Abstract
The discovery of two-dimensional electron gases at the heterointerface between two insulating perovskite-type oxides, such as LaAlO3 and SrTiO3, provides opportunities for a new generation of all-oxide electronic devices. Key challenges remain for achieving interfacial electron mobilities much beyond the current value of approximately 1,000 cm2 V-1 s-1 (at low temperatures). Here we create a new type of two-dimensional electron gas at the heterointerface between SrTiO3 and a spinel γ-Al2O3 epitaxial film with compatible oxygen ions sublattices. Electron mobilities more than one order of magnitude higher than those of hitherto-investigated perovskite-type interfaces are obtained. The spinel/perovskite two-dimensional electron gas, where the two-dimensional conduction character is revealed by quantum magnetoresistance oscillations, is found to result from interface-stabilized oxygen vacancies confined within a layer of 0.9 nm in proximity to the interface. Our findings pave the way for studies of mesoscopic physics with complex oxides and design of high-mobility all-oxide electronic devices.
Similar content being viewed by others
Introduction
High-mobility two-dimensional electron gases (2DEGs) confined in epitaxially grown semiconductor heterostructures form the basis of modern electronic and photonic devices, and have constituted the material basis for the development of quantum transport and mesoscopic physics, for example, the resultant discoveries of the integer and fractional quantum Hall effects1,2. Different from those in semiconductors, strongly correlated electrons in complex oxides with partially occupied d-orbitals give rise to a variety of extraordinary electronic properties, such as high-temperature superconductivity, colossal magnetoresistance, ferromagnetism, ferroelectricity and multiferroicity. Therefore, the high-mobility 2DEGs at atomically engineered complex oxide interfaces not only show promise for multifunctional all-oxide devices with probably even richer behaviour than that in bulk3,4,5,6,7,8,9,10, but would also provide a wealth of opportunities to study mesoscopic physics with strongly correlated electrons confined in nanostructures. Nevertheless, this requires a large-enough electron mobility, so that the characteristic lengths of the system, such as the mean free path or the phase coherence length, become sizeable with respect to the typical dimension of quantum devices.
The enhancement of electron mobilities for complex oxide 2DEGs, however, meets formidable challenges. To date, these 2DEGs have been fabricated exclusively at oxide interfaces between perovskite bilayers4, such as the (001)-oriented polar LaAlO3 (LAO) films grown epitaxially on (001)-oriented non-polar SrTiO3 (STO) single crystals with a TiO2 termination3. The two-dimensional (2D) electron mobility in these perovskite-type oxide interfaces is typically ~1,000 cm2 V−1 s−1 at 2 K (refs 4, 10), with a sheet carrier density, ns, being 1013–1014 cm−2. This Hall mobility is still much lower than those for three-dimensional oxygen-deficient STO single crystals11 and La-doped STO epitaxial films12, amounting to 1.3 × 104 and 3.2 × 104 cm2 V−1 s−1, respectively. The 2DEGs at these perovskite-type oxide interfaces are suggested to result from electronic reconstructions due to a polar discontinuity at the interface3; however, mechanisms such as ion transfer across the interface and formation of defects have also been identified to have important roles on the transport properties13,14. Harnessing the impurities and defects at these polar complex oxide interfaces remains elusive15. Despite deliberate efforts, the highest electron Hall mobility observed in the LAO/STO-based oxide interfaces is limited to the order of 5,000 cm2 V−1 s−1 at 2 K (16,17). Besides interface polarity, we have recently found that chemical redox reactions at the oxide interface between STO single crystals and other complex oxides containing Al, Ti, Zr and Hf elements can provide an alternative approach to creating 2DEGs in complex oxide heterostructures18. Nevertheless, establishing electron confinement with increased carrier mobilities in STO-based heterointerfaces remains a challenge18.
Here we present a novel 2DEG with electron Hall mobilities as large as 1.4 × 105 cm2 V−1 s−1 and ns as high as 3.7 × 1014 cm−2 at 2 K by creating a spinel/perovskite complex oxide interface between epitaxial alumina (Al2O3) films and STO single crystals (Fig. 1a). To our knowledge, it is the first time that complex oxide interfaces based on STO are found to exhibit carrier mobilities larger than any yet reported for either electron-doped STO single crystals11 or optimized epitaxial doped STO films12. Moreover, such a high mobility opens the door to the design of mesoscopic quantum devices based on complex oxides.
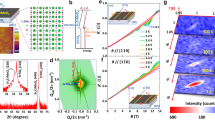
(a) A sketch of the heterostructure. (b) Oxygen sublattices as the backbone to build the spinel/perovskite heterostructure. The compatibility in oxygen sublattices of a γ-Al2O3 surface and the TiO2-terminated STO surface is shown in c and d, respectively. Of note, the tetrahedral cation sites in γ-Al2O3 are not shown. (e) Typical RHEED intensity oscillations for the growth of a 3-uc γ-Al2O3 on STO in a subunit cell layer-by-layer mode. (f) HAADF STEM image of the epitaxial γ-Al2O3/STO interface. Scale bar, 1 nm. Sr ions are brightest, followed by Ti. The faintly visible Al elements can be determined by the averaged line profiles across the interface shown in g. A well-developed TiO2-AlOx heterointerface is defined.
Results
Subunit cell layer-by-layer growth of γ-Al2O3 films
Al2O3 is a widely used oxide and is also one of the best insulating materials in nature, with a band gap normally above 8.0 eV. The synthesis of nanoscale Al2O3 usually results in γ-Al2O3 with a spinel-type structure, rather than the common α-Al2O3 with a corundum structure, because the γ-Al2O3 has a lower surface energy than α-Al2O3 (ref. 19). Remarkably, as illustrated in Fig. 1b–d, despite differences in cation sublattices, the oxygen sublattice of the spinel γ-Al2O3 matches closely with that of the perovskite STO, as the lattice parameter of γ-Al2O3 is twice that of STO (aSTO=3.905 Å, aγ-Al2O3=7.911 Å (ref. 20), lattice mismatch of 1.2%). Such an excellent lattice match between oxygen sublattices, together with the low surface energy of γ-Al2O3, makes it compatible to grow epitaxially γ-Al2O3/STO spinel/perovskite heterostructures in a persistent 2D layer-by-layer growth mode (see Supplementary Fig. S1). Figure 1e shows typical intensity oscillations of the reflection high-energy electron diffraction (RHEED) pattern during the growth of a 3-unit cell (uc) γ-Al2O3 film at a growth temperature of 600 °C. For the epitaxial growth of ionic oxides, when all film components are supplied simultaneously, the oscillation period corresponds to the minimum unit of the chemical composition needed to ensure charge neutrality21,22,23. For γ-Al2O3 grown along the (001) direction, one intensity oscillation corresponds to the growth of one quarter unit cell film (Fig. 1e), as the γ-Al2O3 unit cell consists of four neutral ‘AlOx’ subunit cells with an interlayer distance of about 0.2 nm. Similar subunit cell layer-by-layer film growth has been observed in the epitaxial growth of spinel magnetite (Fe3O4)24. The persistent layer-by-layer, 2D film growth results in a high-quality cubic-on-cubic γ-Al2O3/STO epitaxial heterointerface with no obvious dislocations as confirmed by scanning transmission electron microscopy (STEM) (Fig.1f).
Electrical transport properties of γ-Al2O3/STO interfaces
The investigation of conductivity in our γ-Al2O3/STO heterostructures shows that the interface between the two insulators can become metallic with electrons as the dominant charge carriers (see Supplementary Fig. S2). Of note, under the condition of our film growth, the bare STO substrate remains highly insulating without film deposition. More strikingly, 2DEGs with extremely high Hall electron mobilities are obtained when the γ-Al2O3 film is grown at an oxygen background pressure of 10−4 mbar and a growth temperature of 600 °C (Fig. 2a–c). As shown in Fig. 2, the interfacial conduction depends critically on the thickness, d, of the γ-Al2O3 film. The heterointerface changes from highly insulating to metallic when d is above a threshold thickness of approximately 2 uc (Fig. 2d). At d=2 uc, the interface shows a sheet resistance, Rs, and a carrier density, ns, in the order of 10 kΩ/□ and 2.3 × 1013 cm−2 at T=300 K, respectively, similar to the perovskite-type LAO/STO interface4,6,7,8,9,14,15,16,17. Remarkably, we find a striking Rs decrease of about three orders in magnitude and a Hall mobility as high as μHall~1.1 × 104 cm2 V−1 s−1 at T=2K in the spinel/perovskite γ-Al2O3/STO interface. By carefully controlling the film growth down to a subunit cell level, a great Rs decrease of approximately four orders in magnitude is observed at d=2.5 uc, which is accompanied by the presence of non-linear Hall resistance with respect to magnetic fields at temperatures below 100 K (see Supplementary Fig. S3). A linear fitting to the low-field Hall resistance gives rise to an impressive μHall of approximately 1.4 × 105 cm2 V−1 s−1, with an ns of 3.7 × 1014 cm−2 at 2 K, which is consistent with those obtained by fitting the entire non-linear Hall effect within a two-band model (see Supplementary Fig. S3). Note that the high-mobility 2DEGs with μHall ≥104 cm2 V−1 s−1 at T=2K are only detected in the thickness range of 2 uc≤d<3 uc. Further increasing d deteriorates the electron mobility to less than 1,000 cm2 V−1 s−1, probably due to the significant outward diffusion of the Ti-cations across the interface as observed by electron energy-loss spectroscopy (EELS; see Supplementary Fig. S4).
(a–c) Temperature dependence of sheet resistance, Rs, carrier density, ns, and low-field electron Hall mobility, μHall, for the interface conduction at different film thicknesses. (d,e) Thickness dependence of the sheet conductance, σs, and ns measured at 300 K. High-mobility 2DEGs are obtained at a thickness range of 2 uc≤d<3 uc. The lines are guides to the eye.
2D quantum oscillations of the conduction in γ-Al2O3/STO
The 2D nature of the conduction in our spinel/perovskite heterostructures is indicated by angle-dependent Shubnikov-de Haas (SdH) quantum oscillations, which are superimposed on a huge background of positive magnetoresistance (Fig. 3a). After subtracting the magnetoresistance background, the SdH oscillations become apparent (Fig. 3b) and the extrema positions show a cosine dependence with the angle θ between the magnetic field and the surface normal (Fig. 3c). This reveals the 2D nature of the electron gas formed at our γ-Al2O3/STO interfaces. Besides, the absence of oscillations at θ=90° further confirms that the spatial width of the 2DEG is smaller than at least the cyclotron radius at 15 T, the typical value of which is below 10 nm for our heterostructures. Moreover, the angular dependence of the SdH oscillations measured at high magnetic fields suggests a multiple-subband contribution to charge transport. For instance, an extra feature is observed at θ=50° with Bcosθ=7.2 T, which may result from a π shift of the oscillations due to a spin-split band. Such a phase shift has been observed in the high-mobility 2DEG of GaN/AlGaN interfaces when the Zeeman energy (depending on the total B) and the cyclotron energy (depending on the perpendicular component of B) are equal25.
(a) Longitudinal resistance, Rxx, as a function of magnetic field with visible SdH oscillations (arrowheads) under different tilt angle, θ, at 0.3 K for the d=2.5 uc sample. (b,c) Amplitude of the SdH oscillations, ΔRxx, under different θ versus the reciprocal total magnetic field and the reciprocal perpendicular magnetic field component, respectively. The SdH oscillations depend mainly on the reciprocal perpendicular magnetic field component, particularly in the θ angle of 0°–33°, which suggests a 2D conduction nature of the γ-Al2O3/STO interface.
To confirm the high mobility achieved in our γ-Al2O3/STO 2DEGs, we increased the visibility of the SdH oscillations by cooling one sample (d=2.25 uc) down to 22 mK in a dilution refrigerator. Ultra-low noise measurements allow us to evidence the oscillations down to about 1 T (Fig. 4a), which directly shows that the quantum mobility extracted from the SdH oscillations, μSdH, is in the range of 104 cm2 V−1 s−1, as inferred from the onset of oscillations. Importantly, the low-field dependence of the SdH oscillations reveals the typical behaviour due to a single band. According to theory26, the oscillations amplitude ΔRxx can be described as:
(a) Temperature dependence of the SdH oscillations at θ=0° for the d=2.25 uc sample. (b) Temperature dependence of the scaled oscillation amplitude at B=2.04 T, giving a carrier effective mass of 1.22 me. (c) Dingle plot of the SdH oscillations at 200 mK, giving a total scattering time τ=4.96 × 10−12 s, a related Dingle temperature TD=0.24 K and a consequent quantum mobility μSdH=7.2 × 103 cm2 V−1 s−1.

where,  ,
,  is the cyclotron frequency, m* is the carrier effective mass, kB is Boltzmann’s constant and ħ is Planck’s constant divided by 2π. R0 is the classical resistance in zero field.
is the cyclotron frequency, m* is the carrier effective mass, kB is Boltzmann’s constant and ħ is Planck’s constant divided by 2π. R0 is the classical resistance in zero field.  is the Dingle temperature, τ is the total scattering time. At a fixed magnetic field, m* can be deduced by fitting the temperature-dependent oscillation amplitude with
is the Dingle temperature, τ is the total scattering time. At a fixed magnetic field, m* can be deduced by fitting the temperature-dependent oscillation amplitude with  . As shown in Fig. 4b, for B=2.04 T the fit leads to an effective mass of m*=(1.22±0.03) me (me is the bare electron mass), consistent with those reported for other STO-based heterostructures16,27,28,29,30. At a fixed temperature, TD or τ can be deduced from the slope of the Dingle plot, that is,
. As shown in Fig. 4b, for B=2.04 T the fit leads to an effective mass of m*=(1.22±0.03) me (me is the bare electron mass), consistent with those reported for other STO-based heterostructures16,27,28,29,30. At a fixed temperature, TD or τ can be deduced from the slope of the Dingle plot, that is,  versus 1/B (Fig. 4c for T=200 mK), which gives a τ=4.96 × 10−12 s or TD=0.24 K, corresponding to a quantum mobility μSdH=m* of 7.2 × 103 cm2 V−1 s−1. Such an unprecedented high μSdH in our γ-Al2O3/STO 2DEGs is more than one order of magnitude higher than those observed in the perovskite/perovskite LAO/STO16,17,27 and GaTiO3/STO30 heterostructures, which are typically below 300 cm2 V−1 s−1. Note that the difference between μHall and μSdH in our γ-Al2O3/STO heterostructures could come from a different scattering time (that is, the transport scattering time and the total scattering time, respectively), which has also been reported in the LAO/STO16,17,27 and δ-doped STO heterostructures28,29, as well as the GaAs/AlGaAs heterostructures31. In short, the SdH measurements support the formation of high-mobility 2DEGs at our spinel/perovskite heterointerfaces (see also Supplementary Fig. S5).
versus 1/B (Fig. 4c for T=200 mK), which gives a τ=4.96 × 10−12 s or TD=0.24 K, corresponding to a quantum mobility μSdH=m* of 7.2 × 103 cm2 V−1 s−1. Such an unprecedented high μSdH in our γ-Al2O3/STO 2DEGs is more than one order of magnitude higher than those observed in the perovskite/perovskite LAO/STO16,17,27 and GaTiO3/STO30 heterostructures, which are typically below 300 cm2 V−1 s−1. Note that the difference between μHall and μSdH in our γ-Al2O3/STO heterostructures could come from a different scattering time (that is, the transport scattering time and the total scattering time, respectively), which has also been reported in the LAO/STO16,17,27 and δ-doped STO heterostructures28,29, as well as the GaAs/AlGaAs heterostructures31. In short, the SdH measurements support the formation of high-mobility 2DEGs at our spinel/perovskite heterointerfaces (see also Supplementary Fig. S5).
Spatial confinement of the γ-Al2O3/STO interface 2DEG
To determine the origin and depth-profile for the conduction in the γ-Al2O3/STO heterostructures, angle-resolved X-ray photoelectron spectroscopy (XPS) measurements are performed. We find that the electrons are exclusively accumulated on the otherwise empty 3d shell of Ti4+ on the STO side. The most remarkable XPS result is that the Ti3+ signal in γ-Al2O3/STO heterointerfaces shows strong dependence on the photoelectrons detection angle, φ, with respect to the surface normal. An increase of the Ti3+ signal with increasing φ, as shown in Fig. 5a, is clearly detected for d=2.5 uc with the highest Hall mobility. This further confirms that the conduction in our γ-Al2O3/STO heterointerface is highly confined at the interface region. To make more quantitative analyses, we assume a simple case that the 2DEG extends from the interface to a depth, t, into the STO substrate32. The interface region is further assumed to be stoichiometric, sharp and characterized by a constant fraction, p, of Ti3+ per STO unit cell. Taking into account the attenuation length of photoelectrons, the ratio of Ti3+ to Ti4+ signal, I(Ti3+)/I(Ti4+), as a function of φ can be calculated as32:

where, λ is the electron escape depth in STO. According to the NIST database (NIST Standard Reference Database 71, version 1.2), λ is approximately 2.2 nm for our setup. As shown in Fig. 5b, the best fitting of the experimental I(Ti3+)/I(Ti4+) ratios gives a p~0.31, which equals to an ns ~2.1 × 1014 cm−2 and a t of 0.9 nm. Therefore, the electrons at our γ-Al2O3/STO heterointerface are strongly confined within approximately the first 2 uc of STO surface in proximity to the interface. Note that the ns deduced here is slightly lower than that obtained from Hall data (Fig. 2c). This could be due to the presence of outward diffusion of the Ti-cations into alumina films, where Ti4+ is the dominant component (see Supplementary Figure S4). Such concern is also consistent with the fact that the out-diffused Ti is found to have a negligible contribution to the measured interface conduction. For example, the interface conduction remains unaffected when the capping alumina film is etched away by a 4-M aqueous NaOH solution. This strongly suggests that the effective charge carriers are mainly located on the STO side.
Discussion
As each layer of the (001)-oriented γ-Al2O3/STO heterointerface is nominally charge neutral, the polar discontinuity-induced electronic reconstruction as expected in the LAO/STO interface3 may not contribute here. The presence of Ti3+ is probably a signature of the formation of oxygen vacancies on the STO side. This scenario is consistent with the fact that the interfacial conductivity can be completely removed when the Ti3+ content is significantly suppressed by suitable annealing in 1 bar pure O2 at a temperature higher than 200 °C (see Supplementary Fig. S6). Such an oxygen-vacancy-dominated 2DEG is expected to be formed as a consequence of chemical redox reactions occurring on the STO surface during the film growth of γ-Al2O3, analogous to what has been observed in metallic amorphous STO-based heterostructures grown at room temperature18. Note that the 2DEG at the crystalline γ-Al2O3/STO heterointerface is formed at a high temperature of 600 °C, where the oxygen ions in STO are already highly mobile. This is normally expected to level out any difference in the depth-profile of oxygen distribution in STO18,33. However, this is not the case in the crystalline γ-Al2O3/STO heterostructures as inferred from both Figs 3 and 5. Moreover, the conduction at the interface of thick films, for example, at d=8 uc, can survive the annealing at 300 °C for 24 h in 1 bar pure O2 with only negligible changes in the conductivity (see Supplementary Fig. S6). These features strongly suggest that the oxygen vacancies and the 2DEGs are stabilized by an interface effect, such as by the formation of a space charge region near the heterointerface. It is worth noting that an inherent oxygen ion deficiency has been observed at the grain boundary of STO bicrystals34, where a considerable electron accumulation has also been predicted if the barrier height of the grain boundary is deliberately controlled35. The high electron mobility of STO-based oxide materials at low temperatures is generally related to the polarization shielding of the ionized defect scattering centres driven by the large dielectric constant of STO36. The higher mobility of our spinel/perovskite oxide interface compared with the perovskite-type oxide heterointerface may be due to the better lattice match and, thereby, a more perfect structure and well-defined interface. Though further investigations are needed to reveal how the interface properties increase the mobility and the associated strong suppression of the defect and impurity scattering, our results strongly suggest that defect engineering of oxygen vacancies is crucial for the high mobility of 2DEGs confined at the interface between complex oxides.
In conclusion, we have demonstrated that high-mobility 2DEGs with clear quantum magnetoresistance oscillations and strong spatial confinement can be created at well-defined spinel/perovskite γ-Al2O3/STO oxide interfaces. The strongly spatial confinement of charge carriers achieved directly in the as-deposited spinel/perovskite oxide heterostructures without any post annealing provides the possibility to fabricate multilayers of complex oxides with several 2DEGs. Furthermore, by combining two of the largest groups of oxides, plenty of new physical properties, for instance, interfacial magnetism6 and superconductivity7 as observed in the perovskite-type LAO/STO interface, may be found at the γ-Al2O3/STO heterointerface. Finally, with a large enhancement of the electron mobility, the γ-Al2O3/STO heterointerface probably enables the design of mesoscopic quantum devices based on complex oxide 2DEGs and opens new avenues for oxide nanoelectronics and mesoscopic physics.
Methods
Sample growth
The γ-Al2O3 thin films were grown by pulsed laser deposition37 using a KrF laser (λ=248 nm) with a repetition rate of 1 Hz and laser fluence of 1.5 J cm−2. The target-substrate distance was fixed at 5.6 cm. Commercial α-Al2O3 single crystals were used as targets. Singly TiO2-terminated (001) STO crystals with a size of 5 × 5 × 0.5 mm3 were used as substrates. Note that the TiO2 termination of our substrates is obtained by chemical etching using HCL-HNO3 as acidic solution37, which is found to produce less defects on the STO surface compared with the conventional buffered hydrofluoric acid etch method38,39. The film growth process was monitored by in-situ high pressure RHEED. During deposition, the oxygen pressure was fixed at 10−4 mbar with the deposition temperature changing from room temperature (20 °C) to 700 °C. After film deposition, the samples were cooled down to room temperature at the deposition pressure. The film thickness was determined by both RHEED oscillations and X-ray reflectivity measurements.
Electrical transport measurement
The transport properties of the buried interface were measured using a four-probe Van der Pauw method, with ultrasonically wire-bonded aluminium wires as electrodes, placed at the corners of the square sample. The temperature-dependent electrical transport and Hall-effect measurements were performed in a CRYOGENIC cryogen-free measurement system, with the temperature ranging from 300 K down to 2 K and magnetic fields up to 16 T. To confirm the carrier density and mobility, some Hall-bar patterned samples were also measured, which were prepared directly through a mechanical mask18. Note that the use of a mechanical mask at deposition temperatures higher than 500 °C may have a deleterious effect on the carrier mobility, as the high oxygen ion diffusion can unintentionally disturb the oxygen equilibrium for realizing high mobility. The angle-dependent SdH measurements were performed in a sorption-pumped 3He cryostat with standard lock-in technique at 0.3 K, with magnetic fields up to 15 T by changing the angles manually. The temperature-dependent SdH measurements were performed in a dilution refrigerator with a base temperature of 22 mK and an improved temperature stability, using ultra-low noise electronics. During all the transport measurements, the applied currents were within 1–10 μA (for AC current, the frequency was 327 Hz). Special care was taken to avoid heating effect.
XPS measurement
The XPS measurements were performed in a Kratos Axis UltraDLD instrument, using a monochromatic Al Kα X-ray source with photon energy of 1,486.6 eV. This leads to a kinetic energy of Ti 2p electrons of roughly 1,025 eV. According to the NIST database(NIST Standard Reference Database 71, version 1.2), the electron escape depth is approximately 22 Å in STO at this kinetic energy. The pass energy used for the high resolution scan was 20 eV. The detection angle of the electrons varied between 0° and 60° with respect to the sample normal. For analysing the Ti 2p3/2 peaks (Ti4+ is at a binding energy of 459.5 eV, whereas the Ti3+ is 1.6 eV±0.1 eV lower), a Shirley background was subtracted and the spectra were normalized to the total area below the Ti peaks ([Ti]=[Ti4+]+[Ti3+]=100%).
STEM and EELS measurements
Aberration-corrected STEM measurements were performed by an FEI Titan 80–300ST TEM equipped with a high brightness Shottky emitter (XFEG) and a Gatan Image Filter (Tridiem). High-angle annular dark field (HAADF) images were acquired at 300 kV, where the probe size, convergence angle and HAADF collection angle were 0.8–1 Å, 20 mrad and 46–291 mrad, respectively. For EELS in the STEM, an accelerating voltage of 120 kV (probe size of 1.5–2.0 Å) was used to reduce knock-on damage to the specimen. The energy resolution of EELS was ~0.9 eV. Spectrum imaging was used to collect spectra across the interface. We typically recorded the spectrum images consisting of 40 ten-analysis point lines (that is, 10 × 40 pixel) parallel to the interface and acquired each line by an increment of 0.28 nm. Each spectrum was obtained at a dispersion of 0.1 eV for 0.2–0.4 s. Then the spectra along the lines were summed after removing the spectra from beam-damaged regions according to the HAADF contrast to increase signal/background ratio.
Additional information
How to cite this article: Chen. Y. Z. et al. A high-mobility two-dimensional electron gas at the spinel/perovskite interface of γ-Al2O3/SrTiO3. Nat. Commun. 4:1371 doi: 10.1038/ncomms2394 (2013).
References
Klitzing, K. v., Dorda, G. & Pepper, M. . New methods for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. . Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Ohtomo, A. & Hwang, H. Y. . A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Mannhart, J. & Schlom, D. G. . Oxide interfaces: an opportunity for electronics. Science 327, 1607–1611 (2010).
Irvin, P. et al. Rewritable nanoscale oxide photodetector. Nat. Photon. 4, 849–852 (2010).
Brinkman, A. et al. Magnetic effects at the interface between non-magnetic oxides. Nat. Mater. 6, 493–496 (2007).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
The interface is still the device. Nat. Mater. 11, 91 (2012).
Chakhalian, J., Millis, A. J. & Rondinelli, J. . Whither the oxide interface. Nat. Mater. 11, 92–94 (2012).
Park, J. W. et al. Creation of a two-dimensional electron gas at an oxide interface on silicon. Nat. Commun. 1, 94 (2010).
Frederikse, H. P. R. & Hosler, W. R. . Hall mobility in SrTiO3 . Phys. Rev. 161, 822–827 (1967).
Son, J. et al. Epitaxial SrTiO3 films with electron mobilities exceeding 30 000 cm2 V-1 s-1. Nat. Mater. 9, 482–484 (2010).
Willmott, P. R. et al. Structural basis for the conducting interfaces between LaAlO3 and SrTiO3 . Phys. Rev. Lett. 99, 155502 (2007).
Kalabukhov, A. et al. Effect of oxygen vacancies in the SrTiO3 substrate on the electrical properties of the LaAlO3/SrTiO3 interface. Phys. Rev. B 75, 121404 (2007).
Chambers, S. A. . Understanding the mechanism of conductivity at the LaAlO3/SrTiO3 (001) interface. Surface Sci. 605, 1133–1140 (2011).
Caviglia, A. D. et al. Two-dimensional quantum oscillations of the conductance at LaAlO3/SrTiO3 interfaces. Phys. Rev. Lett. 105, 236802 (2010).
Huijben, M. et al. High mobility interface electron gas by defect scavenging in a modulation doped oxide heterostructure. Preprint at http://arXiv:1008.1896v1 (2010).
Chen, Y. Z. et al. Metallic and insulating interfaces of amorphous SrTiO3-based oxide heterostructures. Nano Lett. 11, 3774–3778 (2011).
McHale, J. M., Auroux, A., Perrotta, A. J. & Navrotsky, A. . Surface energies and thermodynamic phase stability in nanocrystalline aluminas. Science 277, 788–791 (1997).
Zhou, R. S. & Snyder, R. L. . Structures and transformation mechanisms of the η, γ and θ transition aluminas. Acta Cryst. B 47, 617–630 (1991).
Terashima, T. et al. Reflection high-energy electron diffraction oscillations during epitaxial growth of high-temperature superconducting oxides. Phys. Rev. Lett. 65, 2684–2687 (1990).
Rijnders, A. J. H. M. . The initial growth of complex oxides: study and manipulation. PhD thesis Univ. Twente (2001).
Barber, Z. H. . The control of thin film deposition and recent developments in oxide film growth. J. Mater. Chem. 16, 334–344 (2006).
Reisinger, D. et al. Sub-unit cell layer-by-layer growth of Fe3O4, MgO, and Sr2RuO4 thin films. Appl. Phys. A 77, 619–621 (2003).
Knap, W. et al. Spin and interaction effects in Shubnikov-de Haas oscillations and the quantum Hall effect in GaN/AlGaN heterostructures. J. Phys. Condens. Mat. 16, 3421–3432 (2004).
Shoenberg, D. . Magnetic Oscillations in Metals Cambridge Univ. Press: Cambridge, England, (1984).
Ben Shalom, M., Ron, A., Palevski, A. & Dagan, Y. . Shubnikov-de Haas oscillations in SrTiO3/LaAlO3 interface. Phys. Rev. Lett. 105, 206401 (2010).
Jalan, B., Stemmer, S., Mack, S. & Allen, S. J. . Two-dimensional electron gas in δ-doped SrTiO3 . Phys. Rev. B 82, 081103 (2010).
Kozuka, Y. et al. Two-dimensional normal-state quantum oscillations in a superconducting heterostructure. Nature 462, 487–490 (2009).
Moetakef, P. et al. Quantum oscillations from a two-dimensional electron gas at a Mott/band insulator interface. Appl. Phys. Lett. 101, 151604 (2012).
Harrang, J. P. et al. Quantum and classical mobility determination of the dominant scattering mechanism in the two-dimensional electron gas of an AlGaAs/GaAs heterojunction. Phys. Rev. B 32, 8126–8135 (1985).
Sing, M. et al. Profiling the interface electron gas of LaAlO3/SrTiO3 heterostructures with hard X-Ray photoelectron spectroscopy. Phys. Rev. Lett. 102, 176805 (2009).
Mannhart, J. & Schlom, D. G. . Semiconductor physics: the value of seeing nothing. Nature 430, 620–621 (2004).
Jia, C. L. & Urban, K. . Atomic-resolution measurement of oxygen concentration in oxide materials. Science 303, 2001–2004 (2004).
Vollmann, M., Hagenbeck, R. & Waser, R. . Grain-boundary defect chemistry of acceptor-doped titanates: inversion layer and low-field conduction. J. Am. Ceram. Soc. 80, 2301–2314 (1997).
Tufte, O. N. & Chapman, P. W. . Electron mobility in semiconducting strontium titanate. Phys. Rev. 155, 796–802 (1967).
Chen, Y. Z. & Pryds, N. . Imposed quasi-layer-by-layer homoepitaxial growth of SrTiO3 films by large area pulsed laser deposition. Thin Solid Films 519, 6330–6333 (2011).
Zhang, J. et al. Depth-resolved subsurface defects in chemically etched SrTiO3 . Appl. Phys. Lett. 94, 092904 (2009).
Chambers, S. A. et al. Unintentional F doing of SrTiO3 (001) etched in HF acid-structure and electronic properties. Surface Sci. 606, 554–558 (2012).
Acknowledgements
We thank J. Fleig, F. W. Poulsen, N. Bonanos, S. Stemmer and Y.Q. Li for helpful discussions. We also thank K. Thydén, Z.I. Balogh, J.W. Andreasen, E. Johnson, Y. Zhao, X. Tang, W.W. Gao, N.Y. Wu, J. Geyti, K.V. Hansen, K. Engelbrecht and L. Theil Kuhn for their help.
Author information
Authors and Affiliations
Contributions
Y.Z.C. contributed to the concept design, film growth, transport measurements, data analysis, interpretation and writing of the manuscript. N.P. and S.L. contributed to the concept design. N.B. contributed to the XPS measurements and analysis. F.T., D.V.C., N.H.A. and T.S.J. contributed to the transport measurements and analysis. F.M.Q, R.G. and J.D. contributed to the SdH measurements and analysis. T.K. contributed to the STEM and EELS measurements and analysis. W.Z. contributed to the HRTEM measurements and analysis. J.R.S., A.S., J.N., L.L., B. B. and B.G.S discussed the data. All authors extensively discussed the results and the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S6 and Supplementary References (PDF 2501 kb)
Rights and permissions
About this article
Cite this article
Chen, Y., Bovet, N., Trier, F. et al. A high-mobility two-dimensional electron gas at the spinel/perovskite interface of γ-Al2O3/SrTiO3. Nat Commun 4, 1371 (2013). https://doi.org/10.1038/ncomms2394
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2394
This article is cited by
-
Strong Rashba parameter of two-dimensional electron gas at CaZrO3/SrTiO3 heterointerface
Scientific Reports (2023)
-
Non-collinear and asymmetric polar moments at back-gated SrTiO3 interfaces
Communications Physics (2022)
-
Hysteretic temperature dependence of resistance controlled by gate voltage in LaAlO3/SrTiO3 heterointerface electron system
Scientific Reports (2022)
-
A termination-insensitive and robust electron gas at the heterointerface of two complex oxides
Nature Communications (2019)
-
Electronic-reconstruction-enhanced hydrogen evolution catalysis in oxide polymorphs
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.