Abstract
The mid-infrared spectral range (λ~2–20 μm) is of particular importance as many molecules exhibit strong vibrational fingerprints in this region. Optical frequency combs—broadband optical sources consisting of equally spaced and mutually coherent sharp lines—are creating new opportunities for advanced spectroscopy. Here we demonstrate a novel approach to create mid-infrared optical frequency combs via four-wave mixing in a continuous-wave pumped ultra-high Q crystalline microresonator made of magnesium fluoride. Careful choice of the resonator material and design made it possible to generate a broadband, low-phase noise Kerr comb at λ=2.5 μm spanning 200 nm (≈10 THz) with a line spacing of 100 GHz. With its distinguishing features of compactness, efficient conversion, large mode spacing and high power per comb line, this novel frequency comb source holds promise for new approaches to molecular spectroscopy and is suitable to be extended further into the mid-infrared.
Similar content being viewed by others
Introduction
Optical frequency combs1,2, that is, broad spectral bandwidth coherent light sources consisting of equally spaced sharp lines, revolutionized optical frequency metrology one decade ago. They now enable dramatically improved acquisition rates, resolution and sensitivity for molecular spectroscopy mostly in the visible and near-infrared ranges3,4,5,6,7,8. The mid-infrared spectral range (λ~2–20 μm) is known as the ‘molecular fingerprint’ region as many molecules have their characteristic, fundamental vibrational bands in this part of the electromagnetic spectrum. Broadband mid-infrared spectroscopy therefore constitutes a powerful and ubiquitous tool for optical analysis of chemical components that is used in biochemistry, astronomy, pharmaceutical monitoring and material science. Mid-infrared frequency combs have therefore become highly desirable and recent progress in generating such combs by nonlinear frequency conversion9,10,11 has opened access to this spectral region.
Because of its scientific and technological significance, laser technology in the mid-infrared is an active area of research and development. The advent of a compact and versatile coherent light source in this region came after the invention of quantum cascade lasers (QCLs) in 1994 (ref.12). However, QCLs are intrinsically difficult to be passively mode-locked13 and only active mode-locking has been unequivocally demonstrated, creating a limited comb-like spectrum of ~0.3 THz bandwidth14. Today, the most common approach to create frequency combs in the mid-infrared is to frequency down-convert a near-infrared comb through nonlinear processes, such as optical parametric oscillation9,10 or difference frequency generation11.
In this article, we demonstrate a novel, direct route to mid-infrared frequency comb generation based on ultra-high Q (quality factor) crystalline optical microresonators15. The particular advantages of microresonator-based frequency combs are the compact form factor, large comb mode spacing and high power per comb line. The underlying mechanism is cascaded four-wave mixing caused by the third-order Kerr nonlinearity in high-Q whispering-gallery mode (WGM) microresonators, which was first demonstrated in silica microtoroids in the near infrared16,17. In this energy-conserving process, two possibly degenerate photons (frequency ν1 and ν2) are converted to a pair of signal (νS) and idler (νI) photons, such that ν1+ν2=νS+νI. This process can cascade and thereby lead to the formation of an equidistant optical frequency comb (‘Kerr’ comb), whose spectral properties (offset frequency and mode spacing) can be stabilized18. Several microresonator platforms based on this mechanism have demonstrated Kerr frequency comb generation in the near-infrared region15, such as silica microtoroids17,18,19, silicon nitride20,21, Hydex glass22, crystalline fluorides23,24 and fused quartz25, where most optical materials are transparent and characterized by close-to-zero anomalous dispersion. Most of the platforms, however, principally cannot operate in the mid-infrared region. Here, by careful choice of resonator material and design, we demonstrate for the first time mid-infrared Kerr frequency combs based on microresonators. In addition, we have carefully characterized their phase noise and shown that the mid-infrared Kerr combs indeed consist of narrow and mutually coherent lines. The current approach is suitable for extending comb generation further into the mid-infrared.
Results
Crystalline Resonator fabrication and characterization
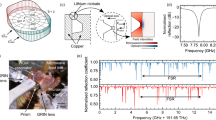
We developed ultra-high Q resonators made of crystalline magnesium fluoride MgF2 for mid-infrared frequency comb generation. The reason for choosing MgF2 is threefold. First, the transparency window of crystalline materials (such as CaF2 and MgF2) extends from the ultraviolet (~160 nm) to the mid-infrared (~7 μm), enabling achievement of ultra-high Q (>108) optical modes in the mid-infrared—in contrast to fused silica or quartz, which exhibit strong absorption above 2.2 μm. Second, the ability to generate optical frequency combs via cascaded four-wave mixing in the presence of self- and cross-phase modulation of the pump requires the group velocity dispersion (GVD) at the pump frequency to be anomalous16,26,27, that is, a free spectral range (FSR) of the cavity that reduces with increasing wavelength. We assess the dispersion properties by carrying out fully vectorial finite element simulations28,29 taking into account geometric effects as well as the intrinsic material dispersion. The resonator dispersion is expressed via the parameter D2=2π (νm+1−2νm+νm−1), where νm is the resonance frequency with azimuthal mode number m. Figure 1b shows a 700-μm-diameter MgF2 crystalline resonator with its dispersion properties shown in Fig. 1c, revealing a GVD that is anomalous over the full mid-infrared transparency range. In contrast to previous work in crystalline (and other) resonators, the present experiments operate in the strongly anomalous dispersion region (D2~κ, where κ is the cavity decay rate). We emphasize that this dispersion region—far from the zero dispersion point, which is at about 1.55 μm—has previously been considered as unfavourable for Kerr comb generation17,20,23 due to the mismatch between cavity resonances and equidistant comb lines. Here, we experimentally demonstrate that the strong anomalous dispersion does not prevent broadband Kerr comb generation in the mid-infrared region. This can be attributed to the nonlinear frequency pulling by self- and cross-phase modulation exceeding the amount of cavity dispersion. Moreover, as detailed below and recently reported30, sufficiently high anomalous dispersion is one way to achieving low-phase noise operation of the comb. The requirement for anomalous dispersion renders other materials, such as Si3N4 microring resonators, which are used successfully at shorter wavelength for Kerr comb generation, unfavourable as their GVD is normal in the mid-infrared31. Third, the sign of the temperature coefficient of the refractive index (dn/dT) and the thermal expansion coefficient α are both positive in MgF2 (at room temperature), which allows the cavity mode to be thermally self-locked to the pump laser frequency32 and enables the stabilization of the repetition rate and offset frequency of microresonator-based frequency combs18. On the contrary, materials with opposite signs of dn/dT and α, such as CaF2, suffer from large thermal oscillatory instabilities and the requirement for active locking (or injection locking) schemes (see Supplementary Note for more information on thermal instability).
(a) Finite element simulation of the optical intensity profile of the fundamental WGM at wavelength 2.45 μm superimposed on a scanning electron microscope image of a 700-μm diameter resonator used in this work, fabricated by polishing and shaping an ultraviolet-grade MgF2 cylinder blank. Scale bar, 10 μm. The radius of curvature of the resonator protrusion, which confines the WGM in the azimuthal direction, is 17 μm. (b) Optical microscope image of the resonator. (c) The figure shows the simulated FSR for fundamental modes with mode number m (FSRm=(νm+1−νm−1)/2, blue curve) and the difference of the FSR between adjacent modes (D2/2π=νm+1−2νm+νm−1, red curve) as a function of the wavelength for the resonator in panel a, exhibiting an anomalous GVD (D2>0) above λ=1.6 μm.
To fabricate the resonators, single-crystal ultraviolet-grade MgF2 was first cut into cylinder blanks with dimensions of several millimetres. The resonators were then shaped and polished on an air-bearing spindle by diamond abrasives to achieve a smooth protrusion which provides an azimuthal WGM confinement, following the methods described in detail in ref. 33. A scanning electron microscope was used to measure the transverse radius of curvature of the resonator of 17 μm (Fig. 1a). The resulting mode area of the WGM was determined in a fully vectorial finite element simulation. Superimposed on Fig. 1a is the intensity profile of the fundamental mode at λ=2.45 μm. From these simulations, we obtained an effective mode area Aeff=60 μm2 and determined the effective nonlinearity of the resonator γeff=2πn2/(λ Aeff)=4.3 × 10−4 m−1W−1, where n2 is the Kerr nonlinearity of MgF2 (1 × 10−20 m2 W−1). The diameters of the resonators typically range from 500 μm to 5 mm, corresponding to a resonator mode spacing in the range of 10–110 GHz. Tapered optical fibres made of silica were used for characterization of the resonators at 1.55 μm. For pre-characterization, the quality factor of the resonances was measured with a tuneable, narrow-linewidth (short-term<100 kHz) fibre laser at λ=1.55 μm, yielding intrinsic Q factors exceeding 109, corresponding to a typical finesse of F=105–106. Additional iterative thermal annealing and polishing steps may further increase the Q factors34.
Generation of mid-infrared frequency comb
We pumped the resonators by a continuous-wave (CW) mid-infrared laser based on an optical parametric oscillator that is tuneable between 2.4 and 2.5 μm with short-term linewidth<100 kHz. Details of the laser source and the experimental set-up can be found in the Methods section and in Fig. 2a. Optical power levels of 200 mW to 1 W were coupled into the resonators by employing a tapered fibre made of low-OH-fused silica (loss ~3.4 dB m−1 at λ=2.5 μm). The resonator and tapered fibre are embedded in a dry-nitrogen-purged environment, as water vapour is highly absorptive in the mid-infrared (prior exposure to air however is not expected to lead to accumulation of water layers as MgF2 crystals are hydrophobic). The output spectra were recorded by an optical spectrum analyser (OSA) with cut-off wavelength at 2.5 μm. Figure 2b shows the optical frequency comb spectrum derived from the 700-μm-diameter resonator pumped with ~600 mW of laser power at λ=2.45 μm. We observed more than 100 modes spaced by 107 GHz (corresponding to a span of over 200 nm), which corresponds to the FSR of the resonator (FSR=c/(2πRneff)), where R is the cavity radius, c is the speed of light in vacuum and neff is the effective refractive index. The resonator has high optical finesse F=1.2 × 105. Optical sidebands can be generated once the parametric threshold is exceeded. The threshold for parametric oscillation can be estimated as the point where the Kerr nonlinearity-induced frequency shift ΔωKerr reaches half the cavity decay rate (the bi-stability point), that is, as ΔωKerr=(n2 ωFPcoupled)/(2π nAeff)=κ/2, where n is the refractive index, n2 the Kerr nonlinearity, Pcoupled the power coupled into the resonator, Aeff the effective modal area, F the cavity finesse, κ the cavity decay rate and ω the optical angular frequency. The estimated threshold for sideband generation is P=4 mW, which matches the experimental observation. The power per generated comb line ranges from microwatts up to several milliwatts, significantly higher than the current state-of-the-art down-converted mid-infrared combs9,10.
(a) The experimental set-up consists of a CW mid- infrared OPO that serves as the pump laser. The pump laser is coupled via a tapered fibre to a crystalline MgF2 microresonator. The generated frequency comb is detected using an optical spectrum analyser (OSA) with a cut-off wavelength of 2.5 μm (PD, photodetector). (b) Frequency comb spectrum recorded by the OSA around λ=2.45 μm with a line spacing of 107 GHz generated from pumping a 700-μm-diameter MgF2 resonator (pump power 600 mW). The grey lines denote frequency components, which are expected to exist based on symmetry around the pump. Inset shows the spectrum taken with a Fourier transform spectrometer, which reveals the overall symmetry of the spectrum. (c) Proof-of-principle mid-infrared Kerr comb absorption spectroscopy experiment. The figure shows the transmittance of 0.5-mm-thick liquid acetone (single-pass) recorded as the relative intensities of the attenuated and unattenuated Kerr comb (shown in panel b) line intensities (red dot) and independently by a Fourier transform spectrometer (grey line). (d) Schematics of the acetone absorption experiment. The shaded part represents the detector system, which in this case is included in the OSA.
Prospects for spectroscopy
Frequency combs have recently demonstrated potential for advances in molecular spectroscopy35,36. To demonstrate that the high power per comb line and the wide mode spacing is well suited for the recording of broadband vibrational spectra in the liquid or solid phase, we performed a proof-of-concept direct comb absorption spectroscopy3 of 0.5 mm-thick layer of liquid acetone using the comb in Fig. 2b as light source and recording the transmission spectra with the OSA. Figure 2d shows the schematics of the comb spectroscopy. The result is shown in Fig. 2c and validated by an independent measurement of the same acetone sample employing a conventional white light source and a Fourier transform spectrometer (FTS). The discrepancy between the FTS and the comb measurements comes from the fact that the power in the resonator has not been stabilized in this work, and the comb line intensities fluctuate on a few seconds time scale required for data taking. Note that if a white light source is used for spectroscopy, a wavelength-calibrated detector system is required, whereas with a frequency comb source the calibration is contained in the known frequencies of the comb modes, and only a detector that can resolve the individual comb components is required. In future experiments employing a mid-infrared disperser and detector array, we expect microresonator-based combs to be suitable light sources for direct molecular fingerprinting3, which would vastly improve the acquisition time and sensitivity. Therefore, new opportunities for real-time spectroscopic investigation and optimization of chemical reactions may come into reach, including industrial real-time process control of, for example, pharmaceutical products.
Phase noise characterization
A key requirement of an optical frequency comb is low phase noise. Although parametric sidebands can already be generated in the weak anomalous dispersion region, it has been shown recently30 that an anomalous dispersion parameter D2 on the order of the cavity decay rate κ leads to intrinsically low-phase noise comb operation. The underlying physical picture is that the ratio κ/D2 determines the position of the primary sidebands relative to the pump, and therefore the pathways of the comb formation process. For κ/D2>>1, the primary sidebands are far away from the pump and spectrally separated sub-combs form before merging, which results in multiple lines in a single optical cavity resonance. This leads to multiple beat notes (or more general phase noise) as well as amplitude noise30. In contrast, due to the strong anomalous dispersion of MgF2 over the entire mid-infrared spectral range (Fig. 1c) and the high Q factors, a ratio of κ/D2≈1 is attained in the mid-infrared. This results in primary sidebands close to the pump, such that intrinsically low-noise operation can be expected, as opposed to the telecom wavelength band where high-phase noise in the form of broad and multiple beat notes is frequently observed in crystalline,30 silicon nitride30,31 and fused quartz25 resonators, and in toroids generating broadband spectra19.
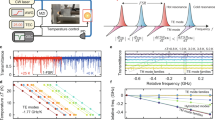
To investigate the noise30 in the generated mid-infrared combs (Fig. 3a), one can either measure the repetition rate beat note, the heterodyne beat notes between a narrow-linewidth CW laser and the comb lines, or the amplitude noise. On the one hand, for a high-phase noise comb state, multiple or broad beat notes will be observed in the radio frequency domain, along with excess low-frequency amplitude noise30; on the other hand, a low-phase noise comb state will have a single and narrow repetition rate or CW heterodyne beat note, and no additional amplitude noise. As ultra-fast mid-infrared detectors capable of detecting the repetition rate of tens of gigahertz frequencies are still in their development stage and not accessible for our experiment, we investigated in this work the phase noise of the mid-infrared Kerr combs by first, measuring the amplitude noise and second, by performing a CW heterodyne beat note measurement. Figure 3b shows two comb spectra derived from a 1-mm-diameter resonator with a line spacing of 70 GHz. Their respective amplitude noise is shown in Fig. 3c along with the detector background noise. No additional noise is observed, indicating that the combs have low phase noise. The experimental set-up and results of the CW heterodyne beat note measurement are shown in Fig. 4. Figure 4b shows the optical comb spectrum investigated, which was derived from the same resonator as in Fig. 3. After measuring the beat of the CW laser with the narrow-linewidth pump (Fig. 4c), the beat notes between the CW laser and different comb modes were recorded (Fig. 4d). All beat notes exhibit the same linewidth corresponding to the employed resolution bandwidth of 300 kHz. Importantly, neither additional linewidth broadening of the comb modes relative to the pump nor multiple beat notes are observed in this measurement, showing that the comb lines exhibit a similar level of phase noise as the CW pump laser. We emphasize that the phase noise in the form of multiple or broad beat notes in Kerr frequency combs does not exhibit a dependence on frequency distance from the pump30.
(a) Illustration of how phase noise of the comb lines can be measured. A low-phase noise comb state (blue) will show a single, narrow repetition rate beat note and CW heterodyne beat note in the radio frequency domain, and no low-frequency amplitude noise; on the other hand, a high-phase noise state (yellow) will show multiple or broad beat notes in repetition rate or CW heterodyne measurement, and also excess low-frequency amplitude noise. Phase noise can thus be determined either by measuring the repetition rate beat note, the CW heterodyne beat note, or the amplitude noise of the comb. (b) Two comb spectra derived from a 1-mm-diameter resonator with a line spacing of 70 GHz. Panel c shows the amplitude noises of the two combs, which are the same as the detector noise background. It proves that the two combs have low phase noise.
(a) Experimental set-up of the CW laser beat note measurement. BS, beam splitter; PD, photodetector. (b) Frequency comb spectrum with a line spacing of 70 GHz used for the beat note measurement. Panel c shows the beat note between the CW laser and the pump, whereas panels d and e show the beat note between the CW laser and the comb modes (marked by the red star and the green dot in b, respectively). All beat notes have a full width at half maximum of ~300 kHz, corresponding to the resolution bandwidth used in the measurement. No other peaks are observed in the measurement with a larger frequency span. Beat notes between the CW laser and other comb modes show the same linewidth.
Discussion
As shown in the simulation in Fig. 1a, the magnitude of D2 is monotonically increasing with wavelength above 1.55 μm in MgF2 resonators (anomalous dispersion). Consequently, intrinsically low-phase noise Kerr combs can be expected across the entire mid-infrared region. This is in contrast to the telecom wavelength region around 1.5 μm, where we could not observe intrinsically low-noise states in the same resonators despite various pumping conditions, in agreement with the understanding of phase noise in ref.30. In the present work, the choice of pump wavelength of λ=2.45 μm originates from the current limitation of the available OSA and the coupling fibre's strongly increasing absorption beyond 2.5 μm. The first reason is not a limiting factor of the system itself and the fibre absorption may be circumvented by employing, for example, a coupling prism37 or tapered chalcogenide fibres38 instead.
Pertaining to the advantages of crystalline microresonator-based mid-infrared frequency comb generators, it is noted that the native mode spacing in the range of 10–110 GHz is one unique feature. On the one hand, the comb repetition rate and carrier envelope offset frequencies are accessible with (suitably fast) photodetectors, electronics and digital signal processing; on the other hand, the comb modes may be individually accessed and even controlled. Indeed, a growing number of emerging applications require combs with large line spacing, such as astronomical spectrograph calibration, arbitrary optical waveform synthesis and spectroscopy15. Line-by-line pulse shaping of individual comb lines39 may prove beneficial to coherent control of chemical reactions. Moreover the ability to dispersively separate the individual modes of the mid-infrared Kerr comb with a single grating onto a detector array enables direct fingerprinting of molecular absorption3.
In summary, a crystalline microresonator-based optical frequency comb in the mid-infrared ‘molecular fingerprint’ region is demonstrated for the first time. This is also the first time that a Kerr comb is generated in the strongly anomalous dispersion region, which was previously considered unfavourable for Kerr comb generation. The high power per comb line and the potential to extend the comb to longer wavelengths makes it a promising candidate for spectroscopic applications. Moreover, the combination of crystalline microresonators with mid-infrared QCLs (which can generate high-CW output power at room temperature) could open the path to novel, simple and compact mid-infrared comb generators. Furthermore, the choice of the microresonator material is not limited to dielectric crystals. As many semiconductors such as silicon (Si), germanium (Ge) and indium phosphide (InP) also exhibit wide transparency windows in the mid-infrared and third-order nonlinearity (see Methods and Supplementary Table S2), a whole class of on-chip microresonator frequency combs for molecular spectrometers based on this approach is conceivable.
Methods
Material choice
The suitable platform for mid-infrared Kerr comb generation should possess the following properties simultaneously: wide transparency window in the mid-infrared; low loss for achieving high-Q cavity; Kerr nonlinearity n2; anomalous GVD; the same signs of thermal coefficient of refractive index dn/dT and thermal expansion coefficient α.
The last criterion comes from the thermal instability described in the Supplementary Note section, which has a key role for stable operation of Kerr combs. In Supplementary Table S1, we list the dielectric crystal materials under consideration with their respective properties. All the materials have positive thermal expansion coefficients. As can be seen from Supplementary Table S1, although most of the fluoride crystals have wide transparency window in the mid-infrared and anomalous GVD, they have negative dn/dT, which would induce thermal instability and render thermal self-locking inapplicable. Silicon nitride has a normal bulk GVD in the mid-infrared, and the current fabrication difficulty to grow Si3N4 waveguides thicker than ~800 nm makes mode confinement and dispersion engineering very challenging. The two suitable materials for mid-infrared Kerr comb generation from the list would be MgF2 and Al2O3. In this work, we choose MgF2 because fluoride crystals (such as CaF2 and MgF2) have lower material absorption therefore could reach higher Q than Al2O3, especially for wavelength longer than 2 μm (ref. 40).
In addition to dielectric crystals, many semiconductor materials also possess wide transparency windows in the mid-infrared and strong Kerr nonlinearity. The advantages of semiconductors are that they allow on-chip integration and are more versatile for waveguide dispersion engineering. Supplementary Table S2 lists several possible semiconductor materials for mid-infrared Kerr comb generation, including silicon (Si), germanium (Ge), aluminium nitride (AlN), gallium arsenide (GaAs) and indium phosphide (InP). The unwanted two-photon absorption is avoided once the photon energy is less than half the bandgap (for example, λ>2.2 μm for silicon), therefore the material loss is lower in the mid-infrared. While we do not find the experimental data on the bulk Kerr nonlinearity n2 in the mid-infrared for AlN, GaAs and InP, it is expected to vary as Eg−4, where Eg is the bandgap of the material41.
Although Si and Ge have normal bulk material GVD in the mid-infrared, it is possible to create a spectral window of anomalous GVD by carefully designing the waveguide geometry. For example, for a Si ring resonator of radius 50 μm, width 900 nm and height 400 nm, it is expected that GVD would be anomalous between 2.0 and 3.2 μm.
Set-up for microresonator-based mid-infrared frequency combs
The employed pump laser is the idler beam of a high-power single-frequency, CW optical parametric oscillator (OPO) (Aculight Argos Model 2400). The pump of the OPO is a 15 W ytterbium-doped fibre-based source operating at 1064, nm, and the OPO is a four-mirror ring-resonant cavity using a temperature-controlled MgO-PPLN crystal as the nonlinear element. The idler beam is tuneable from 2.4 to 3.2 μm with up to 3 W output power, corresponding to a signal beam from 1.9 to 1.6 μm. The idler beam can be fine-tuned by piezoelectric tuning of the pump fibre laser. Both the idler and the signal beams have a specified linewidths of less than 1 MHz.
The tapered-fibre waveguide is made of low-OH-fused silica fibre, which is single mode at 2.5 μm. The idler beam of the OPO was coupled into the tapered fibre by an AR-coated aspherical ZnSe lens. A coupling efficiency of more than 60% was obtained. The optical spectra of the combs were recorded by a Yokogawa long-range OSA.
A second OPO, similar to the pump laser source, is used as the narrow-linewidth CW laser in the beat note measurement. The beat notes are recorded using an extended InGaAs detector with 100 MHz bandwidth.
Additional information
How to cite this article: Wang, C.Y. et al. Mid-infrared optical frequency combs at 2.5 μm based on crystalline microresonators. Nat. Commun. 4:1345 doi: 10.1038/ncomms2335 (2013).
References
Udem T., Holzwarth R., Hänsch T. W. Optical frequency metrology. Nature 416, 233–237 (2002).
Cundiff S. T., Ye J. Colloquium: femtosecond optical frequency combs. Rev. Mod. Phys. 75, 325–342 (2003).
Diddams S. A., Hollberg L., Mbele V. Molecular fingerprinting with the resolved modes of a femtosecond laser frequency comb. Nature 445, 627–630 (2007).
Thorpe M. J. et al. Broadband cavity ringdown spectroscopy for sensitive and rapid molecular detection. Science 311, 1595–1599 (2006).
Mandon J., Guelachvili G., Picqué N. Fourier transform spectroscopy with a laser frequency comb. Nat. Photon. 3, 99–102 (2009).
Coddington I., Swann W. C., Newbury N. R. Coherent multiheterodyne spectroscopy using stabilized optical frequency combs. Phys. Rev. Lett. 100, 013902 (2008).
Bernhardt B. et al. Cavity-enhanced dual-comb spectroscopy. Nat. Photon. 4, 55–57 (2010).
Schliesser A. et al. Frequency-comb infrared spectrometer for rapid, remote chemical sensing. Opt. Express 13, 9029–9038 (2005).
Adler F. et al. Phase-stabilized, 1.5 W frequency comb at 2.8–4.8 mm. Opt. Lett. 34, 1330–1332 (2009).
Leindecker N. et al. Broadband degenerate OPO for mid-infrared frequency comb generation. Opt. Express 19, 6296–6302 (2011).
Maddaloni P. et al. Mid-infrared fibre-based optical comb. New J. Phys. 8, 262 (2006).
Faist J. et al. Quantum cascade laser. Science 264, 553–556 (1994).
Wang C. Y. et al. Coherent instabilities in a semiconductor laser with fast gain recovery. Phys. Rev. A 75, 031802(R) (2007).
Wang C. Y. et al. Mode-locked pulses from mid-infrared quantum cascade lasers. Opt. Express 17, 12929–12943 (2009).
Kippenberg T. J., Holzwarth R., Diddams S. A. Microresonator-based optical frequency combs. Science 332, 555–559 (2011).
Kippenberg T. J., Spillane S. M., Vahala K. J. Kerr-nonlinearity optical parametric oscillation in an ultrahigh-Q toroid microcavity. Phys. Rev. Lett. 93, 083904 (2004).
Del'Haye P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214–1217 (2007).
Del'Haye P. et al. Full stabilization of a microresonator-based optical frequency comb. Phys. Rev. Lett. 101, 053903 (2008).
Del'Haye P. et al. Octave spanning tunable frequency comb from a microresonator. Phys. Rev. Lett. 107, 063901 (2011).
Levy J. S. et al. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nat. Photon. 4, 37–40 (2010).
Foster M. A. et al. Silicon-based monolithic optical frequency comb source. Opt. Express 19, 14233–14239 (2011).
Razzari L. et al. CMOS-compatible integrated optical hyper-parametric oscillator. Nat. Photon. 4, 41–45 (2010).
Savchenkov A. A. et al. Tunable optical frequency comb with a crystalline whispering gallery mode resonator. Phys. Rev. Lett. 101, 093902 (2008).
Liang W. et al. Generation of near-infrared frequency combs from a MgF2 whispering gallery mode resonator. Opt. Lett. 36, 2290–2292 (2011).
Papp S. B., Diddams S. A. Spectral and temporal characterization of a fused-quartz-microresonator optical frequency comb. Phys. Rev. A 84, 053833 (2011).
Matsko A. B. et al. Optical hyperparametric oscillations in a whispering-gallery-mode resonator: Threshold and phase diffusion. Phys. Rev. A 71, 033804 (2005).
Chembo Y. K., Yu N. Modal expansion approach to optical-frequency-comb generation with monolithic whispering-gallery-mode resonators. Phys. Rev. A 82, 033801 (2010).
Oxborrow M. Traceable 2-D finite-element simulation of the whispering-gallery modes of axisymmetric electromagnetic resonators. IEEE Trans. Microw. Theory Tech. 55, 1209–1218 (2007).
Del'Haye P. et al. Frequency comb assisted diode laser spectroscopy for measurement of microcavity dispersion. Nat. Photon. 3, 529–533 (2009).
Herr T. et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photon. 6, 480–487 (2012).
Okawachi Y. et al. Octave-spanning frequency comb generation in a silicon nitride chip. Opt. Lett. 36, 3398–3400 (2011).
Carmon T., Yang L., Vahala K. J. Dynamical thermal behavior and thermal self-stability of microcavities. Opt. Express 12, 4742–4750 (2004).
Hofer J., Schliesser A., Kippenberg T. J. Cavity optomechanics with ultra-high Q crystalline micro-resonators. Phys. Rev. A 82, 031804(R) (2010).
Savchenkov A. A. et al. Optical resonators with ten million finesse. Opt. Express 15, 6768–6773 (2007).
Bernhardt B. et al. Mid-infrared dual-comb spectroscopy with 2.4 μm Cr2+:ZnSe femtosecond lasers. Appl. Phys. B 100, 3–8 (2010).
Adler F. et al. Mid-infrared Fourier transform spectroscopy with a broadband frequency comb. Opt. Express 18, 21861–21872 (2010).
Gorodetsky M. L., Ilchenko V. S. Optical microsphere resonators: optimal coupling to high-Q whispering-gallery modes. J. Opt. Soc. Am. B. 16, 147–154 (1999).
Magi E. C. et al. Enhanced Kerr nonlinearity in sub-wavelength diameter As2Se3 chalcogenide fiber tapers. Opt. Express 15, 10324–10329 (2007).
Ferdous F. et al. Spectral line-by-line pulse shaping of on-chip microresonator frequency combs. Nat. Photon. 5, 770–776 (2011).
Savchenkov A. A. et al. Kilohertz optical resonances in dielectric crystal cavities. Phys. Rev. A 70, 051804 (2004).
Sheikbahae M. et al. Dispersion of bound electronic nonlinear refraction in solids. IEEE J. Quantum Electron. 27, 1296–1309 (1991).
Acknowledgements
T.W.H. and N.P. acknowledge support by the European Associated Laboratory ‘European Laboratory for Frequency Comb Spectroscopy’, the Max Planck Foundation and the Munich Centre for Advanced Photonics. T.J.K. acknowledges funding from the Swiss National Science Foundation and the DARPA QuASAR program. T.J.K. and R.H. acknowledge support by Marie Curie Industry-Academia Partnerships and Pathways and the EU project SOC-II. C.Y.W. acknowledges financial support from a Marie Curie Fellowship (project IRcomb).
Author information
Authors and Affiliations
Contributions
N.P., T.W.H., T.J.K. and C.Y.W. conceived the project. C.Y.W., T.H., P.D. and N.P. constructed the experimental setup. C.Y.W. fabricated the resonators. C.Y.W., T.H. and P.D. took the experimental data. C.Y.W. analyzed the data. T.H. performed the dispersion simulation. A.S. and J.H. contributed to the early development of crystalline resonators and the understanding of thermal instability. N.P., R.H., T.J.K. and T.W.H. supervised the project. C.Y.W. wrote the paper, C.Y.W., T.H. and P.D. made the figures, and all authors joined the discussion and provided comments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure S1, Supplementary Tables S1-S2, Supplementary Note and Supplementary References (PDF 198 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Wang, C., Herr, T., Del’Haye, P. et al. Mid-infrared optical frequency combs at 2.5 μm based on crystalline microresonators. Nat Commun 4, 1345 (2013). https://doi.org/10.1038/ncomms2335
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2335
This article is cited by
-
Dissipative Kerr solitons in semiconductor ring lasers
Nature Photonics (2022)
-
Functional photonic structures for external interaction with flexible/wearable devices
Nano Research (2021)
-
Octave-spanning tunable parametric oscillation in crystalline Kerr microresonators
Nature Photonics (2019)
-
Field-programmable silicon temporal cloak
Nature Communications (2019)
-
Mid infrared gas spectroscopy using efficient fiber laser driven photonic chip-based supercontinuum
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.