Abstract
Precise qubit manipulation is fundamental to quantum computing, yet experimental systems generally have stray coupling between the qubit and the environment, which hinders the necessary high-precision control. Here, we report the first theoretical progress in correcting an important class of errors stemming from fluctuations in the magnetic field gradient, in the context of the singlet–triplet spin qubit in a semiconductor double quantum dot. These errors are not amenable to correction via control techniques developed in other contexts, as here the experimenter has precise control only over the rotation rate about the z axis of the Bloch sphere, and this rate is furthermore restricted to be positive and bounded. Despite these strong constraints, we construct simple electrical pulse sequences that, for small gradients, carry out z axis rotations while cancelling errors up to the sixth order in gradient fluctuations, and for large gradients, carry out arbitrary rotations while cancelling the leading order error.
Similar content being viewed by others
Introduction
A quantum computer would permit exponentially faster algorithms than an ordinary computer for certain important types of problems1. Universal quantum computation requires the ability to perform an entangling two-qubit gate and precise single-qubit rotations around two different axes of the Bloch sphere. Single-electron spin qubits in semiconductor quantum dots potentially have marked advantages in fast two-qubit gating and scalability2, but suffer an embarrassing difficulty in performing fast single-qubit rotations because the strong, high-frequency magnetic fields naïvely required3 heat the sample and are hard to confine to a single qubit4. This problem is circumvented by encoding the qubit in the low-lying singlet–triplet subspace of a two-electron double quantum dot5,6,7,8. Fast electrical control of the exchange coupling, J, via the tilt of the effective double-well potential allows sub-ns rotations about the z axis of the Bloch sphere.
To perform arbitrary rotations of such a qubit, though, one must introduce a difference, ΔB, between the local magnetic fields at each dot, resulting in rotation about the x axis of the Bloch sphere. This can be done either by pumping a nuclear spin polarization gradient9 or by depositing a micromagnet nearby10. However, a problem remains: the local magnetic field typically fluctuates slowly due to second-order nuclear spin flip-flops mediated by the hyperfine coupling to the electron spin11,12 and owing to charge-noise-induced shifts of the double-dot position in the inhomogeneous field. The resulting uncertainty in ΔB introduces a quasi-static random component to the rotation about the x axis that, in the course of ensemble averaging, leads to rapid decoherence of the qubit on the free induction decay timescale of T2*. However, the fact that these errors implement coherent rotations (albeit by an unknown angle) makes it possible to reduce their effect by means of dynamical control; this nice feature is due to the non-Markovian nature of the nuclear spin bath, a situation unique to quantum dot spin qubits. In the case of quantum memory, dynamical decoupling techniques7,12,13,14,15,16,17 can be employed to preserve qubit information long beyond T2*, up to a timescale T2 (which is defined with respect to a specific dynamical decoupling sequence) at which this information is ultimately lost due to dynamical fluctuations. This ability is crucial, because typically T2  104 T2* for localized electron spins in semiconductors—in particular, in GaAs quantum dot systems6,7, T2* ~ 10 ns, T2~0.1 ms, and in Si8, T2* ~ 100 ns with T2 predicted18 to be ~1 ms. However, such echo techniques cannot be performed simultaneously with arbitrary single-qubit rotations, so gate errors are still dominated by statistical fluctuations and depend on the ratio of the gate time to T2* rather than to T2. It is of utmost importance to address this problem because fault-tolerant quantum computation requires extremely precise single-qubit rotations. Thus, the task is to find dynamically corrected gates19,20,21,22,23 applicable to singlet–triplet qubits.
104 T2* for localized electron spins in semiconductors—in particular, in GaAs quantum dot systems6,7, T2* ~ 10 ns, T2~0.1 ms, and in Si8, T2* ~ 100 ns with T2 predicted18 to be ~1 ms. However, such echo techniques cannot be performed simultaneously with arbitrary single-qubit rotations, so gate errors are still dominated by statistical fluctuations and depend on the ratio of the gate time to T2* rather than to T2. It is of utmost importance to address this problem because fault-tolerant quantum computation requires extremely precise single-qubit rotations. Thus, the task is to find dynamically corrected gates19,20,21,22,23 applicable to singlet–triplet qubits.
Finding such gates is challenging because available control in real experimental singlet–triplet spin qubit systems is rather limited: One only has precise control over the rotation rate about the z axis of the Bloch sphere via the exchange interaction, and because of the nature of the exchange interaction, this rotation rate is intrinsically restricted to be positive and bounded. Meanwhile, the rotation around the x axis due to the magnetic field gradient cannot be precisely controlled. These control constraints specific to singlet–triplet qubits render the numerous quantum control techniques developed in other fields, such as nuclear magnetic resonance, inapplicable.
In this work, we show how to perform dynamically corrected single-qubit gates on singlet–triplet qubits, dramatically reducing errors while fully respecting these experimental constraints. We construct simple electrical pulse sequences that, for small magnetic field gradients, carry out rotations about the z axis while cancelling gate errors up to the sixth order in the gradient fluctuations, and for large magnetic field gradients, carry out arbitrary rotations while cancelling the leading order error. This represents an important step forward in the development of singlet–triplet qubits as viable resources for quantum computing.
Results
Model
We consider the Hamiltonian governing the singlet–triplet qubit,

with constraints on the parameters imposed to account for the physical realities of the experiments6,7,8,9,17,24,25. Here h=gμBΔB and fluctuations in ΔB are much slower than typical gate times so that h=h0+δh with h0 a known constant and δh a random, unknown constant. (T2*is inversely proportional to the width of the statistical distribution from which δh is drawn. We estimate the effect of high-frequency noise components in the Supplementary Discussion.) The qubit is manipulated via the electrically controlled exchange coupling, J(t), which is constrained to be positive (except in very high magnetic fields, when it is always negative) and is restricted in magnitude either by the practice of keeping the qubit near the zero-bias point to reduce charge noise sensitivity, or, more intrinsically, by the singlet–triplet splitting of two electrons on a single dot, so that 0 J(t)
J(t) Jmax. The constraint to positive rotations is also relevant to exchange-only coded qubits26,27,28.
Jmax. The constraint to positive rotations is also relevant to exchange-only coded qubits26,27,28.
Our goal is to design a pulse in J(t) that respects these constraints and performs a given rotation in a way that is insensitive to δh. We dub the resulting composite pulse sequence SUPCODE: soft uniaxial positive control for orthogonal drift error. We emphasize that although the singlet–triplet qubit is one of the most experimentally advanced paths towards a scalable quantum computer, the restricted control available does not permit application of existing elegant methods of quantum control. In particular, the positivity of J(t) precludes the prescriptions of refs 19, 20 (which anyway do not accommodate universal single-qubit operations) and ref. 21. Although other works allow a positivity constraint22,23, they are nonetheless precluded by the uncontrolled, always-on gradient h. Below we consider two cases: h0=0, which is directly relevant to experiments with unpumped nuclear spins and no micromagnet6,8, where only rotations about the z axis are desired (for example, for spin echo), and h0~Jmax, which is directly relevant to experiments with pumped nuclear spins9 or a nearby micromagnet10 where full single-qubit control is desired.
SUPCODE for h0=0
For h0=0, we assume for simplicity that the pulse is of a binary form where J(t) alternates between its extremal values of 0 and Jmax. Expanding the evolution operator of the system,  , in powers of δh/Jmax, we choose the time duration of each segment such that the zeroth order term is a rotation about
, in powers of δh/Jmax, we choose the time duration of each segment such that the zeroth order term is a rotation about  by the desired angle and one or more successively higher order terms vanish. We give details in the Methods, and in Supplementary Discussion, we also rigorously show that there is no pulse that cancels all higher orders for finite Jmax. Thus, we find three-, five-, seven-, and nine-piece SUPCODE pulses that perform arbitrary rotations about
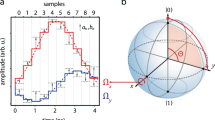
by the desired angle and one or more successively higher order terms vanish. We give details in the Methods, and in Supplementary Discussion, we also rigorously show that there is no pulse that cancels all higher orders for finite Jmax. Thus, we find three-, five-, seven-, and nine-piece SUPCODE pulses that perform arbitrary rotations about  while cancelling undesired terms up to the first, second, second, and third order in δh/Jmax, respectively. (We note that in this special case, the first order cancellation could also be performed via ref. 23.) An example of the five-piece SUPCODE pulse, which cancels first and second order terms in δh/Jmax in the evolution operator (corresponding to second and fourth order terms in the gate error), is shown in Fig. 1. Figure 2 traces the evolution of a particular initial state on the Bloch sphere under a five-piece SUPCODE pulse designed to perform a π/2 rotation about
while cancelling undesired terms up to the first, second, second, and third order in δh/Jmax, respectively. (We note that in this special case, the first order cancellation could also be performed via ref. 23.) An example of the five-piece SUPCODE pulse, which cancels first and second order terms in δh/Jmax in the evolution operator (corresponding to second and fourth order terms in the gate error), is shown in Fig. 1. Figure 2 traces the evolution of a particular initial state on the Bloch sphere under a five-piece SUPCODE pulse designed to perform a π/2 rotation about  . We include an animation showing how this state evolves under the five-piece SUPCODE pulse in Supplementary Movie 1.
. We include an animation showing how this state evolves under the five-piece SUPCODE pulse in Supplementary Movie 1.
 by π/2 .
by π/2 .Here h0=0, and for the purpose of illustration, we have taken δh/Jmax=0.05.  labels the state with the spin-up (spin-down) electron occupying the left (right) dot. Likewise,
labels the state with the spin-up (spin-down) electron occupying the left (right) dot. Likewise,  labels the spin-permuted state.
labels the spin-permuted state.  denotes the singlet state
denotes the singlet state  denotes the non-magnetic triplet state
denotes the non-magnetic triplet state  . The green arrow is the Bloch vector pointing to the final state after the evolution, which is represented as a point on the surface of the Bloch sphere. The black curve shows the trajectory of the state under the five-piece SUPCODE.
. The green arrow is the Bloch vector pointing to the final state after the evolution, which is represented as a point on the surface of the Bloch sphere. The black curve shows the trajectory of the state under the five-piece SUPCODE.
We define the average error per gate, Δ, as

where V is the desired operation, U(Tf) is the actual evolution operator under the composite pulse of duration Tf , and the overlap is averaged over initial states |ψi> distributed uniformly over the Bloch sphere. Fig. 3 shows the average error per gate for the naïve one-piece pulse and the SUPCODE pulses introduced above. We see that for δh/Jmax<10% the SUPCODE pulses have markedly less error. This range is relevant to recent landmark experiments with GaAs7 and silicon-based8 double quantum dots. In the former δh~8 neV and in the latter δh~3 neV, while in both cases Jmax could be several hundred neV. We also see that although the leading order of the error for the nine-piece pulse is higher than that of the other pulses, its coefficient is large enough that for δh/Jmax 2%, it is better to use the five- or seven-piece pulses. This suggests that generating similar pulses with even more pieces likely will not extend the range of values of δh for which low-error rotations are possible.
2%, it is better to use the five- or seven-piece pulses. This suggests that generating similar pulses with even more pieces likely will not extend the range of values of δh for which low-error rotations are possible.
These figures show the average error per gate Δ as functions of δh/Jmax for the rotation around the z axis by (a) φ0=π/2 and (b) φ0=1.7π. The red solid curves are for the uncorrected pulse with quadratic leading order errors in δh. Other curves are showing the three-piece (blue dashed lines), five-piece (black dotted line), seven-piece (magenta dash-dotted lines), and nine-piece (orange dash-dotted lines) SUPCODE pulses that cancel gate error Δ up through second, fourth, fourth and sixth order in δh, respectively.
SUPCODE for h0~Jmax
For h0~Jmax, the noncommutation of the Hamiltonian at different times even for δh=0 makes the previous approach algebraically forbidding. However, in this case, we have the possibility to perform rotations about axes  other than
other than  . We make use of this freedom to construct SUPCODE pulses in a simple way: We first take an uncorrected (that is, designed as if δh=0) rotation
. We make use of this freedom to construct SUPCODE pulses in a simple way: We first take an uncorrected (that is, designed as if δh=0) rotation  and then construct an uncorrected identity operation
and then construct an uncorrected identity operation  designed such that the error in its implementation exactly cancels the leading order error in the original rotation. We represent the uncorrected rotations
designed such that the error in its implementation exactly cancels the leading order error in the original rotation. We represent the uncorrected rotations  in terms of ideal rotations
in terms of ideal rotations  as
as

and

where  and
and  are the first order corrections. For the corrected pulse
are the first order corrections. For the corrected pulse  , it is clear that we want to make
, it is clear that we want to make  . Because there are infinitely many ways to realize the identity operation, there is sufficient freedom to engineer such a cancellation. In particular, we consider parameterized versions of the identity implemented as nested interrupted 2nπ rotations about different axes, with two simple examples being
. Because there are infinitely many ways to realize the identity operation, there is sufficient freedom to engineer such a cancellation. In particular, we consider parameterized versions of the identity implemented as nested interrupted 2nπ rotations about different axes, with two simple examples being

and

where ai and bi are parameters satisfying 0≤ai≤2π, 0≤bi≤Jmax/h0 and n is a positive integer.
As an explicit demonstration of SUPCODE, we show rotations around the x and z axes by arbitrary angles 0<φ<π for the particular case Jmax/h0≥5. (Combinations of these are sufficient for universal one-qubit gates.) About  , the uncorrected rotation is performed by holding J=0 for a time φ/h0, and this is preceded by the identity
, the uncorrected rotation is performed by holding J=0 for a time φ/h0, and this is preceded by the identity  where b1 and b2 are chosen such that errors cancel (see Methods as well as Supplementary Movie 2). About
where b1 and b2 are chosen such that errors cancel (see Methods as well as Supplementary Movie 2). About  , the uncorrected rotation is performed by a three-part pulse29,30
, the uncorrected rotation is performed by a three-part pulse29,30  , and this is preceded by the identity
, and this is preceded by the identity  where a, b3, and b4 are chosen such that errors cancel (see Methods). As shown in Fig. 4 for φ=π/2, SUPCODE does indeed lead to a higher order scaling of the error in δh/h0 (and hence in
where a, b3, and b4 are chosen such that errors cancel (see Methods). As shown in Fig. 4 for φ=π/2, SUPCODE does indeed lead to a higher order scaling of the error in δh/h0 (and hence in  ), and a reduction of error when δh/h0 is less than a few percent. For instance, when δh/h0=5%, errors are typically reduced by an order of magnitude.
), and a reduction of error when δh/h0 is less than a few percent. For instance, when δh/h0=5%, errors are typically reduced by an order of magnitude.
 5.
5.This set of figures shows the average error per gate Δ as functions of δh/h0, for rotations by π/2 about the (a) x axis and (b) z axis. The red curves show the error per gate corresponding to the uncorrected pulses. The corrected pulses, shown by the blue dashed lines, cancel the leading order error. In this figure we used h0 as the energy scale instead of Jmax.
Discussion
The tradeoff of our approach is that SUPCODE rotations are typically over an order of magnitude longer than uncorrected rotations. We note that for a given experimental set of parameters one should try optimizing the pulse sequence, which we have not done for the arbitrarily chosen example above, as both the length and error of the corrected pulses could certainly be reduced by a significant constant factor by searching over different constructions of the identity, Ĩ. Nonetheless, for experiments in GaAs systems with pumped nuclear spins31 (h0~0.6 μeV, δh~30 neV) or micromagnets10 (h0~20 neV, δh~1 neV), the sequences shown here could already deliver substantial improvement over the uncorrected ones.
Realistic deviations from the ideal pulses assumed above would include charge noise, which adds a random quasi-static contribution to the exchange, and finite rise times. The former could be reduced by using a multi-electron variant of the singlet–triplet qubit32 and, in principle, it may even be possible to dynamically correct by adding more degrees of freedom to the pulses. The latter can be compensated for by adjusting pulse parameters given the actual turn-on/off profiles of the pulse for a specific experimental set-up (we give explicit demonstrations in the Supplementary Discussion). Thus, even in nonideal conditions SUPCODE could enable precise spin qubit rotations independent of shot-to-shot variation in the nuclear Overhauser field, also easing tasks such as ensemble-averaged measurements of singlet probability oscillations versus time by reducing hyperfine-induced decay. More importantly, this work allows satisfaction of the quantum error correction threshold within a substantially larger region of the physical parameter space than would otherwise be possible. The fact that T2 has now reached tens of microseconds in GaAs quantum dots7, and milliseconds18 or even seconds in the presence of isotopic purification33 in Si-based structures implies that gate errors are currently dominated not by dynamical fluctuations in the nuclear spin bath, but by the statistical distribution of the magnetic field gradient, and these errors may be efficiently suppressed by SUPCODE.
Methods
Expansion of the evolution operator around h0=0
The evolution operator is defined as

with h=h0+δh. Expanding the evolution operator in powers of δh in the vicinity of h0=0,

where one can show that

and, for n>0,

(note that the product is in descending order in observance of the time-ordering of operators) where



and I is the 2×2 identity matrix and σx, σy, and σz are Pauli matrices.
Thus, for the nth-order term to vanish, one must have

The no-go theorem shown in Supplementary Discussion implies that it is instructive to design pulses that cancel successive orders. In this work, we focus on the piecewise constant pulse, which can be expressed as

where we have defined the dimensionless quantity τk=Jmaxtk for convenience, and tk refers to the duration of a pulse on the kth piece. The total duration of time after the kth piece would be  , with T0≡0 and TN≡Tf indicating the initial and final time. J(t) can then be expressed as
, with T0≡0 and TN≡Tf indicating the initial and final time. J(t) can then be expressed as

where Θ(t) is the Heaviside step function.
Three-piece SUPCODE for h0=0
Our motivation is to cancel successive orders of δh in the expansion with number of pieces N as small as possible. We consider symmetric pulses, that is, J(t)=J(Tf−t), for the h0=0 case. This ensures that U(Tf,0) has no σy component. [To see this fact, note that the operator  can be written in the form Ai=ai0I+aixσx+aizσz with ai0, aix, aiz arbitrary complex numbers. It is then straightforward to show that for any operators A1 and A2 with arbitrary coefficients, A2·A1·A2 can also be written in such a form, free of σy terms. Applying this statement recursively to equation (15), one sees that for any J(t) satisfying J(t)=J(Tf−t) the resulting evolution operator U does not contain σy component.]
can be written in the form Ai=ai0I+aixσx+aizσz with ai0, aix, aiz arbitrary complex numbers. It is then straightforward to show that for any operators A1 and A2 with arbitrary coefficients, A2·A1·A2 can also be written in such a form, free of σy terms. Applying this statement recursively to equation (15), one sees that for any J(t) satisfying J(t)=J(Tf−t) the resulting evolution operator U does not contain σy component.]
One of the simplest ways to cancel the leading order error with strictly positive values of J is via a three-piece pulse sequence. In equation (15), we take N=3 and the three-piece pulse sequence can be characterized by

where φ0 is the desired rotation angle around the z axis. It is straightforward to verify that the evolution operator under this pulse is

Here the deviation from the desired rotation has been suppressed up to second order in δh (which corresponds to the fourth order in equation (2)). This pulse actually sweeps the Bloch vector through an angle φ=2π+φ0, which is the origin of the trivial additional phase factor. It is clear that to achieve error cancellation, the Bloch vector generally must be swept through more than 2π about the z axis as its path is deflected from the ideal (δh=0) path in opposite directions in the 'eastern and western hemispheres'. (One can also explicitly show the necessity of larger angles from equation (10).) Thus the three-piece pulse sequence cancels leading order error simply by ensuring that, in the absence of δh, the Bloch vector spends an equal amount of time in each hemisphere during its rotation.
Five-piece SUPCODE for h0=0
We set N=5 in equation (15), which allows us to cancel the dependence of U(Tf,0) on δh up to the second order (corresponding to the fourth order in equation (2)), using a symmetric pulse with parameters J1=J3=J5=0, J2=J4=Jmax, and

We expand U(Tf,0) as

To make the first order coefficient vanish, one must choose

Plugging equation (21) into equation (20), it suffices to satisfy

to make the second order terms vanish. We choose a root that is positive for 2π<φ<3π, that is

Equations (19), (21), and (23) prescribe the pulse parameters required to achieve a  rotation while cancelling the dependence of U(Tf,0) on δh up to the second order. A plot of these parameters as a function of φ is given in Fig. 1. This pulse is defined for
rotation while cancelling the dependence of U(Tf,0) on δh up to the second order. A plot of these parameters as a function of φ is given in Fig. 1. This pulse is defined for  , which is equivalent to a rotation
, which is equivalent to a rotation  with
with  . Rotation of angles outside the range (0,π) may be achieved by duplicating existing pulse sequences. For example, to achieve a
. Rotation of angles outside the range (0,π) may be achieved by duplicating existing pulse sequences. For example, to achieve a  rotation of φ0=1.2π, one could apply twice the φ0=0.6π (corresponding to φ=2.6π) rotation.
rotation of φ0=1.2π, one could apply twice the φ0=0.6π (corresponding to φ=2.6π) rotation.
As φ→2π, τ1→∞, τ2=π/2, τ3→2τ1. If we want to fix the total duration of the sequence, we let Jmax→∞. The pulse sequence becomes the well-known CPMG pulse13,14. In fact, it can be shown that for a pair of instantaneous π pulses, setting leading order errors to zero while maintaining the time-reversal symmetry of the pulse sequence enforces the Uhrig condition15.
For details of the construction of seven-piece and nine-piece SUPCODE, see Supplementary Methods.
SUPCODE for h0≠0
As described in Results, we perform corrected rotations as  where the implementation of the identity Ĩ is chosen such that the first order errors in δh exactly cancel those from the rotation
where the implementation of the identity Ĩ is chosen such that the first order errors in δh exactly cancel those from the rotation  . Our implementations of Ĩ are of the form
. Our implementations of Ĩ are of the form

For the specific forms Ĩ1,Ĩ2 given in the main text, the parameters ai, bi are constrained by


The particular implementation of Ĩ that will be chosen for a given experimental situation will depend on the particular rotation  as well as the experimental parameters Jmax/h0, with a combinatorial search necessary to find an implementation that (a) cancels the first-order error from
as well as the experimental parameters Jmax/h0, with a combinatorial search necessary to find an implementation that (a) cancels the first-order error from  ; (b) satisfies the constraints of equations (25) and (26); and (c) is close to 'optimal' in some experimentally meaningful sense, such as having the overall shortest duration in time, having the smallest second-order error in δh, or being least sensitive to over-/under-shoot in J(t). As an example of our technique, we found sequences valid for the experimentally relevant regime Jmax/h0≥5, for corrected rotations about angles 0≤φ≤π around the x and z axes. (We have also verified that slightly more complicated identities can be constructed to correct error for pulses with smaller values of Jmax/h0>1.5.) For the x axis rotation, we have
; (b) satisfies the constraints of equations (25) and (26); and (c) is close to 'optimal' in some experimentally meaningful sense, such as having the overall shortest duration in time, having the smallest second-order error in δh, or being least sensitive to over-/under-shoot in J(t). As an example of our technique, we found sequences valid for the experimentally relevant regime Jmax/h0≥5, for corrected rotations about angles 0≤φ≤π around the x and z axes. (We have also verified that slightly more complicated identities can be constructed to correct error for pulses with smaller values of Jmax/h0>1.5.) For the x axis rotation, we have

The first-order term in δh is zero when b1,2 are chosen to satisfy


The solution to these equations are shown in Supplementary Fig. S1. In Supplementary Fig. S1a, we show a specific example of the pulse sequence for π/2 rotation about the x axis, and correspondingly, we show how a given state evolves under this SUPCODE in Supplementary Movie 2. Supplementary Fig. S1c shows solutions for a range of rotation angle 0≤φ≤π.
For the same parameter range, we construct the corrected z axis rotation as

with a and b3,4 satisfying



The solution to these equations is shown in Supplementary Fig. S2. In Supplementary Fig. S2a, we show an example of the pulse sequence appropriate for rotating about the z axis by π/2, while in Supplementary Fig. S2c, we show solutions for 0≤φ≤π.
Additional information
How to cite this article: Wang X. et al. Composite pulses for robust universal control of singlet–triplet qubits. Nat. Commun. 3:997 doi: 10.1038/ncomms2003 (2012).
References
Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information (Cambridge University Press, 2000).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Pioro-Ladriere, M. et al. Electrically driven single-electron spin resonance in a slanting Zeeman field. Nat. Phys. 4, 776–779 (2008).
Levy, J. Universal quantum computation with spin-1/2 pairs and Heisenberg exchange. Phys. Rev. Lett. 89, 147902 (2002).
Petta, J. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Bluhm, H. et al. Dephasing time of GaAs electron-spin qubits coupled to a nuclear bath exceeding 200 μs. Nat. Phys. 7, 109–113 (2011).
Maune, B. M. et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344–347 (2012).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Brunner, R. et al. Two-qubit gate of combined single-spin rotation and interdot spin exchange in a double quantum dot. Phys. Rev. Lett. 107, 146801 (2011).
Reilly, D. J. et al. Measurement of temporal correlations of the Overhauser field in a double quantum dot. Phys. Rev. Lett. 101, 236803 (2008).
Cywiński, L., Witzel, W. M. & Das Sarma, S. Electron spin dephasing due to hyperfine interactions with a nuclear spin bath. Phys. Rev. Lett. 102, 057601 (2009).
Carr, H. Y. & Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 94, 630–638 (1954).
Meiboom, S. & Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 29, 688–691 (1958).
Uhrig, G. S. Keeping a quantum bit alive by optimized π-pulse sequences. Phys. Rev. Lett. 98, 100504 (2007).
Witzel, W. M. & Das Sarma, S. Concatenated dynamical decoupling in a solid-state spin bath. Phys. Rev. B 76, 241303 (2007).
Barthel, C., Medford, J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Interlaced dynamical decoupling and coherent operation of a singlet-triplet qubit. Phys. Rev. Lett. 105, 266808 (2010).
Witzel, W. M., Carroll, M. S., Morello, A., Cywiński, L. & Das Sarma, S. Electron spin decoherence in isotope-enriched silicon. Phys. Rev. Lett. 105, 187602 (2010).
Goelman, G., Vega, S. & Zax, D. B. Squared amplitude-modulated composite pulses. J. Magn. Reson. 81, 423–429 (1989).
Grace, M. D., Dominy, J. M., Witzel, W. M. & Carroll, M. S. Optimized pulses for the control of uncertain qubits. Phys. Rev. A 85, 052313 (2012).
Khodjasteh, K. & Viola, L. Dynamical quantum error correction of unitary operations with bounded controls. Phys. Rev. A 80, 032314 (2009).
Khodjasteh, K., Lidar, D. A. & Viola, L. Arbitrarily accurate dynamical control in open quantum systems. Phys. Rev. Lett. 104, 090501 (2010).
Bensky, G., Brion, E., Carlier, F., Akulin, V. M. & Kurizki, G. Universal dynamical decoupling from slow noise with minimal control. Europhys. Lett. 89, 10011 (2010).
Lai, N. S. et al. Pauli spin blockade in a highly tunable silicon double quantum dot. Sci. Rep. 1, 110 (2011).
Prance, J. R. et al. Single-shot measurement of triplet-singlet relaxation in a Si/SiGe double quantum dot. Phys. Rev. Lett. 108, 046808 (2012).
DiVincenzo, D. P., Bacon, D., Kempe, J., Burkard, G. & Whaley, K. B. Universal quantum computation with the exchange interaction. Nature 408, 339–342 (2000).
Laird, E. A. et al. Coherent spin manipulation in an exchange-only qubit. Phys. Rev. B 82, 075403 (2010).
Shi, Z. et al. Fast hybrid silicon double-quantum-dot qubit. Phys. Rev. Lett. 108, 140503 (2012).
Hanson, R. & Burkard, G. Universal set of quantum gates for double-dot spin qubits with fixed interdot coupling. Phys. Rev. Lett. 98, 050502 (2007).
Ramon, G. Electrically controlled quantum gates for two-spin qubits in two double quantum dots. Phys. Rev. B 84, 155329 (2011).
Bluhm, H., Foletti, S., Mahalu, D., Umansky, V. & Yacoby, A. Enhancing the coherence of a spin qubit by operating it as a feedback loop that controls its nuclear spin bath. Phys. Rev. Lett. 105, 216803 (2010).
Barnes, E., Kestner, J. P., Nguyen, N. T. T. & Das Sarma, S. Screening of charged impurities with multielectron singlet-triplet spin qubits in quantum dots. Phys. Rev. B 84, 235309 (2011).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater 11, 143–147 (2011).
Acknowledgements
This work is supported by LPS-NSA-CMTC and IARPA-MQCO grants.
Author information
Authors and Affiliations
Contributions
J.P.K. and X.W. formulated the problem. The SUPCODE for the h0=0 case was designed by E.B., J.P.K., K.S. and X.W. L.S.B. developed the SUPCODE for h0≠0. S.D.S. supervised the project. All authors discussed the results and prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Figures, Discussion, Methods and References
Supplementary Figures S1–S4, Supplementary Discussion, Supplementary Methods and Supplementary References (PDF 264 kb)
Supplementary Movie 1
The evolution of a given state on the Bloch sphere under the five-piece SUPCODE pulse sequences achieving a π/2 rotation around the z-axis with δh=0.05Jmax. (MOV 278 kb)
Supplementary Movie 2
The evolution of a given state on the Bloch sphere under the SUPCODE pulse sequences at Jmax/h0>=5 achieving a π/2 rotation around the x-axis with δh=0.08h0. (MOV 676 kb)
Rights and permissions
About this article
Cite this article
Wang, X., Bishop, L., Kestner, J. et al. Composite pulses for robust universal control of singlet–triplet qubits. Nat Commun 3, 997 (2012). https://doi.org/10.1038/ncomms2003
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2003
This article is cited by
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
A singlet-triplet hole spin qubit in planar Ge
Nature Materials (2021)
-
Conditional teleportation of quantum-dot spin states
Nature Communications (2020)
-
A noise-resisted scheme of dynamical decoupling pulses for quantum memories
Scientific Reports (2020)
-
A two-qubit gate between phosphorus donor electrons in silicon
Nature (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.