Abstract
The coupling of distinct systems underlies nearly all physical phenomena. A basic instance is that of interacting harmonic oscillators, giving rise to, for example, the phonon eigenmodes in a lattice. Of particular importance are the interactions in hybrid quantum systems, which can combine the benefits of each part in quantum technologies. Here we investigate a hybrid optomechanical system having three degrees of freedom, consisting of a microwave cavity and two micromechanical beams with closely spaced frequencies around 32 MHz and no direct interaction. We record the first evidence of tripartite optomechanical mixing, implying that the eigenmodes are combinations of one photonic and two phononic modes. We identify an asymmetric dark mode having a long lifetime. Simultaneously, we operate the nearly macroscopic mechanical modes close to the motional quantum ground state, down to 1.8 thermal quanta, achieved by back-action cooling. These results constitute an important advance towards engineering of entangled motional states.
Similar content being viewed by others
Introduction
One of the present goals in physics is the explanation of macroscopic phenomena as emerging from the quantum-mechanical laws governing nature on a microscopic scale. This understanding is also important for future quantum information applications1,2,3,4, as many of the most promising platforms are based on nearly macroscopic degrees of freedom. For macroscopic mechanical objects, their potential quantum behaviour5 has been actively investigated with resonators interacting with an electromagnetic cavity mode6. In particular, freezing of the mechanical Brownian motion7,8 down to below one quantum of energy has recently been observed9,10.
Another result of radiation–pressure interaction is the mixing of the normal modes of vibration into linear combinations of the uncoupled phonon and photon modes. This has been verified with optomechanical Fabry–Perot cavity11,12, and by its on-chip microwave analogue13 using an aluminium membrane. All this work is paving the way towards engineering non-classical motional5 and hybrid quantum states1,3,4,14 for basic tests of quantum theory15,16, as well as applications in foreseeable future.
Corresponding phenomena in systems comprising more than two active degrees of freedom17,18,19 have received less attention. In the optomechanical crystal set-up, coupling of mechanical vibrations via radiation–pressure interaction has been demonstrated with the zipper cavity20, however, with some direct interaction between the beams. In the microwave regime, such measurements have remained outstanding. In this work, we take a step further, and examine a multimode system where two micromechanical beams, having resonant frequencies ω1/(2π)=32.1 MHz and ω2/(2π)=32.5 MHz, are each coupled to a microwave on-chip cavity. We obtain the first evidence of hybridization of all the three degrees of freedom. This was made possible by operating, as opposed to the optical set-up, in the good-cavity limit, that is, both ω1 and ω2 were much larger than the cavity decay rate γc. Simultaneously, the mechanical modes are found at low occupation numbers nm, near the quantum ground state, down to nm=1.8±0.5. These are the lowest occupations recorded with nanowire resonators to date, and they occur via the sideband cooling, starting from operation at dilution refrigerator temperatures at a few tens of millikelvin.
Results
Cavity with several mechanical modes
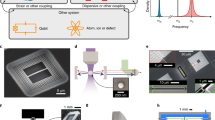
In the optical domain20, a three-mode optomechanical system can be pictured as a Fabry–Perot cavity with both massive mirrors mounted via springs, see Fig. 1a. In the microwave version, (Fig. 1b), the mirrors are replaced by movable capacitors formed by the mechanical resonators. The electromechanical coupling arises when each mechanical resonator (labelled with j), expressed as time-varying capacitors Cj, independently modulates the total capacitance, and hence, the cavity frequency ωc. This is described by the coupling energies gj=(ωc/2C)∂Cj/∂xj. In the actual device (see the micrograph in Fig. 1c), the mechanical resonators are spatially separated by about 100 μm, and we hence expect the direct interaction between the beams via the substrate material to be negligible. We drive the cavity strongly by a microwave pump signal applied at the frequency ωP near the cavity frequency. The pump induces a large cavity field with the number of pump photons  . This allows for a linearized description of the electromechanical interaction and results in substantially enhanced effective couplings
. This allows for a linearized description of the electromechanical interaction and results in substantially enhanced effective couplings  , where
, where  is the zero-point amplitude.
is the zero-point amplitude.
(a) Optomechanical system with both mirrors movable has three degrees of freedom. These are the optical field inside the Fabry–Perot cavity and the displacements x1 and x2 of the mirrors. (b) Analogue of panel a with a microwave-regime cavity represented by the lumped element inductors and capacitors and arbitrary number j=1 … N of mechanical resonators. The system is probed through the coupling capacitor Cc by shining a strong pump microwave tone (frequency ωP), which corresponds to the laser in a, and possibly a weak probe tone (frequency ωin and voltage amplitude Vin) in a dilution refrigerator down to 25 mK temperature. The outgoing wave Vout can be monitored. (c) Images of the all-aluminium superconducting sample, showing four fabrication jigs for a beam. Total of three beams (x1 … x3) were operating. Beams 1 and 2 had large electromechanical couplings g1/2π=1.8 MHz nm−1, g2/2π=2.0 MHz nm−1, whereas the third beam had an order of magnitude smaller coupling. The scale bars are 50 μm on the left and 10 μm on the right.
The general Hamiltonian for N mechanical resonators with frequencies ωj, individually coupled to a common cavity mode, written in a frame rotating with the pump, becomes

Here, a is the annihilation operator for the cavity mode, while bj are those of the mechanical resonators. If one assumes roughly similar mechanical resonators, viz.  and
and  , the cavity becomes nearly resonant to all of them at the red-sideband detuned pump condition Δ=−ωm.
, the cavity becomes nearly resonant to all of them at the red-sideband detuned pump condition Δ=−ωm.
Coupling of the mechanical resonators via the cavity ‘bus’ can be anticipated to be significant if the mechanical spectra begin to overlap when their width increased by the radiation pressure, γeff=γm+γopt, grows comparable to the mechanical frequency spacing. Here, γopt=4G2/γc. The equations of motion following from equation (1) allow one to verify the above assumption. We will in the following focus on two resonators, N=2. The result of such a calculation, which is detailed in the Supplementary Methods, is that they experience an effective coupling with energy G12=G1G2/γc.
In the limit of strong coupling,  , the system is best described as a combination of two ‘bright’ modes with linewidths
, the system is best described as a combination of two ‘bright’ modes with linewidths  , and of a ‘dark’ mode having a long lifetime
, and of a ‘dark’ mode having a long lifetime  . In the latter, the two mechanical resonators oscillate out-of-phase and synchronize into a common frequency (ω1+ω2)/2. In any case, the mode structure can be written with the normal coordinates for mode n, for position quadrature according to
. In the latter, the two mechanical resonators oscillate out-of-phase and synchronize into a common frequency (ω1+ω2)/2. In any case, the mode structure can be written with the normal coordinates for mode n, for position quadrature according to  . Here we used the dimensionless amplitude of the mechanical oscillations
. Here we used the dimensionless amplitude of the mechanical oscillations  , and similarly the dimensionless flux
, and similarly the dimensionless flux  in the cavity. The mode expansion coefficients give the participation ratio of each uncoupled mode. They satisfy
in the cavity. The mode expansion coefficients give the participation ratio of each uncoupled mode. They satisfy  .
.
In the experiment, we use doubly clamped flexural beams, which are made by the use of ion beam milling of aluminium21, having an ultranarrow  nm vacuum slit to the opposite end of the cavity for maximizing the coupling. The cavity is a half-wavelength floating microstrip similar to the one used in Massel et al.22, resonating at ωc/(2π)=6.98 GHz. The total cavity linewidth
nm vacuum slit to the opposite end of the cavity for maximizing the coupling. The cavity is a half-wavelength floating microstrip similar to the one used in Massel et al.22, resonating at ωc/(2π)=6.98 GHz. The total cavity linewidth  MHz is a sum of the internal damping γI/(2π)=1.4 MHz, and the external damping γE/(2π)=4.8 MHz. At the highest powers discussed, however, we obtain a decreased γI/(2π)=0.9 MHz, typical of dielectric loss mechanism.
MHz is a sum of the internal damping γI/(2π)=1.4 MHz, and the external damping γE/(2π)=4.8 MHz. At the highest powers discussed, however, we obtain a decreased γI/(2π)=0.9 MHz, typical of dielectric loss mechanism.
There are a total of three beams as shown in Fig. 1c. Two of the beams have a large zero-point coupling of g1x01/2π=39 Hz and g2x02/2π=44 Hz. The frequencies of beams 1 and 2 are relatively close to each other,  kHz, such that it is straightforward to obtain an effective coupling G12 of the same order. The third beam has an order of magnitude smaller coupling, and hence we neglect it in the full calculation, setting N=2 in equation (1) in what follows.
kHz, such that it is straightforward to obtain an effective coupling G12 of the same order. The third beam has an order of magnitude smaller coupling, and hence we neglect it in the full calculation, setting N=2 in equation (1) in what follows.
The measurements are conducted in a cryogenic temperature below the superconducting transition temperature of the Al film ( K) to reduce losses. We used a dilution refrigerator set-up as in Massel et al.22 down to 25 mK, which allows for a low mechanical mode temperature in equilibrium. Apart from this, cryogenic temperatures or superconductivity are not necessary23.
K) to reduce losses. We used a dilution refrigerator set-up as in Massel et al.22 down to 25 mK, which allows for a low mechanical mode temperature in equilibrium. Apart from this, cryogenic temperatures or superconductivity are not necessary23.
Experimental data
The modes can be probed by adding to the experimental set-up another, the probe, tone11,13,22 with frequency ωin. The maximum pump power we can reach is 4 μW, inducing a coherent  photon occupancy in the cavity, and effective coupling G12=(2π) × 150 kHz (with G1=0.93 MHz, G2=1.0 MHz). In Fig. 2a, we display changes of the cavity absorption by increasing the pump power. The two peaks at the bottom of the cavity dip are due to beams 1 and 2. They broaden with increasing nP, finally leaving behind a narrow dip between them. The overall lineshape is clearly not a sum of two Lorentzian peaks.
photon occupancy in the cavity, and effective coupling G12=(2π) × 150 kHz (with G1=0.93 MHz, G2=1.0 MHz). In Fig. 2a, we display changes of the cavity absorption by increasing the pump power. The two peaks at the bottom of the cavity dip are due to beams 1 and 2. They broaden with increasing nP, finally leaving behind a narrow dip between them. The overall lineshape is clearly not a sum of two Lorentzian peaks.
(a) Measured reflection coefficient S11=Vout/Vin of the probe microwave while a strong pump is applied at the red sideband,  , at increasing pump amplitudes, from bottom to top. A low value of S11 means high resonance absorption. (b,c) Zoomed-in view of panel a. An excellent agreement with the theory is obtained with reflection calculation using a complete model based on equation (1), for two beams 1 and 2 (solid lines). The dashed lines show a fit with an independent-resonator model for beam 1. The narrow feature at 6.982 GHz is due to beam 3. The curves are displaced vertically by 3 dB for clarity. (d) Theory plot for higher nP; the dark mode is expected to become narrower and more and more phonon-like. Here, Δ=−(ω1+ω2)/2. The other parameter values are G/γc=0.28 and 0.63, nP=2 × 109 and 1010, for the lower and upper curve, respectively. (e) Calculated dark mode decomposed into a linear combination of a photon and two phonons. Blue denotes the cavity component Dc, while red (D1) and black (D2) are components of the mechanical resonators 1 and 2, respectively. The parameters are as in panel c. The arrow denotes the highest experimental value. For simplicity, we take
, at increasing pump amplitudes, from bottom to top. A low value of S11 means high resonance absorption. (b,c) Zoomed-in view of panel a. An excellent agreement with the theory is obtained with reflection calculation using a complete model based on equation (1), for two beams 1 and 2 (solid lines). The dashed lines show a fit with an independent-resonator model for beam 1. The narrow feature at 6.982 GHz is due to beam 3. The curves are displaced vertically by 3 dB for clarity. (d) Theory plot for higher nP; the dark mode is expected to become narrower and more and more phonon-like. Here, Δ=−(ω1+ω2)/2. The other parameter values are G/γc=0.28 and 0.63, nP=2 × 109 and 1010, for the lower and upper curve, respectively. (e) Calculated dark mode decomposed into a linear combination of a photon and two phonons. Blue denotes the cavity component Dc, while red (D1) and black (D2) are components of the mechanical resonators 1 and 2, respectively. The parameters are as in panel c. The arrow denotes the highest experimental value. For simplicity, we take  in panels d and e.
in panels d and e.
In Fig. 2c, we show a zoom-in view of the two peaks, together with theoretical predictions. One immediately sees that an attempt to simulate either peak by a single mechanical resonator coupled to cavity (N=1 in the analysis), thereby neglecting the cavity-mediated coupling, fails to explain the lineshape at large  . The full simulation with both beams 1 and 2 included, however, produces a remarkable agreement to the experiment. To create these curves, we further take into account a shift of the mechanical frequencies due to second-order interaction8, given as
. The full simulation with both beams 1 and 2 included, however, produces a remarkable agreement to the experiment. To create these curves, we further take into account a shift of the mechanical frequencies due to second-order interaction8, given as  , where
, where  is the second-order coupling coefficient. The third beam, visible in Fig. 2c as a narrow feature just below 6.982 GHz, was later fitted by running a single-resonator calculation. This is justified because its mixing is negligible owing to weak coupling.
is the second-order coupling coefficient. The third beam, visible in Fig. 2c as a narrow feature just below 6.982 GHz, was later fitted by running a single-resonator calculation. This is justified because its mixing is negligible owing to weak coupling.
The narrow dip between the peaks manifests the onset of the dark mode, where the cavity participation approaches zero with growing Gj, as occurs also in other tripartite systems24. As usual for weakly decaying states, the dark modes can be useful for storage of quantum information20,25. The other two dips (best discerned in the theoretical plots at higher Gj, see Fig. 2d) are the bright modes, and they retain a fully mixed character of all three degrees of freedom. In Fig. 2e, we display the prediction for the mode expansion coefficients with respect to coupling. Asymmetry in the role of the mechanical modes is sensitive to parameters. With the maximum coupling in the experiment ( ), the normal modes are well mixed: the dark mode can be expressed as
), the normal modes are well mixed: the dark mode can be expressed as  .
.
One can also vary the pump detuning, thereby effectively detuning the cavity and the mechanical resonators11,13. An anticrossing of the cavity and mechanical modes is seen in Fig. 3a up to detuning  , above which the system exhibits parametric oscillations. The pertinent simulation, Fig. 3b, portrays the main features of the measurement, except bending of the cavity frequency towards lower value in an upward sweep of Δ. We expect such possibly hysteretic behaviour of the cavity frequency to be due to second-order effects beyond the present linear model.
, above which the system exhibits parametric oscillations. The pertinent simulation, Fig. 3b, portrays the main features of the measurement, except bending of the cavity frequency towards lower value in an upward sweep of Δ. We expect such possibly hysteretic behaviour of the cavity frequency to be due to second-order effects beyond the present linear model.
Sideband cooling
We now turn the discussion into showing how the tripartite system resides nearly in a pure quantum state during the mode-mixing experiments. The mechanical resonators can be sideband cooled with the radiation pressure back-action8,26,27,28 under the effect of the pump, which also creates the mode mixing. Although the ground state of one mode was recently achieved this way9,10, cooling in multimode or nanowire systems is less advanced. The efficiency of cooling with two mechanical resonators is supposed to become hindered at those values of effective coupling where mode mixing starts to set in29. At modest pump powers, relevant for achieving the lowest phonon numbers in the present case, mixing remains insignificant.
The incoherent output spectrum can be due to either a finite phonon number nm, or non-equilibrium population number  of the cavity. The former manifests as a Lorentzian centred at the upper sideband, as in Fig. 4a, with the linewidth γeff=γm+4G2/γc, whereas the latter gives a small emission at broader bandwidth. The analytical approximation8 and experimental details are discussed in Methods.
of the cavity. The former manifests as a Lorentzian centred at the upper sideband, as in Fig. 4a, with the linewidth γeff=γm+4G2/γc, whereas the latter gives a small emission at broader bandwidth. The analytical approximation8 and experimental details are discussed in Methods.
(a) Cavity output spectra representing the thermal motion peaks of beams 1 (left) and 2 (right) measured at 345 mK (red) and 35 mK (black), with nP=4 × 105. (b) Calibration of the detection according to temperature dependence of the mechanical energy  , given by the area of the peak (data for beam 2). The straight line is a linear fit to the data above 120 mK. (c) Output spectra of beam 2 at pump occupation nP, increasing from top to bottom. The curves are shifted vertically by 0.3 y-axis units for clarity. The corresponding mechanical occupations are written on the right. (d) Progress of back-action cooling (beam 2) as a function of pump occupation. The mechanical mode temperature is given by circles, and the cavity temperature by squares. Red: high temperature, 245 mK; blue, base temperature (28 mK). The error bars are from the fits in panel c, given as one s.d. The ideal theoretical behaviour are plotted by the solid lines. Unless the data point for
, given by the area of the peak (data for beam 2). The straight line is a linear fit to the data above 120 mK. (c) Output spectra of beam 2 at pump occupation nP, increasing from top to bottom. The curves are shifted vertically by 0.3 y-axis units for clarity. The corresponding mechanical occupations are written on the right. (d) Progress of back-action cooling (beam 2) as a function of pump occupation. The mechanical mode temperature is given by circles, and the cavity temperature by squares. Red: high temperature, 245 mK; blue, base temperature (28 mK). The error bars are from the fits in panel c, given as one s.d. The ideal theoretical behaviour are plotted by the solid lines. Unless the data point for  , including its error bars, was of positive sign, only the absolute value of the error bar is plotted.
, including its error bars, was of positive sign, only the absolute value of the error bar is plotted.
At low input power, when the cavity back-action damping is small and  , phonon number is set by thermal equipartition
, phonon number is set by thermal equipartition  . This is best observed by the area of the mechanical peak in the output spectrum, as in Fig. 4a, which should be linear in cryostat temperature. The linearity holds down to about 150 mK temperatures (Fig. 4b), below which we observe intermittent heating, which is sensitive to parameters.
. This is best observed by the area of the mechanical peak in the output spectrum, as in Fig. 4a, which should be linear in cryostat temperature. The linearity holds down to about 150 mK temperatures (Fig. 4b), below which we observe intermittent heating, which is sensitive to parameters.
The cooling of beam 2 is observed in the mechanical peaks shown in Fig. 4c (see Methods), and the resulting phonon numbers are displayed in Fig. 4d. At a relatively high temperature of 245 mK, the data points follow theory well up to input powers corresponding to  . At the minimum cryostat temperature of 28 mK, the mode is not thermalized in a manner that depends irregularly on power. We obtain a minimum phonon number in beam 2 of
. At the minimum cryostat temperature of 28 mK, the mode is not thermalized in a manner that depends irregularly on power. We obtain a minimum phonon number in beam 2 of  , where the mechanical mode spends one-third of the time in the quantum ground state. The other mechanical mode, beam 1, cooled simultaneously down to 2.5 quanta, possibly compromised by the slightly smaller coupling. The cooling is quite clearly bottlenecked by heating, by the pump microwave, of the bath to which the mechanical mode is coupled. For the optimum data points, the starting temperature for cooling was raised to 150 mK, and above this it grows roughly quadratically with nP.
, where the mechanical mode spends one-third of the time in the quantum ground state. The other mechanical mode, beam 1, cooled simultaneously down to 2.5 quanta, possibly compromised by the slightly smaller coupling. The cooling is quite clearly bottlenecked by heating, by the pump microwave, of the bath to which the mechanical mode is coupled. For the optimum data points, the starting temperature for cooling was raised to 150 mK, and above this it grows roughly quadratically with nP.
Discussion
The coupling of micromechanical resonators mediated via microwave photons in an on-chip cavity is a basic demonstration of the control of a multimode mechanical system near the quantum limit. The set-up provides a flexible platform for creation and studies of non-classical motional states entangled over the chip30, or over macroscopic distances31,32. The set-up is easily extended to embody nearly arbitrarily many mechanical resonators, hence allowing for designing an electromechanical metamaterial with microwave-tunable properties. For future quantum technology applications even at elevated temperatures23, data may be transferred for storage33 from photonic modes into the dark states, which decay very slowly at the mechanical damping rate.
Methods
Device fabrication
The lithography to define the meandering cavity and jigs for the beams consisted of a single layer of electron-beam exposure, followed by evaporation of 150 nm of aluminium on a fused silica substrate. As the cavity is of planar structure, it has no potentially problematic cross-overs, which tend to have weak spots in superconducting properties and hence could heat up the cavity. We thus expect the cavity to portray a high critical current limited only by the intrinsic properties of the strip. With a 2 μm wide strip, we expect the critical current to be several milliamperes. With the maximum circulating currents in cavity (Fig. 2), about 0.5 mA of the peak value, there was no sign of non-linearity in the cavity response.
The mechanical resonators were defined by focussed ion beam cutting, as in Sulkko et al.21. We used low gallium ion currents of 1.5 pA, which gives the nominal beam width of about 7 nm. To maximize sputtering yield with minimal gallium contamination, we used a single-cutting pass mode. Otherwise, the cut beams tend to collapse to the gate. With the current recipe, fabrication of down to 10 nm gap widths over 5–10 μm distance can be done with about 50% yield.
Theory of cavity-coupled resonators
The Hamiltonian for N mechanical resonators each coupled to one cavity mode via the radiation–pressure interaction is

The pump with the Hamiltonian  induces a large cavity field with the number of pump photons
induces a large cavity field with the number of pump photons  .
.
Under the strong driving, the cavity–mechanics interaction can be linearized individually for each beam, resulting in equation (1). Further details of the calculations are given in the Supplementary Methods.
Sideband cooling
For one beam, the measured output spectrum divided by system gain, Sout(ω), carries information on the phonon number according to8

which is a Lorentzian centred at the cavity frequency. A non-zero base level is due to possible broadband emission from the cavity, due to a thermal state with occupation  . At modest pump (cooling) powers of utmost interest, coupling of the mechanical resonators remains insignificant, and thus we can apply equation (3) separately for each resonator. Some deviations can, however, occur at the highest powers with
. At modest pump (cooling) powers of utmost interest, coupling of the mechanical resonators remains insignificant, and thus we can apply equation (3) separately for each resonator. Some deviations can, however, occur at the highest powers with  .
.
To obtain the phonon number under strong back-action, we fit a Lorentzian to each peak as in Fig. 4c, obtaining independently the base level, amplitude and linewidth for every input power. These values are then compared with equation (3). This leaves, however, yet too many unknowns to obtain the occupations of the mechanics and cavity. This is basically because of uncertainties in the attenuations of both input and amplifier lines, which limit the accuracy of estimating nP. We can obtain a calibration using the linear temperature dependence, and by fitting the dependence of γeff on input power.
As opposed to, for instance, Rocheleau et al.8, the bottleneck for cooling is not heating of the cavity by strong pump, as seen in Fig. 4d, where the cavity temperature is increasing only little up to the optimum cooling powers corresponding to about 0.15 mA of peak current values in cavity. This can be due to the simplistic structure of the cavity.
The above analysis supposes the presence of nearly no non-equilibrium photons in the cavity at zero or low input powers. This situation can be investigated by observing a possible emission from about cavity linewidth under these conditions. A complication arises because the cavity linewidth is so large that a small change is easily overwhelmed by modest standing waves in cabling. We avoided this issue by using temperature dependence of the cavity frequency, due to the kinetic inductance in the long microstrip. Thereby, a broad emission peak moving according to the cavity frequency would be easily distinguishable. We observed no such signal down to the level of  , which justifies the above analysis.
, which justifies the above analysis.
Authors contributions
F.M. and T.H. developed the theory. J.-M.P., S.U.C. and M.A.S. contributed to design and fabrication of the samples, and cryogenic set-up. P.J.H. and M.A.S. conceived the work.
Additional information
How to cite this article: Massel, F. et al. Multimode circuit optomechanics near the quantum limit. Nat. Commun. 3:987 doi: 10.1038/ncomms1993 (2012).
References
Andre A. et al. A coherent all-electrical interface between polar molecules and mesoscopic superconducting resonators. Nat. Phys. 2: 636–642 (2006)
Rosenberg J., Lin Q., Painter O. Static and dynamic wavelength routing via the gradient optical force. Nat. Photonics 3: 478–483 (2009)
Zhu X. et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 478: 221–224 (2011)
Camerer S. et al. Realization of an optomechanical interface between ultracold atoms and a membrane. Phys. Rev. Lett. 107: 223001 (2011)
O’Connell A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464: 697–703 (2010)
Kippenberg T. J., Vahala K. J. Cavity optomechanics: back-action at the mesoscale. Science 321: 1172–1176 (2008)
Metzger C. H., Karrai K. Cavity cooling of a microlever. Nature 432: 1002–1005 (2004)
Rocheleau T. et al. Preparation and detection of a mechanical resonator near the ground state of motion. Nature 463: 72–75 (2010)
Teufel J. D. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475: 359–363 (2011)
Chan J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478: 89–92 (2011)
Gröblacher S., Hammerer K., Vanner M. R., Aspelmeyer M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 460: 724–727 (2009)
Verhagen E., Deleglise S., Weis S., Schliesser A., Kippenberg T. J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 482: 63–67 (2012)
Teufel J. D. et al. Circuit cavity electromechanics in the strong-coupling regime. Nature 471: 204–208 (2011)
LaHaye M. D., Suh J., Echternach P. M., Schwab K. C., Roukes M. L. Nanomechanical measurements of a superconducting qubit. Nature 459: 960–964 (2009)
Leggett A. J. Testing the limits of quantum mechanics: motivation, state of play, prospects. J. Phys. Condens. Matter 14: R415–R451 (2002)
Ansmann M. et al. Violation of Bell’s inequality in Josephson phase qubits. Nature 461: 504–506 (2009)
Metzger C. et al. Self-induced oscillations in an optomechanical system driven by bolometric backaction. Phys. Rev. Lett. 101: 133903 (2008)
Dobrindt J. M., Kippenberg T. J. Theoretical analysis of mechanical displacement measurement using a multiple cavity mode transducer. Phys. Rev. Lett. 104: 033901 (2010)
Heinrich G., Marquardt F. Coupled multimode optomechanics in the microwave regime. Europhys. Lett. 93: 18003 (2011)
Lin Q. et al. Coherent mixing of mechanical excitations in nano-optomechanical structures. Nat. Photonics 4: 236–242 (2010)
Sulkko J. et al. Strong gate coupling of high-Q nanomechanical resonators. Nano Lett. 10: 4884–4889 (2010)
Massel F. et al. Microwave amplification with nanomechanical resonators. Nature 480: 351–354 (2011)
Faust T., Krenn P., Manus S., Kotthaus J. P., Weig E. M. Microwave cavity-enhanced transduction for plug and play nanomechanics at room temperature. Nat. Commun. 3: 728 (2012)
Altomare F. et al. Tripartite interactions between two phase qubits and a resonant cavity. Nat. Phys. 6: 777–781 (2010)
Fleischhauer M., Imamoglu A., Marangos J. P. Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77: 633–673 (2005)
Regal C. A., Teufel J. D., Lehnert K. W. Measuring nanomechanical motion with a microwave cavity interferometer. Nat. Phys. 4: 555–560 (2008)
Schliesser A., Arcizet O., Riviere R., Anetsberger G., Kippenberg T. J. Resolved-sideband cooling and position measurement of a micromechanical oscillator close to the Heisenberg uncertainty limit. Nat. Phys. 5: 509–514 (2009)
Hertzberg J. B. et al. Back-action-evading measurements of nanomechanical motion. Nat. Phys. 6: 213–217 (2010)
Genes C., Vitali D., Tombesi P. Simultaneous cooling and entanglement of mechanical modes of a micromirror in an optical cavity. New J. Phys. 10: 095009 (2008)
Mancini S., Giovannetti V., Vitali D., Tombesi P. Entangling macroscopic oscillators exploiting radiation pressure. Phys. Rev. Lett. 88: 120401 (2002)
Vitali D. et al. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett 98: 030405 (2007)
The LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7: 962–965 (2011)
Safavi-Naeini A. H. et al. Electromagnetically induced transparency and slow light with optomechanics. Nature 472: 69–73 (2011)
Acknowledgements
We thank S. Paraoanu and Lorenz Lechner for useful discussions. This work was supported by the Academy of Finland, by the European Research Council (grants No. 240362-Heattronics and 240387-NEMSQED), and by the Vaisala Foundation.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S4 and Supplementary Methods (PDF 458 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Massel, F., Cho, S., Pirkkalainen, JM. et al. Multimode circuit optomechanics near the quantum limit. Nat Commun 3, 987 (2012). https://doi.org/10.1038/ncomms1993
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1993
This article is cited by
-
Steady-state quantum steering in a largely detuned optomechanical cavity
Quantum Information Processing (2023)
-
Phase-controlled asymmetric optomechanical entanglement against optical backscattering
Science China Physics, Mechanics & Astronomy (2023)
-
Topological phonon transport in an optomechanical system
Nature Communications (2022)
-
Ground-state cooling of mechanical resonators by quantum reservoir engineering
Communications Physics (2021)
-
Vectorial polaritons in the quantum motion of a levitated nanosphere
Nature Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


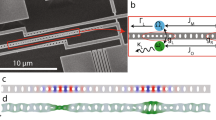



 ,
,  . The pump frequency was slowly swept from left to right. (b) Theory prediction.
. The pump frequency was slowly swept from left to right. (b) Theory prediction.