Introduction

Since the discovery of superconductivity in LaFeAsO1−xFx with Tc=26 K in early 2008 (ref. 1), various types of iron pnictides containing square lattices of Fe2+ have been investigated2,3,4. That maximum was raised to 55 K in Ln-1111-type LnFeAsO1−xFx (Ln denotes lanthanide)5. The compound of LaFeAsO1−xFx is paramagnetic metal with tetragonal symmetry at room temperature and undergoes a tetragonal–orthorhombic transition around 150 K accompanied by a para-antiferromagnetic (AFM) transition6,7. Superconductivity emerges when the transitions are suppressed by carrier doping via element substitution or pressure application. To explain the emergence of superconductivity near the AFM phase, a spin fluctuation model resulting from Fermi surface (FS) nesting between hole and electron pockets was proposed based on density functional theory (DFT) calculations8,9. This model explains the suppression of superconductivity in LaFeAsO1−xFx upon electron doping to the filling level of hole pockets (x=0.2) and the striking difference in the maximum Tc between LnFeAsO1−xFx (26–55 K) and LaFePO (4 K) or between La-1111(26 K) and Sm-1111(55 K)10.

However, the phase diagrams reported so far for LnFeAsO systems are rather incomplete. For instance, the suppression of Tc in over-doping region had not been confirmed for any Ln-1111-types (except La). This situation primarily comes from the low solubility limit of fluorine in LnFeAsO1−xFx (x<0.15–0.20). Recently, we reported the syntheses of (Ce, Sm)FeAsO1−xHx (0<x<0.5) by using the high solubility limit of hydrogen and obtained a complete superconducting dome ranging 0.05<x ≤0.4~0.5 with optimum Tc of 47 K for the Ce-system or 56 K for the Sm-system, agreeing well with that the previous data of each fluorine-doped sample in x<0.15 (refs 11,12). The position and occupancy of hydrogen substituting the oxygen sites were verified by neutron powder diffraction measurement and the charge state of hydrogen was examined by DFT calculations12. The neutron powder diffraction measurement on CeFeAsO1−xDx revealed that hydrogen species exclusively substitute the oxygen sites in the CeO layer, and DFT calculations indicated that the hydrogen 1s band is located at −3 to −6 eV, which is close to level of the oxygen 2p band and the charge state of the hydrogen is −1. These results substantiate the idea that hydrogen exclusively substituting the O2– sites occurs as H−, supplying electrons to the FeAs layer, the same as fluorine does (O2–=H−+e−).

When comparing the superconducting dome of LaFeAsO1−xFx with (Ce, Sm)FeAsO1−xHx, it is found that the dome width is twice as narrow as that of (Ce, Sm)FeAsO1−xHx and the optimum Tc of LaFeAsO1−xFx is much lower than that of (Ce, Sm)FeAsO1−xHx. Moreover, the temperature dependence of resistivity in the normal conducting state indicates that the (Ce, Sm)FeAsO1−xHx behave non-Fermi liquid, that is, ρ(T)~T, whereas LaFeAsO1−xFx obeys Fermi liquid, that is, ρ(T)~T2. These differences remind us the idea that the electron doping via fluorine substitution in LaFeAsO1−xFx is not enough to draw out the genuine physical property of LaFeAsO.

In this Article, we study the LaFeAsO system, the prototype material for the Ln-1111 system, and examine its superconducting properties by using H− in place of F− for electron doping. We report the existence over a wider x range of another Tc dome with higher Tc in addition to the dome reported so far by F− substitution. Not only are there differences in maximum Tc and shape between these two domes, but also the second dome with resistivity characterized by a linear temperature dependence corresponds to that observed in other Ln-1111 systems (except La) with higher Tc. Based on DFT calculations of the crystal structures of these doped samples determined at 20 K, we discuss the origin for the superconductivity.

Results

Two-dome structure

In Fig. 1a,b, we show the temperature dependence of electrical resistivity for LaFeAsO1−xHx. At x=0.01 and 0.04, a kink in resistivity due to structural or magnetic transitions was seen around 150 K (refs 6,7). As x is increased, the transitions are suppressed and the onset Tc appears for x ≥ 0.04, and zero resistivity is attained for x ≥ 0.08. The onset Tc, determined from the intersection of the two extrapolated lines in Fig. 1c,d attains a maximum of 29 K at x=0.08 and decreases to 18 K at x=0.21, forming the first Tc (x) dome. For 0.08≤ x ≤0.21, the temperature dependence of resistivity ρ(T) in the normal state obeys a T2-law, indicating that the system is a strongly correlated metal in Fermi liquid theory13. The Tc (x) and temperature dependence of ρ above Tc agree well with those in LaFeAsO1−xFx (ref. 1). Further electron doping (x > 0.21) continuously enhances Tc to 36 K around x=0.36 for which ρ(T) exhibits T-linear dependence. Figure 1e,f shows the temperature dependence of volume magnetic susceptibility χ for samples with different x. Because of the presence of metal iron impurities, each sample has a positive offset. The diamagnetism due to superconductivity is clear to see for x >0.04. Shielding volume fraction exceeds 40% at 2 K in 0.08≤ x ≤0.46, and then decreases to 20% at x=0.53, forming the second Tc dome in the composition range 0.21<x<0.53. This dome is newly found by the present study.

Figure 1: Electrical and magnetic properties of LaFeAsO1−xHx.
figure 1

(a,b) Electrical resistivity as a function of temperature in x=0.01–0.21 (a) and 0.24–0.53 (b). (c,d) Enlarged ρ–T curves near Tc of LaFeAsO1−xHx with x=0.08–0.21 (c) and 0.24–0.53 (d). The arrows mark the onset Tc. (e,f) Magnetic susceptibility data in x=0.01–0.21 (e) and 0.24–0.53 (f) measured with a zero-field-cooling history and a field of 10 Oe.

Full size image

Pressure effect

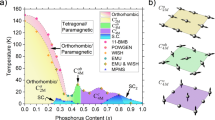
Figure 2a–d shows the changes in ρ(T) for samples with x=0.08, 0.21, 0.30 and 0.46 under applied pressures (P) up to 3 GPa. The onset Tc increases largely with P for x=0.08, 0.21 and 0.30, whereas the Tc for x=0.46 slightly decreases from 33 K to 32 K at P=2.7 GPa. The maximum Tc obtained at x=0.30 under P=2.6 GPa is 46 K, which is distinctly higher than the maximum Tc (43 K) in the LaFeAsO1−xFx under high pressure14. The Tc valley around x=0.21 under ambient pressure disappears, resulting in the one-dome structure as observed in other Ln-1111 series. Figure 2e summarizes the Ts and Tc under ambient pressure in the LaFeAsO1−xHx and LaFeAsO1−xFx (ref. 15) along with Tc at P=3 GPa of LaFeAsO1−xHx. Two superconducting domes are evident and each has maximum Tc around x=0.08 and 0.36. The first dome is located adjacent to the orthorhombic and AFM phase and is almost the same as previously reported for LaFeAsO1−xFx, whereas the second dome appears adjacent to the first dome. At P=3 GPa, the two domes merge into a wider dome having a closed shape and a range similar to those in CeFeAsO1−xHx with maximum Tc=47 K (ref. 12). This unification of the two domes on applying high pressure may be understood as lattice compression; the reduction of the a-axis (~1% under 3 GPa) in LaFeAsO1−xFx is assumed to bring it close to a LaFeAsO1−xHx lattice16. Then, a 1%-reduction of a-axis for LaFeAsO1−xHx draws its lattice close to that of CeFeAsO1−xHx under an ambient pressure12.

Figure 2: Temperature dependence of the electrical resistivity of LaFeAsO1−xHx below 3 GPa and phase diagrams of LaFeAsO1−x(H, F)x.
figure 2

(a–d) Temperature dependence of resistivity as a function of static pressure at x=0.08 (a), 0.21 (b), 0.30 (c) and 0.46 (d). The insets show pressure dependence of Tc. (e) Electronic phase diagram for LaFeAsO1−xHx (filled symbols) and LaFeAsO1−xFx (ref. 15; open symbols). The Tc under ambient (squares) and 3 GPa (inverted triangles) was determined from the intersection of the two extrapolated lines around superconducting transition and Ts (circles) was taken as the anomaly kink in the ρ–T curve7.

Full size image

Lanthanide cation substitution effect

Here we consider the relation between the two domes of the La-system and the domes of the other Ln-1111 systems. To compare the temperature dependence of resistivity of LaFeAsO1−xHx with that of other Ln-1111 systems, we performed power-law fitting, ρ=ρ0+ATn (ρ0: residual resistivity) in the temperature range above Tc to 150 K (Supplementary Fig. S1). Figure 3a shows the relation between the exponents n and x for LnFeAsO1−xHx (Ln=La, Ce, Sm and Gd; The sample preparation and temperature dependence of electrical resistivity and volume magnetic susceptibility for newly found GdFeAsO1−xHx are summarized in Supplementary Fig. S2 and in the Supplementary Methods.). Fermi liquid-like behaviour, n=2, is observed only in low-x LaFeAsO1−xHx, whereas non-Fermi liquid behaviuor, n<2, is observed for high-x LaFeAsO1−xHx and for the entire range of x in the other systems. Figure 3b shows the plot of Tc versus exponent n for the same systems. As n approaches unit for each system, Tc becomes a maximum, indicating that this feature of the second dome in LaFeAsO1−xHx is commonly seen for domes in other Ln-1111; that is, the first dome is unique to La-1111, whereas the second is universally to all four systems. Figure 3c–f shows the x-variation in Tc for all four systems. The optimal x in the Tc dome continuously shifts to lower x when comparing Ln=La through to Gd.

Figure 3: Effect of lanthanide cation.
figure 3

(a) Relation between the exponent n and x in LnFeAsO1−xHx (Ln=La (pink circles), Ce (yellow triangles), Sm (green inverted triangles) and Gd (blue pentagons)). The exponent n was obtained by fitting the power-law form ρ=ρ0+ATn. The fitting was performed for a linear region in log [ρ(T)–ρ0] versus log T plot. If the shielding volume fraction is <20%, we set the Tc as 0 K to represent an over-doped region. The dashed line denotes Fermi liquid state (n=2). (b) Tc versus power-law exponent n of LnFeAsO1−xHx (Ln=La (pink circles), Ce (yellow triangles), Sm (green inverted triangles) and Gd (blue pentagons)). (c–f) Variation in the Tc-dome in LnFeAsO1−xHx with Ln=La (f), Ce (e), Sm (d) and Gd (c). The arrows mark the optimal Tc.

Full size image

Discussion

We have found an unusual two-dome structure in Tc for the LaFeAsO1−xHx system, the higher Tc dome being associated with a universal structure of LnFeAsO1−xHx systems generally. To understand these dome structures, we calculated the electronic state of these materials using the crystal structures determined at 20 K. The electron doping via substitution of O2– sites with H− ion was modelled in virtual crystal approximation assuming hydrogen acts as a quasi-fluorine ion supplying an electron to the FeAs layer12, that is, the oxygen (Z=8) sites were substituted for virtual atoms which have a fractional nuclear charge (Z=8+x), where x is hydrogen fraction. Figure 4a–d shows the two-dimensional cross-sections of FS for the various doping levels. These compositions, x=0.08, 0.21, 0.36 and 0.40, correspond to the top of first dome, Tc valley, the top of the second dome and over-doping region, respectively. At x=0.08, the size of an outer dxy (x, y and z coordination is given by the Fe square lattice) or inner dyz,zx hole pockets at the Γ point is close to that of two electron pockets at the M point, indicating that nesting in the (π π) direction between the hole and the electron pockets is strong. As x increases, the nesting monotonically weakens because the hole pockets are gradually reduced but the electron pockets are expanded. It is pointed out that as the pnictogen height, hPn, from the Fe plane increases, the dxy hole pocket is enlarged; nesting then becomes better10. In the present case, although hAs increases with x as shown in Fig. 4e, the size of the dxy hole pocket remains almost unchanged irrespective of x. This result may be understood by considering that expansion of dxy hole pocket by structural modification is cancelled by reduction due to the up-shift of Fermi level (EF) by electron doping.

Figure 4: Electronic structure of LaFeAsO1−xHx.
figure 4

(a–d) Two-dimensional Fermi surface of LaFeAsO1−xHx with x=0.08 (a), 0.21 (b), 0.36 (c) and 0.40 (d). The blue arrow represents the nesting vector in the (π π) direction. The contribution of Fe-dxy and dyz,zx orbitals are coloured green and pink, respectively21. (e) Hydrogen doping dependence of As–Fe–As angle in FeAs4 tetrahedron (orange circles) and arsenic height hAs from the Fe plane (dark sky-blue diamonds). The angles and hAs are determined from Synchrotron X-ray diffraction measurements at 20 K. The solid lines are as a visual guide. The dashed line denotes the regular tetrahedron angle. (f–i) Band structures of LaFeAsO1−xHx with x=0.08 (f), 0.21 (g), 0.36 (h) and 0.40 (i). Insets show close-up views of the low energy region. The contribution of Fe-dxy and dyz,zx orbitals are coloured green and pink, respectively. (j) Variation in energy level of relevant Fe 3d bands at Γ point with x. The inset is the band structure of LaFeAsO0.92H0.08. The Γdxy (filled green inverted triangles) and Γanti-dxy (open green triangles) signify the bonding and anti-bonding states, respectively, for a bond primary composed of two Fe dxy orbitals in a unit cell. Also shown is the energy level of degenerate dyx,zx band (Γdyz,zx indicated by filled pink squares). The solid and dashed lines are as a visual guide. (k–n) Total DOS (solid black line) and partial DOS of dxy (solid green line) and dyz,zx (solid pink line) orbitals of LaFeAsO1−xHx with x=0.08 (k), 0.21 (l), 0.36 (m) and 0.40 (n). The sum of the partial DOS of dxy and dyz,zx orbitals is also shown (dotted blue line).

Full size image

Nesting between hole and electron pockets is the most important glue in the spin fluctuation model8,9. The decrease in Tc from x=0.08 through 0.21 may be understood as a reduction in spin fluctuations due to weakening of the nesting in a similar manner to LaFeAsO1−xFx. It is, however, difficult to understand by the FS nesting that the experimental findings that Tc (x) increases over a wider dome range of 0.21<x<0.53 and optimizes at 36 K around x=0.36.

Figure 4f–i shows band structures near EF for sample composition x=0.08, 0.21, 0.36 and 0.40. As the unit cell contains two irons, there are ten bands around the EF derived from bonding and anti-bonding of 3d orbitals of the two neighbouring irons that cross the EF around the Γ and M points. The unoccupied bands move continuously lower with x. In particular, the bands derived from the anti-bonding orbital between the dxy orbitals, which we shall call the 'anti-dxy bands' hereafter, and the band derived from the degenerate dyz,zx bonding orbitals are lowered in energy and cross the bonding-dxy band around x=0.36, forming degenerate states of Fe 3dxy,yz,zx three bands near EF as seen in Fig. 4j. After this triply-degenerate state is formed, the anti-dxy band and bonding dyz,zx band create a new band below EF at x=0.40 by reconstruction (see inset of Fig. 4i). Note in Fig. 4e that the As–Fe–As angle of FeAs4 tetrahedron is far from that of regular tetrahedron (109.5°) in the optimally doped region (x=0.33−0.46). The band structures of LaFeAsO1−xHx (x=0.08, 0.21, 0.36 and 0.40) with only structural change are shown in Supplementary Fig. S3. Although the magnitude of the energy difference between these three bands becomes small with x, the band crossing is not caused only by the structural change, indicating that not only the change in local structure around iron but also asymmetric occupation of doped electrons in the bonding-dyz,zx, dxy and anti-bonding-dxy, affect the band shift. As the bonding dyz,zx and dxy bands are almost flat along the Γ-Z direction, their band crossing at x=0.36 form a shoulder in the total density of states (DOS) at EF (Fig. 4m), indicating an electronic instability of the system arising from degeneration of the dxy and dyz,zx bands. In such a situation, structural transitions, for instance band Jahn-Teller distortion, may occur to reduce the energy of the system. However, in the present results, any structural transition could not be observed at least down to 20 K in samples with 0.08≤ x ≤0.40.

Table 1 summarizes the characteristics of each Tc dome described above. The primary question is what the origin is for the second dome, that is, the dome in the Ln-1111 with higher Tc. The resistivity above Tc changes from quadratic to linear dependence as x approaches the top of the second dome region. As the nesting between hole and electron pockets monotonically is weakened with x, it is rationally considered that the contribution of FS nesting to the second Tc dome is not dominant. In addition, the calculated DOS shows the presence of a shoulder of the DOS (EF) at x=0.36 related by the degeneracy of three bands derived from Fe-dyz,zx and dxy orbitals. Given these results, the band degeneracy appears to have an important role in emergence of the second dome. For the iron-based superconductors, there is another pairing model derived from a large softening of a shear modulus observed near the tetragonal–orthorhombic transition of parent compounds17,18,19. This model tells that the Fe-d orbitals are possible to order when their degeneracy in Fe-dyz,zx orbitals is removed at the structural transition and the fluctuations of this orbital ordering are shown capable of inducing superconductivity18,19. If we follow the orbital fluctuation model, the second dome and T-linear resistivity in the present system might be understood as results of electron pairing and carrier scattering by the fluctuations of the degenerated Fe-dxy,yz,zx orbitals, respectively.

Table 1 Characteristics of two Tc domes in LaFeAsO1−xHx.
Full size table

Finally, we consider why the two-dome structure is only found in LaFeAsO1−xHx and not (Ce-Gd)FeAsO1−xHx. The degeneracy of three bands derived from Fe-3dyz,zx and dxy orbitals is realized when energy splitting between the 3dyz,zx and dxy bands mainly derived from distortion of FeAs4 tetrahedron is cancelled out by asymmetric occupation of doped electrons in the these three bands. The magnitude of the energy difference between these three bands becomes small on going from La ion to Ce–Gd ions in LnFeAsO because the As–Fe–As angle of FeAs4 tetrahedron continuously approach to the angle (109.5°) of a regular tetrahedron as the lanthanide ion is changed from La (114°) to Gd (110°)20. In particular, this deviation in the La-system is rather large compared with the other system. Therefore, the threefold degeneracy in (Ce-Gd)FeAsO1−xHx on electron doping is expected to occur in lower x than that (x=0.35) in LaFeAsO1−xHx. As a consequence, we think that the second dome primarily originating from the band degeneracy is separated from the first dome from FS nesting. The present discussion on orbital fluctuation model is based on DFT calculations. Further effort is required to confirm the validity of this idea on decisive experimental evidences such as angular-resolved photoemission and elastic shear modulus measurements using the single crystals.

Methods

Synthesis, structural and chemical analyses of LaFeAsO1−xHx

As reported previously, LaFeAsO1−xHx was synthesized by solid-state reactions using starting materials La2O3, LaAs, LaH2, FeAs and Fe2As under high pressure11. The phase purity and structural parameters at room temperature were determined by powder X-ray diffraction measurements with MoKα1 radiation. The structure parameters at low temperatures were determined by synchrotron X-ray diffraction measurements at 20 K using the BL02B2 beam-line in the SPring-8, Japan. Hydrogen content in the synthesized samples was evaluated by thermogravimetric mass spectroscopy, and the chemical composition with the exception of hydrogen was determined with a wavelength-dispersive-type electron-probe microanalyzer.

Electric and magnetic measurement

Resistivity and magnetic susceptibility at ambient pressure were measured using a physical property measurement system with a vibrating sample magnetometer attachment. Electrical resistivity measurements under high pressure were performed by the dc four-probe method. Pressures were applied at room temperature and maintained using a piston-cylinder device. A liquid pressure-transmitting medium (Daphne oil 7373) was used to maintain hydrostatic conditions.

Density functional theory calculations

The electronic structure for LaFeAsO1−xHx was derived from non-spin-polarized DFT calculations using the WIEN2K code22 using the generalized gradient approximation Perdew–Burke–Ernzerhof functional23 and the full-potential linearized augmented plane wave plus localized orbitals method. To ensure convergence, the linearized augmented plane wave basis set was defined by the cutoff RMTKMAX=9.0 (RMT: the smallest atomic sphere radius in the unit cell), with a mesh sampling of 15×15×9 k points in the Brillouin zone.

Additional information

How to cite this article: Iimura, S et al. Two-dome structure in electron-doped iron arsenide superconductors. Nat. Commun. 3:943 doi: 10.1038/ncomms1913 (2012).