Abstract
Graphene has extraordinary electronic and optical properties and holds great promise for applications in photonics and optoelectronics. Demonstrations including high-speed photodetectors, optical modulators, plasmonic devices, and ultrafast lasers have now been reported. More advanced device concepts would involve photonic elements such as cavities to control light–matter interaction in graphene. Here we report the first monolithic integration of a graphene transistor and a planar, optical microcavity. We find that the microcavity-induced optical confinement controls the efficiency and spectral selection of photocurrent generation in the integrated graphene device. A twenty-fold enhancement of photocurrent is demonstrated. The optical cavity also determines the spectral properties of the electrically excited thermal radiation of graphene. Most interestingly, we find that the cavity confinement modifies the electrical transport characteristics of the integrated graphene transistor. Our experimental approach opens up a route towards cavity-quantum electrodynamics on the nanometre scale with graphene as a current-carrying intra-cavity medium of atomic thickness.
Similar content being viewed by others
Introduction
Graphene, an atomic monolayer formed by carbon hexagons, is a material with extraordinary electrical and optical properties1,2,3. Consequently, there is a growing interest in graphene optoelectronics4 and first demonstrations of graphene-based photodetectors5, optical modulators6, plasmonic devices7,8 and ultra-fast lasers9 have been reported. Because of its two-dimensional geometry, graphene is ideally suited for enclosure within a planar λ/2 microcavity, a photonic structure that confines optical fields between two highly reflecting mirrors with a spacing of only one half wavelength of light. The optical confinement could provide a powerful means of controlling the otherwise featureless optical absorption10 as well as the spectrally broad thermal emission11,12 of graphene. The concept of optical confinement of graphene enables a new class of functional devices as, for example, spectrally selective and highly directional light emitters, detectors and modulators. Moreover, it opens up the opportunity for investigating fundamental, cavity-induced modifications of light–matter interaction in graphene.
According to Fermi's golden rule13, the spontaneous photon emission (absorption) rate is determined by the local photonic mode density that can be significantly altered inside an optical microcavity14. The cavity-induced confinement enables the enhancement15 or the inhibition16 of the light emission (absorption) rate of the intra-cavity medium. The in-plane transition dipole moment of the intra-cavity medium couples to the longitudinal cavity mode of the cavity with wavelength-dependent efficiency, and the coupling strength is maximized at the antinode of the optical field located at the cavity centre17,18. Figure 1 visualizes the principle of confining graphene by a planar optical cavity.
Visualization of a graphene layer located at the centre of a planar optical λ/2 microcavity. Optical fields with wavelength λ are confined in the direction perpendicular to the cavity mirrors with spacing L. The optical coupling is maximized if the graphene layer is oriented parallel to the cavity mirrors.
The cavity-induced rate enhancement, or Purcell-effect, has already been demonstrated with quasi 2D quantum wells, as well as quasi 1D and 0D systems such as atoms, molecules, quantum dots and other nanoparticles14. However, embedding a truly 2D material such as graphene into a planar cavity has not been reported so far. Yet such an approach is highly desirable for two main reasons. First, the coupling area, that is, the spatial overlap between graphene and the cavity, can be extended to the micrometre scale within the two dimensions of the cavity plane, whereas preserving the optical confinement of graphene with respect to the cavity normal on the length scale of λ/2 (see Fig. 1). This is important because optical transitions in graphene are associated with in-plane transition dipole moments (π–π* transitions), thus rendering the 1D planar cavity confinement highly efficient. Second, the Fermi energy and density-of-states of graphene can be tuned easily by directly connecting it to electrodes, thus enabling charge carrier control, electrical transport and heating within the active area of the cavity. Graphene hence opens a unique experimental approach towards cavity-quantum electrodynamics on the nanometre scale with a current-carrying intra-cavity medium of atomic thickness.
In this paper, we report the monolithic integration of a graphene transistor with a planar optical microcavity. We find that both photocurrent generation as well as electrically excited thermal light emission of graphene can be controlled by the spectral properties of the microcavity. The device constitutes a first implementation of a cavity-enhanced graphene light detector, as well as a demonstration of a fully integrated, narrow-band thermal light source. Most importantly, the optical confinement of graphene by the microcavity profoundly modifies the electrical transport characteristics of the integrated graphene transistor.
Results
Device design
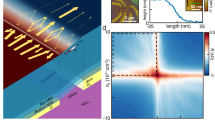
Figure 2a outlines our novel integration principle: an electrically contacted single layer of graphene is embedded between two optically transparent, dielectric thin films made of Si3N4 and Al2O3, respectively. The dielectric layers are enclosed by two metallic (Ag, Au) mirrors with a spacing L that determines the resonance wavelength λcavity of the microcavity (see Methods and ref. 18). A novel multi-step manufacturing process (see Methods) allows us to define device area and cavity mirror spacing with nanometre precision and to build a series of devices that satisfy the specific requirements of different optoelectronic experiments. For photocurrent studies, we designed the cavity resonance to match the tuning range of the laser system at hand (~580 nm). For thermal emission studies, we designed the cavity resonance to be spectrally located within the detection range of the spectroscopic unit (~925 nm). In principle, all the measurements can be performed on the same device, whereas the efficiencies of light absorption and emission are largely determined by the optical properties of the cavity.
(a) Schematic representation and electrical interconnection of the device. Inset: cross-sectional view of the device. The graphene sheet is embedded between two Ag mirrors and separated by two dielectric layers (Si3N4; Al2O3). The thickness L of the dielectric stack between the cavity mirrors determines the resonance wavelength λ of the optical microcavity. Also shown is a visualization of the intensity profile of the fundamental λ/2 cavity mode. (b) Top-view scanning electron microscope false colour image of the device; graphene sheets (yellow), Pd contacts (blue) Ag mirror (red). Scale bar, 2 μm. (c) Optical white light transmission micrograph of the device. The fundamental cavity mode is spectrally located at λcavity=585 nm, which appears green to the eye. Scale bar, 4 μm. (d) Optical transmission spectrum of the device (black line) measured with white light illumination reveals the cavity resonance at λcavity=585 nm having a cavity-Q of 20. The measured laser-induced photocurrent amplitude (red dots) samples the spectral profile of the optical cavity resonance. (e) Electrical transfer (left) and output (right) characteristics of the device; the fit (red solid line) to the transfer data (open symbols) is explained in the main text.
Microcavity-controlled light detection
Figure 2b–e reports the device characterization by electrical, optical and optoelectronic measurements: to characterize the electronic device properties, we measure both electrical transfer and output characteristics of the integrated graphene transistor (Fig. 2e). We apply a bias voltage along the graphene sheet and use one of the metallic cavity mirrors as a gate electrode (Fig. 2a). We fit the measured electrical transfer characteristics based on the model reported in ref. 19 and extract the device parameters that demonstrate the quality of the graphene sheet and the Pd-graphene contacts: we find a carrier mobility μ=2350 cm2 V−1 s−1, a residual carrier density n0=4.9×1011 cm−2, an electrical-resistance ratio Rmax/Rmin=5, and a specific contact resistance Rc=0.265 kΩ μm.
To characterize the optical properties of the device, we illuminate the cavity with white light from the top (see Fig. 2a) and spectrally analyse the transmitted light. This way, we determine the resonance wavelength λcavity and the cavity quality factor Q=λcavity /Δλcavity, where Δλcavity is the spectral full-width-at-half-maximum (FWHM) of the peak at λcavity in the measured transmission spectrum. In the present case (Fig. 2d), we obtain λcavity =585 nm and cavity-Q=20.
We employ photocurrent generation in graphene20 to probe electronically the optical absorption of the graphene layer inside the device. We focus a laser beam on one of the microcavity mirrors, tune the laser wavelength across the optical resonance, and measure the photocurrent generated inside the biased graphene layer by means of a lock-in technique. The functional dependence of the photocurrent amplitude on laser wavelength (Fig. 2d, red circles) matches the spectral profile of the cavity resonance as measured by white light transmission micro-spectroscopy (Fig. 2d, solid line). By tuning the laser wavelength to λlaser =583 nm, on resonance with the microcavity, we obtain a photocurrent amplitude of 23.3 nA, while we measure only 1.2 nA for laser illumination at λlaser =633 nm. The photocurrent modulation by a factor of 20 demonstrates that the device acts as a light detector with spectral selectivity. In contrast, the photocurrent amplitude of a non-confined graphene transistor varies by less than a factor of two if we tune the laser excitation wavelength across the same spectral interval.
Microcavity-controlled thermal light emission
We now investigate the light-emission properties of non-confined graphene and compare it to the microcavity-controlled graphene transistor. By applying a bias voltage across the non-confined graphene device using source and drain electrodes (Fig. 3a), the electrical current heats up the graphene layer and thermal light emission sets in, as reported previously11,12. As shown in Fig. 3b, the electrically excited, thermal emission spectrum of graphene in free, non-confined space exhibits a featureless exponential tail that shifts from the near-infrared towards the visible spectral range as a function of injected electrical power. The temperature values are extracted by fitting the measured emission spectra based on a model of a two-dimensional black body (see Methods and ref. 21).
(a) The schematic visualizes how thermal light emission is generated by applying a drain bias and how thermal radiation couples to the optical cavity mode. (b) Thermal near-infrared emission spectra measured for a cavity-confined (open circles) and a non-confined (filled squares) graphene transistor. The emission spectra of the cavity-controlled graphene transistor displays the optical resonance of the cavity at λcavity=925 nm. The left y-axis is the intensity of the non-confined emission (log scale), whereas the right y-axis is the intensity of the confined emission (linear scale). The indicated temperatures are derived by fitting the non-confined thermal radiation spectra to Planck's law (see Methods). (c) Simulated spectra of cavity-controlled thermal radiation (solid lines) and non-confined thermal radiation (dashed lines) modelled by assuming that the cavity resonance is spectrally located at λcavity =925 nm and has a spectral full width at half maximum of 30 nm. (d) Spectrally integrated light intensity as function of electrical power for three devices with different channel sizes (red 1×1 μm2, blue 2×2 μm2, purple 4×4 μm2). The solid lines are T3 fits assuming that the dissipated electrical power is proportional to the temperature T in the graphene sheet.
In contrast, the thermal emission spectrum of a microcavity-controlled graphene transistor displays a single, narrow peak at λcavity=925 nm having a FWHM of 50 nm (Fig. 3b), providing a 140-fold spectral narrowing as compared with the simulated free-space thermal spectrum at T=650 K. It is important to note that this is not merely a spectral filtering effect, but that thermal radiation cannot be emitted by the graphene layer at all if the thermal radiation wavelength λthermal is larger than λcavity because of the optical confinement, or, in other words, the cavity-induced inhibition of spontaneous emission. This constitutes the first demonstration of a current-driven, microcavity-controlled thermal light source. The spectral peak position of the emission peak does not shift as a function of injected electrical power. The simulated emission spectra in Fig. 3c reproduce the overall shape of their experimental counterparts very well (for details, see Methods). Further data analysis reveals that microcavity-controlled thermal radiation is emitted into a narrow lobe with a total angular width of 24° (FWHM) only (see Supplementary Methods and Supplementary Fig. S1). The integral over the microcavity-controlled light intensity is plotted as function of the injected electrical power in Fig. 3d for three different devices. The power dependences reveal that the integrated light intensity is proportional to T3 as expected from the Stefan-Boltzmann law in two dimensions21. Here we assume that the electrical power density p  T, which is validated by measurements in non-confined space (see Supplementary Fig. S2).
T, which is validated by measurements in non-confined space (see Supplementary Fig. S2).
We now establish the physical concept of cavity-controlled thermal light generation in graphene. The graphene layer initially heats up due to carrier scattering. The emission of long-wavelength thermal radiation at λthermal>λcavity is however inhibited by the cavity. As the temperature in the graphene sheet increases as a function of the electrical power density p, the thermal distribution inside the graphene layer spectrally shifts towards λcavity (Fig. 3b) and, at a threshold temperature Tcavity, eventually enables the emission of a significant fraction of photons at λthermal λcavity. We note that the temperature Tcavity and the corresponding threshold power density pcavity depend on device parameters, that is, the carrier mobility μ, the channel area and λcavity. For the device in Fig. 3b, we find Tcavity≈650 K and pcavity=90 kW cm−2. Based on Wien's law in two dimensions,21 we estimate that the graphene layer would have to be heated up to Tcavity,optimum≈hc/3.92kBλcavity≈4,000 K to maximize the light output at λcavity=925 nm. In this case, the intensity maximum of the thermal-radiation distribution would overlap with the cavity resonance at λcavity, resulting in a peak population of the cavity mode by thermal photons. Note that we designed microcavity devices specifically for performing the thermal emission spectroscopy in the near-infrared to take advantage of the favourable experimental conditions, that is, the high sensitivity and detection yield of the CCD array at hand. The optimum light-emitting performance, however, is expected to be in the mid-infrared spectral range. Assuming device operation at, for example, Tcavity =650 K, we estimate a maximum thermal light output at λthermal≈5.6 μm. Future work should hence extend the spectral range towards the terahertz regime.
λcavity. We note that the temperature Tcavity and the corresponding threshold power density pcavity depend on device parameters, that is, the carrier mobility μ, the channel area and λcavity. For the device in Fig. 3b, we find Tcavity≈650 K and pcavity=90 kW cm−2. Based on Wien's law in two dimensions,21 we estimate that the graphene layer would have to be heated up to Tcavity,optimum≈hc/3.92kBλcavity≈4,000 K to maximize the light output at λcavity=925 nm. In this case, the intensity maximum of the thermal-radiation distribution would overlap with the cavity resonance at λcavity, resulting in a peak population of the cavity mode by thermal photons. Note that we designed microcavity devices specifically for performing the thermal emission spectroscopy in the near-infrared to take advantage of the favourable experimental conditions, that is, the high sensitivity and detection yield of the CCD array at hand. The optimum light-emitting performance, however, is expected to be in the mid-infrared spectral range. Assuming device operation at, for example, Tcavity =650 K, we estimate a maximum thermal light output at λthermal≈5.6 μm. Future work should hence extend the spectral range towards the terahertz regime.
Transport in microcavity-controlled graphene transistors
Finally, we discuss modifications of electrical transport in optically confined graphene by correlating the electrical current and the spectrally integrated thermal radiation.
In Fig. 4a–c, we show the electrical output characteristics of a graphene transistor in non-confined space. The electrical current in the graphene layer saturates in the high bias regime, whereas thermal light emission sets in as it shifts into the detection range. Performing the same experiment for a cavity-controlled graphene transistor with identical dimensions, we find that the electrical output characteristic is qualitatively different (see Fig. 4d–f) and we can identify three different regimes by comparing electrical transport and light emission properties. In the sub-threshold regime (I), the electrical current saturates and the graphene layer heats up while the cavity-induced inhibition of spontaneous emission for λthermal>λcavity prevents off-resonant thermal radiation. In the threshold regime (II), the temperature of the graphene sheet has reached the critical value Tcavity enabling light emission at λthermal λcavity. In the above-threshold regime (III), the initial electrical current saturation is lifted and the electrical resistance drops as function of electrical power density.
λcavity. In the above-threshold regime (III), the initial electrical current saturation is lifted and the electrical resistance drops as function of electrical power density.
(a) Schematic illustration of the sample layout. (b) Normalized and integrated emitted light intensity (blue) and electrical current (red) as a function of bias voltage measured with a non-confined graphene transistor and (c) the integrated light intensity (blue) and the electrical resistance (red) plotted as a function of electrical power density. (d) Schematic illustration of the sample layout. (e) Normalized integrated emitted light intensity (blue) and electrical current (red) as a function of bias voltage measured with a microcavity-controlled graphene transistor and (f), the integrated light intensity (blue) and the electrical resistance (red) plotted as a function of electrical power density. Three regimes can be identified: (I) sub-threshold, (II) threshold and (III) above threshold, respectively.
Discussion
We have observed electrical transport modifications similar to those shown in Fig. 4 in all functional graphene-cavity devices (a total of five), that is, those that allowed for thermal light generation (see Supplementary Fig. S3). In all cases, the saturation currents in regime I were lower than those obtained in the non-confined reference devices (same contacts and dielectric layers, no metal mirrors). One can rationalize this observation by assuming that the onset of current saturation in graphene depends on temperature and that the degree of self heating is determined by the thermal coupling of graphene to its local environment, captured by the thermal conductance r as suggested in ref. 22. The saturation current j in the graphene layer would then be proportional to r. This implies that cavity-induced variations of r with respect to the non-confined reference value r0 will lead to variations of the saturation current j and, accordingly, to the temperature in the graphene layer. In this scenario, the cavity-induced inhibition of the radiative thermal relaxation leads to enhanced self heating of the graphene layer and an onset of current saturation at lower electrical power levels as compared with the non-confined case. Based on the experimental transport data and the self-heating model presented in ref. 22, we estimate temperature changes as high as ΔT=100 K when compared with the same graphene transistor in non-confined space (see Supplementary Methods and Supplementary Fig. S4). In this context, we point out that the amount of heat that is radiatively dissipated from the graphene sheet is very small, orders of magnitude smaller than the amount of energy that is dissipated non-radiatively11 (see Supplementary Fig. S5). It is clear then that a proper model of electrical transport and its temperature dependence in a microcavity-controlled graphene transistor should account for the current-induced self-heating of graphene that is affected by both the non-radiative heat transfer through dielectric interfaces and metal contacts, and the microcavity-controlled, radiative heat transfer.
In summary, we have demonstrated that a microcavity-controlled graphene transistor can act as a spectrally selective light detector and emitter with greatly enhanced sensitivity. Moreover, we have found that the cavity-induced optical confinement modifies graphene's electrical transport characteristics, an effect that may have important implications for nanoelectronics as well as cavity quantum electrodynamics.
Note added in proof: A photodetection study of graphene inside a planar optical microcavity was reported while this work was under consideration (Furchi, M. et al. Microcavity-integrated graphene photodetector. Nano Lett. doi: 10.1021/nl204512x (2012)).
Methods
Device fabrication
Graphene sheets are produced via micromechanical cleavage of graphite on Si substrates covered with 300 nm of SiO2 layer23. Single-layer graphene is identified by a combination of optical microscopy and Raman spectroscopy24,25. Three layers of 950 K poly(methyl methacrylate) (PMMA) are then spin coated on the substrates where flakes are deposited. The samples are subsequently immersed in de-ionized (DI) water at 90 °C for 2 h, resulting in the detachment of the polymer film, due to the intercalation of water at the polymer–SiO2 interface. Graphene flakes stick to the PMMA film, and can thus be removed from the original substrate. The target substrate is a suspended Si3N4 layer [n(Si3N4)≈2] with a thickness of 50 nm and an area of 50×50 μm2, supported by a Si frame having a thickness of 200 μm. We defined metallic markers by e-beam lithography and e-beam evaporation of 5 nm Ti and 50 nm Au on the target substrate. These markers are used for orientation during the transfer process and re-alignment for all following e-beam lithography steps. The PMMA+graphene film is transferred onto the suspended Si3N4 layer. Because a thin layer of water is trapped at the substrate–polymer interface, the latter can be moved across the target substrate allowing accurate positioning of a chosen graphene flake onto a specific location on the Si3N4 membrane. The sample is then left to dry, and finally PMMA is dissolved by acetone drop casting followed by immersion, resulting in the gentle release of the selected graphene flake on the target substrate. Success of the transfer is confirmed by Raman spectroscopy, which also proves the absence of process-induced structural defects. Metallic contacts are fabricated by e-beam lithography and sequential deposition of 0.5 nm Ti and 50 nm Pd by e-beam evaporation. In a next step, the selected single-layer graphene are shaped by oxygen plasma etching into different sizes (0.5×0.5 μm2, 1×1 μm2, 2×2 μm2 and 4×4 μm2). We then deposit a nucleation layer of 2 nm Al on top of the single-layer graphene to ensure homogeneous growth26, followed by an Al2O3 layer (n(Al2O3)≈1.7) grown by atomic layer deposition of varying thickness. The chosen thicknesses of the intra-cavity dielectrics determine the resonance wavelength of the optical microcavity. To make the devices electrically accessible, we pattern openings over the large contact pads by e-beam lithography and etch away the Al2O3 in 40% phosphoric acid by weight at a temperature of T=50 °C (etch rate ~10 nm/2 min) utilizing the PMMA resist as the etch mask. Cavity mirrors are prepared by depositing a 30 nm Ag (Au) globally on the backside of the sample by e-beam evaporation. An additional e-beam lithography step is necessary for the local definition of the top cavity mirror followed by deposition of 60 nm Ag (Au) to ensure devices can still be addressed electrically (see Supplementary Figs S6 and S7).
Simulation of microcavity spectra
Transmission and reflection spectra of the planar microcavity are simulated by using a transfer matrix method for multilayer stacks27. The stack used in the simulation consists of Ag(60 nm)/Al2O3(0–100 nm)/Si3N4(50 nm)/Ag(30 nm). The simulations reproduce well the experimental results obtained from a set of reference samples (see Supplementary Fig. S8).
The thermal emission spectra of graphene in free, non-confined space are fitted with the spectral density model of the two-dimensional black-body radiation given in ref. 21 and the temperature is extracted for each electrical power density level. The microcavity-controlled thermal emission spectra of graphene are then simulated for the same temperatures by superimposing a single Lorentzian at λcavity=925 nm with a FWHM of 30 nm on the spectral density of the two-dimensional black-body radiation discussed above. Note that, as compared with the measured white-light transmission spectrum of the same device, the peak in the thermal emission spectrum is blue shifted by 20 nm and broadened by a factor of 2 (see Supplementary Fig. S1). This is mainly due to the detection with high numerical aperture, NA=0.8, leading to wavelength-dependent variations of the collection efficiencies for on- and off-axis cavity emissions18, an effect that is not accounted for in the present model.
Additional information
How to cite this article: Engel, M. et al. Light-matter interaction in a microcavity-controlled graphene transistor. Nat. Commun. 3:906 doi: 10.1038/ncomms1911 (2012).
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Geim, A. K. Graphene: Status and prospects. Science 324, 1530–1534 (2009).
Avouris, P. H. Graphene: Electronic and photonic properties and devices. Nano Lett. 10, 4285–4294 (2010).
Bonaccorso, F., Sun, Z., Hasan, T. & Ferrari, A. C. Graphene photonics and optoelectronics. Nat. Photon. 4, 611–622 (2010).
Xia, F. et al. Ultrafast graphene photodetector. Nat. Nanotechnol. 4, 839–843 (2009).
Liu, M. et al. A graphene-based broadband optical modulator. Nature 474, 64–67 (2011).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Echtermeyer, T. J. et al. Strong plasmonic enhancement of photovoltage in graphene. Nat. Commun. 2, 458 (2011).
Sun, Z. et al. Graphene mode-locked ultrafast laser. ACS Nano 4, 803–807 (2010).
Nair, R. R. et al. Fine structure constant defines visual transparency of graphene. Science 320, 1308 (2008).
Freitag, M. et al. Thermal infrared emission from biased graphene. Nat. Nanotechnol. 5, 497–501 (2010).
Berciaud, S. et al. Electron and optical phonon temperatures in electrically biased graphene. Phys. Rev. Lett. 104, 227401 (2010).
Fermi, E. Quantum theory of radiation. Rev. Mod. Phys. 4, 87–132 (1932).
Vahala, K. J. Optical microcavities. Nature 424, 839–846 (2003).
Purcell, E. M., Torrey, H. C. & Pound, R. V. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 37–38 (1946).
Kleppner, D. Inhibited spontaneous emission. Phys. Rev. Lett. 47, 233–236 (1981).
Bjoerk, G. & Yamamoto, Y. in Spontaneous Emission and Laser Oscillation in Microcavities (eds Yokoyama, H. and Ujihara, K.) (CRC Press, Boca Raton, 1995).
Steiner, M. et al. Controlling molecular broadband-emission by optical confinement. New J. Phys. 10, 123017 (2008).
Kim, S. et al. Realization of a high mobility dual-gated graphene field-effect transistor with Al2O3 dielectric. Appl. Phys. Lett. 94, 062107 (2009).
Lee, E. J. H. et al. Contact and edge effects in graphene devices. Nat. Nanotechnol. 3, 486–490 (2008).
Kim, H., Lim, S. C. & Lee, Y. H. Size effect of two-dimensional thermal radiation. Phys. Lett. A 375, 2661–2664 (2011).
Perebeinos, V. & Avouris, P. H. Inelastic scattering and current saturation in graphene. Phys. Rev. B 81, 195442 (2010).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Casiraghi, C. et al. Rayleigh imaging of graphene and graphene layers. Nano Lett. 7, 2711–2717 (2007).
Ferrari, A. C. et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 97, 187401 (2006).
Wang, X., Tabakman, S. M. & Dai, H. Atomic Layer Deposition of Metal Oxides on Pristine and Functionalized Graphene. J. Am. Chem. Soc. 130, 8152–8153 (2008).
Hecht, E. Optics 4th edn (MA: Addison-Wesley Publishing Company, 2001).
Acknowledgements
We acknowledge S. Linden (University of Bonn) for support with the optical simulations, D.B. Farmer (IBM TJ Watson Research Center) for atomic layer deposition, R. Ferlito (CSS, IBM TJ Watson Research Center) for Ag mirror deposition and B.A.Ek (IBM TJ Watson Research Center) for expert technical assistance. M.E. and R.K. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) and the State of Baden-Württemberg through the DFG-Center for Functional Nanostructures (CFN) within subproject B 1.9. A.C.F. acknowledges funding from EU grants NANOPOTS, GENIUS, RODIN and EPSRC grants EP/GO30480/1 and EP/G042357/1, Royal Society Wofson Research Merit Award.
Author information
Authors and Affiliations
Contributions
The experiments were conceived, designed and carried out by M.E. and M.S., A.L. performed graphene exfoliation and transfer. The manuscript was written by M.E. and M.S. with input from R.K., P.A., A.C.F., and H.v.L.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S8, Supplementary Methods and Supplementary References (PDF 2805 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Engel, M., Steiner, M., Lombardo, A. et al. Light–matter interaction in a microcavity-controlled graphene transistor. Nat Commun 3, 906 (2012). https://doi.org/10.1038/ncomms1911
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1911
This article is cited by
-
A flat-based plasmonic fiber probe for nanoimaging
Nano Research (2023)
-
A complete numerical analysis of the impact of disorder and defect cavities on achieving complete optical absorption in monolayer graphene with supporting random structures
Optical and Quantum Electronics (2023)
-
On photo-induced electrons in graphene-plasmonic nanoparticles
Applied Physics A (2023)
-
Graphene perfect absorber with loss adaptive Q-factor control function enabled by quasi-bound states in the continuum
Scientific Reports (2021)
-
High-responsivity graphene photodetectors integrated on silicon microring resonators
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.