Abstract
Although the interaction between light and motion in cavity optomechanical systems is inherently nonlinear, experimental demonstrations to date have allowed a linearized description in all except highly driven cases. Here, we demonstrate a nanoscale optomechanical system in which the interaction between light and motion is so large (single-photon cooperativity C0≈103) that thermal motion induces optical frequency fluctuations larger than the intrinsic optical linewidth. The system thereby operates in a fully nonlinear regime, which pronouncedly impacts the optical response, displacement measurement and radiation pressure backaction. Specifically, we measure an apparent optical linewidth that is dominated by thermo-mechanically induced frequency fluctuations over a wide temperature range, and show that in this regime thermal displacement measurements cannot be described by conventional analytical models. We perform a proof-of-concept demonstration of exploiting the nonlinearity to conduct sensitive quadratic readout of nanomechanical displacement. Finally, we explore how backaction in this regime affects the mechanical fluctuation spectra.
Similar content being viewed by others
Introduction
In cavity optomechanics, the interaction between light in an optical cavity and the motion of a mechanical resonator enables sensitive optical readout of displacement, as well as manipulation of the motion of the resonator through optical forces1. This has allowed demonstrations of sideband and feedback cooling of the mechanical resonator near its quantum ground state2,3,4,5, squeezing of light6,7,8 and of the mechanical zero-point fluctuations9,10,11, entanglement12 and state transfer13 between the optical and mechanical degrees of freedom, as well as detection of radiation pressure shot noise14,15 and non-classical correlations16,17,18,19. In all of these examples, the coupling between fluctuations of the optical field and the mechanical displacement can be regarded as linear for all intents and purposes.
However, the optomechanical interaction is inherently nonlinear. Indeed, the cavity optomechanical interaction Hamiltonian reads  , where
, where 
 is the annihilation (creation) operator for the optical cavity field,
is the annihilation (creation) operator for the optical cavity field,  is the displacement operator for the mechanical resonator and ħ is the reduced Planck constant. The photon–phonon coupling rate g0=(∂ωc/∂x)xzpf quantifies the change of the cavity frequency ωc due to a displacement the size of the zero-point fluctuations of the resonator xzpf. This interaction Hamiltonian leads to nonlinear behaviour, as the equations of motion it generates contain products of two operators. The linearized form of the interaction
is the displacement operator for the mechanical resonator and ħ is the reduced Planck constant. The photon–phonon coupling rate g0=(∂ωc/∂x)xzpf quantifies the change of the cavity frequency ωc due to a displacement the size of the zero-point fluctuations of the resonator xzpf. This interaction Hamiltonian leads to nonlinear behaviour, as the equations of motion it generates contain products of two operators. The linearized form of the interaction  does not contain the nonlinear terms, but usually suffices to describe the dynamics of fluctuations1. This form emerges when the cavity field is written as the sum
does not contain the nonlinear terms, but usually suffices to describe the dynamics of fluctuations1. This form emerges when the cavity field is written as the sum  of an average coherent field
of an average coherent field  and fluctuations
and fluctuations  , and the term containing
, and the term containing  is neglected by assuming
is neglected by assuming  . The linearization is generally valid if the fluctuations
. The linearization is generally valid if the fluctuations  , insofar as they are induced by mechanical motion, do not approach or exceed the coherent field
, insofar as they are induced by mechanical motion, do not approach or exceed the coherent field  . However, the assumption that
. However, the assumption that  is not valid if mechanical fluctuations shift the cavity completely in and out of resonance with the optical drive, that is, when they produce a cavity frequency shift comparable to the optical linewidth κ. Then, nonlinear processes become crucially important, and qualitatively different effects can occur.
is not valid if mechanical fluctuations shift the cavity completely in and out of resonance with the optical drive, that is, when they produce a cavity frequency shift comparable to the optical linewidth κ. Then, nonlinear processes become crucially important, and qualitatively different effects can occur.
In the quantum domain, intriguing implications of this nonlinearity are expected in the single-photon strong-coupling regime when the coupling rate g0 exceeds the optical and mechanical loss rates κ and Γ, respectively. There, quantum-level mechanical fluctuations induce a nonlinear response, creating non-classical states of both light and motion when the mechanical frequency Ωm approaches the optical linewidth as well20,21,22. In the so-called bad-cavity limit (κ>Ωm), the nonlinearity of the interaction provides a useful path towards creating motional quantum states, for example through performing quadratic measurements of displacement (proportional to  )23,24,25,26,27.
)23,24,25,26,27.
In macroscopic or chip-based optomechanical implementations, the breakdown of linearity when  ≳
≳ has so far only been experimentally relevant for mechanical resonators driven to large amplitude, for example through optomechanical parametric amplification. In that case, nonlinear effects determine the maximum amplitude of optomechanical self-oscillation1,28,29,30,31,32 and can lead to complex nonlinear dynamical phenomena such as chaos33,34,35.
has so far only been experimentally relevant for mechanical resonators driven to large amplitude, for example through optomechanical parametric amplification. In that case, nonlinear effects determine the maximum amplitude of optomechanical self-oscillation1,28,29,30,31,32 and can lead to complex nonlinear dynamical phenomena such as chaos33,34,35.
Here, we establish and explore the regime where even intrinsic Brownian motion induces cavity frequency fluctuations larger than the optical linewidth. In this regime, the nonlinear nature of the cavity optomechanical interaction becomes important in all essential phenomena, including optomechanical displacement measurement and radiation pressure backaction. The regime is defined by  ≳
≳ , where
, where  is the average phonon occupancy of the mechanical mode with frequency Ωm, in thermal equilibrium at a temperature T and kB is the Boltzmann constant. It is clear from this condition that any optomechanical system in which the ratio g0/κ is increased will enter this regime before reaching the single-photon strong-coupling regime, unless the mechanical resonator is pre-cooled to its ground state. The condition can equivalently be expressed as C0≳
is the average phonon occupancy of the mechanical mode with frequency Ωm, in thermal equilibrium at a temperature T and kB is the Boltzmann constant. It is clear from this condition that any optomechanical system in which the ratio g0/κ is increased will enter this regime before reaching the single-photon strong-coupling regime, unless the mechanical resonator is pre-cooled to its ground state. The condition can equivalently be expressed as C0≳ , that is, the single-photon cooperativity C0≡4g02/κΓ being larger than the ratio of optical decay rate and mechanical thermal decoherence rate
, that is, the single-photon cooperativity C0≡4g02/κΓ being larger than the ratio of optical decay rate and mechanical thermal decoherence rate  . In our experiments, we follow a strategy of exploiting subwavelength optical confinement36 to reach a single-photon cooperativity around 103; two to three orders of magnitude larger than typical values in nanoscale optomechanical systems to date1,37,38, and only comparable with cold-atom implementations15,39. In the systems demonstrated here, the apparent optical linewidth is dominated by the transduced thermal motion over a wide range of temperatures, and the transduction becomes extremely nonlinear. We numerically implement a model that describes transduction in this regime, in contrast to the conventional analytical description, which fails for fluctuations that approach the linewidth. Moreover, we analyse how the nonlinear response of the radiation pressure force to stochastic fluctuations alters the shape of mechanical fluctuation spectra. Finally, we provide a proof-of-concept demonstration of exploiting the nonlinearity to conduct sensitive quadratic readout of nanomechanical displacement.
. In our experiments, we follow a strategy of exploiting subwavelength optical confinement36 to reach a single-photon cooperativity around 103; two to three orders of magnitude larger than typical values in nanoscale optomechanical systems to date1,37,38, and only comparable with cold-atom implementations15,39. In the systems demonstrated here, the apparent optical linewidth is dominated by the transduced thermal motion over a wide range of temperatures, and the transduction becomes extremely nonlinear. We numerically implement a model that describes transduction in this regime, in contrast to the conventional analytical description, which fails for fluctuations that approach the linewidth. Moreover, we analyse how the nonlinear response of the radiation pressure force to stochastic fluctuations alters the shape of mechanical fluctuation spectra. Finally, we provide a proof-of-concept demonstration of exploiting the nonlinearity to conduct sensitive quadratic readout of nanomechanical displacement.
Results
Sliced photonic crystal nanobeam
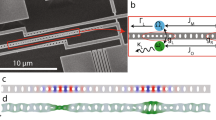
Figure 1a shows the optomechanical system we employ. It combines low-mass, megahertz-frequency, nanomechanical modes with subwavelength optical field confinement in a sliced photonic crystal nanobeam36, to establish strong optomechanical interactions with photon–phonon coupling rates g0 in the range of tens of MHz. The fundamental mechanical resonance of the sliced nanobeam, shown in Fig. 1b, strongly influences the gap distance d in the middle of the beam. The motion of the resonator in this mechanical mode is associated with a simulated effective mass of 1.5 pg, leading to relatively large zero-point fluctuations  . As shown in the optical field profile of the fundamental cavity resonance of the structure in Fig. 1c, the nanoscale gap in the middle of the beam confines the light to a small area, which makes the optical cavity resonance frequency ωc strongly dependent on the gap size d between the two halves of the nanobeam. With the fabricated gap size of 45–50 nm, we simulated the optical frequency change due to a displacement of the beams to be ∂ω/∂x/2π=0.8 THz nm−1, where x≡d/2. This leads to an expected optomechanical coupling rate of g0/2π=35 MHz. We decrease the optical cavity decay rate and increase the outcoupling at normal incidence by engineering the angular radiation spectrum of the sliced nanobeam structure40,41 (Methods section). The resultant simulated optical decay rate is 8.8 GHz, showing that the sliced nanobeam design is capable of combining large optomechanical interactions with relatively low optical losses (Q>104). We believe that further optimization along these lines could, in principle, lead to still larger optical quality factors.
. As shown in the optical field profile of the fundamental cavity resonance of the structure in Fig. 1c, the nanoscale gap in the middle of the beam confines the light to a small area, which makes the optical cavity resonance frequency ωc strongly dependent on the gap size d between the two halves of the nanobeam. With the fabricated gap size of 45–50 nm, we simulated the optical frequency change due to a displacement of the beams to be ∂ω/∂x/2π=0.8 THz nm−1, where x≡d/2. This leads to an expected optomechanical coupling rate of g0/2π=35 MHz. We decrease the optical cavity decay rate and increase the outcoupling at normal incidence by engineering the angular radiation spectrum of the sliced nanobeam structure40,41 (Methods section). The resultant simulated optical decay rate is 8.8 GHz, showing that the sliced nanobeam design is capable of combining large optomechanical interactions with relatively low optical losses (Q>104). We believe that further optimization along these lines could, in principle, lead to still larger optical quality factors.
(a) Electron microscope image of a silicon sliced nanobeam. The shown part is free-standing and has a thickness of 250 nm. The scale bar is 2 μm and is valid for a–c. (b) Simulated displacement profile of the fundamental mechanical resonance, which strongly modifies the gap size. (c) Simulated transverse electric field of the fundamental optical cavity resonance. The inset shows an enlarged view of the cavity region (scale bar 1 μm), formed by a tapered variation of the distances between, and sizes of, the holes. (d) Schematic diagram of the employed balanced homodyne interferometer measurement set-up. The reflection from the sliced nanobeam is interfered with the light from the reference arm, enabling near-quantum-limited measurement of fluctuation spectra even with low power incident on the sample (see Methods section for details).
We employ a balanced homodyne detection scheme, schematically shown in Fig. 1d, to study the fluctuations imparted on the light in the nanobeam cavity through the optomechanical interaction (Methods section). Figure 2a depicts fluctuation spectra recorded with an electronic spectrum analyser, showing the two fundamental mechanical resonances of one device, measured at 3 K with the laser on-resonance with the cavity. We ascribe the two resonances to the two half-beams moving at slightly different natural frequencies, instead of the ideal antisymmetric eigenmode depicted in Fig. 1b. The fact that in this device the two resonances are nearly of equal strength indicates that the two half-beams are mechanically coupled at a rate smaller than their intrinsic frequency difference36, and thus moving approximately independent of each other; stronger mechanical coupling would result in hybridization into symmetric and antisymmetric eigenmodes with different optical transduction strengths.
(a) Recorded optically measured spectra of the two fundamental mechanical resonances with frequencies f1 and f2 (PSD, power spectral density; optical power incident on sample: 11.3 nW). Grey noise spectra were recorded with the signal arm of the interferometer blocked. Black lines show the Lorentzian fit, used to determine the linewidths (full width at half maximum) shown in the figure. The displacement spectral density scale on the right-hand side assumes linear transduction of the known thermal motion of the structure at the cryostat temperature. (b) Detuning dependence of the measured transduced thermal motion, measured as the band power at f1, the lowest mechanical frequency, at room temperature and at 3 K. The black solid and dashed lines show fits with a Voigt lineshape squared (Methods section), with the widths (full width at half maximum) shown. (c) Schematic representation of thermal-motion-induced linewidth broadening: the thin orange lines represent the intrinsic cavity response at a few example detunings, while the thick brown line shows the overall response resulting from averaging over the fluctuating detuning. (d) Optical linewidth versus temperature. The solid line is a fit with a model that assumes a constant Lorentzian intrinsic linewidth κ convolved with a Gaussian with a width LG that depends on  . The asymptotes (blue) of the fit function allow us to extract κ and the optomechanical coupling rates g0,i for the two mechanical modes (i=1, 2). Extracted values are shown in the figure.
. The asymptotes (blue) of the fit function allow us to extract κ and the optomechanical coupling rates g0,i for the two mechanical modes (i=1, 2). Extracted values are shown in the figure.
Modification of optical response
The signal strength of the transduced motion around the cavity resonance wavelength of 1457.5 nm, measured at 3 K and at room temperature, is shown in Fig. 2b as a function of laser detuning. The fluctuations are recorded while continuously sweeping the piezo-mounted mirror over multiple interferometer fringes, thus averaging the measured signal quadratures. As we analyse in detail elsewhere (La Gala et al., manuscript in preparation), the resulting signal strength acquires a simple single-peaked detuning dependence with a maximum when the laser is tuned to the cavity resonance (Methods section). As Fig. 2b shows, the apparent linewidth of the optical resonance is strongly influenced by temperature. We infer from this that the frequency fluctuations of the cavity due to the thermal motion of the mechanical resonator dominate the response which occurs when they are larger than the intrinsic optical linewidth. This is illustrated in Fig. 2c: while the intrinsic optical response of the cavity is Lorentzian with linewidth κ (orange thin lines), the distribution of cavity frequency fluctuations due to thermal motion has a Gaussian spectrum (brown thick line), whose linewidth LG is related to the root-mean-square (r.m.s.) value of the frequency fluctuations δωr.m.s. as  . In the bad-cavity limit we consider here, we model the observed cavity response as a Voigt lineshape, which is a convolution between the Lorentzian cavity response and the Gaussian distribution of cavity resonance frequencies due to the Brownian motion. We note that the measured electronic power spectral density is proportional to the square of the optical response, which leads to a smaller apparent linewidth in the detuning dependence shown in Fig. 2b. In the following, we only report the extracted linewidth (Methods section), which directly corresponds to the optical loss rate κ in the low-temperature limit, and the full width at half maximum of the frequency fluctuation distribution in the high-temperature limit.
. In the bad-cavity limit we consider here, we model the observed cavity response as a Voigt lineshape, which is a convolution between the Lorentzian cavity response and the Gaussian distribution of cavity resonance frequencies due to the Brownian motion. We note that the measured electronic power spectral density is proportional to the square of the optical response, which leads to a smaller apparent linewidth in the detuning dependence shown in Fig. 2b. In the following, we only report the extracted linewidth (Methods section), which directly corresponds to the optical loss rate κ in the low-temperature limit, and the full width at half maximum of the frequency fluctuation distribution in the high-temperature limit.
As the thermomechanical displacement variance is given by  (assuming dynamical backaction is negligible), the induced frequency fluctuations due to a single-mechanical mode at frequency Ωm are characterized by a r.m.s. amplitude
(assuming dynamical backaction is negligible), the induced frequency fluctuations due to a single-mechanical mode at frequency Ωm are characterized by a r.m.s. amplitude

which reveals a square-root dependence on temperature. In case multiple independent mechanical modes are coupled to the optical cavity, the variances of the cavity frequency fluctuations are added, that is,  , which preserves the overall temperature dependence. Figure 2d shows the full measured temperature dependence of the apparent linewidth, which exhibits the expected square-root dependence on temperature at higher temperatures. We fit the data points using an equation that approximates the linewidth of the Voigt lineshape (Methods section), with a fixed Lorentzian contribution due to the intrinsic optical loss and a Gaussian contribution that follows equation (1). The resulting fit curve is shown in Fig. 2d, together with its asymptotes (thin blue lines). These asymptotes allow us to directly extract the intrinsic optical linewidth κ and the variance of thermal-motion-induced frequency fluctuations of the cavity, without further calibration. There are two mechanical resonances that show significant coupling to the optical cavity resonance as shown in Fig. 2a, and we derive the ratio between their coupling strengths from the ratio between the signal strengths at the two mechanical resonance frequencies36. Using this ratio and the measured resonance frequencies, we obtain g0/2π=24.7 and 25.4 MHz for the two mechanical modes, which corresponds closely to the predicted value for an ideal antisymmetric mode of 35 MHz, since
, which preserves the overall temperature dependence. Figure 2d shows the full measured temperature dependence of the apparent linewidth, which exhibits the expected square-root dependence on temperature at higher temperatures. We fit the data points using an equation that approximates the linewidth of the Voigt lineshape (Methods section), with a fixed Lorentzian contribution due to the intrinsic optical loss and a Gaussian contribution that follows equation (1). The resulting fit curve is shown in Fig. 2d, together with its asymptotes (thin blue lines). These asymptotes allow us to directly extract the intrinsic optical linewidth κ and the variance of thermal-motion-induced frequency fluctuations of the cavity, without further calibration. There are two mechanical resonances that show significant coupling to the optical cavity resonance as shown in Fig. 2a, and we derive the ratio between their coupling strengths from the ratio between the signal strengths at the two mechanical resonance frequencies36. Using this ratio and the measured resonance frequencies, we obtain g0/2π=24.7 and 25.4 MHz for the two mechanical modes, which corresponds closely to the predicted value for an ideal antisymmetric mode of 35 MHz, since  .
.
This large optomechanical coupling rate, combined with the extracted optical decay rate of κ/2π=20.4 GHz and the mechanical decay rate of Γ/2π=100 Hz (measured at 3 K), means that this device has a single-photon cooperativity  . The single-photon cooperativity is a metric that combines optomechanical coupling and losses1,38. It signals the inverse of the number of intracavity photons needed to perform a measurement at the standard quantum limit, if all photons escaping the cavity could be employed towards that measurement. Interestingly, the combination of quadrature-averaged detection with temperature-dependent linewidth measurement allows direct extraction of C0, with no other calibration than that of the mechanical bath temperature. The extremely high value we report here, which exceeds previously reported nano-optomechanical architectures by two to three orders of magnitude1,37,38, highlights the prospects of such systems for measurement-based quantum control of motion.
. The single-photon cooperativity is a metric that combines optomechanical coupling and losses1,38. It signals the inverse of the number of intracavity photons needed to perform a measurement at the standard quantum limit, if all photons escaping the cavity could be employed towards that measurement. Interestingly, the combination of quadrature-averaged detection with temperature-dependent linewidth measurement allows direct extraction of C0, with no other calibration than that of the mechanical bath temperature. The extremely high value we report here, which exceeds previously reported nano-optomechanical architectures by two to three orders of magnitude1,37,38, highlights the prospects of such systems for measurement-based quantum control of motion.
Nonlinear transduction
When the relative cavity fluctuations δωr.m.s./κ are large, a typical mechanical oscillation samples the full width of the optical Lorentzian lineshape. Since this lineshape is nonlinear, higher-order harmonics are expected to appear in the transduced optical fluctuation spectrum. At room temperature, the cavity frequency fluctuations due to both mechanical modes have an amplitude  . As shown in Fig. 3a, at room temperature the measurement signal indeed contains fluctuations at (mixed) integer multiples of the two fundamental mechanical resonances, that is
. As shown in Fig. 3a, at room temperature the measurement signal indeed contains fluctuations at (mixed) integer multiples of the two fundamental mechanical resonances, that is  , where j, k∈{0, 1, 2, …}. Around the fundamental frequencies near 3.3 MHz, we observe odd mixing terms up to ninth order (for example a peak is visible at f5,−4=5f1−4f2), and around the sum frequency at 6.6 MHz, even mixing terms up to tenth order can be identified.
, where j, k∈{0, 1, 2, …}. Around the fundamental frequencies near 3.3 MHz, we observe odd mixing terms up to ninth order (for example a peak is visible at f5,−4=5f1−4f2), and around the sum frequency at 6.6 MHz, even mixing terms up to tenth order can be identified.
(a) Power spectral density of transduced thermal motion, measured at room temperature (295 K). (b) Power spectral density of the group of peaks around the fundamental mechanical frequencies f1, f2 and around f1+f2, at room temperature (blue) and at 3 K (red). The orange arrows indicate the ratio between the maximum first- and second-order transduction (dashed lines). (c) Ratio between the 3 second-order peaks around f1+f2 and the peaks at the fundamental frequencies f1, f2 as a function of the relative cavity fluctuations δωr.m.s./κ. Device 1 is the same device presented in the other figures; device 2 is a similar device with different parameters from which more measurements are shown in Supplementary Note 2; room-temperature measurements from two recent publications are indicated with data points I (ref. 24) and II (ref. 36). The dashed line indicates the prediction from an analytical model with an order-by-order approximation, while the black data points connected with solid lines represent a calculation based on a numerically generated time trace to simulate thermal motion. (d) Expected band power at the fundamental frequency f as well as at 2f and 3f, as a function of the relative cavity fluctuations, normalized to the band power for f at δωr.m.s./κ=10−2. Solid, dashed, and dash-dotted lines follow the order-by-order approximation, while the coloured points are the outcome of our numerical model.
At a temperature of 3 K, the ratio between the cavity frequency fluctuations, caused by both mechanical modes, and the intrinsic optical linewidth is δωr.m.s./κ=0.34, which still leads to significant higher-order transduction. Figure 3b shows a direct comparison of the spectra obtained at room temperature and at 3 K. As a measure for the higher-order transduction, we take the ratio between the second- and first-order transduction. The ratio between the orders is independent of other parameters, such that it gives direct insight in the strength of the nonlinearity. This ratio is clearly larger at higher temperature (its inverse is indicated with arrows in Fig. 3b). The difference in the signal-to-noise ratio between low and high temperatures is due to the mechanical linewidth being smaller at low temperatures (by a factor of 2) as well as a redistribution of modulation power among higher harmonics, as explained in the following.
Higher-order transduction (for a single-mechanical mode) has previously been described with an analytical model that is based on a Taylor expansion of the measurement output around the average detuning23,24,36. For low-amplitude modulation, the higher-order terms in this expansion can be approximated as independent. Mathematically, this is based on an order-by-order approximation  . The resulting expression for the maximum signal power measured at the (multiple of the) resonance frequency kΩ is
. The resulting expression for the maximum signal power measured at the (multiple of the) resonance frequency kΩ is

where A is a constant that depends on the optical power as well as the coupling efficiency to the cavity (for details, see Methods section and La Gala et al., manuscript in preparation).
In Fig. 3c, the dashed line shows the ratio between the second- and first-order transduction that follows from this order-by-order approximation, (2δωr.m.s./κ)2. The data points labelled I and II, which represent room-temperature measurements reported in refs 24 and 36, respectively, are still well-explained by the order-by-order approximation. For the devices under study, δωr.m.s./κ is so large that this approach breaks down. This is shown by our temperature sweep data, where we take the fitted area  under the peaks at the fundamental frequencies and at twice the frequency (labelled in Fig. 3a), and plot their ratio:
under the peaks at the fundamental frequencies and at twice the frequency (labelled in Fig. 3a), and plot their ratio:  . This ratio reduces to A2f/Af if the two frequencies f1, f2 coincide, which supports directly comparing it to the single-mode prediction of the order-by-order approximation. The red circles indicate the results for the same device presented in the other figures, while the blue squares represent a different device with g0/2π=10.8 MHz and κ/2π=9.0 GHz (Supplementary Note 2).
. This ratio reduces to A2f/Af if the two frequencies f1, f2 coincide, which supports directly comparing it to the single-mode prediction of the order-by-order approximation. The red circles indicate the results for the same device presented in the other figures, while the blue squares represent a different device with g0/2π=10.8 MHz and κ/2π=9.0 GHz (Supplementary Note 2).
Where the order-by-order approximation breaks down, the nonlinear transduction still follows the prediction of our full model, in which we calculate the expected homodyne output from a numerical time-domain simulation of the thermal motion (Methods section). We then Fourier transform the simulated signal and plot the ratio of the band powers, noting that the numerical result does not depend on whether we include one or two mechanical resonances when plotted against total relative cavity fluctuations δωr.m.s./κ. This full model prediction is shown by the black dots connected by solid lines in Fig. 3c. The numerical simulation follows the experimentally observed trend, and shows that the ratio between second- and first-order transduction saturates close to unity at higher fluctuation amplitudes. We note that only such a numerical approach correctly takes into account the statistics of the transduced motion: the strongly nonlinear conversion of displacement to optical field precludes an analysis based solely on one or several moments of the displacement distribution. In other words, a single peak in the fluctuation spectrum at kΩm can no longer be dominantly associated with a specific scattering process involving k phonons, but also contains contributions due to k+2, k+4, … phonons. Although some of the data lie below the expected curve we note that this cannot be explained by poor thermalization of the sample. If the sample would not be thermalized at low temperatures, our estimate of κ would be too high and our estimate of δωr.m.s. too low. Both such misestimations would lead to data points that lie above the predicted trend (black line) in Fig. 3c, which is not what we observe. Independent measurements that vary optical power and radiation heat load also indicate good thermalization of the sample (Supplementary Notes 1 and 2).
Using the numerical model, we calculate the absolute signal power due to thermal motion at the fundamental frequency f and its multiples 2f and 3f (points in Fig. 3d). For cavity frequency fluctuations δωr.m.s./κ larger than about 10%, both linear and higher-order transduction no longer follow the order-by-order approximation given in equation (2) (black lines), which predicts monotonic increases in signal strength. Instead, we recognize an optimum single-harmonic signal strength due to cavity frequency fluctuations, beyond which larger fluctuations cause the cavity to be off-resonance most of the time. This reduces the transduction at a single harmonic in the optical signal, instead distributing energy equally among an increasing number of harmonics as the system operates deeper in the nonlinear regime.
Quadratic measurement of motion
A measurement that is directly sensitive to the square of displacement, x2, can be used to estimate the energy of the mechanical resonator. In the resolved-sideband regime, displacement-squared optomechanical coupling hence provides a means to perform quantum non-demolition measurements of the phonon number42,43,44,45,46. But also in the bad-cavity limit, measurements of x2 have been proposed as a possible route to preparing non-classical (superposition) states of motion of the mechanical resonator23,24,47,48. It is important then to suppress both linear measurement and backaction, either through structural design or through active feedback schemes24. Measurements of x2 can be performed using the nonlinear transduction we study here, by detecting the transduced motion at twice the fundamental frequency, 2f, provided that the sample temperature is low enough such that the order-by-order approximation is valid. This gives rise to an effective quadratic coupling rate given by  (ref. 48), which amounts to 2π × 32 kHz in the device presented here. To put that number in perspective, one can compare it to the quadratic coupling rate
(ref. 48), which amounts to 2π × 32 kHz in the device presented here. To put that number in perspective, one can compare it to the quadratic coupling rate  in devices that are designed such that the frequency is directly proportional to the square of the displacement. A state-of-the-art double-slotted photonic crystal system recently demonstrated45 a quadratic coupling rate of μ0/2π=245 Hz.
in devices that are designed such that the frequency is directly proportional to the square of the displacement. A state-of-the-art double-slotted photonic crystal system recently demonstrated45 a quadratic coupling rate of μ0/2π=245 Hz.
In Fig. 4 we show selective linear and quadratic measurements of mechanical displacement at 3 K. Figure 4a shows the strength of the first- and second-order transduction (proportional to x and x2, respectively, in the order-by-order approximation) as a function of the piezo mirror position that controls the homodyne phase, which is now no longer continuously swept. The data follow the expected sinusoidal dependence.
(a) Transduction of first (f2) and second (f1+f2) order peaks (orange and light blue data points, respectively) while sweeping the piezo mirror position, with 10.5 nW optical power incident on the sample. The solid lines show sinusoidal fits to the data. The horizontal scale was derived from the fit to the band power of f2, and the data at f1+f2 was shifted horizontally by about 3% to compensate for measurement drift. (b) Spectra at f2 and 2f2 at optimal mirror positions for linear and quadratic transduction (red and light blue data points, respectively), taken with 12.8 nW of incident optical power. The black solid lines are Lorentzian fits, whose area was used to calibrate the vertical scale.
We obtained the spectra in Fig. 4b by positioning the piezo mirror at the optimum points for first- and second-order transduction, depicted by the red and blue data points, respectively. The vertical scale was calibrated by using the order-by-order approximation, where the area under the peaks in the spectrum is proportional to the variance of the thermal motion of the structure, which here provides a lower limit for the sensitivity. This analysis yields an imprecision for the displacement-squared measurement of 2.0 × 10−25 m2 Hz−1/2. To provide some context for this value, with the current mechanical linewidth this level of imprecision corresponds to the ability to measure a phonon occupation of 752 with a signal-to-noise ratio of 1, which is an improvement over the measurement sensitivity in the proof-of-concept experiment reported in ref. 24 by approximately a factor 50. In the data shown here, the suppression of linear transduction is 28 dB, which could be further improved by implementing a feedback loop to lock the homodyne interferometer phase to a desired value.
It is important to note that our numerical model, as shown in Fig. 3d, predicts second-order transduction at only 10% of the strength of the order-by-order approximation for δωr.m.s./κ≈0.34, which is the size of the relative cavity fluctuations in our device at 3 K. Therefore, we expect that if this device is cooled further, to the point where the order-by-order approximation accurately predicts the transduction, an even lower imprecision noise of 6.3 × 10−26 m2 Hz−1/2 would be recovered without any further optimization. This would be comparable to a phonon occupation of 238. In the regime where the order-by-order approximation holds, this imprecision, expressed as a phonon number nimp scales as

with η the coupling efficiency to our cavity, Pin the incident optical power, and ξ a constant incorporating the technical homodyne detector measurement efficiency for both signal and local oscillator (Supplementary Note 3). With relatively modest improvements an imprecision at the single-phonon level could be within reach, for example by improving g0 and κ by factors of  and 2, respectively, as well as increasing η to 40% from the 1.3% estimated in the current device (Supplementary Note 4), for example by employing waveguide-based coupling strategies49. The powers used for acquiring the data above are also low, corresponding to an average cavity occupation of ∼0.2 photons. At higher powers, the mechanical spectrum was affected by low-frequency noise of the laser through the effects explored in the next section, an effect that could be ameliorated by for example shorter measurement times.
and 2, respectively, as well as increasing η to 40% from the 1.3% estimated in the current device (Supplementary Note 4), for example by employing waveguide-based coupling strategies49. The powers used for acquiring the data above are also low, corresponding to an average cavity occupation of ∼0.2 photons. At higher powers, the mechanical spectrum was affected by low-frequency noise of the laser through the effects explored in the next section, an effect that could be ameliorated by for example shorter measurement times.
It is important to note that to use such measurements to create quantum superposition states, significant further advances are needed: first, the nonlinear measurement rate should exceed the thermal decoherence rate, requiring an imprecision  . As such, lower bath temperature and larger intracavity photon number would be highly beneficial. Second, active feedback at the mechanical frequency would be needed to suppress quantum backaction associated with the existent linear coupling. As noted by Brawley et al.24, suppressing this to the single-phonon level requires a measurement efficiency ζ that satisfies g02/κ2>(1−ζ)/(8ζ), where ζ=hη, and h is the quantum efficiency of our measurement set-up (Supplementary Notes 3 and 4). Fulfilling this thus requires a strong investment in reaching near-unity extraction efficiencies and larger optical quality factors in these devices.
. As such, lower bath temperature and larger intracavity photon number would be highly beneficial. Second, active feedback at the mechanical frequency would be needed to suppress quantum backaction associated with the existent linear coupling. As noted by Brawley et al.24, suppressing this to the single-phonon level requires a measurement efficiency ζ that satisfies g02/κ2>(1−ζ)/(8ζ), where ζ=hη, and h is the quantum efficiency of our measurement set-up (Supplementary Notes 3 and 4). Fulfilling this thus requires a strong investment in reaching near-unity extraction efficiencies and larger optical quality factors in these devices.
Radiation pressure force with large cavity fluctuations
The nonlinear regime not only impacts optical transduction of motion, but also pronouncedly affects the mechanical fluctuations themselves through its influence on radiation pressure backaction. The strongest manifestation of backaction in the regime where the cavity reacts nearly instantaneously to the mechanical motion  is the optical spring effect, which alters the mechanical resonance frequency depending on the detuning between a drive laser frequency and the cavity resonance1. Figure 5a,d show experimentally obtained spectrograms at low temperature (3 K, incident optical power 20.6 nW) and at room temperature (295 K, incident optical power 124 nW) around the fundamental harmonic of one of the mechanical modes, while Fig. 5c,f show several cross sections at selected detunings. At low temperature, the observed effect is very similar to the normal (linearized) optical spring effect, where a blue-detuned laser shifts the mechanical frequency upwards and vice versa for red detuning. However, we additionally observe a broadening of the obtained spectra both when the laser is red- and blue-detuned by ∼10 GHz (
is the optical spring effect, which alters the mechanical resonance frequency depending on the detuning between a drive laser frequency and the cavity resonance1. Figure 5a,d show experimentally obtained spectrograms at low temperature (3 K, incident optical power 20.6 nW) and at room temperature (295 K, incident optical power 124 nW) around the fundamental harmonic of one of the mechanical modes, while Fig. 5c,f show several cross sections at selected detunings. At low temperature, the observed effect is very similar to the normal (linearized) optical spring effect, where a blue-detuned laser shifts the mechanical frequency upwards and vice versa for red detuning. However, we additionally observe a broadening of the obtained spectra both when the laser is red- and blue-detuned by ∼10 GHz ( ). At room temperature, the spectra also become asymmetric: instead of a symmetric Lorentzian lineshape, the peak in spectra close to the optical resonance has a much steeper edge on one side than on the other side. In addition, the shift of the peak due to the optical spring effect usually scales linearly with the incident optical power, but the data set at room temperature shows a smaller, rather than a larger shift than the data set at 3 K, even though the used optical power is five times higher.
). At room temperature, the spectra also become asymmetric: instead of a symmetric Lorentzian lineshape, the peak in spectra close to the optical resonance has a much steeper edge on one side than on the other side. In addition, the shift of the peak due to the optical spring effect usually scales linearly with the incident optical power, but the data set at room temperature shows a smaller, rather than a larger shift than the data set at 3 K, even though the used optical power is five times higher.
(a,d) Experimental spectrograms, showing transduced mechanical spectra (horizontal axis) versus the optical laser frequency (vertical axis) at two different experimental conditions: (a) cooled at 3 K, incident laser power 20.6 nW; (d) room temperature, 295 K, with incident laser power 124 nW. (b,e) Simulated spectrograms corresponding to those shown in (a,d), obtained by calculating frequency shifts for a large number of motional amplitudes sampled from a thermal distribution, and averaging Lorentzian lineshapes with centre frequencies given by the calculated shifts. The colour bar below panel (e) is shared for all the spectrograms (PSD, power spectral density). (c,f) Individual spectra at various detunings (coloured symbols), overlaid with the corresponding simulated spectrum (solid black lines). Spectra were offset by a factor of 102 between them to avoid overlap.
To account for these observations, we again need to take the large fluctuations of the cavity frequency due to thermal motion into consideration. The typical optomechanical model for the optical spring effect is based on the linearized equations of motion1, which do not apply in the nonlinear regime we reach here. To model a single-mechanical mode, we instead calculate an effective spring constant from the first Fourier coefficient of the radiation pressure force, while the resonator oscillates harmonically, x(t)=x0 cos Ωt. For this, we express the radiation pressure force in the cavity as

where  with
with  the average detuning between the laser and cavity frequency, and ncmax is the maximum number of photons in the cavity when it is driven at resonance. The effective spring constant can be directly rescaled to obtain the frequency shift (Supplementary Note 5). As before, we numerically sample a thermal distribution to model the behaviour of the system, in this case by averaging over 104 different amplitudes x0, such that the displacement variance equals that from both mechanical modes in the experiment. Finally, we average the same number of Lorentzian lineshapes with the centre frequencies given by the simulated frequency shifts and their widths set to the median linewidth measured in the experiment, to approximate the intrinsic linewidth at that temperature (Supplementary Note 5). The resulting simulated spectra are shown in Fig. 5b,e and plotted as black solid lines in Fig. 5c,f. To allow overlaying the simulated spectra with the experimental cross sections, we rescaled all the simulated spectra such that the maximum value of the spectrum closest to resonance matched the experimental value. The model reproduces the broadening of the peaks as well as the asymmetry for the high-temperature data. At room temperature, a strong edge at larger frequency shifts is observed in the model, which is absent in the measurements. We attribute this to the presence of two mechanical modes, which will tend to soften this effect. An interesting feature in this model is that the spectra obtained with the laser on-resonance are not affected at all, and we indeed observed experimentally that at
the average detuning between the laser and cavity frequency, and ncmax is the maximum number of photons in the cavity when it is driven at resonance. The effective spring constant can be directly rescaled to obtain the frequency shift (Supplementary Note 5). As before, we numerically sample a thermal distribution to model the behaviour of the system, in this case by averaging over 104 different amplitudes x0, such that the displacement variance equals that from both mechanical modes in the experiment. Finally, we average the same number of Lorentzian lineshapes with the centre frequencies given by the simulated frequency shifts and their widths set to the median linewidth measured in the experiment, to approximate the intrinsic linewidth at that temperature (Supplementary Note 5). The resulting simulated spectra are shown in Fig. 5b,e and plotted as black solid lines in Fig. 5c,f. To allow overlaying the simulated spectra with the experimental cross sections, we rescaled all the simulated spectra such that the maximum value of the spectrum closest to resonance matched the experimental value. The model reproduces the broadening of the peaks as well as the asymmetry for the high-temperature data. At room temperature, a strong edge at larger frequency shifts is observed in the model, which is absent in the measurements. We attribute this to the presence of two mechanical modes, which will tend to soften this effect. An interesting feature in this model is that the spectra obtained with the laser on-resonance are not affected at all, and we indeed observed experimentally that at  the effect is much smaller if not entirely absent.
the effect is much smaller if not entirely absent.
We also observe that at higher optical powers, beyond ∼100 nW at 3 K, the influence of the nonlinear regime on the optical spring effect leads to imprinting of low-frequency noise on the mechanical motion as random drifting of the mechanical frequency. At higher powers still, self-oscillation regularly occurs. However, the fluctuations due to thermal motion can be larger than the amplitude at which a self-oscillating state would normally saturate, leading to highly complex dynamics. We believe this leads to observed irregular behaviour, including random hopping of the oscillation frequency between the two mechanical modes, and occasional occurrence of instabilities for both blue and red detuning. Further study and modelling is needed to explore this regime.
Discussion
Our analysis of both nonlinear transduction and backaction relies on a numerical model instead of an analytical description, as the typical order-by-order approximation to describe transduction breaks down at large relative cavity fluctuation strengths. This breakdown is related to the fact that the Taylor expansion used to describe the intracavity field24 as a function of the relative detuning  does not converge for all u. For example, at average detuning
does not converge for all u. For example, at average detuning  , the intracavity field can be written as
, the intracavity field can be written as

which does not converge for |u|>1. At this detuning, u=2δω/κ represents the cavity frequency fluctuations due to the thermal motion, meaning the power series does not converge when the mechanical motion changes the cavity frequency by more than a linewidth. Therefore, this model cannot be used to extrapolate the expected sensitivity of optomechanical measurements in the nonlinear regime we describe here. Our numerical model relies on a direct calculation of the optical response to mechanical motion, which can be performed for any cavity frequency change δω. It is however crucial to correctly simulate the distribution of mechanical amplitudes within the thermal mechanical state.
We have demonstrated the effects of the optomechanical nonlinearity in a system that operates in the regime  ≳1, and described how it modifies the optical response, transduction, and backaction over a wide range of temperatures. It is to be expected that a growing number of optomechanical systems will operate in this regime as parameters continue to improve, and the single-photon strong coupling regime (g0>κ, Γ) is approached. Indeed, various characteristics of the nonlinear regime we demonstrate are reminiscent of the expected effects due to quantum fluctuations in the single-photon strong coupling regime, including a modification of the optical response and the appearance of strong higher-order sidebands in optical fluctuation spectra. Whereas our sliced photonic crystal nanobeam devices demonstrate these effects for the bad-cavity limit, the regime has equally important impact for devices in the resolved-sideband regime
≳1, and described how it modifies the optical response, transduction, and backaction over a wide range of temperatures. It is to be expected that a growing number of optomechanical systems will operate in this regime as parameters continue to improve, and the single-photon strong coupling regime (g0>κ, Γ) is approached. Indeed, various characteristics of the nonlinear regime we demonstrate are reminiscent of the expected effects due to quantum fluctuations in the single-photon strong coupling regime, including a modification of the optical response and the appearance of strong higher-order sidebands in optical fluctuation spectra. Whereas our sliced photonic crystal nanobeam devices demonstrate these effects for the bad-cavity limit, the regime has equally important impact for devices in the resolved-sideband regime  , although precise manifestations are expected to vary. In particular, the optical excitation spectrum will be altered by displaying multiple discrete sidebands20,21. Moreover, backaction forces acquire an additional delay factor due to the longer lifetime of cavity excitation, which will lead to fluctuating damping and driving forces affecting the motion. As the manipulation of mechanical thermal noise is a topic of interest, for example, in sensing applications, it could be worthwhile to investigate the effects of the combination of dynamical backaction and the optomechanical nonlinearity. Notably, it would allow manipulating thermal fluctuations beyond a Gaussian distribution. Similar aims in the bad-cavity limit could be reached through nonlinear measurement, such as the displacement-squared measurements we demonstrated.
, although precise manifestations are expected to vary. In particular, the optical excitation spectrum will be altered by displaying multiple discrete sidebands20,21. Moreover, backaction forces acquire an additional delay factor due to the longer lifetime of cavity excitation, which will lead to fluctuating damping and driving forces affecting the motion. As the manipulation of mechanical thermal noise is a topic of interest, for example, in sensing applications, it could be worthwhile to investigate the effects of the combination of dynamical backaction and the optomechanical nonlinearity. Notably, it would allow manipulating thermal fluctuations beyond a Gaussian distribution. Similar aims in the bad-cavity limit could be reached through nonlinear measurement, such as the displacement-squared measurements we demonstrated.
Interestingly, the alteration of the optical response due to thermal motion provides a new method to directly determine the intrinsic optical linewidth κ and the optomechanical coupling rate g0: the ratio of different harmonics of the transduced mechanical spectrum allows retrieving the relative frequency fluctuations δωr.m.s./κ. Together with a measurement of the optical excitation linewidth (Methods section, equation (13)) this uniquely determines both g0 and κ. This method only requires further knowledge of the bath temperature and the mechanical frequency. We note that there is no need for any other calibration, including characterization of optical powers.
The large single-photon cooperativity C0 in the structures we present here offers prospects beyond the exploitation of the optomechanical nonlinearity, in particular for quantum measurement and control of mechanical motion. For example, the requirement for feedback cooling to the ground state (thermal occupancy below 1) is that the cooperativity  , where nc is the number of photons in the cavity5,50,51. In our sliced nanobeam structure, the measurement sensitivity is currently limited by the coupling efficiency, which we estimate to be η≈1.3% (Supplementary Note 4). The double-period modulation method we use to improve the coupling efficiency of a photonic crystal nanobeam cavity at normal incidence has previously been shown41 to yield a simulated collection efficiency of more than 20%. Therefore we expect that by either improving the optical design, or by employing waveguide-based coupling schemes49,51, the coupling can be further increased in our current free-space set-up. For example, with a detection efficiency of 2/9, ground state preparation would be in reach at a very modest minimum cavity occupation of nc>17 photons with the demonstrated parameters. Finally, the large optomechanical coupling strength in combination with low loss provides other opportunities for measurement-based control in the bad-cavity limit, such as conditional state preparation of the mechanical resonator by pulsed measurements52, or quantum state swapping between the optical and mechanical degrees of freedom27.
, where nc is the number of photons in the cavity5,50,51. In our sliced nanobeam structure, the measurement sensitivity is currently limited by the coupling efficiency, which we estimate to be η≈1.3% (Supplementary Note 4). The double-period modulation method we use to improve the coupling efficiency of a photonic crystal nanobeam cavity at normal incidence has previously been shown41 to yield a simulated collection efficiency of more than 20%. Therefore we expect that by either improving the optical design, or by employing waveguide-based coupling schemes49,51, the coupling can be further increased in our current free-space set-up. For example, with a detection efficiency of 2/9, ground state preparation would be in reach at a very modest minimum cavity occupation of nc>17 photons with the demonstrated parameters. Finally, the large optomechanical coupling strength in combination with low loss provides other opportunities for measurement-based control in the bad-cavity limit, such as conditional state preparation of the mechanical resonator by pulsed measurements52, or quantum state swapping between the optical and mechanical degrees of freedom27.
Methods
Sliced photonic crystal nanobeam design
Eigenfrequency calculations were performed using finite element software (COMSOL Multiphysics). For optical simulations, perfectly matched layers were used to allow the extraction of the optical radiation losses. To estimate ∂ωc/∂x, the optical frequency shift due to mechanical motion, x (half of the gap size) was increased by 1 nm the full length of the nanobeam, leading to a change in the simulated eigenfrequency.
The sliced nanobeam design confines light in the transverse direction due to total internal reflection, while along the nanobeam the photonic crystal patterning creates a bandgap for light. An optical cavity is formed by a defect region in the middle with holes of different shape and periodicity, which is tapered to the periodic outer region over 5 holes to minimize optical losses40. In addition, we create a low-efficiency outcoupling grating in the structure by making the hole sizes alternatingly 5% wider and narrower. This double-period modulation allows part of the cavity field to scatter out at normal incidence41, which is efficiently collected by our free-space optical measurement set-up. Our experimental results indicate that this strategy increases the coupling efficiency to the optical cavity from approximately 0.1% to 1–2% (Supplementary Note 4).
Fabrication
Devices were fabricated from a silicon-on-insulator substrate (SOITEC), with a 250 nm silicon device layer on top of 3 μm silicon oxide. Patterns were written using electron-beam lithography in an 80 nm layer of spincoated HSQ resist (FOX-15, Dow Corning) and developed using TMAH. The silicon layer was etched in an inductively coupled plasma etcher using a combination of Cl2 and HBr/O2 gases. Finally, the nanobeams were released to be free-standing by wet etching with HF, which also dissolves leftover resist and oxide-based deposits formed during plasma etching. The wet etch was followed by critical point drying to prevent collapse of the nanobeams. The device layer of silicon-on-insulator wafers typically contains compressive stress, which can induce buckling of the nanobeams even when using critical point drying. We avoided this by incorporating stress-relief features in the support structure around the free-standing nanobeams. We note that the fabricated devices exhibit optical quality factors that are somewhat lower (by a factor ∼2) compared to the designed value, likely due to remaining surface roughness, and structural deviation from the designed pattern.
Measurement set-up
A closed-cycle cryostat (Montana Cryostation C2) was used to control the sample temperature between 3 and 300 K. We used an aspheric lens positioned outside the cryostat window with an effective focal length of 8 mm a numerical aperture of 0.55 to focus the laser beam (New Focus Velocity 6725, linewidth ≤200 kHz) on the sample and to collect the reflection in free space. A balanced detector with two nominally identical photodiodes (New Focus 1817-FS) detected the output of the homodyne interferometer, schematically shown in Fig. 1c. The detector signal was then Fourier transformed and the spectrum recorded with an electronic real-time spectrum analyser (Agilent MXA). The optical power in the reference arm was 135 μW or more, ensuring that the optical shot noise was at least as large as the electronic noise. The pressure in the cryostat was typically 0.3 mbar at room temperature, and well below 10−4 mbar at cryogenic temperatures.
Sample thermalization
A measurement of the power dependence of the transduced signal (Supplementary Note 1) was performed to verify that the measurement of the thermal motion of the nanobeam is not influenced by additional heating by the laser beam down to the lowest temperature. We then used the temperature sensor placed next to the sample in the cryostat to calibrate the scale for the displacement power spectral density Sxx in Figs 2a and 4b. Measurements with different thermal radiation heat loads show that the presence of a cold window ensures that the sample is thermalized at all temperatures (Supplementary Note 2).
Balanced homodyne interferometer signal
The optical response of the balanced homodyne interferometer probing our cavity optomechanical system is a function of the average detuning  between the laser frequency and the cavity frequency, the frequency shift of the cavity due to mechanical motion δω, the homodyne phase θ, the cavity linewidth κ, and various constant factors such as the coupling efficiency to the cavity, and the optical power used for the measurement. To obtain the full expression, we start by describing the reflection from our nanobeam cavity using input-output theory
between the laser frequency and the cavity frequency, the frequency shift of the cavity due to mechanical motion δω, the homodyne phase θ, the cavity linewidth κ, and various constant factors such as the coupling efficiency to the cavity, and the optical power used for the measurement. To obtain the full expression, we start by describing the reflection from our nanobeam cavity using input-output theory

with η the coupling efficiency, sc is the amplitude of the reflected light and sin the amplitude of the input light. The term ceiφ is due to non-resonant scattering from the nanobeam structure or the substrate. The total detuning  is the sum of the laser detuning and the shift caused by mechanical motion. If φ=0, the resulting reflectivity shows a Lorentzian response, while other values will lead to the more general case of a Fano lineshape.
is the sum of the laser detuning and the shift caused by mechanical motion. If φ=0, the resulting reflectivity shows a Lorentzian response, while other values will lead to the more general case of a Fano lineshape.
Using balanced homodyne detection, with the light in the reference arm, or local oscillator, described as sLO=|sLO|eiθ and the input to the cavity sin taken to be real, the output of the detector is proportional to a virtual optical power P

Substituting  yields the relationship between the measurement output P and the displacement x.
yields the relationship between the measurement output P and the displacement x.
Optomechanical transduction with order-by-order approximation
We consider the Taylor expansion of the measurement output P for small fluctuations δω around 

For harmonic fluctuations δω=δω0 cos Ωmt, the individual terms of this expansion contribute at different frequencies. To leading order,  , which means the higher-orders are completely spectrally separated, and we can consider this expansion order-by-order. If multiple mechanical modes are coupled to the optical cavity, the expansion will also include cross terms ∝ cos(Ω1t)j−k cos(Ω2t)k, which are spectrally separated from higher-order terms in the same regime where the approximation holds for a single-mechanical mode. This means we can account for multiple modes by simply adding the variances they contribute in a specific order, and in the following we consider a single mode for simplicity.
, which means the higher-orders are completely spectrally separated, and we can consider this expansion order-by-order. If multiple mechanical modes are coupled to the optical cavity, the expansion will also include cross terms ∝ cos(Ω1t)j−k cos(Ω2t)k, which are spectrally separated from higher-order terms in the same regime where the approximation holds for a single-mechanical mode. This means we can account for multiple modes by simply adding the variances they contribute in a specific order, and in the following we consider a single mode for simplicity.
We measure the power spectral density SPP(Ω), whose integral over frequency gives the variance 〈P2〉. Averaging over the homodyne phase, the detuning dependence for (∂kP/∂ωk)2 has a simple Lorentzian lineshape, raised to the power (k+1), as we analyse elsewhere (La Gala et al., manuscript in preparation). The maximum contribution is therefore at resonance ( =0) and can be expressed as
=0) and can be expressed as

where A2=8PinPLOη2 is a constant prefactor that depends on the optical powers Pin, PLO in the signal and reference arm, respectively, and on the coupling efficiency to the cavity η.
We now calculate the band power at a frequency kΩm, where only the kth term of the Taylor expansion contributes, as

Since δω=(∂ωc/∂x)δx, we can use the properties of the higher moments of x. For thermal motion, and again using the order-by-order approximation24,53, we use

which can be directly substituted into equation (10) to obtain

used in equation (2).
Supplementary Fig. 1 shows a spectrogram demonstrating the detuning dependence of the nonlinear transduction.
Power spectral density and Voigt linewidth
We plot the power spectral density of the electronic output signal of our measurement set-up, which has units of W Hz−1. This corresponds to a power spectral density of a (virtual) optical power P, SPP, which has units of W2 Hz−1. As a consequence, the Lorentzian detuning dependence of the optomechanical transduction leads to a Lorentzian-squared dependence in the power spectral density. Similarly, we observe the square of the Gaussian distribution of cavity frequencies due to thermal motion. Therefore, we fit the square of a Voigt lineshape, which models the convolution of a Lorentzian and a Gaussian lineshape, to our data, and extract the linewidth of the non-squared Voigt lineshape. This value then directly corresponds to either the optical loss rate κ or the amplitude of the frequency fluctuations δωr.m.s., in the respective limits where  or vice versa.
or vice versa.
We use an empirical equation for the linewidth of a Voigt lineshape54

where κ is the linewidth of the Lorentzian lineshape and  is the linewidth of the Gaussian lineshape. To fit the linewidth as a function of temperature, we substitute
is the linewidth of the Gaussian lineshape. To fit the linewidth as a function of temperature, we substitute  . To account for multiple independent mechanical modes, we can calculate the individual optomechanical coupling rates from the asymptote of the fit curve if we know the ratio between the transduced peaks in the spectrum36. The variances due to the modes j add up,
. To account for multiple independent mechanical modes, we can calculate the individual optomechanical coupling rates from the asymptote of the fit curve if we know the ratio between the transduced peaks in the spectrum36. The variances due to the modes j add up,  , which means equation (1) is modified to
, which means equation (1) is modified to

Numerical model for nonlinear transduction
Time traces for the mechanical displacement x were generated for one or two resonance frequencies Ωm. To simulate thermal motion, we randomly change the amplitude A and phase  of harmonic motion x=A cos(Ωmt+
of harmonic motion x=A cos(Ωmt+ ). The points at which A and
). The points at which A and  are changed are taken from a Poissonian distribution with mean time between jumps taken to be the mechanical damping time Γ. The new amplitude is taken from an exponential distribution characterized by a mean proportional to the average thermal occupation
are changed are taken from a Poissonian distribution with mean time between jumps taken to be the mechanical damping time Γ. The new amplitude is taken from an exponential distribution characterized by a mean proportional to the average thermal occupation  , while the phase is taken from a uniform distribution. A time trace of the measurement output P was generated from the position time trace using our full model for the transduction (equation (7)) and phase-averaging the homodyne measurement. The discrete Fourier transform of this time trace allowed us to extract the signal strength at Ωm and at higher-order multiples or mixing terms.
, while the phase is taken from a uniform distribution. A time trace of the measurement output P was generated from the position time trace using our full model for the transduction (equation (7)) and phase-averaging the homodyne measurement. The discrete Fourier transform of this time trace allowed us to extract the signal strength at Ωm and at higher-order multiples or mixing terms.
Data availability
All relevant data is available upon request.
Additional information
How to cite this article: Leijssen, R. et al. Nonlinear cavity optomechanics with nanomechanical thermal fluctuations. Nat. Commun. 8, 16024 doi: 10.1038/ncomms16024 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Teufel, J. D. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Verhagen, E., Deléglise, S., Weis, S., Schliesser, A. & Kippenberg, T. J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 482, 63–67 (2012).
Wilson, D. J. et al. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature 524, 325–329 (2015).
Brooks, D. W. C. et al. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature 488, 476–480 (2012).
Safavi-Naeini, A. H. et al. Squeezed light from a silicon micromechanical resonator. Nature 500, 185–189 (2013).
Purdy, T. P., Yu, P.-L., Peterson, R. W., Kampel, N. S. & Regal, C. A. Strong Optomechanical Squeezing of Light. Phys. Rev. X 3, 031012 (2013).
Wollman, E. E. et al. Quantum squeezing of motion in a mechanical resonator. Science 349, 952–955 (2015).
Pirkkalainen, J.-M., Damskägg, E., Brandt, M., Massel, F. & Sillanpää, M. A. Squeezing of quantum noise of motion in a micromechanical resonator. Phys. Rev. Lett. 115, 243601 (2015).
Lecocq, F., Clark, J. B., Simmonds, R. W., Aumentado, J. & Teufel, J. D. Quantum Nondemolition measurement of a nonclassical state of a massive object. Phys. Rev. X 5, 041037 (2015).
Palomaki, T. A., Teufel, J. D., Simmonds, R. W. & Lehnert, K. W. Entangling mechanical motion with microwave fields. Science 342, 710–713 (2013).
Palomaki, T. A., Harlow, J. W., Teufel, J. D., Simmonds, R. W. & Lehnert, K. W. Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 495, 210–214 (2013).
Purdy, T. P., Peterson, R. W. & Regal, C. A. Observation of radiation pressure shot noise on a macroscopic object. Science 339, 801–804 (2013).
Murch, K. W., Moore, K. L., Gupta, S. & Stamper-Kurn, D. M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat. Phys. 4, 561–564 (2008).
Riedinger, R. et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 530, 313–316 (2016).
Sudhir, V. et al. Quantum correlations of light due to a room temperature mechanical oscillator for force metrology. Preprint at http://arxiv.org/abs/1608.00699 (2016).
Purdy, T. P., Grutter, K. E., Srinivasan, K. & Taylor, J. M. Observation of optomechanical quantum correlations at room temperature. Preprint at http://arxiv.org/abs/1605.05664 (2016).
Kampel, N. S. et al. Improving broadband displacement detection with quantum correlations. Phys. Rev. X 7, 021008 (2017).
Nunnenkamp, A., Børkje, K. & Girvin, S. M. Single-Photon Optomechanics. Phys. Rev. Lett. 107, 063602 (2011).
Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 107, 063601 (2011).
Lemonde, M.-A., Didier, N. & Clerk, A. A. Enhanced nonlinear interactions in quantum optomechanics via mechanical amplification. Nat. Commun. 7, 11338 (2016).
Doolin, C. et al. Nonlinear optomechanics in the stationary regime. Phys. Rev. A 89, 053838 (2014).
Brawley, G. A. et al. Nonlinear optomechanical measurement of mechanical motion. Nat. Commun. 7, 10988 (2016).
Vanner, M. R., Hofer, J., Cole, G. D. & Aspelmeyer, M. Cooling-by-measurement and mechanical state tomography via pulsed optomechanics. Nat. Commun. 4, 2295 (2013).
Khosla, K. E., Vanner, M. R., Bowen, W. P. & Milburn, G. J. Quantum state preparation of a mechanical resonator using an optomechanical geometric phase. New J. Phys. 15, 043025 (2013).
Bennett, J. S. et al. A quantum optomechanical interface beyond the resolved sideband limit. New J. Phys. 18, 053030 (2016).
Kippenberg, T. J., Rokhsari, H., Carmon, T., Scherer, A. & Vahala, K. J. Analysis of radiation-pressure induced mechanical oscillation of an optical microcavity. Phys. Rev. Lett. 95, 033901 (2005).
Marquardt, F., Harris, J. G. E. & Girvin, S. M. Dynamical multistability induced by radiation pressure in high-finesse micromechanical optical cavities. Phys. Rev. Lett. 96, 103901 (2006).
Vahala, K. et al. A phonon laser. Nat. Phys. 5, 682–686 (2009).
Bagheri, M., Poot, M., Li, M., Pernice, W. P. H. & Tang, H. X. Dynamic manipulation of nanomechanical resonators in the high-amplitude regime and non-volatile mechanical memory operation. Nat. Nanotechnol. 6, 726–732 (2011).
Krause, A. G. et al. Nonlinear radiation pressure dynamics in an optomechanical crystal. Phys. Rev. Lett. 115, 233601 (2015).
Carmon, T., Cross, M. & Vahala, K. Chaotic quivering of micron-scaled on-chip resonators excited by centrifugal optical pressure. Phys. Rev. Lett. 98, 167203 (2007).
Wu, J. et al. Mesoscopic chaos mediated by Drude electron-hole plasma in silicon optomechanical oscillators. Preprint at http://arxiv.org/abs/1608.05071 (2016).
Navarro-Urrios, D. et al. Nonlinear dynamics and chaos in an optomechanical beam. Nat. Commun. 8, 14965 (2017).
Leijssen, R. & Verhagen, E. Strong optomechanical interactions in a sliced photonic crystal nanobeam. Sci. Rep. 5, 15974 (2015).
Meenehan, S. M. et al. Pulsed Excitation dynamics of an optomechanical crystal resonator near its quantum ground state of motion. Phys. Rev. X 5, 041002 (2015).
Schilling, R. et al. Near-field integration of a SiN nanobeam and a SiO2 microcavity for Heisenberg-limited displacement sensing. Phys. Rev. Appl. 5, 054019 (2016).
Brennecke, F., Ritter, S., Donner, T. & Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. Science 322, 235–238 (2008).
Quan, Q. & Lončar, M. Deterministic design of wavelength scale, ultra-high Q photonic crystal nanobeam cavities. Opt. Express 19, 18529 (2011).
Tran, N.-V.-Q., Combrié, S., Colman, P., De Rossi, A. & Mei, T. Vertical high emission in photonic crystal nanocavities by band-folding design. Phys. Rev. B 82, 075120 (2010).
Thompson, J. D. et al. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 452, 72–75 (2008).
Miao, H., Danilishin, S., Corbitt, T. & Chen, Y. Standard quantum limit for probing mechanical energy quantization. Phys. Rev. Lett. 103, 100402 (2009).
Clerk, A. A., Marquardt, F. & Harris, J. G. E. Quantum measurement of phonon shot noise. Phys. Rev. Lett. 104, 213603 (2010).
Paraïso, T. K. et al. Position-squared coupling in a tunable photonic crystal optomechanical cavity. Phys. Rev. X 5, 041024 (2015).
Kaviani, H. et al. Nonlinear optomechanical paddle nanocavities. Optica 2, 271–274 (2015).
Jacobs, K., Tian, L. & Finn, J. Engineering superposition states and tailored probes for nanoresonators via open-loop control. Phys. Rev. Lett. 102, 057208 (2009).
Vanner, M. R. Selective linear or quadratic optomechanical coupling via measurement. Phys. Rev. X 1, 021011 (2011).
Gröblacher, S., Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Highly efficient coupling from an optical fiber to a nanoscale silicon optomechanical cavity. Appl. Phys. Lett. 103, 181104 (2013).
Genes, C., Vitali, D., Tombesi, P., Gigan, S. & Aspelmeyer, M. Ground-state cooling of a micromechanical oscillator: comparing cold damping and cavity-assisted cooling schemes. Phys. Rev. A 77, 033804 (2008).
Krause, A. G., Blasius, T. D. & Painter, O. Optical read out and feedback cooling of a nanostring optomechanical cavity. Preprint at http://arxiv.org/abs/1506.01249 (2015).
Vanner, M. R. et al. Pulsed quantum optomechanics. Proc. Natl Acad. Sci. USA 108, 16182–16187 (2011).
Hauer, B., Maciejko, J. & Davis, J. Nonlinear power spectral densities for the harmonic oscillator. Ann. Phys. 361, 148–183 (2015).
Olivero, J. & Longbothum, R. Empirical fits to the Voigt line width: a brief review. J. Quant. Spectrosc. Radiat. Transf. 17, 233–236 (1977).
Acknowledgements
We thank Thijs Kleijntjens for assistance in setting up the balanced homodyne interferometer. This work is part of the research programme of the Netherlands Organisation for Scientific Research (NWO), and supported by the European Union's Horizon 2020 research and innovation programme under grant agreement No 732894 (FET Proactive HOT). E.V. gratefully acknowledges an NWO-Vidi grant for financial support. J.T.M. thankfully acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 707364.
Author information
Authors and Affiliations
Contributions
R.L., J.T.M. and E.V. conceived the experiment. L.F. and R.L. fabricated the devices. G.R.L.G., L.F., J.T.M. and R.L. carried out numerical simulations, carried out experiments and analysed the results. R.L., J.T.M. and E.V. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Leijssen, R., La Gala, G., Freisem, L. et al. Nonlinear cavity optomechanics with nanomechanical thermal fluctuations. Nat Commun 8, ncomms16024 (2017). https://doi.org/10.1038/ncomms16024
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms16024
This article is cited by
-
Quadrature nonreciprocity in bosonic networks without breaking time-reversal symmetry
Nature Physics (2023)
-
Nonlinear interactions between vibration modes with vastly different eigenfrequencies
Communications Physics (2023)
-
Active-feedback quantum control of an integrated low-frequency mechanical resonator
Nature Communications (2023)
-
Non-Hermitian chiral phononics through optomechanically induced squeezing
Nature (2022)
-
Integrated optical-readout of a high-Q mechanical out-of-plane mode
Light: Science & Applications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.