Abstract
Unique superconductivity at surfaces/interfaces, as exemplified by LaAlO3/SrTiO3 interfaces, and the high transition temperature in ultrathin FeSe films, have triggered intense debates on how superconductivity is affected in atomic and electronic reconstructions. The surface of superconducting cubic spinel oxide LiTi2O4 is another interesting system because its inherent surface electronic and atomic reconstructions add complexity to superconducting properties. Investigations of such surfaces are hampered by the lack of single crystals or high-quality thin films. Here, using low-temperature scanning tunnelling microscopy and spectroscopy, we report an unexpected small superconducting energy gap and a long coherence length on the surface of LiTi2O4(111) epitaxial thin films. Furthermore, we find that a pseudogap opening at the Fermi energy modifies the surface superconductivity. Our results open an avenue for exploring anomalous superconductivity on the surface of cubic transition-metal oxides, where the electronic states are spontaneously modulated involving rich many-body interactions.
Similar content being viewed by others
Introduction
Recent advances in the atomic-scale synthesis and characterization of two-dimensional superconductors have kindled significant interest in their exotic electronic, orbital and magnetic structures1,2,3,4,5,6. In addition to the ultrathin superconducting films on substrates7,8,9,10,11,12,13,14,15,16,17,18,19,20, surfaces of cubic-structure superconducting transition-metal oxides provide another interesting platform, because the spontaneous electronic and atomic reconstructions on surfaces are expected to modify superconductivity. A particularly interesting system is the spinel oxide (AB2O4) superconductor. In this system, the cubic pyrochlore sublattice of B-atoms provides large degeneracy (frustration) of charge, spin and orbital states in bulk21,22, and a prominent degeneracy lifting at the surface is expected to lead rich electronic states on the surface. None of the previous studies, however, has revealed the electronic signature of modulated superconductivity on their surfaces.
Lithium titanate, LiTi2O4, is the only oxide superconductor with spinel structure23,24,25,26, and exhibits the highest superconducting transition temperature (Tc) with ∼13.7 K of any spinel superconductors27,28,29,30,31,32. It is known as a 3d0.5 metallic system (one half of an electron per Ti atom resides in the 3d states), and medium-coupling Bardeen–Cooper–Schrieffer (BCS) superconductivity with s-wave pairing symmetry has been proposed33,34,35,36. Recent transport data with epitaxial films showed an angle-dependent anomalous magnetoresistance, which is possibly related to a spin and orbital fluctuation effect22. On the basis of this data, the similarity between LiTi2O4 and high Tc cuprates has been discussed22. Although superconducting properties of bulk LiTi2O4 have been investigated extensively, studies of the superconductivity at LiTi2O4 surfaces have been hindered by the lack of single crystals and high-quality thin films. Recently, high-quality epitaxial LiTi2O4 thin films were successfully grown using pulsed laser deposition (PLD)37,38,39; however, investigations of the superconductivity on LiTi2O4 surfaces remain unexplored. Recently, we have developed a scanning tunnelling microscope (STM) combined with a PLD system40, and in situ investigation of the LiTi2O4 surface without exposing to air has became possible.
Here we report modified superconductivity at the surfaces of LiTi2O4(111) epitaxial thin films, using STM/scanning tunnelling spectroscopy (STM/STS) and first-principles density functional theory (DFT) calculations. From the atomic-scale observations of superconductivity, we present measurements of the unexpected small superconducting energy gap Δ and a long coherence length ξ values. Furthermore, we found that a superconducting gap exists on large energy scale pseudogap states. These results provide the spectroscopic evidence of spontaneous superconducting modification on the surface of cubic transition-metal oxides, paving an interesting path to explore exotic superconductivity involving rich interactions.
Results
Preparation of higher Tc sample with flat surface
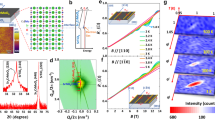
We found that low-temperature film deposition using PLD followed by post-deposition annealing increases Tc up to 13 K, together with improved surface flatness. We first compare the STM images of the films grown at substrate temperature Ts of 600 °C (Fig. 1a) and 400 °C (Fig. 1b). The former temperature is the typical growth temperature reported in the previous studies22,37,38,39. While many triangular-shaped islands are observed on both surfaces, the height of the islands is much smaller in the latter film, indicating that the surface roughness is strongly dependent on the growth temperatures. As the Ts is reduced from 600 to 400 °C, the root mean square (RMS) value of surface roughness, RRMS, improved from 0.86 (Fig. 1a) to 0.40 nm (Fig. 1b). To further improve the surface roughness, we investigated the post-deposition annealing effect on the film grown at Ts=400 °C; thin films were annealed at 600 °C in ultrahigh vacuum for an hour. Expectedly, the film became flatter to RRMS=0.28 nm (Fig. 1c). Furthermore, this RRMS value was improved to 0.21 nm for the film deposited at Ts=300 °C followed by the above-mentioned annealing (Fig. 1d and Supplementary Fig. 1).
(a,b) STM topographic images of as-deposited thin film at substrate temperature of 600 °C (a) and 400 °C (b). (c,d) STM images after post-deposition annealing (PDA) for films deposited at 400 °C (c) and 300 °C (d). Note that b,c are taken with using the same film. a–c are obtained at 77 K and d is obtained at 4.2 K (all the STM images were observed at a sample-bias voltage of +300 mV and a tunnelling current is about 10 pA). Scale bar, 80 nm (a–d). (e) Growth temperature dependence of root mean square of surface roughness (RRMS) values: as-grown samples (blue symbols) and after PDA (red symbols). The value of RRMS is evaluated from topographic images observed at a sample-bias voltage of +300 mV and a tunnelling current of 10 pA (scan area of 400 nm). (f) Temperature dependence of the field-cooled dc magnetic susceptibility for the LiTi2O4 films in a magnetic field of 50 Oe, which was applied parallel to the (111) plane. Clear diamagnetism is observed.
Importantly, this annealing process increases Tc values (Fig. 1f), in addition to the flattening of the surfaces. While the Tc values of the films grown at Ts=500 and 600 °C show 12.0 K and 12.5 K, respectively, the Tc increases up to 13.0 K for the films after annealing (red curves in Fig. 1f). The Tc value of ∼13 K is one of the highest values among reported values for LiTi2O4 epitaxial thin films22,37,38,39. We confirmed from X-ray diffraction that the films exhibit rocking-curve full-width at half-maximum of 0.36° for 444 peak, and that the lattice is fully relaxed from SrTiO3(111) substrate (Supplementary Fig. 2). The above results show that the quality of the sample is quite high. In the following investigations, we focus on the films deposited at Ts=300 °C followed by the post-deposition annealing in vacuum at 600 °C.
Atomic-scale order on LiTi2O4(111) film surface
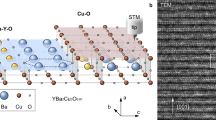
We observed, on the atomic level, a well-ordered triangular lattices and defects. Figure 2a shows the wide-area STM image of the LiTi2O4 surface, where flat terraces and dark spots with peculiar defect shapes were observed. In the close-up image (Fig. 2c), strong topographic corrugations (shown in blue) are observed together with weak topographic corrugations (shown in red), displaying three-fold symmetry. This is consistent with the inherent three-fold rotational symmetry along the [111] axis in a spinel system. The unit cell size was found to be ∼0.6 nm (Fig. 2c), which was independent of the location and sample-bias voltages Vs. This size well matches that of the unit cell of LiTi2O4 bulk (111) plane. We concluded that the protrusions of the triangular lattice originate from Ti atoms on the surface, as discussed later together with the nature of the defects (dark spots).
(a) Filled-state STM image of LiTi2O4(111) surface (11.6 nm × 11.6 nm, sample-bias voltage Vs of −900 mV, tunnelling current Iset of 30 pA). (b) Empty-state STM image (4 nm × 4 nm, Vs=+30 mV, Iset=30 pA). (c) Zoomed-up image (1.7 nm × 1.7 nm, Vs=+30 mV, Iset=30 pA) of b. The image shows three-fold symmetry representing the spinel crystal structure. Scale bars, 2 nm (a), 0.8 nm (b) and 0.3 nm (c).
Superconductivity in tunnelling spectra measurements
In addition to the atomic-scale corrugations, we observed clear signature of superconductivity in tunnelling spectra measurements at 4.2 K. The wide- and narrow-energy-range spectra were obtained at the area far from defects (see cross in Fig. 3a). To evaluate the superconducting gap Δ quantitatively, we analysed tunnelling spectra (Fig. 3b–d) using the Dynes formula41 convoluted with an energy derivative of the Fermi–Dirac function F.
(a) A topographic image obtained with a sample-bias voltage Vs of +30 mV and a tunnelling current of 30 pA. Scale bar, 2 nm. The red cross in a indicates the position where the spectra shown in b–d were obtained. (b,c) Tunnelling spectrum (dI/dV) obtained at a wide energy region (Vs of −190 mV to +190 mV and −100 mV to +50 mV, for a,b, respectively.) (c) High-resolution tunnelling spectrum for Vs between ±6 mV near the Fermi energy. Experimental curve (black dots) and fitted curve (red line) are shown in the same figure. See main body for the details of the fitting procedure. The energy windows of numerical derivative to obtain conductance spectrum were 15, 1.5 and 0.3 mV for a–c, respectively. The yellow region represents the Vs range of −6 to 6 mV. All the images and spectra were obtained at 4.2 K.

Here we assume that the normal-state density of states (DOS) near EF has a linear dependence with energy E, expressed as (a+bE), and Γ is the spectral broadening factor. The fitting parameters a, b, Δ and Γ are determined with fixed temperature T=4.2 K. We fitted our spectra (Fig. 3d) with a single-component isotropic pairing gap, and we obtained Δ=1.716±0.004 meV and Γ=0.321±0.004 meV. According to the BCS gap function, assuming the same Tc for surfaces and bulk (13 K), the obtained Δ value can be regarded as a gap value in the T=0 K limit. With using bulk Tc, the obtained 2Δ/kBTc value of 3.0 is unexpectedly small. In contrast, the 2Δ/kBTc values reported in polycrystalline LiTi2O4 samples range from 3.5 to 4.0 in point-contact spectroscopy33,34 and Andreev reflection36. A recent report using epitaxial LiTi2O4 thin films claims 2Δ/kBTc=4.07 from point-contact spectroscopy22, and thus the obtained value of 3.0 is much smaller than that of all the previous reports. Furthermore, the present value is even smaller than that for the weak coupling limit for s-wave BCS superconductivity of 3.52. We discuss later the possible origins of this unexpectedly small 2Δ/kBTc.
Coherence length on the surface
To further study the superconductivity on the surface, we investigated the value of ξ from the electronic structures around a magnetic vortex core. We first analysed the Vs dependent conductance (dI/dV) map around a single vortex core by applying an external magnetic field of 1.5 T perpendicular to the surface at 4.2 K (Fig. 4a–e). At Vs=−8 mV and +8 mV, we observed uniform conductance over the scanned region (Fig. 4a,e), whereas conductance values were depressed around the centre of images at Vs=−4 mV and +4 mV (Fig. 4b,d). This depressed conductance is a consequence of suppressed coherence peaks. In contrast, the conductance map at Vs=0 mV clearly represents enhanced conductance in the centre region (Fig. 4c). This enhanced zero-bias conductance around the centre region is because of pair breaking. These energy evolutions of conductance map indicate signatures of a vortex core (Fig. 4a–e), and the evolution of tunnelling spectra along line A–B in Fig. 4a clearly shows a typical spatial evolution of spectral shape across a vortex core (Fig. 4f).
A single vortex core is investigated at the temperature of 4.2 K with applying a magnetic field of 1.5 T normal to the surface. (a–e) Conductance mappings around an isolated single vortex core with various sample-bias voltages. A STM tip is stabilized at a tunnelling current of 30 pA and a sample-bias voltage of −10 mV. The energy window of numerical derivative to obtain conductance spectrum is 1 mV. Scale bars, 6 nm (a–e). (f) Spatial evolution of tunnelling spectra across the vortex centre (the line is shown in c). (g) Averaged spectra as a function of distance from vortex centre <r>. (h) Zero-bias conductance (ZBC) obtained from g. Coherence length of ∼12 nm is obtained by fitting the ZBC (see main text for details). A total 3,600 spectra (60 × 60) were taken with equal spacing in the region (a–e). We classified the area of Fig. 4a–e into 20 regions based on the distance from vortex centre (see also Supplementary Fig. 3). Interval of <r>, which is 5.758 nm, is set as error bars for x axis in h.
To evaluate ξ, we analysed the zero-bias conductance data as a function of the radial distance from the vortex core centre r (Supplementary Fig. 3). We first extracted the zero-bias conductance Z as a function of mean distance r. Then, we fitted the Z(r) by the exponential decay function Z(r)=Z(∞)+Aexp(−r/ξ), where A is a constant and Z(∞) is the normalized zero-bias conductance away from the vortex core42. From the fitting, we obtained ξ=12±1 nm (Fig. 4h), A=0.505±0.02 and Z(∞)=0.512±0.03. This ξ value is much larger than the ξGL values obtained from the upper critical field (Hc2) using the formula Hc2=Φ0/2πξGL2 (Φ0 is the magnetic flux quanta) based on Ginzburg–Landau theory. For epitaxial LiTi2O4 thin films, the ξGL values estimated from macroscopic measurements are 4.1–4.7 nm (refs 22, 37). Whereas excellent agreement between ξ and ξGL values have been reported in other superconducting systems such as Fe-based superconductors42,43, the values of ξ obtained on the surface of LiTi2O4 are much larger than the estimated ξGL obtained from transport measurement techniques. The deviation of ξ from ξGL also implies that there is a difference in superconductivity between surface and bulk.
Discussion
To understand the superconductivity on the LiTi2O4(111) surface, we performed first-principles calculations. We first calculated the bulk electronic structures to understand the triangular lattice observed in the STM images. Figure 5a shows the calculated partial DOS for bulk. The Ti 3d states predominantly contribute near EF, and the influence of Li atoms should be negligible to the STM images. Thus, the main protrusions of the triangular lattice observed in the topographic image (indicated by blue colour in Fig. 2) correspond to Ti atoms on the surface.
(a) Calculated DOS for bulk LiTi2O4. (b) Crystal structure with bulk continuum, together with four bulk-cut planes represented by broken lines. Vertical axis is along the (111) crystal orientation. (c) The topographic image of a defect on the surface (a sample-bias voltage of +30 mV, a tunnelling current of 30 pA). Scale bar, 0.6 nm (c). Top view of TiL2- (d) and TiLi1- (e) terminated surfaces. See b for the colour of the circles. (f) Calculated DOS for the topmost Ti atoms in TiL2- and TiLi1-terminated surfaces. DOS for bulk is shown again for clarity. Here 0 on the horizontal axes in a,f correspond to the Fermi energy.
To further understand the LiTi2O4(111) surface, we calculated the electronic structures of four possible bulk-cut surfaces: two-types of O-terminated, Kagome-lattice Ti-terminated, and TiLi2-terminated surfaces (see four dotted lines in Fig. 5b). These surfaces were optimized structurally and the electronic states of the reconstructed surfaces were investigated. Both the two O-terminated surfaces resulted in an insulating band structure (Supplementary Fig. 4a,b), which is inconsistent with the experimental metallic tunnelling spectra (Fig. 3). For the Kagome-lattice Ti-terminated surface, the simulated charge density plot (Supplementary Fig. 4c) also shows inconsistency with the experimental topographic image (Fig. 2). Consequently, neither the O-terminated nor the Kagome-lattice Ti-terminated surface reproduced the experimental results (Supplementary Fig. 4). On the other hand, TiLi2-terminated surface shows metallic states, and the arrangement of the protrusions and their nearest neighbour distance (0.6 nm) observed in the STM image (Fig. 2) can be explained by the framework of Ti-triangular lattice of TiLi2 layer.
We focus on the TiLi2-terminated surface, and further investigate the effect of Li-layer deficiency near surface since Li may be easily deficient during depositions process due to its high volatility. The TiLi2-terminated surface contains a triangular lattice of Ti atoms, and two layers of Li atoms: Li atoms displaced towards the vacuum (hereafter called higher Li layer, dark green circle in Fig. 5b) and those displaced towards the bulk (hereafter called lower Li layer, light green circle in Fig. 5b). Three possible models of surface terminations are considered: a stoichiometric TiLi2-terminated surface, a surface without the higher Li layer (TiLi1-terminated surface), and a surface without both higher and lower Li layer (TiLi0-terminated surface) (Fig. 5b).
On the basis of the following discussion, we could exclude TiLi0-terminated surface by showing that Li atoms reside at the vicinity of the topmost Ti-triangular lattice. Figure 5c shows a close-up image of the dark spots observed in the wide-area STM image (Fig. 3a). Three oval protrusions are observed, and this image indicates that a defect centre is around the middle of the three oval protrusions. Considering that the ovals are at the Ti sites, and taking into account the crystal structure of spinel system, the defects could be identified as a point-Li defect. Indeed, the dark contrast around this point-Li defect, observed at a negative sample-bias voltage of −900 meV, is consistent with hole-doping nature of Li vacancy (Fig. 2a). These results demonstrate that Li atoms reside at the vicinity of the topmost Ti-triangular lattice. Accordingly, the results exclude TiLi0 termination, and the surface of the films is terminated with either TiLi2 or TiLi1 structure. We note that the density of point-Li defects on the surface is <2% of Li atoms. Thus, we speculate that the impact of the presence of point-Li defects on superconductivity can be negligible25, unless the defects on the surfaces induce local magnetic moments.
We now compare the DOS at EF, N(EF), of a bulk and that of the TiLi2- and TiLi1- terminated surfaces, and reveal that both surfaces have smaller N(EF) than that of the bulk. Our DFT calculations for bulk show a peak structure at EF (Fig. 5a), which is consistent with previous calculations using the linear muffin-tin orbital method44 and full-potential linearized augmented plane wave45. The simulated peak structure at EF is also consistent with an experimental report of large normal-state electronic-specific heat, which is a measure of N(EF) for bulk35. On the TiLi2- (Fig. 5d) and TiLi1- (Fig. 5e) terminated surfaces, a broken lattice symmetry normal to the surface lifts the degeneracy of the t2g orbitals and modifies the orbital states on the surface. Compared to the bulk, we observed reduction of the N(EF) at the topmost Ti atoms for both TiLi2 and TiLi1 (Fig. 5f). Because the smaller N(EF) leads to lower Tc according to the BCS theory, the calculation naively suggest suppressed superconductivity on the surface.
Based on the above discussions, we present here coherent interpretation of the experimental results. As we experimentally observed a pseudogap state (shaded red in Fig. 3a,b), which is expected to be absent in bulk, the modified superconductivity on the surface is a reasonable hypothesis. Indeed, using bulk Tc and surface Δ, the 2Δ/kBTc value becomes anomalously small. This is puzzling since the value 3.0 is much smaller than that for a weak coupling limit of BCS superconductors (3.52). However, this puzzle can be explained by considering the presence of a non-superconducting or reduced-Tc surface layer. Moreover, the large ξ value can possibly be understood as the reduced N(EF) due to pseudogap formation on the surface. The Fermi velocity vF is proportional to 1/N(EF); therefore, based on the formula ξ = vF/D derived from BCS theory, the larger vF together with smaller D on a surface increases ξ more than that for the bulk value. Beyond the framework of the less-interacting picture, it is an interesting future subject to investigate relations between modified superconductivity, pseudogap formation and frustration effects on this (111) oriented spinel oxide surface.
In summary, we have investigated superconductivity in the atomically well-defined surface of LiTi2O4(111) thin films, using STM/STS and first-principles calculations. We provided spectroscopic evidence of modified superconductivity on the surface, originating from the formation of a pseudogap in the DOS. Our study has made an essential first step towards exploring superconducting phenomena emerging from spontaneous atomic and electronic reconstruction on surfaces, including different film orientation46, of superconducting cubic transition-metal oxides.
Methods
Samples and characterizations
We used a low-temperature STM connected with a PLD chamber. This system enables us to investigate thin film surfaces immediately after their deposition, without exposing surfaces to air. The base pressure of the PLD chamber was 5 × 10−11 Torr. Thin films of LiTi2O4 are grown on Nb(0.05 wt %)-doped SrTiO3(111) substrate using PLD with a KrF excimer laser (wavelength λ=248 nm). We used Li4Ti5O12 target for PLD film growth to compensate the Li loss during depositions. Substrates were annealed at 1,000 °C for an hour in oxygen under a partial pressure PO2=5 × 10−7 Torr before film depositions. Substrates were resistively heated, and their temperatures were monitored using a pyrometer. We deposited film at a substrate temperature Ts=300 °C under PO2=5 × 10−7 Torr followed by post-deposition annealing at 600 °C in ultrahigh vacuum for one hour. During thin film depositions, pulse repetition and fluence were set at 2 Hz and 1 J cm−2, respectively. Film thickness, measured ex situ using a DEKTAK 3030ST mechanical profiler, was determined to be about 100 nm. The STM data shown in Fig. 1a-c were taken at liquid-nitrogen temperature (77 K). The rest of STM data were taken at liquid-helium temperature (4.2 K). We obtained differential conductance values (dI/dV) from the numerical derivatives of I (tunnelling current) − V (voltage) curves. For ex situ characterization, we measured X-ray diffraction pattern and temperature dependence of magnetization after in situ STM/STS measurements.
First-principles calculations
For the first-principles calculations, we used DFT with the code Quantum ESPRESSO, with the generalized gradient approximation and ultra-soft pseudopotential scheme47,48,49,50,51. Cutoff energies for the Kohn–Sham orbitals and charge density of 32.5 and 45 Ry are imposed. The Brillouin-zone summation is evaluated using 3 × 3 × 1 and 12 × 12 × 1 k-point sampling for the structure optimizations and the DOS calculations, respectively. For the DOS broadening, we applied a simple Gaussian broadening method with broadening parameter of 0.005 Ry. Convergence criteria of the structure optimization are 10 × 10−3 for forces and 10 × 10−4 for energy. For the calculation of the near-surface atomic/electronic structures, we use the symmetric slab model with four unit cells along the (111) direction on each side. In the structure optimization, the topmost surface structures are initiated from bulk cuts. The atomic positions of the Ti atoms at the centre of the symmetric slab model along the (111) direction are fixed during optimization. Spin degrees of freedom and electron–electron correlations are not included in the calculation.
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
Additional information
How to cite this article: Okada, Y. et al. Scanning tunnelling spectroscopy of superconductivity on surfaces of LiTi2O4(111) thin films. Nat. Commun. 8, 15975 doi: 10.1038/ncomms15975 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bozovic, I., Logvenov, G., Belca, I., Narimbetov, B. & Sveklo, I. Epitaxial strain and superconductivity in La2-xSrxCuO4 thin films. Phys. Rev. Lett. 89, 107001 (2002).
Gozar, A. et al. High-temperature interface superconductivity between metallic and insulating copper oxides. Nature 455, 782–785 (2008).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat. Phys. 7, 767–771 (2011).
Li, L., Richter, C., Mannhart, J. & Ashoori, R. C. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nat. Phys. 7, 762–766 (2011).
Scheurer, M. S. & Schmalian, J. Topological superconductivity and unconventional pairing in oxide interfaces. Nat. Commun. 6, 6005 (2014).
Gor’kov, L. P. & Rashba, E. I. Superconducting 2D system with lifted spin degeneracy: mixed singlet-triplet state. Phys. Rev. Lett. 87, 037004 (2001).
Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931 (2012).
Ge, J. F. et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3 . Nat. Mater. 14, 285–289 (2015).
Shiogai, J., Ito, Y., Mitsuhashi, T., Nojima, T. & Tsukazaki, A. Electric-field-induced superconductivity in electrochemically etched ultrathin FeSe films on SrTiO3 and MgO. Nat. Phys. 12, 42–46 (2016).
Miyata, Y., Nakayama, K., Sugawara, K., Sato, T. & Takahashi, T. High-temperature superconductivity in potassium-coated multilayer FeSe thin films. Nat. Mater. 14, 775–779 (2015).
Guo, Y. et al. Superconductivity modulated by quantum size effects. Science 306, 1915 (2004).
Qin, S., Kim, J., Niu, Q. & Shih, C. K. Superconductivity at the two-dimensional limit. Science 324, 1314–1317 (2009).
Nishio, T., Ono, M., Eguchi, T., Sakata, H. & Hasegawa, Y. Superconductivity of nanometer-size Pb islands studied by low-temperature scanning tunneling microscopy. Appl. Phys. Lett. 88, 113115 (2006).
Zhang, T. et al. Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 6, 104 (2010).
Uchihashi, T., Mishra, P., Aono, M. & Nakayama, T. Macroscopic superconducting current through a silicon surface reconstruction with indium adatoms: Si(111)−(✓7 × ✓3)−In. Phys. Rev. Lett. 107, 207001 (2011).
Yoshizawa, S. et al. Imaging Josephson vortices on the surface superconductor Si(111)−(✓7 × ✓3)−In using a scanning tunneling microscope. Phys. Rev. Lett. 113, 247004 (2014).
Brun, C. et al. Remarkable effects of disorder on superconductivity of single atomic layers of lead on silicon. Nat. Phys. 10, 444–450 (2014).
Joe, Y. I., Abbamonte, P. & Geck, J. Orbital textures and charge density waves in transition-metal dichalcogenides. Nat. Phys. 11, 328–331 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2 . Science 350, 1353–1357 (2015).
Lee, S. et al. Frustrated magnetism and cooperative phase transitions in spinels. J. Phys. Soc. Japan 79, 011004 (2010).
Jin, K. et al. Anomalous magnetoresistance in the spinel superconductor LiTi2O4 . Nat. Commun. 6, 7183 (2015).
Bragg, W. The structure of magnetite and the spinels. Nature 95, 561–561 (1915).
Johnston, D. C., Prakash, H. & Zachariasen, W. H. High temperature superconductivity in Li-Ti-O ternary system. Mat. Res. Bull 8, 777–784 (1973).
Johnston, D. C. Superconducting and normal state properties of Li1+xTi2−xO4 spinel compounds. I. Preparation, crystallography, superconducting properties, electrical resistivity, dielectric behavior, and magnetic susceptibility. J. Low Temp. Phys. 25, 145 (1976).
Callum, R. W., Johnston, D. C., Luengo, C. A. & Maple, M. P. Superconducting and normal state properties of Li1+xTi2−xO4 spinel compounds. II. Low-temperature heat capacity. J. Low Temp. Phys. 25, 177 (1976).
Robbins, M., Willens, R. H. & Miller, R. C. Superconductivity in the spinels CuRh2S4 and CuRh2Se4 . Solid State Commun. 5, 933 (1967).
Shelton, R. N., Johnston, D. C. & Adrian, H. Measurement of the pressure dependence of Tc for superconducting spinel compounds. Solid State Commun. 20, 1077 (1976).
Hagino, T. et al. Superconductivity in spinel-type compounds CuRh2S4 and CuRh2Se4 . Phys. Rev. B 51, 12673 (1995).
Ito, M. et al. Pressure-induced superconductor-insulator transition in the spinel compound CuRh2S4 . Phys. Rev. Lett. 91, 077001 (2003).
Cao, G. et al. Suppression of metal-to-insulator transition and appearance of superconductivity in Cu1−xZnxIr2S4 . Phys. Rev. B 64, 214514 (2001).
Luo, H. et al. Superconductivity in the Cu(Ir1-xPtx)2Se4 spinel. Phys. Rev. B 87, 214510 (2013).
Ng, K. W., Khim, Z. G., Shum, D. P. & Wolf, E. L. Vacuum tunneling spectroscopy of this film and bulk polycrystalline superconductors. Surf. Sci. 181, 37–45 (1987).
Ekino, T. & Akimitsu, J. Superconducting energy gap in spinel compound Li1+xTi2−xO4 from electron tunneling. Physica B 165, 1599 (1990).
Sun, C. P. et al. Magnetic field dependence of low-temperature specific heat of the spinel oxide superconductor LiTi2O4 . Phys. Rev. B 70, 054519 (2004).
Tang, L. et al. Electrical resistivity and Andreev reflection spectroscopy of the superconducting oxide spinel LiTi2O4 . Phys. Rev. B 73, 184521 (2006).
Chopdekar, R. V., Wong, F. J., Takamura, Y., Arenholz, E. & Suzuki, Y. Growth and characterization of superconducting spinel oxide LiTi2O4 thin films. Physica C 469, 1885–1891 (2009).
Kumatani, A. et al. Growth processes of lithium titanate thin films deposited by using pulsed laser deposition. Appl. Phys. Lett. 101, 123103 (2012).
Oshima, T., Niwa, M., Yokoyama, K. & Ohtomo, A. Pulsed-laser deposition of superconducting LiTi2O4 ultrathin films. J. Cryst. Growth 419, 153–157 (2015).
Iwaya, K., Shimizu, R., Hashizume, T. & Hitosugi, T. Systematic analyzes of vibration noise of a vibration isolation system for high-resolution scanning tunneling microscopes. Rev. Sci. Instrum 82, 083702 (2011).
Dynes, R. C., Narayanamurti, V. & Garno, J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509 (1978).
Song, C. L. et al. Suppression of superconductivity by twin boundaries in FeSe. Phys. Rev. Lett. 109, 137004 (2012).
Song, C. L. et al. Dopant clustering, electronic inhomogeneity, and vortex pinning in iron-based superconductors. Phys. Rev. B 87, 214519 (2013).
Satpathy, S. & Martint, R. M. Electronic structure of the superconducting oxide spinel LiTi2O4 . Phys. Rev. B 36, 7269 (1987).
Massidda, S., Yu, J. & Freeman, A. J. Electronic structure and properties of superconducting LiTi2O4 . Phys. Rev. B 38, 11352 (1988).
He, G. et al. Anisotropic electron-phonon coupling in the spinel oxide superconductor LiTi2O4 . Phys. Rev. B 95, 054510 (2017).
Giannozzi, P. et al. Quantum espresso. J. Phys. Condens. Matter 21, 395502 (2009).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 136, B864 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, 1133 (1965).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892 (1990).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Acknowledgements
We thank Y. Takagi and K. Yamamoto for experimental assistance, and T. Hanaguri, T. Machida, Y. Yoshida, H. Kawasoko and K. Sato for useful discussions. Y.O. acknowledges funding from JSPS KAKENHI Grant Nos. 26707016 and 25886004. T.H. acknowledges funding from JSPS KAKENHI Grant Nos. 26246022, 26106502, 26108702, 26610092, JST-PRESTO and JST-CREST programme. S.W. acknowledges funding from JSPS KAKENHI Grant No. 15H03561. This work was supported by the World Premier Research Center Initiative (WPI), promoted by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. We thank P. Han for the critical reading of this manuscript.
Author information
Authors and Affiliations
Contributions
Y.O. pursued film growth, STM/STS measurements and data analysis. Y.A. performed the first-principles calculations. Y.O., R.S., S.S. and T.H. discussed the experimental results. Y.A., E.M. and S.W. discussed the theoretical calculations. All authors discussed the conclusions of this paper. Y.O. and T.H. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Okada, Y., Ando, Y., Shimizu, R. et al. Scanning tunnelling spectroscopy of superconductivity on surfaces of LiTi2O4(111) thin films. Nat Commun 8, 15975 (2017). https://doi.org/10.1038/ncomms15975
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15975
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.