Abstract
To know the properties of a particle or a wave, one should measure how its energy changes with its momentum. The relation between them is called the dispersion relation, which encodes essential information of the kinetics. In a magnet, the wave motion of atomic spins serves as an elementary excitation, called a spin wave, and behaves like a fictitious particle. Although the dispersion relation of spin waves governs many of the magnetic properties, observation of their entire dispersion is one of the challenges today. Spin waves whose dispersion is dominated by magnetostatic interaction are called pure-magnetostatic waves, which are still missing despite of their practical importance. Here, we report observation of the band dispersion relation of pure-magnetostatic waves by developing a table-top all-optical spectroscopy named spin-wave tomography. The result unmasks characteristics of pure-magnetostatic waves. We also demonstrate time-resolved measurements, which reveal coherent energy transfer between spin waves and lattice vibrations.
Similar content being viewed by others
Introduction
Spin waves (SWs) can be classified into the following three classes: exchange, dipole-exchange and pure-magnetostatic spin waves1,2,3,4. Exchange SWs refer to a type of spin waves in which the dispersion relations are dominated by exchange interaction; neutron scattering has been used to measure their dispersion relations5. Dipole-exchange SWs refer to a type of spin waves affected both by exchange interaction and magnetostatic dipole interaction; Brillouin light scattering holds an unchallenged position in their observation6,7,8. The third type is pure-magnetostatic SWs whose dispersion is explained without exchange interaction1,2,3,4. Spin waves in the magnetostatic regime are characterized by complicated and anisotropic dispersion relations; for instance, their slope may even become negative for the so-called backward volume magnetostatic waves. Although they are currently employed in spintronics and micromagnetics9,10,11,12,13, a dispersion spectroscopy of pure-magnetostatic waves is still missing; to observe the dispersion requires a new concept in spin-wave spectroscopy.
The most traditional principle of spectroscopy is diffraction caused by periodic structures, such as a grating or a crystal lattice14. Many methods of neutron and optical scattering spectroscopy, including Brillouin light scattering, are based on this mechanism5,6,7,8,10,13.
Another powerful principle of spectroscopy is the Fourier transform (FT) method, which has recently become more attractive because of advances in optical- and data-processing technologies as demonstrated by phonon-polariton spectroscopy15,16,17,18. In the FT method, all possible waves are excited at once, and power spectra are obtained by calculating the FT of the excited waveform. Such methods have been introduced in some fields including FT infrared spectroscopy (FTIR)17 and NMR spectroscopy15, and rapidly turned into versatile tools spread all over the world.
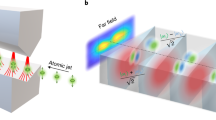
In the following, we present spin-wave FT spectroscopy which can reconstruct the dispersion curves of spin waves: we name it spin-wave tomography (SWaT). An ultrashort light pulse is focused on a very small surface area of a magnet to excite spin waves11,19,20,21,22,23,24,25. When the pulse duration and the excitation area are infinitesimally small, the pulse consists of all temporal and spatial wave components according to the Fourier theorem. Then, spin waves of all wave vectors can be created simultaneously and propagate radially from the excitation point. The created spin waves are detected using a magneto-optical imaging technique26 (see Methods section for details). By Fourier transforming the observed propagating waveform with respect to time and spatial coordinates, power spectra of the spin-wave propagation are obtained as a function of the frequency f and the wavenumber vector k. The spin-wave dispersion relations are then read from the spectra (Supplementary Note 1). The lateral sample size should be larger than the spin-wave decay length to avoid extrinsic standing-wave formation caused by reflection of the spin waves at the sample edges. This method gives access to the spin-wave dispersion with wavelengths typically larger than a micrometre. This is the principle of the SWaT developed here. To obtain the spectra, clear Faraday rotation signals with high spatial resolution are indispensable. Thanks to a recently developed technique to acquire absolute Faraday rotation angles as a function of time and position26, we report here the dispersion structures of pure-magnetostatic spin waves observed with SWaT.
Results
SWaT measurements
Figure 1 illustrates our experimental setup. A 100 fs-duration intense laser pump pulse was focused to a small round area (7 μm2) of a 4.0 μm-thick LuIG (001) film (see Methods section for details). The pump pulse excites spin waves by photo-magnetic effects, predominantly photo-induced demagnetization11,19,22 and magnetoelasticity24,27,28,29 (see below). The temporal evolution of the excited magnetization texture was obtained from the polarization rotation angle of the probe beam, which represents the local magnetization component along the light propagation via the optical Faraday effect26,30. To acquire temporal evolution data, the time delay t between the pump and the probe pulses was scanned. By Fourier transforming the temporal and spatial dependence of the Faraday rotation angle, we obtained power spectra of the Faraday rotation: SWaT power spectra, which reflect the k-dependent dynamical magnetic susceptibility31 (Supplementary Note 1).
Spin-wave tomography (SWaT) is based on the observation of the propagation dynamics of spin waves with the pump-and-probe magneto-optical imaging method. Various modes of spin waves are excited simultaneously by the illumination of the pump laser pulse in magnetic materials. The propagation dynamics of the spin waves are measured through the Faraday effect on the probe pulse (θF), which is proportional to the magnetization along the direction normal to the sample surface (mz). The images of θF are obtained by analyzing the transmission images (Iα) observed at various angles of the analyzer (α)26. The spin-wave dispersion relations are reconstructed by Fourier transforming the propagating waveform of the spin waves.
Figure 2a shows a spectrum for a non-magnetic Gd3Ga5O12 (GGG) crystal that does not carry spin waves obtained by the above SWaT method as a function of the wavenumber k along the [100] direction and the frequency f. We confirm that no signals appear in the spectrum for this non-magnetic medium, and then move on to measurements on magnetic materials.
(a) A SWaT spectrum obtained for a paramagnetic GGG substrate without spontaneous magnetization. (b) SWaT spectra for the LuIG sample with wavenumber k parallel to the magnetization M, which was aligned along the [100] axis by an in-plane magnetic field H. We observe three different dispersion curves, which are schematically shown in (d). TA, LA and MV represent the transverse acoustic phonon, the longitudinal acoustic phonon and the magnetostatic volume mode branches, respectively. The white dashed curves are calculated by a magnetostatic spin wave theory4 with the following parameters: saturation magnetization 4πMs=780 G, cubic anisotropy Kc=2.3 × 103 erg cm−3 and uniaxial magnetic anisotropy Ku=−1.2 × 104 erg cm−3. (c) A schematic of the experimental configuration. φ is defined as the angle between k of spin waves and the orientation of M. (d) A schematic of the three branches observed in (b). (e) A three-dimensional contour plot (at the intensity of 0.7 in the scale shown in (a) of the SWaT intensity representing spin waves (red) and phonons (blue). The direction of M is indicated by the green arrow.
In Fig. 2b, we show a SWaT spectrum obtained for a ferrimagnetic LuIG (001) film with a magnetic field (H) applied in the [100] direction. Here, k is set along the [100] direction (φ=0°, where φ is defined in Fig. 2c). In Fig. 2b, importantly, clear signals (orange colour) appear around 0.5 GHz-2.0 GHz that are labelled as magnetostatic volume wave (MV) (Fig. 2d,e). The signals shift towards higher frequencies almost proportional to the external magnetic field H. This proves that the signals are caused by magnetic excitations.
Notable is that the spectra in Fig. 2b disclose a dispersion curve with negative slope; the signal frequency f decreases with increasing k, which is a distinct feature of backward volume magnetostatic modes that are expected to be prominent near k=0. The experimental signal (orange colour in Fig. 2b) is well reproduced by an analytical expression for backward volume magnetostatic modes4 (dashed white curve in Fig. 2b). This is evidence for the observation of pure-magnetostatic spin-wave dispersion curves (Supplementary Movie 1). Higher-order standing spin waves are less visible in the transmission Faraday experiments due to their oscillations along the thickness direction4.
In all the spectra measured for LuIG, we observed low-frequency signals, labelled as transverse acoustic (TA) phonon and longitudinal acoustic (LA) phonon in Fig. 2b, each of which exhibits a linear k dependence (f ∝ k). The TA (LA) signal is assigned to transverse (longitudinal) acoustic phonon dispersion, since its slope, v=3.0 km s−1 (6.2 km s−1), is consistent with the transverse (longitudinal) sound velocity32. This means that low-frequency lattice vibrations are coupled to magnetization oscillations, and the present method is sufficiently sensitive to pick them up.
Angular dependence of SWaT
In Fig. 3a, we show the k-direction dependence of the obtained SWaT spectra for LuIG (Supplementary Movie 1). With changing the direction of k, the dispersion drastically changes, again consistent with magnetostatic spin wave theory4. The slope of the MV dispersion changes from negative to positive when the angle (φ) between k and M (Fig. 2c) is around 30°. This is caused by the uniaxial magnetocrystalline anisotropy along the surface normal; the experimental results are well reproduced by a theoretical calculation4 including this uniaxial anisotropy, shown as the white dashed curves in Fig. 3a. The dispersion signal labelled as DE in Fig. 3a can be assigned to a spin wave called a magnetostatic Damon-Eshbach mode4. The dispersion curves of MV and DE show negative and positive slopes, respectively, consistent with microwave absorption data33. For comparison, in Fig. 3b, we show numerically calculated power spectra of the pure-magnetostatic spin waves for the k directions in Fig. 3a; the temporal evolution of the out-of-plane magnetization distribution generated by a sudden change in the magnetization at the origin was calculated by solving the Landau–Lifshitz–Gilbert equation34. The parameters are the same as those used for the fits in Fig. 3a. The measured dispersion curves are well reproduced by the calculations for all k directions. This demonstrates again that the observed dispersion signals pertain to pure-magnetostatic spin waves, and that SWaT works properly and is powerful enough to directly map them.
(a) Experimentally obtained angular dependence of the SWaT spectra for various k directions. The angle (φ) between k and M is shown at the top of each figure. The branches of spin waves labelled as DE and MV represent the magnetostatic Damon–Eshbach and magnetostatic volume modes, respectively. The white dashed curves are calculated by magnetostatic spin wave theory4. (b) Spin-wave dispersion obtained by a micromagnetic simulation (see text) with the same parameters as in (a). The white dashed lines represent the phonon dispersion.
Time-resolved SWaT
Finally, we present time-resolved spectra that provide information about the spin-wave excitation mechanism and the role of phonons. Time-resolved SWaT spectra were obtained by clipping out data over a time interval, Δt, centred around a time, tc, using a Gaussian window function and performing the SWaT analysis for the clipped data (Supplementary Note 2). Here, we set Δt as 2.8 ns corresponding to the frequency resolution of ∼0.4 GHz.
We observed significant difference in the time evolution of the spectral intensity under the external magnetic fields of 560 Oe (Fig. 4a) and 40 Oe (Fig. 4b,c). This is attributed to the difference in the dominant spin-wave excitation mechanisms: the photo-induced demagnetization or the magnetoelastic coupling. Figure 4a shows time-resolved SWaT spectra for LuIG under the magnetic field of 560 Oe (see also Supplementary Movie 1). The spin wave branches are already recognizable in the spectra at tc=2 ns. At this magnetic field, the spin waves appear to be excited mainly by the photo-induced demagnetization process11,19,22; the spin wave spectral intensity is unchanged when the pump pulse polarization is changed among clockwise, anticlockwise and linear, excluding the possibility of the inverse Faraday effect21,29,35,36 or photo-induced magnetic anisotropy23 as excitation mechanisms. The demagnetizing field is changed by the laser light in the pumped area, and the resulting impulse can contribute to the spin-wave emission11,19,22. At H=40 Oe, on the other hand, the spectral intensity at k∼0.8 × 104 rad cm−1 and k ∼ 1.5 × 104 rad cm−1 in the spectra gradually increases over time (Fig. 4b). This implies an energy transfer from phonons (LA and TA) to spin waves via the crossing points of their dispersion curves. At these points, the spin waves can be excited directly by phonons via magnetoelastic coupling (Supplementary Note 3), known as magnetoelastic waves, although phonons are less visible in the Faraday rotation. The difference in the dominant excitation mechanisms in Fig. 4a,b is due to the strong magnetic field dependence in the magnetoelastic waves, of which the intensity significantly reduces with increasing the external field (Supplementary Note 4). Consequently, spin waves are dominantly generated by the photo-induced demagnetization at 560 Oe, while the magnetoelastic coupling is the dominant mechanism at 40 Oe.
(a,b) Time-resolved SWaT spectra with k parallel to M under in-plane magnetic fields of 560 Oe (a) and 40 Oe (b) respectively. The data was obtained by applying a time-window with the width of 2.8 ns centred at the time delay noted in each figure. (c) A three-dimensional contour plot (at the intensity of 0.97 in the scale shown in Fig. 2a) of the SWaT intensity obtained under the in-plane magnetic field of 40 Oe. The data shown in (b) was extracted along the cross-section shown as the yellow plane. (d) Temporal evolution of the time-resolved SWaT spectra obtained along the dashed white line in (b). The data was obtained by applying a time-window with the width of 1.0 ns. (e) A result of numerical calculations of the time-resolved SWaT spectra shown in (d).
Figure 4d shows the temporal evolution of the SWaT spectral intensity along the dashed line in Fig. 4b for 10 ns. Interestingly, a streak pattern appears below the dispersion-crossing frequency of ∼0.7 GHz. This streak is attributed to the beat pattern between spin-wave and phonon modes, which interfere near the intersection point while satisfying momentum and energy conservation (Supplementary Note 3). In fact, a numerical calculation shown in Fig. 4e, in which the Landau–Lifshitz–Gilbert equation is solved combined with the magnetoelastic coupling to transverse acoustic phonons, well reproduces the observed streak pattern.
Discussion
Finally, let us discuss the advantages of SWaT. As we demonstrated, SWaT can be employed as a new technique for the dispersion spectroscopy of pure-magnetostatic waves. The SWaT is a non-contact and non-destructive spectroscopy for magnetic excitation and phonons that can be applied even to minute and thin samples. SWaT measurements can also be made under various environments, such as strong electric fields, strong magnetic fields, varying temperature and high pressure. As a result of this versatility, SWaT might find potential applications in the evaluation of the spin-wave dispersion not only in magnetic materials, but also in, for instance, topological insulators and magnetic films attached on superconductors. The obtained dispersion of spin waves would form the basis for the development of spintronics and magnonics devices. Moreover, time-resolved measurements of SWaT may be utilized for the real-time imaging of interaction between fundamental excitations in solids, like electronic quasiparticles, phonons and spin waves.
Methods
Sample
We used a 4.0 μm-thick film of Bi-doped iron garnet Lu2.3Bi0.7Fe4.2-Ga0.8O12 (LuIG) grown on a Gd3Ga5O12 (001) substrate, which is a well-established material for magneto-optical imaging37,38. The saturation magnetization of the sample (4πMs) was measured to be 780 G using a vibrating sample magnetometer. The magneto-optical properties of LuIG films were reported in refs 37, 38. At the wavelength of the probe pulse (630 nm), the sample shows a large Faraday rotation angle of 5.2 degrees and a high transmissivity of 41%. All the measurements were performed at room temperature.
Ultrafast time-resolved magneto-optical imaging
Propagation dynamics of the optically-excited spin waves were observed using an ultrafast time-resolved magneto-optical imaging system with sub-picosecond time resolution, sub-micrometre spatial resolution and millidegree resolution in the light polarization rotation angle26. This system, schematically represented in Fig. 1, is based on an all-optical two-colour pump-probe technique for the time-resolved measurements in combination with a rotation analyser method to obtain magneto-optical images. As a light source, we used a 100 fs amplified laser system with the center wavelength of 800 nm and a repetition frequency of 1 kHz. The output of the laser was divided into two beams: the pump and the probe beams. The beam with the original wavelength (800 nm) was used for the pump. The probe wavelength was tuned with an optical parametric amplifier to 630 nm. The pump pulse was circularly polarized and focused to a small round area (7 μm2) on the sample surface. The probe beam illuminated the sample with a focus size of ∼1 mm. The probe fluence (0.2 mJ cm−2) was much weaker than the pump fluence (1.2 J cm−2). To measure the photo-induced change in the magnetization distribution, we measured light polarization images of the transmitted probe beam using the rotation analyzer method, composed of an analyzer (a Glan-Taylor prism) and a CCD (charge-coupled device) camera. The analyzer angle (α) was controlled with a motorized rotation stage. For the measurements, we scan α from −10 degrees to 10 degrees, and the CCD camera measures the light intensity images of the transmitted probe beam as a function of α, which we denote as I(α). Furthermore, I(α) is given by I(α)=Itsin2 (θF−α)+Ib, where It, θF and Ib represent the transmitted light intensity, the Faraday rotation angle and the background signal, respectively. By fitting the obtained I(α) data with this equation, we obtained three images of It, θF and Ib simultaneously. The quantity θF reflect the magnetic properties of the sample. SWaT spectra were obtained by performing spatial and temporal FT of the θF data set. A Hanning window was employed for the FT along the time axis to reduce noise.
Data availability
The data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Hashimoto, Y. et al. All-optical observation and reconstruction of spin wave dispersion. Nat. Commun. 8, 15859 doi: 10.1038/ncomms15859 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Stancil, D. D. & Prabnakar, A. Spin Waves: Theory and Applications Springer (2009).
Sparks, M. Guide-curve theory for infinite-film spin-wave frequencies. AIP Conf. Proc. 5, 1113 (1972).
Kalinikos, B. A. Excitation of propagating spin waves in ferromagnetic films. IEE Proc. H 127, 4–10 (1980).
Hurben, M. J. & Patton, C. E. Theory of magnetostatic waves for in-plane magnetized anisotropic films. J. Magn. Magn. Mater. 163, 39–69 (1996).
Chatterji, T. Neutron Scattering from Magnetic Materials Elsevier (2006).
Sandweg, C. W. et al. Wide-range wavevector selectivity of magnon gases in Brillouin light scattering spectroscopy. Rev. Sci. Instrum. 81, 073902 (2010).
Serga, A. A. et al. Brillouin light scattering spectroscopy of parametrically excited dipole-exchange magnons. Phys. Rev. B 86, 134403 (2012).
Sebastian, T., Schultheiss, K., Obry, B., Hillebrands, B. & Schultheiss, H. Micro-focused Brillouin light scattering: imaging spin waves at the nanoscale. Front. Phys. 3, 1–23 (2015).
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262–266 (2010).
Serga, A. A., Chumak, A. V. & Hillebrands, B. YIG magnonics. J. Phys. D: Appl. Phys. 43, 264002 (2010).
Lenk, B., Ulrichs, H., Garbs, F. & Münzenberg, M. The building blocks of magnonics. Phys. Rep. 507, 107–136 (2011).
An, T. et al. Unidirectional spin-wave heat conveyer. Nat. Mater. 12, 549–553 (2013).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Boyd, R. W. Nonlinear Optics Academic Press (2008).
Ernst, R. R., Bodenhausen, G. & Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions Oxford University Press (1987).
Yang, C., Wu, Q., Xu, J., Nelson, K. A. & Werley, C. A. Experimental and theoretical analysis of THz-frequency, direction-dependent, phonon polariton modes in a subwavelength, anisotropic slab waveguide. Opt. Exp. 18, 26351–26364 (2010).
Smith, B. C. Fundamentals of Fourier Transform Infrared Spectroscopy 2nd edn. CRC Press (2011).
Ofori-Okai, B. K., Sivarajah, P., Werley, C. A., Teo, S. M. & Nelson, K. A. Direct experimental visualization of waves and band structure in 2D photonic crystal slabs. New J. Phys. 16, 053003 (2014).
van Kampen, M. et al. All-optical probe of coherent spin waves. Phys. Rev. Lett. 88, 227201 (2002).
Ulrichs, H., Lenk, B. & Münzenberg, M. Magnonic spin-wave modes in CoFeB antidot lattices. Appl. Phys. Lett. 97, 092506 (2010).
Satoh, T. et al. Directional control of spin-wave emission by spatially shaped light. Nat. Photon. 6, 662–666 (2012).
Au, Y. et al. Direct excitation of propagating spin waves by focused ultrashort optical pulses. Phys. Rev. Lett. 110, 097201 (2013).
Yoshimine, I. et al. Phase-controllable spin wave generation in iron garnet by linearly polarized light pulses. J. Appl. Phys. 116, 043907 (2014).
Ogawa, N. et al. Photodrive of magnetic bubbles via magnetoelastic waves. Proc. Natl Acad. Sci. USA 112, 8977–8981 (2015).
Bossini, D. et al. Macrospin dynamics in antiferromagnets triggered by sub-20 femtosecond injection of nanomagnons. Nat. Commun. 7, 10645 (2015).
Hashimoto, Y. et al. Ultrafast time-resolved magneto-optical imaging of all-optical switching in GdFeCo with femtosecond time-resolution and a μm spatial-resolution. Rev. Sci. Instrum. 85, 063702 (2014).
Kittel, C. Interaction of spin waves and ultrasonic waves in ferromagnetic crystals. Phys. Rev. 110, 836–841 (1958).
Chikazumi, S. Physics of Ferromagnetism Oxford University Press (1997).
Shen, K. & Bauer, G. E. W. Laser-induced spatiotemporal dynamics of magnetic films. Phys. Rev. Lett. 115, 197201 (2015).
Zvezdin, A. K. & Kotov, V. A. Modern Magnetooptics and Magnetooptical Materials Institute of Physics Publishing (1997).
White, R. M. Quantum Theory of Magnetism: Magnetic Properties of Materials Springer (2007).
Spencer, E. G. & LeCraw, R. C. Magnetoacoustic resonance in yttrium iron garnet. J. Appl. Phys. 30, S149 (1959).
Khivintsev, Y. V., Filimonov, Y. A. & Nikitov, S. A. Spin wave excitation in yttrium iron garnet films with micron-sized antennas. Appl. Phys. Lett. 106, 052407 (2015).
Donahue, M. & Porter, D. Oommf User’s Guide, Version 1.0. Interagency Report NISTIR 6376 National Institute of Standards and Technology (1999).
Kimel, A. V. et al. Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 435, 655–657 (2005).
Kalashnikova, A. M. et al. Impulsive excitation of coherent magnons and phonons by subpicosecond laser pulses in the weak ferromagnet FeBO3 . Phys. Rev. B 78, 104301 (2008).
Helseth, L. E., Hansen, R. W., Il’yashenko, E. I., Baziljevich, M. & Johansen, T. H. Faraday rotation spectra of bismuth-substituted ferrite garnet films with in-plane magnetization. Phys. Rev. B 64, 174406 (2001).
Hansteen, F. et al. Optical and magnetooptical properties of bismuth and gallium substituted iron garnet films. Thin Solid Films 455–456, 429–432 (2004).
Acknowledgements
We thank Dr S. Sermin, A. van Roij and A. Toonen for technical support. We thank Dr K. Aoshima for the saturation magnetization measurements of the sample. This work was financially supported by JST-ERATO Grant Number JPMJER1402, JST-ERATO Grant Number JPNJER1601, Grant-in-Aid for Scientific Research on Innovative Area, ‘Nano Spin Conversion Science' (26103004, 26103005 and 26103006), Grant-in-Aid for Scientific Research (Grant Nos. 25247056, 25220910, and 26220601), JSPS Core-to-Core Program, A. Advanced Research Networks, JSPS ‘Postdoctoral Fellowship for Overseas Researcher’ No P16326 and World Premier International Research Center Initiative (WPI), all from MEXT, Japan, Graduate Program in Spintronics, Tohoku University, de Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO), de Stichting voor Fundamenteel Onderzoek der Materie (FOM), FOM program Exciting Exchange, the EU-FP7 projects FemtoSpin (grant no. 281043), ERC-2013-AdG-339813-EXCHANGE, EU-FET Grant InSpin 612759 and DFG 257 Priority Programme 1538 ‘Spin-Caloric Transport’ (BA 2582954/2).
Author information
Authors and Affiliations
Contributions
Y.H. performed the measurements and analysed the data with input by Y.T., S.D. and R.I. Y.H., S.D. and R.I. carried out the numerical analysis. Y.O., K.Sh., K.Sa. and G.B. developed the theory. T.J. contributed to the sample fabrication. A.K., T.R. and E.S. planned and supervised the study. Y.H., K.Sa., K.Sh. and E.S. wrote the manuscript with review and input from D.B., T.S., T.R. and B.H. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes and Supplementary References (PDF 91 kb)
Supplementary Video
This supplementary movie demonstrates two data. One is the angular dependence of the SWaT spectra obtained at in-plane magnetic field of 40 Oe. Another is the temporal changes of two SWaT spectra obtained at in-plane magnetic elds of 40 Oe and 560 Oe. (MOV 3864 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hashimoto, Y., Daimon, S., Iguchi, R. et al. All-optical observation and reconstruction of spin wave dispersion. Nat Commun 8, 15859 (2017). https://doi.org/10.1038/ncomms15859
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15859
This article is cited by
-
Coherent oscillation between phonons and magnons
Communications Physics (2022)
-
Coherent spin-wave transport in an antiferromagnet
Nature Physics (2021)
-
Tuning spin excitations in magnetic films by confinement
Nature Materials (2021)
-
Bi-reflection of spin waves
Communications Physics (2020)
-
Room temperature and low-field resonant enhancement of spin Seebeck effect in partially compensated magnets
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.