Abstract
While it has long been known that some highly adsorbing microporous materials suddenly become inaccessible to guest molecules below certain temperatures, previous attempts to explain this phenomenon have failed. Here we show that this anomalous sorption behaviour is a temperature-regulated guest admission process, where the pore-keeping group’s thermal fluctuations are influenced by interactions with guest molecules. A physical model is presented to explain the atomic-level chemistry and structure of these thermally regulated micropores, which is crucial to systematic engineering of new functional materials such as tunable molecular sieves, gated membranes and controlled-release nanocontainers. The model was validated experimentally with H2, N2, Ar and CH4 on three classes of microporous materials: trapdoor zeolites, supramolecular host calixarenes and metal-organic frameworks. We demonstrate how temperature can be exploited to achieve appreciable hydrogen and methane storage in such materials without sustained pressure. These findings also open new avenues for gas sensing and isotope separation.
Similar content being viewed by others
Introduction
Selective admission of guest molecules into microporous solids is the cornerstone of a range of key applications such as gas separation1,2,3,4,5, storage6,7 and recognition8,9. However, in many important cases the size difference between relevant molecules can be of order 0.1 Å (refs 10, 11), and materials with the appropriately sized micropores necessary for discrimination are often very difficult to find12. If the accessibility of the micropores could be actively regulated by external stimuli, such as heat13, light14 or electrical field, the material’s utility could be fundamentally enhanced. In 1959, Breck showed that at temperatures below 170 K, the admission of Ar and N2 molecules into 4A zeolite was dramatically reduced15. Recently, other microporous materials including molecular trapdoor zeolites3,16,17 and certain metal-organic frameworks (MOFs)13,18,19,20,21,22 have been reported to exhibit similar properties, with negligible N2 surface area at 77 K but considerable adsorption at ambient temperatures. Many other zeolites also exhibit such a pore-blocking effect towards inert gases including caesium chabazites23, RHO24,25 and K-KFI26. While observations of this phenomenon imply pore accessibility can be regulated by temperature, neither the underlying science nor the process by which this regulation occurs is fully understood.
To elucidate a mechanism by which the admission of guest molecules can be thermally regulated, this work presents experimental data and ab initio calculations that explain the phenomenon for several types of microporous materials including trapdoor zeolites, supramolecular hosts27,28 and MOFs. Furthermore, a physical model is proposed to provide a quantitative description of temperature-regulated guest admission. Finally, we demonstrate a new application of this temperature-regulated gas admission phenomenon in which appreciable storage of H2 can be achieved without sustained external pressure via encapsulation within the material’s pore space. Importantly, the amount of hydrogen encapsulated greatly exceeds the equilibrium adsorption capacity of the material at comparable conditions.
Results
Experimental study of temperature-regulated guest admission
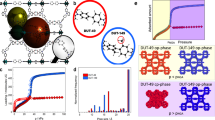
To exemplify the phenomenon of temperature-regulated guest admission, we show in Fig. 1 how pore accessibility can be abruptly and reversibly switched on/off across a narrow temperature range for four different guest molecules on a trapdoor16 chabazite, r2KCHA (potassium chabazite with Si/Al ratio of 2.2). This material is a typical small-pore zeolite in which eight-membered oxygen rings (8MRs) govern the access of guest molecules to internal cavities (Supplementary Figs 1 and 2). Geometrically, the 8MR is large enough for simple gas molecules such as H2 and Ar to pass through, but in trapdoor zeolites like r2KCHA, this access is blocked by large cations which occupy the energetically favourable site (SIII′) at the centre of the 8MR doorway16,17, as exemplified by a low N2 surface area at 77 K, which for r2KCHA was 21 m2 g−1. A sharp transition in the pore accessibility with temperature is clearly apparent for r2KCHA in the uptake of H2, Ar, N2 and CH4 (Fig. 1d). The ultra-low adsorption capacities observed for these molecules at 149, 197, 233 and 233 K, respectively, transition to considerable capacities with an increase of only 30–70 K. This is contrary to the normal dependence of physisorption capacity on temperature29,30, as illustrated in Supplementary Fig. 3.
(a) Illustration of the structure of an ideal potassium chabazite crystal, highlighting the eight-membered oxygen ring (8MR) which sets the nominal pore aperture diameter to be 3.8 Å (distance between opposing oxygen atoms). The centre of the 8MR pore aperture (cation site SIII′) is occupied by the potassium cation, reducing the nominal accessible pore aperture to 0.6 Å, as determined from the Synchrotron PXRD data. (b) Rietveld refinement of a representative Synchrotron PXRD pattern for trapdoor potassium chabazite with a Si/Al ratio of 2.2 (r2KCHA). (c) Left axis: fractional occupancy of SIII′ sites by K+ cations indicating blockage of 8MR pores over the experimental temperature range. Estimated uncertainty 1.5%. Right axis: evolution of the 8MR dimensions D1, D2 and D3 (inset) of r2KCHA suggesting pore contraction with increasing temperature, ruling out the possibility of thermally induced pore dilation. 0.3% uncertainty. (d) Adsorption isotherms for hydrogen, argon, nitrogen and methane, respectively, on r2KCHA showing restricted pore accessibility at low temperatures (crossed blue symbols) but no restriction at high temperatures (red open symbols), and comparison with GCMC calculated equilibrium capacities (lines) for nitrogen and methane.
One popular hypothesis for temperature-dependent pore accessibility is thermal expansion of the pore size31,32. We excluded this possibility by in situ synchrotron powder X-ray diffraction (PXRD) measurements of r2KCHA (Fig. 1b,c) over the temperature range of 213–363 K under vacuum and N2, respectively. The Rietveld refined PXRD data as detailed in Supplementary Note 1 and Supplementary Tables 1 and 2 show that while the accessible opening remained less than 1 Å, the 8MR diameter actually contracted slightly by 0.18 Å with increasing temperature. Such negligible negative thermal expansion is not uncommon in zeolites or other microporous materials33,34. Similarly, potential explanations based on restricted diffusion (kinetic) effects were excluded through adsorption rate measurements (detailed in Supplementary Fig. 4 and Supplementary Note 2).
Another possible mechanism is the migration of the pore-keeping cation from the 8MR centre to a secondary stable site at sufficiently high temperatures above a threshold, as suggested by Shang et al.16 for a caesium-exchanged chabazite. However, the PXRD data, which also resolved the locations of the extra-framework cations, eliminate this explanation in the case of r2KCHA. Figure 1c shows that the favourable cation site SIII′ at the centre of the 8MR doorways remains fully occupied by K+ across the entire temperature range. Superficially this temperature-independent cation position suggests that the admission of N2 into the r2KCHA pores should remain negligible at least up to 363 K. The question then arises how H2, Ar, N2 and CH4 were admitted while the pore entrance was seemingly blocked.
Ab initio DFT studies of gas admission
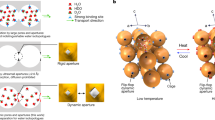
We explored whether guest admission in r2KCHA is regulated by the temporary and reversible deviation of the pore-keeping K+ cation from the SIII′ site by calculating the associated potential energy surfaces using ab initio DFT (density functional theory). The admission process was simulated as consisting of two concurrent parts: the pore-keeping K+ cation deviates temporarily from the 8MR’s centre (SIII′) as a result of an interaction with the guest molecule, which allows the guest molecule to pass through the transient opening in the 8MR doorway. Accordingly, the energy barrier (ΔEtotal) of this coupled gas admission process contains two interdependent components: ΔEtotal=ΔEhost+ΔEguest, where ΔEhost accounts for the potential energy change of the cation’s temporary deviation in the presence of a gas, and ΔEguest is the potential energy barrier a guest molecule passing through the temporarily opened doorway must overcome, due to the cation and framework. We used an iterative method within the DFT calculations to capture the energy profiles associated with the simultaneous movement of the cation and the gas molecule (Supplementary Note 3).
We identified that the transient deviation of the K+ cation follows the pathway from SIII′ to SIII (Fig. 2), that is, from the centre of an 8MR to the site above the adjacent 4MR plane (see Supplementary Figs 5–7 for detailed justification). As illustrated in Fig. 2a,b, if the cation deviated temporarily to the potential energy saddle point along the SIII′-to-SIII path, these guest molecules would have more than enough room to pass through the 8MR doorway; that is, the cation does not need to reach the secondary stable site SIII to admit guest molecules. By mapping ΔEtotal in the presence of different guest molecules as a function of cation position along the SIII′-to-SIII pathway, we determined the minimum energy required for the admission of each gas. In all cases the minimum ΔEtotal of the system was achieved before the cation deviation reached the saddle point in Fig. 2a,b. Examples for Ar and CH4 are shown in Fig. 2c,d, and ΔEtotal for the four gases follows the order H2 (0.75 eV) <Ar (1.16 eV) <N2 (1.19 eV) <CH4 (1.30 eV). The trajectories determined by DFT calculations (Fig. 2e–h) clearly show that a partially opened 8MR doorway is sufficient for the admission of these molecules. However, they also illustrate that the deviation distance of the cation, that is, the opening of the doorway, is not necessarily proportional to the size of the guest molecule (Fig. 2g,h), indicating that this guest admission process is not simply steric in nature.
(a) Energy profile for the deviation of the potassium cation following the SIII′-to-SIII path. (b) The position of the saddle point relative to the original cation site SIII′, which if reached would completely unblock the 8MR doorway to incoming guests. (c,d) Examples of DFT-calculated energy barriers experienced by the door-keeping cation of the host zeolite, the interacting guest molecule (c, argon and d, methane, respectively) and their sum as a function of cation position. With the increasing deviation there is a trade-off between the increase in the cation’s potential energy and a decrease in the potential energy barrier experienced by the guest molecule. (e–h) Total energy barriers and trajectories for the admission of guest molecules H2, Ar, N2 and CH4, respectively. Higher energy barriers must be overcome for the admission of larger guest molecules; however, larger molecules do not necessarily require the cation’s deviation to be greater in extent because there are two (guest and host) contributions to the total energy barrier.
GCMC calculated adsorption equilibrium
We conducted Grand Canonical Monte Carlo (GCMC) simulations to compute the equilibrium adsorption isotherms for CH4 and N2 on r2KCHA at all temperatures, using force field parameters derived from both experiment and literature35,36. A 3 × 3 × 3 supercell was built to take into account the temperature-dependent pore accessibility (Supplementary Figs 8 and 9). Good agreement between the GCMC-calculated and experimentally measured adsorption capacities was achieved across the whole temperature range (Supplementary Figs 10 and 11), including during the transition from accessible to inaccessible pores with decreasing temperature. More details about the determination of the simulation parameters are presented in Supplementary Note 4 and summarized in Supplementary Tables 3–6 (refs 37, 38).
A quantitative model for regulated guest admission
To derive a physically based function able to describe the observed temperature dependence of the guest admission process, we start with a comparison between the minimum energy barrier ΔEtotal and the thermal energy of the system. The system’s thermal energy Etherm is the sum of the kinetic energy of the guest molecule interacting with the pore-keeping groups and the thermal vibrational energy of those groups in the framework of the regulated pores. A general expression for the mean thermal energy Ētherm is (ref. 39):

where s is the number of harmonic oscillators (or degrees of freedom) of the system, k is the Boltzmann constant and c(T, v) is a function of the absolute temperature T and the oscillators’ vibrational frequencies v. In systems of harmonic oscillators where the number of degrees of freedom is large (for example, 102–103 Da as for the pore-structures considered here) the energy distribution will be Gaussian39,40. Accordingly, the probability density distribution of their thermal energies, Etherm, is:

Here σ is the standard deviation of the distribution function, representing its width in terms of energy. The cumulative probability that a given oscillator will admit a guest molecule is then:

Identifying the threshold temperature, T0, at which the system’s mean thermal energy is equal to ΔEtotal, and substituting the expression for Ētherm from equation (1) into equation (3) gives:

Drahos and Vékey suggest that below 1,000 K, both c(T, υ) and σ can be well approximated by linear functions of temperature40. Accordingly, the final analytical expression for the fraction of pore-keeping oscillators that allow guest molecule admission as a function of temperature is:

where β characterizes the width of the system-specific distribution in temperature. The product of βT in equation (5) is the standard deviation of the cumulative distribution function, indicating that the width of the distribution is asymmetrical and broader at higher temperatures (Supplementary Fig. 12).
This temperature-dependent distribution function for the accessibility of internal sites can be readily incorporated into a classical model of equilibrium adsorption capacity Q(P, T), such as Langmuir, Sips, Toth or BET30, to enable a quantitative description of temperature-regulated guest admission:

Here Q(P, T) is the classical isotherm as a function of temperature and pressure. The pre-factor in square brackets contains the fraction of accessible adsorption sites determined by the temperature-dependent distribution function, Φ, together with the fraction of external surface sites and defects always available for adsorption, ɛ. For near-perfect adsorbent crystals with sufficiently large grain size ɛ will be negligible. Alternatively ɛ can be estimated through surface area analysis with specific gases. The fraction Φ can also be found from GCMC calculations.
We name the above method of describing the stimuli-dependent availability of adsorption sites as the LJM model, and accordingly LJM-Toth and LJM-Langmuir denote models (Supplementary equations 2 and 3) for heterogeneous and homogeneous adsorption, respectively. The LJM model introduces only two new parameters, namely T0 and β, to describe the temperature dependence of the pore accessibility. All other parameters describing the adsorption occur within the classical isotherm equations. To determine T0 and β reliably, equation (6) should be regressed to adsorption isotherms measured over a sufficiently wide temperature range spanning the material’s transition from inaccessible to accessible pores. The physical significance of T0 and β was further established when it was found that including Φ into the GCMC calculations enabled accurate prediction of adsorption capacities measured in the transitional region. In principle, LJM models are compatible with ideal adsorbed solution theory41 and other multicomponent isotherm models (Supplementary Note 5) and can also be used to calculate the isosteric heat of adsorption (Supplementary Fig. 13)42,43.
Demonstration for trapdoor zeolites
The LJM model was used to describe successfully the temperature-regulated admission of several non-polar guest species on three classes of microporous materials across ranges of at least 108 K. First, adsorption isotherms were measured for H2, Ar, N2 and CH4 on the molecular trapdoor zeolite r2KCHA, and regressed by the LJM-Langmuir model (Fig. 3). The experimental, GCMC and LJM capacities are all in good agreement across the pore-accessible, transitional and pore-inaccessible regions. The quality of the fits to the data is high: for example, measurements of the r2KCHA—N2 system spanned 14 isotherms (195–343 K) over the pressure range of 1–120 kPa with 312 data points in total. Description of the eight N2 isotherms below 273 K would be impossible without the two LJM parameters. The regression had an R2=0.992 with all parameter values being physically meaningful. Similar results were obtained for the other three gases as shown in Supplementary Table 7.
Experimentally measured data together with the GCMC calculations and a demonstration of the LJM model’s ability to quantify the effect of temperature-regulated guest admission. (a) H2 at 11 different temperatures; (b) Ar at 7 temperatures; (c) N2 at 14 temperatures; (d) CH4 at 13 temperatures. Only 1/6th of the isobar data points measured and used in the regression are shown here for clarity. Full isotherm/isobar data across the experimental pressure range 2–120 kPa can be found in Supplementary Figs 14–17. The full set of N2 and CH4 GCMC calculations are presented in Supplementary Figs 10 and 11. Solid symbols denote experimental data, hollow symbols represent the GCMC calculated capacities, and solid curves correspond to the LJM-Langmuir model. The dotted lines represent the threshold admission temperature T0 determined using the LJM model.
Correlating the experimentally determined T0 values with the DFT calculated energy barriers ΔEtotal for the admission of H2, Ar, N2 and CH4 on r2KCHA produced a striking relationship. As shown in Fig. 4a, T0 is linearly proportional to the square root of ΔEtotal. This relationship is consistent with the use of equations (1), (3) and (4) in the derivation of the LJM model and supports the interpretation of T0 as the temperature at which the mean thermal energy of the adsorption system reaches a threshold value sufficient to overcome the guest admission energy barrier ΔEtotal. Furthermore, the experimental T0 are proportional to the kinetic diameters10,12 d of the guest molecules: in the context of the mechanism elucidated by the DFT results, this property will facilitate the design of tuneable molecular sieves and thermally gated membranes from zeolites. A third interesting correlation observed in the experimental data (Fig. 4b–d) relates to the order of the distribution width β and the molecular mass of each guest species: H2 (30 K), CH4 (50 K), N2 (57 K) and Ar (118 K). This result has important implications for the potential use of temperature-regulated sieving to separate isotopes (for example, hydrogen-deuterium-tritium44).
(a) Left axis: Linear correlation between the square root of the total energy barrier ΔEtotal and the threshold guest admission temperature T0, indicating a consistency between the DFT calculations, framework used to derive the LJM model, and the experimental data. Right axis: linear relationship between T0 and the apparent pore size of r2KCHA based on the guest molecule’s kinetic diameter10,12. (b) Accessibility of adsorption sites as a function of temperature for guest molecules of H2, CH4, N2 and Ar as calculated by  in equation (6). The lower and upper cut-offs are 0.1 and 99.9% of the accessibility of the internal sites, respectively, and the initial value of the curve represents the fraction of external sites ɛ. (c) Corresponding differential site accessibility for the four different guest molecules on r2KCHA. (d) Corresponding width of the transitional temperature range (as characterized by β in the LJM model) for the admission of different guest species, showing heavier molecules tend to have larger distribution widths.
in equation (6). The lower and upper cut-offs are 0.1 and 99.9% of the accessibility of the internal sites, respectively, and the initial value of the curve represents the fraction of external sites ɛ. (c) Corresponding differential site accessibility for the four different guest molecules on r2KCHA. (d) Corresponding width of the transitional temperature range (as characterized by β in the LJM model) for the admission of different guest species, showing heavier molecules tend to have larger distribution widths.
Demonstration for calixarenes and MOFs
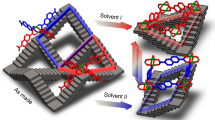
Calixarenes are typical supramolecular host materials composed of macro-cyclic polyphenols. The cyclic tetramer calix[4]arene has a stable basket conformation and is known to accommodate small guest molecules, such as CH4 and N2 (refs 27, 28). Its host–guest inclusion complex formation has similar characteristics to physisorption. In this study, methane adsorption isotherms were measured on p-t-butylcalix[4]arene between 195 and 303 K at pressures up to 120 kPa (Supplementary Fig. 18). The data were regressed successfully to the LJM-Langmuir model (Fig. 5a), revealing a threshold temperature of 230 K for CH4 admission. The results can be interpreted in terms of the cooperative rotation of the tert-butyl groups producing a ‘turnstile’ effect which regulates the admission of guests into the CX[4] cavity45.
(a) Typical bell-shaped isobars for the adsorption of CH4 on p-t-butylcalix[4]arene showing good agreement between the experimental data (points) and the LJM model (solid curves). A threshold admission temperature of 230 K was determined by the model’s regression. Inset: molecular structure of p-t-butylcalix[4]arene showing the accessibility of its basket-shaped cavity is kept by four thermally responsive t-butyl groups. (b) Representative adsorption isobars for CH4 on CuTEI, a MOF nanocage whose ligand 5-((triisopropylsilyl)ethynyl)isophthalic acid (TEI) provides a turnstile-type configuration. Symbols denote experimental data, solid curves the fitting by LJM-Toth model, and dashed curves the inevitable overestimation of the guest uptake using conventional physisorption models. Inset: illustration of the turnstile type pore keeping group in CuTEI (the cage structure of the CuTEI was adapted from Fig. 1 in Chem. Commun. 46, 7352–7354 (2010) with permission from The Royal Society of Chemistry). For clarity, less than 1/5th of the data points used in the regression are presented in a,b. The full data set is available in the Supplementary Table 8.
Adsorption data reported for a number of MOFs also exhibit the bell-shaped isobars characteristic of the temperature-dependent gas admission effect13,20,22,46. Interestingly, all these MOFs have pore-keeping groups responsive to temperature changes (Supplementary Fig. 19). For example, adsorption capacity data have been presented for a porous coordination nanocage, CuTEI13, the exterior of which is covered by turnstile-like triisopropylsilyl groups that regulate access to the nanocage. Regression of the LJM-Toth model to the 93 literature data collected between 113 and 273 K produced a reasonable fit (Fig. 5b), with T0=145 K, suggesting a much smaller energy barrier for CH4 admission compared with CX[4]. This result highlights the importance of examining the possibility of temperature-dependent pore accessibility changes in ‘designer’ microporous materials, especially those generated and screened purely by computer13,47, to avoid substantial over-estimation of lower-temperature adsorption capacities.
Reversible hydrogen and methane encapsulation and release
The storage of H2 and CH4 in porous media such as MOFs and carbons with large surface areas is a widely studied approach for achieving high volumetric energy density with relatively low regeneration cost. Common drawbacks of such approaches include the unavoidable use of thick-walled vessels to contain the high pressure and/or limited reversibility of the storage process6,48. The temperature-regulated guest admission mechanism identified here offers substantial potential for such applications because pre-dosed gas can be encapsulated and prevented from escaping by lowering the system temperature below T0. We explored this concept (Fig. 6a) by dosing the r2KCHA trapdoor zeolite at ambient temperature with H2 at various pressures up to 10 MPa using a set up shown in Supplementary Fig. 20. After quenching to cryogenic temperatures, the system was evacuated to remove all the free gaseous hydrogen, leaving only the hydrogen trapped inside the chabazite’s intracrystal cavities. No H2 was evolved over an extended period under vacuum as long as the temperature remained well-below T0=170 K. The appreciable quantity of hydrogen stored at this low pressure and low temperature condition was then measured by returning the system to ambient temperature (Fig. 6a) thereby completely releasing the stored H2. The cumulative amount of H2 evolved varied with the initial dosing pressure, which for 10 MPa amounted to about 0.95 wt%. This result demonstrates the ability to store physically substantial quantities of H2 in materials with temperature-regulated pore accessibility without sustained external pressure. The encapsulation capacity is proportional to the intracrystal pore volume as opposed to the surface area: in this example the H2 encapsulated was 30 times greater than the maximum adsorption capacity at the same storage temperature. These preliminary results suggest the possibility of storing 3–7 wt% H2 at ambient pressures by quenching a chabazite initially dosed at ambient temperature to 70–250 MPa (Supplementary Note 6 and Supplementary Fig. 21). A potential deployment method for the on-board fuel gas storage via gas encapsulation has been exemplified in Supplementary Fig. 22. The encapsulation temperature could be elevated to near ambient by using heavier door-keeping cations, for example, Rb+, while the storage capacity could be increased by designing a composite material with a high porosity core and a trapdoor shell. Figure 6b also shows the controlled release of H2 through the manipulation of system temperature, thereby enabling a nano-regulator for molecular transport. The encapsulation/decapsulation of CH4 was also demonstrated with trapdoor r2KCHA and supramolecular p-t-butylcalix[4]arene and visualized by igniting the CH4 being evolved from the materials, generating a sustained or abrupt flame, respectively (Supplementary Movies 1 and 2).
(a) Four-step procedure for reversible encapsulation and decapsulation of H2 in materials with temperature-regulated guest admission: (1) At temperatures above the threshold, T0, high-pressure dosing is used to store a significant quantity of H2 within the material’s pore volume. (2) The material is quenched to below T0 so the door-keeping group closes off access between the pore space and the environment. (3) H2 remains encapsulated inside the material’s pore space even when the external pressure is replaced with a vacuum as long as the temperature is below T0. (4) Controlled decapsulation of the gas into the low pressure environment is achieved by bringing the system temperature above T0, with the cumulative amount evolved providing a measure of the initial storage. This storage and release cycle is fully reversible and regulated by heat transfer. (b) Measured amount of H2 decapsulated from r2KCHA during step (4) as a function of system re-heating temperature after dosing with different initial pressures. Inset: cyclical performance of H2 encapsulated at a dosing pressure of 10 MPa by following the above four-step procedure across five consecutive experiments, showing steady and repeatable H2 storage capacity (see Supplementary Table 9 for detailed data).
Discussion
We have elucidated a mechanism for the important but poorly understood phenomenon of temperature-regulated guest admission in several typical microporous materials. Such admission processes involve the temporary and reversible displacement of a pore-blocking group as a result of interactions with the guest molecule. The adsorption model developed here to describe the dependence of guest admission on temperature for four gases on three classes of materials allows for robust quantification of this effect, which has not been possible to date. The variation in the admission threshold temperature with the guest’s size offers new opportunities for thermo-regulated sieving applications. Similarly, the dependence in the width of the pore accessibility distribution on the guest’s molecular mass has the potential to enable sophisticated gas sensing and separation processes. With the trapdoor zeolite, we also demonstrated the ability to physically encapsulate and store appreciable amounts of H2 and CH4 without sustained external pressure, and the ability to regulate its release by thermally controlled decapsulation. These findings should help illuminate new paths for gas and energy storage by molecular encapsulation.
Methods
Synthesis of microporous samples
Chabazite with Si/Al ratio of 2.2 was synthesized from zeolite Y following the reported method16, and then ion exchanged to the potassium form with a typical procedure: 5 g of chabazite in 200 ml of 1 M KCl was refluxed at 343 K under stirring for 24 h, followed by filtration and washing with deionized water 2–3 times. The above ion exchange procedure was repeated twice to obtain fully exchanged potassium chabazite (labelled as r2KCHA). p-t-butylcalix[4]arene was synthesized according to the reported procedure27,28. After the synthesis, the sample was heated under vacuum at 140 °C for 24 h to completely remove any possible entrapped solvent toluene from the calixarene cavity, ensuring it was vacant. The sample was sublimed at 280 °C under vacuum to give the final product used in the analysis49.
Sample characterization
The species of inorganic ions and Si/Al ratios of the chabazites were determined by inductively coupled plasma-mass spectroscopy. For in situ synchrotron PXRD experiments, the zeolite powder was degassed on Micromeritics ASAP 2010 (623 K for 12 h below 1 Pa), transferred to a 0.7 mm quartz capillary, and sealed in an Ar glove bag. Then the capillary was decanted at one end and mounted on the synchrotron PXRD machine with the open end being connected to vacuum/gas line. Before the experiments, the sample was re-degassed in situ, followed by cooling to 213 K. For the scans under vacuum, the sample was heated from 213 to 363 K at 5 K min−1, during which XRD data were collected at a series of temperature points; the sample was held at each set point for 60 s before scanning for 600 s. For the scans in N2, a similar procedure was adopted and the only difference is that N2 was dosed into the capillary slowly to 1 bar at 423 K before cooling to 213 K and the N2 pressure was kept at 1 bar. N2 was introduced at a relatively high temperature to assure the gas was admitted and the behaviour of the zeolite sample truly reflected the presence of the gas. A Mythen-II detector was used for data collection with a X-ray wavelength of 0.5894 Å for all zeolites.
The purity of p-t-butylcalix[4]arene was verified by nuclear magnetic resonance (Supplementary Figs 23 and 24) and high performance liquid chromatography, and no impurities were detected by either technique. The crystal structure of the p-t-butylcalix[4]arene was also identified by synchrotron PXRD with an X-ray wavelength of 0.77502 Å (Supplementary Fig. 25).
Gas adsorption measurements
Before the isotherm measurements, the samples were thoroughly dehydrated and degassed by heating stepwise to 413 K for p-t-butylcalix[4]arene and 623 K for r2KCHA under high vacuum overnight on a Micromeritics ASAP2010/2020 analyser. After degas the samples were cooled to room temperature and backfilled with He. Adsorption isotherms on r2KCHA were measured in the temperature range of 77–343 K for N2, 77–303 K for H2, 197–305 K for Ar and 195–353 K for CH4 and at pressures up to 120 kPa. Temperatures of 77 and 195 K were achieved with liquid nitrogen and ethanol-dry ice baths, respectively. Other non-standard cryogenic temperatures below 243 K were achieved using a solid–liquid thermostatic bath of water–ethanol in different ratios. CH4 isotherms on p-t-butylcalix[4]arene were measured in the temperature range from 195 to 323 K. The rate of adsorption of CH4 on r2KCHA was measured at 333, 279 and 195 K using the reported procedure and equipment50, representing the fully pore accessible, transitional and pore inaccessible temperature ranges, respectively.
Density functional theory calculations
Ab initio DFT calculations were employed to determine the energy barriers associated with the guest admission process as well as the snapshots of the trajectories of the gas molecules and the door-keeping cations in r2KCHA. The Vienna Ab initio Simulation Package51 was used with the projector augmented waves approach52 and the dispersion-corrected DFT-D3 functional53.
Grand Canonical Monte Carlo calculations
Adsorption isotherms for CH4 and N2 at all temperatures were computed by the GCMC method using the RASPA software35,36. The structures of the trapdoor r2KCHA determined from synchrotron PXRD experiments were used to construct the molecular model for GCMC. A 3 × 3 × 3 supercell was built to calculate adsorption equilibria for blocked pores. See Supplementary Note 4 for simulation details, and the Crystallographic Information Files of a cubic unit cell and the supercell appended separately.
Hydrogen and methane encapsulation
The experimental procedure illustrated in Fig. 6a used 5.93 g of r2KCHA with dosing and quenching temperatures of 323 and 77 K, respectively. The setup for conducting the reversible hydrogen encapsulation and decapsulation experiment is detailed in Supplementary Fig. 20. No activation or degas was needed between repeated cycles. In a similar setup, the encapsulation/decapsulation of methane with both r2KCHA (6.06 g) and p-t-butylcalix[4]arene (3.27 g) was demonstrated by igniting the CH4 evolved (Supplementary Movies 1 and 2).
Data availability
All data generated or analysed during this study are included in this published article (and its Supplementary Information Files). The Crystallographic Information File data are available in the Dryad Digital Repository http://datadryad.org/ via doi:10.5061/dryad.2426m.
Additional information
How to cite this article: Li, G. et al. Temperature-regulated guest admission and release in microporous materials. Nat. Commun. 8, 15777 doi: 10.1038/ncomms15777 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Herm, Z. R. et al. Separation of hexane isomers in a metal-organic framework with triangular channels. Science 340, 960–964 (2013).
Kuznicki, S. M. et al. A titanosilicate molecular sieve with adjustable pores for size-selective adsorption of molecules. Nature 412, 720–724 (2001).
Moliner, M., Martínez, C. & Corma, A. Synthesis strategies for preparing useful small pore zeolites and zeotypes for gas separations and catalysis. Chem. Mater. 26, 246–258 (2013).
Hudson, M. R. et al. Unconventional, highly selective CO2 adsorption in zeolite SSZ-13. J. Am. Chem. Soc. 134, 1970–1973 (2012).
Nugent, P. et al. Porous materials with optimal adsorption thermodynamics and kinetics for CO2 separation. Nature 495, 80–84 (2013).
Murray, L. J., Dinca, M. & Long, J. R. Hydrogen storage in metal-organic frameworks. Chem. Soc. Rev. 38, 1294–1314 (2009).
Kuc, A., Zhechkov, L., Patchkovskii, S., Seifert, G. & Heine, T. Hydrogen sieving and storage in fullerene intercalated graphite. Nano Lett. 7, 1–5 (2007).
Davis, M. E. Ordered porous materials for emerging applications. Nature 417, 813–821 (2002).
Bein, T., Brown, K., Frye, G. C. & Brinker, C. J. Molecular sieve sensors for selective detection at the nanogram level. J. Am. Chem. Soc. 111, 7640–7641 (1989).
Auerbach, S. M., Carrado, K. A. & Dutta, P. K. Handbook of zeolite science and technology CRC (2003).
Nair, S., Tsapatsis, M., Toby, B. H. & Kuznicki, S. M. A study of heat-treatment induced framework contraction in strontium-ETS-4 by powder neutron diffraction and vibrational spectroscopy. J. Am. Chem. Soc. 123, 12781–12790 (2001).
Li, J.-R., Kuppler, R. J. & Zhou, H.-C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 38, 1477–1504 (2009).
Zhao, D., Yuan, D., Krishna, R., van Baten, J. M. & Zhou, H.-C. Thermosensitive gating effect and selective gas adsorption in a porous coordination nanocage. Chem. Commun. 46, 7352–7354 (2010).
Lyndon, R. et al. Dynamic photo-switching in metal-organic frameworks as a route to low-energy carbon dioxide capture and release. Angew. Chem. Int. Ed. 52, 3695–3698 (2013).
Breck, D. W., Eversole, W. G., Milton, R. M., Reed, T. B. & Thomas, T. L. Crystalline zeolites. I. the properties of a new synthetic zeolite, type A. J. Am. Chem. Soc. 78, 5963–5972 (1956).
Shang, J. et al. Discriminative separation of gases by a ‘molecular trapdoor’ mechanism in chabazite zeolites. J. Am. Chem. Soc. 134, 19246–19253 (2012).
De Baerdemaeker, T. & De Vos, D. Gas separation: trapdoors in zeolites. Nat. Chem. 5, 89–90 (2013).
Ma, S., Sun, D., Wang, X.-S. & Zhou, H.-C. A mesh-adjustable molecular sieve for general use in gas separation. Angew. Chem. Int. Ed. 46, 2458–2462 (2007).
Ma, S., Sun, D., Yuan, D., Wang, X.-S. & Zhou, H.-C. Preparation and gas adsorption studies of three mesh-adjustable molecular sieves with a common structure. J. Am. Chem. Soc. 131, 6445–6451 (2009).
Kim, H. et al. Temperature-triggered gate opening for gas adsorption in microporous manganese formate. Chem. Commun. 4697–4699 (2008).
Deng, H., Olson, M. A., Stoddart, J. F. & Yaghi, O. M. Robust dynamics. Nat. Chem. 2, 439–443 (2010).
Gao, Q., Xu, J., Cao, D., Chang, Z. & Bu, X. H. A rigid nested metal-organic framework featuring a thermoresponsive gating effect dominated by counterions. Angew. Chem. Int. ed. 55, 15027–15030 (2016).
Shang, J. et al. Determination of composition range for ‘molecular trapdoor’ effect in chabazite zeolite. J. Phys. Chem. C 117, 12841–12847 (2013).
Lozinska, M. M. et al. Understanding carbon dioxide adsorption on univalent cation forms of the flexible zeolite Rho at conditions relevant to carbon capture from flue gases. J. Am. Chem. Soc. 134, 17628–17642 (2012).
Lozinska, M. M. et al. Cation gating and relocation during the highly selective ‘trapdoor’ adsorption of CO2 on univalent cation forms of zeolite Rho. Chem. Mater. 26, 2052–2061 (2014).
Remy, T. et al. Adsorption and separation of CO2 on KFI zeolites: effect of cation type and Si/Al ratio on equilibrium and kinetic properties. Langmuir 29, 4998–5012 (2013).
Thallapally, P. K., Kirby, K. A. & Atwood, J. L. Comparison of porous and nonporous materials for methane storage. New J. Chem. 31, 628–630 (2007).
Atwood, J. L., Barbour, L. J., Thallapally, P. K. & Wirsig, T. B. A crystalline organic substrate absorbs methane under STP conditions. Chem. Commun. 51–53 (2005).
Yang, R. T. Gas separation by adsorption processes Vol. 3 (Imperial College Press (1997).
Do, D. D. Adsorption analysis: equilibria and kinetics Ch. 5 (Imperial College Press (1998).
Breck, D. W. Zeolite molecular sieves: structure, chemistry, and use Wiley (1974).
Breck, D. W. Crystalline molecular sieves. J. Chem. Edu. 41, 678 (1964).
Miller, W., Smith, C. W., Mackenzie, D. S. & Evans, K. E. Negative thermal expansion: a review. J. Mater. Sci. 44, 5441–5451 (2009).
Queen, W. L. et al. Site-specific CO2 adsorption and zero thermal expansion in an anisotropic pore network. J. Phys. Chem. C 115, 24915–24919 (2011).
Dubbeldam, D., Calero, S., Ellis, D. E. & Snurr, R. Q. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 42, 81–101 (2016).
Dubbeldam, D., Torres-Knoop, A. & Walton, K. S. On the inner workings of Monte Carlo codes. Mol. Simul. 39, 1253–1292 (2013).
Fang, H. et al. Identification of high-CO2-capacity cationic zeolites by accurate computational screening. Chem. Mater. 28, 3887–3896 (2016).
Fang, H. et al. First principles derived, transferable force fields for CO2 adsorption in Na-exchanged cationic zeolites. Phys. Chem. Chem. Phys. 15, 12882–12894 (2013).
Vékey, K. Internal energy effects in mass spectrometry. J. Mass Spectrom. 31, 445–463 (1996).
Drahos, L. & Vékey, K. Determination of the thermal energy and its distribution in peptides. J. Am. Soc. Mass Spectrom. 10, 323–328 (1999).
Myers, A. L. & Prausnitz, J. M. Thermodynamics of mixed-gas adsorption. AIChE J. 11, 121–127 (1965).
Kapoor, A., Ritter, J. A. & Yang, R. T. An extended Langmuir model for adsorption of gas-mixtures on heterogeneous surfaces. Langmuir 6, 660–664 (1990).
Li, G., Xiao, P. & Webley, P. Binary adsorption equilibrium of carbon dioxide and water vapor on activated alumina. Langmuir 25, 10666–10675 (2009).
Physick, A. J. W. et al. Novel low energy hydrogen-deuterium isotope breakthrough separation using a trapdoor zeolite. Chem. Eng. J. 288, 161–168 (2016).
Ananchenko, G. S. et al. A molecular turnstile in para-octanoyl calix[4]arene nanocapsules. Chem. Commun. 707–709 (2007).
Zhang, J.-P. & Chen, X.-M. Exceptional framework flexibility and sorption behavior of a multifunctional porous cuprous triazolate framework. J. Am. Chem. Soc. 130, 6010–6017 (2008).
Liu, B. & Smit, B. Comparative molecular simulation study of CO2/N2 and CH4/N2 separation in zeolites and metal-organic frameworks. Langmuir 25, 5918–5926 (2009).
Li, G. et al. Hydrogen storage in Pd nanocrystals covered with a metal-organic framework. Nat. Mater. 13, 802–806 (2014).
Atwood, J. L., Barbour, L. J., Jerga, A. & Schottel, B. L. Guest transport in a nonporous organic solid via dynamic van der Waals cooperativity. Science 298, 1000–1002 (2002).
Xiao, G., Li, Z., Saleman, T. L. & May, E. F. Adsorption equilibria and kinetics of CH4 and N2 on commercial zeolites and carbons. Adsorption 23, 131–147 (2016).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Grimme, S. et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. The Journal of Chemical Physics. 132, 154104 (2010).
Acknowledgements
G.L. is the recipient of an Australian Research Council Discovery Early Career Researcher Award (DE140101824). This research was undertaken on the powder X-ray diffraction beamline at the Australian Synchrotron, Victoria, Australia. J.S., P.A.W. and J.Z.L. acknowledge the Australian Research Council for providing the funding (DP130103708) and acknowledge National Computational Infrastructure at Australian National University for providing the computational resource. D.S.S. was supported as part of the Center for Understanding and Control of Acid Gas-Induced Evolution of Materials for Energy (UNCAGE-ME), an Energy Frontier Research Center funded by U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award #DE-SC0012577. E.F.M. and G.L. acknowledge support from the Australian Research Council through IC150100019. G.L., J.S. and E.F.M. thank Professors Yinong Liu and Michael Johns, Drs Michael Moldover and Hanjun Fang for helpful discussions.
Author information
Authors and Affiliations
Contributions
G.L., J.S., J.Z.L., P.A.W. and E.F.M. conceived and designed the experiments. J.S., G.L., N.J. and A.G. performed the synthesis and measured the adsorption isotherms. Q.G. and X.Z. performed the synchrotron PXRD study and Q.G. did the Rietveld refinement. J.S. and J.Z.L. conducted the ab initio DFT calculations and J.S., J.Z.L., G.L., P.A.W. and E.F.M. analysed the data. R.V.A. and D.S.S. performed the GCMC calculations. G.L., N.J. and E.F.M. derived the temperature-regulated guest admission model. G.L., J.S., R.V.A. and E.F.M. wrote the paper. All authors discussed the results and commented on the manuscript. G.L. and J.S. contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Tables, Supplementary Notes and Supplementary References (PDF 2389 kb)
Supplementary Movie 1
Ignition of methane evolved from trapdoor chabazites generating a sustained flame. (MP4 12174 kb)
Supplementary Movie 2
Ignition of methane evolved from p-t-butylcalix[4]arene generating an abrupt flame. (MP4 9929 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, G., Shang, J., Gu, Q. et al. Temperature-regulated guest admission and release in microporous materials. Nat Commun 8, 15777 (2017). https://doi.org/10.1038/ncomms15777
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15777
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.