Abstract
Extreme variations of Earth’s magnetic field occurred in the Levant region around 1000 BC, when the field intensity rapidly rose and fell by a factor of 2. No coherent link currently exists between this intensity spike and the global field produced by the core geodynamo. Here we show that the Levantine spike must span >60° longitude at Earth’s surface if it originates from the core–mantle boundary (CMB). Several low intensity data are incompatible with this geometric bound, though age uncertainties suggest these data could have sampled the field before the spike emerged. Models that best satisfy energetic and geometric constraints produce CMB spikes 8–22° wide, peaking at O(100) mT. We suggest that the Levantine spike reflects an intense CMB flux patch that grew in place before migrating northwest, contributing to growth of the dipole field. Estimates of Ohmic heating suggest that diffusive processes likely govern the ultimate decay of geomagnetic spikes.
Similar content being viewed by others
Introduction
A key challenge to understanding the geodynamo process is to characterize and explain the most extreme spatial and temporal variations of Earth’s magnetic field. Dipole dominance, high- and low-latitude intense flux patches and weak variations in the Pacific hemisphere1,2 are robust characteristics of the field over the past few hundred years. Similar features have been reproduced in geodynamo simulations3 and have been used as criteria for assessing whether simulations produce Earth-like behaviour4,5,6. Whether these kinds of spatial variations can reflect long-term behaviour of the geomagnetic field requires detailed observations preceding the historical period.
The highest geomagnetic field intensities on record have been recovered from archeomagnetic artefacts from the Levantine region dated at around 1000 BC. At this time the global field was unusually strong, with an increasing7,8,9 axial dipole moment (ADM) of ∼95–100 ZAm2. Yet the intensities recorded in Jordan10 and Israel11 around 980 BC correspond to local virtual ADMs (VADMs) of approximately 200 ZAm2. The detection of high VADMs in Turkey to the North12, in Georgia13 to the East, and highs 150–300 years earlier in China to the North-East14 lends support for a somewhat broader regional extent for this extreme feature, and an increasing number of high quality intensity data from distinct archaeological sites in Syria15 provide additional temporal context for Middle Eastern intensity variations over the past 9,000 years. However, the morphology and spatial extent of the Levantine spike are presently unknown. Recent work suggests the existence of a second geomagnetic spike in North America that may be coeval with the Levantine spike16. Here we focus on the Levant region before discussing the issue of multiple spikes.
The Levantine geomagnetic spike is shown in Fig. 1, which presents six sets of spatially binned paleointensity data from sites with ages younger than 5000 BC and northern hemisphere locations from 15 to 60° E as downloaded from the online Geomagia.v3 database17 (http://geomagia.gfz-potsdam.de/) on 4 December, 2015. We use the VADM representation for the data to minimize geographical effects due to axial dipole variation and show all data with age and intensity uncertainties as assigned (or not) by the original authors. The spike is clearly visible in the 10–40° N, 30–45° E geographic bin in Fig. 1e, but not elsewhere. Previous attempts to relate the rate of field changes inferred from the spike to fluid flow at the top of the core require velocities that are much faster than those corresponding to present secular variation and flow morphologies that are very different to those obtained from frozen flux inversions of geomagnetic data or from the present generation of geodynamo simulations18,19
Archeomagnetic and volcanic VADM data drawn from the Geomagia.v3 database17 and plotted in geographic bins as noted in individual panels. Error bars are as assigned by the original authors, and where given are typically ±1 s.d. for radiocarbon ages, and ±1 s.d. about the mean VADM. However, in some publications the methodology is not reported and in some cases errors in both ages and intensity may be ±2 s.d. or 1 s.e. Please see the Geomagia.v3 database17 for more detailed information on the errors. (a–c) present a longitudinal transect from 15 to 60° E, and data from 40 to 70° N in latitude, and d–f are the same longitude bins as directly above, but for latitudes 10–40° N. The spike is clearly visible in e at about 1000 BC, while other bins (except c which is more or less flat) exhibit lower peaks around 500 BC. Light coloured lines represent predictions of axial dipole moment (ADM) from recent Holocene field models9, CALS10k.2 (red) and HFM.OL1.A1 (blue), while darker blue and red colours are VADM predictions for the average location of data in each bin. ADM increases to a peak value at about 300 AD, while VADM predictions are more regionally variable but still do not match the peak of the spike.
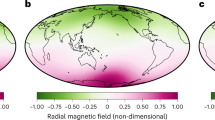
The 2,138 archeomagnetic intensity data shown in Fig. 1 form a subset of a much larger globally distributed collection of observations (>80,000 over the interval 8000 BC to 1660 AD), that is dominated by directions and relative paleointensities from sediments and has been used to produce recent Holocene field models. A selection of maps of radial magnetic field, Br, at the core–mantle boundary (CMB) are predicted from snapshots of the CALS10k.2 model9 and shown in Fig. 2. From 2000 BC, flux at high northern latitudes moves equator-ward, slightly weakening the dipole. By 1500 BC a small flux patch has emerged under NE Africa/Saudi Arabia, which intensifies until 1000 BC before later moving north and west. This patch may be related to the Levantine spike although there is no obvious signature in the surface intensity (Fig. 4b), and the VADM predicted by CALS10k.2 is much weaker than the observed values (Fig. 1e) around 1000 BC.
Maps of Br at the core–mantle boundary (CMB) predicted from model CALS10k.2 at (a) 2000 BC, (b) 1500 BC, (c) 1000 BC and (d) 750 BC. All scales for Br range from −900 to 900 μT. Note the incipient flux patch under Saudi Arabia at 1500 BC in b that grows into a relatively strong flux patch centred on 25° N in c. By 750 BC it appears to have moved west and north to merge with a patch lying to the south of the UK. There is no spike signature in the associated surface intensity (Fig. 4b), because of low resolution in the CALS10k.2 model.
(a) Black circles give age uncertainty estimates, σage, for 4,128 paleointensity estimates spanning the interval 0–10 ka used in the construction of the CALS10k.2 Holocene field model9 as described in the text. Green circles highlight the 143 data lying in the interval 1150–850 BC. Red circles mark estimates associated with the peak value at each of the 23 sites used in Fig. 4. (b) Black, green and red symbols as in the upper panel but now showing σlab. Blue circles show σt, which incorporates uncertainty effects arising from dating (σage) and age bias Δ arising from the discrepancy in the assigned age relative to the date of the Levantine spike, taken here to be 1000 BC (Methods). The total uncertainty is  , with the rate of intensity change ∂F/∂t taken to be 0.15 μT yr−1.
, with the rate of intensity change ∂F/∂t taken to be 0.15 μT yr−1.
Contours of field intensity, F (μT), at Earth’s surface (r=a) from the CHAOS-4 model2 at 2010 (a) the CALS10k.2 global field model at 1000 BC (b) and CALS10k.2 at 1000 BC plus a superposed best-fitting spike at 20° N, 40° E with amplitude A=400 mT and s.d. of σ=1° at the CMB (c). Symbols show paleointensities for samples dated at 1150–1050 BC (triangles), 1049–950 BC (squares) and 949–850 BC (circles). Symbol colours are blue (40–50 μT), green (51–60 μT), yellow (61–70 μT), orange (71–90 μT), red (91–115 μT) and black (>115 μT). White triangles in a–c mark the north pole of the dipole field. (d) Longitudinal cross-section through the spike in c, at Earth’s surface (blue, right ordinate) and the CMB (r=c, red, left ordinate). The horizontal dashed line marks the width at half maximum δ2(a). Available data within 20°±15° N are shown corrected to 20° N using the formula for an axial dipole field,  , where θ is colatitude. Error bars correspond to the uncertainties in Fig. 3b. Open and closed symbols cannot be simultaneously matched by the model.
, where θ is colatitude. Error bars correspond to the uncertainties in Fig. 3b. Open and closed symbols cannot be simultaneously matched by the model.
In this study we first map the spatial extent of the Levantine spike, showing that the region of anomalously high intensities, where the field strength rose and fell by a factor of 2, is confined to only 20° longitude. We then create a model of the spike by assuming, as in previous studies10,11,18,19,20, that it is a product of the geodynamo process that generates Earth’s internal magnetic field through motions of the liquid iron core. In this model the synthetic spike is entirely determined by its amplitude, width and location, all specified at the CMB. We find that even the thinnest CMB spikes (<1° wide) produce a surface feature that spans at least 60° in longitude. Models that trade off matching the surface spike intensity, minimizing L1 misfit to the available data, and satisfying core energy constraints produce CMB spikes 8–22° wide, peaking at O(100) mT. Such extreme behaviour is not observed in global models of the recent magnetic field and does not appear to have been identified in the current generation of geodynamo simulations.
Results
Spatial map of the levantine geomagnetic spike
To create an approximate spatial map of the Levantine spike seen at Earth’s surface we consider the Jordanian and Israeli data to be coeval and centred at 1000 BC. Although there is evidence for two distinct spikes separated by 1–2 centuries in the observations11 we do not make this distinction here, instead focussing on a single potential deep-seated cause at the CMB. We assigned an uncertainty to the spike age of ±100 years, which is similar to the age uncertainty on the Jordanian data and to the average age uncertainty of the paleointensity data used to construct CALS10k.2. We then selected all absolute intensity data from the Geomagia.v3 database17 with assigned ages in the range 1000±150 BC, yielding 143 data in 23 locations. Data without any prescribed age uncertainty were assigned the average value from the CALS10k.2 paleointensity data, namely σage=110 years (Fig. 3a). A given datum is considered to be coeval with the spike if their ages overlap within the uncertainties.
Further data selection is hampered by the significant complexities associated with paleointensity error estimation. Differences in host material, conditions at the time of remanence acquisition, laboratory protocols, age controls and documentation mean that it is very hard to define paleointensity errors that can be compared across different samples21,22. Improvements to paleointensity determination inevitably mean that older samples were not subjected to the same strict selection criteria used recently on the Levantine artefacts. In view of these difficulties we adopt the reasonable strategy of retaining all of the data, thus achieving critical mass and avoiding potential bias associated with specific protocols at the expense of requiring robust L1 measures for data misfit. An alternative approach would be to reject data where the paleointensity uncertainty is anomalously high. We compared the age and intensity uncertainties for all archeomagnetic paleointensity data used to construct CALS10k.2 (Fig. 3). The overall intensity uncertainty was assumed to arise from three factors (Methods): intensity uncertainty as a product of the laboratory measurements, σlab; age uncertainty based on dating the sample, σage; and age difference, Δ, between the sample age and the time of the spike, taken to be 1000 BC. The total uncertainty  , where ∂F/∂t is the rate of intensity change. Values of σlab<5 μT were considered to be unrealistically low9 and so these data were assigned an uncertainty of σlab=5 μT. Representative values of σt calculated using
, where ∂F/∂t is the rate of intensity change. Values of σlab<5 μT were considered to be unrealistically low9 and so these data were assigned an uncertainty of σlab=5 μT. Representative values of σt calculated using  , similar to the historical geomagnetic field1, provide evidence for the influence of age uncertainties (Fig. 3b, Supplementary Table 1). Nevertheless, the 143 global data that constrain the spatial structure of the Levantine spike are clearly typical of the overall CALS10k.2 data set, reinforcing the view that there is no justification for further data rejection at this stage.
, similar to the historical geomagnetic field1, provide evidence for the influence of age uncertainties (Fig. 3b, Supplementary Table 1). Nevertheless, the 143 global data that constrain the spatial structure of the Levantine spike are clearly typical of the overall CALS10k.2 data set, reinforcing the view that there is no justification for further data rejection at this stage.
To visualize the spike, we select at each of the 23 locations the datum with peak intensity (Fig. 4b–d, Supplementary Table 1). Some low values occur in the Levantine region at times nominally ranging from 1150 BC to 1025 BC (open symbols in Fig. 4d). Age uncertainties mandate their inclusion here, highlighting the issue that constraining absolute ages across the region remains difficult despite the high quality stratigraphic constraints possible within some individual sites11. Nevertheless, the spike is remarkably localized: normal intensities in Bulgaria23, India and Ukraine suggest a longitudinal extent of only 20°. There are no high-intensity features comparable to the spike in satellite2, historical1 or Holocene7,8 geomagnetic field models (compare Fig. 4a–c).
Model of the levantine spike
We assume that the geomagnetic spike is the surface expression of short wavelength structure in the radial magnetic field, Br, at the CMB (Methods). We do not consider how the spike might be produced, only the consequences of its existence. Holocene field models like CALS10k.2 (Figs 2c and 4b) are too smooth to show the spike in the field intensity at Earth’s surface7,8 and so we create a synthetic spike field,  , that is combined with the field
, that is combined with the field  predicted from a representative model (Fig. 4b). A representation of the spike is required in both physical space using spherical polar coordinates (r, θ, φ), and in wavenumber space using spherical harmonics of degree l and order m. This motivates the circular Fisher–Von Mises probability density function as a suitable choice for the spatial form of
predicted from a representative model (Fig. 4b). A representation of the spike is required in both physical space using spherical polar coordinates (r, θ, φ), and in wavenumber space using spherical harmonics of degree l and order m. This motivates the circular Fisher–Von Mises probability density function as a suitable choice for the spatial form of  . A spike centred at (θc, φc) in spherical coordinates is then defined entirely by the amplitude A and s.d. σ of the distribution. Assuming an insulating mantle, the total radial field is simply
. A spike centred at (θc, φc) in spherical coordinates is then defined entirely by the amplitude A and s.d. σ of the distribution. Assuming an insulating mantle, the total radial field is simply  .
.
Values of A, σ, θc and φc are varied simultaneously to match the observed spike intensity and width. Any single peak in intensity can always be produced by varying A and σ. Spike width is defined with respect to the peak intensity  . The latitudinal extent of the spike is hard to estimate, partly because there is little coeval data north and south of Jordan and Israel and partly because of the latitudinal increase in dipole field strength. We therefore define the regional spike width δx(r) as the longitudinal range over which F>Fmax/x, where x is a parameter that is >1. At 1000 BC the CALS10k.2 and PFM9K field models7,8 give F(a)≈60–65 μT at latitude λ=30° north, where a is Earth’s radius; together with the value of Fmax(a) from Fig. 4d, we obtain x≈1.6–2.0. Individual data (Fig. 4b) yield a similar result and so we focus on x=2, although using x=1.6 makes little difference.
. The latitudinal extent of the spike is hard to estimate, partly because there is little coeval data north and south of Jordan and Israel and partly because of the latitudinal increase in dipole field strength. We therefore define the regional spike width δx(r) as the longitudinal range over which F>Fmax/x, where x is a parameter that is >1. At 1000 BC the CALS10k.2 and PFM9K field models7,8 give F(a)≈60–65 μT at latitude λ=30° north, where a is Earth’s radius; together with the value of Fmax(a) from Fig. 4d, we obtain x≈1.6–2.0. Individual data (Fig. 4b) yield a similar result and so we focus on x=2, although using x=1.6 makes little difference.
With  =0, decreasing σ towards zero reduces the width of the surface spike towards a minimum of
=0, decreasing σ towards zero reduces the width of the surface spike towards a minimum of  (Supplementary Figs 1–3), much larger than the observed value of δ2(a)≈20°. This behaviour can be understood by considering the limit of a delta function spike (σ→0) at the CMB, which has equal power at all wavenumbers. The field decays with increasing r as (a/r)l+2 (Methods) and so the small-scale structure that is added to the CMB spike by decreasing σ is geometrically attenuated; the field exhibits no spike-like feature at Earth’s surface (Fig. 5). A suite of models with
(Supplementary Figs 1–3), much larger than the observed value of δ2(a)≈20°. This behaviour can be understood by considering the limit of a delta function spike (σ→0) at the CMB, which has equal power at all wavenumbers. The field decays with increasing r as (a/r)l+2 (Methods) and so the small-scale structure that is added to the CMB spike by decreasing σ is geometrically attenuated; the field exhibits no spike-like feature at Earth’s surface (Fig. 5). A suite of models with  =0 predict that the dominant surface expression of the spike is a change in the l=1 dipole component of the field for all 0.5°≤σ≤40° and 200≤A≤800 mT, although in relative terms it does not make a large immediate change to an existing dipole moment. With
=0 predict that the dominant surface expression of the spike is a change in the l=1 dipole component of the field for all 0.5°≤σ≤40° and 200≤A≤800 mT, although in relative terms it does not make a large immediate change to an existing dipole moment. With  defined by the CALS10k.2 field model at 1000 BC the spike is much wider, even for small values of σ, owing to lateral intensity variations in the field model (compare Supplementary Fig. 3 and Fig. 4d).
defined by the CALS10k.2 field model at 1000 BC the spike is much wider, even for small values of σ, owing to lateral intensity variations in the field model (compare Supplementary Fig. 3 and Fig. 4d).
Spatial power spectrum Rl for CALS10k.2 at 1000 BC, a representative spike, and spike plus CALS10k.2 as a function of spherical harmonic degree l at Earth's surface (a) and the core–mantle boundary (CMB) (b). The parameters for the spike model are the same as those in Fig. 4. Note the different scales for the abscissa in a,b and the attenuation of power at high l as the radius increases from the CMB to the surface. The inset in b shows a blow-up of the range l=0–10.
The predicted minimum spike width cannot be further reduced by adding time dependence or dynamics associated with the dynamo to the model. The problem is purely geometrical: the source is very far from the observation point. Allowing for finite mantle conductivity will smooth and delay core signals24, but does not move the source significantly closer to the surface because the mantle is thought to be weakly conductive everywhere except in a thin layer above the CMB25. The case of multiple closely spaced CMB spikes separated by a distance Δ at the CMB has also been investigated. When Δ<5° the corresponding surface feature appears as one large spike (Supplementary Figs 1 and 3). With Δ≈5° the surface feature has a flat top due to smearing of adjacent spikes. At large separations (for example, Δ=15° , Supplementary Fig. 2). the individual spikes are visible as a broad high-intensity region at the surface. In principle, a CMB magnetic flux distribution consisting of concentric rings of alternately signed flux would create a narrow high-intensity field structure at the Earth’s surface, however, such a configuration is not thought to be likely for a dynamo-generated field and has not been investigated here. The thinnest surface feature is obtained with only one spike at the CMB (Supplementary Figs 3 and 4). This, together with the available data distribution (Fig. 4), strongly suggests that the spike cannot be centred under the Near East.
To constrain spike morphology and position we generated 750 models with  defined by the CALS10k.2 field model at 1000 BC and a range of amplitudes, widths and locations (A, σ, θc and φc). Normalized model misfit for the n=143 data
defined by the CALS10k.2 field model at 1000 BC and a range of amplitudes, widths and locations (A, σ, θc and φc). Normalized model misfit for the n=143 data  was initially evaluated using both L1 and L2 measures of difference from the model predictions,
was initially evaluated using both L1 and L2 measures of difference from the model predictions,  . We define
. We define  for which we should expect values of L1=1.128 and L2∼1, respectively26 if we have accurate estimates of
for which we should expect values of L1=1.128 and L2∼1, respectively26 if we have accurate estimates of  . The
. The  are calculated as described above (Fig. 3) both with and without the age bias term Δ and for various values of ∂F/∂t. Since models with minimum L1 (and L2) are too smooth to fit the high-intensity Near East data we also require that a suitable model fits the observed intensity at the location of the spike, initially taken to be Israel.
are calculated as described above (Fig. 3) both with and without the age bias term Δ and for various values of ∂F/∂t. Since models with minimum L1 (and L2) are too smooth to fit the high-intensity Near East data we also require that a suitable model fits the observed intensity at the location of the spike, initially taken to be Israel.
The presence of outliers precluded obtaining reasonable fits using the L2 quadratic misfit measure. We therefore focus on L1. With ∂F/∂t=0.15 μT yr−1 (Fig. 3) the best fits to the spike correspond to L1∼2. This is higher than expected based on our uncertainty estimates. It is possible that the average lab uncertainties in paleointensity measurements of 5–10% are too low owing to the issues described above21. Alternatively, setting ∂F/∂t=0.15 μT yr−1 could be too conservative during a time of rapid dipole growth and occasional extreme regional field variations and this is supported by the rates of change of ≥1 μT yr−1 inferred from data in the Levant region around 1000 BC (refs 18, 27). A small increase of ∂F/∂t to 0.2 μT yr−1 gives values of L1 within the acceptable range (Fig. 6), which does not seem unreasonable. Larger values of ∂F/∂t shift the data in Fig. 6 to lower L1 since this gives more weight to the age uncertainties, which already represent the main contribution to σt for ∂F/∂t=0.15 μT yr−1.
Two representations of the same 750 models with different parameter dependencies highlighted. The grey shaded region marks the spike intensity in Israel10 with generous error bars applied. Best-fitting models, outlined by the rectangles, provide the best trade-off between matching the spike intensity and minimizing L1 misfit. (a) Highlights dependence on location: φc is indicated by colours while θc is shown by shape. (b) CMB spike location is fixed at θc=70° and φc=40° to illustrate dependence on A and σ. Models with thin spikes (low σ) located south east of Jordan are preferred.
Adding a synthetic spike to the CALS10k.2 1000 BC field improves the fit to the high-intensity Levantine data while retaining a satisfactory L1 misfit to the overall data set (Fig. 6). There is a relatively poor fit to some data (for example, Hawaii, Mali, Switzerland, China) whether or not the spike is present (Fig. 4b,c), reflecting the localized nature of the spike field. However, even the best-fitting spikes (Fig. 4c) are unable to match both the low (for example, Syrian, Egyptian and Cypriot) and high-intensity data in the Levantine region. This could be because the spike feature changed so fast18 that the approach of selecting all data in a 300 year window bracketing the main spike event is incorrect, though very rapid changes are not compatible with present core flows18 based on the frozen flux approximation. A potentially more satisfactory explanation is that the discrepancy arises due to inaccuracies in the dating and age bias (note that Syrian, Egyptian and Cypriot data are all nominally at older ages than the Jordanian and Israeli data, while data in Mali and India are nominally younger). What is clear is that the high and low Levantine intensity data cannot be simultaneously matched by changing the spike geometry.
Best-fitting model spikes are obtained when the spike is centred south East of Jordan around (λc, φc)=20° N, 40° E (Figs 4 and 6b), close to the position of a relatively strong CMB flux patch in the CALS10k.2 field (Fig. 2c). This location is favoured because it reduces the field intensity in south East Europe, which tends to be slightly over-predicted. Supplementary Fig. 5 shows that the best trade-off between minimizing weighted L1 misfit and fitting the spike intensity in Israel is achieved for the same parameter combinations regardless of the weighting applied in the misfit calculation. We, therefore, consider that the constraints on spike location and geometry shown in Fig. 6 are plausible given the present availability and quality of data.
At the CMB the best-fitting model spikes are strong and thin, with 400 mT≤A≤600 mT and 0<σ<18° The corresponding CMB field intensities range from O(1) mT for very wide spikes (σ=18°), comparable to the peak historical field1, to 1 T for thin spikes (σ=0.5°). While the latter value seems absurdly high it cannot be ruled out using surface magnetic field observations alone as long as the CMB field is so localized that it is obscured from detection (that is, there is significant power at harmonic degrees beyond l≈20 as in Fig. 5). The present root mean square (RMS) CMB field strength,  , including the small scales, can be inferred using numerical geodynamo simulations28 and studies of Earth’s nutations29,30 and length-of-day variations31, and may be as large as 1 mT. Assuming a similar value around 1000 BC eliminates only the very thin spikes: all models with σ≥4° and A≤600 mT have
, including the small scales, can be inferred using numerical geodynamo simulations28 and studies of Earth’s nutations29,30 and length-of-day variations31, and may be as large as 1 mT. Assuming a similar value around 1000 BC eliminates only the very thin spikes: all models with σ≥4° and A≤600 mT have  <1.7 mT.
<1.7 mT.
Significant regional variations in field direction are predicted by our model (Fig. 8), which could in principle provide additional constraints on its validity. However, the archeomagnetic slag samples used to identify the original intensity spike are unsuitable for accompanying directional measurements, while only two results were available in the Geomagia database between 1150 and 850 BC in the geographic bin containing the spike (Fig. 1e). Recent work on samples from fired ovens from Tel Megiddo, Israel11 have recovered steep inclination values of up to 75° at around the time of the spike, which are unusual at that latitude, while Turkish data with high VADMs are accompanied by slightly lower inclinations than in Israel suggesting they might lie slightly further from the centre of the spike. The predicted model directions are in line with these limited observations.
Intensity F in μT at the core–mantle boundary (a), and Earth’s surface (b) for a model with one geomagnetic spike under Texas (A=600 mT, σ=1°) and another spike under the Levant (A=400 mT, σ=1°). Maps of declination (c) and inclination (d) in degrees at Earth’s surface are also shown. Symbols in b are the same as in Fig. 4. Symbols in c,d show I=50–53° and D≈−10° for Halls Cave (Fig. 9 in ref. 16), I=65–75° and D≈−5–20° in Israel (Fig. 6 of ref. 11), and I=65° and D≈0° in Turkey (Fig. 7 in ref. 12).
A final independent constraint on the spike is obtained by estimating its contribution to the core energy budget. In a steady dynamo, magnetic energy created through work done by fluid motions on the field is balanced by energy lost via Ohmic heating, denoted Ψ. Together with estimates of core physical properties, Ψ constrains the core cooling rate and provides an estimate of the CMB heat flow, Qcmb, which can be compared to independent estimates32 of Qcmb=5–15 TW. We use a standard model for the energy budget33 and two sets of core material properties34 that were calculated for two different values of the inner core boundary density jump35, Δρ=0.6 and 0.8 gm cc−1 (ref. 36) (Methods). We estimate the Ψ due to the spike using a solution for the minimum Ohmic heating associated with the observable magnetic field37, denoted Ψm. This estimate omits ΨD, the part of Ψ due to the main dynamo process, and so provides a conservative estimate of Qcmb. Estimates of ΨD range from 0.5 to 10 TW (ref. 38), when accounting for recent results giving an increased core electrical conductivity39. We take ΨD=4 TW as an example and assume Ψm and ΨD can be added to obtain a simple estimate of Ψ (Methods).
With ΨD=0 none of our spikes require a CMB heat flow exceeding 15 TW, while with ΨD=4 TW only the strongest (A≥600 mT) and thinnest (σ=0.5°) spikes require Qcmb>15 TW (Fig. 7). The presence of the spike is only apparent in the gross energetics for σ<2°, where the CMB heat flow required to maintain the spike alone is the same order of magnitude as that required to maintain the whole dynamo. We view this as unlikely and so favour spikes with σ>2° at the CMB. Relaxing the steady state assumption does not change the results (Methods).
Applying the constraints provided by paleomagnetic data, estimates of CMB field strength and the core energy budget to the best-fitting synthetic spikes (marked by rectangles in Fig. 6), we infer the model parameter values A≈400 mT and σ≈4–10°. These values correspond to a CMB spike width of δ2(c)≈8–22° and a surface width of δ2(a)≈60°.
It is interesting to consider how the above results are affected by the presence of multiple CMB spikes. We consider the specific case of a recent sediment record from Texas16, which is apparently coeval with the Levantine spike and also shows rapid changes to very high field strength. Assigning different amplitudes and widths to a pair of spikes allows us to obtain models with slightly lower L1 misfits and a ∼10% increase in ADM compared to models with a single spike under the Levant. For example, the model in Fig. 8 has L1=0.46, a dipole moment of 116 ZAm2 and ADM of 115 ZAm2 compared to L1≈1.18, dipole moment of 105 ZAm2 and ADM of 102 ZAm2 for the single-spike model in Fig. 4c. This change in ADM is within the errors of the data8,9, while the associated directional deviations are compatible with the limited directional data accompanying recent studies11,12,16 (Fig. 8). As in the single-spike case the Ohmic heating can be kept to an acceptable level as long as neither spike is too thin.
Discussion
Our model shows that the instantaneous surface expression of high intensities must extend over a broad geographical area, estimated to be ≈60° longitude. Some of the data in Fig. 4 are inconsistent with this result, but the issue cannot be rectified by appealing to unresolved small scales in the core field. Ideally we would identify low-quality intensity estimates and those with poor age control and remove them from the analysis. The estimates presented in Supplementary Table 1 indicate that total uncertainties exceeding 45% of the measurement (with ∂F/∂t=0.2 μT yr−1) pertain to data from Japan, Mali, Czech Republic, India, Greece, Syria and Egypt. It is tempting to remove these data, since this would all but resolve the inconsistencies in the Near East shown in Fig. 4. However, as described above, quantification of uncertainty remains a challenge even with gold standard paleointensity protocols. Our uncertainty assessment has its own limitations, including reliance on the consistency of individual laboratory and dating errors and the poorly known rate of intensity change in the Levant around 1000 BC. The simplest explanation, suggested by the sample dates and age uncertainties, is that the low intensity samples found in Syria, Egypt and Cyprus sampled the field before the emergence of the spike.
On the basis of synthetic spike models that provide the best fit to the available data and assuming that low intensity samples in the region did not sample the spike field we suggest that the Levantine geomagnetic spike reflects an intense and localized near-equatorial flux patch on the CMB, perhaps reminiscent of features seen in the modern field40. The available data east and west of the Levant both suggest a VADM peak of ∼150 ZAm2 around 500 BC (Fig. 1d,f), which argues against pure east–west drift of this patch, while flux patches produced by rotationally constrained dynamos do not usually cross the equator41. This suggests that the patch either emerged from within the core and subsequently decayed in the same place, or grew in the equatorial region and migrated northwards (and westward).
Equatorial growth and subsequent northward migration of the spike is an appealing scenario because this would contribute to the ≈15–20% increase in dipole field strength42 seen in Holocene field models at that time7,8. Changes in the present dipole field strength are predominantly due to meridional advection by a large-scale anti-cyclonic gyre43. We envisage that a similar circulation could have transported the Levantine flux patch westward in the equatorial region before advecting it northward around American longitudes. The equatorial flux patch under Saudi Arabia in the CALS10k.2 model appears to follow a similar evolution (Fig. 2), suggesting that this patch may be a low-resolution image of the Levantine spike, although the exact evolution of this feature remains uncertain owing to the available temporal resolution of the CALS10k.2 field model44,45. In this scenario the tantalising evidence for an intensity spike recently identified in Texas16 (interpreted as a second intense flux spot on the CMB) would also enhance the dipole, since normal flux under North America is located near the northward leg of the gyre and so would also be swept towards the pole46.
A complication to this simple scenario is the possible occurrence of another Levantine spike11 that emerged after the main peak in 1000 BC. Current evidence for this second later spike is not clear-cut: an initial determination of a second spike at 890 BC (ref. 10) was rejected based on stronger selection criteria11, with new data suggesting a second spike around 800 BC. One plausible explanation is that these surface features reflect the propagation of multiple intense flux patches on the CMB. Alternatively, the two intensity highs might sample the edges of a single-flux patch.
Constraints on the spatial structure of geomagnetic spikes also provide additional insights into their temporal evolution. Theoretical calculations of rapid intensity changes require knowledge of the CMB magnetic field at scales that cannot be resolved by current observations18. Our results show that the power spectrum of the small-scale field associated with a spike (Fig. 5) cannot be obtained by a simple extrapolation of the observable field, which predicts decreasing power with increasing harmonic degree. It may also be possible to incorporate the energetic requirements for sustaining a given spike as constraints in core flow inversions. Furthermore, estimates of the Ohmic heating associated with geomagnetic spikes show that diffusion is likely to be important for the dynamics. Indeed, diffusion may ultimately be responsible for the decay of the spike as this process would be much faster than diffusive decay of a dipole field39 because the spike is so thin. We speculate that radial diffusion, which has been hitherto neglected in evolutionary models of the spike, is crucial to reconciling the rapid observed temporal variations (Fig. 1) with flow at the top of the core. Since radial diffusion is not directly constrained by geomagnetic observations one possibility is to incorporate a parameterization of the effect in core flow models using results from numerical geodynamo simulations47.
The present constraints on extreme geomagnetic field variations can guide the locations of future paleomagnetic acquisitions with a view to improving spatial coverage of the Levantine spike and to identifying new extreme geomagnetic events. Our results predict that the Levantine spike may have actually reached peak values south east of Israel, in which case paleointensity determinations from north-eastern Africa and Saudi Arabia would provide important constraints on the spike geometry. More directional data around 1000 BC, particularly east and west of the predicted spike location, are also essential to better quantify field behaviour in and around the Levantine region. The role of diffusion in controlling decay of geomagnetic spikes can, in principle, be tested in geodynamo simulations, although it remains to be seen whether the current generation of models produce the extremely spatially localized intensity variations that characterize the Levantine spike. Simulations can also be used to examine the origin of geomagnetic spikes. Potential mechanisms could include the expulsion of very strong toroidal flux concentrations48 (though this might produce a pair of equatorially symmetric spikes, which is not presently observed), or the concentration of magnetic flux near the CMB by a convergent downwelling flow49.
Methods
Treatment of paleointensity uncertainties
We assume that three effects contribute uncertainty when using paleointensity data to constrain the Levantine geomagnetic spike: intensity uncertainty as a product of the laboratory measurements, σlab; age uncertainty based on dating the sample, σage; and age difference, Δ, between the sample and the time of the spike (here taken as 1000 BC). The impact of both the latter contributions depend on the rate of change of the field and so the mean square error  can be written as
can be written as  , where
, where  =(∂F/∂t)2Δ2. For an individual intensity datum the contributions to
=(∂F/∂t)2Δ2. For an individual intensity datum the contributions to  were summed in quadrature. σlab was initially set to the uncertainty assigned by the original authors where available. Assigned uncertainties of <5 μT were considered to be unrealistically low9, and so these data were assigned an uncertainty of 5 μT. Data without intensity uncertainty were also assigned a value of σlab=5 μT. σage was taken from the original publications where this information was provided, otherwise it was set to the average value for the entire CALS10k.2 paleointensity data set, σage=110 years. The bias term
were summed in quadrature. σlab was initially set to the uncertainty assigned by the original authors where available. Assigned uncertainties of <5 μT were considered to be unrealistically low9, and so these data were assigned an uncertainty of 5 μT. Data without intensity uncertainty were also assigned a value of σlab=5 μT. σage was taken from the original publications where this information was provided, otherwise it was set to the average value for the entire CALS10k.2 paleointensity data set, σage=110 years. The bias term  arises because the estimated age of some samples is quite different from the assumed age of the spike; these samples are still included since the age uncertainties are such that they could be coeval with the spike. We estimate Δ as the age difference between 1000 BC and the nominal age of the sample, and use this to evaluate bias expected because of secular variation arising from the age mis-match.
arises because the estimated age of some samples is quite different from the assumed age of the spike; these samples are still included since the age uncertainties are such that they could be coeval with the spike. We estimate Δ as the age difference between 1000 BC and the nominal age of the sample, and use this to evaluate bias expected because of secular variation arising from the age mis-match.
The rate of intensity change, ∂F/∂t, in the Levant around 1000 BC is poorly constrained. Values as high as 4–5 μT yr−1 have been postulated from the data10, while theoretical bounds18 based on the frozen flux approximation suggest 0.6–1.2 μT yr−1. We consider three values of ∂F/∂t=0.1, 0.15 and 0.20 μT yr−1. The middle value is close to the maximum value found for the gufm1 historical field model1 spanning the period 1590–1990 AD.
Spike model
We make the standard assumption that the mantle is an insulator, which means that the toroidal field is zero on the CMB (radius r=c). For r>c the magnetic field B can be written as the gradient of a scalar ψ,

and the constraint

implies ∇2ψ=0, which is Laplace’s equation. In this case knowledge of the radial component Br is enough to determine ψ everywhere50. The solution for ψ is standard37 and can be used to obtain the three components of B. In spherical polar coordinates (r, θ, φ) the radial component Br is given by

Here  are spherical harmonics of degree l and order m and a is the radius of Earth’s surface. In practice the infinite series is truncated at l=Lmax. The complex coefficients
are spherical harmonics of degree l and order m and a is the radius of Earth’s surface. In practice the infinite series is truncated at l=Lmax. The complex coefficients  used in our code are related to the familiar Gauss coefficients
used in our code are related to the familiar Gauss coefficients  and
and  by
by  =2lRe(clm) and
=2lRe(clm) and  =−2lIm(clm) for m≠0 and
=−2lIm(clm) for m≠0 and  =lRe(c) and
=lRe(c) and  =0 for m=0.
=0 for m=0.
We insert a spike into Br at the CMB described by a Fisher–Von Mises probability distribution51. This form is chosen because it naturally conforms to the geometry of a spherical surface, and is easily adjusted in angular width and scale. We write

where

is the dot product of the vectors pointing from r=0 to the centre of the spike at (θc, φc) and from r=0 to the point under consideration. The amplitude of the spike is denoted A and the invariance κ of the Fisher distribution is related to the angular standard deviation, σ, by (ref. 51)

Since we are interested in the limiting case of very thin spikes we have chosen, without loss of generality, a circular spike with equal standard deviations in latitude and longitude,  . Multiple spikes can be inserted into Br, each with unique amplitude A and σ and separated by a distance Δ.
. Multiple spikes can be inserted into Br, each with unique amplitude A and σ and separated by a distance Δ.
Creating a spike in Br leaves open the possibility of also creating a monopole field, which violates Maxwell’s equations, but this is easily prevented by the introduction of the second term in equation (4). Because the Fisher distribution is a probability density function, the first term in equation (4) integrates to A. The second term uniformly distributes field across the core surface to ensure  in accordance with equation (2).
in accordance with equation (2).
Equation (3) provides a simple means of relating the spectral representations of the field at the surface and CMB. Equation (4) specifies the spike in physical space and so a method is needed to convert between the two. We use the standard spectral transform method52 with 3/2Lmax θ points and 3Lmax φ points, which ensures an exact transform between physical and spectral space. The spectral representation also makes it easy to combine two fields together. Since Laplace’s equation is linear, addition of the spike field  and the observed field
and the observed field  can be done on each harmonic individually.
can be done on each harmonic individually.
We compute the following quantities using the spectral representation:
Power spectrum37:

Minimum Ohmic heating37

Core energy budget
The energy and entropy equations that encapsulate the gross thermodynamics of core convection and the geodynamo are described in detail elsewhere38. The standard model for powering the geodynamo assumes that motion of the core fluid, a mixture of iron plus lighter elements, arises due to cooling and the presence of any radiogenic elements. Cooling leads to freezing of the solid inner core from the centre of the planet because the melting curve is steeper than the ambient temperature profile. As the inner core grows latent heat is released and the light elements partition favourably into the liquid phase, providing a source of gravitational energy. Averaging over a timescale that is long compared to that associated with convection but short compared to the evolutionary timescale of the planet it is assumed that convection mixes the entropy and light elements uniformly throughout the outer core such that the temperature varies adiabatically. The mantle is assumed to be electrically insulating. The global steady state energy equation relates the heat flowing across the CMB, Qcmb, to the heat sources inside the core and can be written symbolically as

Here Qs is the sensible heat stored in the core, QL is the latent heat released as the inner core grows, Qg is the gravitational energy, Qr is the heat released by any radiogenic elements and Tcmb is the CMB temperature. The quantities A and B represent integrals over core material properties. Equation (9) does not contain the magnetic field because magnetic energy is converted locally to heat by Ohmic dissipation. The field does appear in the entropy equation, which can be written symbolically as

where EJ≥0 is the Ohmic dissipation, Ek≥0 is the entropy due to thermal conduction, and the terms on the right-hand side are the entropies associated with the heat sources in equation (9). In writing equations (9) and (10) we have neglected small terms representing pressure heating due to core contraction, barodiffusion (pressure-driven diffusion of light elements) and heat of reaction. Viscous dissipation has also been neglected in equation (10); it is expected to be much smaller than the Ohmic dissipation because the kinematic viscosity is about 106 times smaller than the magnetic diffusivity39 and because magnetic fields tend to suppress small-scale motions53.
Equations (9) and (10) relate the Ohmic dissipation to the CMB heat flow through the cooling rate at the CMB,  . The quantities A and B are integrals over depth-varying profiles of core material properties38. We calculate these quantities using a model33 that incorporates the Preliminary Reference Earth Model (PREM)35 density and represents the melting and adiabatic temperature profiles by polynomials. The density jump at the inner core boundary, Δρ, determines the amount of light element in the outer core, which in turn affects the melting temperature and the values of all transport properties including the thermal and electrical conductivities, k and σc respectively. Normal modes give
. The quantities A and B are integrals over depth-varying profiles of core material properties38. We calculate these quantities using a model33 that incorporates the Preliminary Reference Earth Model (PREM)35 density and represents the melting and adiabatic temperature profiles by polynomials. The density jump at the inner core boundary, Δρ, determines the amount of light element in the outer core, which in turn affects the melting temperature and the values of all transport properties including the thermal and electrical conductivities, k and σc respectively. Normal modes give  gm cc−1 (ref. 36) and this uncertainty produces a comparable change in A and B to that obtained by combining the uncertainties in all other parameters34. We therefore consider changes in Δρ to reflect uncertainty in the calculation and focus on two values, Δρ=0.6 and 0.8 gm cc−1, with the corresponding parameters taken from a recent review34. Radiogenic heating is not included.
gm cc−1 (ref. 36) and this uncertainty produces a comparable change in A and B to that obtained by combining the uncertainties in all other parameters34. We therefore consider changes in Δρ to reflect uncertainty in the calculation and focus on two values, Δρ=0.6 and 0.8 gm cc−1, with the corresponding parameters taken from a recent review34. Radiogenic heating is not included.
The CMB heat flow is set by mantle convection; it does not necessarily equal the heat conducted out of the core down the adiabatic gradient. Recent reviews32,38 estimate Qcmb=5–15 TW, although >13 TW is probably needed at the present day34,54 in light of the recent upward revision to the core thermal and electrical conductivities39,55. The Ohmic dissipation is hard to constrain, partly because the dissipation is thought to occur on small length scales that are not resolved by surface observations56, and partly because part of the magnetic field is confined within the core. We seek a conservative estimate of the Ohmic dissipation and note that

where μ0 is the permeability of free space and Tmax≈5,500 K is the maximum temperature inside the core34. The Ohmic heating Ψ can be calculated directly in numerical geodynamo simulations, although these models are currently restricted to running in a parameter space far removed from that thought appropriate to Earth’s core. Older estimates of this type found Ψ≈0.5–1 TW (refs 28, 57), while recent work suggests Ψ=3–8 TW (ref. 58). Thermodynamic modelling constrained by output from one particular dynamo simulation59 yielded the estimate Ψ≈1–2 TW.
The estimates of Ψ above are based on temporal averages of the field as is appropriate for investigating long-term dynamo behaviour. As such they do not contain short-term features like geomagnetic spikes that get averaged out. We therefore assume that these Ψ estimates, denoted ΨD, represent the Ohmic heating associated with processes acting in the bulk of the core that are responsible for most of the field generation and that we may add to this a contribution Ψm due to the geomagnetic spike at the CMB:

As a conservative estimate for Ψm, we use an analytical solution for the minimum Ohmic heating associated with the observable part of the field given in equation (8) above.
On short timescales the basic assumptions of the model must be re-evaluated. Lateral variations in seismic velocity or density have never been detected60 and are expected to be small even if the core is not adiabatic throughtout61. Lateral temperature variations at the top of the core inferred from the observed magnetic field are 106 times smaller than the absolute temperature there62, backing up the seismic evidence. Seismic models of radial structure agree that the core is very close to adiabatic and well-mixed35,60, except perhaps in thin layers near the top63 and bottom64, but these layers are too thin (O(100) km) to have a significant effect in the calculation. Moreover, numerical models of rotating thermal convection with fixed flux boundaries find that the motion tends to reduce the super-adiabatic temperature difference across the domain as the driving force is increased towards Earth-like values65. The assumptions of an adiabatic and well-mixed core therefore seem appropriate when modelling short-term core energetics.
Fluctuations of the fluid velocity, v, that maintains the well-mixed adiabatic state need not average out on short timescales. The CMB is modelled as a simple boundary, that is, a spherical surface with no lateral variations in thermal or electrical properties. These assumptions together with the usual no-slip velocity boundary condition imply that v enters the governing equations (1) and (2) only through the rate of change of kinetic energy KE,  , which should be added to the left-hand side of equation (9) and the right-hand side of equation (10). (All (v·∇) terms are transformed to surface integrals that vanish on using the boundary conditions.) The field B should also be time-dependent and the term
, which should be added to the left-hand side of equation (9) and the right-hand side of equation (10). (All (v·∇) terms are transformed to surface integrals that vanish on using the boundary conditions.) The field B should also be time-dependent and the term  added to equations (9) and (10), where ME is the magnetic energy. A rough estimate of the magnetic and kinetic energies can be obtained by assuming a constant field B0 and velocity v0. Values of B0=1–10 mT are chosen; the highest value is 5–10 times present-day estimates for the RMS CMB field strength and four times higher than the core-averaged value inferred from nutations66. For v0 the range 10−4–10−3 m s−1 is selected, corresponding to roughly 1–10 times the present-day RMS flow speed at the top of the core inferred from geomagnetic secular variation67. With these values we obtain 7 × 1019≤ME≤7 × 1020 J and 8 × 1015 ≤ KE ≤ 8 × 1016 J. To make a meaningful contribution to the present-day energy budget of ≈13 TW, d(ME)/dt and d(KE)/dt must contribute at least 1 TW. The timescale Δt over which the estimated change in ME and KE would produce 1 TW of power can be estimated from d(ME)/dt≈ME/ΔtM and d(KE)/dt≈KE/ΔtK. The required change in kinetic energy would have to occur in <1 year, even for flow speeds ten times the present-day CMB value, which seems unlikely. Values of ΔtM 20–2,000 years, which also appear unlikely since the largest observed changes in the dipole moment (factor of 3) take 10,000–100,000 years68.
added to equations (9) and (10), where ME is the magnetic energy. A rough estimate of the magnetic and kinetic energies can be obtained by assuming a constant field B0 and velocity v0. Values of B0=1–10 mT are chosen; the highest value is 5–10 times present-day estimates for the RMS CMB field strength and four times higher than the core-averaged value inferred from nutations66. For v0 the range 10−4–10−3 m s−1 is selected, corresponding to roughly 1–10 times the present-day RMS flow speed at the top of the core inferred from geomagnetic secular variation67. With these values we obtain 7 × 1019≤ME≤7 × 1020 J and 8 × 1015 ≤ KE ≤ 8 × 1016 J. To make a meaningful contribution to the present-day energy budget of ≈13 TW, d(ME)/dt and d(KE)/dt must contribute at least 1 TW. The timescale Δt over which the estimated change in ME and KE would produce 1 TW of power can be estimated from d(ME)/dt≈ME/ΔtM and d(KE)/dt≈KE/ΔtK. The required change in kinetic energy would have to occur in <1 year, even for flow speeds ten times the present-day CMB value, which seems unlikely. Values of ΔtM 20–2,000 years, which also appear unlikely since the largest observed changes in the dipole moment (factor of 3) take 10,000–100,000 years68.
The spike is not a global feature at the CMB and cannot extend too far into the core without exceeding the available dissipation (Fig. 7). Moreover, RMS field strengths for even the thinnest spikes are comparable to the previous estimates. We therefore conclude that the time-dependent terms make a negligible contribution to the energy budget even in the presence of a spike. Clearly this does not imply that the spike itself is a static feature of the field.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Additional information
How to cite this article: Davies, C. & Constable, C. Geomagnetic spikes on the core-mantle boundary. Nat. Commun. 8, 15593 doi: 10.1038/ncomms15593 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Jackson, A., Jonkers, A. R. T. & Walker, M. R. Four centuries of geomagnetic secular variation from historical records. Philos. Trans. R. Soc. Lond. A 358, 957–990 (2000).
Olsen, N. et al. The CHAOS-4 geomagnetic field model. Geophys. J. Int. 197, 815–827 (2014).
Christensen, U. R. & Wicht, J. in Treatise on Geophysics, Vol. 8 (ed. Schubert, G.) 245–282 (Elsevier, 2007).
Christensen, U. R., Aubert, J. & Hulot, G. Conditions for Earth-like geodynamo models. Earth Planet. Sci. Lett. 296, 487–496 (2010).
Davies, C. J. & Constable, C. G. Insights from geodynamo simulations into long-term geomagnetic field behaviour. Earth Planet. Sci. Lett. 404, 238–249 (2014).
Mound, J., Davies, C. & Silva, L. Inner core translation and the hemispheric balance of the geomagnetic field. Earth Planet. Sci. Lett. 424, 148–157 (2015).
Korte, M., Constable, C. G., Donadini, F. & Holme, R. Reconstructing the Holocene geomagnetic field. Earth Planet. Sci. Lett. 312, 497–505 (2011).
Nilsson, A., Holme, R., Korte, M., Suttie, N. & Hill, M. Reconstructing Holocene geomagnetic field variation: new methods, models and implications. Geophys. J. Int. 198, 229–248 (2014).
Constable, C., Korte, M. & Panovska, S. Persistent high paleosecular variation activity in the Southern Hemisphere for at least 10,000 years. Earth Planet. Sci. Lett. 453, 78–86 (2016).
Shaar, R. et al. Geomagnetic field intensity: how high can it get? How fast can it change? Constraints from iron age copper slag. Earth Planet. Sci. Lett. 301, 297–306 (2011).
Shaar, R. et al. Large geomagnetic field anomalies revealed in bronze to iron age archeomagnetic data from Tel Megiddo and Tel Hazor, Israel. Earth Planet. Sci. Lett. 442, 173–185 (2016).
Ertepinar, P. et al. Archaeomagnetic study of five mounds from Upper Mesopotamia between 2500 and 700 BCE: further evidence for an extremely strong geomagnetic field ca. 3000 years ago. Earth Planet. Sci. Lett. 357–358, 84–98 (2012).
Shaar, R., Tauxe, L., Gogichaishvili, A., Rathert, M. C. & Devidze, M. Absolute geomagnetic field intensity in Georgia during the past 6 millennia. Latinmag Lett. 3, 1–4 (2013).
Cai, S. et al. Archaeointensity results spanning the past 6 kiloyears from eastern China and implications for extreme behaviors of the geomagnetic field. Proc. Natl Acad. Sci. USA 114, 39–44 (2017).
Gallet, Y. et al. New Late Neolithic (c. 7000–5000 BC) archeointensity data from Syria. Reconstructing 9,000 years of archeomagnetic field intensity variations in the Middle East. Phys. Earth Planet. Inter. 238, 89–103 (2015).
Bourne, M. D. et al. High-intensity geomagnetic field ‘spike’ observed at ca. 3,000 cal BP in Texas, USA. Earth Planet. Sci. Lett. 442, 80–92 (2016).
Brown, M. C. et al. GEOMAGIA50.v3: 1. General structure and modifications to the archeological and volcanic database. Earth, Planets Space 67, 83 (2015).
Livermore, P. W., Fournier, A. & Gallet, Y. Core-flow constraints on extreme archeomagnetic intensity changes. Earth Planet. Sci. Lett. 387, 145–156 (2014).
Fournier, A., Gallet, Y., Usoskin, I., Livermore, P. W. & Kovaltsov, G. A. The impact of geomagnetic spikes on the production rates of cosmogenic 14C and 10Be in the Earth’s atmosphere. Geophys. Res. Lett. 42, 2759–2766 (2015).
Shaar, R. et al. Decadal-scale variations in geomagnetic field intensity from ancient Cypriot slag mounds. Geochem. Geophys. Geosyst. 16, 195–214 (2015).
Tauxe, L. & Yamazaki, T. Treatise on Geophysics, 2nd edn, Vol. 5 (ed. Schubert, G.) 509–563 (Elsevier, 2015).
Suttie, N., Holme, R., Hill, M. J. & Shaw, J. Consistent treatment of errors in archaeointensity implies rapid decay of the dipole prior to 1840. Earth Planet. Sci. Lett. 304, 13–21 (2011).
Kovacheva, M., Kostadinova-Avramova, M., Jordanova, N., Lanos, P. & Boyadzhiev, Y. Extended and revised archaeomagnetic database and secular variation curves from Bulgaria for the last eight millennia. Phys. Earth Planet. Inter. 236, 79–94 (2014).
Backus, G. E. Application of mantle filter theory to the magnetic jerk of 1969. Geophys. J. R. Astron. Soc. 74, 713–746 (1983).
Buffett, B. A., Matthews, P. M. & Herring, T. A. Modeling of nutation and precession: effects of electromagnetic coupling. J. Geophys. Res. 107, 2070 (2002).
Parker, R. L. Geophysical Inverse Theory Princeton University Press (1994).
Shaar, R., Ron, H., Tauxe, L., Kessel, R. & Agnon, A. Paleomagnetic field intensity derived from non-SD: testing the Thellier IZZI technique on MD slag and a new bootstrap procedure. Earth Planet. Sci. Lett. 310, 213–224 (2011).
Christensen, U. R. & Aubert, J. Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Int. 166, 97–114 (2006).
Mathews, P. M., Herring, T. A. & Buffett, B. A. Modelling of nutation and precession: new nutation series for nonrigid Earth and insights into the Earth’s interior. J. Geophys. Res. 107, 2068 (2002).
Koot, L. & Dumberry, M. The role of the magnetic field morphology on the electromagnetic coupling for nutations. Geophys. J. Int. 195, 200–210 (2013).
Gillet, N., Jault, D., Canet, E. & Fournier, A. Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465, 74–77 (2010).
Lay, T., Hernlund, J. & Buffett, B. A. Core-mantle boundary heat flow. Nat. Geosci. 1, 25–32 (2009).
Davies, C. J. Cooling history of Earth’s core with high thermal conductivity. Phys. Earth Planet. Inter. 247, 65–79 (2015).
Davies, C., Pozzo, M., Gubbins, D. & Alfè, D. Constraints from material properties on the dynamics and evolution of Earth’s core. Nat. Geosci. 8, 678–685 (2015).
Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Masters, G. & Gubbins, D. On the resolution of density within the Earth. Phys. Earth Planet. Inter. 140, 159–167 (2003).
Backus, G. E., Parker, R. L. & Constable, C. G. Foundations of Geomagnetism Cambridge University Press (1996).
Nimmo, F. in Treatise on Geophysics 2nd edn, Vol. 8 (ed. Schubert, G.) 27–55 (Elsevier, 2015).
Pozzo, M., Davies, C. J., Gubbins, D. & Alfè, D. Transport properties for liquid silicon-oxygen-iron mixtures at Earth’s core conditions. Phys. Rev. B 87, 14110 (2013).
Jackson, A. Intense equatorial flux spots on the surface of the Earth’s core. Nature 424, 760–763 (2003).
Roberts, P. H. & King, E. M. On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76, 1–55 (2013).
Olson, P. & Amit, H. Changes in earth’s dipole. Naturwissenschaften 93, 519–542 (2006).
Finlay, C. C., Aubert, J. & Gillet, N. Gyre-driven decay of the Earth’s magnetic dipole. Nat. Commun. 7, 1–8 (2016).
Amit, H. G., Korte, M., Aubert, J., Constable, C. & Hulot, G. The time-dependence of intense archeomagnetic flux patches. J. Geophys. Res. 116, B12106 (2011).
Terra-Nova, F., Amit, H. & Hartmann, G. A. The time dependence of reversed archeomagnetic flux patches. J. Geophys. Res. 120, 691–704 (2015).
Gillet, N., Jault, D. & Finlay, C. C. Planetary gyre, time-dependent eddies, torsional waves, and equatorial jets at the Earth’s core surface. J. Geophys. Res. 120, 3991–4013 (2015).
Amit, H. & Christensen, U. R. Accounting for magnetic diffusion in core flow inversions from geomagnetic secular variation. Geophys. J. Int. 175, 913–924 (2008).
Bloxham, J. The expulsion of magnetic flux from the Earth’s core. Geophys. J. R. Astron. Soc. 87, 669–678 (1986).
Olson, P., Christensen, U. R. & Glatzmaier, G. A. Numerical modeling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104, 10,310–383,404 (1999).
Constable, C. G. & Parker, R. L. Statistics of the geomagnetic secular variation for the past 5 m.y. J. Geophys. Res. 93, 11569–11581 (1988).
Fisher, R. Dispersion on a sphere. Proc. R. Soc. Ser. A. 217, 295–305 (1953).
Young, R. E. Finite amplitude thermal convection in a spherical shell. J. Fluid Mech. 63, 695–721 (1974).
Zhang, K. Spherical shell rotating convection in the presence of a toroidal magnetic field. Philos. Trans. R. Soc. Lond. A 448, 245–268 (1995).
Buffett, B. A. Geomagnetic fluctuations reveal stable stratification at the top of the Earth’s core. Nature 507, 484–487 (2014).
Gomi, H. et al. The high conductivity of iron and thermal evolution of the Earth’s core. Phys. Earth Planet. Inter. 224, 88–103 (2013).
Jackson, A. & Livermore, P. W. On ohmic heating in the Earth’s core I: nutation constraints. Geophys. J. Int. 177, 367–382 (2009).
Buffett, B. A. & Christensen, U. R. Magnetic and viscous coupling at the core-mantle boundary: Inferences from observations of the Earth’s nutations. Geophys. J. Int. 171, 145–152 (2007).
Stelzer, Z. & Jackson, A. Extracting scaling laws from numerical dynamo models. Geophys. J. Int. 193, 1265–1276 (2013).
Roberts, P. H., Jones, C. A. & Calderwood, A. R. in Earth’s Core and Lower Mantle 100–129 (Contributions from the 7th Symposium SEDI 2000, (2003).
Masters, T. G. in Encyclopedia of Geomagnetism and Paleomagnetism (eds Gubbins, D. & Herrero-Bervera, E.) 82–85 (Springer, 2007).
Stevenson, D. J. Limits on lateral density and velocity variations in the Earth’s outer core. Geophys. J. Int. 88, 311–319 (1987).
Bloxham, J. & Jackson, A. Lateral temperature variations at the core-mantle boundary deduced from the magnetic field. Geophys. Res. Lett. 17, 1997–2000 (1990).
Helffrich, G. & Kaneshima, S. Outer-core compositional stratification from observed core wave speed profiles. Nature 468, 807–809 (2010).
Souriau, A. & Poupinet, G. The velocity profile at the base of the liquid core from PKP(BC+Cdiff) data: an argument in favor of radial inhomogeneity. Geophys. Res. Lett. 18, 2023–2026 (1991).
King, E., Stellmach, S. & Buffett, B. Scaling behaviour in Rayleigh-Bènard convection with and without rotation. J. Fluid Mech. 717, 449–471 (2013).
Buffett, B. A. Tidal dissipation and the strength of the Earth’s internal magnetic field. Nature 468, 952–954 (2010).
Holme, R. in Treatise on Geophysics Vol. 8 (ed. Schubert, G.) 107–130 (Elsevier, 2007).
Biggin, A. J., Strik, G. H. M. a & Langereis, C. G. The intensity of the geomagnetic field in the late-Archaean: new measurements and an analysis of the updated IAGA palaeointensity database. Earth, Planets Space 61, 9–22 (2009).
Acknowledgements
C.D. is supported by Natural Environment Research Council independent research fellowship NE/L011328/1 and a Green scholarship at IGPP. C.C. acknowledges support from NSF grants EAR-1246826 and EAR-1623786.
Author information
Authors and Affiliations
Contributions
C.D. and C.C. designed the project and wrote the paper. C.D. developed the numerical model of the spike and the core energy budget. C.C. developed the error analysis applied to the paleointensity data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Table and Supplementary References (PDF 1238 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Davies, C., Constable, C. Geomagnetic spikes on the core-mantle boundary. Nat Commun 8, 15593 (2017). https://doi.org/10.1038/ncomms15593
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15593
This article is cited by
-
Modeling geomagnetic spikes: the Levantine Iron Age anomaly
Earth, Planets and Space (2023)
-
Waves in planetary dynamos
Reviews of Modern Plasma Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.