Abstract
Semiconductor InAs/GaAs quantum dots grown by the Stranski–Krastanov method are among the leading candidates for the deterministic generation of polarization-entangled photon pairs. Despite remarkable progress in the past 20 years, many challenges still remain for this material, such as the extremely low yield, the low degree of entanglement and the large wavelength distribution. Here, we show that with an emerging family of GaAs/AlGaAs quantum dots grown by droplet etching and nanohole infilling, it is possible to obtain a large ensemble of polarization-entangled photon emitters on a wafer without any post-growth tuning. Under pulsed resonant two-photon excitation, all measured quantum dots emit single pairs of entangled photons with ultra-high purity, high degree of entanglement and ultra-narrow wavelength distribution at rubidium transitions. Therefore, this material system is an attractive candidate for the realization of a solid-state quantum repeater—among many other key enabling quantum photonic elements.
Similar content being viewed by others
Introduction
Solid-state sources that emit single pairs of entangled photons are a key element in quantum information technology. Polarization-entangled photons from atomic cascades were first used to test Bell’s inequality1,2, but demonstrating scalable applications with single atoms is clearly a technological challenge. In 1988, Shih and Alley3 reported that the photon pairs generated from spontaneous parametric down conversion4 are polarization entangled and can violate Bell’s inequality, opening the door for various polarization-entanglement-based experiments. However, spontaneous parametric down conversion sources are characterized by Poissonian statistics, that is, a tradeoff has to be made between the source brightness and the multiphoton emission probability. This lack of on-demand single-photon generation fundamentally limits their applications in complex quantum protocols.
Semiconductor InAs/GaAs quantum dots (QDs) grown by the Stranski–Krastanov method are among the leading candidates for the deterministic generation of polarization-entangled photons5,6,7,8,9,10. As proposed by Benson et al.5, the cascaded emission in single QDs from the biexciton  to the ground state via the intermediate exciton states
to the ground state via the intermediate exciton states  produces polarization-entangled photon pairs
produces polarization-entangled photon pairs  , where R and L denote right- and left-handed circular polarization, respectively. In real InAs/GaAs semiconductor QDs, however, the anisotropy in strain, composition and shape reduces the QD symmetry and mixes the two bright exciton states, resulting in two non-degenerate bright exciton states
, where R and L denote right- and left-handed circular polarization, respectively. In real InAs/GaAs semiconductor QDs, however, the anisotropy in strain, composition and shape reduces the QD symmetry and mixes the two bright exciton states, resulting in two non-degenerate bright exciton states  split by the fine structure splitting (FSS)11. The final two-photon state has a time-varying form
split by the fine structure splitting (FSS)11. The final two-photon state has a time-varying form  , where T1 is the radiative lifetime of the exciton, S the FSS and H and V horizontal and vertical linear polarization, respectively12. To reduce the phase shift between the |HH〉 and |VV〉 two-photon components and to obtain a high degree of entanglement, the experimental strategies are to reduce the FSS S and/or the exciton lifetime T1.
, where T1 is the radiative lifetime of the exciton, S the FSS and H and V horizontal and vertical linear polarization, respectively12. To reduce the phase shift between the |HH〉 and |VV〉 two-photon components and to obtain a high degree of entanglement, the experimental strategies are to reduce the FSS S and/or the exciton lifetime T1.
This is unfortunately no easy task. In the last decade there have been extensive efforts to generate entangled photons with InAs/GaAs QDs. The probability of finding suitable QDs in an as-grown sample is <10−2 (refs 13, 14), thus necessitating the use of post-growth tuning techniques (such as thermal annealing, the optical Stark effect, magnetic, electric and strain fields) to eliminate the FSS15. On the one hand, the fact that every single QD needs to be independently engineered imposes a great challenge for the practical application of QD-based devices. On the other hand, due to the electron–nuclear spin hyperfine interactions16,17, the degree of entanglement of InAs/GaAs QD-based sources is generally low even at zero FSS. The best result so far yields an entanglement fidelity F=0.82 and concurrence C=0.75 (ref. 18). Alternatively, one can reduce the exciton lifetime T1 by using the Purcell enhancement in a cavity, or perform time gating before a significant phase shift T1S/ħ between |HH〉 and |VV〉 takes place. The practical implementation of the former requires a simultaneous Purcell enhancement of both X and XX emissions6, which is a nontrivial task. The latter discards a large portion of photons and reduces the source brightness significantly. Applying post selection, fidelities up to F=0.86 have been achieved using an InAsP QD containing InP nanowire19.
Based on the above discussion, it is possible to obtain a large ensemble of QD-based polarization-entangled photon emitters by simultaneously incorporating a highly symmetric confinement potential, a short radiative lifetime and a weak electron–nuclear spin hyperfine interaction. The first attempt was reported by Juska et al.13, where arrays of symmetric In0.25Ga0.75As1−δNδ QDs were grown on the GaAs (111)B surface. They were able to obtain areas with an impressive 15% of entangled photon emitters with fidelities F in the range of 0.5 up to 0.72. Although the FSS is consistently below 4 μeV for these novel QDs, the exciton lifetime is quite long (1.8±0.6 ns). Nevertheless, the violation of Bell’s inequality was recently shown in electrically injected pyramidal QDs20. Kuroda et al.21 demonstrated the generation of entangled photons (with fidelity up to F=0.86) using highly symmetric GaAs/AlGaAs QDs grown on the GaAs (111)A surface by droplet epitaxy. Although the exciton lifetime is short (560 ps), the FSS are relatively large (with a mean value of 10±5 μeV) and the hyperfine interaction of the exciton with nuclear spins is significant in this system21.
In this work, we show that a large ensemble of as-grown polarization-entangled photon emitters can be obtained, using an emerging family of GaAs/AlGaAs QDs grown by droplet etching and nanohole infilling. These QDs exhibit very small FSS (with a mean value of 4.8±2.4 μeV) and short radiative lifetime (T1<220 ps). Under pulsed resonant two-photon excitation, a coherent excitation of the biexciton state can be achieved (with pronounced Rabi oscillations up to 7π), and all measured QDs emit single pairs of entangled photons with ultra-high purity and high degree of entanglement (fidelity F up to 0.91, concurrence C=0.90). The QDs presented in this work offer a deterministic wavelength control and ultra-narrow wavelength distribution, specifically tailored to match the optical transitions of rubidium. Thereby, we envision a hybrid quantum repeater that incorporates QD-generated entangled photon qubits interfaced with a rubidium vapour-based quantum memory.
Results
Sample growth
The QDs presented in this work are fabricated by solid-source molecular beam epitaxy. The in situ droplet etching22,23 is used to create self-assembled nanoholes with ultra-high in-plane symmetry24,25, which are subsequently filled and capped to obtain embedded solid-state quantum emitters26,27. Figure 1a shows a sketch of the processes involved in the QD formation. The initial point is a GaAs (001) substrate that has been deoxidized and overgrown with a GaAs buffer layer followed by 200 nm of AlxGa1−xAs. During the growth As2 is provided by a cracker cell running at 650 °C. First, Al is deposited under low arsenic pressure (<10−8 mbar), forming droplets on the surface at 630 °C. Driven by concentration gradients, the concurring dissolution of As through the droplets and diffusion of Al towards the substrate induces the formation of nanoholes with high symmetry. In a following annealing step at 630 °C the structures crystallize under a re-established As atmosphere of 10−7 mbar. Then, the nanoholes are filled with GaAs and subsequently overgrown by AlxGa1−xAs to obtain the isolated QDs with three-dimensional carrier confinement.
(a) Processing steps during the growth of GaAs/AlGaAs quantum dots (QDs): Al is deposited under low arsenic pressure, forming droplets on the surface of AlGaAs grown on a GaAs (001) substrate. The concurring dissolution of As through the droplets and diffusion of Al towards the substrate (illustrated by arrows) induces the formation of nanoholes with high symmetry. In a following annealing step the structures crystallize under a re-established As atmosphere. Then, the nanoholes are filled with GaAs and subsequently overgrown by AlGaAs to obtain isolated QDs with three-dimensional carrier confinement. (b) Exciton emission wavelength distribution for two different samples with GaAs infilling amounts of 2 nm (blue) and 2.75 nm (green) for more than 50 dots measured on each sample. Red markers indicate the rubidium D1 and D2 transition lines at 794.9 and 780.2 nm, respectively. Inset: sketch of envisioned interface between entangled photons from a QD and an atomic quantum memory based on the Raman scheme53. (c) Occurrence of the exciton fine structure splitting, comparing the GaAs/AlGaAs QDs (blue) with InAs/GaAs QDs (grey). Inset: scheme of the biexciton (XX) decay indicating the spin-related fine structure splitting S between the intermediate exciton states (X).
Envisioning a hybrid QD–atomic interface as a promising solid-state quantum memory28,29, it is desirable to match the QD emission with atomic transitions, illustrated by the inset in Fig. 1b. For this purpose several samples with varying GaAs infilling amounts have been grown, targeting the Rb D1 and D2 transition lines at a wavelength of 794.9 and 780.2 nm, respectively. Figure 1b shows the exciton wavelength distribution for two different samples with 2 nm (blue) and 2.75 nm (green) GaAs deposited at a growth rate of 0.47 and 0.5 μm h−1, accordingly. The statistics on more than 50 QDs across an area of 1 cm2 on each sample show an unprecedented control on the central emission wavelengths, with mean values of 779.8±1.6 nm and 796.3±1.3 nm. The wavelength distributions, or the so-called inhomogeneous broadenings, are among the narrowest for semiconductor QDs and are about 5 times smaller than that of a typical self-assembled InAs/GaAs QD sample. A similarly narrow inhomogeneous broadening can be observed in pyramidal QDs20,30.
Together with the high homogeneity, the QDs also exhibit high symmetry due to the negligible intermixing and a virtually strain-free interface between GaAs and AlGaAs. Previous work suggests that a reduction of the amount of deposited Al and an increase of the deposition rate can enhance the nanohole symmetry25. Following this trend, a single pulse of 0.09 nm excess Al at a growth rate of 0.8 μm h−1 (corresponding to AlAs growth) was used for our samples. The optimized growth protocols lead to high-quality QDs. Figure 1c shows the statistical distribution of the FSS for the GaAs/AlGaAs QD sample studied in this work (blue) and for a typical InAs/GaAs QD sample grown by partial capping and annealing (grey). The total number of measured dots is 45 and 114, respectively. The GaAs QDs feature an average FSS of only 4.8±2.4 μeV that is among the best values reported so far13,21,25. With these superior spectral properties, the investigated samples are promising candidates for the generation of polarization-entangled photons.
Resonant excitation of the biexciton
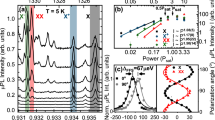
The major challenge to the realization of entangled photon pair emission from droplet-etched GaAs/AlGaAs QDs is the effective excitation of the biexciton (XX) state. In pyramidal GaAs/AlGaAs QDs the biexciton has been observed31, as well as in QDs based on GaAs/AlGaAs quantum well thickness flucutations32,33. So far there are only few reports about the observation of a biexciton in GaAs/AlGaAs QDs grown by local droplet etching21,27, presumably due to the low internal population probability under nonresonant excitation. Due to the optimized growth process we are able to observe strong XX emissions even with above-band excitations. We select a QD from the sample emitting close to the Rb D2 transition (∼780.2 nm) and excite it by pumping the surrounding higher-bandgap AlGaAs with a pulsed laser. The resulting spectrum (Fig. 2a), which is relatively clean in a broad range, shows several different excitonic transitions: The transition with the highest intensity is the exciton emission (X) at λ=778.5 nm. Among several red-shifted transitions, the XX emission is the strongest (λ=780.1 nm).
(a) Quantum dot (QD) emission spectrum for pulsed above-band excitation. The dominant exciton (X) and the biexciton (XX) transition are observed, which are spectrally close to other excitonic species. (b) Resonant excitation of the XX state using a two-photon excitation scheme. This efficient and coherent pumping mechanism results in a pure spectrum featuring primarily the XX–X cascade. The centric residual laser signal is strongly suppressed by using notch filters. (c) Intensity-autocorrelation measurement of the XX and X transition showing the coincidences plotted over the delay time τ. Very pure single-photon emission is confirmed by  and
and  . (d) Measurement of the fluorescence lifetime T1 for the XX and X state. The respective fit functions (solid lines) denote the convolution between an exponential decay and the detector response function. Short radiative lifetimes of T1,XX=112 ps and T1,X=134 ps are determined. (e) Fluorescence intensities of the XX and X emissions as a function of the pulse area θ, obtained by excitation laser power-dependent measurements. Rabi oscillations up to 7π are observed for both transitions. An offset is added to the XX values for better visibility, with the dotted lines indicating zero intensity.
. (d) Measurement of the fluorescence lifetime T1 for the XX and X state. The respective fit functions (solid lines) denote the convolution between an exponential decay and the detector response function. Short radiative lifetimes of T1,XX=112 ps and T1,X=134 ps are determined. (e) Fluorescence intensities of the XX and X emissions as a function of the pulse area θ, obtained by excitation laser power-dependent measurements. Rabi oscillations up to 7π are observed for both transitions. An offset is added to the XX values for better visibility, with the dotted lines indicating zero intensity.
To efficiently excite and to coherently drive the XX transition, we pump the two-photon resonance of the XX state by using a pulsed laser that lies spectrally in between the X and XX transitions. This excitation scheme has already been proven very effective in case of InAs/GaAs QDs34. Making use of tunable notch filters we can effectively suppress the laser background. Hence, a very pure spectrum showing mostly the XX and X emissions can be observed (Fig. 2b). The integrated intensities are the same for both emissions, strongly indicating a close to unity efficiency for the cascaded emission process34.
To obtain the evidence of pure single-photon emissions from both XX and X, we perform an autocorrelation measurement at π-pulse excitation using a standard Hanbury Brown and Twiss setup and the results are shown in Fig. 2c. The autocorrelation function g(2)(τ) plotted over the photon arrival delay τ shows a clear absence of counts at zero delay and proves the ultra-high purity single-photon emission. The background-corrected correlation function is measured to be  for XX and
for XX and  for X.
for X.
Next, we measure the luminescence lifetime T1 by recording an intensity correlation between the excitation laser pulse and the arrival time of the photons (see Fig. 2d). The XX shows a simple exponential decay, which is fitted taking into account the convolution with the detector response function. The X decay shows a longer rise time since the state has to be populated first by the decay of the XX state. The extracted lifetimes are T1,XX=112 ps and T1,X=134 ps, and these are among the lowest values recorded for as-grown semiconductor QDs. The ideal lifetime-limited linewidth of the exciton emission is therefore ΔE=4.9 μeV, close to the mean value of the FSS in our sample.
To further evaluate the resonant two-photon excitation scheme, we record the intensity of XX and X photons while changing the excitation power. The result is summarized in Fig. 2e by plotting the intensity over the pulse area θ that is proportional to the square root of the excitation power. Clear Rabi oscillations are observed, which are oscillations of the intensity due to a coherent rotation on the Bloch sphere between the ground state |0〉 and the excited state |XX〉. The abscissa is normalized in units of π to the first maximum of the XX intensity, where the pulse area is equal to π. Intensity oscillations up to 7π are observed. The mean intensity is decreasing for higher excitation powers, which may be caused by several different factors like chirp in the excitation pulse or scattering processes in the QD34. Increasing the power also leads to an increase in the oscillation frequency. This is a fingerprint of the two-photon excitation process in clear contrast to one-photon resonant excitation, where the frequency remains constant.
Evaluating the degree of entanglement
After realizing an efficient coherent control over the XX decay in GaAs QDs we now evaluate the degree of entanglement in the polarization of the emitted photons. A QD with a FSS of S=2.3 μeV is chosen in the experiment, since it represents a large portion (∼22%) of QDs in the sample (see Fig. 1c). The QD is excited with π-pulses for an efficient preparation of the biexciton state. To measure the degree of polarization correlation we send the stream of XX and X photons onto a 50:50 beam splitter. Each subsequent signal arm contains a quarter-wave plate, a half-wave plate and a polarizer to select the polarization in an arbitrary basis. After spectral selection of XX and X photons in the first and second signal arm, respectively, they are sent to single-photon detectors. Coincidence counting hardware is used to obtain the second-order correlation function  between XX and X photons for the selected polarization direction.
between XX and X photons for the selected polarization direction.
Figure 3a shows six cross-correlation measurements obtained for three bases of co-polarized and cross-polarized photons: the rectilinear (HV), diagonal (DA) and circular (RL) basis. As expected for an ideal entangled two-photon state  , a strong bunching (antibunching) at τ=0 is observed for co-polarization (cross-polarization) in the rectilinear and orthogonal bases, whereas this behaviour is reversed for the circular basis set. The correlation contrast for a chosen basis set is given by17
, a strong bunching (antibunching) at τ=0 is observed for co-polarization (cross-polarization) in the rectilinear and orthogonal bases, whereas this behaviour is reversed for the circular basis set. The correlation contrast for a chosen basis set is given by17
(a) Cross-correlation measurements between the biexciton and exciton emission for co- and cross-polarized photons in the rectilinear (H, horizontal; V, vertical), diagonal (D, diagonal; A, antidiagonal) and circular (R, right-handed; L, left-handed) polarization bases. For better visibility an offset in the delay time τ is added in the cross-polarized case. From these measurements on a quantum dot (QD) with a finite fine structure splitting of S=2.3 μeV a fidelity F=0.88±0.03 to the state  is deduced. (b,c) Real (b) and imaginary (c) part of the two-photon density matrix as reconstructed from 16 correlation measurements of the same QD by employing the maximum likelihood technique. The fidelity and concurrence extracted from this matrix are F=0.91 and C=0.90, respectively.
is deduced. (b,c) Real (b) and imaginary (c) part of the two-photon density matrix as reconstructed from 16 correlation measurements of the same QD by employing the maximum likelihood technique. The fidelity and concurrence extracted from this matrix are F=0.91 and C=0.90, respectively.

with  denoting the second-order correlation function at zero delay in collinear, and
denoting the second-order correlation function at zero delay in collinear, and  in orthogonal bases. For the three illustrated basis sets the following contrasts are obtained:
in orthogonal bases. For the three illustrated basis sets the following contrasts are obtained:



The fidelity F of the measured quantum state to the ideal state  can then be obtained by17
can then be obtained by17

which exceeds the classical limit F=0.5 by more than 12 standard deviations.
A more comprehensive picture of the measured entangled two-photon state is given by the density matrix representation. We performed cross-correlation measurements for 16 different base combinations to account for the 16 unknown variables in the density matrix ρ. The measured values for g(2)(0) are then used to construct a density matrix following the procedure presented in ref. 35. Since the thereby obtained density matrix violates important basic properties like positive semidefiniteness, the maximum likelihood estimation is employed to find the appropriate density matrix that is the closest to the measured results. The resulting matrix is shown in Fig. 3, split into the real part (Fig. 3b) and imaginary part (Fig. 3c). The strongest features are observed in the outer-diagonal real-part matrix elements, which are close to 0.5, while all other elements are close to zero. This is in agreement with the expected entangled state  whose density matrix should have only non-zero values of 0.5 in the outer-diagonal elements. The small (but non-zero) real values in the off-diagonal elements indicate a weak spin scattering process in the QD. The finite imaginary off-diagonal values represent a small phase difference between |HH〉 and |VV〉, presumably caused by the joint effect of a finite FSS and an accumulated phase due to the optical setup. From this density matrix, we obtain a fidelity F (after background corrections34) to the state
whose density matrix should have only non-zero values of 0.5 in the outer-diagonal elements. The small (but non-zero) real values in the off-diagonal elements indicate a weak spin scattering process in the QD. The finite imaginary off-diagonal values represent a small phase difference between |HH〉 and |VV〉, presumably caused by the joint effect of a finite FSS and an accumulated phase due to the optical setup. From this density matrix, we obtain a fidelity F (after background corrections34) to the state  of
of

which is very close to the value of 0.88±0.03 obtained from the 6 cross-correlation measurements in Fig. 3a.
Another measure for nonclassical properties of a quantum state is the concurrence C35. Using the acquired density matrix, a value of C=0.90 (raw data without correction: C=0.81) is obtained. This is not only surpassing the best value measured for InAs/GaAs QDs with zero FSS18, but is also the highest value obtained for any QD entangled photon source so far. The high values for fidelity and concurrence are especially remarkable considering the finite fine structure splitting of S=2.3 μeV, which already significantly degrades the entanglement in case of InAs/GaAs QDs17,36.
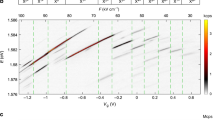
Since the phase shift T1S/ħ between |HH〉 and |VV〉 states is significantly reduced due to the very short lifetime T1 in this system, we expect that the generation of entangled photons should be also possible for QDs with even higher values of S. Therefore, we select six dots representing the whole range of FSS measured in the sample. By measuring six cross-correlations in three basis sets for each dot, their entanglement fidelities F are obtained. Figure 4 shows the values of F plotted as a function of the FSS (black circles), overlaid on the FSS distribution in the sample (grey histogram). The data from Zhang et al.36 including a Lorentzian fit are shown as a reference for typical InAs/GaAs QDs (orange line). Remarkably, all of the measured dots show a clear signature of entangled photon emission with F>0.5. Even the QD with S=9.8 μeV, which represents the QDs with the largest FSS in our sample, shows a fidelity F=0.59±0.05. We want to highlight that the measured dots were not preselected according to certain conditions apart from their FSS. All measurements lead to the conclusion that nearly 100% of the QDs in this sample show entangled photon emission.
The data points and traces illustrate the entanglement fidelity (left axis) and the grey histogram bars the occurrence of quantum dots (right axis), both plotted over the fine structure splitting S. All measured GaAs/AlGaAs quantum dots (QDs) from the sample (black circles) emit entangled photons with a fidelity above the classical limit of F=0.5 (dashed line) even for the largest values of S=9.8 μeV (F=0.59). The highest fidelity is measured to be F=0.91 at a nonvanishing S=2.3 μeV. For comparison, fidelity values of InAs/GaAs QDs taken from ref. 36 are plotted in orange, together with a Lorentzian fit. The fidelity uncertainties are obtained using error propagation and Poisson statistics for the coincidence counts. The uncertainties for S are determined by least square regression of polarization-dependent fluorescence measurements. Using a theoretical model, the fidelity F(T1, S) is plotted for two radiative lifetimes T1=120 ps (red) and T1=220 ps (blue), representing the range of all measured values for T1 in the sample. The applied model implies that both cross-dephasing and spin scattering processes are significantly suppressed in this material system. Together with the fine structure splitting distribution (grey histogram), the fidelity measurements strongly indicate that close to 100% of the QDs in the sample are polarization-entangled photon emitters.
Another outstanding feature of this material system are the significantly higher fidelities compared with that of the typical InAs/GaAs QDs, mostly originating from the weak electron–nuclear spin hyperfine interactions in this type of QDs16,17,37. To better understand the obtained values, we plot two theoretical curves showing the fidelity over the FSS for radiative lifetimes of T1=120 ps (red curve) and T1=220 ps (blue curve), the typical range for the measured exciton lifetimes. We modelled the fidelity following the work by Hudson et al.17 that includes the influence of the FSS and lifetime τ as well as cross-dephasing and spin scattering:

with

Here, k denotes the probability that the measured photon pairs originate from the dot. We estimate it to be k=0.97 due to the measured autocorrelation measurements presented in Fig. 2b. The factor  denotes the fraction of the QD emission that is unaffected by both cross-dephasing and spin-scattering processes, while
denotes the fraction of the QD emission that is unaffected by both cross-dephasing and spin-scattering processes, while  only considers spin-scattering processes. Since the presented data show no trend that would lead to F<0.5 for large FSS, we expect the influence of spin scattering processes on the entanglement to be negligible in this material system. Considering spin scattering due to the Overhauser field of the nuclear spins present in the dot, a spin-scattering time of TSS=15 ns can be assumed38. This is, however, two orders of magnitudes longer than the measured radiative lifetimes and therefore barely contributes to the degradation of the fidelity. On the other hand, in typical InAs/GaAs QDs this effect can be significantly stronger in case of high concentrations of spin-9/2 indium38, leading to much lower fidelity values for InAs/GaAs QDs in Fig. 4 (ref. 36). Since the fidelities at small FSS are very high for the GaAs/AlGaAs QDs, we neglect cross-dephasing processes in the model. It is clear that the trend in all our fidelity measurements can be well represented by the employed model.
only considers spin-scattering processes. Since the presented data show no trend that would lead to F<0.5 for large FSS, we expect the influence of spin scattering processes on the entanglement to be negligible in this material system. Considering spin scattering due to the Overhauser field of the nuclear spins present in the dot, a spin-scattering time of TSS=15 ns can be assumed38. This is, however, two orders of magnitudes longer than the measured radiative lifetimes and therefore barely contributes to the degradation of the fidelity. On the other hand, in typical InAs/GaAs QDs this effect can be significantly stronger in case of high concentrations of spin-9/2 indium38, leading to much lower fidelity values for InAs/GaAs QDs in Fig. 4 (ref. 36). Since the fidelities at small FSS are very high for the GaAs/AlGaAs QDs, we neglect cross-dephasing processes in the model. It is clear that the trend in all our fidelity measurements can be well represented by the employed model.
Discussion
In this work, we propose a new type of solid-state polarization-entangled photon source based on an emerging family of GaAs/AlGaAs QDs. These QDs can be grown with unprecedented wavelength control, ultra-small FSS and short radiative lifetime. The efficient and coherent excitation of the biexciton state in the GaAs/AlGaAs QDs is achieved by employing a resonant two-photon excitation scheme. The combination of a highly symmetric confinement potential, a short radiative lifetime and a weak electron–nuclear spin interaction in this material system enables entanglement fidelities up to F=0.91 and a concurrence of C=0.90. These are among the highest values ever reported for QD-based entangled photon sources. Most remarkably, the whole set of measurements draws an unambiguous conclusion that we have obtained a large ensemble of entangled photon emitters on a single semiconductor wafer, with almost 100% of QDs in the sample having fidelities F>0.5. Moreover, a great fraction of QDs are expected to exhibit high fidelities F>0.8 without any post-growth tuning.
We envision that a number of key enabling quantum photonic elements can be practically implemented by using this novel material system. A particularly important example is a quantum repeater as the backbone for long-range quantum communication. One requirement for a quantum repeater is the storage of entangled photon pairs within a quantum memory at a millisecond timescale39,40. Promising candidates for exceedingly long coherent storage are ensembles of laser-cooled atoms41,42,43,44, single trapped atoms45, impurity-doped crystals46,47 and optomechanical systems48. A potential material system for the storage of photons in the telecom wavelength range is erbium-doped Y2SiO5 (ref. 49). However, the storage capabilities of the latter do not yet exceed the nanosecond timescale. Thus, the QDs presented in this work are specifically tailored to match the optical transitions of rubidium that is among the most mature storage candidates. Thereby, we envision a hybrid quantum repeater that incorporates QD-generated entangled photon qubits that can be mapped reversibly in and out of a rubidium vapour-based quantum memory.
To fully reach that goal, however, high source brightness and photon indistinguishability also have to be ensured, for example by implementing QDs into microcavities. Additionally, entangled photons from different sources have to be spectrally matched to meet the requirements for quantum interference. Different strategies have been experimentally implemented to address this issue50,51. Furthermore, efficient frequency conversion of the photons after storage to the telecom wavelength range would be desirable for practical long-range quantum communication.
During the preparation of the manuscript we noted a similar work by Huber et al.52 that was executed at the same time. Both works are rather complementary to each other: while their focus lies on high entanglement fidelities and good indistinguishability values of a few selected dots, we show an exceptionally high yield to obtain strongly entangled photon sources for rubidium hybrid systems.
Methods
Optical excitation
The photoluminescence experiments were conducted at T=4 K by placing the sample in either a helium bath or a helium flow cryostat. As excitation laser for the above band and two-photon excitation, a pulsed Ti:Sa laser with 76 MHz repetition rate was used, which generated pulses with a duration of 3 ps. To spectrally narrow the laser pulse it was sent to a home-built pulse-shaping setup before it was coupled into a single-mode fibre. The excitation laser was then sent to the sample in the cryostat using a beam sampler and focused by a lens or an objective that was also used for the collection of the QD emission. We used half-ball solid immersion lenses to increase the photon collection from the sample. The fluorescence signal was coupled into a polarization-maintaining single-mode fibre. To suppress the resonant laser background, two consecutive tunable notch filters were employed before signal detection with a spectrometer.
Correlation measurements
To measure entanglement, the collected light from the QD was split by a 50:50 beam splitter into two arms, each containing a quarter-wave plate, a half-wave plate and a polarizer. The two beams were then coupled into polarization-maintaining single-mode fibres. After eliminating the residual laser using notch filters, each light path was fed into a monochromator to select the XX or X transition, respectively. The streams of photons were then detected by avalanche photodiodes, whose signals were processed by a time-correlated single photon counter. The integration times in the presented measurements ranged from 20 to 30 min for each correlation measurement, with count rates in the range of 2,500 c.p.s. up to 5,000 c.p.s. and a time binning of 64 ps.
Characterization of optical properties
We measured the FSS of the sample by rotating the half-wave plate in the entanglement measurement setup by α while rotating the quarter-wave plate by 2α. By obtaining high-resolution spectra for multiple values of α it was possible to fit the emission lines and determine an oscillation amplitude of the peaks spectral centre position with sub-μeV accuracy that corresponds to the FSS. The FSS in the InAs/GaAs QD reference sample was determined using the same method, but simply by rotating a half-wave plate in front of a linear polarizer. The lifetimes T1 were obtained using an avalanche photodiode with a short response function that was measured by using 3 ps laser pulses to be FWHM ≈100 ps. The measured response function was used to obtain the convoluted theoretical fits.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Additional information
How to cite this article: Keil, R. et al. Solid-state ensemble of highly entangled photon sources at rubidium atomic transitions. Nat. Commun. 8, 15501 doi: 10.1038/ncomms15501 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Freedman, S. J. & Clauser, J. F. Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938 (1972).
Aspect, A., Grangier, P. & Roger, G. Experimental tests of realistic local theories via Bell’s theorem. Phys. Rev. Lett. 47, 460 (1981).
Shih, Y. & Alley, C. O. New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion. Phys. Rev. Lett. 61, 2921 (1988).
Burnham, D. C. & Weinberg, D. L. Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett. 25, 84 (1970).
Benson, O., Santori, C., Pelton, M. & Yamamoto, Y. Regulated and entangled photons from a single quantum dot. Phys. Rev. Lett. 84, 2513–2516 (2000).
Dousse, A. et al. Ultrabright source of entangled photon pairs. Nature 466, 217–220 (2010).
Stevenson, R. M. et al. A semiconductor source of triggered entangled photon pairs. Nature 439, 179–182 (2006).
Akopian, N. et al. Entangled photon pairs from semiconductor quantum dots. Phys. Rev. Lett. 96, 130501 (2006).
Hafenbrak, R. et al. Triggered polarization-entangled photon pairs from a single quantum dot up to 30K. New J. Phys. 9, 315 (2007).
Muller, A., Fang, W., Lawall, J. & Solomon, G. S. Creating polarization-entangled photon pairs from a semiconductor quantum dot using the optical Stark effect. Phys. Rev. Lett. 103, 217402 (2009).
Bayer, M. et al. Fine structure of neutral and charged excitons in self-assembled In(Ga)As/(Al)GaAs quantum dots. Phys. Rev. B 65, 195315 (2002).
Stevenson, R. M. et al. Evolution of entanglement between distinguishable light states. Phys. Rev. Lett. 101, 170501 (2008).
Juska, G., Dimastrodonato, V., Mereni, L. O., Gocalinska, A. & Pelucchi, E. Towards quantum-dot arrays of entangled photon emitters. Nat. Photonics 7, 527–531 (2013).
Gong, M. et al. Statistical properties of exciton fine structure splitting and polarization angles in quantum dot ensembles. Phys. Rev. B 89, 205312 (2014).
Plumhof, J. D., Trotta, R., Rastelli, A. & Schmidt, O. G. Experimental methods of post-growth-tuning of the excitonic fine structure splitting in semiconductor quantum dots. Nanoscale Res. Lett. 7, 336 (2012).
Welander, E., Hildmann, J. & Burkard, G. Influence of hyperfine interaction on the entanglement of photons generated by biexciton recombination. Preprint at https://arxiv.org/abs/1409.6521 (2014).
Hudson, A. J. et al. Coherence of an entangled exciton-photon state. Phys. Rev. Lett. 99, 266802 (2007).
Trotta, R., Wildmann, J. S., Zallo, E., Schmidt, O. G. & Rastelli, A. Highly entangled photons from hybrid piezoelectric-semiconductor quantum dot devices. Nano Lett. 14, 3439–3444 (2014).
Versteegh, M. A. et al. Observation of strongly entangled photon pairs from a nanowire quantum dot. Nat. Commun. 5, 6298 (2014).
Chung, T. H. et al. Selective carrier injection into patterned arrays of pyramidal quantum dots for entangled photon light-emitting diodes. Nat. Photonics 10, 782–787 (2016).
Kuroda, T. et al. Symmetric quantum dots as efficient sources of highly entangled photons: violation of Bell’s inequality without spectral and temporal filtering. Phys. Rev. B 88, 041306 (2013).
Wang, Z. M., Liang, B. L., Sablon, K. A. & Salamo, G. J. Nanoholes fabricated by self-assembled gallium nanodrill on GaAs(100). Appl. Phys. Lett. 90, 113120 (2007).
Stemmann, A., Heyn, C., Köppen, T., Kipp, T. & Hansen, W. Local droplet etching of nanoholes and rings on GaAs and AlGaAs surfaces. Appl. Phys. Lett. 93, 123108 (2008).
Atkinson, P., Zallo, E. & Schmidt, O. G. Independent wavelength and density control of uniform GaAs/AlGaAs quantum dots grown by infilling self-assembled nanoholes. J. Appl. Phys. 112, 054303 (2012).
Huo, Y. H., Rastelli, A. & Schmidt, O. G. Ultra-small excitonic fine structure splitting in highly symmetric quantum dots on GaAs (001) substrate. Appl. Phys. Lett. 102, 152105 (2013).
Rastelli, A. et al. Hierarchical self-assembly of GaAs/AlGaAs quantum dots. Phys. Rev. Lett. 92, 166104 (2004).
Graf, A. et al. Excitonic states in GaAs quantum dots fabricated by local droplet etching. Phys. Rev. B 89, 115314 (2014).
Akopian, N., Wang, L., Rastelli, A., Schmidt, O. G. & Zwiller, V. Hybrid semiconductor-atomic interface: slowing down single photons from a quantum dot. Nat. Photonics 5, 230–233 (2011).
Pan, J. W. et al. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777 (2012).
Leifer, K. et al. Narrow (≈4 meV) inhomogeneous broadening and its correlation with confinement potential of pyramidal quantum dot arrays. Appl. Phys. Lett. 91, 081106 (2007).
Hartmann, A., Ducommun, Y., Kapon, E., Hohenester, U. & Molinari, E. Few-particle effects in semiconductor quantum dots: observation of multicharged excitons. Phys. Rev. Lett. 84, 5648–5651 (2000).
Ghali, M., Ohtani, K., Ohno, Y. & Ohno, H. Generation and control of polarization-entangled photons from GaAs island quantum dots by an electric field. Nat. Commun. 3, 661 (2012).
Hours, J., Senellart, P., Peter, E., Cavanna, A. & Bloch, J. Exciton radiative lifetime controlled by the lateral confinement energy in a single quantum dot. Phys. Rev. B 71, 161306 (2005).
Müller, M., Bounouar, S., Jöns, K. D., Glässl, M. & Michler, P. On-demand generation of indistinguishable polarization-entangled photon pairs. Nat. Photonics 8, 224–228 (2014).
James, D. F., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Zhang, J. et al. High yield and ultrafast sources of electrically triggered entangled-photon pairs based on strain-tunable quantum dots. Nat. Commun. 6, 10067- (2015).
Ulhaq, A. et al. Vanishing electron g factor and long-lived nuclear spin polarization in weakly strained nanohole-filled GaAs/AlGaAs quantum dots. Phys. Rev. B 93, 165306 (2016).
Chekhovich, E. A. et al. Nuclear spin effects in semiconductor quantum dots. Nat. Mater. 12, 494–504 (2013).
Afzelius, M., Gisin, N. & de Riedmatten, H. Quantum memory for photons. Phys. Today 68, 42–47 (2015).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Julsgaard, B., Sherson, J., Cirac, J. I., Fiurasek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004).
Chaneliere, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833–836 (2005).
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005).
Specht, H. P. et al. A single-atom quantum memory. Nature 473, 190–193 (2011).
de Riedmatten, H., Afzelius, M., Staudt, M. U., Simon, C. & Gisin, N. A solid-state light-matter interface at the single-photon level. Nature 456, 773–777 (2008).
Hedges, M. P., Longdell, J. J., Li, Y. & Sellars, M. J. Efficient quantum memory for light. Nature 465, 1052–1056 (2010).
Aspelmeyer, M., Meystre, P. & Schwab, K. Quantum optomechanics. Phys. Today 65, 29–35 (2012).
Lauritzen, B. et al. Telecommunication-wavelength solid-state memory at the single photon level. Phys. Rev. Lett. 104, 080502 (2010).
Chen, Y. et al. Wavelength-tunable entangled photons from silicon-integrated III-V quantum dots. Nat. Commun. 7, 10387 (2016).
Zhang, J. et al. Electric-field-induced energy tuning of on-demand entangled-photon emission from self-assembled quantum dots. Nano Lett. 17, 501–507 (2017).
Huber, D. et al. Highly indistinguishable and strongly entangled photons from symmetric GaAs quantum dots. Nat. Commun. 8, 15506 (2017).
Ding, D.-S. et al. Raman quantum memory of photonic polarized entanglement. Nat. Photonics 9, 332–338 (2015).
Acknowledgements
The work was financially supported by the ERC Starting Grant No. 715770 (QD-NOMS), the BMBF Q.Com-H (16KIS0106) and the European Union Seventh Framework Programme 209 (FP7/2007–2013) under Grant Agreement No. 601126 210 (HANAS). We thank E. Zallo, N. Akopian, K.D. Jöns and A. Rastelli for help and fruitful discussions, and Y. Li, X. Zhang, B. Eichler, R. Engelhard, S. Nestler, S. Baunack and S. Harazim for technical support.
Author information
Authors and Affiliations
Contributions
F.D. conceived the experiment and supervised the project together with O.G.S. who directed the research. The samples were grown by R.K. and the optical measurements were performed by M.Z. and R.K. with help from B.H. and Y.C. Data Analysis was performed by R.K. and M.Z. with help from J.Z. The manuscript was written by R.K., M.Z. and F.D. with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Keil, R., Zopf, M., Chen, Y. et al. Solid-state ensemble of highly entangled photon sources at rubidium atomic transitions. Nat Commun 8, 15501 (2017). https://doi.org/10.1038/ncomms15501
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15501
This article is cited by
-
Oscillating photonic Bell state from a semiconductor quantum dot for quantum key distribution
Communications Physics (2024)
-
Applications of single photons to quantum communication and computing
Nature Reviews Physics (2023)
-
Quantum interference of identical photons from remote GaAs quantum dots
Nature Nanotechnology (2022)
-
A tuneable telecom wavelength entangled light emitting diode deployed in an installed fibre network
Communications Physics (2020)
-
A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability
Nature Nanotechnology (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.