Abstract
The pseudogap in the cuprate high-temperature superconductors was discovered as a suppression of the Knight shift and spin relaxation time measured in nuclear magnetic resonance (NMR) experiments. However, theoretical understanding of this suppression in terms of the magnetic susceptiblility of correlated itinerant fermion systems was so far lacking. Here we study the temperature and doping evolution of these quantities on the two-dimensional Hubbard model using cluster dynamical mean field theory. We recover the suppression of the Knight shift and the linear-in-T spin echo decay that increases with doping. The relaxation rate shows a marked increase as T is lowered but no indication of a pseudogap on the Cu site, and a clear downturn on the O site, consistent with experimental results on single layer materials but different from double layer materials. The consistency of these results with experiment suggests that the pseudogap is well described by strong short-range correlation effects.
Similar content being viewed by others
Introduction
The pseudogap in the cuprates was discovered as a reduction of the Knight shift (Ks) and spin relaxation time T1 measured in nuclear magnetic resonance (NMR) experiments1,2,3,4,5. Subsequent experimental research6,7 has resulted in its detection in a wide range of materials and experimental probes for dopings smaller than optimal doping and temperatures smaller than 300 K. In single particle experiments, the pseudogap shows as a clear suppression of the density of states near the antinodal, but not the nodal, point of the Brillouin zone and is well described by non-perturbative numerical simulations8,9,10,11,12,13,14,15 of fermion model systems.
Unlike single-particle probes, NMR provides a direct measure of a two-particle quantity, the magnetic (spin) susceptibility. The complete theoretical understanding of the two-particle signals measured in NMR is difficult, requiring two components: a precise relation of the NMR signal to correlation functions16,17,18 and the low-energy spin susceptibility, and a reliable calculation of the spin susceptibility itself. While the first aspect has been well understood, directly obtaining the spin susceptibility of a correlated system has proven to be a formidable task, and as a result theoretical calculations of the NMR response have been limited to analytic or semi-analytic methods19,20, high temperature21 or sign-problem-free attractive models22. While these calculations provide a qualitative understanding of NMR signals outside the strong correlation regime, they either do not contain a pseudogap in the single particle quantities or are obtained on an attractive model and therefore are difficult to relate to the pseudogap in cuprate NMR spectra which is expected to originate from a repulsive interaction.
Recent advances in the numerical simulation of interacting fermionic lattice models23 have made simulation of susceptibilities possible. In particular, a combination of cluster dynamical mean field methods24 with continuous-time25 auxiliary field26,27 impurity solver extensions to two-particle functions28 now allow for the unbiased calculation of generalized susceptibilities29. These methods are controlled, in the sense that they become exact as cluster size is increased, and treat short range correlations within the cluster exactly, while longer ranged correlations are approximated in a mean field way.
In this paper we employ these new techniques to obtain the spin susceptibility of the Hubbard Hamiltonian,  (see methods), from which we can compute all aspects of NMR probes. Specifically we show calculations for NMR experiments such as: the Knight shift, the spin echo decay time (T2G) and the relaxation rate
(see methods), from which we can compute all aspects of NMR probes. Specifically we show calculations for NMR experiments such as: the Knight shift, the spin echo decay time (T2G) and the relaxation rate  . We focus on the temperature and doping dependence of these quantities for which a large body of experimental NMR work exists. Our results show remarkable similarity (both in temperature and doping dependence) to the experimentally measured quantities, indicating that the single-orbital Hubbard model, away from half filling and with an interaction strength close to the bandwidth captures much of the two-particle physics observed in experiment. Further, we isolate the role of pseudogap physics in each NMR probe.
. We focus on the temperature and doping dependence of these quantities for which a large body of experimental NMR work exists. Our results show remarkable similarity (both in temperature and doping dependence) to the experimentally measured quantities, indicating that the single-orbital Hubbard model, away from half filling and with an interaction strength close to the bandwidth captures much of the two-particle physics observed in experiment. Further, we isolate the role of pseudogap physics in each NMR probe.
Results
Knight shift
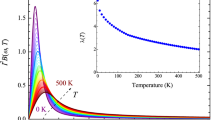
In Fig. 1 we present the simulated NMR Knight shift as a function of temperature T/t for a several dopings x. For these parameters, the largest Tc on the hole doped side is Tc=0.03t at x=0.09. At large doping x=0.1453 (triangle, solid blue line), the simulated Knight shift monotonically increases as T is reduced. Doped cases show a maximum at a temperature  , indicated by filled symbols. As the density decreases from x=0.0841 to x=0, this
, indicated by filled symbols. As the density decreases from x=0.0841 to x=0, this  gradually moves to higher T. At all temperatures studied, the overall magnitude of the Knight shift increases as doping is increased.
gradually moves to higher T. At all temperatures studied, the overall magnitude of the Knight shift increases as doping is increased.
Knight shift KS∝χm as a function of temperature T/t (lower x axis) for a series of doping levels computed at U=6t, t′=−0.1t obtained from 8-site DCA. Filled symbols: the peak positions of the Knight shift. Arrows: onset of normal state pseudogap obtained by analytical continuation of the single particle spectral function at K=(0, π). Upper x axis: T/t in units of Kelvin assuming t∼0.3 eV.
Several features in Fig. 1 described above are consistent with what is observed in NMR experiment on high Tc cuprates, and we show side-by-side comparison to those data in the supplement. Firstly, in the underdoped regime the downturn of χ as T is lowered is widely observed in Ks at various nuclei sites, see, for example, Fig. 8 in ref. 4 on YBa2Cu3O6.63 and Fig. 7 in ref. 30 on YBa2Cu4O8; and similar data for χ(T) is found in squid magnetometry of La2−xSrxCuO4 (ref. 31), which has historically been interpreted as the onset of the pseudogap phase4. Secondly, the increasing Knight shift with increasing doping is observed in a wide range of compounds, including La2−xSrxCuO4 (refs 31, 32), YBa2CuO7−x and YBa2Cu4O8 (ref. 18) and Y1−xPrxBa2Cu3O7 (ref. 18).
At high temperature, there is a distinct difference between the susceptibility measured in the bilayer material YBa2CuO6.63, which displays a broad maximum at 500 K and remains approximately constant up to 630 K (ref. 30), and that of the single layer material La2−xSrxCuO4 (refs 31, 33), where measurements indicate a slowly decreasing Knight shift above T. This discrepancy may be caused by magnetic coupling of copper-oxygen planes in the bilayer materials. Our calculations, which are done on a purely two-dimensional system, are consistent with measurements performed on single layer materials.
Extracting pseudogap energy scales
The arrows in Fig. 1 indicate the onset temperature of the pseudogap in the single particle spectral function calculated by analytical continuation of the single particle Green’s function34 using the maximum entropy method35,36. From the temperature evolution of AK=(π, 0)(ω), we define T as the temperature at which a suppression of the density of states appears near zero frequency (see Supplementary Fig. 1). In agreement with refs 37, 38, and as observed in a study of an attractive model39,  exhibits the same dependence on temperature and doping level as T, showing crossover temperatures identified with single-particle quantities (density of states) and two-particle quantities (Knight shift) to be the same. (While this work uses lattice susceptibility to calculate the Knight shift, ref. 37 identifies T based on cluster susceptibility, whose doping dependence is not consistent with NMR experiment.)
exhibits the same dependence on temperature and doping level as T, showing crossover temperatures identified with single-particle quantities (density of states) and two-particle quantities (Knight shift) to be the same. (While this work uses lattice susceptibility to calculate the Knight shift, ref. 37 identifies T based on cluster susceptibility, whose doping dependence is not consistent with NMR experiment.)
Figure 2 expands further upon the data in Fig. 1, including additional doping levels at x=0.0178 and x=0.0585 for temperatures above the superconducting Tc and below  as an Arrhenius plot. Once a gap has fully opened, the resulting curves become straight lines within uncertainties, allowing us to interpret our data as thermal excitations over a rigid gap and to extract an energy scale from the slopes using χm(T)=χ0 exp(−Δpg(2p)/T). The inset of Fig. 2 shows the comparison between the pseudogap energy determined by this method (open symbols) and the corresponding pseudogap energy extracted from the peak-to-peak distance of the single particle spectral function at the antinode (filled symbols). The two energy gaps are proportional as a function of doping. The distinct energy scales are however expected since Δpg(2p) averages over the Brillouin zone while Δpg(1p) only considers the antinodal momenta. As a result, their actual gap values in this case differ by a factor of 75, independent of doping. Similar comparisons for experimental data on YBa2Cu4O8 yield values of Δpg(1p)≈150 meV and Δpg(2p)=7.75 meV, a difference of a factor of 20 (refs 5, 7, 40, 41, 42). Potentially, a quantitative comparison of this ratio to experiment it might allow for a more precise determination of model parameters than considering single-particle properties alone.
as an Arrhenius plot. Once a gap has fully opened, the resulting curves become straight lines within uncertainties, allowing us to interpret our data as thermal excitations over a rigid gap and to extract an energy scale from the slopes using χm(T)=χ0 exp(−Δpg(2p)/T). The inset of Fig. 2 shows the comparison between the pseudogap energy determined by this method (open symbols) and the corresponding pseudogap energy extracted from the peak-to-peak distance of the single particle spectral function at the antinode (filled symbols). The two energy gaps are proportional as a function of doping. The distinct energy scales are however expected since Δpg(2p) averages over the Brillouin zone while Δpg(1p) only considers the antinodal momenta. As a result, their actual gap values in this case differ by a factor of 75, independent of doping. Similar comparisons for experimental data on YBa2Cu4O8 yield values of Δpg(1p)≈150 meV and Δpg(2p)=7.75 meV, a difference of a factor of 20 (refs 5, 7, 40, 41, 42). Potentially, a quantitative comparison of this ratio to experiment it might allow for a more precise determination of model parameters than considering single-particle properties alone.
Extraction of Δpg(2p) from Knight shift data via χm(T)=χ0 exp(−Δpg(2p)/T). Open symbols: data of Fig. 1 plotted as log(χm) versus β. Dashed lines: linear fits to the data in exponentially decaying regime. Inset: comparison between pseudogap energy extracted from the slope of Arrhenius plot (open symbols, right y axis) and from the single particle spectral function at K=(0, π) (filled symbols, left y axis).
Spin echo decay time
Figure 3 shows the spin echo decay time T2G, a measure of indirect spin–spin coupling, calculated according to equation (5). Owing to the divergence of lattice susceptibility near (π, π), we use the cluster susceptibility. This quantity shows a linear rise with temperature in the normal state and increases as doping is increased. The inset of Fig. 3 plots these data as  , the spin echo decay rate.
, the spin echo decay rate.  becomes less temperature dependent as more charge carriers are added. Otherwise, and consistent with experiment, T2G is rather featureless in the normal state and shows no marked change upon entering the pseudogap region.
becomes less temperature dependent as more charge carriers are added. Otherwise, and consistent with experiment, T2G is rather featureless in the normal state and shows no marked change upon entering the pseudogap region.
The linear increase of T2G depicted in Fig. 3 is similar to data obtained on YBa2Cu4O8 in NMR experiments reported in Fig. 3 of ref. 43 and Fig. 3 of ref. 44, and NQR experiment (Fig. 4 of ref. 30). The change of magnitude of a factor of 4 from 100 to 700 K is comparable in this calculation and experiment. The increase of  as charge carriers are added is similarly observed in YBa2Cu3O7−x experiment, see, for example, Fig. 8 of ref. 45 and Fig. 11 of ref. 18. We find no indication of a change of slope around ∼500 K as discussed in Fig. 4 of ref. 30.
as charge carriers are added is similarly observed in YBa2Cu3O7−x experiment, see, for example, Fig. 8 of ref. 45 and Fig. 11 of ref. 18. We find no indication of a change of slope around ∼500 K as discussed in Fig. 4 of ref. 30.
Spin relaxation rate
Figure 4 shows the simulated spin-lattice relaxation rate multiplied by the inverse temperature, (T1T)−1, as a function of T for three dopings (see equation (6)) with structure factors corresponding to copper and oxygen nuclei. All results are obtained at an interaction strength of U=6t using the cluster susceptibility. (T1T)−1 for 63Cu (solid line) rises rapidly when temperature is reduced. As doping is reduced, the value of (T1T)−1 decreases, and no clear indication of the pseudogap onset temperature is visible. In contrast, (T1T)−1 for 17O (solid line) has peaks at about the same temperatures as  . (T1T)−1 for both 63Cu and 17O become doping independent at even higher temperature (see Supplemental Material).
. (T1T)−1 for both 63Cu and 17O become doping independent at even higher temperature (see Supplemental Material).
(T1T)−1 plotted as a function of temperature at U=6t, t′=−0.1t, for x=0 to x=0.145, by 8-site DCA. (a) Solid lines: symmetry factors corresponding to 63Cu site. (b) Dashed line: 17O site (See Supplemental Material for explanation of uncertainties). Values in units of  18.
18.
While reliable results for T1 from other theoretical methods are absent in the pseudogap regime, our results can directly be compared to real-frequency RPA calculations for T1 in the weak coupling regime19. These calculations are neither limited by the momentum resolution of dynamical cluster approximation (DCA), nor do they suffer from the limitations of analytic continuation. Therefore they provide a stringent check on the precision with which we can obtain relaxation rates. Our simulations show that  smoothly decreases towards zero as temperature is reduced, in good agreement with RPA for U=2t (ref. 19), hinting at limitations of the random phase approximation in the intermediate coupling regime where deviations are apparent (see Supplemental Material).
smoothly decreases towards zero as temperature is reduced, in good agreement with RPA for U=2t (ref. 19), hinting at limitations of the random phase approximation in the intermediate coupling regime where deviations are apparent (see Supplemental Material).
The experimentally measured spin-lattice relaxation rates are strongly material dependent. One common feature found for the planar Cu site in YBCO materials in the normal state is that (T1T)−1 increases slowly and linearly as T decreases in a large range of temperature above T (refs 4, 40). As T is lowered below T, it shows a decrease towards Tc. In contrast, experiments in LSCO materials show that (T1T)−1 for the planar Cu site increases rapidly as temperature is decreased until Tc, with a larger rate as the doping level is decreased (see ref. 32, Fig. 4). (T1T)−1 data for planar 17O in LSCO are proportional to the Knight shift in the range from 100 to 200 K (ref. 46). Doping-independent (T1)−1 is observed in NQR experiment on LSCO above 700 K (Fig. 2 in ref. 47), and NMR experiment on YBa2(Cu1−xZnx)4O8 above 150 K (Fig. 2 in ref. 48). A comparison of these two types of materials is made in ref. 45. Our result is consistent with the experimental result of LSCO and inconsistent with YBCO. We attribute this to the presence of interplanar spin couplings in the latter materials49, whose existence is confirmed by neutron-scattering experiment50, and surmise that more complicated bilayer models might be required to yield consistent result for the YBCO spin-lattice relaxation rates, also suggested from previous theoretical work51.
Temperature dependence of momentum-dependent susceptibility
Expanding upon the previous section, we comment further on the distinct behaviour of the 63Cu and 17O signals in the calculated (T1T)−1 data of Fig. 4. Both calculations originate from the same spin susceptibility, and are distinguished only by the convolution with 63F|| and 17F|| structure factors, which are q-dependent functions.
In order to make these effects transparent, we present cuts in the Q=(qx, qy) plane of the static spin susceptibility on the matsubara axis, χ(iν0, qx, qy), in Fig. 5a. Plotted are 8-site DCA results, which therefore have only 4-distinct values at the M, Γ, X points and at Q=(π/2, π/2). As the temperature decreases, we see that the X=(π, 0) point has no temperature dependence. There does exist temperature dependence at both Q=(π/2, π/2) and Γ. However, the predominant effect with reduced temperature is the strong temperature dependence of the susceptibility near M=(π, π), which shows a continual increase upon decreasing temperature. This is distinct behaviour from the Γ point, which shows increasing behaviour until T/t=T=0.083, after which it decreases (see inset of Fig. 5b. The contribution at Γ=(0, 0) is precisely the NMR Knight shift (see Fig. 1).
The impact of the strong antiferromagnetic (π, π) scattering vector is compounded by the influence of the Form factors 63F|| and 17F||. These are plotted in Fig. 5b. We see than for the Cu sites, the 63F|| picks up both contributions of temperature dependence from M=(π, π) and near Γ=(0, 0). However, the signal is completely dominated by the monotonic increase with decreasing temperature of the susceptibility at the M-point. For oxygen sites, the 17F|| suppresses the growth of the susceptibility near (π, π), emphasizing instead the temperature dependence in the remaining regions around the Γ point. It is for this reason that NMR probes show site selective pseudogap behaviour (observed on oxygen NMR and not in copper NMR).
Discussion
We have shown results for the doping and temperature evolution of the Knight shift, the relaxation time and the spin echo decay time in the pseudogap regime of the two-dimensional Hubbard model from state-of-the art numerical simulation. Our results were obtained using an eight-site DCA calculation that treats short ranged correlations exactly and approximates longer ranged correlations in a mean field way. In this work, our goal has not been explaining the original of the pseudogap, but instead elucidating what is actually being measured in NMR probes in the presence of a pseudogap. These calculations show trends in temperature and doping evolution that are in remarkable agreement with experiment on single layer compounds and deviate when compared to the relaxation rate of double layer compounds, indicating that both the relation of experimental quantities to the generalized susceptibility and the calculation of the susceptibility in the pseudogap regime are well under control. Within these calculations, we demonstrate that the observation of a downturn in both Knight shift and  on oxygen sites originates from the same underlying effect, namely temperature dependence of the static susceptibility in the vicinity of q=(0, 0), and explain how such effects are washed out for
on oxygen sites originates from the same underlying effect, namely temperature dependence of the static susceptibility in the vicinity of q=(0, 0), and explain how such effects are washed out for  on copper sites.
on copper sites.
Further, the agreement of the calculated two-particle quantities with NMR experiment and relation to single-particle features of the pseudogap (T and Δpg) suggests that the salient aspects of the physics of the cuprate pseudogap are contained within the simple single-orbital Hubbard model14,52. Phenomena absent from this calculation, for example, stripes, charge ordering, multi-orbital effects53,54 or nematic order, may occur in addition to the physics realized here but do not seem to be the primary cause of the pseudogap observed in the cuprates via NMR probes.
The marked difference between multi layer and single layer materials suggests that inter-layer correlations, absent in these calculations, have a strong effect on the relaxation time. Providing reliable calculations of such effects, along with providing a description of the full momentum and frequency dependence of the susceptibility measured in neutron spectroscopy55, remains an interesting open challenge.
Methods
Susceptibilities
We study the single orbital Hubbard model in two dimensions with nearest and next nearest hopping parameters in the normal state,

where μ is the chemical potential, k momentum, i labels sites in real-space, U the interaction and the dispersion is given by 

The generalized susceptibility χ (refs 56, 57) is written in imaginary time in terms of the one-particle  =
= and two-particle
and two-particle  =
= Green’s functions as
Green’s functions as  =
= −
−
 . Its Fourier transform is
. Its Fourier transform is

where ω and ω′ are fermionic Matsubara frequencies, ν is a bosonic Matsubara frequency, σ and σ′ are ↑ or ↓ spin labels and k, k′ and q are initial, final and transfer momenta respectively. ph denotes the Fourier transform convention56. The main object of interest, the spin susceptibility, is then defined as

Knight shift
According to the Mila–Rice–Shastry model16,17 for hyperfine coupling with itinerant Cu2+ holes in high Tc cuprates, the Knight shift KS measured in NMR experiment is proportional to the uniform spin susceptibility,

Spin echo decay rate
For the 63Cu nuclear spin echo decay rate 631/T2G in paramagnetic state of high Tc cuprates58 showed that

where  (q, ν=0) denotes the real part of the real-frequency dynamical spin susceptibility at momentum q and frequency ν=0 and N is number of q points sampled in the first Brillouin zone. The prefactor 0.69 originates from the natural abundance of 63Cu (ref. 59), and 63Feff is defined in ref. 18 with hyperfine coupling constants A and B as
(q, ν=0) denotes the real part of the real-frequency dynamical spin susceptibility at momentum q and frequency ν=0 and N is number of q points sampled in the first Brillouin zone. The prefactor 0.69 originates from the natural abundance of 63Cu (ref. 59), and 63Feff is defined in ref. 18 with hyperfine coupling constants A and B as  , A||=−4B. For simplicity we set B≡1 and consider only proportionality. With this, both KS and T2G can be calculated directly from a susceptibility on the Matsubara axis since χ(q, ν=0)=χ(q, iν=0).
, A||=−4B. For simplicity we set B≡1 and consider only proportionality. With this, both KS and T2G can be calculated directly from a susceptibility on the Matsubara axis since χ(q, ν=0)=χ(q, iν=0).
Spin-lattice relaxation rate
The spin-lattice relaxation rate 1/T1 is related to the imaginary part of dynamical spin susceptibility on the real axis,

where αF||(q) differs for 63Cu and 17O, as defined in ref. 18.

The calculation of  (q, ν)/ν within a Matsubara formalism requires analytical continuation35. However, the quantity S(q, τ), defined as the real-to-k-space Fourier transform of
(q, ν)/ν within a Matsubara formalism requires analytical continuation35. However, the quantity S(q, τ), defined as the real-to-k-space Fourier transform of  , satisfies
, satisfies

(see ref. 22 for details) such that in the limit T→0

Numerical method
The direct numerical solution of equations (4), (5) and (8) for the Hubbard Hamiltonian equation (1) is intractable. We therefore employ the DCA24 which approximates the momentum dependence of the many-body self-energy and irreducible vertex functions by an approximated function that is constant on a set of Nc ‘patches’ in momentum space24,60. The method is a non-perturbative short correlation length approximation and is controlled in the sense that as Nc is increased it converges to the exact limit23,27,61. Throughout this paper we use Nc=8, a compromise between accuracy and efficiency that has previously been shown to capture much of the single-particle12,13,14,34,62 and two-particle28,29 physics observed in experiment and shows a qualitatively correct phase diagram for the pseudogapped and superconducting phases63,64,65,66. The interaction strength U=6t is large enough to exhibit a clear pseudogap state but presumably slightly smaller than seen in experiment, having an optimal doping and pseudogap onset closer to half filling29. We use a next-nearest neighbour hopping of t′=−0.1t, and do not allow for long ranged ordered antiferromagnetic or superconducting states.
Data availability
The computer code and data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Chen, X. et al. Simulation of the NMR response in the pseudogap regime of the cuprates. Nat. Commun. 8, 14986 doi: 10.1038/ncomms14986 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Warren, W. W. et al. Cu spin dynamics and superconducting precursor effects in planes above T c in YBa2Cu3O6.7 . Phys. Rev. Lett. 62, 1193–1196 (1989).
Alloul, H., Ohno, T. & Mendels, P. 89Y nmr evidence for a fermi-liquid behavior in YBa2Cu3O6+x . Phys. Rev. Lett. 63, 1700–1703 (1989).
Walstedt, R. E. et al. 63Cu nmr shift and linewidth anomalies in the t c=60 k phase of Y-Ba-Cu-O. Phys. Rev. B 41, 9574–9577 (1990).
Takigawa, M. et al. Cu and O nmr studies of the magnetic properties of YBa2Cu3O6.63 (t c=62 k). Phys. Rev. B 43, 247–257 (1991).
Walstedt, R. E. The NMR Probe of High-Tc Materials Vol. 228 (Springer Tracts in Modern Physics Springer (2008).
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Progr. Phys. 62, 61 (1999).
Hüfner, S., Hossain, M. A., Damascelli, A. & Sawatzky, G. A. Two gaps make a high-temperature superconductor? Rep. Progr. Phys. 71, 062501 (2008).
Huscroft, C., Jarrell, M., Maier, T., Moukouri, S. & Tahvildarzadeh, A. N. Pseudogaps in the 2d hubbard model. Phys. Rev. Lett. 86, 139–142 (2001).
Tremblay, A.-M. S., Kyung, B. & Sénéchal, D. Pseudogap and high-temperature superconductivity from weak to strong coupling. towards a quantitative theory (review article). Low Temp. Phys. 32, 424–451 (2006).
Macridin, A., Jarrell, M., Maier, T., Kent, P. R. C. & D’Azevedo, E. Pseudogap and antiferromagnetic correlations in the hubbard model. Phys. Rev. Lett. 97, 036401 (2006).
Kyung, B. et al. Pseudogap induced by short-range spin correlations in a doped mott insulator. Phys. Rev. B 73, 165114 (2006).
Werner, P., Gull, E., Parcollet, O. & Millis, A. J. Momentum-selective metal-insulator transition in the two-dimensional hubbard model: an 8-site dynamical cluster approximation study. Phys. Rev. B 80, 045120 (2009).
Gull, E., Parcollet, O., Werner, P. & Millis, A. J. Momentum-sector-selective metal-insulator transition in the eight-site dynamical mean-field approximation to the hubbard model in two dimensions. Phys. Rev. B 80, 245102 (2009).
Gull, E., Ferrero, M., Parcollet, O., Georges, A. & Millis, A. J. Momentum-space anisotropy and pseudogaps: a comparative cluster dynamical mean-field analysis of the doping-driven metal-insulator transition in the two-dimensional hubbard model. Phys. Rev. B 82, 155101 (2010).
Sordi, G., Sémon, P., Haule, K. & Tremblay, A.-M. S. Strong coupling superconductivity, pseudogap, and mott transition. Phys. Rev. Lett. 108, 216401 (2012).
Mila, F. & Rice, T. Analysis of magnetic resonance experiments in YBa2Cu3O7 . Phys. C 157, 561–570 (1989).
Shastry, B. S. t−J model and nuclear magnetic relaxation in high-tc materials. Phys. Rev. Lett. 63, 1288–1291 (1989).
Barzykin, V. & Pines, D. Magnetic scaling in cuprate superconductors. Phys. Rev. B 52, 13585–13600 (1995).
Bulut, N., Hone, D. W., Scalapino, D. J. & Bickers, N. E. Knight shifts and nuclear-spin-relaxation rates for two-dimensional models of CuO2 . Phys. Rev. B 41, 1797–1811 (1990).
Bulut, N. & Scalapino, D. J. Analysis of nmr data in the superconducting state of YBa2Cu3O7 . Phys. Rev. Lett. 68, 706–709 (1992).
Bulut, N., Scalapino, D. J. & White, S. R. Comparison of monte carlo and diagrammatic calculations for the two-dimensional hubbard model. Phys. Rev. B 47, 2742–2753 (1993).
Randeria, M., Trivedi, N., Moreo, A. & Scalettar, R. T. Pairing and spin gap in the normal state of short coherence length superconductors. Phys. Rev. Lett. 69, 2001–2004 (1992).
LeBlanc, J. P. F. et al. Solutions of the two-dimensional hubbard model: benchmarks and results from a wide range of numerical algorithms. Phys. Rev. X 5, 041041 (2015).
Maier, T., Jarrell, M., Pruschke, T. & Hettler, M. H. Quantum cluster theories. Rev. Mod. Phys. 77, 1027–1080 (2005).
Gull, E. et al. Continuous-time monte carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349–404 (2011).
Gull, E., Werner, P., Parcollet, O. & Troyer, M. Continuous-time auxiliary-field monte carlo for quantum impurity models. Europhys. Lett. 82, 57003 (2008).
Gull, E. et al. Submatrix updates for the continuous-time auxiliary-field algorithm. Phys. Rev. B 83, 075122 (2011).
Lin, N., Gull, E. & Millis, A. J. Two-particle response in cluster dynamical mean-field theory: formalism and application to the raman response of high-temperature superconductors. Phys. Rev. Lett. 109, 106401 (2012).
Chen, X., LeBlanc, J. P. F. & Gull, E. Superconducting fluctuations in the normal state of the two-dimensional hubbard model. Phys. Rev. Lett. 115, 116402 (2015).
Curro, N. J., Imai, T., Slichter, C. P. & Dabrowski, B. High-temperature 63Cu(2) nuclear quadrupole and magnetic resonance measurements of YBa2Cu4O8 . Phys. Rev. B 56, 877–885 (1997).
Nakano, T. et al. Magnetic properties and electronic conduction of superconducting La2−x Srx cuo4 . Phys. Rev. B 49, 16000–16008 (1994).
Ohsugi, S., Kitaoka, Y., Ishida, K., qing Zheng, G. & Asayama, K. Cu nmr and nqr studies of high-t c superconductor La2–xSrxCuO4 . J. Phys. Soc. Jpn 63, 700–715 (1994).
Johnston, D. C. Magnetic susceptibility scaling in La2−xSrxCuO4−y . Phys. Rev. Lett. 62, 957–960 (1989).
Lin, N., Gull, E. & Millis, A. J. Physics of the pseudogap in eight-site cluster dynamical mean-field theory: photoemission, raman scattering, and in-plane and c-axis conductivity. Phys. Rev. B 82, 045104 (2010).
Jarrell, M. & Gubernatis, J. Bayesian inference and the analytic continuation of imaginary-time quantum monte carlo data. Phys. Rep. 269, 133–195 (1996).
Levy, R., LeBlanc, J. P. F. & Gull, E. Implementation of the maximum entropy method for analytic continuation. Preprint at https://arxiv.org/abs/1606.00368 (2016).
Vidhyadhiraja, N. S., Macridin, A., Sen, C., Jarrell, M. & Ma, M. Quantum critical point at finite doping in the 2d hubbard model: a dynamical cluster quantum monte carlo study. Phys. Rev. Lett. 102, 206407 (2009).
Sordi, G., Sémon, P., Haule, K. & Tremblay, A.-M. S. c-axis resistivity, pseudogap, superconductivity, and widom line in doped mott insulators. Phys. Rev. B 87, 041101 (2013).
Trivedi, N. & Randeria, M. Deviations from fermi-liquid behavior above T c in 2d short coherence length superconductors. Phys. Rev. Lett. 75, 312–315 (1995).
Tomeno, I. et al. Nmr study of spin dynamics at planar oxygen and copper sites in YBa2Cu4O8 . Phys. Rev. B 49, 15327–15334 (1994).
Bankay, M., Mali, M., Roos, J. & Brinkmann, D. Single-spin fluid, spin gap, and d -wave pairing in YBa2Cu4O8: a nmr and nqr study. Phys. Rev. B 50, 6416–6425 (1994).
Williams, G. V. M., Tallon, J. L., Quilty, J. W., Trodahl, H. J. & Flower, N. E. Absence of an isotope effect in the pseudogap in YBa2Cu4O8 as determined by high-resolution 89Y nmr. Phys. Rev. Lett. 80, 377–380 (1998).
Corey, R. L. et al. 63Cu(2) nuclear quadrupole and nuclear magnetic resonance studies of YBa2Cu4O8 in the normal and superconducting states. Phys. Rev. B 53, 5907–5914 (1996).
Stern, R., Mali, M., Roos, J. & Brinkmann, D. Spin pseudogap and interplane coupling in Y2Ba4Cu7O15: A 63Cu nuclear spin-spin relaxation study. Phys. Rev. B 51, 15478–15483 (1995).
Berthier, C., Julien, M. H., Horvatić, M. & Berthier, Y. NMR studies of the normal state of high temperature superconductors. J. Phys. I 6, 2205–2236 (1996).
Walstedt, R. E., Shastry, B. S. & Cheong, S.-W. Nmr, neutron scattering, and the one-band model of La2−x Srx CuO4 . Phys. Rev. Lett. 72, 3610–3613 (1994).
Imai, T., Slichter, C. P., Yoshimura, K. & Kosuge, K. Low frequency spin dynamics in undoped and Sr-doped La2CuO4 . Phys. Rev. Lett. 70, 1002–1005 (1993).
qing Zheng, G. et al. 63Cu nqr/nmr study of zn-substituted YBa2Cu4O8 effect of impurity on spin-gap-like behavior. J. Phys. Soc. Jpn 62, 2591–2594 (1993).
Takigawa, M., Hults, W. L. & Smith, J. L. Comparison of nuclear spin relaxation rates at y and o sites in YBa2Cu3O7−y . Phys. Rev. Lett. 71, 2650–2653 (1993).
Tranquada, J. M., Gehring, P. M., Shirane, G., Shamoto, S. & Sato, M. Neutron-scattering study of the dynamical spin susceptibility in YBa2Cu3O6.6 . Phys. Rev. B 46, 5561–5575 (1992).
Millis, A. J. & Monien, H. Spin gaps and spin dynamics in La2−xSrxCuo4 and YBa2Cu3O7−δ . Phys. Rev. Lett. 70, 2810–2813 (1993).
Alloul, H. What is the simplest model that captures the basic experimental facts of the physics of underdoped cuprates? C. R. Phys. 15, 519–524 (2014).
Varma, C. M. Non-fermi-liquid states and pairing instability of a general model of copper oxide metals. Phys. Rev. B 55, 14554–14580 (1997).
Varma, C. M. Theory of the pseudogap state of the cuprates. Phys. Rev. B 73, 155113 (2006).
Li, Y. et al. Hidden magnetic excitation in the pseudogap phase of a high-tc superconductor. Nature 468, 283–285 (2010).
Rohringer, G., Valli, A. & Toschi, A. Local electronic correlation at the two-particle level. Phys. Rev. B 86, 125114 (2012).
Maier, T. A., Jarrell, M., Schulthess, T. C., Kent, P. R. C. & White, J. B. Systematic study of d-wave superconductivity in the 2d repulsive hubbard model. Phys. Rev. Lett. 95, 237001 (2005).
Pennington, C. H. & Slichter, C. P. Theory of nuclear spin-spin coupling in yba2 cu3 o7−δ . Phys. Rev. Lett. 66, 381–384 (1991).
Imai, T., Slichter, C. P., Yoshimura, K., Katoh, M. & Kosuge, K. Spin-spin correlation in the quantum critical regime of La2CuO4 . Phys. Rev. Lett. 71, 1254–1257 (1993).
Fuhrmann, A., Okamoto, S., Monien, H. & Millis, A. J. Fictive-impurity approach to dynamical mean-field theory: a strong-coupling investigation. Phys. Rev. B 75, 205118 (2007).
LeBlanc, J. P. F. & Gull, E. Equation of state of the fermionic two-dimensional hubbard model. Phys. Rev. B 88, 155108 (2013).
Gull, E. & Millis, A. J. Superconducting and pseudogap effects on the interplane conductivity and raman scattering cross section in the two-dimensional hubbard model. Phys. Rev. B 88, 075127 (2013).
Gull, E., Parcollet, O. & Millis, A. J. Superconductivity and the pseudogap in the two-dimensional hubbard model. Phys. Rev. Lett. 110, 216405 (2013).
Gull, E. & Millis, A. J. Energetics of superconductivity in the two-dimensional hubbard model. Phys. Rev. B 86, 241106 (2012).
Gull, E. & Millis, A. J. Pairing glue in the two-dimensional hubbard model. Phys. Rev. B 90, 041110 (2014).
Gull, E. & Millis, A. J. Quasiparticle properties of the superconducting state of the two-dimensional hubbard model. Phys. Rev. B 91, 085116 (2015).
Bauer, B. et al. The alps project release 2.0: open source software for strongly correlated systems. J. Stat. Mech. Theor. Exp. 2011, P05001 (2011).
Acknowledgements
We thank R. Walstedt and A.J. Millis for insightful and productive discussions on experimental data and on theory. We acknowledge the Simons Collaboration on the Many-Electron Problem for methods development and NSF grant 1606348 for application to NMR. Our simulations made use of the ALPS67 library and were performed on XSEDE using TG-DMR130036.
Author information
Authors and Affiliations
Contributions
X.C. performed the simulation and prepared the figures. X.C., J.P.F.L. and E.G. implemented computer codes, analysed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no financial competing interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Discussion, Supplementary Methods, Supplementary Results and Supplementary References (PDF 923 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, X., LeBlanc, J. & Gull, E. Simulation of the NMR response in the pseudogap regime of the cuprates. Nat Commun 8, 14986 (2017). https://doi.org/10.1038/ncomms14986
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms14986
This article is cited by
-
Explaining the pseudogap through damping and antidamping on the Fermi surface by imaginary spin scattering
Communications Physics (2022)
-
Particle-hole asymmetry in the dynamical spin and charge responses of corner-shared 1D cuprates
Communications Physics (2021)
-
Pairfield fluctuations of a 2D Hubbard model
npj Quantum Materials (2019)
-
Stripe order from the perspective of the Hubbard model
npj Quantum Materials (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

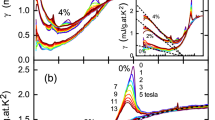



 . Decay rates are in units of
. Decay rates are in units of  63γn where 63γn is nuclear gyromagnetic ratio.
63γn where 63γn is nuclear gyromagnetic ratio.
