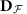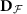Abstract
Interacting bosons or fermions give rise to some of the most fascinating phases of matter, including high-temperature superconductivity, the fractional quantum Hall effect, quantum spin liquids and Mott insulators. Although these systems are promising for technological applications, they also present conceptual challenges, as they require approaches beyond mean-field and perturbation theory. Here we develop a general framework for identifying the free theory that is closest to a given interacting model in terms of their ground-state correlations. Moreover, we quantify the distance between them using the entanglement spectrum. When this interaction distance is small, the optimal free theory provides an effective description of the low-energy physics of the interacting model. Our construction of the optimal free model is non-perturbative in nature; thus, it offers a theoretical framework for investigating strongly correlated systems.
Similar content being viewed by others
Introduction
Many-body physics of non-interacting systems reduces to the description of a single particle and thus is well understood. In contrast, the understanding of interacting systems remains one of the major open problems of both condensed matter and high-energy physics. Complete analytical solutions are possible in the so-called integrable systems1, which are not robust to perturbations. More generally, one relies on mean-field approaches, density functional theory or perturbation theory to expand around known solvable instances. Such methods can be employed when correlations are weak or interactions induce small corrections to the original state. Many interesting phenomena, however, have non-perturbative origin, such as superconductivity or the fractional quantum Hall effect. Although important insights about such systems have been obtained using variational ansätze2,3,4,5, this approach requires non-trivial physical intuition about the nature of the emerging free quasiparticles. A question of paramount importance arises: is it possible to directly identify the free effective model that is most similar to a given interacting one?
Here we introduce the concept of the interaction distance,  , which quantifies the effect of interactions on the ground state of a many-body system. At the same time, we identify the optimal free theory closest to the given interacting model. Our approach employs quantum information inspired techniques to study the correlations of a system witnessed in its entanglement spectrum and to build a general diagnostic tool of interactions. Typically, we find
, which quantifies the effect of interactions on the ground state of a many-body system. At the same time, we identify the optimal free theory closest to the given interacting model. Our approach employs quantum information inspired techniques to study the correlations of a system witnessed in its entanglement spectrum and to build a general diagnostic tool of interactions. Typically, we find  to be small when mean-field theory is applicable, whereas non-trivial behaviour emerges near critical regions. Using the example of the quantum Ising model, we demonstrate that the interaction distance can be calculated efficiently. We envision that finding the optimal free description of interacting systems can help formulate suitable variational ansätze in a variety of areas, ranging from condensed matter to high energy physics. Alternatively, it could be used to develop efficient numerical simulations of interacting systems that scale favourably with the system size.
to be small when mean-field theory is applicable, whereas non-trivial behaviour emerges near critical regions. Using the example of the quantum Ising model, we demonstrate that the interaction distance can be calculated efficiently. We envision that finding the optimal free description of interacting systems can help formulate suitable variational ansätze in a variety of areas, ranging from condensed matter to high energy physics. Alternatively, it could be used to develop efficient numerical simulations of interacting systems that scale favourably with the system size.
Results
Overview
The interaction distance  , introduced below, quantifies the distance between the reduced density matrix of a many-body state and the closest free-particle reduced density matrix. We demonstrate that
, introduced below, quantifies the distance between the reduced density matrix of a many-body state and the closest free-particle reduced density matrix. We demonstrate that  can be calculated efficiently from the entanglement spectrum6 and when this distance is small
can be calculated efficiently from the entanglement spectrum6 and when this distance is small  leads to the optimal free model that best describes the low-energy properties of the interacting system. Near critical regions,
leads to the optimal free model that best describes the low-energy properties of the interacting system. Near critical regions,  behaves non-trivially and its finite-size scaling can be related to the properties of the model under renormalization group flow. As an example, we apply our method to the one-dimensional (1D) quantum Ising model in the presence of transverse and longitudinal fields. We demonstrate that this model has
behaves non-trivially and its finite-size scaling can be related to the properties of the model under renormalization group flow. As an example, we apply our method to the one-dimensional (1D) quantum Ising model in the presence of transverse and longitudinal fields. We demonstrate that this model has  ≈0 across the whole phase diagram and we identify its optimal free description. Finally, we present a particular model with non-zero interaction distance in the thermodynamic limit, thus demonstrating its intrinsic interacting nature.
≈0 across the whole phase diagram and we identify its optimal free description. Finally, we present a particular model with non-zero interaction distance in the thermodynamic limit, thus demonstrating its intrinsic interacting nature.
Interaction distance and optimal free model
Consider an arbitrary many-body system prepared in its ground state,  . For simplicity, here we consider fermionic systems defined on a lattice, although our approach can be generalized to other systems, as we discuss below. Partitioning the system in two regions, A and its complement B, defines the reduced density matrix ρ=trB
. For simplicity, here we consider fermionic systems defined on a lattice, although our approach can be generalized to other systems, as we discuss below. Partitioning the system in two regions, A and its complement B, defines the reduced density matrix ρ=trB
 . The entanglement Hamiltonian HE=−ln ρ has eigenvalues {E}, known as the entanglement spectrum6. The entanglement spectrum captures the correlations in the ground state. Moreover, the universal properties of the actual Hamiltonian of the interacting system are reflected in HE6,7,8,9. For this reason, we diagnose the effect of interactions and identify the optimal free model exclusively through ground-state correlations.
. The entanglement Hamiltonian HE=−ln ρ has eigenvalues {E}, known as the entanglement spectrum6. The entanglement spectrum captures the correlations in the ground state. Moreover, the universal properties of the actual Hamiltonian of the interacting system are reflected in HE6,7,8,9. For this reason, we diagnose the effect of interactions and identify the optimal free model exclusively through ground-state correlations.
We introduce the interaction distance between the interacting ρ and the free σ reduced density matrices

where  is the trace distance and
is the trace distance and  is the manifold of all free fermion states. It is worth noting that unlike previous works10,11,12,13,14,15,16, the manifold
is the manifold of all free fermion states. It is worth noting that unlike previous works10,11,12,13,14,15,16, the manifold  contains all Gaussian states in any set of fermionic quasiparticle operators {c}. The trace distance has a physical interpretation in terms of distinguishability between ρ and σ when measuring observables17. Alternative state-distance measures can equally well be employed18. The quantity
contains all Gaussian states in any set of fermionic quasiparticle operators {c}. The trace distance has a physical interpretation in terms of distinguishability between ρ and σ when measuring observables17. Alternative state-distance measures can equally well be employed18. The quantity  has a geometric interpretation as the distance of the density matrix ρ from
has a geometric interpretation as the distance of the density matrix ρ from  .
.
To compute  , we need to perform the minimization in equation (1). We can show that this problem can be reduced to varying only the spectrum of σ. Consider the basis where ρ is diagonal and its entanglement spectrum {E} is available. A general σ∈
, we need to perform the minimization in equation (1). We can show that this problem can be reduced to varying only the spectrum of σ. Consider the basis where ρ is diagonal and its entanglement spectrum {E} is available. A general σ∈ need not be diagonal in the same basis as ρ. However, the trace distance between ρ and σ is minimized when σ commutes with ρ, that is, it is simultaneously diagonal with ρ and their eigenvalue spectra are rank ordered19. Indeed, if there existed a σ which minimized
need not be diagonal in the same basis as ρ. However, the trace distance between ρ and σ is minimized when σ commutes with ρ, that is, it is simultaneously diagonal with ρ and their eigenvalue spectra are rank ordered19. Indeed, if there existed a σ which minimized  but did not commute with ρ, then that minimum would not be a global one. As a consequence, the eigenstates of the optimal model σ are the same as the eigenstates of ρ. Thus, the minimization for obtaining
but did not commute with ρ, then that minimum would not be a global one. As a consequence, the eigenstates of the optimal model σ are the same as the eigenstates of ρ. Thus, the minimization for obtaining  now involves a variation with respect to the eigenvalues of σ that can be given in terms of its entanglement spectrum.
now involves a variation with respect to the eigenvalues of σ that can be given in terms of its entanglement spectrum.
Having to minimize only with respect to the spectrum of σ is a significant simplification of the optimization problem. A further exponential simplification is possible if we consider the structure of its entanglement spectrum. Consider N single-particle entanglement energies { } with allowed occupations {ni, i=1,…, N; ni=0, 1} corresponding to the independent modes {c} obeying Fermi-Dirac statistics. The full entanglement spectrum {Ef} of σ contains exponentially many levels, 2N, as a function of subsystem size N. However, a special property of free systems is that due to Wick’s theorem their entanglement spectrum can be built from a set of single-particle entanglement energies
} with allowed occupations {ni, i=1,…, N; ni=0, 1} corresponding to the independent modes {c} obeying Fermi-Dirac statistics. The full entanglement spectrum {Ef} of σ contains exponentially many levels, 2N, as a function of subsystem size N. However, a special property of free systems is that due to Wick’s theorem their entanglement spectrum can be built from a set of single-particle entanglement energies  i according to20
i according to20

where E0 is a normalization constant. The index k runs over the many-body spectrum, and for each k there are associated occupations ni(k)∈{0,1}. Hence, the interaction distance,  , can be cast as a minimization with respect to the N-many single-particle energies
, can be cast as a minimization with respect to the N-many single-particle energies

As N increases at most linearly with system size, expression (3) provides the means to efficiently compute the interaction distance and obtain the optimal free model of any state of an interacting theory whenever its entanglement spectrum {E} is accessible.
According to (3) the interaction distance is zero when the entanglement spectrum of ρ satisfies the combinatorial structure given in (2) for certain single-particle energies, { }. This generalizes our concept of free models. In general, no
}. This generalizes our concept of free models. In general, no  ’s exist that satisfy all these constraints as their number grows exponentially with the system size, while the number of
’s exist that satisfy all these constraints as their number grows exponentially with the system size, while the number of  ’s grows only linearly. Owing to the properties of the trace distance18 we have that the interaction distance takes values
’s grows only linearly. Owing to the properties of the trace distance18 we have that the interaction distance takes values  ∈[0,1]. The condition
∈[0,1]. The condition  =0 corresponds to a system that can be exactly described by the free fermions {c}, while
=0 corresponds to a system that can be exactly described by the free fermions {c}, while  =1 is the maximal distance a state can be from a free description. When
=1 is the maximal distance a state can be from a free description. When  is approximately zero, then the deviation in expectation values or correlation functions between ρ and the approximation σ is bounded. In particular, the interaction distance is sensitive only to deviations in the low lying entanglement spectrum, which dominate the expectation values of physical observables.
is approximately zero, then the deviation in expectation values or correlation functions between ρ and the approximation σ is bounded. In particular, the interaction distance is sensitive only to deviations in the low lying entanglement spectrum, which dominate the expectation values of physical observables.
At this point we might wonder what significance the bipartition holds in definition (1) of the interaction distance. From a quantum information point of view, the partial trace serves as a quantum channel through which we view the ground state. This channel is Gaussian if it maps a Gaussian state to another Gaussian state21. The combinatorial structure of (2) describes the eigenvalue spectrum of any Gaussian density matrix. In matching the spectrum we are testing compatibility between canonical operators in which the original state is a Gaussian state and the quantum channel is Gaussian, and our ability to describe the state in terms of modes separable to A and B. If there exist such modes then  is zero.
is zero.
A useful insight in the form of the modes {c} is given by a constructive derivation of (3) from (1) . The canonical algebra of {c} is invariant under arbitrary unitary transformations on σ. Hence, these transformations keep σ in  and
and  contains all of its unitary orbits. Optimizing for the minimum
contains all of its unitary orbits. Optimizing for the minimum  involves the following steps. First,
involves the following steps. First,  is decomposed into equivalence classes which are the mentioned unitary orbits. Within each class, the trace distance is minimized by a certain representative σ with which ρ commutes19. Then,
is decomposed into equivalence classes which are the mentioned unitary orbits. Within each class, the trace distance is minimized by a certain representative σ with which ρ commutes19. Then,  is obtained by taking the minimum over representatives of each class. As within these unitary orbits the trace distance is minimized when σ and ρ are simultaneously diagonal, the free modes {c} are given as Schmidt vectors corresponding to the single-particle entanglement levels {
is obtained by taking the minimum over representatives of each class. As within these unitary orbits the trace distance is minimized when σ and ρ are simultaneously diagonal, the free modes {c} are given as Schmidt vectors corresponding to the single-particle entanglement levels { } for which we have optimized. Note that the unitarily transformed modes are, in general, a nonlinear combination of the original modes, though they still describe a free model. From the optimal state σ, we can identify an effective free physical Hamiltonian in terms of the emergent quasiparticles {c} and we refer to this as the optimal free model. It can be found via a non-unique procedure22,23 which utilizes the two-point correlations of {c} with respect to σ.
} for which we have optimized. Note that the unitarily transformed modes are, in general, a nonlinear combination of the original modes, though they still describe a free model. From the optimal state σ, we can identify an effective free physical Hamiltonian in terms of the emergent quasiparticles {c} and we refer to this as the optimal free model. It can be found via a non-unique procedure22,23 which utilizes the two-point correlations of {c} with respect to σ.
General optimal free description
To determine the value of  we have chosen in (2) the statistics of the free quasiparticles to be fermionic. Generalizing further, we could allow for an optimal free description with respect to other quasiparticle statistics than the constituent fermions of the original interacting system. However, systems that comprize quasiparticles with different mutual statistics have in general Hilbert spaces of unequal dimension. This can be directly resolved in the following way. The entanglement spectrum of a pure state
we have chosen in (2) the statistics of the free quasiparticles to be fermionic. Generalizing further, we could allow for an optimal free description with respect to other quasiparticle statistics than the constituent fermions of the original interacting system. However, systems that comprize quasiparticles with different mutual statistics have in general Hilbert spaces of unequal dimension. This can be directly resolved in the following way. The entanglement spectrum of a pure state  can be found from the Schmidt decomposition,
can be found from the Schmidt decomposition,  ≅VAΣ
≅VAΣ , where the state has been reinterpreted as a map between the Hilbert spaces of the A and B parts. The isometries VA and VB map from A to B through an intermediate space
, where the state has been reinterpreted as a map between the Hilbert spaces of the A and B parts. The isometries VA and VB map from A to B through an intermediate space  , the entanglement Hilbert space on which the matrix of singular values Σ and the related entanglement Hamiltonian, HE, are defined. One can increase the dimension of
, the entanglement Hilbert space on which the matrix of singular values Σ and the related entanglement Hamiltonian, HE, are defined. One can increase the dimension of  by the addition of zero singular values to Σ and the addition of linearly independent columns to VA and VB so that they remain full-rank, without changing the correlations in
by the addition of zero singular values to Σ and the addition of linearly independent columns to VA and VB so that they remain full-rank, without changing the correlations in  . If the dimension of
. If the dimension of  is made to exceed the Hilbert space dimension of either subsystem then the isometries serve as projectors removing non-physical states with high entanglement energy. This fact allows us to compare interacting systems with optimal free models that may have different Hilbert space dimension.
is made to exceed the Hilbert space dimension of either subsystem then the isometries serve as projectors removing non-physical states with high entanglement energy. This fact allows us to compare interacting systems with optimal free models that may have different Hilbert space dimension.
Efficiency of computing 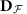
In the following we shall demonstrate with two examples that the interaction distance,  , is a versatile quantity that can be evaluated numerically or analytically. Importantly, the calculation of
, is a versatile quantity that can be evaluated numerically or analytically. Importantly, the calculation of  requires only the knowledge of the ground state; thus, it is more efficient than other possible measures, for example, based on directly comparing the structure of actual energy spectra.
requires only the knowledge of the ground state; thus, it is more efficient than other possible measures, for example, based on directly comparing the structure of actual energy spectra.
When ρ is the reduced density matrix of a gapped 1D system, then  can be numerically determined efficiently with L, the linear size of the system. Gapped 1D states have area-law entanglement24, which bounds the number of significant levels in the entanglement spectrum in the thermodynamic limit. Below we use the well-known density matrix renormalization group algorithm (DMRG)25 to efficiently obtain ground states of finite 1D systems. Moreover, in this case the low lying {
can be numerically determined efficiently with L, the linear size of the system. Gapped 1D states have area-law entanglement24, which bounds the number of significant levels in the entanglement spectrum in the thermodynamic limit. Below we use the well-known density matrix renormalization group algorithm (DMRG)25 to efficiently obtain ground states of finite 1D systems. Moreover, in this case the low lying { } in (2), and as a consequence the state σ, will converge exponentially fast with L. Thus, the minimization procedure in (3) is also efficient (see Methods), as it need only involve a finite number of significant levels determined by the correlation length, even in the thermodynamic limit.
} in (2), and as a consequence the state σ, will converge exponentially fast with L. Thus, the minimization procedure in (3) is also efficient (see Methods), as it need only involve a finite number of significant levels determined by the correlation length, even in the thermodynamic limit.
For critical 1D systems, logarithmic corrections to the area law are possible, which leads to the polynomial complexity in determining ρ. For critical 1D states, a multi-scale renormalization ansatz26 can be implemented to obtain the entanglement spectrum. If the system is gapless, the number of significant entanglement levels will increase but only polynomially with system size L; hence, the optimization procedure for determining the single-particle energies  remains efficient.
remains efficient.
Finally, in higher-dimensional systems, our method is reliant on the efficiency of the current methods in the literature for computing the entanglement spectrum of the ground state. For two-dimensional (2D) systems, one can use iterative methods such as the Lanczos algorithm to access only the ground state in the exact diagonalization framework. Furthermore, Monte-Carlo algorithms27 and 2D tensor networks28,29 can be used in a variety of systems to variationally approximate the ground state. Then the typical runtime complexity of  for an entanglement spectrum from a disk partition is polynomial in the correlation length and thus efficient.
for an entanglement spectrum from a disk partition is polynomial in the correlation length and thus efficient.
Finite-size scaling of 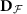
The quantity  , through its dependence on the entanglement spectrum, inherits the information about both short- and long-wavelength properties of the system. As pointed out by Li and Haldane6, the entanglement spectrum of a gapped phase exhibits a generic separation into the universal long-wavelength part and a non-universal short-distance part, the two being separated by the entanglement gap6. Assuming that the linear size of the system’s quasiparticles,
, through its dependence on the entanglement spectrum, inherits the information about both short- and long-wavelength properties of the system. As pointed out by Li and Haldane6, the entanglement spectrum of a gapped phase exhibits a generic separation into the universal long-wavelength part and a non-universal short-distance part, the two being separated by the entanglement gap6. Assuming that the linear size of the system’s quasiparticles,  , is much smaller than the linear size of the partition A, the long-wavelength information corresponds to correlated quasiparticle excitations across the entanglement partition, whereas the short-distance physics is associated with internal structure of the quasiparticles. The non-universal part is thus a boundary effect which is insensitive to variation in the subsystem size. In the thermodynamic limit, the non-universal part is exponentially suppressed in a gapped phase6, as seen from (3), and
, is much smaller than the linear size of the partition A, the long-wavelength information corresponds to correlated quasiparticle excitations across the entanglement partition, whereas the short-distance physics is associated with internal structure of the quasiparticles. The non-universal part is thus a boundary effect which is insensitive to variation in the subsystem size. In the thermodynamic limit, the non-universal part is exponentially suppressed in a gapped phase6, as seen from (3), and  then predominantly describes the universal properties of the system.
then predominantly describes the universal properties of the system.
At critical points where the quasiparticles remain well defined, that is,  stays finite, a large but finite system of linear size
stays finite, a large but finite system of linear size  chops off some of the correlations between the quasiparticles. We surmize that the finite-size scaling of
chops off some of the correlations between the quasiparticles. We surmize that the finite-size scaling of  near such critical regions follows the ansatz
near such critical regions follows the ansatz

where f is an undetermined function, and ζ and ν are the critical exponents. The constant θ≥0, which vanishes in the standard power-law scaling ansatz30, accommodates the fact that the interaction distance is bounded from above,  . A simple scaling analysis (see Methods) shows that ν is the correlation length exponent, whereas ζ determines the effect of interactions in the renormalization group sense. For example, when interactions are relevant,
. A simple scaling analysis (see Methods) shows that ν is the correlation length exponent, whereas ζ determines the effect of interactions in the renormalization group sense. For example, when interactions are relevant,  should remain non-zero as L increases, which dictates ζ≤0. On the other hand, when interactions are irrelevant, it is expected that
should remain non-zero as L increases, which dictates ζ≤0. On the other hand, when interactions are irrelevant, it is expected that  decreases with L near the critical regions, in which case ζ>0. However, it is noteworthy that it is possible for interactions to be irrelevant and still yield finite
decreases with L near the critical regions, in which case ζ>0. However, it is noteworthy that it is possible for interactions to be irrelevant and still yield finite  in the thermodynamic limit. This is because,
in the thermodynamic limit. This is because,  may be sensitive to non-universal (short distance) properties of the system, which can give a residual non-zero contribution parametrized by θ.
may be sensitive to non-universal (short distance) properties of the system, which can give a residual non-zero contribution parametrized by θ.
Application to Ising model
For concreteness we consider the example of the 1D ferromagnetic (FM) and antiferromagnetic (AFM) Ising model in both transverse, hz, and longitudinal, hx, fields (see ref. 31 for a recent review). By using exact diagonalization to determine the entanglement spectrum, we compute  across the phase diagram and examine its scaling around criticality and its convergence in the thermodynamic limit. Finally, we find optimal free-fermion models for each point (hz,hx) of the phase space.
across the phase diagram and examine its scaling around criticality and its convergence in the thermodynamic limit. Finally, we find optimal free-fermion models for each point (hz,hx) of the phase space.
The interacting Hamiltonians are given by

where H+ stands for FM and H− for AFM with periodic boundary conditions. In the presence of only transverse field (hx=0), model (5) maps to free fermions via the Jordan-Wigner transformation. A non-zero longitudinal field, hx, introduces non-local interactions between fermions. A quantum critical point at hz=1 separates an ordered and a disordered phase of the free system which are related by a self-duality32. The FM model has a single critical point at (hz=1, hx=0), whereas the AFM model has a critical line connecting (hz=1, hx=0) with the classical point (hz=0, hx=2)33.
Minimizing the interaction distance over the phase diagram we find that  decays with L away from critical regions as shown in Fig. 1, with the variational parameters {
decays with L away from critical regions as shown in Fig. 1, with the variational parameters { } converging exponentially (see Methods). Thus, the model can be faithfully described by a free theory in these regions of the phase diagram. The exceptions only occur infinitesimally close to the FM critical point and at the AFM classical critical point. This is remarkable because these models are non-integrable and a priori have strong quantum fluctuations due to all energy scales being comparable in magnitude.
} converging exponentially (see Methods). Thus, the model can be faithfully described by a free theory in these regions of the phase diagram. The exceptions only occur infinitesimally close to the FM critical point and at the AFM classical critical point. This is remarkable because these models are non-integrable and a priori have strong quantum fluctuations due to all energy scales being comparable in magnitude.
(a) The FM and (b) the AFM model at system size L=16 with periodic boundary conditions. The interaction distance (log scale) takes non-negligible values only in the vicinity of the critical point and critical line which are sketched in red. The scaling behaviour of  along the dashed lines is given in Fig. 2.
along the dashed lines is given in Fig. 2.
Strong correlations build up near criticality where the effect of interactions is most significant and  can take higher values. These regions, however, shrink around criticality as L increases. To examine this we consider the finite-size scaling of
can take higher values. These regions, however, shrink around criticality as L increases. To examine this we consider the finite-size scaling of  using ansatz (4) , as shown in Fig. 2, along the paths hz=1 (FM) and hx=hz (AFM) shown in Fig. 1. It is noteworthy that, despite being near criticality, the values of
using ansatz (4) , as shown in Fig. 2, along the paths hz=1 (FM) and hx=hz (AFM) shown in Fig. 1. It is noteworthy that, despite being near criticality, the values of  remain small
remain small  for both models; thus, we set θ=0 in the ansatz (4). We obtain critical exponents ζFM≈−1.4 and ζAFM≈1.11, showing that interactions have a dramatically different effect in the two models. In the FM case the interactions are a singular perturbation to the critical point, whereas in the AFM case their effect diminishes as L increases. This behaviour is consistent with the shrinking of the significant high
for both models; thus, we set θ=0 in the ansatz (4). We obtain critical exponents ζFM≈−1.4 and ζAFM≈1.11, showing that interactions have a dramatically different effect in the two models. In the FM case the interactions are a singular perturbation to the critical point, whereas in the AFM case their effect diminishes as L increases. This behaviour is consistent with the shrinking of the significant high  regions around criticality. Furthermore, the critical exponent νFM≈0.533, is approximately equal to that of the correlation length
regions around criticality. Furthermore, the critical exponent νFM≈0.533, is approximately equal to that of the correlation length  =8/15 (ref. 34). Similarly, νAFM≈1.252 which is within 20% accuracy to the correlation length critical exponent for the same cut
=8/15 (ref. 34). Similarly, νAFM≈1.252 which is within 20% accuracy to the correlation length critical exponent for the same cut  ≈1.052, which we obtain numerically. We account for the deviation in νAFM by small system sizes and the fact that we are not perturbing with an operator that has a well-defined scaling dimension. The critical scaling behaviour of
≈1.052, which we obtain numerically. We account for the deviation in νAFM by small system sizes and the fact that we are not perturbing with an operator that has a well-defined scaling dimension. The critical scaling behaviour of  is independently verified by employing the variational DMRG method rather than exact diagonalization, which can efficiently probe significantly larger system sizes (see Methods).
is independently verified by employing the variational DMRG method rather than exact diagonalization, which can efficiently probe significantly larger system sizes (see Methods).
 for a number of systems sizes of (a) the FM model and (c) the AFM model along the dashed lines given in Fig. 1. We obtain the critical exponents νFM≈0.533, ζFM≈−1.4 and νAFM≈1.252, ζAFM≈1.11 by fitting to (4). (b,d) show the scaling collapse of
for a number of systems sizes of (a) the FM model and (c) the AFM model along the dashed lines given in Fig. 1. We obtain the critical exponents νFM≈0.533, ζFM≈−1.4 and νAFM≈1.252, ζAFM≈1.11 by fitting to (4). (b,d) show the scaling collapse of  , where xL=(g−gc)L1/ν and
, where xL=(g−gc)L1/ν and  . This demonstrates the applicability of the scaling ansatz (4).
. This demonstrates the applicability of the scaling ansatz (4).
Finally, we are in position to identify the optimal free model that describes the interacting system given by an instance of (5). In particular, we identify the free Ising model H±( ,0) with transverse field
,0) with transverse field  , whose ground state’s entanglement spectrum matches σ’s obtained from (1) for each point (hz,hx). This is simply obtained by minimizing D(σ(hz,hx), σf(
, whose ground state’s entanglement spectrum matches σ’s obtained from (1) for each point (hz,hx). This is simply obtained by minimizing D(σ(hz,hx), σf( ,0)) over
,0)) over  . As a result we observe that in the FM case, adding infinitesimal interactions to the free Ising model with hz<1 maps the model to a free Ising with hz>1 in a discontinuous way, as shown in Fig. 3a. When hz>1, the introduction of interactions maps the model to a neighbouring free model continuously. In the AFM case, the interactions are irrelevant. Indeed, Fig. 3b shows that the whole phase diagram maps trivially to the free model even very near criticality.
. As a result we observe that in the FM case, adding infinitesimal interactions to the free Ising model with hz<1 maps the model to a free Ising with hz>1 in a discontinuous way, as shown in Fig. 3a. When hz>1, the introduction of interactions maps the model to a neighbouring free model continuously. In the AFM case, the interactions are irrelevant. Indeed, Fig. 3b shows that the whole phase diagram maps trivially to the free model even very near criticality.
(a) The FM model and (b) the AFM model both at system size L=16. Contours indicate the transverse-field  , dashed lines for those in the symmetry broken phase and solid otherwise (including the critical value
, dashed lines for those in the symmetry broken phase and solid otherwise (including the critical value  =1). The background colour plot gives the distance min
=1). The background colour plot gives the distance min D(σ,σf) (log scale) signifying the success of the mapping. In this way the interacting system is given a description in terms of a free-fermion model. The region near the hz=0 classical axis of the AFM is removed (grey region) because our calculations do not resolve all symmetries of the system.
D(σ,σf) (log scale) signifying the success of the mapping. In this way the interacting system is given a description in terms of a free-fermion model. The region near the hz=0 classical axis of the AFM is removed (grey region) because our calculations do not resolve all symmetries of the system.
The distance min D(σ,σf) is shown by the colour scale in Fig. 3. We see that away from criticality σ can be mapped to the free Ising model with a high fidelity. In the thermodynamic limit we expect the critical line of the AFM to also be identified with a free Ising model, because min
D(σ,σf) is shown by the colour scale in Fig. 3. We see that away from criticality σ can be mapped to the free Ising model with a high fidelity. In the thermodynamic limit we expect the critical line of the AFM to also be identified with a free Ising model, because min D(σ,σf) decreases with L and the conformal field theory, which describes the point (hz=1, hx=0), also governs the entire critical line31. This analysis reveals that the optimal free model is local and fermionic throughout the phase diagrams, except at the critical point of the FM model and the classical critical point of the AFM model whose ground state is macroscopically degenerate.
D(σ,σf) decreases with L and the conformal field theory, which describes the point (hz=1, hx=0), also governs the entire critical line31. This analysis reveals that the optimal free model is local and fermionic throughout the phase diagrams, except at the critical point of the FM model and the classical critical point of the AFM model whose ground state is macroscopically degenerate.
Maximally interacting model
In the above analysis, we found for the Ising model that the interaction distance vanishes in the thermodynamic limit in almost the entire phase diagram. For that model we identified the optimal free fermion model that effectively describes it throughout the phase space. We now present a truly interacting model that cannot be approximated by free fermions, that is, has a non-zero  in the thermodynamic limit, even away from criticality. In our analytical approach, we first construct the entanglement spectrum that gives a non-zero
in the thermodynamic limit, even away from criticality. In our analytical approach, we first construct the entanglement spectrum that gives a non-zero  with respect to free fermions. Then, we identify the physical system and emergent quasiparticles that correspond to the derived entanglement spectrum.
with respect to free fermions. Then, we identify the physical system and emergent quasiparticles that correspond to the derived entanglement spectrum.
We consider the simple case where the entanglement Hamiltonian comprises two fermionic modes. We aim to maximize the interaction distance with respect to the entanglement spectrum {Emax} which consists of four levels. We perform a maximization of the interaction distance from free-fermion entanglement spectra generated by two single-particle energies,  1,
1, 2. It can be analytically proven (see Supplementary Note 2) that the maximum interaction distance in this case is
2. It can be analytically proven (see Supplementary Note 2) that the maximum interaction distance in this case is

where the maximization is performed with respect to the eigenvalues {λ} of ρ. The spectrum of the reduced state ρmax that maximizes  is the maximally mixed rank-3 spectrum {λmax}={
is the maximally mixed rank-3 spectrum {λmax}={ ,
,  ,
,  , 0}, with entanglement spectrum {Emax}={ln 3, ln 3, ln 3,∞}.
, 0}, with entanglement spectrum {Emax}={ln 3, ln 3, ln 3,∞}.
We would now like to find the parent physical system which exhibits such correlations in the ground state so that it saturates the maximum of  . As the entanglement spectrum {Emax} has a three-fold degeneracy, it is natural to consider models which support fractionalized excitations. In particular, a
. As the entanglement spectrum {Emax} has a three-fold degeneracy, it is natural to consider models which support fractionalized excitations. In particular, a  quantum clock model effectively describes the edge physics of a 2D topological phase35 and can in principle be realized in the laboratory35,36,37,38,39. The
quantum clock model effectively describes the edge physics of a 2D topological phase35 and can in principle be realized in the laboratory35,36,37,38,39. The  Hamiltonian in the topological phase at its renormalization fixed point is
Hamiltonian in the topological phase at its renormalization fixed point is

where τj are non-Hermitian clock operators which commute between sites and can be represented locally as τj=diag(1, ei2π/3, e−i2π/3) satisfying  .
.
The ground state of (7) hosts topologically protected parafermionic zero-modes exponentially localized on open boundaries40. These correspond to three-fold degeneracy in the entanglement spectrum {E}={ln 3, ln 3, ln 3} from maximally entangled pairs of parafermions across each virtual boundary. We have seen in a previous section that we can increase the dimension of the entanglement Hilbert space  by introducing completely uncorrelated states that correspond to infinite entanglement energy. Hence, the entanglement spectrum of the
by introducing completely uncorrelated states that correspond to infinite entanglement energy. Hence, the entanglement spectrum of the  model reproduces the aforementioned {Emax}. As a result we have readily identified a truly interacting model that gives
model reproduces the aforementioned {Emax}. As a result we have readily identified a truly interacting model that gives  with respect to free fermions in the thermodynamic limit. Importantly, we have managed to analytically identify the ground state of the corresponding interacting model by considering only the structure of its correlations.
with respect to free fermions in the thermodynamic limit. Importantly, we have managed to analytically identify the ground state of the corresponding interacting model by considering only the structure of its correlations.
Discussion
In this study we have identified, for a given interacting theory, the optimal free state which is closest to its ground state and introduced the interaction distance between them. Quantifying interactions in such generic terms gives a fresh perspective into the physics of interacting systems. Indeed, our approach extends beyond mean-field theory, which is valid for weak correlations and spatial dimensions above the upper-critical dimension, or perturbation theory which requires weak couplings. Optimizing with respect to the correlations present in the ground state captures faithfully the low energy physics of the interacting system reproducing the observables with bounded error.
We have numerically determined the interaction distance for the 1D Ising model in the presence of transverse and longitudinal fields. We used both exact diagonalization as well as DMRG, thus demonstrating the efficiency in determining  for large 1D gapped systems using standard techniques. Further, our diagnostic
for large 1D gapped systems using standard techniques. Further, our diagnostic  shows that the ground state of this interacting model in its gapped phases is well described by a free state, requiring exponentially less information to represent than the exact ground state. We expect that this could be generalized to an efficient algorithm for finding a representative (nearly) free state, similar to the DMRG method which constructs a low Schmidt rank approximation to gapped 1D ground states. Alternatively, our method can be combined with analytical wave functions, as in the case of the Bethe ansatz41 or the trial wave functions in the quantum Hall effect5,42,43.
shows that the ground state of this interacting model in its gapped phases is well described by a free state, requiring exponentially less information to represent than the exact ground state. We expect that this could be generalized to an efficient algorithm for finding a representative (nearly) free state, similar to the DMRG method which constructs a low Schmidt rank approximation to gapped 1D ground states. Alternatively, our method can be combined with analytical wave functions, as in the case of the Bethe ansatz41 or the trial wave functions in the quantum Hall effect5,42,43.
We have also verified that there exist quantum states for which  ≠0, such as the
≠0, such as the  quantum clock model. Other possible candidates are systems that give rise to exotic phases such as high-Tc superconductors and states with intrinsic topological order, where interactions play a crucial role. This could establish
quantum clock model. Other possible candidates are systems that give rise to exotic phases such as high-Tc superconductors and states with intrinsic topological order, where interactions play a crucial role. This could establish  as an interaction order parameter identifying truly interacting systems, in terms of fermions or bosons, from nearly free ones such as the Ising model. Furthermore, as we have shown for the Ising Model and the
as an interaction order parameter identifying truly interacting systems, in terms of fermions or bosons, from nearly free ones such as the Ising model. Furthermore, as we have shown for the Ising Model and the  model, it is possible to directly identify a parent Hamiltonian for the optimal free state.
model, it is possible to directly identify a parent Hamiltonian for the optimal free state.
In introducing our interaction distance, we have generalized the meaning of freedom in many-body quantum states by choosing the mutual statistics of the free modes we are optimizing over. Varying the statistics of the free modes used in our optimization corresponds to changing the free manifold  from which the interaction distance is measured. Our construction can be immediately generalized to soft-core bosons by promoting the occupation m of each mode in equation (2) to a variational parameter taking values 1≤m<∞. Taking this further, the single-body levels themselves can become occupation dependent. Such a modification could accommodate fractionalized excitations in strongly-correlated states44. Another interesting generalization would be to introduce the notion of entanglement temperature45, which shifts the sensitivity of the measure to other parts of the entanglement spectrum, reflecting entanglement on different length scales. Finally, we mention that methods for measuring entanglement spectra in optical lattices have recently been proposed46. Hence, the interaction distance can be determined for exotic states realized in cold atom systems.
from which the interaction distance is measured. Our construction can be immediately generalized to soft-core bosons by promoting the occupation m of each mode in equation (2) to a variational parameter taking values 1≤m<∞. Taking this further, the single-body levels themselves can become occupation dependent. Such a modification could accommodate fractionalized excitations in strongly-correlated states44. Another interesting generalization would be to introduce the notion of entanglement temperature45, which shifts the sensitivity of the measure to other parts of the entanglement spectrum, reflecting entanglement on different length scales. Finally, we mention that methods for measuring entanglement spectra in optical lattices have recently been proposed46. Hence, the interaction distance can be determined for exotic states realized in cold atom systems.
Methods
Optimization
The optimization to find σ and  in (3) is performed by a Monte Carlo basin-hopping strategy47 using the Nelder–Mead simplex algorithm for local minimization within basins of the cost function
in (3) is performed by a Monte Carlo basin-hopping strategy47 using the Nelder–Mead simplex algorithm for local minimization within basins of the cost function  . This global strategy was selected to counteract an observed tendency for local methods to get trapped in local minima. The initial guess for this search is found as follows. The normalization constant E0 is the lowest entanglement energy of the input entanglement spectrum {E}. We iteratively construct an approximate set of single-particle entanglement energies starting from an empty set. First, we take the lowest remaining level in the spectrum and subtract E0 to produce a new single-particle level
. This global strategy was selected to counteract an observed tendency for local methods to get trapped in local minima. The initial guess for this search is found as follows. The normalization constant E0 is the lowest entanglement energy of the input entanglement spectrum {E}. We iteratively construct an approximate set of single-particle entanglement energies starting from an empty set. First, we take the lowest remaining level in the spectrum and subtract E0 to produce a new single-particle level  k. Then we remove the many-body levels, which are closest to the new combinatorial levels generated according to (2) by the additional single-particle level. This process is repeated until the input spectrum is exhausted. We can also introduce a truncation of the entanglement spectrum cutting off high entanglement energies, making the construction of the initial guess terminate faster. The minimization of D(σ, σf) to identify the optimal free model for the Ising Hamiltonian (5) is calculated using a local Nelder–Mead method.
k. Then we remove the many-body levels, which are closest to the new combinatorial levels generated according to (2) by the additional single-particle level. This process is repeated until the input spectrum is exhausted. We can also introduce a truncation of the entanglement spectrum cutting off high entanglement energies, making the construction of the initial guess terminate faster. The minimization of D(σ, σf) to identify the optimal free model for the Ising Hamiltonian (5) is calculated using a local Nelder–Mead method.
Finite-size scaling
We perform the finite-size scaling according to an ansatz (4). The parameters of the collapse were estimated using the method of ref. 48. From the scaling ansatz (4) and for a trial set of scaling parameters gc,ν and ζ, the scaled values xL=(g−gc)L1/ν and  are calculated from each unscaled data point
are calculated from each unscaled data point  . From this collection of scaled data points (xL,yL) across all L, we implicitly define a so-called master curve that best represents them. This curve y(x) is defined around a point x as the linear regression calculated by taking the scaled data points immediately left and right of x for each system size L. We characterize the deviation of the scaled points (xL,yL) from the master curve y(xL) using the χ2 statistic. This measure is used as the cost function for an optimization problem over the scaling parameters gc, ν, ζ and θ, which can be solved using the same techniques as the previous problems.
. From this collection of scaled data points (xL,yL) across all L, we implicitly define a so-called master curve that best represents them. This curve y(x) is defined around a point x as the linear regression calculated by taking the scaled data points immediately left and right of x for each system size L. We characterize the deviation of the scaled points (xL,yL) from the master curve y(xL) using the χ2 statistic. This measure is used as the cost function for an optimization problem over the scaling parameters gc, ν, ζ and θ, which can be solved using the same techniques as the previous problems.
In Fig. 4a, we show  calculated from the entanglement spectrum using DMRG25, which extends our results from Fig. 2 in the FM case to larger system sizes inaccessible to exact diagonalization. In Fig. 4b, we show the scaling collapse. We obtain critical exponents ν, ζ, which are consistent with those found with exact diagonalization and ν is consistent with known results of CFT34. There are two differences compared with results in Fig. 2. First, with our larger sizes we become sensitive to the upper bound of
calculated from the entanglement spectrum using DMRG25, which extends our results from Fig. 2 in the FM case to larger system sizes inaccessible to exact diagonalization. In Fig. 4b, we show the scaling collapse. We obtain critical exponents ν, ζ, which are consistent with those found with exact diagonalization and ν is consistent with known results of CFT34. There are two differences compared with results in Fig. 2. First, with our larger sizes we become sensitive to the upper bound of  , which gives us θ≈0.025. The fact that θ is non-zero is readily apparent in the saturation behaviour visible in the unscaled data and is demanded for consistency with an upper bound. Second, in accordance with common practice, we perform DMRG using open boundary conditions, which changes the non-universal function f in the scaling ansatz (4).
, which gives us θ≈0.025. The fact that θ is non-zero is readily apparent in the saturation behaviour visible in the unscaled data and is demanded for consistency with an upper bound. Second, in accordance with common practice, we perform DMRG using open boundary conditions, which changes the non-universal function f in the scaling ansatz (4).
 for the FM Ising model calculated from the density matrix renormalization group.
for the FM Ising model calculated from the density matrix renormalization group.(a) DMRG results retaining χ states for χ=32 (dots), 64 (lines) and 128 (crosses) states. The result is already converged for χ=64 for the biggest system size L=1,024. (b) Scaling collapse according to ansatz (4) with the critical exponents ν≈0.533, ζ≈−1.4 and saturation parameter θ≈0.025. The collapsed variables xL=(g−gc)L1/ν and  . (c) Comparison between
. (c) Comparison between  calculated for entanglement spectra provided via DMRG (points), for χ=16 entanglement levels, and exact diagonalization (lines) for the same system. The results for these system sizes accessible by exact diagonalization agree. All results in this figure are calculated for open boundary conditions where DMRG is most natural.
calculated for entanglement spectra provided via DMRG (points), for χ=16 entanglement levels, and exact diagonalization (lines) for the same system. The results for these system sizes accessible by exact diagonalization agree. All results in this figure are calculated for open boundary conditions where DMRG is most natural.
To verify our DMRG results we compare  obtained by DMRG and exact diagonalization with open boundary conditions. We confirm that they are in excellent agreement, as shown in Fig. 4c. Between iterations in DMRG, the ground state is approximated by retaining a reduced number of entanglement states. They correspond to the greatest Schmidt weights. The interaction distance is insensitive to these approximations inherent in DMRG, because the induced error is comparable to the truncation error which is typically kept to be 10−14. We demonstrate that our DMRG calculations are converged in the number of retained states χ in Fig. 4a. Close to criticality, due to the logarithmic growth in entanglement, we need to retain more states for larger L. The result is already converged for χ=64 at the largest L studied, which justifies our approximation in retaining this number of states in the finite-size scaling. It is worth noting that the single-particle entanglement energies converge exponentially away from criticality exponentially (as discussed in Supplementary Note 1).
obtained by DMRG and exact diagonalization with open boundary conditions. We confirm that they are in excellent agreement, as shown in Fig. 4c. Between iterations in DMRG, the ground state is approximated by retaining a reduced number of entanglement states. They correspond to the greatest Schmidt weights. The interaction distance is insensitive to these approximations inherent in DMRG, because the induced error is comparable to the truncation error which is typically kept to be 10−14. We demonstrate that our DMRG calculations are converged in the number of retained states χ in Fig. 4a. Close to criticality, due to the logarithmic growth in entanglement, we need to retain more states for larger L. The result is already converged for χ=64 at the largest L studied, which justifies our approximation in retaining this number of states in the finite-size scaling. It is worth noting that the single-particle entanglement energies converge exponentially away from criticality exponentially (as discussed in Supplementary Note 1).
Data availability
All data presented in this work are available from the authors upon request. Statement of compliance with EPSRC policy framework on research data: this publication is theoretical work that does not require supporting research data.
Additional information
How to cite this article: Turner, C. J. et al. Optimal free descriptions of many-body theories. Nat. Commun. 8, 14926 doi: 10.1038/ncomms14926 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Sutherland, B. Beautiful Models: 70 Years of Exactly Solved Quantum Many-body Problems World Scientific (2004).
Feynman, R. P. Atomic theory of the two-fluid model of liquid helium. Phys. Rev. 94, 262–277 (1954).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Gutzwiller, M. C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 10, 159–162 (1963).
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
Li, H. & Haldane, F. D. M. Entanglement spectrum as a generalization of entanglement entropy: identification of topological order in non-abelian fractional quantum Hall effect states. Phys. Rev. Lett. 101, 010504 (2008).
Calabrese, P. & Lefevre, A. Entanglement spectrum in one-dimensional systems. Phys. Rev. A 78, 032329 (2008).
Qi, X.-L., Katsura, H. & Ludwig, A. W. W. General relationship between the entanglement spectrum and the edge state spectrum of topological quantum states. Phys. Rev. Lett. 108, 196402 (2012).
Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. General theorem relating the bulk topological number to edge states in two-dimensional insulators. Phys. Rev. B 74, 045125 (2006).
Genoni, M. G., Paris, M. G. A. & Banaszek, K. Quantifying the non-Gaussian character of a quantum state by quantum relative entropy. Phys. Rev. A 78, 060303 (2008).
Marian, P. & Marian, T. A. Relative entropy is an exact measure of non-Gaussianity. Phys. Rev. A 88, 012322 (2013).
Gertis, J., Friesdorf, M., Riofro, C. A. & Eisert, J. Estimating strong correlations in optical lattices. Phys. Rev. A 94, 053628 (2016).
Schilling, C., Gross, D. & Christandl, M. Pinning of fermionic occupation numbers. Phys. Rev. Lett. 110, 040404 (2013).
Byczuk, K., Kuneš, J., Hofstetter, W. & Vollhardt, D. Quantification of correlations in quantum many-particle systems. Phys. Rev. Lett. 108, 087004 (2012).
Gottlieb, A. D. & Mauser, N. J. Nonfreeness and related functionals for measuring correlation in many-fermion states. Preprint at https://arxiv.org/abs/1510.04573 (2015).
Zhang, J. M. & Kollar, M. Optimal multiconfiguration approximation of an n-fermion wave function. Phys. Rev. A 89, 012504 (2014).
Fuchs, C. A. & van de Graaf, J. Cryptographic distinguishability measures for quantum-mechanical states. IEEE Trans. Inf. Theory 45, 1216–1227 (1999).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information Cambridge Univ. Press (2011).
Markham, D., Miszczak, J. A., Puchała, Z. & Życzkowski, K. Quantum state discrimination: a geometric approach. Phys. Rev. A 77, 042111 (2008).
Peschel, I. Calculation of reduced density matrices from correlation functions. J. Phys. A 36, L205 (2003).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Fidkowski, L. Entanglement spectrum of topological insulators and superconductors. Phys. Rev. Lett. 104, 130502 (2010).
Holevo, A. S. & Werner, R. F. Evaluating capacities of bosonic gaussian channels. Phys. Rev. A 63, 032312 (2001).
Hastings, M. B. An area law for one-dimensional quantum systems. J. Stat. Mech. Theor. Exp. 2007, P08024 (2007).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Vidal, G. Class of quantum many-body states that can be efficiently simulated. Phys. Rev. Lett. 101, 110501 (2008).
Zhang, S. Quantum Monte Carlo Methods for Strongly Correlated Electron Systems Springer (2004).
Verstraete, F., Murg, V. & Cirac, J. I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 57, 143–224 (2008).
Orús, R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann. Phys. 349, 117–158 (2014).
Fisher, M. E. & Barber, M. N. Scaling theory for finite-size effects in the critical region. Phys. Rev. Lett. 28, 1516–1519 (1972).
Dutta, A. et al. Quantum Phase Transitions in Transverse Field Models Cambridge Univ. Press (2015).
Kramers, H. A. & Wannier, G. H. Statistics of the two-dimensional ferromagnet. Part I. Phys. Rev. 60, 252–262 (1941).
Ovchinnikov, A. A., Dmitriev, D. V., Krivnov, V. Y. & Cheranovskii, V. O. Antiferromagnetic Ising chain in a mixed transverse and longitudinal magnetic field. Phys. Rev. B 68, 214406 (2003).
Zamolodchikov, A. B. Integrals of motion and S-matrix of the (scaled) T=T c Ising model with magnetic field. Int. J. Mod. Phys. A 04, 4235–4248 (1989).
Alicea, J. & Fendley, P. Topological phases with parafermions: theory and blueprints. Annu. Rev. Condensed Matter Phys. 7, 119–139 (2016).
Klinovaja, J., Yacoby, A. & Loss, D. Kramers pairs of majorana fermions and parafermions in fractional topological insulators. Phys. Rev. B 90, 155447 (2014).
Vaezi, A. Fractional topological superconductor with fractionalized majorana fermions. Phys. Rev. B 87, 035132 (2013).
Cheng, M. Superconducting proximity effect on the edge of fractional topological insulators. Phys. Rev. B 86, 195126 (2012).
You, Y.-Z. & Wen, X.-G. Projective non-abelian statistics of dislocation defects in a rotor model. Phys. Rev. B 86, 161107 (2012).
Jermyn, A. S., Mong, R. S. K., Alicea, J. & Fendley, P. Stability of zero modes in parafermion chains. Phys. Rev. B 90, 165106 (2014).
Bethe, H. Zur Theorie der Metalle. Zeitschr. Phys. 71, 205–226 (1931).
Read, N. & Rezayi, E. Beyond paired quantum Hall states: parafermions and incompressible states in the first excited Landau level. Phys. Rev. B 59, 8084–8092 (1999).
Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nuclear Phys. B 360, 362–396 (1991).
Davenport, S. C., Rodríguez, I. D., Slingerland, J. K. & Simon, S. H. Composite fermion model for entanglement spectrum of fractional quantum Hall states. Phys. Rev. B 92, 115155 (2015).
Chandran, A., Khemani, V. & Sondhi, S. L. How universal is the entanglement spectrum? Phys. Rev. Lett. 113, 060501 (2014).
Pichler, H., Zhu, G., Seif, A., Zoller, P. & Hafezi, M. Measurement protocol for the entanglement spectrum of cold atoms. Phys. Rev. X 6, 041033 (2016).
Wales, D. J. & Doye, J. P. K. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 101, 5111–5116 (1997).
Houdayer, J. & Hartmann, A. K. Low-temperature behavior of two-dimensional gaussian Ising spin glasses. Phys. Rev. B 70, 014418 (2004).
Acknowledgements
We thank M. Barkeshli, B. Doyon, P. Fendley, G. Giedke, J. Garcia-Ripoll, S. Iblisdir, A. Läuchli, T. Neupert, D. Poilblanc, A. Polkovnikov, K. Shtengel and S. Simon for inspiring conversations and useful comments. This work was supported by the EPSRC grants EP/I038683/1, EP/M50807X/1 and EP/P009409/1.
Author information
Authors and Affiliations
Contributions
All authors contributed to developing the ideas, analysing the results and writing the manuscript. C.J.T. implemented the algorithm.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Notes and Supplementary References (PDF 165 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Turner, C., Meichanetzidis, K., Papić, Z. et al. Optimal free descriptions of many-body theories. Nat Commun 8, 14926 (2017). https://doi.org/10.1038/ncomms14926
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms14926
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.