Abstract
Reduced rainfall increases the risk of forest dieback, while in return forest loss might intensify regional droughts. The consequences of this vegetation–atmosphere feedback for the stability of the Amazon forest are still unclear. Here we show that the risk of self-amplified Amazon forest loss increases nonlinearly with dry-season intensification. We apply a novel complex-network approach, in which Amazon forest patches are linked by observation-based atmospheric water fluxes. Our results suggest that the risk of self-amplified forest loss is reduced with increasing heterogeneity in the response of forest patches to reduced rainfall. Under dry-season Amazonian rainfall reductions, comparable to Last Glacial Maximum conditions, additional forest loss due to self-amplified effects occurs in 10–13% of the Amazon basin. Although our findings do not indicate that the projected rainfall changes for the end of the twenty-first century will lead to complete Amazon dieback, they suggest that frequent extreme drought events have the potential to destabilize large parts of the Amazon forest.
Similar content being viewed by others
Introduction
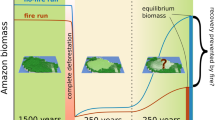
The Amazon forest has been listed as one of the tipping elements of the Earth system1. Large-scale vegetation shifts resulting from reduced rainfall probably occurred in glacial times2,3 and might occur under twenty-first century climate change in combination with increasing deforestation, logging and fire4,5,6,7,8. It is an open question whether these stressors can trigger self-amplified forest loss in the Amazon basin9,10. Self-amplified forest loss may happen due to the strong coupling of vegetation and regional climate (Fig. 1). On the one hand, the vegetation state depends on the rainfall regime6,11. With decreasing precipitation, forest resilience (defined here as the ability of the forest to recover from perturbations12) decreases12,13 and the forest might shift to an alternative low tree-cover (TC) state11,14,15 as a result of perturbations such as fire and extreme drought events8. On the other hand, forest loss amplifies drought16,17 by reducing dry-season evapotranspiration rates18,19,20 and thereby weakening atmospheric moisture recycling, which is estimated to amount to 25–50% of total Amazonian rainfall21,22,23. As a consequence, a decrease in oceanic moisture inflow could trigger vegetation–atmosphere feedbacks and lead to self-amplified forest loss.
(a) Vegetation–atmosphere system in equilibrium. (b) Initial forest loss triggered by decreasing oceanic moisture inflow. This reduces local evapotranspiration and the resulting downwind moisture transport. (c) As a result, the rainfall regime is altered in another location, leading to further forest loss and reduced moisture transport.
Intensification of the Amazonian hydrological cycle has been observed in the last decades, with the wet season getting wetter and the dry season getting drier in southern and eastern Amazonia24,25,26. This is partly explained by a reduction in oceanic moisture inflow caused by a sea-surface-temperature-induced northward displacement of the intertropical convergence zone24,25. Whether these anomalies will persist in the future is uncertain and climate model predictions in Amazonia vary from strong drying to modest wetting27. However, recent projections constrained with observations show a widespread drying during the extended dry season (June–November)27. Furthermore, while the spatial variability of precipitation during the Last Glacial Maximum (LGM, around 21,000 yr BP) was roughly similar to the present conditions, rainfall may have been lower over large parts of the Amazon basin28,29,30 due to reduced dry-season oceanic moisture inflow induced by lower evaporation from the cooler sea surface31.
Despite progress in recent years, the complex and nonlinear vegetation–rainfall interactions that may cause self-amplified Amazon forest loss are still poorly represented in process-based vegetation–climate models32,33. Here we provide a new perspective on the stability of the Amazon vegetation–rainfall system and the potential of self-amplified Amazon forest loss by applying a complex-network approach. Such an inter-disciplinary approach is powerful for analysing cascading effects and has been applied to study, for example, contagion in financial systems34, the spread of innovations in society35, catastrophic species extinctions36, cascading failure in power grids37 or the collapse of marine ecosystems38. Recently, complex networks representing statistical similarities in climatic fields were used to improve forecasts of Indian monsoon timing39, extreme floods in the central Andes40 and El Niño events41. Here, we use the reconstruction of moisture recycling networks23 obtained from atmospheric moisture tracking22,42 of synthesis climate data (see Methods). In these networks, nodes represent individual vegetation grid cells within the Amazon basin that are linked by monthly water fluxes from the source (evapotranspiration) to the sink (rainfall). Thus, rainfall in each node has an oceanic and a continental component22. The ability of such networks to represent real moisture recycling processes has been shown in a previous detailed analysis of networks’ topology23. Combining moisture recycling networks23 and an empirical indicator of forest resilience11 in a unified cascade model35 allows us to evaluate the strength and extent of vegetation–atmosphere feedbacks in a spatially explicit way while relying on observations.
Results
Forest shifts
For each node, the rainfall regime is characterized by mean annual precipitation (MAP) and maximum cumulative water deficit (MCWD), a measure of the intensity of the dry season43. MAP and MCWD are well-suited climatic variables to explain the variability of vegetation distribution in the tropics6. Under a range of these variables, two TC states can be found (Supplementary Fig. 1): (1) an intermediate TC state (5⩽TC<55%), comprising deciduous forest, shrubs and herbaceous and (2) a high TC state (TC⩾55%) corresponding to evergreen forest (hereafter simply called forest) (Fig. 2a). The probability of forest for different rainfall regimes is derived from satellite data (see Methods). This probability is used as an indicator of forest resilience11 (Fig. 3a). Figure 2b shows that forest resilience decreases with reduced MCWD and MAP. In our interpretation, a forest with lower resilience is more likely to shift to a lower TC state in response to perturbations such as extreme drought and fire. In our modelling approach, forest nodes can shift stochastically based on thresholds in resilience (see Methods).
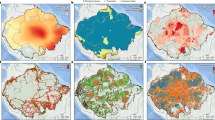
(a) Frequency distribution of tree-cover (TC) data (MOD44B v5 for the period 2001–2010) and associated land-cover types (from GLC2000 classification). (b) Probability of finding forest (TC⩾55%) as a function of mean annual precipitation (MAP) and maximum cumulative water deficit (MCWD) calculated from a logistic regression model (equations4 and 5) using monthly rainfall data (TRMM 3B42 for the period 2000–2012).
(a) Amazon forest resilience calculated from a logistic regression model (equations 4 and 5) based on monthly rainfall data (CRU) for the period 1961–2012. (b) Simulated changes in evapotranspiration during the extended dry season (June-November) after complete forest loss calculated from a regression model (equations 15 and 16) fitted to synthesis hydro-climate data (1989–2005). The color scale has been truncated at 25%. (c) Fraction of total precipitation during the extended dry season (June–November) that last evaporated from the ocean, calculated from atmospheric moisture tracking22,42 of synthesis hydro-climate data (1989–2005). Arrows represent vertically integrated moisture fluxes.
Evapotranspiration and rainfall changes after forest loss
Changes in evapotranspiration are evaluated using a statistical model based on multiple synthesis hydro-climate data (see Methods). The model accounts for the most important factors controlling monthly evapotranspiration in the Amazon basin as identified by flux tower measurements19: atmospheric demand (monthly potential evapotranspiration) and access of subsurface water during seasonal drought (carry-over factor). A complete Amazon deforestation experiment allows us to compare our estimations with existing studies. The spatio-temporal variability of evapotranspiration changes (Fig. 3b, see also Supplementary Figs 2 and 3) is in line with simulations from a recent mesoscale land-surface model17 and measurements from flux towers20. Our estimates of mean annual evapotranspiration change for complete Amazon forest loss (−108 mm per year, see Supplementary Table 1) is at the lower end of estimates from multiple recent climate models (−110 to −510 mm per year, median −219 mm per year)44. Likewise, our estimates of MAP change over the Amazon basin (−32 mm per year) are much lower than the values from regional (70–475 mm per year)44 and global (140–640 mm per year, mean 324 mm per year)45 climate models. However, the upper-uncertainty 95th percentile bound of our estimate (−274 mm per year, −13%) corresponds much closer to the mean rainfall changes simulated by multiple climate models (−324 mm per year, −12%)45,46. Based on this knowledge, our upper uncertainty bound can be considered as a realistic estimate. This result is consistent across all data sets used in this study (Supplementary Table 1).
Self-amplified forest loss under dry-season intensification
We simulate cascading effects in the vegetation–rainfall system (see Methods and Supplementary Fig. 4) triggered by gradual reduction of the contribution of oceanic moisture inflow to total precipitation during the extended dry season (June-November, Fig. 3c). Self-amplified forest loss increases nonlinearly with decreasing oceanic moisture inflow (gray shadings in Fig. 4a). This results from (1) a nonlinear decrease of forest resilience (Fig. 4b), (2) a stronger reduction of evapotranspiration after forest loss (Fig. 4c) and (3) an increased contribution of moisture recycling to total rainfall (Fig. 4b) under reduced dry-season oceanic moisture inflow. These findings are robust for different evapotranspiration input data sets and models (Supplementary Fig. 5), as well as cascade model settings (Supplementary Fig. 6).
(a) Fraction of the Amazon basin covered by forest (median of all 1,000 realizations of the cascade model as lines, 95% bounds shown by coloured bars on the right side of the plot). The difference between forest cover using the one-way coupling ‘P→veg’ (blue line) and the fully coupled system ‘P←veg’ (red line) quantifies the additional forest loss due to self-amplifying effects (grey area). Results obtained considering the upper bound of the 95% confidence interval (CI) in estimated evapotranspiration change after forest loss are shown (dashed lines). For comparison, the maximum possible forest loss for a complete failure of moisture recycling is also shown (orange line). (b) Mean Amazon forest resilience (green line, left axis) and mean fraction of oceanic moisture that contributes to total rainfall (black line, right axis), calculated using the model version ‘P→veg’. Whereas the 95% CI for the former is shown (dashed green lines), no error bars can be displayed for the latter but uncertainties associated with input data are shown in Supplementary Fig. 5a. (c) Mean evapotranspiration change (ΔE) after complete Amazon forest loss, calculated using the model version ‘veg→P’. The upper bound of the 95% CI of evapotranspiration reduction is shown (dashed black line).
While initial forest loss induced by reduced oceanic moisture inflow is sensitive to the underlying resilience thresholds, the additional forest loss attributed to vegetation–atmosphere feedbacks is more robust (Supplementary Fig. 6). Under a breakdown of oceanic moisture inflow during the extended dry season, this additional forest loss amounts to between 11–19% of the Amazon basin, depending on the thresholds. Among all the underlying processes represented, the largest uncertainties arise from the estimated changes in evapotranspiration (Fig. 4c). Considering these uncertainties, the additional forest loss attributed to vegetation–atmosphere feedbacks could amount up to 25–38% of the Amazon basin, depending on the thresholds (light gray shadings in Fig. 4a and Supplementary Fig. 6).
LGM and twenty-first century
Climate simulations of the LGM31 indicate that oceanic moisture inflow during that time was reduced at the end of the dry season, resulting in a mean Amazonian rainfall decrease of 50% during the extended dry season (see Methods). Estimated change in vegetation cover (Fig. 5a) results from a large-scale shift of forests in the southern and eastern part of the Amazon basin (Fig. 5b). Oceanic moisture inflow reduction leads to initial forest shifts in the south-eastern part of the Amazon basin (light blue regions in Fig. 5c), triggering self-amplifying forest loss in regions located further south and west (red regions in Fig. 5c). Similar patterns are found using different resilience thresholds (Supplementary Figs 7 and 8). Additional forest loss due to self-amplified effects for the LGM occurs in 10–13% of the Amazon basin and up to 18–23% when uncertainties in evapotranspiration estimates are considered (Supplementary Table 2).
(a,d) Most frequent vegetation cover for 1,000 realizations of the cascade model. (b,e) Shifting frequency of Amazon forest. (c,f) Share of cascading effects in causing forest shifts (see Methods). Results are shown (a–c) for the `LGM' scenario and (d–f) for the ‘end of twenty-first century’ scenario (see Methods).
A severe, stylized rainfall change scenario for the end of the twenty-first century following recent statistical projections27, for which Amazonian rainfall reduction during the extended dry season is reduced by 40% induced by oceanic moisture inflow decrease, can lead to similar dynamics (Fig. 5c). Depending on the resilience thresholds, forest loss due to self-amplified effects occurs in 1–7% of the Amazon basin or up to 14% when uncertainties in evapotranspiration estimates are taken into account (Supplementary Table 2).
Effect of heterogeneity
Given the risk of self-amplified forest loss, understanding the specific properties and mechanisms that stabilize the system is of key interest. Previous modelling studies indicated the importance of spatial heterogeneity for the stability of ecosystems47,48,49 and complex networks in general35. Here we assess the effect of heterogeneity in the response of forest nodes to changing climatic conditions on the stability of the Amazon vegetation–rainfall system. Theoretically, while a completely homogeneous forest would shift completely if it crosses a uniquely defined critical rainfall regime, heterogeneity in the forest response would result in forest nodes shifting at different critical rainfall regimes. Such heterogeneity may arise, for instance, from spatial variability in forest adaptability to drought, in land surface properties controlling water availability for trees and in disturbances to the forest. To evaluate the importance of such heterogeneity, we investigate the effect of the width of the bell-shaped resilience threshold distribution on cascade size (see Methods) under complete breakdown of dry-season oceanic moisture inflow. Figure 6 shows that larger heterogeneity in forest resilience thresholds reduces the frequency of high-order cascades by more than 50%, regardless of the model settings (Supplementary Fig. 9). In other words, if individual forest nodes shift at different critical rainfall regimes, propagation of forest loss is usually stopped in the early stage of the cascade. Hence, variability in the Amazon forest’s sensitivity to altered rainfall regime seems to alleviate the risk of long-term self-amplified forest loss.
Frequency distribution of cascade sizes with increasing heterogeneity of the forest resilience thresholds based on 1,000 realizations of the cascade model. Note that with increasing heterogeneity (σ), the frequency of high-order cascades (cascade size=4) decreases and the frequency of low-order cascades (cascade size=2) increases.
Sensitivity to evapotranspiration model and data
Effects of forest loss and rainfall change on evapotranspiration are typically sensitive to the underlying model and input data50,51. To assess the sensitivity of our results, we performed additional analyses using a generalized linear model (equation (17) and for different input evapotranspiration data (satellite observations and/or measurements, simulations from land-surface models, output from atmospheric reanalyses and the merged synthesis of all these three categories52). We find that these choices do not affect our results. Firstly, the spatio-temporal variability of simulated evapotranspiration changes after forest loss is consistent for all input data sets and for the two statistical models considered (Supplementary Figs 2 and 3). Secondly, similar dynamics are found regarding the effect of decreasing oceanic moisture inflow on simulated changes of evapotranspiration after forest loss (Supplementary Fig. 5c,d). This gives us confidence that our main findings are robust with respect to different choices of evapotranspiration model and input data. However, the absolute changes might vary depending on the evapotranspiration data. The results shown in the main part of the manuscript are therefore based on the merged synthesis evapotranspiration data set.
Discussion
Our results highlight the key role of regional dynamic vegetation–atmosphere interactions in the Amazon basin, which are not considered in most previous modelling studies assessing the likelihood of Amazon forest dieback for the future5,6,53,54 or for the LGM3,55. As it does not resolve the underlying processes of forest dieback, our method is not suited to provide information on the ‘real-world’ time scale of self-amplified forest loss. Our study should be seen as a sensitivity analysis rather than a projection of the system dynamics, as it omits some key feedbacks important for regulating forest cover. In particular, wind fields are considered to be static, which is a possible drawback of our approach as forest loss is expected to alter atmospheric circulation patterns. However, this effect might be relatively weak over the Amazon compared to changes in the amount of water transported17. We do not account for the effects of changing temperature and atmospheric CO2 concentrations on the hydrological cycle and on forest resilience, the latter remaining highly uncertain6,53,54.
Our results for the LGM show a self-amplified expansion of the intermediate TC state (encompassing savannas and/or deciduous forests) at the expense of the high TC state (evergreen forests). Although we do not account for all processes of vegetation dynamics, this finding is in line with recent observations of Amazonian speleothem records indicating a reduced moisture recycling during this period29,30. This gives us confidence that vegetation–atmosphere interactions, as represented in our modelling approach, probably play a major role in explaining Amazonian precipitation and vegetation changes. Furthermore, our results suggest that self-amplified forest loss triggered by oceanic moisture inflow reductions similar to LGM conditions did not affect the western Amazonia. A more resilient forest area related to more climatically stable conditions in this region, which is also suggested by paleoenvironmental records3,29,30,56, might have been crucial in the biogeographic history of one of the world’s most species-rich terrestrial ecosystems.
For the end of the century, in agreement with previous studies53,54,57, we find that projected rainfall reduction does not lead to complete dieback of the Amazon forest. However, if extreme drought events become more frequent or intense in the future, as suggested by some studies based on current trends25 and climate projections51,58, these may push the system towards large-scale self-amplified forest loss in a step-wise process without similarly drastic changes in the long-term mean rainfall regime. Indeed, the main mechanisms responsible for large-scale self-amplifying forest loss identified in our study might occur during such extreme drought events. Firstly, we found that the reduction of evapotranspiration after forest loss is more pronounced with increasing water deficit, consistent with measurements from flux towers20. This is due to the fact that, compared to forest, vegetation states with lower TC are less able to access subsurface water and thereby to maintain high evapotranspiration rates during drought18,19,20. Secondly, we find that the contribution of moisture recycling to total rainfall increases with reduced oceanic moisture inflow, consistent with paleoprecipitation records29. These two effects have probably already occurred during recent drought years17. Further efforts are needed to assess the effect of inter-annual rainfall variability on the stability of the Amazon vegetation–rainfall system and potential time lags in the response of the coupled system.
By fully coupling vegetation and rainfall, our study goes beyond previous efforts combining moisture-tracking algorithms with statistical16 or mechanistic17 climate models. Existing coupled models still poorly represent nonlinear regional interactions between biosphere and atmosphere, as shown by large discrepancies in predictions depending on model structure and settings9,59. Misrepresented key processes include (1) access of subsurface water by tropical trees, leading to an underestimation of the reduction of evapotranspiration after forest loss (by around 1 mm per day)55,60, (2) moisture recycling, leading to biases in moisture fluxes61 and (3) forest responses to drought5,6,7. In our statistical model, all abovementioned processes are included by applying vegetation and hydro-climate data, which are either observation-based or merged from multiple data sets. Our findings are robust against choices of evapotranspiration model and data, to which insights about the hydrological cycle are usually sensitive50,51.
This work adds to previous studies that suggested the importance of heterogeneity for ecosystems’ stability32,33,47,62,63 and the Amazon forests in particular48,49. However, none of these studies considered spatial interactions among vegetation patches32,33,48,49,62 or interactions were represented non-realistically47,63. Our results illustrate the importance of maintaining the structural and functional diversity of Amazon forests to reduce the risk of long-term self-amplified forest loss. This should be incorporated into future conservation management strategies and calls for cross-regional and -national approaches.
Methods
Hydro-climate data
The input data for the construction of moisture recycling networks and calibration of the evapotranspiration model cover the time period 1989–2005 for tropical South America (between 14.25° North and 23.5° South). The precipitation data are an average of four observation-based data sets: Climate Research Unit (CRU), the Global Precipitation Climatology Centre (GPCC), the Global Precipitation Climatology Project (GPCP) and the unified Climate Prediction Center (CPC) from the National Oceanic and Atmospheric Administration. A description of the precipitation data sets is provided in Appendix A in ref. 52. The potential evapotranspiration data are based on the Penman–Monteith equation which is forced by temperature, humidity and wind speed from reanalysis data corrected to remove biases at various time scales by merging with observation-based data50,64. The evapotranspiration data sets are taken from LandFlux-EVAL and are merged synthesis products from different categories: derived from satellite observations and/or measurements (‘diagnostic’), simulations from land-surface models and output from atmospheric reanalyses. In the preparation of the merged LandFlux-EVAL data, the long-term evapotranspiration by the energy balance was constrained (latent heat flux cannot exceed net surface radiation) but not by the available water (mean annual evapotranspiration can exceed precipitation). Evapotranspiration, precipitation and potential evapotranspiration data sets are available at monthly time scale and for a 1° longitude and latitude grid. Consistencies between these data sets are shown by Budyko curves (Supplementary Fig. 10). Wind fields and specific humidity data are taken from the six-hourly ERA-Interim reanalysis product65.
Data for forest resilience
Calculation of forest resilience is based on TC data from the Moderate Resolution Imaging Spectroradiometer (MODIS) Vegetation Continuous Fields MOD44B v5 (ref. 66) averaged for the period 2001–2010. The land-cover map is taken from the Global Land Cover 2000 (GLC 2000) Database67. To account only for natural distribution of the vegetation, human-modified landscapes and water bodies (GLC2000 classes 16–18 and 20–23) have been excluded from the analysis. TC and land-cover data are available at 1 km resolution of longitude and latitude, and have been sampled at the centroid of each precipitation grid cell.
For visualization of current forest resilience in the MAP-MCWD space (Fig. 2), precipitation data are derived from the Tropical Rainfall Measuring Mission (TRMM) 3B-42 v7 (ref. 68) for the years 2000–2012. These data have the advantage of their high spatial resolution (0.25° grid) and their ability to represent temporal and spatial variability over tropical South America69,70,71. For calibration of the logistic regression model to simulate self-amplified forest loss, precipitation data are derived from CRU, which have lower spatial resolution (0.5° grid) but longer duration (1961–2012).
Vegetation–cover data for the evapotranspiration model
Vegetation cover for the evapotranspiration model calibration is based on MOD44B v5 (ref. 66) TC data for the year 2001. To fit with the grid of the LandFlux-EVAL product, TC data have been upscaled to 1° resolution using the most frequent value. The Andes mountains were excluded from the analysis as evapotranspiration in this region is mainly determined by temperature rather than by rainfall. Artificial landscapes were not excluded. To exclude the Andes from the analysis, we use a natural-vegetation-cover map at 1° resolution that is based on a consensus of two global natural-vegetation-cover maps widely used in climate studies, as well as several regional maps from different sources72. The classes that represent the Andes region and that were excluded from the analysis are ‘desert’, ‘semi-desert’, ‘tundra’ and ‘grasslands’.
Vegetation-cover data for initial conditions in the cascade model
The initial vegetation cover for the cascade model is based on two different data sets, depending on whether grid cells are within the Amazon basin (area of interest) or outside the Amazon basin (boundary conditions). Within the Amazon basin, initial vegetation cover is derived from satellite monitoring of the vegetation73 for the year 2003. This data set distinguishes between forest (here set as ‘high TC state’), non-forest (here set as ‘intermediate TC state’) and deforested area (here set as ‘treeless state’). The initial vegetation cover outside the Amazon basin is based on MOD44B v5 (ref. 66) TC data for the year 2001. To fit with the grid of moisture recycling networks, both vegetation data sets were upscaled to 1.5° resolution by selecting the most frequent value found in the original data.
Vegetation classification from TC data
Following previous studies11,14, TC data were used to classify treeless (5%
Moisture recycling networks
Following a previous study23, moisture recycling networks were built with the atmospheric moisture-tracking model WAM-2layers V2.3.01 (refs 22, 42). As requested by WAM-2layers settings, all data have been spatially interpolated to a 1.5° grid using the nearest-neighbour algorithm. The temporal resolution of WAM-2layers is 3 h, to which monthly evapotranspiration and precipitation data have been downscaled using the temporal dynamics of ERA-Interim products. The output of WAM-2layers is averaged to monthly moisture transport between grid cells. Hence, in the networks, for each pair of grid cells (or nodes) j and k and for a given month, the weight of the arrow originating from j and pointing towards k (mj,k) is the monthly amount of water that comes from evapotranspiration in j and falls as rain over k.
For each grid cell k and for each month, the sum of all incoming arrows (∑j(mj,k)) is the amount of precipitation over k that originates from the continent. Hence, 1−∑j(mj,k)/Pk, with Pk being the total monthly precipitation in k, is the fraction of total precipitation that last evaporated from the ocean (Fig. 3a). Note that it corresponds to 1−ρ, with ρ being the continental precipitation recycling ratio22.
(Maximum) climatological water deficit
The MCWD is the most negative value of the climatological water deficit (C). For each grid cell k and for each month t (ref. 6):



with Pk,t being the precipitation in month t and grid cell k. The MCWD is an indicator of ‘meteorologically induced’ water stress43 and therefore evapotranspiration is fixed (Efix=3.3 mm per day). Efix is an approximation of evapotranspiration rate under favourable climatic conditions, which we found to be reached both in high and lower TC regions.
Forest resilience
We calculate the resilience of the vegetation based on ref. 11, but including MCWD in the calculation as well instead of MAP only. MCWD was calculated on monthly rainfall data averaged for the entire period (rather than for each year individually) following a previous study6.
The binomial distribution of forest (TC⩾55%) was fitted to a logistic regression model using the Matlab function ‘glmfit’:


with x corresponding to MAP and y to MCWD. For statistical stability, data points with extreme hydro-climatic values (y=0 and y<800 mm) were excluded from the analysis. Estimates of the parameters are shown in Supplementary Table 5.
Potential landscapes
We estimated under which conditions high and intermediate TC are alternative stable states by performing potential analysis74 on the TC data set following an existing method11. We computed stability landscapes of TC by determining how the probability density of TC changes with MAP (0 to 2,500 mm per year in steps of 25 mm per year) and MCWD (−800 to 0 mm per year in steps of 80 mm per year). At each step of the climatic variable (MAP or MCWD), TC values were weighted by applying a Gaussian kernel on the climatic variable with a standard deviation of 5% of the total range considered. Subsequently, the probability density of TC was estimated using the Kernel smoothing function in Matlab (ksdensity) with a bandwidth according to Silverman’s rule of thumb. Maxima (minima) in these probability densities are considered to be stable (unstable) states, whereby local fluctuations in the densities were filtered out11. Forest is bistable under climatic conditions below the highest values of MAP and MCWD at which a stable intermediate TC state is inferred (respectively 2,000 and −88 mm per year) (Supplementary Fig. 1).
Simple evapotranspiration model on a monthly time scale
To estimate changes in local evapotranspiration with changing rainfall or vegetation state, we use a nonlinear regression adapted from a simple evapotranspiration model on a monthly scale, hereafter called ‘Gerrits’ model’75. Evapotranspiration (E) includes evaporation of intercepted water by the surfaces (canopy, understory, forest floor and the top layer of the soil) (Ei) and transpiration by the vegetation (Et), while evaporation from deeper soil and open water are neglected. In Gerrits’ model, monthly transpiration is modelled as a simple threshold process that is a function of monthly precipitation P:

where A is a carry-over factor that represents the transpiration rate at P=0 and relates to the access of the vegetation to subsurface water during seasonal drought. It depends on vegetation-rooting depth and soil moisture. Bt is the slope between effective rainfall (rainfall minus interception evaporation) and transpiration. This slope can be estimated as Bt=1−ω−ω(exp(−ω)) with ω=Sb/Dt where Sb is the soil moisture below which transpiration is constrained. Dt is the monthly potential transpiration (that is, the atmospheric demand for evaporation once the interception process has first absorbed its part of the available energy). In Gerrits’ model, monthly evaporation from interception is modelled as:

where Bi is the potential amount of monthly interception (in terms of storage capacity). The authors75 also provide numerical derivation of the processes that takes into account the distribution of the expected number of rain days per month. For simplicity, we only use the analytical derivation.
Here, we assume that limits of Ei and Et can be combined to derive the overall limiting factors of E. Because there is no interception with no rainfall, E is limited at P=0 by A. In addition, the upper limit of E is the potential evapotranspiration Ep. We can thus model E as:







To account for depletion of subsurface water, here we consider that A is a variable that is modelled as a linear function of the climatological water deficit (C, see equations 1). Here, C is estimated individually for each year (rather than on the average for the entire period). We call p1=1/(1−Bt) and p2=Bi. Our evapotranspiration model becomes:


with p1, p2, p3, p4 parameters. While these parameters depend typically on land-surface properties (soil and vegetation) and daily rainfall characteristics75, for simplicity we consider here only the vegetation control. These parameters are estimated for each vegetation state (high TC, intermediate TC, treeless) using iterative least-squares estimation based on the function ‘nlinfit’ in Matlab with initial values set to 1.
The estimated parameters and the corresponding standard errors for each category of evapotranspiration input data set are shown in Supplementary Table 4. To account for uncertainties associated with the parameters, we perform simulations for which evapotranspiration rates in high and low TC states nodes are replaced by the 95% upper bound and 5% lower bound of the estimates, respectively.
Generalized linear model
To assess the sensitivity of our results to the choice of evapotranspiration model, we performed additional analyses using a generalized linear model:

in which p5, p6, p7, p8, p9 are parameters. Using a generalized linear mixed-effects model would be more appropriate due to dependency of the observations (spatio-temporal data). However, the use of a generalized linear model already reproduces sufficiently well the results based on our evapotranspiration model (equations 15 and 16).
Cascade model
Our approach has been largely inspired by the ‘Watts model’35, which simulates cascades that are found in social systems, such as the spread of innovations. Typically, individuals must decide between two alternative actions and their decisions depend explicitly on the actions of other individuals with whom they interact. The Watts model is based on a random network, in which each node might shift between alternative states depending on the states of their neighbours according to a simple threshold rule. Here, our model is based on moisture recycling networks and the threshold rule is related to local forest resilience that depends on the total incoming moisture. Initially, each node is assigned a resilience threshold drawn from a normal distribution with mean φ and standard deviation σ.
A simulation run comprises the following steps (Supplementary Fig. 4). First, moisture of oceanic and continental origin propagates through the network using moisture recycling networks and the simple evapotranspiration model (equation 16). This occurs on a monthly time scale, where the strongest effects of varying vegetation states on evapotranspiration can be observed, as shown by flux tower measurements18,19,20. In this step, it is assumed that with the moisture recycling link between two nodes, mj,k (from j to k) changes linearly with total evapotranspiration in the source node (in j). This implies that atmospheric circulation following vegetation shifts are not considered and that rainfall is assumed to be linearly correlated to atmospheric moisture. Second, the rainfall regime characterized by the MAP and the MCWD are calculated for each node. Third, the forest resilience is calculated for each node (equation 5). Fourth, a critical transition occurs in all nodes for which the forest resilience crosses the individual threshold, without any time lag. Fifth, local evapotranspiration is updated in nodes where shifts occur. The model runs with nodes updating their status until equilibrium in vegetation cover is reached.
The resilience thresholds are fixed for the duration of the simulation and potential spatial correlations are not considered. Results are shown for 1,000 random realizations of the initial condition. In the main text, it is assumed that φ=0.5, which best reproduces vegetation cover under current rainfall conditions (Supplementary Fig. 12), and σ=0.05, which limits the occurrence of shifts (Supplementary Fig. 13) to the zone where high TC and intermediate TC states can both exist (Supplementary Fig. 1). Results for other plausible values of φ, ranging from 0.4 to 0.6, are shown in Supplementary Figs 6–8.
We use different model settings: a fully coupled vegetation–rainfall system (‘P←veg’), a one-way coupled system in which changes in vegetation states do not affect precipitation (‘P→veg’) and a one-way coupled system in which changes in precipitation do not affect vegetation states (‘veg→P’) (Supplementary Fig. 4). Several metrics are of interest: first, the difference between forest loss in P←veg and P→veg, which quantifies the additional forest loss due to self-amplified effects; second, the relative difference between the shifting frequency in P←veg and P→veg, which quantifies the share of cascading effect in forest loss (‘share of cascading effect’); third, the number of model iterations until equilibrium (‘cascade size’) in the fully coupled version (P←veg). The cascade size can be interpreted as a time span of the cascade, but only on a relative scale (for comparison between high- and low-order cascades). We note that only nodes in which the shifting frequency exceeds 3% are accounted for.
Experiments of dry-season oceanic moisture inflow reduction
We present two different set-ups to study the effects of decreasing monthly oceanic moisture inflow during the extended dry season (June–November) with the period 1989–2005 as baseline. In a first setup, oceanic moisture inflow is homogeneously decreased by 2 mm per day increments until this inflow ceases completely in most of the Amazon basin (up to 8 mm per day reduction for each month of the extended dry season).
In a second setup, two stylized scenarios (end of twenty-first century and LGM) are generated based on long-term precipitation change estimations for the extended dry season in the Amazon basin drawn from previous studies27,31. The first scenario (end of twenty-first century) follows the upper bound of projected precipitation reduction for the end of the twenty-first century (2060–2099) based on a combination of observation-based data and the ensemble mean of CMIP5 climate models27. In this scenario, monthly oceanic moisture inflow is reduced homogeneously by [0.8, 1.0, 1.1, 1.3, 1.0, 0.8] mm per day (in June-November). If the resulting amount of oceanic moisture inflow becomes negative, it is set to zero. Averaged over the Amazon basin during the extended dry season, it corresponds to an oceanic moisture inflow reduction of 57% and a total rainfall reduction of 38% (calculated from step 1 of the cascade model).
The second scenario (LGM) follows a reconstruction of Amazonian rainfall during the LGM from a regional climate model, in which the effect of vegetation on climate has been turned off (Fig. 13b in Cook et al.31). Here, monthly oceanic moisture inflow is reduced by [0, 1, 2, 6, 10, 6] mm per day (June–November). Averaged over the Amazon basin during the extended dry season, it corresponds to an oceanic moisture inflow reduction of 76% and a total rainfall reduction of 52% (calculated from step 1 of the cascade model). The ability of this scenario to represent accurately LGM rainfall conditions depends on the quality of the sea-surface temperature reconstruction used as forcing data, as well as on the climate model parameterization. The latter was optimized to reproduce South American climate under present conditions sufficiently well31. Furthermore, the total rainfall reduction is in agreement with recent observation-based paleoprecipitation reconstructions30. Supplementary Table 3 summarizes the different model settings, scenarios and initial conditions used to produce the figures.
Data availability
The data can be downloaded from http://www.un-spider.org/links-and-resources/data-sources/land-cover-map-glc2000-jrc (GLC2000 land-cover map), https://data.iac.ethz.ch/landflux/ (LandFlux-EVAL evapotranspiration), http://hydrology.princeton.edu/data.pdsi.php (Potential evapotranspiration), ftp://ftp.glcf.umd.edu/glcf/Global_VCF/Collection_5/ (MOD44B v5 TC), http://www.csr.ufmg.br/simamazonia/ (Amazonian vegetation classification for 2003) http://mirador.gsfc.nasa.gov/cgi-bin/mirador/presentNavigation.pl?tree=project data set=TRMM_3B42_daily.007 project=TRMM dataGroup=Gridded version=007 (TRMM 3B-42 v7 precipitation). The precipitation data from CRU, GPCC, GPCP and CPC can be downloaded using links given in a previous study (ref. 75) and the merged synthesis product has been obtained from the author of that study (B.M.) upon request. The natural-vegetation-cover classification is accessible from Instituto Nacional de Pesquisas Espaciais (INPE)—Centro de Previso de Tempo e Estudos Climticos (CPTEC). The moisture recycling networks and the computer code of the models developed in this study are available from the corresponding author D.C.Z., upon reasonable request. A basic version of the WAM-2layers model is available through the link https://github.com/ruudvdent/WAM2layersPython.
Additional information
How to cite this article: Zemp, D. C. et al. Self-amplified Amazon forest loss due to vegetation–atmosphere feedbacks. Nat. Commun. 8, 14681 doi: 10.1038/ncomms14681 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Lenton, T. M. et al. Tipping elements in the Earth’s climate system. Proc. Natl Acad. Sci. USA 105, 1786–1793 (2008).
Rull, V., Montoya, E., Nogué, S., Vegas-Vilarrúbia, T. & Safont, E. Ecological palaeoecology in the neotropical gran sabana region: Long-term records of vegetation dynamics as a basis for ecological hypothesis testing. Perspect. Plant Ecol. Evol. Syst. 15, 338–359 (2013).
Mayle, F. E., Beerling, D. J., Gosling, W. D. & Bush, M. B. Responses of Amazonian ecosystems to climatic and atmospheric carbon dioxide changes since the last glacial maximum. Philos. Trans. R. Soc. B 359, 499–514 (2004).
Oyama, M. D. & Nobre, C. A. A new climate-vegetation equilibrium state for tropical South America. Geophys. Res. Lett. 30, 2199 (2003).
Nepstad, D. C., Stickler, C. M., Soares-Filho, B. & Merry, F. Interactions among Amazon land use, forests and climate: prospects for a near-term forest tipping point. Philos. Trans. R. Soc. B 363, 1737–1746 (2008).
Malhi, Y. et al. Exploring the likelihood and mechanism of a climate-change-induced dieback of the Amazon rainforest. Proc. Natl Acad. Sci. USA 106, 20610–20615 (2009).
Coe, M. T. et al. Deforestation and climate feedbacks threaten the ecological integrity of south-southeastern Amazonia. Philos. Trans. R. Soc. B 368, 20120155 (2013).
Brando, P. M. et al. Abrupt increases in Amazonian tree mortality due to drought-fire interactions. Proc. Natl Acad. Sci. USA 111, 6347–6352 (2014).
Betts, R. et al. The role of ecosystem-atmosphere interactions in simulated Amazonian precipitation decrease and forest dieback under global climate warming. Theor. Appl. Climatol. 78, 157–175 (2004).
Davidson, E. A. et al. The Amazon basin in transition. Nature 481, 321–328 (2012).
Hirota, M., Holmgren, M., van Nes, E. H. & Scheffer, M. Global resilience of tropical forest and savanna to critical transitions. Science 334, 232–235 (2011).
Verbesselt, J. et al. Remotely sensed resilience of tropical forests. Nat. Clim. Change 6, 1028–1031 (2016).
Poorter, L. et al. Biomass resilience of neotropical secondary forests. Nature 530, 211–214 (2016).
Staver, A. C., Archibald, S. & Levin, S. A. The global extent and determinants of savanna and forest as alternative biome states. Science 334, 230–232 (2011).
Xu, C. et al. Remotely sensed canopy height reveals three pantropical ecosystem states. Ecology 97, 2518–2521 (2016).
Spracklen, D., Arnold, S. & Taylor, C. Observations of increased tropical rainfall preceded by air passage over forests. Nature 489, 282–285 (2012).
Bagley, J. E., Desai, A. R., Harding, K. J., Snyder, P. K. & Foley, J. A. Drought and deforestation: has land cover change influenced recent precipitation extremes in the Amazon? J. Clim. 27, 345–361 (2014).
von Randow, C. et al. Comparative measurements and seasonal variations in energy and carbon exchange over forest and pasture in South West Amazonia. Theor. Appl. Climatol. 78, 5–26 (2004).
Da Rocha, H. R. et al. Patterns of water and heat flux across a biome gradient from tropical forest to savanna in Brazil. J. Geophys. Res. 114, G00B12 (2009).
von Randow, R. C., von Randow, C., Hutjes, R. W., Tomasella, J. & Kruijt, B. Evapotranspiration of deforested areas in central and southwestern Amazonia. Theor. Appl. Climatol. 109, 205–220 (2012).
Eltahir, E. A. & Bras, R. L. Precipitation recycling in the Amazon basin. Q. J. Roy. Meteor. Soc. 120, 861–880 (1994).
van der Ent, R. J., Savenije, H. H. G., Schaefli, B. & Steele-Dunne, S. C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 46, W09525 (2010).
Zemp, D. C. et al. On the importance of cascading moisture recycling in South America. Atmos. Chem. Phys. 14, 13337–13359 (2014).
Fu, R. et al. Increased dry-season length over southern Amazonia in recent decades and its implication for future climate projection. Proc. Natl Acad. Sci. USA 110, 18110–18115 (2013).
Marengo, J. A., Tomasella, J., Alves, L. M., Soares, W. R. & Rodriguez, D. A. The drought of 2010 in the context of historical droughts in the Amazon region. J. Geophys. Res. 38, LI2703 (2011).
Gloor, M. et al. Intensification of the Amazon hydrological cycle over the last two decades. Geophys. Res. Lett. 40, 1729–1733 (2013).
Boisier, J. P., Ciais, P., Ducharne, A. & Guimberteau, M. Projected strengthening of Amazonian dry season by constrained climate model simulations. Nat. Clim. Change 5, 656–660 (2015).
Mosblech, N. A. et al. North Atlantic forcing of Amazonian precipitation during the last ice age. Nat. Geosci. 5, 817–820 (2012).
Cheng, H. et al. Climate change patterns in Amazonia and biodiversity. Nat. Commun. 4, 1411 (2013).
Wang, X. et al. Hydroclimate changes across the Amazon lowlands over the past 45,000 years. Nature 541, 204–207 (2017).
Cook, K. & Vizy, E. South American climate during the Last Glacial Maximum: delayed onset of the South American monsoon. J. Geophys. Res. 111, D02110 (2006).
Scheffer, M., Holmgren, M., Brovkin, V. & Claussen, M. Synergy between small-and large-scale feedbacks of vegetation on the water cycle. Glob. Change Biol. 11, 1003–1012 (2005).
van Nes, E. H., Hirota, M., Holmgren, M. & Scheffer, M. Tipping points in tropical tree cover: linking theory to data. Glob. Change Biol. 20, 1016–1021 (2014).
Gai, P. & Kapadia, S. Contagion in financial networks. Proc. R. Soc. A 466, 2401–2423 (2010).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002).
Thébault, E. & Fontaine, C. Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856 (2010).
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).
Fox, R. J. & Bellwood, D. R. Herbivores in a small world: network theory highlights vulnerability in the function of herbivory on coral reefs. Funct. Ecol. 28, 642–651 (2014).
Stolbova, V., Surovyatkina, E., Bookhagen, B. & Kurths, J. Tipping elements of the Indian monsoon: Prediction of onset and withdrawal. Geophys. Res. Lett. 43, 3982–3990 (2016).
Boers, N. et al. Prediction of extreme floods in the eastern Central Andes based on a complex networks approach. Nat. Commun. 5, 5199 (2014).
Ludescher, J. et al. Very early warning of next El Niño. Proc. Natl Acad. Sci. USA 111, 2064–2066 (2014).
van der Ent, R. J., Wang-Erlandsson, L., Keys, P. & Savenije, H. Contrasting roles of interception and transpiration in the hydrological cycle-part 2: Moisture recycling. Earth Syst. Dynam. 5, 471–489 (2014).
Aragao, L. E. O. et al. Spatial patterns and fire response of recent Amazonian droughts. Geophys. Res. Lett. 34, L07701 (2007).
Lejeune, Q., Davin, E. L., Guillod, B. P. & Seneviratne, S. I. Influence of Amazonian deforestation on the future evolution of regional surface fluxes, circulation, surface temperature and precipitation. Clim. Dyn. 44, 2769–2786 (2015).
Lawrence, D. & Vandecar, K. Effects of tropical deforestation on climate and agriculture. Nat. Clim. Change 5, 27–36 (2015).
Spracklen, D. & Garcia-Carreras, L. The impact of Amazonian deforestation on Amazon basin rainfall. Geophys. Res. Lett. 42, 9546–9552 (2015).
van Nes, E. H. & Scheffer, M. Implications of spatial heterogeneity for catastrophic regime shifts in ecosystems. Ecology 86, 1797–1807 (2005).
Levine, N. M. et al. Ecosystem heterogeneity determines the ecological resilience of the Amazon to climate change. Proc. Natl Acad. Sci. USA 113, 793–797 (2016).
Sakschewski, B. et al. Resilience of Amazon forests emerges from plant trait diversity. Nat. Clim. Change 6, 1032–1036 (2016).
Sheffield, J., Wood, E. F. & Roderick, M. L. Little change in global drought over the past 60 years. Nature 491, 435–438 (2012).
Trenberth, K. E. et al. Global warming and changes in drought. Nat. Clim. Change 4, 17–22 (2014).
Mueller, B. et al. Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis. Hydrol. Earth Syst. Sci. 17, 3707–3720 (2013).
Rammig, A. et al. Estimating the risk of Amazonian forest dieback. New Phytol. 187, 694–706 (2010).
Huntingford, C. et al. Simulated resilience of tropical rainforests to CO2-induced climate change. Nat. Geosci. 6, 268–273 (2013).
Kleidon, A. & Lorenz, S. Deep roots sustain Amazonian rainforest in climate model simulations of the last ice age. Geophys. Res. Lett. 28, 2425–2428 (2001).
Colinvaux, P. A., De Oliveira, P. & Bush, M. Amazonian and neotropical plant communities on glacial time-scales: the failure of the aridity and refuge hypotheses. Quat. Sci. Rev. 19, 141–169 (2000).
Malhi, Y. et al. Climate change, deforestation, and the fate of the Amazon. Science 319, 169–172 (2008).
Cox, P. M. et al. Increasing risk of Amazonian drought due to decreasing aerosol pollution. Nature 453, 212–215 (2008).
Good, P., Jones, C., Lowe, J., Betts, R. & Gedney, N. Comparing tropical forest projections from two generations of Hadley Centre Earth System models, HadGEM2-ES and HadCM3LC. J. Clim. 26, 495–511 (2013).
Miguez-Macho, G. & Fan, Y. The role of groundwater in the Amazon water cycle: 1. Influence on seasonal streamflow, flooding and wetlands. J. Geophys. Res. 117, D15114 (2012).
Yin, L., Fu, R., Shevliakova, E. & Dickinson, R. E. How well can CMIP5 simulate precipitation and its controlling processes over tropical South America? Clim. Dyn. 41, 3127–3143 (2013).
Claussen, M., Bathiany, S., Brovkin, V. & Kleinen, T. Simulated climate-vegetation interaction in semi-arid regions affected by plant diversity. Nat. Geosci. 6, 954–958 (2013).
Staal, A., Dekker, S. C., Xu, C. & van Nes, E. H. Bistability, spatial interaction, and the distribution of tropical forests and savannas. Ecosystems 19, 1080–1091 (2016).
Sheffield, J., Goteti, G. & Wood, E. F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 19, 3088–3111 (2006).
Dee, D. et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597 (2011).
DiMiceli, C. et al. Annual global automated MODIS vegetation continuous fields (MOD44B) at 250 m spatial resolution for data years beginning day 65, 2000-2010, collection 5, percent tree cover (University of Maryland, College Park, MD, USA, 2011).
Bartholomé, E. & Belward, A. S. GLC2000: a new approach to global land cover mapping from Earth observation data. Int. J. Remote Sens. 26, 1959–1977 (2005).
Huffman, G. J. et al. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 8, 38–55 (2007).
Franchito, S. H., Rao, V. B., Vasques, A. C., Santo, C. M. & Conforte, J. C. Validation of TRMM precipitation radar monthly rainfall estimates over Brazil. J. Geophys. Res. 114, D0210 (2009).
Rozante, J. R., Moreira, D. S., de Goncalves, L. G. G. & Vila, D. A. Combining TRMM and surface observations of precipitation: Technique and validation over South America. Weather Forecast. 25, 885–894 (2010).
Kim, J.-E. & Alexander, M. J. Tropical precipitation variability and convectively coupled equatorial waves on submonthly time scales in Reanalyses and TRMM. J. Clim. 26, 3013–3030 (2013).
Lapola, D. M., Oyama, M. D., Nobre, C. A. & Sampaio, G. A new world natural vegetation map for global change studies. An. Acad. Bras. Ciênc. 80, 397–408 (2008).
Soares-Filho, B. S. et al. Modelling conservation in the Amazon basin. Nature 440, 520–523 (2006).
Livina, V. N., Kwasniok, F. & Lenton, T. M. Potential analysis reveals changing number of climate states during the last 60 kyr. Clim. Past 6, 77–82 (2010).
Gerrits, A., Savenije, H., Veling, E. & Pfister, L. Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model. Water Resour. Res. 45, W04403 (2009).
Acknowledgements
We thank Ruud van der Ent for developing and sharing the atmospheric-moisture tracking model used in this study, Egbert van Nes for providing code for Supplementary Fig. 1 and Brigitte Mueller for providing the precipitation multi-data set used in this study. We also thank Hermann Behling, A.J. Han Dolman, Jonathan F. Donges, Dieter Gerten, Milena Holmgren, Patrick Keys, Peter Puetz, Thomas Kneib, Marten Scheffer, Kirsten Thonicke and Liubov Tupikina for discussion and comments. We are thankful to Pierre Manceaux for his contribution to the design of the figures and to Alison Schlums for proof-read. This paper was developed within the scope of the IRTG 1740/TRP 2011/50151-0, funded by the DFG/FAPESP. D.C.Z. acknowledges the financial support from EU-FP7 ROBIN project under grant agreement 283093. H.M.J.B. acknowledges the financial support from FAPESP through grants number 11/50151-0 and 13/50510-5. L.W.-E. acknowledges the financial support from The Swedish Research Council Formas through grant number 1364115. A.S. acknowledges the financial support from SENSE Research School, A.R. the EU-FP7 project AMAZALERT (ProjectID 282664) and M.H. the project Microsoft/FAPESP 2013/50169-1, and C.F.S. the financial support by the German Federal Ministry for the Environment, Nature Conservation and Nuclear Safety (16_II_148_Global_A_IMPACT).
Author information
Authors and Affiliations
Contributions
D.C.Z. and C.-F.S. conceived the study, D.C.Z. conducted the analysis and wrote the paper with the support of all co-authors. A.R. supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures and Supplementary Tables (PDF 5509 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zemp, D., Schleussner, CF., Barbosa, H. et al. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat Commun 8, 14681 (2017). https://doi.org/10.1038/ncomms14681
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms14681
This article is cited by
-
Remotely sensing potential climate change tipping points across scales
Nature Communications (2024)
-
Transformation starts at the periphery of networks where pushback is less
Scientific Reports (2024)
-
Critical transitions in the Amazon forest system
Nature (2024)
-
Notable shifts beyond pre-industrial streamflow and soil moisture conditions transgress the planetary boundary for freshwater change
Nature Water (2024)
-
Tropical deforestation causes large reductions in observed precipitation
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.