Abstract
To minimize the lattice thermal conductivity in thermoelectrics, strategies typically focus on the scattering of low-frequency phonons by interfaces and high-frequency phonons by point defects. In addition, scattering of mid-frequency phonons by dense dislocations, localized at the grain boundaries, has been shown to reduce the lattice thermal conductivity and improve the thermoelectric performance. Here we propose a vacancy engineering strategy to create dense dislocations in the grains. In Pb1−xSb2x/3Se solid solutions, cation vacancies are intentionally introduced, where after thermal annealing the vacancies can annihilate through a number of mechanisms creating the desired dislocations homogeneously distributed within the grains. This leads to a lattice thermal conductivity as low as 0.4 Wm−1 K−1 and a high thermoelectric figure of merit, which can be explained by a dislocation scattering model. The vacancy engineering strategy used here should be equally applicable for solid solution thermoelectrics and provides a strategy for improving zT.
Similar content being viewed by others
Introduction
Thermoelectric materials attract increasing interest, driven by the world-wide demand for clean energy1. Based on either the Seebeck or Peltier effects, thermoelectrics can be used for power generation or for refrigeration, respectively. Thermoelectrics use the charge carriers inside a material as a working medium, therefore enabling a vibration-free and emission-free solution to the direct conversion between heat and electricity. The biggest challenge is to enhance the conversion efficiency, which is mostly limited by the materials’ dimensionless figure of merit, zT=S2T/ρ(κE+κL), where S is the Seebeck coefficient, ρ is the electric resistivity, κE and κL are the electronic and the lattice contribution to the thermal conductivity, and T is the absolute temperature.
Owing to the strong coupling between S, ρ and κE, two straightforward strategies for improving zT are to increase the electrical performance via the power factor S2/ρ and to reduce the independent material property, lattice thermal conductivity κL. The former strategy has been recently demonstrated by the band engineering concept2,3,4,5,6,7,8,9,10 and the later one can be accomplished by a few approaches that include nanostructuring11,12,13,14, alloying15,16 and lattice anharmonicity17,18.
Among all the demonstrated approaches for achieving a low lattice thermal conductivity mentioned above, the essential commonality is the strengthened phonon scattering, but in different ways. Specifically, nanostructuring increases boundary scattering and alloying introduces point defect scattering, whereas anharmonic lattice vibrations lead to a strong inherent phonon–phonon scattering. These different scattering mechanisms collectively contribute to shorten the overall relaxation time (τtot) of phonons, each with a characteristic frequency (ω) dependence, leading to a low lattice thermal conductivity. More quantitatively, boundary scattering by nanostructures leads to a relaxation time, τB∝ω0, which enables effective scattering of low-frequency phonons; point defect scattering in alloys results in a relaxation time, τPD∝ω−4, effectively scattering the high-frequency phonons, and the inherent phonon–phonon scattering by anharmonic lattice vibrations has respectively a relaxation time, τU,N∝ω−2, for Umklapp (τU) and normal (τN) processes, which enables effective scattering on phonons with all frequencies.
Although it is rarely focused on, dislocation scattering is another process that can be effective at reducing lattice thermal conductivity in thermoelectrics19,20. The frequency dependence of phonon scattering on dislocation strian fields (τDS∝ω−1) and dislocation cores (τDC∝ω−3) makes this mechanism particularly effective at scattering mid-range frequency phonons, phonons missed by the previously discussed scattering mechanisms21,22. Even with scattering by grain boundary dislocations, which are known to have much shorter range strain fields than lattice dislocations23, a large κL reduction has been recently observed experimentally20. Therefore, it is believed that phonon scattering by dislocations, whether in the grain boundary structure or in the lattice, is an effective approach for advancing thermoelectrics.
Dislocations are generally undesired in semiconductors and ceramics24,25 when the thermal conductivity is not a major functionality, due to their detrimental effects on the mechanical properties, carrier mobility and optical properties26,27,28. To achieve an effective κL reduction by dislocations in thermoelectric semiconductors, a simple estimation shows that the density of uniformly distributed dislocations within the grains (ND) needs to be approaching 1012 cm−2 or higher29, being at least two orders of magnitude higher than that can be normally obtained in semiconductors30. The most straightforward way to introduce dislocations into a material is through plastic deformation. However, most thermoelectrics do not readily plastically deform and dislocations must be introduced by other means.
In thermoelectrics, dislocations have been introduced through the precipitation of secondary phases where misfit dislocations mediate the lattice mismatch at coherent phase boundaries16. A large density of grain boundary dislocations has also been achieved by liquid-phase compaction (ND=2 × 1011 cm−2)20. Another method for introducing a large density of dislocations is through the introduction of a large concentration of vacancies31. On thermal annealing these vacancies will diffuse forming vacancy clusters of lower energy, these vacancy clusters then collapse into closed loops of edge dislocations. This mechanism was initially observed in metals32 and has since been observed in ionic crystals33. In addition, vacancies in a material facilitate dislocation climb and at vacancy concentrations far from equilibrium the resulting dislocation motion can increase the dislocation content (that is, the activation of Bardeen–Herring sources)34,35.
Frank34 highlights a situation where the concentration of point defects is far from equilibrium, which is common in semiconducting materials31. When annealed, the resulting dislocation motion via climb will result in an increase in dislocation content34. Although these mechanisms are well understood for ionic crystals where vacancies are produced through Frenkel defects or Schottky pairs, they are likely to be more complicated in systems where vacancies are introduced via charge compensation doping and one vacancy-type dominates. These mechanisms lead to a strategy for obtaining uniformly distributed dense dislocations through vacancy engineering in thermoelectric materials.
Compared with the solvent compound, when a solute of a smaller cation-to-anion ratio is dissolved forming a solid solution, either vacancies at the cation site or interstitial anions would be expected. Anion interstitials generally have a much larger defect formation energy than that of a cation site vacancy, because typically the anion radius is larger than that of the cation. This leads to the preferred formation of cation vacancies. Thus, the formation of dislocations would be expected due to the collapse of cation vacancy clusters. It is expected that the density of the dislocations can be easily controlled by tuning the composition of the solid solution.
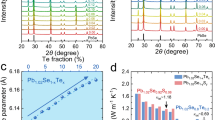
This work focuses on the thermoelectric properties of PbSe-Sb2Se3 solid solutions (Pb1−xSb2x/3Se) to demonstrate this strategy. To maintain a charge-balanced, undoped semiconductor within the solid solution, with rock salt structure, it is believed that for three Pb sites replaced by two Sb atoms and a third site becomes vacant. The resulting cation vacancies lead to a high density of uniformly distributed dislocations (Fig. 1a,b). These dislocations provide a strong scattering of phonons in the mid-range of frequencies (τDC∝ω−3, τDS∝ω−1). This is in addition to the point defect scattering (τPD∝ω−4) from the Sb/Pb substitution for high-frequency phonons and strong inherent phonon–phonon scattering (τU,N∝ω−2) for phonons at all frequencies. This full frequency spectrum scattering of phonons, with an emphasis on the mid-frequency phonons, leads to the low value lattice thermal conductivity (κL), compared with intrinsic PbSe36, approaching the amorphous limit estimated by assuming a phonon mean free path of minimal distance37 in a broad temperature range (Fig. 1c). Most importantly, the ultralow lattice thermal conductivity of ∼0.4 Wm−1 K−1 leads to higher zT than previously reported in PbSe (Fig. 1d). This vacancy engineering strategy for dislocation scattering to reduce the lattice thermal conductivity should be widely applicable in thermoelectric solid solutions.
Uniformly distributed dense dislocations in Pb0.95Sb0.033Se solid solution (a) and Pb0.97Sb0.02Se solid solution (b). The temperature-dependent lattice thermal conductivity (c) and thermoelectric figure of merit (d) for Pb1−xSb2x/3Se (x=0.01, 0.03, 0.04, 0.05 and 0.07) with or without Ag doping. The lattice thermal conductivity of PbSe36 (grey line) and estimated minimal lattice thermal conductivity (black line) are included for comparison. Dislocations due to cation vacancies lead to the lowest lattice thermal conductivity and the highest zT in PbSe thermoelectrics.
Results
Microstructure and formation mechanisms of dislocations
The powder X-ray diffraction (XRD) indicates all the materials obtained here crystalize in NaCl structure with high phase purity (Supplementary Fig. 1a). The formation of Pb1−xSb2x/3Se solid solution in this work can be evident from the linear decrease in lattice parameter with increasing x (Supplementary Fig. 1b), which agrees well with the Vegard’s law. Neither precipitates nor nanometre-scale grains are observed according to our XRD analyses and transmission electron microscope (TEM) observations.
As the cation-to-anion ratio in Sb2Se3 is 1/3 smaller than that in PbSe, formation of a rock-salt structured Pb1−xSb2x/3Se solid solution would lead to x/3 negatively charged vacancies at the Pb site per formula unit rather than interstitial Se. Pb deficiency can be observed in the energy dispersive X-ray spectroscopy analysis. These Pb vacancies can increase the dislocation content through a number of mechanisms that have been observed in ionic crystals33,23,38,39. One possibility is the activation of Bardeen–Herring sources (the climb analogue to the Frank–Read source) where vacancy diffusion facilitates dislocation climb34. These sources act as dislocation multiplication sites and are diffusion-limited processes. In addition, dislocations in ionic crystals can have an electrostatic charge23,38. These charged regions interact with the negatively charged Pb vacancies retarding the motion of the dislocations via glide stopping their annihilation with each other or at a surface.
The samples in this study were annealed at 1,023 K for 2 days, giving the system sufficient thermal energy to activate the above mentioned, diffusion-limited dislocation nucleation and multiplication processes. These dislocations can subsequently climb, glide and tangle into the complex dislocation network seen in Fig. 1a,b. Although these mechanisms are well understood for ionic crystals where vacancies are produced through Frenkel defects or Schottky pairs, they are likely to be more complicated in systems where vacancies are introduced via charge compensation doping and one vacancy type dominates. Different thermal histories, composition and synthesis methods may explain why other Pb1−xSbxSe studies show the formation of Sb-rich impurity phases but not dislocations40.
According to the theory of impurity diffusion, in particular in cubic crystals with vacancies41,42,43, the existence of vacancies will significantly retard the diffusion of the substitutional impurities because of the coulombic interaction between them34,36,44,45, whereas the diffusion of vacancies themselves can be largely accelerated when they are bound with dislocations46. Therefore, the substitutional Sb impurity on the Pb sites do not diffuse fast enough to form an aggregation of Sb-rich phases as confirmed by the TEM observations for Pb1−xSb2x/3Se. This mechanism may further explain the formation of Sb-rich impurity phases but not dislocations in Pb1−xSbxSe, which may have fewer cation vacancies40.
Density of dislocation
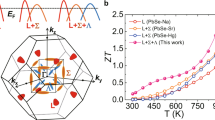
An example of a typical dislocation in the high-resolution annular bright field scanninge TEM (STEM) image in Fig. 2a. Starting from the core (centre of the image) of the dislocation, one (001) and two (111) extra half planes of atoms are observed and marked by yellow arrows. The Burgers vectors of the dislocation is determined to be BD=1/2[0 1], which is generally observed in NaCl structures47. Based on a few low magnification STEM images, the average areal dislocation density (ND) is estimated to be ∼4 × 1012 cm−2; this is an extremely high value compared with that typically reported in semiconductors30.
1], which is generally observed in NaCl structures47. Based on a few low magnification STEM images, the average areal dislocation density (ND) is estimated to be ∼4 × 1012 cm−2; this is an extremely high value compared with that typically reported in semiconductors30.
A high-resolution annular bright field (ABF) STEM image (a) shows the detailed dislocations in the sample with x=0.05. The black arrows give a complete Burgers loop of a dislocation and the yellow arrows show one (001) and two (111) extra half planes of atoms. The estimated Burger’s vector (red arrow) for the observed dislocations is BD=1/2[0 1]. The inset shows the structural model of PbSe projected in [110] direction with red dots standing for Pb, whereas yellow ones for Se. Neither precipitates nor nanometre-scale grains are observed. The synchrotron XRD pattern (b) and the peak broadening analysis by the modified Williamson–Hall plot (red line) in which the slope and intercept reveal the dislocation density and the crystallite size (c).
1]. The inset shows the structural model of PbSe projected in [110] direction with red dots standing for Pb, whereas yellow ones for Se. Neither precipitates nor nanometre-scale grains are observed. The synchrotron XRD pattern (b) and the peak broadening analysis by the modified Williamson–Hall plot (red line) in which the slope and intercept reveal the dislocation density and the crystallite size (c).
To estimate the density of dislocations more macroscopically and to compare with that determined by the local TEM observations, synchrotron XRD (Fig. 2b) was carried out and the modified Williamson–Hall model48,49 was employed for the high zT sample Pb0.95Sb0.033Se. According to this method, the broadening of the diffraction peaks strongly relate to the dislocation density and the crystallite size via: ΔK=0.9/d+(πA2BD2/2)ND1/2K2C±O(K4C2) with details shown in Supplementary Table 3. With the experimentally measured K and ΔK, the dislocation density can be determined via the slope of the modified Williamson–Hall plot as shown in Fig. 2c. The estimated dislocation density is ∼5 × 1012 m−2 for Pb0.95Sb0.033Se, which agrees well with the result determined by the TEM observations. Similarly, the modified Williamson–Hall plots, according to our normal XRD results, qualitatively show that the density of dislocations for Pb1−xSb2x/3Se (x=0∼0.07) solid solutions increase with increasing Sb concentration (Supplementary Fig. 2).
Lattice thermal conductivity and modelling
The lattice thermal conductivity (Fig. 1c), determined by subtracting the electronic contribution via the Wiedemann–Franz law from the measured thermal conductivity, decreases with increasing Sb2Se3 content, meaning a strengthened phonon scattering with increasing x. To ensure that the uniformly distributed dense dislocations are indeed responsible for the observed ultralow lattice thermal conductivity, modelling is carried out based on the Debye approximation with different scattering sources for phonons.
First, the literature values of κL, which are an average on a few degenerately doped polycrystalline PbSe samples, is used to estimate the ratio (=4) of N- to U-processes for the phonon–phonon scattering36. Second, the point defect scattering parameters including both mass and strain contributions are determined according to the literature50,51,52. Third, the scattering by dislocations can be calculated21 with the experimental Burger vector and the dislocation density. Klemens’ expression for edge dislocation scattering was used. Besides our measured transverse and longitudinal sound velocities of υL=3,150 ms−1 and υT=1,600 ms−1, respectively, other parameters including Gruneisen parameter of 1.7 (ref. 53) and Poisson ratio of 0.243(ref. 54) are taken from the literature. More details for the modelling can be found in the Supplementary Tables 1 and 2.
Next, one can calculate the temperature-dependent lattice thermal conductivity using the following equation55:

where kB is the Boltzmann constant, υ is average sound speed, ℏ is the reduced Plank constant, θD is Debye temperature, τtot is the total relaxation time and x=ℏω/kBT. The total relaxation time includes the contributions from phonon–phonon, point defect and dislocation scattering by:

As shown in Fig. 3a, the model prediction agrees well with the measurements for the high thermoelectric figure of merit sample (x=0.05). It is then clear that the lattice thermal conductivity (κL) additionally decreases by at least 30% in the entire temperature range due to dislocation scattering. Assuming all the initially produced vacancies remains in the solid solution as random point defects, the lattice thermal conductivity is predicted to be as the blue dashed line (Fig. 3a), which is well above the model prediction including the contribution from dislocation scattering (green solid line). Therefore, dislocation scattering is believed to be the main reason for the observed κL reduction. Importantly, the nearly full phonon frequency spectrum scattering leads to a comparable κL with the theoretical minimum (κLmin=0.37 Wm−1 K−1) obtained by the Cahill’s model37. Comparing the dislocations in samples with x=0.03 (Fig. 1b), x=0.04 (Supplementary Fig. 3a,b), x=0.05 (Fig. 1a) and x=0.07 (Supplementary Fig. 3c,d), a roughly linear increase in the density of the dislocations (ND) with increasing x is observed. Using this simple linear approximation between ND and x, the above model further enables a nice prediction on κL versus x at a given temperature, as shown in Fig. 3b. This confirms the dislocation scattering is indeed helpful for reducing the lattice thermal conductivity.
Temperature- (a) and composition- (b) dependent lattice thermal conductivity (symbols) for Pb1−xSb2x/3Se solid solution. Taking into account the frequency (ω)-dependent terms for phonon relaxation time including ω−2 for phonon–phonon (black line in Fig. 3a), ω−4 for point defect (solid blue line) and ω−1+ω−3 for dislocation scattering (olive line), a model based on the Debye approximation (curves) predicts the experimental results. The dashed blue line shows the model prediction, assuming all the Pb vacancies stabilize as random point defects rather than dislocations. The comparison of the dislocations between the x=0.05 (Fig. 1a) and the x=0.03 (Fig. 1b) samples indicates a nearly linear increase in dislocation density with increasing x, further enabling a reliable model prediction on κL versus x.
The model-predicted frequency-dependent accumulative reduction in κL (Supplementary Fig. 4) indeed shows the significant effect of dislocations for mid-frequency phonon scattering in Pb0.95Sb0.33Se. The predicted accumulative κL due to Umklapp and normal scattering in pure PbSe, further helps us understand the important range of mean free path56 that contributes to heat conduction. It is also worthy to note that the mechanical strength does not degrade a lot due to the existence of dense in-grain dislocations here (Supplementary Table 4).
Transport properties
In spite of the strong scattering of phonons, one needs also to be careful when evaluating the thermoelectric properties, because the formation of solid solutions may change the band structure, whereas the existence of dislocations may affect the scattering of charge carriers. To clarify this possibility, the Hall carrier concentration-dependent room-temperature Seebeck coefficient is shown in Fig. 4a. It is seen that both the literature PbSe36 and the current Pb1−xSb2x/3Se solid solution show nearly the same relationship between Seebeck coefficient and Hall carrier concentration. This indicates the band parameters such as the density-of-states effective mass remains unchanged. Therefore, they both can be described by a single Kane band model.
Hall carrier concentration-dependent Seebeck coefficient (a) at room temperature and temperature-dependent Hall mobility (b) for Pb1−xSb2x/3Se solid solution. Although the band structure of PbSe remains nearly immune to alloying with Sb2Se3, the resulting dislocation scattering reduces the mobility.
The temperature-dependent Hall mobility (Fig. 4b) helps understand the carrier scattering mechanism. With increasing x, thus an increase in dislocation density, it is shown that at T<500 K the Hall mobility (μH) decreases much slower with increasing temperature as compared with a relationship of μH∼T−2.25 that is normally expected for n-PbSe53. This can be understood, because a temperature-dependent mobility of μH∼T1.5 will be observed in case of carrier scattering dominated by dislocations57, which is similar with that of ionized impurity scattering. This type of scattering can be effectively screened here, because of the high dielectric constant of PbSe53; therefore, a high mobility can still be obtained. Similar dielectric screening effects for a high mobility has been found in semiconductors and graphene58,59,60. However, the temperature-dependent Hall mobility in Pb1−xSbxSe40, without dense dislocations as in Pb1−xSb2x/3Se, does not indicate a T1.5-type contribution to the Hall mobility. The electronic transport of Pb1−xSbxSe40 without dislocations show normal n-type doped PbSe36 behaviour.
The temperature-dependent thermal conductivity (κ), Seebeck coefficient (S) and resistivity (ρ) are shown in Fig. 5a–c, respectively. With increasing x, the reduced thermal conductivity is largely from the lattice thermal conductivity reduction due to the vacancy-induced dislocations. It should be noted that the Lorenz factor is determined by the single Kane band model to estimate the electronic thermal conductivity (κE). At T<600 K, the decrease in resistivity in the heavily alloyed samples can be explained by the resulting dislocation scattering on carriers (Fig. 4b). The decrease in ρ and S at T>700 K is probably due to the existence of minority carriers, which is normally seen in narrow band gap semiconductors.
Discussion
In summary, this work presents a method to create uniformly distributed dense dislocations throughout the entire grains of Pb1−xSb2x/3Se solid solutions by the introduction of cation vacancies. Owing to the strong phonon scattering by dislocation cores and strain fields, the lattice thermal conductivity reaches the theoretical minimum and, therefore, a high figure of merit zT is obtained. Unlike previously demonstrated approaches focusing on the scattering of phonons with either low or high frequencies, this work proposes a vacancy engineering strategy for well-dispersed dense dislocations, enabling an effective demonstration of mid-range frequency phonon scattering for low lattice thermal conductivity. This strategy emphasizes a thermal effect, which is independent of other existing strategies, such as band engineering, for increasing the electrical performance2. Therefore, a combination with other strategies offers great potential for further improvements of thermoelectrics.
Methods
Synthesis
Starting with pure elements (Pb 99.99%, Sb 99.99%, Se 99.999%), Pb1−xSb2x/3Se solid solutions with x from 0 to 9% were prepared by melting at 1,400 K for 6 h, followed by quenching in water and annealing at 1,023 K for 2 days. An Ag doping of ≤1% at the Pb site was also used to help control the carrier concentration precisely. The ingot materials were ground into fine powders for hot pressing58 at 973 K for 1 h under a uniaxial pressure of ∼90 MPa under vacuum. The disk samples for measurements were ∼2 mm in diameter and ∼1.5 mm in thickness, and the density (d) is higher than 96% of theoretical value.
Characterization
The phase impurity was characterized by lab XRD (Dandong Haoyuan Instrument Co. Ltd). The samples for (S)TEM observation were prepared by mechanical polishing, dimpling and ion milling with liquid nitrogen. TEM and STEM imaging including in high-angle annular dark field and annular bright field modes, as well as energy dispersive X-ray spectroscopy element mapping were carried out by JEOL ARM 200 equipped with a probe corrector and an image corrector. Synchrotron XRD measurements were carried out at the beamline number 14B of the Shanghai Synchrotron Radiation Facility. The energy of monochromatic X-ray beam was 10 keV, corresponding to a wavelength of 0.687 nm. The reflection mode was applied and the signal was recorder by a NaI(Tl) scintillation detector. The beam size is 0.5 × 1 mm. The line profiles were recorded with a step size of 0.02° and a dwell time of 3 s.
Transport property measurements
The electrical properties including Seebeck coefficient, resistivity and Hall coefficient were simultaneously measured on the samples during both heating and cooling in vacuum. The Seebeck coefficient in the in-plane direction was obtained from the slope of the thermoelectric voltage versus temperature gradients59. The in-plane resistivity and Hall coefficient were measured using the Van der Pauw technique under a reversible magnetic field of 1.5 T. The uncertainty of each transport property measurement is ∼5%. The thermal diffusivity DT was measured by the laser flash method (Netzsch LFA 457) and the thermal conductivity κ was calculated from κ=dDTCp, where Cp is the heat capacity determined by Cp(kB/atom)=(3.07+0.00047(T/K-300))60,61. The sound velocity was measured by an ultrasonic pulse-receiver (Olympus-NDT) equipped with an oscilloscope (Keysight). The uncertainty for each measurement of transport property is ∼5%.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Chen, Z. et al. Vacancy-induced dislocations within grains for high-performance PbSe thermoelectrics. Nat. Commun. 8, 13828 doi: 10.1038/ncomms13828 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457–1461 (2008).
Pei, Y. et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 473, 66–69 (2011).
Liu, W. et al. Convergence of conduction bands as a means of enhancing thermoelectric performance of n-type Mg2Si1−xSnx solid solutions. Phys. Rev. Lett. 108, 166601 (2012).
Pei, Y. et al. Stabilizing the optimal carrier concentration for high thermoelectric efficiency. Adv. Mater. 23, 5674–5678 (2011).
Xie, H. et al. Beneficial contribution of alloy disorder to electron and phonon transport in half-Heusler thermoelectric materials. Adv. Funct. Mater. 23, 5123–5130 (2013).
Pei, Y., LaLonde, A. D., Heinz, N. A. & Snyder, G. J. High thermoelectric figure of merit in PbTe alloys demonstrated in PbTe–CdTe. Adv. Energy Mater. 2, 670–675 (2012).
Pei, Y., Wang, H., Gibbs, Z. M., LaLonde, A. D. & Snyder, G. J. Thermopower enhancement in Pb1-xMnxTe alloys and its effect on thermoelectric efficiency. NPG Asia Mater. 4, e28 (2012).
Lin, S. et al. Tellurium as a high-performance elemental thermoelectric. Nat. Commun. 7, 10287 (2016).
Jian, Z. et al. Significant band engineering effect of YbTe for high performance thermoelectric PbTe. J. Mater. Chem. C 3, 12410–12417 (2015).
Li, W. et al. Band and scattering tuning for high performance thermoelectric Sn1−xMnxTe alloys. J. Mater. 1, 307–315 (2015).
Hsu, K. F. et al. Cubic AgPbmSbTe2+m: bulk thermoelectric materials with high figure of merit. Science 303, 818–821 (2004).
Biswas, K. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Poudel, B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638 (2008).
Pei, Y., Lensch-Falk, J., Toberer, E. S., Medlin, D. L. & Snyder, G. J. High thermoelectric performance in PbTe due to large nanoscale Ag2Te precipitates and La doping. Adv. Funct. Mater. 21, 241–249 (2011).
Vining, C. B. in CRC Handbook of Thermoelectrics ed. Rowe D. M. Ch. 28, CRC Press (1995).
Schemer, H. & Scherrer, S. in CRC Handbook of Thermoelectrics ed. Rowe D. M. Ch. 19, CRC Press (1995).
Zhao, L.-D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377 (2014).
Morelli, D. T., Jovovic, V. & Heremans, J. P. Intrinsically minimal thermal conductivity in cubic I-V-VI2 semiconductors. Phys. Rev. Lett. 101, 035901 (2008).
He, J. Q., Girard, S. N., Kanatzidis, M. G. & Dravid, V. P. Microstructure-lattice thermal conductivity correlation in nanostructured PbTe0.7S0.3 thermoelectric materials. Adv. Funct. Mater. 20, 764–772 (2010).
Kim, S. I. et al. Thermoelectrics. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 348, 109–114 (2015).
Klemens, P. G. The scattering of low-frequency lattice waves by static imperfections. Proc. Phys. Soc. A68, 1113–1128 (1955).
Adams, A., Baumann, F. & Stuke, J. Thermal conductivity of selenium and tellurium single crystals and phonon drag of tellurium. Phys. Stat. Solid. (b) 23, K99–K104 (1967).
Hirth, J. P. Theory of Dislocations 2nd Edn John Willey & Sons (1982).
de Kock, A. J. R. The elimination of vacancy‐cluster formation in dislocation‐free silicon crystals. J. Electrochem. Soc. 118, 1851–1856 (1971).
Mott, N. F. CXVII. A theory of work-hardening of metal crystals. LED Phil. Mag. J. Sci. 43, 1151–1178 (2010).
Jin, N. Y. Formation of dislocation structures during cyclic deformation of F.C.C. crystals—I. Formation of PSBs in crystals oriented for single-slip. Acta Metall. 37, 2055–2066 (1989).
Read, W. T. LXXXVII. Theory of dislocations in germanium. LED Phil. Mag. J. Sci. 45, 775–796 (2009).
Meyer, M. Some electrical and optical effects of dislocations in semiconductors. J. Appl. Phys. 38, 4481 (1967).
Koehler, J. S. A calculation of the changes in the conductivity of metals produced by cold-work. Phys. Rev. 75, 106–117 (1949).
Dexter, D. L. & Seitz, F. Effects of dislocations on mobilities in semiconductors. Phys. Rev. 86, 964–965 (1952).
Tan, T. Y., You, H.-M. & Gösele, U. M. Thermal equilibrium concentrations and effects of negatively charged Ga vacancies in n-type GaAs. Appl. Phys. A 56, 249–258 (1993).
Hirsch, P. B., Silcox, J., Smallman, R. E. & Westmacott, K. H. Dislocation loops in quenched aluminium. Philos. Mag. 3, 897–908 (1958).
Suzuki, T., Ueno, M., Nishi, Y. & Fujimoto, M. Dislocation loop formation in nonstoichiometric (Ba,Ca)TiO3 and BaTiO3 ceramics. J. Am. Ceram. Soc. 84, 200–206 (2001).
Frank, F. Dislocations and point defects. Discuss. Farad. Soc. 23, 122–127 (1957).
Hollmon, J., Maurer, R., Seitz, F. & Shockley, W. in Imperfections in Nearly Perfect Crystals. Symposium held at Pocono Manor, Penna, USA, 12–14 October 1950 (eds Shockley W., Hollomon J. H., Maurer R. and Seitz F.), pp490 (Wiley: New York; Chapman and Hall: London, 1952).
Wang, H., Pei, Y., LaLonde, A. D. & Snyder, G. J. Weak electron-phonon coupling contributing to high thermoelectric performance in n-type PbSe. Proc. Natl Acad. Sci. USA 109, 9705–9709 (2012).
Cahill, D. G., Watson, S. K. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131 (1992).
Whitworth, R. W. Charged dislocations in ionic crystals. Adv. Phys. 24, 203–304 (1974).
Johnston, W. G. & Gilman, J. J. Dislocation multiplication in lithium fluoride crystals. J. Appl. Phys. 31, 632–643 (1960).
Lee, Y. et al. Contrasting role of antimony and bismuth dopants on the thermoelectric performance of lead selenide. Nat. Commun. 5, 3640 (2014).
Lidiard, A. B. CXXXIII. Impurity diffusion in crystals (mainly ionic crystals with the sodium chloride structure). LED Phil. Mag. J. Sci. 46, 1218–1237 (2009).
Hu, S. M. General theory of impurity diffusion in semiconductors via the vacancy mechanism. Phys. Rev. 180, 773–784 (1969).
Nichols, C. S., Van de Walle, C. G. & Pantelides, S. T. Mechanisms of dopant impurity diffusion in silicon. Phys. Rev. B 40, 5484–5496 (1989).
Christoph Mueller, D., Alonso, E. & Fichtner, W. Arsenic deactivation in Si: electronic structure and charge states of vacancy-impurity clusters. Phys. Rev. B 68, 045208 (2003).
Ranki, V., Nissila, J. & Saarinen, K. Formation of vacancy-impurity complexes by kinetic processes in highly As-doped Si. Phys. Rev. Lett. 88, 105506 (2002).
Stark, J. P. The diffusivity, mobility, and correlation factor for solute vacancy diffusion in an edge dislocation in a face-centered-cubic crystal. J. Appl. Phys. 62, 3077 (1987).
Prasad, D. S., Munirathnam, N. R., Rao, J. V. & Prakash, T. L. Purification of tellurium up to 5N by vacuum distillation. Mater. Lett. 59, 2035–2038 (2005).
Ungár, T., Dragomir, I., Revesz, A. & Borbély, A. The contrast factors of dislocations in cubic crystals: the dislocation model of strain anisotropy in practice. J. Appl. Crystallogr. 32, 992–1002 (1999).
Ungar, T., Ott, S., Sanders, P., Borbély, A. & Weertman, J. Dislocations, grain size and planar faults in nanostructured copper determined by high resolution X-ray diffraction and a new procedure of peak profile analysis. Acta Mater. 46, 3693–3699 (1998).
Pei, Y. & Morelli, D. Vacancy phonon scattering in thermoelectric In2Te3-InSb solid solutions. Appl. Phys. Lett. 94, 122112 (2009).
Abeles, B. Lattice thermal conductivity of disordered semiconductor alloys at high temperatures. Phys. Rev. 131, 1906–1911 (1963).
Tian, Z. et al. Inelastic x-ray scattering measurements of phonon dispersion and lifetimes in PbTe1−x Sex alloys. J. Phys. Condens. Matter 27, 375403 (2015).
Ravich, Y. I., Efimova, B. A. & Smirnov, I. A. Semiconducting Lead Chalcogenides Plenum Press (1970).
Wang, H., Wang, J., Cao, X. & Snyder, G. J. Thermoelectric alloys between PbSe and PbS with effective thermal conductivity reduction and high figure of merit. J. Mater. Chem. A 2, 3169–3174 (2014).
Callaway, J. & Vonbaeyer, H. C. Effect of point imperfections on lattice thermal conductivity. Phys. Rev. 120, 1149–1154 (1960).
Tian, Z. et al. Phonon conduction in PbSe, PbTe, and PbTe1−xSex from first-principles calculations. Phys. Rev. B 85, 184303 (2012).
Ng, H. M., Doppalapudi, D., Moustakas, T. D., Weimann, N. G. & Eastman, L. F. The role of dislocation scattering in n-type GaN films. Appl. Phys. Lett. 73, 821 (1998).
LaLonde, A. D., Ikeda, T. & Snyder, G. J. Rapid consolidation of powdered materials by induction hot pressing. Rev. Sci. Instrum. 82, 025104 (2011).
Zhou, Z. H. & Uher, C. Apparatus for Seebeck coefficient and electrical resistivity measurements of bulk thermoelectric materials at high temperature. Rev. Sci. Instrum. 76, 023901 (2005).
Pei, Y., LaLonde, A. D., Wang, H. & Snyder, G. J. Low effective mass leading to high thermoelectric performance. Energ. Environ. Sci. 5, 7963–7969 (2012).
Blachnik, R. & Igel, R. Thermodynamic properties of IV-VI compounds lead chalcogenides. Z. Naturforsch. B 29, 625–629 (1974).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant Numbers 51422208, 11474219, 51401147 and 11374332), the National Recruitment Program of Global Youth Experts (1000 Plan), the fundamental research funds for the central universities, the Bayer-Tongji Eco-Construction & Material Academy (TB20140001) and the Solid-State Solar-Thermal Energy Conversion Center (S3TEC), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award number DE-SC0001299.
Author information
Authors and Affiliations
Contributions
Y.P. designed this work. Z.C., W.L., S.L. and J.S. synthesized the samples and carried out the transport property measurements. Y.C. and B.G. performed the (scanning) TEM observations. Z.C., Y.P., B.G., R.H. and G.J.S. analysed the transport properties, the microstructures and the linkage between. Z.C., Y.P., R.H. and G.J.S. discussed the formation mechanism of the dense dislocations via the vacancy engineering approach. All authors wrote and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Tables, Supplementary Discussion, Supplementary References. (PDF 808 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, Z., Ge, B., Li, W. et al. Vacancy-induced dislocations within grains for high-performance PbSe thermoelectrics. Nat Commun 8, 13828 (2017). https://doi.org/10.1038/ncomms13828
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13828
This article is cited by
-
Vacancies tailoring lattice anharmonicity of Zintl-type thermoelectrics
Nature Communications (2024)
-
Influence of point defects and multiscale pores on the different phonon transport regimes
Communications Materials (2023)
-
Phonon engineering significantly reducing thermal conductivity of thermoelectric materials: a review
Rare Metals (2023)
-
Lattice modulation and electronic band optimization in Q-doped SnTe-GeTe alloys (Q = Bi, Sb, and Ag)
Science China Materials (2023)
-
Evolution of defect structures leading to high ZT in GeTe-based thermoelectric materials
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.