Abstract
It is well known that the topological phenomena with fractional excitations, the fractional quantum Hall effect, will emerge when electrons move in Landau levels. Here we show the theoretical discovery of the fractional quantum Hall effect in the absence of Landau levels in an interacting fermion model. The non-interacting part of our Hamiltonian is the recently proposed topologically non-trivial flat-band model on a checkerboard lattice. In the presence of nearest-neighbouring repulsion, we find that at 1/3 filling, the Fermi-liquid state is unstable towards the fractional quantum Hall effect. At 1/5 filling, however, a next-nearest-neighbouring repulsion is needed for the occurrence of the 1/5 fractional quantum Hall effect when nearest-neighbouring repulsion is not too strong. We demonstrate the characteristic features of these novel states and determine the corresponding phase diagram.
Similar content being viewed by others
Introduction
As one of the most significant discoveries in modern condensed matter physics, fractional quantum Hall effect (FQHE)1 has attracted intense theoretical and experimental studies in the past three decades. The wavefunctions proposed by Laughlin2,3,4 first explained FQHE by introducing fractionally charged quasi-particles. Later, the ideas of flux attachment and the composite Fermi-liquid theory5 have provided a rather simple but deep understanding of the nature of the FQHE. Among many of its interesting and unique properties, two of the most striking features of FQHE are the following: fractionalization, where quasi-particle excitations carry fractional quantum numbers and even fractional statistics of the constituent particles, and topological degeneracy, where the number of degenerate ground states responds non-trivially to the changing of the topology of the underlying manifold. These two phenomena are the central ideas of the topological ordering6. In addition, on the potential application side, they are also the essential components in the studies of topological quantum computation7.
Since 1988, great efforts have been made to study quantum Hall effects in lattice models without Landau levels. The first such example is the theoretical model proposed by Haldane8, where it was demonstrated that in a half-filled honeycomb lattice, an integer quantum Hall state can be stabilized upon the introduction of imaginary hoppings. This study was brought to the forefront again recently owing to a major breakthrough in which a brand new class of topological states of matter, known as the time-reversal invariant Z2 topological insulators, was discovered (see refs 9,10 and references therein). From the topological point of view, both Haldane's model and Z2 topological insulators can be considered as generalizations of the integer quantum Hall effect. Unlike the FQHE, they do not support fractional excitations, and the ground states here have no topological degeneracy.
For fractional states, fractional Z2 topological insulators are found to be theoretically possible11. However, it is unclear how to realize such states with lattice models. This difficulty originates from the strong coupling nature of the fractionalized states. In contrast to the integer quantum Hall effect and the Z2 topological insulators, where all their essential topological properties can be understood within a non-interacting picture, the interaction effects are expected to have a vital role in stabilizing a fractionalized topological state. In fact, without interactions, a fractional quantum Hall system will become a Fermi liquid due to the fractional filling factor.
Most recently, a series of models with topologically non-trivial nearly flat-band models have been proposed13,14,15. These lattice models have topologically non-trivial bands (different from early proposal16), similar to Haldane's model and Z2 topological insulators, and their bandwidth can be tuned to be much smaller than the band gap, resulting in a nearly–flat-band structure. In particular, based on the mechanism of quadratic band touching13,14, a large class of flat-band models have been explicitly obtained with the ratio of the band gap to the bandwidth reaching the high value of 20–50. Owing to the strong analogy between these nearly flat bands and the Landau levels, it was conjectured that in these models, FQHE (or fractional topological insulators) can be stabilized in the presence of repulsive interactions. However, the conjecture is challenged by competing orders, for example, the charge-density wave, and thus the fate of these systems are unclear. More importantly, the flux attachment picture5 may also break down, and it is very interesting to examine the nature of the corresponding emergent fractionalized quantum state, if it can be realized in such a model without Landau levels.
Here we report the discovery of FQHE at filling factor 1/3 and 1/5 in models with topologically non-trivial nearly flat bands14, based on exact calculations of finite-size systems. The existence of the FQHE are confirmed by using two independent methods, both of which are well established and have been widely adopted in the study of the traditional FQHE. We have studied both the characteristic low-energy spectrum and the topologically invariant Chern numbers17,18,19,20,21,22 of the low-energy states. The first method directly detects the topological degeneracy and the other is related to the phenomenon of fractionalization.
Results
Phase diagram
We consider the following Hamiltonian on a checkerboard lattice:

where H0 describe the short-range hoppings in the two-band checkerboard-lattice model defined in ref. 14, ni is the on-site fermion particle number operator. The nearest-neighbouring (NN) and next-nearest-neighbouring (NNN) bonds are represented by 〈i, j〉 and 〈〈i, j〉〉, respectively.
The effect of the NN (U) and NNN (V) interactions are summarized in the phase diagrams Figure 1a and b. At filling factor 1/3, the FQHE emerges by turning on a relatively small U. Interestingly, the FQHE phase remains robust at the large U limit, where particles avoid each other at NN sites and can only be destroyed by an intermediate V. At filling factor 1/5, the FQHE occurs in most region of the parameter space as long as the NNN repulsion V exceeds a critical value Vc, whose value drops to zero for larger U. The observed FQHE states are characterized by nearly p-fold (P=3 and 5 for filling factors 1/3 and 1/5 respectively) degenerating ground states with the momentum quantum numbers of these states related to each other by a unit momentum translation of each particle as an emergent symmetry, a finite spectrum gap separating the ground-state manifold (GSM) from the low-energy excited states with a magnitude dependent on the interaction strengths U and V, and the GSM carrying a unit total Chern number as a topological invariant protected by the spectrum gap, resulting in a fractional effect of 1/p quantum for each energy level in the GSM. We identify the quantum phase transition on the basis of the spectrum-gap collapsing. As shown in Figure 1, the Fermi-liquid phase with gapless excitations is found for relatively strong NNN interaction at 1/3 filling and for relatively weak NNN interaction at 1/5 filling. This observation is consistent with Haldane's pseudopotential theory3, and previous studies on ordinary FQHE, where a FQHE state is found to be sensitive to interactions and other microscopic details (for example, the thickness of the two-dimensional electron gas23).
(a) At 1/3 and (b) 1/5 filling number in the parameter space of the nearest-neighbour (U) and next- nearest-neighbour (V) interaction strengths for different system sizes. In both (a) and (b), two phases are observed, the Fermi-liquid phase (labelled as FL) and the fractional-quantum-Hall phase (labelled as FQH). The dashed lines in both figures mark the phase boundaries at different system size. The thick grey lines mark the averaged phase boundary over different systems sizes and the error bar mark the averaged deviations.
Low-energy spectrum and topological degeneracy
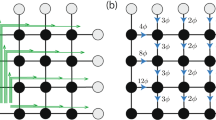
Consider a system of Nx×Ny unit cells (Ns=2NxNy sites) with twisted boundary conditions:  , where T(Nj) is the translation operator with j=x and y representing the x and y directions, respectively. Note that the filling factor is defined as the ratio of the number of particles (Np) over the number of unit cells (Nx×Ny). In the absence of impurities, the total momentum of the many-body state is a conserved quantity, and thus the Hamiltonian can be diagonalized in each momentum sector for systems with Ns=24 to 60 sites (depending on filling factors). We consider periodic boundary conditions (θ1=θ2=0) first. Figure 2a illustrates the evolution of the low-energy spectrum with changing U for V=0 and Ns=2×4×6 (Nx=4 and Ny=6) at particle-filling factor ν=1/3. Here the NN hopping strength (t)is set to unity. We denote the momentum of a state q=(2πkx/Nx, 2πky/Ny) by using two integers (kx, ky) as shown in Figure 2. For vanishing NN interaction U=0.0 (the bottom panel of Fig. 2a), the ground state has k=(0,0) whereas no particular structure is observed in other k sectors. For a weak interaction U=0.2, we find an interesting change in the spectrum. Here the energies of two states with momenta (kx, ky)=(0, 2) and (0, 4) have been lowered substantially. For a stronger interaction, the energies of the three states with kx=0 and ky=0, 2, 4 form a nearly degenerate GSM6 at U>0.3. In the mean time, a sizable spectrum gap opens up, separating the GSM from the other excited states as shown in the top panel of Figure 2a for U=1.0. The obtained threefold ground state near degeneracy and a robust spectrum gap are the characteristic features of the 1/3 FQHE phase, which emerge with the onset of the NN repulsion U. By increasing the NNN repulsion V to a certain critical value Vc, we have observed the collapse of the spectrum gap, which determines the boundary of the 1/3 FQHE phase, as shown in Figure 1a. Further evidence of the FQHE based on topological quantization will be presented later in Figure 3.
, where T(Nj) is the translation operator with j=x and y representing the x and y directions, respectively. Note that the filling factor is defined as the ratio of the number of particles (Np) over the number of unit cells (Nx×Ny). In the absence of impurities, the total momentum of the many-body state is a conserved quantity, and thus the Hamiltonian can be diagonalized in each momentum sector for systems with Ns=24 to 60 sites (depending on filling factors). We consider periodic boundary conditions (θ1=θ2=0) first. Figure 2a illustrates the evolution of the low-energy spectrum with changing U for V=0 and Ns=2×4×6 (Nx=4 and Ny=6) at particle-filling factor ν=1/3. Here the NN hopping strength (t)is set to unity. We denote the momentum of a state q=(2πkx/Nx, 2πky/Ny) by using two integers (kx, ky) as shown in Figure 2. For vanishing NN interaction U=0.0 (the bottom panel of Fig. 2a), the ground state has k=(0,0) whereas no particular structure is observed in other k sectors. For a weak interaction U=0.2, we find an interesting change in the spectrum. Here the energies of two states with momenta (kx, ky)=(0, 2) and (0, 4) have been lowered substantially. For a stronger interaction, the energies of the three states with kx=0 and ky=0, 2, 4 form a nearly degenerate GSM6 at U>0.3. In the mean time, a sizable spectrum gap opens up, separating the GSM from the other excited states as shown in the top panel of Figure 2a for U=1.0. The obtained threefold ground state near degeneracy and a robust spectrum gap are the characteristic features of the 1/3 FQHE phase, which emerge with the onset of the NN repulsion U. By increasing the NNN repulsion V to a certain critical value Vc, we have observed the collapse of the spectrum gap, which determines the boundary of the 1/3 FQHE phase, as shown in Figure 1a. Further evidence of the FQHE based on topological quantization will be presented later in Figure 3.
(a) For 1/3 filling with V=0, U=0 to 1.0 (U increases from bottom panel up) and Ns=2×4×6 sites; (b) For 1/5 filling with U=1 and V=0 to V=1 and Ns=2×6×5. We have shifted the ground-state energy to zero for comparison. Nearly degenerate GSM and the large gap between GSM and excited states, observed in (a) at large U and (b) at large V indicate the formation of the fractional quantum Hall states.
The total Berry phase as a function of Nmesh/Ntot, which measures the ratio of the area in the boundary phase space for (a) 1/3 filling at Ns=30; (b) 1/5 filling at Ns=40. In fractional quantum Hall phase, a linear curve is observed whose slope is determined by filling factor, as expected. In the Fermi-liquid phase, we observed large fluctuation and non-universal behaviours, indicating the absence of the topological quantization.
In Figure 2b, we present the formation of the 1/5 FQHE by showing the energy spectrum at particle filling factor ν=1/5 with increasing V at U=1 for a system with Ns=2×6×5 (Nx=6 and Ny=5). From the bottom panel to the top panel, five states with momenta (2, ky) (ky=0, ..., 4) form the nearly degenerate GSM with the increase of V, whereas a large spectrum gap is formed at V=1.0. The same feature of the energy spectrum is observed for the whole regime of the 1/5 FQHE above the critical Vc line shown in the phase diagram Figure 1b while Vc drops to near zero for larger U.
We note that there is a small energy difference between the states in the GSM in both filling factors. This is a finite-size effect21,24 as each of these states has to fit into the lattice structure. The finite-size effect is substantially smaller for 1/5 FQHE comparing with the 1/3 case due to the lower particle density. Interestingly, for all cases that we have checked for different system sizes (Ns=24–60), the members of the GSM are always related to each other through a momentum space translation as an emerging symmetry of the system. Namely, if (k1, k2) is the momentum quantum number for a state in the GSM, then another state in the GSM can be found in the momentum sector (k1+Ne, k2+Ne) modulo (Nx, Ny). This relation of the quantum numbers of the GSM demonstrates the correlation between the real space and momentum space in a manner precisely resembling the FQHE in a uniform magnetic field. For the case where the particle number Np is integer multiples of both Nx and Ny (for example, Ns=2×3×6 and Ns=2×5×5 at 1/3 and 1/5 fillings, respectively), all the states of the GSM are indeed observed to fall into the same momentum sector as expected.
Fractional quantization of topological number
To further establish the existence of the FQHE here, we study the topological property of the GSM by numerically inserting flux into the system using generalized boundary phases. As first realized by Thouless and co-workers17,18,19, a topological quantity of the wavefunction, known as the first Chern number, distinguishes the quantum Hall states from other topological trivial states. In particular, one can detect the fractionalization phenomenon in FQHE by examining the Chern number of the GSM through inserting flux into the system20,21,22. The results of this calculation are shown in Figure 3. With details presented in the Methods part, the total Berry phase as a function of Nmesh/Ntot should be a linear function with slope 2π/3 and 2π/5 for the FQHE with filling factors 1/3 and 1/5, respectively. This agrees very well with the observation shown in Figure 3. On the other hand, for the Fermi-liquid phase, strong fluctuations and non-universal behaviours of the Berry phase are found, suggesting the absence of topological quantization.
FQHE at strong coupling limit
We further examine the phase at strong coupling limit for lower filling factor ν=1/5, where 1/5 FQHE demonstrates less sensitivity to either large U or V. We show the lowest 20 eigenvalues as a function of U in Figure 4, while we always set V=U for simplicity. At small U, we see the flatness of the spectrum in consistent with a Fermi-liquid phase with small energy dispersion. As we increase U>Uc=0.35, all the lowest five states remain nearly degenerate, whereas higher energy states jump a step up making a robust gap between them and the GSM. In fact, the 1/5 FQHE persists into infinite U and V limit as we have checked by projecting out the configurations with double or more occupancy between a site and all its NN and NNN sites. Physically, this can be understood as particles at lower filling having enough phase space within the lower Hubbard band, and thus the FQHE remains intact. It would be very interesting to establish a variational state for the FQHE on the flatband model, which will be investigated in the future.
Discussion
Finally, it is important to emphasize that the fractional topological phases we found are very stable and the same effect survives even if the hopping strengths are tuned by an amount of ∼10%. On the experimental side, it is known that checker-board lattice we studied can be found in condensed matter systems (for example, the thin films of LiV2O4, MgTi2O4, Cd2Re2O7, etc.), and the imaginary hopping terms we required can be induced by spin–orbit coupling and/or spontaneous symmetry breaking25. In addition, this lattice model also has the potential to be realized in optical lattice system using ultra-cold atomic gases, in which the tuning of the parameters are much easier compared with condensed matter systems. On the basis of these observations, we conclude that there is no fundamental challenge preventing the experimental realization of these novel fractional topological states, but further investigation is still needed to discover the best experimental candidates.
Methods
Calculation of Chern number for many-body state
The Chern number of a many-body state can be obtained as:

where the closed path integral is along the boundary of a unit cell 0≤θ≤2π with j=x and y, respectively. The Chern number C is also the Berry phase (in units of 2π) accumulated for such a state when the boundary phase evolves along the closed path. Equation (2) can also be reformulated as an area integral over the unit cell C=(1/2π)∫dθ1dθ2F, where F(θ1, θ2) is the Berry curvature. To determine the Chern number accurately20,22, we divide the boundary-phase unit cell into about Ntot=200 to 900 meshe. The curvature F(θ1, θ2) is then given by the Berry phase of each mesh divided by the area of the mesh. The Chern number is obtained by summing up the Berry phases of all the meshes.
Chern number quantization in FQHE
We find that the curvature is in general a very smooth function of θj inside FQHE regime. For an example, the ground-state total Berry phase sums up to 0.325×2π, slightly away from the 1/3 quantization for a system with Ns=30, U=1 and V=0 at 1/3 filling. Physically, as we start from one state with momentum (kx, ky) in the GSM, it evolves to another state with a different momentum kx→kx+Ne (ky→ky+Ne), when the boundary phase along x (y) direction is increased from 0 to 2π. Thus, with the insertion of a flux, states evolve to each other within the GSM. We observe that only the total Berry phase of the GSM is precisely quantized to 2π and the total Chern number C=1 for all different choices of parameters inside either the 1/3 or 1/5 FQHE regime of Figure 1. When states in the GSM have the same momentum, the Chern number of each state is an integer due to non-crossing condition of the energy levels with the same quantum number, while the total Chern number remains the same21,22.
Fluctuating Chern number in other phases
As we move across the phase boundary from the FQHE state into the Fermi-liquid phase, there is no well-defined nearly degenerate GSM or spectrum gap, and the Berry curvature in general shows an order of magnitude bigger fluctuations. The obtained total Chern integer varies with system parameters (for example, U and V). To illustrate this feature, we start from the lowest-energy eigenstate and continuously increase the boundary phases for three periods, which allows the first state to evolve into other states and eventually return back to itself. In Figure 3, we plot the accumulated total Berry phase as a function of the ratio of the total meshes included Nmesh over the total number of meshes Ntot in each period. For the system in the 1/3 FQHE phase with Ns=30, U=1 and V=0, the total Berry phase follows a straight line in all three periods, well fitted by  , indicating a nearly perfect linear law of the Berry phase to the area in the phase space with a deviation around 10%. In the Fermi-liquid phase with Ns=30, U=1 and V=2, we see step-like jumps of the total Berry phase, with a magnitude in the order of 2π, in sharp contrast to the linear law in the FQHE phase. The total Chern number for the Fermi-liquid state sums up to three, indicating the decorrelation between three states. Different integer values for the Chern number are found in this region (including negative ones) with changing system parameters, demonstrating a measurable fluctuating Hall conductance if particles are charged. For 1/5 FQHE state, by following up the Berry phase of five periods for the ground state as shown in Figure 3b, we observe the same linear law with a slope of 2π/5 and the total Chern number is quantized to one. Interestingly, a negative integer Chern number for Fermi-liquid state for the parameters U=1 and V=0.1 is observed confirming the non-universal nature of the topological number for such a gapless system. We conjecture that the Fermi-liquid phase may be unstable towards Anderson localization, especially at lower filling factors, similarly to the conventional FQHE systems21.
, indicating a nearly perfect linear law of the Berry phase to the area in the phase space with a deviation around 10%. In the Fermi-liquid phase with Ns=30, U=1 and V=2, we see step-like jumps of the total Berry phase, with a magnitude in the order of 2π, in sharp contrast to the linear law in the FQHE phase. The total Chern number for the Fermi-liquid state sums up to three, indicating the decorrelation between three states. Different integer values for the Chern number are found in this region (including negative ones) with changing system parameters, demonstrating a measurable fluctuating Hall conductance if particles are charged. For 1/5 FQHE state, by following up the Berry phase of five periods for the ground state as shown in Figure 3b, we observe the same linear law with a slope of 2π/5 and the total Chern number is quantized to one. Interestingly, a negative integer Chern number for Fermi-liquid state for the parameters U=1 and V=0.1 is observed confirming the non-universal nature of the topological number for such a gapless system. We conjecture that the Fermi-liquid phase may be unstable towards Anderson localization, especially at lower filling factors, similarly to the conventional FQHE systems21.
Additional information
How to cite this article: Sheng, D.N. et al. Fractional quantum Hall effect in the absence of Landau levels. Nat. Commun. 2:389 doi: 10.1038/ncomms1380 (2011).
References
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
Haldane, F. D. M. Fractional quantization of the Hall effect: a hierarchy of incompressible quantum fluid states. Phys. Rev. Lett. 51, 605–608 (1983).
Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1984).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Wen, X. G. & Niu, Q. Ground-state degeneracy of the fractional quantum Hall states in the presence of a random potential and on high-genus riemann surfaces. Phys. Rev. B 41, 9377–9396 (1990).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Haldane, F. D. M. Model for a quantum Hall effect without landau levels: condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.- L. & Zhang, S.- C. Topological insulators and superconductors. Rev. Mod. Phys. (in the press). Preprint at//arxiv.org/abs/1008.2026.
Levin, M. & Stern, A. Fractional topological insulators. Phys. Rev. Lett. 103, 196803 (2009).
Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Tang, E., Mei, J.- W. & Wen, X.- G. High temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).
Sun, K., Gu, Z., Katsura, H. & Sarma, S. D. Nearly-flat bands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Wu, C. et al. Flat bands and Wigner crystalization in the honeycomb optical lattice. Phys. Rev. Lett. 99, 70401 (2007).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Niu, Q., Thouless, D. J. & Wu, Y.- S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).
Arovas, D. P., Bhatt, R. N., Haldane, F. D. M., Littlewood, P. B. & Rammal, R. Localization, wave-function topology, and the integer quantized Hall effect. Phys. Rev. Lett. 60, 619–622 (1988).
Huo, Y. & Bhatt, R. N. Current carrying states in the lowest landau level. Phys. Rev. Lett. 68, 1375–1378 (1992).
Sheng, D. N. et al. Disorder-driven collapse of the mobility gap and transition to an insulator in the fractional quantum Hall effect. Phys. Rev. Lett. 90, 256802 (2003).
Wan, X. et al. Mobility gap in fractional quantum Hall liquids: effects of disorder and layer thickness. Phys. Rev. B 72, 075325 (2005).
Peterson, M. R., Jolicoeur, T. & DasSarma, S. Orbital landau level dependence of the fractional quantum Hall effect in quasi-two-dimensional electron layers: finite-thickness effects. Phys. Rev. B 78, 155308 (2008).
Tao, R. & Haldane, F. D. M. Impurity effect, degeneracy, and topological invariant in the quantum Hall effect. Phys. Rev. B 33, 3844–3850 (1986).
Sun, K., Yao, H., Fradkin, E. & Kivelson, S. A. Topological insulators and nematic phases from spontaneous symmetry breaking in 2D fermi systems with a quadratic band crossing. Phys. Rev. Lett. 103, 046811 (2009).
Acknowledgements
This work is supported by DOE Office of Basic Energy Sciences under grant DE-FG02-06ER46305 (DNS), the NSF grant DMR-0958596 (for instrument), the State Key Program for Basic Researches of China under Grant Nos. 2009CB929504 and 2007CB925104, and the NSFC 10874066 and 11074110 (LS). Z.C.G. is supported in part by the NSF Grant No. NSFPHY05-51164. K.S. acknowledges the support from JQI-NSF-PFC, AFOSR-MURI, ARO-DARPA-OLE, and ARO-MURI.
Author information
Authors and Affiliations
Contributions
All authors planned and designed theoretical and numerical studies. D.N.S. and L.S. obtained numerical results, whereas Z.-C.G. and K.S. worked more on theoretical analysis of results. All contributed in completing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Sheng, D., Gu, ZC., Sun, K. et al. Fractional quantum Hall effect in the absence of Landau levels. Nat Commun 2, 389 (2011). https://doi.org/10.1038/ncomms1380
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1380
This article is cited by
-
Polarization-driven band topology evolution in twisted MoTe2 and WSe2
Nature Communications (2024)
-
Fractional quantum anomalous Hall effect in multilayer graphene
Nature (2024)
-
Dual quantum spin Hall insulator by density-tuned correlations in TaIrTe4
Nature (2024)
-
Thermodynamic evidence of fractional Chern insulator in moiré MoTe2
Nature (2023)
-
1/4 is the new 1/2 when topology is intertwined with Mottness
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.