Abstract
Pair production can be triggered by high-intensity lasers via the Breit–Wheeler process. However, the straightforward laser–laser colliding for copious numbers of pair creation requires light intensities several orders of magnitude higher than possible with the ongoing laser facilities. Despite the numerous proposed approaches, creating high-energy-density pair plasmas in laboratories is still challenging. Here we present an all-optical scheme for overdense pair production by two counter-propagating lasers irradiating near-critical-density plasmas at only ∼1022 W cm−2. In this scheme, bright γ-rays are generated by radiation-trapped electrons oscillating in the laser fields. The dense γ-photons then collide with the focused counter-propagating lasers to initiate the multi-photon Breit–Wheeler process. Particle-in-cell simulations indicate that one may generate a high-yield (1.05 × 1011) overdense (4 × 1022 cm−3) GeV positron beam using 10 PW scale lasers. Such a bright pair source has many practical applications and could be basis for future compact high-luminosity electron–positron colliders.
Similar content being viewed by others
Introduction
Pair production is one of the fundamental quantum electrodynamics (QED) effects, which is potentially interesting for a variety of applications1,2,3, such as fundamental nuclear and particle physics, laboratory astrophysics and plasma physics, radiography for material science and medical applications. For example, GeV and even TeV positron beams are required for studying highly energetic astrophysical phenomena in laboratories and realizing electron–positron (e−e+) collider for high-energy particle physics3,4. Schwinger has predicted the critical electric field5 Es≈1.32 × 1018 V m−1 for spontaneous creation of pairs out of vacuum by a laser beam. This field corresponds to a light intensity roughly 1029 W cm−2, which is seven orders of magnitude higher than attainable in current laboratories4. It has also predicted that pairs can be produced via the Trident and Bethe–Heitler (BH) processes6,7 from lasers interaction with high-Z targets. So far, the major way of producing positrons with lasers in experiments relies upon the BH process, which is based on the decay of bremsstrahlung γ-rays from electrons in high-Z targets. It is shown that energetic positrons could be obtained by direct laser–solid interactions8,9,10 or by laser-driven electrons colliding with solid targets11,12,13,14. However, the positrons obtained have a low density of ∼1016−17 cm−3 with a laser energy conversion efficiency to positrons around ∼0.02% only15,16. There is a need to significantly enhance the positron yield, density and energy, as well as the laser energy conversion for the aforementioned applications.
Under extremely high laser intensities, the laser–matter interaction enters the near-QED regime and the following two critical processes are involved: (1) high-energy photons emission by relativistic electrons quivering in ultraintense laser fields17 (e−+nγlaser→γphoton+e−, where γlaser represents a laser photon); and (2) pairs creation by real photon–photon annihilation, that is, the multi-photon Breit–Wheeler (BW) process18 (γphoton+mγlaser→e−+e+). The first process is essentially the nonlinear Compton scattering of laser photons by relativistic electrons, while the second generally occurs under extreme laser conditions by photons colliding with the electromagnetic waves, for example, the laser fields. The first such an experiment was carried out by using the conventional paradigm at SLAC19. It is demonstrated that a 46 GeV linac-accelerated electron beam colliding with a 1018 W cm−2 laser is able to produce a few pairs (106±14), which shows a relatively weak QED effect.
State-of-art laser systems20 are capable of delivering a laser pulse with intensity up to 2 × 1022 W cm−2. The next-generation multi-PW lasers (for example, the XCELS and ELI facilities (the next generation of laser facilities, such as Exawatt Center for Extreme Light Studies (XCELS) and Extreme Light Infrastructure (ELI). Available at http://www.xcels.iapras.ru and http://www.eli-np.ro)) are expected to reach ∼1024 W cm−2 and beyond. This opens the door for studying light–matter interactions as well as QED effects in unexplored domains1,4,21,22. Diverse schemes have been proposed for energetic e−e+ pairs production via the BW process using ultrarelativistic lasers23,24,25,26,27,28,29,30,31. It is shown that using multiple colliding lasers25 for pair cascades in vacuum can reduce the required laser intensity down to ∼1026 W cm−2. This intensity is significantly smaller than the Schwinger value. An alternative scheme26,27 relies on the energetic electrons from a laser-driven gas jet or thin solid target by using either two counter-propagating lasers or a single laser. The positron beam produced is very bright and energetic. However, the required laser intensity is as high as ∼1024 W cm−2, still two orders of magnitude higher than that of the available lasers. Another challenge is the target transparence27 to the incident super intense lasers, which leads to the low efficiency of the BW process. By comparison, the laser-hohlraum scheme28 invokes the single-photon BW process with a much lower laser intensity but achieves a positron yield at the 105 level only. More recently, it is proposed to combine the laser wakefield acceleration (LWFA32) with the positron generation by colliding the accelerated electron beam with a counter-propagating laser pulse29,30. The resulting positron yield can be up to ∼109 (predicted by Blackburn et al.29), with a maximum density <1020 cm−3 (simulations by Lobet et al.30). This configuration allows for a compact linac, while the extraction and application of the produced positrons depend on additional laser and beam facilities, which is of significant importance for particle physics experiments, for example, a linear e−e+ collider. To date, an all-optical collider based on laser–plasma interactions for high-energy physics has yet to be realized.
For prolific pair creation via the BW process, high-energy and density γ photons are essential. The latter can be obtained by nonlinear Compton scattering33,34, bremsstrahlung radiation of electrons in a solid target28 or synchrotron radiation of electrons in a laser beam reflected from a thick foil27. Instead of using a solid or gas plasmas, here we present an efficient non-conventional scheme to generate extremely dense γ photons and copious numbers of e−e+ pairs by focusing two counter-propagating lasers at currently affordable laser intensity ∼1022 W cm−2 onto two near-critical-density (NCD) plasmas. The proposed scheme requires two steps. First, bright γ photons are produced by radiation-reaction trapped electrons in both NCD plasmas; second, the dense γ photons emitted from one NCD plasma collide with the focused counter-propagating laser in the other to initiate the multiple-photon BW process. We have carried out full three-dimensional (3D) particle-in-cell (PIC) simulations with collective QED effects incorporated. We demonstrate that the positron yield obtained is up to 1.05 × 1011, which is 106-fold more than that obtained from the laser-hohlraum scheme28 and is two orders of magnitude larger than those by using the LWFA-accelerated electrons29,30. The peak positron density is as high as 4 × 1022 cm−3 with a cutoff energy of several GeV. This overdense e−e+ pair plasma source may find many practical applications and could serve as a compact linear collider with high luminosity.
Results
Overview of the scheme
When an electron absorbs multiple laser photons in the nonlinear Compton scattering process, it can radiate a high-energy photon. The radiated photons propagate through the laser fields and interact with the laser waves to produce e−e+ pairs via the multi-photon BW process. The probabilities of γ-photon emission and positron creation are determined by two relativistic and gauge invariant parameters35 (see Methods):  and
and  , where E⊥ is the local electric field perpendicular to the electron velocity β,
, where E⊥ is the local electric field perpendicular to the electron velocity β,  is the Schwinger electric field, and ħk(ħω) is the emitted photon momentum (energy). When a laser propagates parallel with an electron beam, it leads to η≅0, which is undesirable for high-energy γ photon emission and positron production; If the laser counter-propagates with the energetic electron beam, there is η≅1, which has been extensively investigated in past years19,26,29,30. Here we propose to use two lasers and two electron beams in an all-optical configuration realized simply by a pair of counter-propagating laser pulses in NCD plasmas. This enables one to have two sets of laser-electron beam colliding with η1≅1 and η2≅1 simultaneously (equivalent to a real η larger than 1), which could significantly enhance the γ photon emission and the pair production via the BW process.
is the Schwinger electric field, and ħk(ħω) is the emitted photon momentum (energy). When a laser propagates parallel with an electron beam, it leads to η≅0, which is undesirable for high-energy γ photon emission and positron production; If the laser counter-propagates with the energetic electron beam, there is η≅1, which has been extensively investigated in past years19,26,29,30. Here we propose to use two lasers and two electron beams in an all-optical configuration realized simply by a pair of counter-propagating laser pulses in NCD plasmas. This enables one to have two sets of laser-electron beam colliding with η1≅1 and η2≅1 simultaneously (equivalent to a real η larger than 1), which could significantly enhance the γ photon emission and the pair production via the BW process.
Radiation-reaction effect and radiation trapping of electrons
In extreme laser fields, the radiation damping force36,37,38 exerting on electrons could be expressed as  , where e is the charge unit, me is the electron mass, and β is the normalized electron velocity by the light speed in vacuum c, B and E are the magnetic and electric fields. Here we keep only the main term proportional to
, where e is the charge unit, me is the electron mass, and β is the normalized electron velocity by the light speed in vacuum c, B and E are the magnetic and electric fields. Here we keep only the main term proportional to  in the strong relativistic case. It is shown that the damping force fd becomes significant enough to compensate for the Lorenz force fL=q(E+β × B), under laser intensity >1022 W cm−2, and it has to be taken into account in modelling laser–plasma interaction. As a result, the electron motion is profoundly altered. Instead of being scattered off transversely, electrons are trapped inside the laser field and perform extreme oscillations in the laser polarization direction. This is the radiation trapping effect39,40, which could lead to efficient synchrotron-like γ-ray emission. However, the simple test electron model39 suggests a threshold laser amplitude required to enter this regime, that is,
in the strong relativistic case. It is shown that the damping force fd becomes significant enough to compensate for the Lorenz force fL=q(E+β × B), under laser intensity >1022 W cm−2, and it has to be taken into account in modelling laser–plasma interaction. As a result, the electron motion is profoundly altered. Instead of being scattered off transversely, electrons are trapped inside the laser field and perform extreme oscillations in the laser polarization direction. This is the radiation trapping effect39,40, which could lead to efficient synchrotron-like γ-ray emission. However, the simple test electron model39 suggests a threshold laser amplitude required to enter this regime, that is,

where r0 is the laser focal spot radius normalized by the wavelength λ0 and re=e2/mec2 is the classical electron radius. It is shown that the threshold is dependent on the laser focal size. In order to excite the multi-photon BW process with synchrotron-like γ rays, the threshold laser amplitude should meet  , which is currently inaccessible. Therefore, in our scheme we first employ two cone-targets to focus the lasers. Instead of using a gas plasma or solid, we choose NCD plasmas filled inside the cones to increase the laser energy absorption and conversion so that more background electrons are provided and accelerated to enhance the γ-rays emission and positrons production.
, which is currently inaccessible. Therefore, in our scheme we first employ two cone-targets to focus the lasers. Instead of using a gas plasma or solid, we choose NCD plasmas filled inside the cones to increase the laser energy absorption and conversion so that more background electrons are provided and accelerated to enhance the γ-rays emission and positrons production.
The scheme takes advantage of the radiation damping and trapping effect in the near-QED regime39,40. Figure 1 presents the schematic drawing of our basic configuration, where two counter-propagating laser pulses interact with the NCD plasmas inside a double-cone-targets. In this scheme, high-energy-density γ photons are emitted by the trapped energetic electrons in the NCD plasmas at the laser axis, which are accelerated by the intense laser fields. When the γ-photons collide with the focused counter-propagating laser waves from another direction, e−e+ pairs are efficiently produced via the multi-photon BW process. A positron beam produced in one NCD plasma can interact with the electron beam accelerated in the other NCD plasma, behaving like a microscopic e−e+ collider.
Two counter-propagating ultraintense laser pulses are focused from two directions onto the near-critical-density plasmas filled inside two cones (purple). The quivering electrons in the ultraintense laser fields experience large radiation-reaction forces by emitting photons so that a large number of electrons are trapped in the laser fields. These trapped electrons perform extreme oscillations in the transverse direction and emit bright γ rays (red- and blue–yellow) around the laser axis. Finally, copious numbers of e−e+ pairs are created via the multi-photon Breit–Wheeler process.
Here we demonstrate the feasibility of the scheme by using full 3D PIC code EPOCH with QED effects incorporated (see Methods). To benchmark the simulation results, we also perform a series of reference simulations using the QED-PIC code Virtual Laser–Plasma Lab. (VLPL37,41), which can reproduce the main results presented below.
3D PIC simulation results
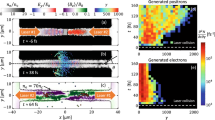
Figure 2 illustrates the simulation results at t=36T0 (T0≈3.3 fs is the laser cycle), when both lasers overlap in the double-cone junction. It is shown that the laser intensity can be greatly boosted due to the coupling effect of nonlinear plasma effects and tightly focusing of the laser pulse in the cone42,43,44. The strengthened laser ponderomotive force accelerates the electrons both radially and forward with considerable radiation emitted. When the radiation damping effect is taken into account, electrons undergo a strong backward damping force. This force increases with the time and becomes comparable to the laser ponderomotive force. As a consequence, a large number of electrons are kicked back to the laser fields radially and accumulate near the laser axis, forming a dense electron bunch as shown in Fig. 2a. These electrons are ultrarelativistic with a cutoff energy of ∼5 GeV (Fig. 3a) and are well collimated around the laser axis with a peak density up to 40nc ( is the critical density). Additional simulations without the NCD plasmas and cone, respectively, indicate that the reduction of the laser threshold for the electron trapping is ultimately attributed to the nonlinear effect of the laser in the NCD plasmas-filled cone, which demonstrates the advantages of the cone structure over a plasma channel40. These trapped electrons travel almost along the laser-axis, inducing a strong poloidal self-generated magnetic field40,43. This results in additional pinching effect on the electrons. Therefore, the electron trapping or pinching near the laser axis originates from the radiation damping force and is remarkably enhanced by the magnetic pinching effect.
is the critical density). Additional simulations without the NCD plasmas and cone, respectively, indicate that the reduction of the laser threshold for the electron trapping is ultimately attributed to the nonlinear effect of the laser in the NCD plasmas-filled cone, which demonstrates the advantages of the cone structure over a plasma channel40. These trapped electrons travel almost along the laser-axis, inducing a strong poloidal self-generated magnetic field40,43. This results in additional pinching effect on the electrons. Therefore, the electron trapping or pinching near the laser axis originates from the radiation damping force and is remarkably enhanced by the magnetic pinching effect.
Density distribution of electrons (a), γ photons (b) and positrons (c) at t=36T0. Both lasers enter the simulation box at t=0T0 and arrive at the open mouths of the double-cone-target at t=5T0. Two dense electron bunches are formed around the laser axis in the double-cone due to the radiation trapping effect, with high energy (∼5 GeV) and a high density (∼40 nc).
The trapped electrons co-move with the focused laser in the cone and keep oscillating with an amplitude of ∼2 μm in the laser field for a long time (Fig. 2a). During the process, two oxhorn-like electron bunches close to the cone mouths are also formed, resulting from the strong return currents in the cone. These trapped electrons emit a great deal of γ photons. At t=36T0, the photon density is up to 850nc (Fig. 2b) and the cutoff energy is about several GeV (Fig. 3b). The corresponding average photon energy density is around 1018 J m−3, which is 107 higher than the threshold for high-energy-density physics45. The production of such relativistic γ photons is crucial to studying the plasma dynamics and collective QED effects in laser–matter interactions46,47,48, which has many applications in diverse frontiers1,21,23, especially laboratory astrophysics.
The photon emission is mainly contributed by two processes: (1) the trapped electrons perform oscillations in the laser fields, like betatron oscillations in the bubble regime32,49,50; (2) the trapped high-energy electrons collide head-on with the opposite-propagating lasers, so that energetic photons are emitted by nonlinear Compton backscattering. Here the first process dominates the radiation over the second because the photon spectrum as seen in Fig. 3b is a typical synchrotron-like spectrum, while the scattered photons in the ultrahigh laser field limit via the second process would be only peaked at51 ξ/(1+ξ)Ee,max≈1.5 GeV. Here the parameters are ξ=4Eeħω0/(mec2)2≈0.18, Ee,max≈10GeV at t=34T0, where ħω0≈1.2 eV is the laser photon energy. However, the second process enhances the high-energy γ-photon emission at later times (Supplementary Fig. 1; Supplementary Note 1). On the contrary, the photon emission by positrons created is a small fraction, since these positrons have a much smaller flux, energy, and density as compared with the trapped electrons in the laser fields.
These photons are distributed mainly around the laser axis with a cone angle θγ∼1/γe<1 mrad with respect to the cone axis in both cones. Later, they collide with the focused counter-propagating laser waves from the opposite directions, initiating the multi-photon BW process. Here, the BH process is intrinsically inefficient because of the low-Z NCD plasmas and the thin Al cone thickness8,9,10,11,12,13,14. Therefore, this process can be reasonably ignored in our simulations. Figure 2c presents the positron density distribution at t=36T0. A maximum positron density of ∼4 × 1022 cm−3 can be obtained with energies up to 1.6 GeV (Fig. 3c). This peak density is much higher than that reported in the both BW and BH experiments as well as relevant simulations8,9,10,11,12,13,14,15,16,19,27,28,29,30,31. The total positron yield is as high as 1.05 × 1011, which is more than an order of magnitude larger than that in laser foil interactions27, although our laser intensity is lower by more than an order of magnitude. As compared with the recent LWFA-aided scheme29,30, both the positron yield and density are two orders of magnitude higher.
Figure 3d presents the evolution of the laser energy conversion efficiency to the trapped electrons, γ photons, and positrons left in the simulation box. As the laser energy is soaked up and the electron energy grows, the damping process attenuates the laser wave and the laser energy is transferred to electrons and photons, and finally to positrons. At t=38T0, the positron energy approaches a maximum and then decreases by emitting photons in a similar way to electrons in the laser fields. The laser energy conversion efficiencies to the photons and positrons are peaked at 14.9% and 0.14%, respectively. With the same laser parameters, the efficiency of the positron production in our scheme is much higher than that of the LWFA-aided scheme29,30, making it very competitive as a compact positron source.
Parametric influences and robustness of the scheme
The robustness of the scheme is further demonstrated by using different laser intensities and NCD plasmas, as summarized in Fig. 4. Here the laser duration is changed to 8T0to save time, while other parameters are kept the same except for a0 and ne. As expected, both the photon emission and positrons creation are enhanced with the increase of the laser intensity. In the following, we compare our simulation results with theoretical predictions.
(a) The electron radiation power (red line) and the function g(η) (black dashed line) as a function of the parameter η in our scheme. The red asterisks represent the simulation results. The laser energy conversion efficiency to (b) the γ-photons and (c) positrons with different laser intensities and plasma densities. Here the green dashed line in b shows the fitted results. Note that there exists a laser threshold intensity in (c), ath∼120, for efficient positron production in our configuration. (d) The positron yield as a function of the laser intensity, based on the equation (3) and PIC simulations.
The quantum-corrected instantaneous radiation power by an electron is given by ref. 52, Prad=(4πmec3/3λC)αη2g(η)=PCg(η), where λC is the Compton wavelength, α=e2/ħc=1/137 is the fine-structure constant, PC=(4πmec3/3λC)αη2 is the classical power, and  with F(η, χ) being the quantum-corrected synchrotron spectrum function as given by Erber35. Figure 4a shows the evolution of the radiation power. For comparison, we also give in Fig. 4a the simulation result calculated by collecting all γ photons’ energy and then dividing this by the total number of trapped electrons. The radiation time is estimated to be of order of several laser cycles. We see that our simulation results agree well with the theoretical predictions, considering the fact that we neglect the low energy photons (<1 MeV) in the simulations. The numerical scaling of the laser energy conversion efficiency to the γ photons with different laser intensities and NCD plasmas is shown in Fig. 4b. By increasing the laser intensity, the laser energy conversion to the γ-photons increases at first and then saturates when the laser field amplitude a0>800. This can be attributed to the rapid annihilation of the high-energy γ-photons via the BW process. Note that the γ-photon emission is significantly limited by the number and energy of the trapped electrons.
with F(η, χ) being the quantum-corrected synchrotron spectrum function as given by Erber35. Figure 4a shows the evolution of the radiation power. For comparison, we also give in Fig. 4a the simulation result calculated by collecting all γ photons’ energy and then dividing this by the total number of trapped electrons. The radiation time is estimated to be of order of several laser cycles. We see that our simulation results agree well with the theoretical predictions, considering the fact that we neglect the low energy photons (<1 MeV) in the simulations. The numerical scaling of the laser energy conversion efficiency to the γ photons with different laser intensities and NCD plasmas is shown in Fig. 4b. By increasing the laser intensity, the laser energy conversion to the γ-photons increases at first and then saturates when the laser field amplitude a0>800. This can be attributed to the rapid annihilation of the high-energy γ-photons via the BW process. Note that the γ-photon emission is significantly limited by the number and energy of the trapped electrons.
In the simulations, we also observe a linear increase of the laser energy conversion to the positrons’ kinetic energy, as illustrated in Fig. 4c. This tendency is valid for all considered NCD densities and laser intensities with a0>100. Qualitatively, the energy conversion efficiency can be approximately written as

where f(a0,ne) is a factor dependent on the laser and NCD plasmas, and is a constant under a given initial condition, a0(t)=a0g(t), and g(t) is the temporal profile of the laser pulse. This implies there exists a threshold laser intensity or field amplitude, that is, ath∼120, for efficient pair creation in our configuration (Fig. 4c). We can understand the underlying physics simply in this way: when such a laser pulse is focused in the NCD plasmas-filled cone-target, its electric field amplitude can be increased by more than three times (depending on its focusing location in the cone), which has been confirmed by additional simulations using the same cone configuration as above. As a result, one obtains an enhanced laser amplitude, which approximates the equivalent theoretical laser threshold for the electron trapping in our cone-target,  , assuming a focusing spot radius of r0′≈0.3r0.
, assuming a focusing spot radius of r0′≈0.3r0.
We finally compare the laser energy conversion efficiency in the simulations with theoretical predictions. Here the laser electric field can be increased up to  due to the enhanced pinching and focusing effect of the cone. The corresponding two critical parameters are given by ηf∼3 and χf∼2, which indicate effective excitation of both processes during the laser-NCD plasmas interaction. If we take χ=0.1 for example (see Methods), the required photon energy for pair creation is only 26 MeV, which is in reasonable agreement with the average energy of the γ-photons in our simulations. Considering χf≳1 in our case, the characteristic positron energy is given by53
due to the enhanced pinching and focusing effect of the cone. The corresponding two critical parameters are given by ηf∼3 and χf∼2, which indicate effective excitation of both processes during the laser-NCD plasmas interaction. If we take χ=0.1 for example (see Methods), the required photon energy for pair creation is only 26 MeV, which is in reasonable agreement with the average energy of the γ-photons in our simulations. Considering χf≳1 in our case, the characteristic positron energy is given by53  , while the laser energy is
, while the laser energy is  . Thus we can estimate the final maximum positron yield by:
. Thus we can estimate the final maximum positron yield by:

which is plotted in Fig. 4d. It is shown that our simulation results validate these theoretical estimations, especially for higher laser intensities. This further demonstrates the robustness of our scheme and validation of the simulations. If we scale our results to the upcoming lasers such as the XCELS (the next generation of laser facilities, such as Exawatt Center for Extreme Light Studies (XCELS) and Extreme Light Infrastructure (ELI). Available at http://www.xcels.iapras.ru and http://www.eli-np.ro), we can estimate the positron yield approaching ∼1014 with peak density of ∼1025 cm−3 and energy of tens GeV.
Schematic of a possible experimental arrangement
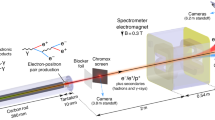
A possible experimental arrangement of the scheme with two 10 PW ELI-NP laser beams is illustrated in Fig. 5. Instead of using a double-cone-targets, we can focus the two laser beams on two gas, foam or cluster jets to produce NCD plasmas54,55. Carbon-Nano-Tube foams56 can be also used for NCD plasma generation, which has been extensively applied in laser–plasma interactions. One can vary the gap between the two jets to optimize the γ-photon emission and pair production. The focusing mirrors have small holes on the interaction axis in order to separate the electrons, γ-photons, and positrons, and to diagnose their interaction dynamics on axis. The background radiation can be reduced by burying the gamma detectors into the electron beam-dump23, which is positioned on the axis of the two laser interaction, as schematically shown in Fig. 5.
Two counter-propagating 10 PW laser beams are focused by off axis parabolic mirrors on two gas or foam or cluster jets with near-critical-density, generating electron beams (EB), positron beams (PB) and γ-ray beams (GB). The focusing mirrors have small holes in the centre to extract the electrons (e−), positrons (e+) and γ-rays (γ), and to observe their interactions on axis.
The femtosecond synchronization57 of the two femtosecond laser pulses can be obtained because both pulses are split from the same pulse in our configuration (after the laser oscillator), travel nearly identical optical paths (in the laser amplifier chains) and the small temporal differences are compensated at the end. Indeed synchronization of ±50 fs has already been demonstrated experimentally with the two 0.5 PW laser beams of the Astra-Gemini Laser at STFC in the UK57 and the method described can be further improved. Because of the copious numbers of positrons and electrons expected, the measurement of the number and spectrum of electron–positron pairs and of γ-photons can be done in a single-laser-shot12,23, that is, there is no need to accumulate many shots as is typical in particle and nuclear physics experiments. The detectors could also be gated to the picosecond time-window of the laser shot in order to further increase the Signal-to-Noise ratio. Various interesting physics processes are likely to occur at the interaction area, including nonlinear Compton scattering, multi-photon BW process, e−e+ collider and γγ collider as discussed below.
Discussion
Production of high-energy-density pair plasmas within a few tens of laser periods may open up new possibilities of studying astrophysical collective QED phenomena1,21 and high-energy particle physics3,4 in laboratories. Our scheme provides an efficient way to produce high-energy-density electrons and positrons, γ photons, and potentially other particles through their interactions, resulting in many applications. For example, this configuration is particularly suitable for applications as a non-conventional table-top e−e+ collider: the positron/electron beams and trapped energetic electron beams are generated in both NCD plasmas; when the electron beams in one NCD plasma collide head-on with the positron beams in the other NCD plasma (Supplementary Fig. 2; Supplementary Fig. 3; Supplementary Note 2), a compact e−e+ collider is expected, as indicated in Fig. 5. In the case of the future ELI facility (the next generation of laser facilities, such as Exawatt Center for Extreme Light Studies (XCELS) and Extreme Light Infrastructure (ELI). Available at http://www.xcels.iapras.ru and http://www.eli-np.ro; assume I0∼1024 W cm−2), the total positron number predicted is about 6 × 1013, with about 3 × 1011 positrons in the energy range between 2 and 2.5 GeV. This number is million times higher than detectable in current laser–plasma experiments so that the signal is strong enough to be detected in a single-laser-shot12,23. Assuming equal beams and Gaussian profiles in all dimensions with a beam size, conservatively, for example,  , it is estimated that the peak geometric luminosity of such a 4−5 GeV centre-of-mass (CM) e−e+ collider is as high as 1033 cm−2 s−1, which is comparable to the state-of-art colliders worldwide3. One may even scale the proposed scheme to TeV CM e−e+ collision, which is a unique feature of our scheme as compared with the others8,9,10,11,12,13,14,15,16,26,27,28,29,30,31.
, it is estimated that the peak geometric luminosity of such a 4−5 GeV centre-of-mass (CM) e−e+ collider is as high as 1033 cm−2 s−1, which is comparable to the state-of-art colliders worldwide3. One may even scale the proposed scheme to TeV CM e−e+ collision, which is a unique feature of our scheme as compared with the others8,9,10,11,12,13,14,15,16,26,27,28,29,30,31.
In our scheme, the low-emittance high-energy-density γ-photons in one NCD plasma can also collide with the other γ-photons from the second NCD plasma, which is a second γγ collider51 (Supplementary Fig. 1; Supplementary Note 1), an add-on to the e−e+ collider. Compared with the conventional linear colliders3, these new conceptual colliders based on laser–plasma interactions have many advantages, such as pure e−e+ collisions, low expense, compact size, and high luminosity, which may enable investigations in far-ranging scientific domains4,21,58 in future, for example, testing nonlinear phenomena such as mass-shift, spin-dependent effects, quantum gravity and so on.
In summary, we have presented a scheme on the generation of extremely dense e−e+ pairs via the multi-photon BW process at affordable laser intensity ∼1022 W cm−2 with the upcoming 10s PW lasers. In this scheme, bright γ rays are first produced by radiation-reaction trapped energetic electrons in the NCD plasmas. The photons then collide with the focused counter-propagating lasers to initiate the multi-photon BW process. A high-yield (1.05 × 1011) overdense (4 × 1022 cm−3) GeV positron beam is thus produced with a laser energy conversion efficiency as high as 0.14%. This highly energetic system may serve as a test bed for a variety of nonlinear QED physics and may be applied as a compact electron-position collider.
Methods
Two critical parameters in strong electromagnetic fields
The probability of photon emission and pair production can be written in terms of a differential optical depth35,  and dτ±/dt=(2παc/λC)(mec2/ħω)χT±(χ), respectively. Here η controls the photon emissivity via the quantum-corrected synchrotron function F(η,χ), and χ determines pair creation via the function
and dτ±/dt=(2παc/λC)(mec2/ħω)χT±(χ), respectively. Here η controls the photon emissivity via the quantum-corrected synchrotron function F(η,χ), and χ determines pair creation via the function  . In our case, the two key parameters equals
. In our case, the two key parameters equals  and
and  , since the terms β × c B and
, since the terms β × c B and  are parallel to the transverse laser field
are parallel to the transverse laser field  . The Lorentz factor for electrons in the cone is assumed to be
. The Lorentz factor for electrons in the cone is assumed to be  , where ħω0 is the laser photon energy and Ef is the focused laser transverse electric field. Then, we obtain
, where ħω0 is the laser photon energy and Ef is the focused laser transverse electric field. Then, we obtain  , where E0=mecω0/e. The characteristic photon energy can be described classically using the theory of synchrotron radiation as26
, where E0=mecω0/e. The characteristic photon energy can be described classically using the theory of synchrotron radiation as26  . Thus the parameter χ is rewritten as
. Thus the parameter χ is rewritten as  . It is shown that, as η ≳1 and χ≳1, the BW process dominates the positron production and quantum effects intervene significantly. Considering only χ≳0.1 in the photon–photon annihilation, the BW process also occurs, although it is relatively inefficient.
. It is shown that, as η ≳1 and χ≳1, the BW process dominates the positron production and quantum effects intervene significantly. Considering only χ≳0.1 in the photon–photon annihilation, the BW process also occurs, although it is relatively inefficient.
Numerical modelling
The open-source PIC code EPOCH27,59 is used to perform the 3D simulations. The code has been equipped with the synchrotron radiation module, the radiation-reaction module, and the pair creation module (BW process), allowing self-consistent modelling of laser–plasmas interactions in the near-QED regime. In the code, the BW process is modelled by a probabilistic Monte Carlo algorithm52,59, which has been extensively applied recently. For simplicity, the e−e+ annihilation is ignored in the code.
In the simulations, two counter-propagating linearly polarized laser pulses are incident from the left and right boundaries of the box simultaneously, which have the same temporal-spatial profiles, that is, a transversely Gaussian distribution with a=a0exp(−r2/r02) and a square temporal profile with a duration of τL=12T0. Here the laser parameters are, respectively, a0=150, r0=5λ0, T0=3.3fs, r2=y2+z2, and λ0=1μm, which indicates a laser peak intensity of I0≈3 × 1022 W cm−2. Exposed in such a strong laser field, both electrons and protons can be pushed forward. The simulation box size is x × y × z=60λ0 × 16λ0 × 16λ0, sampled by cells of 3,000 × 240 × 240 with 27 macroparticles per cell. For simplicity, two symmetric aluminium cones are used to focus the incident laser pulses, both of which have a length of 50λ0 and a plasma density of n0=390nc. The left and right radius of each cone mouth are R=6 μm and r=1.5 μm, respectively. To enhance the laser energy absorption, the double-cone-targets are filled with NCD hydrogen plasmas, which has an initial density of ne=3nc. These parameters are tunable in simulations. For reference, we also compared the simulation results to the case with a Gaussian temporal pulse profile, which shows a comparable positron yield and density (Supplementary Fig. 4; Supplementary Fig. 5; Supplementary Note 3). Note that we only count the photons with energy >1 MeV in above simulations.
Data availability
The data that support the findings of this study are available from the corresponding authors on request.
Additional information
How to cite this article: Zhu, X.-L. et al. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat. Commun. 7, 13686 doi: 10.1038/ncomms13686 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Di Piazza, A., Müller, C., Hatsagortsyan, K. Z. & Keitel, C. H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 84, 1177–1288 (2012).
Danielson, J. R., Dubin, D. H. E., Greaves, R. G. & Surko, C. M. Plasma and trap-based techniques for science with positrons. Rev. Mod. Phys. 87, 247–306 (2015).
Abramowicz, H. & Caldwell, A. C. HERA collider physics. Rev. Mod. Phys. 71, 1275–1409 (1999).
Mourou, G. A., Tajima, T. & Bulanov, S. V. Optics in the relativistic regime. Rev. Mod. Phys. 78, 309–371 (2006).
Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 82, 664 (1951).
Bethe, H. & Heitler, W. On the stopping of fast particles and on the creation of positive electrons. Proc. R. Soc. Lond. A 146, 83–112 (1934).
Nakashima, K. & Takabe, H. Numerical study of pair creation by ultraintense lasers. Phys. Plasmas 9, 1505 (2002).
Cowan, T. E. et al. High energy electrons, nuclear phenomena and heating in petawatt laser-solid experiments. Laser Part. Beams 17, 773–783 (1999).
Chen, H. et al. Relativistic positron creation using ultraintense short pulse lasers. Phys. Rev. Lett. 102, 105001 (2009).
Liang, E. et al. High e+/e− ratio dense pair creation with 1021W·cm−2 laser irradiating solid targets. Sci. Rep. 5, 13968 (2015).
Gahn, C. et al. Generating positrons with femtosecond-laser pulses. Appl. Phys. Lett. 77, 2662 (2000).
Sarri, G. et al. Table-Top Laser-Based Source of Femtosecond, Collimated, Ultrarelativistic Positron Beams. Phys. Rev. Lett. 110, 255002 (2013).
Sarri, G. et al. Generation of neutral and high-density electron-positron pair plasmas in the laboratory. Nat. Commun. 6, 6747 (2015).
Xu, T. et al. Ultrashort megaelectronvolt positron beam generation based on laser-accelerated electrons. Phys. Plasmas 23, 033109 (2016).
Chen, H. et al. Relativistic Quasimonoenergetic Positron Jets from Intense Laser-Solid Interactions. Phys. Rev. Lett. 105, 015003 (2010).
Müller, C. & Keitel, C. H. Antimatter: Abundant positron production. Nat. Photon. 3, 245–246 (2009).
Di Piazza, A., Hatsagortsyan, K. Z. & Keitel, C. H. Quantum radiation reaction effects in multiphoton Compton scattering. Phys. Rev. Lett. 105, 220403 (2010).
Breit, G. & Wheeler, J. A. Collision of Two Light Quanta. Phys. Rev 46, 1087 (1934).
Burke, D. L. et al. Positron Production in Multiphoton Light-by-Light Scattering. Phys. Rev. Lett. 79, 1626 (1997).
Yanovsky, V. et al. Ultra-high intensity-300-TW laser at 0.1 Hz repetition rate. Opt. Express 16, 2109 (2008).
Marklund, M. & Shukla, P. K. Nonlinear collective effects in photon-photon and photon-plasma interactions. Rev. Mod. Phys. 78, 591–640 (2006).
Ritus, V. I. Quantum effects of the interaction of elementary particles with an intense electromagnetic field. J. Russ. Laser Res. 6, 497–617 (1985).
Turcu, I. C. E. et al. HPLS-TDR2: high field physics and QED experiments at ELI–NP: technical design report. Rom. Rep. Phys. 68, supplement, S145–S231 (2016).
Sokolov, I. V., Naumova, N. M., Nees, J. A. & Mourou, G. A. Pair Creation in QED-Strong Pulsed Laser Fields Interacting with Electron Beams. Phys. Rev. Lett. 105, 195005 (2010).
Bulanov, S. S. et al. Multiple Colliding electromagnetic pulses: a way to lower the threshold of e+e− pair production from vacuum. Phys. Rev. Lett. 104, 220404 (2010).
Bell, A. R. & Kirk, J. G. Possibility of Prolific Pair Production with High-Power Lasers. Phys. Rev. Lett. 101, 200403 (2008).
Ridgers, C. P. et al. Dense electron-positron plasmas and ultraintense γ rays from laser-irradiated solids. Phys. Rev. Lett. 108, 165006 (2012).
Pike, O. J., Mackenroth, F., Hill, E. G. & Rose, S. J. A photon-photon collider in a vacuum hohlraum. Nat. Photon. 8, 434–436 (2014).
Blackburn, T. G., Ridgers, C. P., Kirk, J. G. & Bell, A. R. Quantum radiation reaction in laser–electron-beam collisions. Phys. Rev. Lett. 112, 015001 (2014).
Lobet, M., Davoine, X., d'Humières, E. & Gremillet, L. Generation of high-energy electron-positron beams in the collision of a laser-accelerated electron beam and a multi-petawatt laser. Preprint at http://arxiv.org/abs/1510.02301 (2015).
Chang, H. X. et al. Generation of overdense and high-energy electron-positron-pair plasmas by irradiation of a thin foil with two ultraintense lasers. Phys. Rev. E 92, 053107 (2015).
Pukhov, A. & Meyer-ter-Vehn, J. Laser wake field acceleration: the highly non-linear broken-wave regime. Appl. Phys. B 74, 355 (2002).
Thomas, A. G. R. et al. Strong radiation-damping effects in a gamma-ray source generated by the interaction of a high-intensity laser with a wakefield-accelerated electron beam. Phys. Rev. X 2, 041004 (2012).
Bulanov, S. S., Schroeder, C. B., Esarey, E. & Leemans, W. P. Electromagnetic cascade in high-energy electron, positron, and photon interactions with intense laser pulses. Phys. Rev. A 87, 062110 (2013).
Erber, T. High-energy electromagnetic conversion processes in intense magnetic fields. Rev. Mod. Phys. 38, 626–659 (1966).
Landau, L. D. & Lifshitz, E. M. The Classical Theory Of Fields vol. 2, Butterworth-Heinemann (1980).
Yu, T. P. et al. Dynamics of laser mass-limited foil interaction at ultra-high laser intensities. Phys. Plasmas 21, 053105 (2014).
Chen, M., Pukhov, A., Yu, T. P. & Sheng, Z. M. Radiation reaction effects on ion acceleration in laser foil interaction. Plasma Phys. Contr. Fus. 53, 014004 (2011).
Ji, L. L. et al. Radiation-reaction trapping of electrons in extreme laser fields. Phys. Rev. Lett. 112, 145003 (2014).
Zhu, X. L. et al. Enhanced electron trapping and γ ray emission by ultra-intense laser irradiating a near-critical-density plasma filled gold cone. New J. Phys. 17, 053039 (2015).
Pukhov, A. Three-dimensional electromagnetic relativistic particle-in-cell code VLPL (Virtual Laser Plasma Lab). J. Plasma Phys. 61, 425 (1999).
Kodama, R. et al. Plasma devices to guide and collimate a high density of MeV electrons. Nature 432, 1005–1008 (2004).
Zhu, X. L. et al. Ultra-bright, high-energy-density γ-ray emission from a gas-filled gold cone-capillary. Phys. Plasmas 22, 093109 (2015).
Yu, T. P. et al. High-energy-density electron jet generation from an opening gold cone filled with near-critical-density plasma. J. Appl. Phys. 117, 023105 (2015).
Davidson, R. C. et al. Frontiers in High Energy Density Physics: The X-Games of Contemporary Science National Academies Press (2003).
Lobet, M. et al. Ultrafast Synchrotron-Enhanced Thermalization of Laser-Driven Colliding Pair Plasmas. Phys. Rev. Lett. 115, 215003 (2015).
Nerush, E. N. et al. Laser field absorption in self-generated electron-positron pair plasma. Phys. Rev. Lett. 106, 035001 (2011).
Zhang, P., Ridgers, C. P. & Thomas, A. G. R. The effect of nonlinear quantum electrodynamics on relativistic transparency and laser absorption in ultra-relativistic plasmas. New J. Phys. 17, 043051 (2015).
Cipiccia, S. et al. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nat. Phys 7, 867–871 (2011).
Yu, T. P. et al. Bright Betatronlike X Rays from Radiation Pressure Acceleration of a Mass-Limited Foil Target. Phys. Rev. Lett. 110, 045001 (2013).
Telnov, V. Principles of photon colliders. Nucl. Instr. and Meth. in Phys. Res. A 355, 3–18 (1995).
Ridgers, C. P. et al. Modelling gamma-ray photon emission and pair production in high-intensity laser-matter interactions. J. Comput. Phys. 260, 273 (2014).
Fedotov, A. M., Narozhny, N. B., Mourou, G. & Korn, G. Limitations on the Attainable Intensity of High Power Lasers. Phys. Rev. Lett. 105, 080402 (2010).
Fukuda, Y. et al. Energy increase in multi-MeV ion acceleration in the interaction of a short pulse laser with a cluster-gas target. Phys. Rev. Lett. 103, 165002 (2009).
Chen, S. N. et al. Density and temperature characterization of lonf-scale length, near-critical density controlled plasma produced from ultra-low density plastic foam. Sci. Rep 6, 21495 (2016).
Ma, W. et al. Directly synthesized strong, highly conducting, transparent single-walled carbon nanotube films. Nano Lett. 7, 2307–2311 (2007).
Corvan, D. J. et al. Femtosecond-scale synchronization of ultra-intense focused laser beams. Preprint at http://arxiv.org/abs/1409.4243 (2014).
Schroeder, C. B. et al. Physics considerations for laser-plasma linear colliders. Phys. Rev. ST Accel. Beams 13, 101301 (2010).
Arber, T. D. et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Contr. Fus. 57, 113001 (2015).
Acknowledgements
We acknowledge the fruitful discussions with M.Y. Yu, F. Pegoraro, C. Plostinar, and M. Zhong. The work was supported by the National Natural Science Foundation of China (Project Nos. 11622547, 11474360, 11175255, 91230205 and 11374210), the National Basic Research Program of China (Grant No. 2013CBA01504), a Leverhulme Trust Research Project Grant, the U.K. EPSRC (Grant No. EP/N028694/1), Plasma HEC Consortium EPSRC Grant (No. EP/L000237/1), the Science Challenge Program (Grant No. JCKY2016212A505), and the Research Project of NUDT (JQ14-02-02). The EPOCH code was developed as part of the UK EPSRC grants EP/G056803/1 and EP/G055165/1. All simulations were performed on TianHe High Performance Computers.
Author information
Authors and Affiliations
Contributions
X.-L.Z. and T.-P.Y. conceived the scheme and X.-L.Z carried out all simulations. T.-P.Y. and X.-L.Z. performed the data analysis and wrote the manuscript. Z.-M.S., Y.Y. and A.P. clarified details of the physics and contributed to the writing of the manuscript. I.C.E.T. proposed the schematics of the experiment and evaluated its feasibility with ELI-NP facilities. All authors discussed the results, commented on the manuscript, and agreed on the contents.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Notes 1-3 and Supplementary References. (PDF 1023 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhu, XL., Yu, TP., Sheng, ZM. et al. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat Commun 7, 13686 (2016). https://doi.org/10.1038/ncomms13686
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13686
This article is cited by
-
Forward-looking insights in laser-generated ultra-intense γ-ray and neutron sources for nuclear application and science
Nature Communications (2022)
-
Towards bright gamma-ray flash generation from tailored target irradiated by multi-petawatt laser
Scientific Reports (2022)
-
All-optical quasi-monoenergetic GeV positron bunch generation by twisted laser fields
Communications Physics (2022)
-
Dominance of γ-γ electron-positron pair creation in a plasma driven by high-intensity lasers
Communications Physics (2021)
-
Efficient generation of relativistic near-single-cycle mid-infrared pulses in plasmas
Light: Science & Applications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.