Abstract
Electric field effects in ferromagnetic metal/dielectric structures provide a new route to control domain wall dynamics with low-power dissipation. However, electric field effects on domain wall velocities have only been observed so far in the creep regime where domain wall velocities are low due to strong interactions with pinning sites. Here we show gate voltage modulation of domain wall velocities ranging from the creep to the flow regime in Ta/Co40Fe40B20/MgO/TiO2 structures with perpendicular magnetic anisotropy. We demonstrate a universal description of the role of applied electric fields in the various pinning-dependent regimes by taking into account an effective magnetic field being linear with the electric field. In addition, the electric field effect is found to change sign in the Walker regime. Our results are consistent with voltage-induced modification of magnetic anisotropy. Our work opens new opportunities for the study and optimization of electric field effect at ferromagnetic metal/insulator interfaces.
Similar content being viewed by others
Introduction
Electric field control of magnetic domain wall (DW) motion in transition-metal ferromagnets1,2,3,4,5,6,7 has attracted great interest due to the possibility to achieve DW control with low-power dissipation for memory and logic circuits. One important example is racetrack memory8, where a gate voltage can be exploited to assist manipulation of DWs under spin-polarized currents1. This would allow the reduction of the generally large critical currents needed to depin and shift DWs in narrow wires. Another example concerns DW logic circuits9, for which local modulation of DW motion can lead to programmable DW energy landscapes. In both cases, the key is whether the electric field enables both efficient depinning for stored DWs and control of DW propagation.
Materials with perpendicular magnetic anisotropy (PMA) are particularly attractive for DW devices as they exhibit narrow DWs10, enabling high-density storage. Recently, the electric field effect on DW dynamics has been demonstrated in Pt/Co/oxide films with PMA involving oxides with relatively high dielectric constant such as AlOx (refs 3, 6), HfO2 (ref. 4) or GdOx (ref. 5). However, significant modulation of DW velocity under gate voltage has been shown only in the creep regime where DWs propagate at relatively low speeds (<0.1 m s−1) through thermal activation over local energy barriers3,4,5,6 originating from the random disorder10,11. The efficient gate-voltage control in the creep regime has been explained in terms of modulation of the activation energy barriers3,4,5,6 through voltage-induced changes of the interfacial magnetic anisotropy12,13,14,15,16. With increasing DW velocity in the creep regime, the electric field effect was found to be strongly reduced due to the decrease of the activation energies with applied magnetic fields5. So far, there has been no reports on the experimental observation of electric field effects beyond the creep regime, particularly in the depinning and flow regimes17,18,19,20.
Here we report the observation of voltage modulation of DW motion over different dynamical regimes where velocities range from 10−8 to 20 m s−1. In addition, we demonstrate that this behaviour can be understood over the full range of DW dynamics by electric field-induced modulation of the magnetic anisotropy. Our approach makes use of Ta/CoFeB/MgO films with PMA, for which the density of pinning sites and the damping are very low21,22,23 with respect to other PMA materials such as Co/Pt19,24 or Co/Ni18,25. In addition, PMA at the CoFeB/MgO interface can be manipulated efficiently through gate voltage control15,16. These materials are considered as the most promising, not only for spin transfer torque magnetic random access memory26,27 but also for DW-based memories28, as a combination of spin Hall effect and Dzyaloshinskii–Moriya interaction leads to efficient DW propagation under current29,30,31.
Results
Voltage effect on DW velocity in the depinning regimes
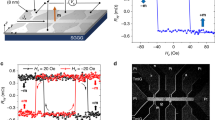
In this study, DW velocity under electric field was measured in both as-grown and annealed Ta(5 nm)/Co40Fe40B20(1 nm)/MgO(2 nm)/TiO2(20 nm)/ITO samples using magneto-optic Kerr microscopy under combined electric and magnetic fields. By applying a top gate voltage VG between the bottom Ta/CoFeB and top ITO electrodes (shown schematically in Fig. 1a), electrons can either accumulate or deplete at the CoFeB/MgO interface. For the experiments shown, positive (negative) voltage corresponds to electron accumulation (depletion) at the CoFeB/MgO interface. It is noteworthy that, to avoid any temperature rise, the experiments were performed under low leakage current below 20 nA, which corresponds to gate voltages ranging from −1.5 to 1.5 V. The maximum voltage corresponds to electric field of 0.37 V nm−1 below the voltage breakdown of MgO (>1 V nm−1). Figure 1b shows typical differential Kerr images of magnetic DW motion in an annealed CoFeB structure for various gate voltages of VG=−1.5, 0 and +1.5 V. The dark regions indicate the motion of the DW under a magnetic field pulse of μ0H=8 mT during Δt=45 μs under voltage. The voltage VG was applied in the region of the 50 μm-wide ITO strip as indicated by the dashed rectangle. The DW displacement below the ITO strip at VG=−1.5 V is smaller than that at VG=0 V, whereas the DW displacement at VG=1.5 V is larger, indicating an opposite effect of electric field for different polarities. Figure 2a–c shows the dependence of DW velocity on the gate voltage in the annealed sample for different values of μ0H. In all field ranges, the DW velocity increases (decreases) with positive (negative) voltage VG. As indicated in Figure 2d, the effect of gate voltage on DW velocity is found to be relatively large in the low-field regime, but it strongly decreases with increasing magnetic field. It is noteworthy that these results do not depend on the direction of magnetic fields (Supplementary Fig. 1) and were demonstrated in several devices with different width of ITO electrodes (Supplementary Fig. 2).
(a) The gate voltage VG is applied between the ITO strip and the CoFeB film. The magnetic field H is applied perpendicular to the film plane. (b) DW displacement measured by polar Kerr microscopy at applied magnetic fields μ0H of 8 mT with 45 μs duration under voltage VG of −1.5, 0 and 1.5 V, respectively. The DW displacement is obtained from the difference between the polar Kerr images after and before magnetic field pulses. The right (left) boundary in the dark part in the image shows the DW position before (after) applying the magnetic field pulse and the arrow indicates the direction of DW motion. Top gate voltage VG is applied in the region indicated by the dashed rectangle.
(a–c) DW velocity as a function of VG for different magnetic fields μ0H of 3, 9 and 29 mT, respectively. (d) Ratio of DW velocity v1.5V/v−1.5V as a function of the applied field. Electric field effect is detected up to the high velocity regime. The error bars of DW velocity are given by repeating the measurements for several times in one device. As DW motion is intrinsically stochastic due to thermal activation over energy barriers, a distribution of DW velocity is expected.
To determine the role of voltage on the various dynamic regimes, we have measured the dependence of DW velocity v on the applied magnetic field H for various voltages ranging from −1.5 to 1.5 V. Figure 3 shows the DW velocity versus μ0H for typical gate voltages VG=−1.5, 0 and 1.5 V for the annealed sample. Three DW dynamical regimes are observed, including the creep, intermediate depinning and depinning regimes11,17,19,20,22. In all regimes the DW velocity increases (decreases) under positive (negative) voltage. In the creep regime where μ0H<8 mT (Fig. 3b), the DW velocity can be expressed as
(a) Velocity as a function of H under voltages VG of −1.5 V (open squares), 0 V (solid squares) and 1.5 V (open circles). (b) Velocity (in logarithmic scale) as a function of H−1/4 under voltages VG of −1.5 V (open squares), 0 V (solid squares) and 1.5 V (open circles). The symbols correspond to the experimental data, and the lines to the fitting (equations (1) and (2)). The error bars of DW velocity are given by repeating the measurements for several times in one device.

where UC is a characteristic energy related to the disorder-induced pinning potential, kB the Boltzmann constant, T the temperature and Hdep the depinning field at which the Zeeman energy is equal to the DW pinning energy. The exponent 1/4 fits the data well and is theoretically predicted for interactions of one-dimensional DWs with two-dimensional weak random disorder in thin magnetic films with PMA11. This regime allows us to determine the values of UC(Hdep)1/4/(kBT) and lnv0 as a function of the applied voltage as shown in Figure 4a,b. UC(Hdep)1/4/(kBT) decreases (increases) with positive (negative) voltages values, whereas lnv0 remains fairly constant. In agreement with ref. 19, close above Hdep a critical depinning regime is observed for μ0H>12 mT, where the velocity fits as

This regime allows us to determine accurately the value of Hdep as a function of the gate voltages as shown in Fig. 4c. Hdep decreases with increasing voltage. We find a linear variation of the depinning field with voltage that can be described by

where Hdep0=12 mT and L∼0.05 V−1. Finally, by using the value of μ0Hdep determined from equation (2) into equation (1), the characteristic energy UC is found to be independent of the voltage as indicated in Fig. 4d. Although a dependence of UC on anisotropy is expected in the creep theory10,11, this feature is consistent with recent results of modulation of anisotropy in Pt/Co/Pt32 and Ta/CoFeB/MgO33 films. Between these two regimes for 8 mT<μ0H<12 mT, an intermediate depinning regime occurs, which corresponds to the tails of the creep regime20 where the energy barriers vanish linearly as ΔE∼(H/Hdep−1) approaching Hdep.
Voltage effect on anisotropy and DW depinning field
Our results are consistent with electric field-induced change of perpendicular anisotropy as described below. In our structure, the dielectric layer consists of a 2 nm-thick MgO (dielectric constant ɛMgO∼9.7) and 20 nm-thick TiO2 (dielectric constant ɛTiO2∼100) films. A positive (negative) gate voltage of VG=+1 V (−1 V) corresponds to an electric field of ∼0.25 V nm−1 and an accumulation (depletion) of ∼0.01 electron per Co(Fe) atom at the CoFeB/MgO interface. The results here show that positive voltage increases the DW velocity. This is consistent with recent studies showing that positive voltage give rise to a reduction of the effective anisotropy Keff in Ta/CoFeB/MgO structures15,16,34,35,36. Indeed, as the depinning field Hdep depends on Keff as Hdep∼(Keff)1/2 (refs 10, 11, 33), a reduction of Keff under positive voltage leads to a reduction of Hdep and thus an increase of DW velocity following equations (1) and (2). It is noteworthy that the variation of Hdep gives rise to a depinning efficiency of 2.3 mT V−1 nm.
In a recent study36, we have used ionic liquid to apply electric fields on larger scales in Ta/CoFeB/MgO structures grown under the same conditions, which allows us to measure the variation of the anisotropy field under electric field. The results are found to be consistent with a linear variation of the effective anisotropy under voltage, confirming previous studies15,16,34,35. Thus, considering Keff=Keff0(1−aVG), where Keff0 is the effective anisotropy at zero voltage, a is the modulation ratio of Keff per V and VG the gate voltage, the depinning field Hdep∼(Keff)1/2 can be written as

where Hdep0 is the propagation field at zero voltage (Supplementary Note 1). This is consistent with our finding of a linear variation of Hdep with voltage (see equation (3)) considering a/2=L. Using L=0.05 V−1 deduced from the fit to Fig. 4c, we find that the modulation ratio of Keff is a∼10% per V. As the modulation of Keff is related to the modulation of the interface anisotropy at the CoFeB/MgO interface and Keff0∼105 J m−3 in our films, the typical modulation ratio of interface anisotropy KefftCoFeB where tCoFeB=1 nm is then 40 fJ m−1 V−1 in agreement with previous studies on Ta/Co40Fe40B20/MgO (ref. 15).
Effective magnetic field under voltage
In the creep and intermediate depinning regime where DW velocities follow an exponential behaviour, the energy barrier depends on H/Hdep that can be written H/Hdep=(1+LVG)H/Hdep0. This indicates that the DW velocity under voltage follows the same expressions as the ones at zero voltage by replacing the magnetic field H by an effective magnetic field Heff=(1+LVG)H (Supplementary Fig. 3), that is, the energy barrier is given by Heff/Hdep0. This is shown in Fig. 5a where the DW velocity v is plotted against Heff under typical VG of −1.5, 0 and 1.5 V, respectively. The behaviour in the DW creep regime is also shown in Fig. 5b where v (in logarithmic scale) is plotted against (Heff)−1/4. All the curves can be superimposed by considering the effective magnetic field instead of the applied magnetic field. It is interesting to observe that it is also the case in the depinning regime above Hdep where the DW velocity depends on (H−Hdep)1/4. As LVG<<1, (H−Hdep)1/4≈(Heff−Hdep0)1/4, which indicates that the universal description given by Heff is quantitatively applicable over the full range of the pinning-dependent regimes.
(a) Velocity v as a function of (1+LVG)H under voltages VG of −1.5 V (open squares), 0 V (solid squares) and 1.5 V (open circles), where L=0.05 V−1. (b) Velocity v (in logarithmic scale) as a function of [(1+LVG)H]−1/4 under voltages VG of −1.5 V (open squares), 0 V (solid squares) and 1.5 V (open circles), where L=0.05 V−1. The error bars of DW velocity are given by repeating the measurements for several times in one device.
Voltage effect on magnetic DW velocity in the Walker regime
Figure 6 shows DW velocity at high fields in an as-grown Ta(5 nm)/Co40Fe40B20(1 nm)/MgO(2 nm)/TiO2(20 nm)/ITO structure, for which the PMA is lower due to the amorphous character of the CoFeB layer19. In this case, the beginning of the flow regime occurs at lower fields than the annealed sample (Supplementary Fig. 4), which allows us to study the influence of electric field on the flow regime. As shown in Fig. 5a, the velocity v at VG=0 as a function of the magnetic field increases up to μ0H=27 mT. Interestingly, for μ0H>27 mT, a new regime where the DW velocity decreases with increasing H is observed. This additional regime beyond the depinning regime corresponds to the instability regime above the Walker breakdown that is partially hidden by the depinning regime as we have recently observed17,18,21,31. For μ0H<27 mT, the DW velocity increases with positive VG, as shown in Figure 5b. Interestingly, Fig. 5c shows that for μ0H=30 mT in the negative mobility regime, instead the DW velocity decreases with increasing VG, indicating a reversal of the electric field effect. In this regime, the DW velocity exhibits a non-trivial dependence on the effective anisotropy. First, we note that the Walker field can be written HW=NyMSα/2, where Ny is the demagnetizing factor across the wall given as tCoFeB/(tCoFeB+Δ), α is the damping parameter and Δ is the DW width that can be written Δ=(A/Keff+Nyμ0MS2/2)1/2. The typical value of HW is around 0.8 mT in our films22 lower than Hdep. As HW depends on Δ−1, HW is expected to vary as (Keff)1/2 such as Hdep. Thus, a positive voltage (reduction of Keff) results in a decrease of HW, which, as first approximation, translates the Walker regime to lower fields reducing the DW velocity above HW as we observed. This is further supported by micromagnetic simulations (Supplementary Fig. 5), which shows that in the Walker regime indeed a reduction of anisotropy gives rise to a reduction of DW velocity.
(a) Velocity v as a function of H in the range from 11 to 34 mT at zero voltage. Inset shows v in the H range from 0.6 to 34 mT. (b,c) Velocity v as a function of VG under magnetic field μ0H of 6 and 30 mT, respectively. The error bars of DW velocity are given by repeating the measurements for several times in one device.
Discussion
In conclusion, beyond the important finding of the universal description of electric field-induced DW motion, the possibility to both obtain depining efficiency up to 2.5 mT V−1 nm and control DW velocity up to the flow regime in CoFeB/MgO structures opens new perspectives for low power spintronic applications such as solid state memories and logic devices. We believe that these electric field effects can be used to lower the energy barrier for stored DWs, leading to a smaller spin-polarized currents to depin and move them. In addition, as the depinning fields of CoFeB/MgO can be as small as 2 mT, on/off operations are feasible, which is of interest for logic devices. Furthermore, electric field effects can be very useful in the flow regime to speed up DW motion between two storing positions. The control of DW motion is obtained through interface anisotropy modulation due to charge accumulation/depletion at the ferromagnetic metal/dielectric interfaces. To overcome the limited charge modulation related to the static breakdown of the dielectric layer, pulsed gate voltages together with optimized dielectrics layers can provide much larger electric field, which could be an avenue for higher efficiencies.
Methods
Fabrication of Ta/CoFeB/MgO/TiO2/ITO structure
The Ta(5 nm)/Co40Fe40B20(1 nm)/MgO(2 nm)/Ta(5 nm) films were deposited on Si/SiO2 wafers by magnetron sputtering. Atomic force microscopy and X-ray reflectivity indicate high structural quality with very low interface roughness37,38. Selected films were annealed at 300 °C for 2 h. To apply an electric field effect in CoFeB/MgO structures, a high dielectric constant layer is required to be deposited on top of the MgO layer. The top 5 nm-thick Ta layer was gently removed using ion beam etching monitored by secondary ion beam spectroscopy, and then a 20 nm-thick TiO2 dielectric layer was sputtered on the MgO layer from a Ti target with mixed Ar and O2 gas (Supplementary Fig. 6). Finally, 100 nm-thick sputtered ITO (In2O3:Sn) stripes with width ranging from 10 to 50 μm were patterned on top of the TiO2 layer as the top electrode by optical lithography and lift-off process. ITO was used as the top electrode, because it is not only a good electrical conductor (conductivity∼7 Ω−1 m−1), but also is transparent for visible light, so that it is possible to use Kerr microscopy for visualizing magnetic domains. By applying a top gate voltage VG between the bottom Ta/CoFeB and the top ITO, electrons can accumulate or deplete at the CoFeB/MgO interface. Here, positive (negative) gate voltage corresponds to electron accumulation (depletion) in the CoFeB layer. The leakage current was measured to be less than a few nA for gate voltages VG<1.5 V and <100 nA at the maximum gate voltage (Supplementary Fig. 6), and thus Joule heating influence on DW motion is negligible.
Magnetic DW velocity measurement by polar Kerr microscopy
The polar Kerr microscopy was performed using a diode with the blue light (455 nm in wavelength) and a × 50 objective lens. The analyser was set to ∼87° (analyser and polarizer almost crossed) and the exposure time was 2 s. To measure DW velocity under an applied perpendicular magnetic field H, we used the following procedures: first, the sample was saturated with a magnetic field of −20 mT fixed for >10 s. Second, several positive magnetic field pulses of +3 mT with duration of around 10 s were applied, until the nucleation of a single DW below the ITO strip was observed. A reference Kerr image was taken at zero applied magnetic field after the first set of magnetic field pulses. Third, another magnetic field pulse was applied, resulting in a DW displacement. The amplitude of the second set of magnetic field pulses ranged from 0.6 to 35 mT and their durations Δt from 100 s (long pulse) to 9 μs (short pulse). The magnetic field pulse was generated from a coil with 1 cm diameter, which was fixed very close to the sample, and the rise time of magnetic field was ∼4 μs. After the second set of magnetic field pulses were applied, a second Kerr image was taken as soon as the magnetic field was back to zero. The DW displacement during Δt was obtained by the difference between the two Kerr images, which gave the DW velocity v. The velocity measured under the short magnetic field pulses was determined by the slope of the DW displacement versus magnetic field pulse duration.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Lin, W. et al. Universal domain wall dynamics under electric field in Ta/CoFeB/MgO devices with perpendicular anisotropy. Nat. Commun. 7, 13532 doi: 10.1038/ncomms13532 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Yamanouchi, M., Chiba, D., Matsukura, F. & Ohno, H. Current-assisted domain wall motion in ferromagnetic semiconductors. Jpn J. Appl. Phys. 45, 3854–3859 (2006).
Logginov, A. S. et al. Room temperature magnetoelectric control of micromagnetic structure in iron garnet films. Appl. Phys. Lett. 93, 182510 (2008).
Schellekens, A. J., van den Brink, A., Franken, J. H., Swagten, H. J. M. & Koopmans, B. Electric-field control of domain wall motion in perpendicularly magnetized materials. Nat. Commun. 3, 847 (2012).
Chiba, D. et al. Electric-field control of magnetic domain-wall velocity in ultrathin cobalt with perpendicular magnetization. Nat. Commun. 3, 888 (2012).
Bauer, U., Emori, S. & Beach, G. S. D. Voltage-gated modulation of domain wall creep dynamics in an ultrathin metallic ferromagnet. Appl. Phys. Lett. 101, 172403 (2012).
Bernand-Mantel, A. et al. Electric-field control of domain wall nucleation and pinning in a metallic ferromagnet. Appl. Phys. Lett. 102, 122406 (2013).
Bauer, U., Emori, S. & Beach, G. S. D. Voltage-controlled domain wall traps in ferromagnetic nanowires. Nat. Nanotechnol. 8, 411–416 (2013).
Parkin, S. S. P., Hayashi, M. & Thomas, L. Magnetic domain-wall racetrack memory. Science 320, 190–194 (2008).
Allwood, D. A. et al. Submicrometer ferromagnetic NOT gate and shift register. Science 296, 2003–2006 (2002).
Ferré, J. in Spin Dynamics in Confined Magnetic Structures I eds Hillebrands B., Ounadjela K.) Vol. 83, p 127–168Springer-Verlag: Berlin Heidelberg, (2002).
Lemerle, S. et al. Domain wall creep in an Ising ultrathin magnetic film. Phys. Rev. Lett. 80, 849–852 (1998).
Weisheit, M. et al. Electric field-induced modification of magnetism in thin-film ferromagnets. Science 315, 349–351 (2007).
Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechnol. 4, 158–161 (2009).
Niranjan, M. K., Duan, C.-G., Jaswal, S. S. & Tsymbal, E. Y. Electric field effect on magnetization at the Fe/MgO(001) interface. Appl. Phys. Lett. 96, 222504 (2010).
Endo, M. et al. Electric-field effects on thickness dependent magnetic anisotropy of sputtered MgO/Co40Fe40B20/Ta structures. Appl. Phys. Lett. 96, 212503 (2010).
Kita, K., Abraham, D. W., Gajek, M. J. & Worledge, D. C. Electric-field-control of magnetic anisotropy of Co0.6Fe0.2B0.2/oxide stacks using reduced voltage. J. Appl. Phys. 112, 033919 (2012).
Metaxas, P. J. et al. Creep and flow regimes of magnetic domain-wall motion in ultrathin Pt/Co/Pt films with perpendicular anisotropy. Phys. Rev. Lett. 99, 217208 (2007).
Yamada, K. et al. Influence of instabilities on high-field magnetic domain wall velocity in (Co/Ni) nanostrips. Appl. Phys. Express 4, 113001 (2011).
Gorchon, J. et al. Pinning-dependent field-driven domain wall dynamics and thermal scaling in an ultrathin Pt/Co/Pt magnetic film. Phys. Rev. Lett. 113, 027205 (2014).
Jeudy, V. et al. Universal pinning energy barrier for driven domain walls in thin ferromagnetic films. Phys. Rev. Lett. 117, 057201 (2016).
Devolder, T. et al. Damping of CoxFe80-xB20 ultrathin films with perpendicular magnetic anisotropy. Appl. Phys. Lett. 102, 022407 (2013).
Burrowes, C. et al. Low depinning fields in Ta-CoFeB-MgO ultrathin films with perpendicular magnetic anisotropy. Appl. Phys. Lett. 103, 182401 (2013).
Tetienne, J.-P. et al. Nanosacle imaging and control of domain wall hoping with a nitrogen vacancy center microscope. Science 344, 1366–1369 (2014).
Mizukami, S. et al. Gilbert damping in perpendicularly magnetized Pt/Co/Pt films investigated by all-optical pump-probe technique. Appl. Phys. Lett. 96, 152502 (2010).
Mizukami, S. et al. Gilbert damping in Ni/Co multilayer films exhibiting large perpendicular anisotropy. Appl. Phys. Express 4, 013005 (2011).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Worledge, D. C. et al. Spin torque switching of perpendicular Ta/CoFeB/MgO-based magnetic tunnel junctions. Appl. Phys. Lett. 98, 022501 (2011).
Fukami, S. et al. Current-induced domain wall motion in perpendicularly magnetized CoFeB nanowire. Appl. Phys. Lett. 98, 082504 (2011).
Thiaville, A., Rohart, S., Jué, E., Cros, V. & Fert, A. Dynamics of Dzyaloshinskii domain walls in ultrathin magnetic films. Europhys. Lett. 100, 57002 (2012).
Ryu, K.-S., Thomas, L., Yang, S.-H. & Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 8, 527–533 (2013).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Shepley, P. M. et al. Modification of perpendicular magneticanisotropy and domain wall velocity in Pt/Co/Pt by voltage-induced strain. Sci. Rep. 5, 7921 (2015).
Herrera Diez, L. et al. Controlling magnetic domain wall motion in the creep regime in He+-irradiated CoFeB/MgO films with perpendicular anisotropy. Appl. Phys. Lett. 107, 032401 (2015).
Wang, W. G., Li, M., Hageman, S. & Chien, C. L. Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 11, 64–68 (2012).
Kanai, S., Martin Gajek, M., Worledge, M., Matsukura, F. & Ohno, H. Electric field-induced ferromagnetic resonance in a CoFeB/MgO magnetic tunnel junction under dc bias voltages. Appl. Phys. Lett. 105, 242409 (2014).
Liu, Y. T. et al. Ionic-liquid gating of perpendicularly magnetised CoFeB/MgO thin films. J. Appl. Phys. 120, 023901 (2016).
Mantovan, R. et al. Perpendicular magnetic anisotropy in Ta/CoFeB/MgO systems synthesized on treated SiN/SiO2 substrates for magnetic memories. Thin Solid Films 533, 75–78 (2013).
Lamperti, A., Ahn, S.-M., Ocker, B., Mantovan, R. & Ravelosona, D. Interface width evaluation in thin layered CoFeB/MgO multilayers including Ru or Ta buffer layer by X-ray reflectivity. Thin Solid Films 533, 79–82 (2013).
Acknowledgements
This work was partly funded by the European Community’s Seventh Framework Programme FP7 under grant agreement 257707 (MAGWIRE); the French Agence Nationale de la Recherche (ANR) through the projects ELECMADE, FRIENDS, DIPMEN and COMAG; and by RTRA, C'Nano IdF and LABEX NanoSaclay. Work at UCSD supported by the National Science Foundation under award number DMR-1312750. We thank S. Eimer for experimental assistance, J.P. Adam for micromagnetic simulation, and L. Herrera Diez, L. Ranno, A. Marty, A. Bernand-Mantel, D. Givord, J.P. Jamet, A. Thiaville and V. Jeudy for fruitful discussions.
Author information
Authors and Affiliations
Contributions
W.L. and D.R. designed the experiment. B.O. optimized the deposition of Ta/CoFeB/MgO/Ta films. W.L. fabricated the Ta/CoFeB/MgO/TiO2/ITO structures with the help of G.A. and K.G. W.L. and N.V. performed polar Kerr microscopy measurement and analysed the data. W.L. gave the phenomenological physics description and wrote the manuscript. N.V., E.E.F. and D.R. contributed to the manuscript revision. W.Z. discussed the work. D.R. managed the study.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Note 1, Supplementary References. (PDF 1045 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lin, W., Vernier, N., Agnus, G. et al. Universal domain wall dynamics under electric field in Ta/CoFeB/MgO devices with perpendicular anisotropy. Nat Commun 7, 13532 (2016). https://doi.org/10.1038/ncomms13532
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13532
This article is cited by
-
Skin-effect-mediated magnetoionic control of charge transport in thick layers
Scientific Reports (2024)
-
Spin-orbit-torque-induced magnetic domain wall motion in Ta/CoFe nanowires with sloped perpendicular magnetic anisotropy
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.