Abstract
Thermal conductivity of two-dimensional (2D) materials is of interest for energy storage, nanoelectronics and optoelectronics. Here, we report that the thermal conductivity of molybdenum disulfide can be modified by electrochemical intercalation. We observe distinct behaviour for thin films with vertically aligned basal planes and natural bulk crystals with basal planes aligned parallel to the surface. The thermal conductivity is measured as a function of the degree of lithiation, using time-domain thermoreflectance. The change of thermal conductivity correlates with the lithiation-induced structural and compositional disorder. We further show that the ratio of the in-plane to through-plane thermal conductivity of bulk crystal is enhanced by the disorder. These results suggest that stacking disorder and mixture of phases is an effective mechanism to modify the anisotropic thermal conductivity of 2D materials.
Similar content being viewed by others
Introduction
Two-dimensional (2D) layer-structured materials consist of atomic layers with strong intra-layer covalent bonding stacked together by weak van der Waals bonds. Transition metal dichalcogenides, an important class of 2D materials, have attracted extensive research interest recently due to their unique electronic and chemical properties1. In particular, molybdenum disulfide (MoS2) has been extensively studied for potential applications in nanoelectronics, optoelectronics and flexible electronic devices2,3,4,5. Although the thermal conductivity of single, few-layer and bulk MoS2 has been reported recently, the effects of structural and compositional disorder on the anisotropic thermal conductivity of layered materials, which usually occurs during crystal growth, fabrication and applications (for example, in energy storage, thermoelectrics and nanoelectronics), have not yet been systematically characterized6,7,8.
Guest ions can be intercalated into the van der Waals gaps in MoS2. Intercalation causes changes in the electronic structure, and optical and electrical properties9. Intercalation can also induce structural and compositional disorder, including variations in layer spacing, interaction strengths between adjacent layers and phase transitions10,11,12. By monitoring the potential during electrochemical intercalation, we can control the amount of intercalated ions. Therefore, intercalation provides an effective way to systematically vary the structural and compositional disorder of many 2D materials, and enables investigations of how disorder affects their thermal conductivity.
To understand how thermal conductivity of highly anisotropic materials can be affected by disorder, here we study the thermal conductivity of both pristine and lithium ion-intercalated bulk and thin-film MoS2. In the bulk sample, the MoS2 basal planes are oriented parallel to the surface; whereas, in the thin-film sample, the MoS2 basal planes are vertically aligned. The thermal conductivity of LixMoS2 samples with different degrees (x) of electrochemical interaction of lithium ions were measured by time-domain thermoreflectance (TDTR). We show that lithium ion intercalation has drastically different effects on thermal transport in these different forms of MoS2 due to the differences in crystalline orientation and initial structural disorder. Our most striking observation is that the thermal anisotropy ratio in bulk LixMoS2 crystals increases from 52 (x=0) to 110 (x=0.34) as a result of lithiation-induced stacking disorder and phase transitions. The thermal anisotropy ratio is the ratio of in-plane to through-plane thermal conductivity, an important material parameter in thermal management. The increase in thermal anisotropy with increasing disorder is counter-intuitive: previous studies show that structural disorder typically decreases the thermal anisotropy ratio13,14. Our analysis suggest that the enhanced thermal anisotropy ratio in LixMoS2 bulk crystal is likely due to the combination of phonon-focusing effects and pronounced differences in the in-plane and through-plane length scale of the lithiation-induced disorder.
Results
Sample preparation
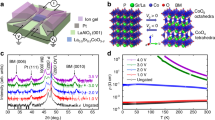
The MoS2 thin-film samples with vertically aligned basal planes were grown by rapid sulfurization of a Mo thin film15. Bulk samples of MoS2 were obtained by mechanical exfoliation of bulk MoS2 crystals (SPI Supplies). The cross-sectional transmission electron microscopy (TEM) image in Fig. 1a reveals that the film thickness is ≈200 nm after chemical-vapour deposition (CVD) growth and the MoS2 atomic layers are predominantly aligned perpendicular to the substrate with the edges of the MoS2 layers exposed to the surface. A typical plan-view TEM image of the vertically aligned MoS2 thin film is shown in Fig. 1b. The thin film is polycrystalline with randomly oriented strip-like or columnar grains. The cross-sectional area of those columnar grains is ∼10 nm wide and several tens of nanometres long. Bulk MoS2 samples, with typical thickness of 10–20 μm, were prepared by standard Scotch tape assisted mechanical exfoliation. A plan-view TEM image of the bulk MoS2 sample is shown in Fig. 1c, where the high-quality atomic plane of MoS2 can be seen.
Spectra obtained at (a) low frequencies and (b) high frequencies. The y-axis is the signal intensity normalized by laser power (S/P) in the unit of counts per second per milliwatt (cps mW−1). The bulk spectrum is shifted up by 50 cps mW−1. Raman spectra for bulk LixMoS2 samples at different degrees of lithiation (x=0, 0.34 and 0.68) at (c) low frequencies, (d) high frequencies. The x=0.34 and x=0 spectra are shifted up by 65 and 130 cps mW−1, respectively.
Thin-film (black) and bulk (red) MoS2 samples, compared with data by Wang et al.55 (dashed line) for thin-film LixMoS2.
(a) Schematics of bulk and thin-film LixMoS2 samples for TDTR measurements. (b) Thermal conductivity of LixMoS2 samples with different degrees of lithiation x. Blue squares: through-plane thermal conductivity of thin-film MoS2; black squares: through-plane thermal conductivity of bulk MoS2; black open squares: in-plane thermal conductivity of bulk MoS2. The minimum thermal conductivity for bulk and thin-film samples are plotted as black and blue dashed lines, respectively. The total uncertainties of the measured thermal conductivity are calculated by taking into account the systematic errors that propagate from uncertainties in the film thickness, laser spot size, and thermal properties of the transducer film and substrate.
Further structural analysis of bulk and thin-film MoS2 samples before lithiation were carried out by X-ray diffraction and Raman spectroscopy. In X-ray diffraction, bulk samples show a strong (002) peak located at 2θ=14.4o, and (004), (006) and (008) peaks with decaying magnitudes, indicating that the basal planes of the bulk sample are parallel to the surface. The thin-film samples have two peaks located at 32.8o and 58.5o, which are due to the diffraction from (100) and (110) planes of individual columnar grains, consistent with our conclusion from the TEM images that the basal planes are vertically aligned (see details in Fig. 5). In contrast to the bulk sample, (002) peak is not observed in the X-ray diffraction spectrum of the thin-film sample because the normal to the (002) planes is parallel to the substrate surface.
(a) X-ray diffraction spectra for MoS2 thin-film samples on sapphire substrate. The two diffraction peaks coincide with the standard X-ray diffraction powder patterns of MoS2 (100) and (110). Therefore, the dominant lattice orientation in the MoS2 thin-film samples are (100) and (110). The diffraction peak at 32.8° and 58.5° corresponds to a lattice constant of 2.73 and 1.58 Å, respectively. (b) Lattice spacing d between MoS2 layers in bulk MoS2 samples. The error bars are calculated by taking into account the experimental errors and the systematic errors that propagate from uncertainties in the fitting of X-ray diffraction spectra. The inset plot is the change of MoS2 (002) peak position with x in LixMoS2.
Figure 2a,b present the Raman spectra of the bulk and thin-film MoS2 samples. To probe the low-frequency interlayer  phonon mode, we used three reflective volume Bragg grating filters (BragGrate notch filters) in combination with a single-pass monochromator to access frequency shifts as small as ∼10 cm−1. The E1g mode (286 cm−1) is observed only in the thin-film samples while the
phonon mode, we used three reflective volume Bragg grating filters (BragGrate notch filters) in combination with a single-pass monochromator to access frequency shifts as small as ∼10 cm−1. The E1g mode (286 cm−1) is observed only in the thin-film samples while the  mode (32 cm−1) is only present in the bulk samples, as expected. According to the Raman selection rules, the E1g mode is forbidden in backscattering experiment on the basal plane of bulk MoS2 (refs 16, 17). However, when the incident light scatters on the surface of edge-terminated MoS2, the corresponding scattering Raman tensor undergoes a rotation transformation, leading to a non-zero differential scattering cross-section and hence the E1g mode can be observed. The observation of the E1g mode in thin-film samples therefore indicates that the basal planes of MoS2 are vertically aligned, consistent with the TEM and X-ray diffraction data. The absence of the
mode (32 cm−1) is only present in the bulk samples, as expected. According to the Raman selection rules, the E1g mode is forbidden in backscattering experiment on the basal plane of bulk MoS2 (refs 16, 17). However, when the incident light scatters on the surface of edge-terminated MoS2, the corresponding scattering Raman tensor undergoes a rotation transformation, leading to a non-zero differential scattering cross-section and hence the E1g mode can be observed. The observation of the E1g mode in thin-film samples therefore indicates that the basal planes of MoS2 are vertically aligned, consistent with the TEM and X-ray diffraction data. The absence of the  mode (which is not forbidden by selection rules) in thin-film samples is probably due to the randomly oriented columnar grains and stacking disorder in CVD-grown samples. In addition, although both A1g at 383 cm−1 and
mode (which is not forbidden by selection rules) in thin-film samples is probably due to the randomly oriented columnar grains and stacking disorder in CVD-grown samples. In addition, although both A1g at 383 cm−1 and  at 408 cm−1 modes are present in bulk and thin-film MoS2, the peak intensity of the out-of-plane
at 408 cm−1 modes are present in bulk and thin-film MoS2, the peak intensity of the out-of-plane  mode is similar to that of the in-plane
mode is similar to that of the in-plane  mode in the bulk sample and ∼3 times that of the
mode in the bulk sample and ∼3 times that of the  mode in the thin-film sample under the same measurement condition. Such preferred excitation of an out-of-plane mode is also consistent with the vertical-aligned crystal texture of the thin-film sample considering the polarization dependence of the Raman scattering cross-section15.
mode in the thin-film sample under the same measurement condition. Such preferred excitation of an out-of-plane mode is also consistent with the vertical-aligned crystal texture of the thin-film sample considering the polarization dependence of the Raman scattering cross-section15.
We carried out electrochemical intercalation of lithium ions in both bulk and thin-film MoS2 to study how lithiation affects the thermal conductivity differently in MoS2 samples with different orientations. Lithium ion intercalation of thin-film MoS2 samples was performed through a galvanostatic discharge process in a glass vial inside a glovebox; electrochemical intercalation of bulk MoS2 samples as performed using a coin cell battery setup18. In both cases, MoS2 samples were used as the working electrode, and the lithium foil was used as the counter and reference electrode.
The discharge curves for thin-film and bulk MoS2 samples are shown in Fig. 3. On lithium ion intercalation, a well-defined plateau is observed at potentials between 1.1 and 1.2 V, as the host lattice of MoS2 undergoes a phase transition from 2H to 1T phase19. The voltage dip at the initial stage of the discharge curve for bulk MoS2 sample is caused by the mass transport limitation of lithium ions. The voltage gradually recovers when the lithium ion transport is facilitated by defects formed during intercalation. The voltage dip was not observed in the discharge process of thin-film MoS2, which can be attributed to the high density of the edge sites in edge-terminated thin-film samples.
We describe the lithium ion intercalation process in the range of 1.1–3.0 V as reaction (1):

We calculate the average lithium composition from the electronic charge transferred to MoS2, based on the theoretical specific charge capacity for full intercalation of 167 mA h g−1 (ref. 19). Hence, by controlling the duration of the galvanostatic discharge process as shown in Fig. 3, vertically aligned LixMoS2 thin-film (x=33 at%, 46 at%, 68 at% and 100 at%) and lithiated bulk samples (20 at%, 40 at%, 60at%, 80 at% and 100 at%) with various lithiation content (x) were prepared.
Since the charge transfer during electrochemical intercalation can have a contribution from complicated side reactions, the actual degree of lithiation (x) for each sample might be different from the calculated values. To determine the actual x in bulk MoS2 samples, inductively coupled plasma mass spectroscopy measurements were performed on one fully lithiated bulk sample. The mass ratio of Li, Mo and S atoms is calculated by measuring the element masses in the bulk LixMoS2 sample with metal coating (total mass≈1 mg). The measured x is 86 at% suggesting reasonable agreement between calculated and measured lithium contents for the lithiation process. The actual x in other bulk LixMoS2 samples is then scaled by the same factor of 0.86.
Thermal conductivity
MoS2 samples (schematics shown in Fig. 4a) were characterized by TDTR to determine the change in thermal conductivity caused by lithium ion intercalation. The TDTR data of both thin-film and bulk LixMoS2 samples are presented as a function of x in Fig. 4b. The through-plane thermal conductivity of thin-film LixMoS2 decreases monotonically from ≈3.4 W m−1 K−1 (x=0) to ≈1.7 W m−1 K−1 (x=1) with increasing lithium content. The through-plane thermal conductivity of bulk LixMoS2 decreases first from ≈2.0 W m−1 K−1 (x=0) to ≈0.4 W m−1 K−1 (x=0.34) and then increases to ≈1.6 W m−1 K−1 (x=0.86). The in-plane thermal conductivity follows a similar trend, which decreases from ≈105 W m−1 K−1 (x=0) to ≈45 W m−1 K−1 (x=0.34) and then increases to ≈80 W m−1 K−1 (x=0.86).
To understand such a drastic decrease of thermal conductivity, we calculated the minimum thermal conductivity  of LixMoS2 using a simplified model by Cahill et al.20 at the high-temperature limit. The minimum thermal conductivity is
of LixMoS2 using a simplified model by Cahill et al.20 at the high-temperature limit. The minimum thermal conductivity is  , where kB is the Boltzmann constant, n is the atomic density (atoms cm−3), vL is the longitudinal speed of sound, and vt is the transverse speed of sound21. Atomic densities of Mo and S atoms in LixMoS2 thin films was measured by Rutherford backscattering spectrometry; vL is measured by picosecond acoustics; vt is measured by detecting surface acoustic waves using a phase-shift mask22. We accounted for the change of atomic density and longitudinal speed of sound due to lithiation. More details can be found in the ‘Methods’ section and the Supplementary Methods.
, where kB is the Boltzmann constant, n is the atomic density (atoms cm−3), vL is the longitudinal speed of sound, and vt is the transverse speed of sound21. Atomic densities of Mo and S atoms in LixMoS2 thin films was measured by Rutherford backscattering spectrometry; vL is measured by picosecond acoustics; vt is measured by detecting surface acoustic waves using a phase-shift mask22. We accounted for the change of atomic density and longitudinal speed of sound due to lithiation. More details can be found in the ‘Methods’ section and the Supplementary Methods.
In thin-film LixMoS2 samples, the polycrystalline structure with randomly oriented columnar grains is transverse isotropic so that this conventional minimum thermal conductivity model can be applied. In the bulk LixMoS2 samples, however, the strongly anisotropic structure introduces a significant phonon-focusing effect23, which suppresses the through-plane average group velocity due to the relatively high in-plane group velocity. We adopted the modified minimum thermal conductivity model recently proposed by Zhen et al.41 (equation S(7) in their Supplementary Material) and followed their procedure to calculate the minimum thermal conductivity of bulk LixMoS2 (see details in Supplementary Note 1 with parameters shown in Supplementary Table 1).
If the measured lowest through-plane thermal conductivity of bulk or thin-film LixMoS2 agrees with the predicted minimum thermal conductivity, the phonons are glass-like lattice vibrations in a disordered crystal at this composition. The calculated minimum thermal conductivity of bulk and thin-film LixMoS2 is plotted in Fig. 4b as dashed lines. Both measured through-plane thermal conductivity of bulk and thin-film LixMoS2 is higher than the predicted minimum thermal conductivity, which suggests that a significant fraction of the phonons in these samples are propagating modes.
Interlayer distance characterization
Large expansion in layer spacing along the c-axis is often observed after intercalation of large-diameter molecules or ions11,24. We collected X-ray diffraction spectra for bulk LixMoS2 samples with different amount of lithium ion intercalation (0≤x≤0.86) to determine the change in layer spacing due to lithium ion intercalation. Samples were placed inside an air-tight sample holder with a beryllium (Be) window in an argon-filled glovebox before they were transferred out for X-ray diffraction characterization. Figure 5b shows that the (002) peak of the pristine MoS2 is located at 14.40o, and the peak position downshifts to 14.28o for Li0.86MoS2. The corresponding layer spacing is 6.16 and 6.19 Å for pristine MoS2 and Li0.86MoS2, respectively, a 0.5% change in lattice constant. We estimate the uncertainty of the lattice spacing measurement as ≈0.6%. The weak dependence of lattice constant on lithium content is consistent with the fact the effective ionic radius of lithium ion25 (76 pm) is slightly smaller than the octahedral site in the van der Waals gap of in MoS2. If we assume an effective ionic radius of S2− as 1.84 Å, and close packing of S2− atoms, the radius of the octahedral site is 76 pm (ref. 25). Our measurement on the layer spacing of Li0.86MoS2 agrees with recent observations reporting on minimal change in interlayer distance of LiMoS2 (refs 26, 27).
Elastic constants
We further measured elastic properties using pump-probe techniques to help understand the thermal conductivity change in our samples. Polycrystalline MoS2 thin films with vertically aligned basal planes are transverse isotropic, which has five effective independent averaged elastic constants:  ,
,  ,
,  ,
,  and
and  . Figure 6 plots the effective
. Figure 6 plots the effective  and
and  elastic constants of thin-film LixMoS2. The elastic constant
elastic constants of thin-film LixMoS2. The elastic constant  of LixMoS2 thin film decreases from 147 GPa (x=0) to 121 GPa (x=1). Even though the density of LixMoS2 thin films increases by 11% from x=0 to x=1, the decrease of longitudinal speed of sound from 5,720 ms−1 to 4,930 ms−1 (measured by picosecond acoustics) dominates the decrease of
of LixMoS2 thin film decreases from 147 GPa (x=0) to 121 GPa (x=1). Even though the density of LixMoS2 thin films increases by 11% from x=0 to x=1, the decrease of longitudinal speed of sound from 5,720 ms−1 to 4,930 ms−1 (measured by picosecond acoustics) dominates the decrease of  . The elastic constant
. The elastic constant  increases from 22 GPa (x=0) to 32 GPa (x=0.34) and then decreases to 18 GPa (x=1). We do not yet understand the trend of the elastic constants of thin-film LixMoS2 changing with x. One possible reason is the combined effect of increasing binding energy due to the intercalation of lithium ions and increasing structural and compositional disorder (for example, point defects and mixture of phases). More measurement details are described in the ‘Methods’ section and Supplementary Methods.
increases from 22 GPa (x=0) to 32 GPa (x=0.34) and then decreases to 18 GPa (x=1). We do not yet understand the trend of the elastic constants of thin-film LixMoS2 changing with x. One possible reason is the combined effect of increasing binding energy due to the intercalation of lithium ions and increasing structural and compositional disorder (for example, point defects and mixture of phases). More measurement details are described in the ‘Methods’ section and Supplementary Methods.
 (square) decreases from 147 GPa (x=0) to 121 GPa (x=1).
(square) decreases from 147 GPa (x=0) to 121 GPa (x=1).  (diamond) increases from 22 GPa (x=0) to 32 GPa (x=0.34) and then decreases to 18 GPa (x=1). As comparison, the C33 of bulk LixMoS2 samples (circle) are also plotted. C33 gradually changes from 52 GPa (x=0) to 58 GPa (x=0.86) with a transition point at x≈0.34. The error bars are calculated by taking into account the experimental errors and the systematic errors that propagate from uncertainties in the Al film thickness, LixMoS2 film density and the input elastic constants.
(diamond) increases from 22 GPa (x=0) to 32 GPa (x=0.34) and then decreases to 18 GPa (x=1). As comparison, the C33 of bulk LixMoS2 samples (circle) are also plotted. C33 gradually changes from 52 GPa (x=0) to 58 GPa (x=0.86) with a transition point at x≈0.34. The error bars are calculated by taking into account the experimental errors and the systematic errors that propagate from uncertainties in the Al film thickness, LixMoS2 film density and the input elastic constants.
The elastic constants of bulk LixMoS2 samples C33 are also plotted in Fig. 6. C33 gradually changes from 52 GPa (x=0) to 58 GPa (x=0.86) with a transition point at x ≈0.34, which suggests a phase transition in bulk LixMoS2.
Raman spectroscopy
We used Raman spectroscopy to further characterize lithiation-induced structural and compositional disorder of bulk LixMoS2 to gain more insights about other phonon scattering mechanisms that could lead to the thermal conductivity change. All bulk LixMoS2 samples except pristine MoS2 were loaded inside the glovebox into a home-made air-free sample holder sealed by O-ring and screw-on connectors and measured through the glass window of the holder. As shown in Fig. 2c,d, the intensity of the low-frequency peak at ∼32 cm−1 corresponding to the  shear mode in 2H-MoS2 decreases as the degree of lithiation (x) increases. The decreasing peak intensity of
shear mode in 2H-MoS2 decreases as the degree of lithiation (x) increases. The decreasing peak intensity of  mode is attributed to the increasing stacking disorder resulting from the lithium ion intercalation. In the 2H to 1T phase transition, the stacking of Mo atom planes changes from ABA (two molecular layers per unit cell) to AA (one molecular plane per unit cell)28,29. As the atomic structure of the MoS2 layer changes from prismatic aBa (2H) structure to octahedral aBc (1T) (upper letters correspond to Mo planes, lowercase letters correspond to the S planes)30, the high-frequency
mode is attributed to the increasing stacking disorder resulting from the lithium ion intercalation. In the 2H to 1T phase transition, the stacking of Mo atom planes changes from ABA (two molecular layers per unit cell) to AA (one molecular plane per unit cell)28,29. As the atomic structure of the MoS2 layer changes from prismatic aBa (2H) structure to octahedral aBc (1T) (upper letters correspond to Mo planes, lowercase letters correspond to the S planes)30, the high-frequency  and A1g modes redshift from 383 to 377 cm−1 and 408 to 402 cm−1, respectively, as the lithium content increases from x=0 to x=0.86. The observed redshift is mainly attributed to the intra-layer shift of the S atom during the 2H to 1T phase change31.
and A1g modes redshift from 383 to 377 cm−1 and 408 to 402 cm−1, respectively, as the lithium content increases from x=0 to x=0.86. The observed redshift is mainly attributed to the intra-layer shift of the S atom during the 2H to 1T phase change31.
Discussion
Lithium ion intercalation into van der Waals gap could change the thermal transport of MoS2 due to several distinct mechanisms. First, the 2D layer spacing might change as a result of lithiation10,11,19. In addition, a recent theoretical work found that intercalated lithium ions enhances the binding energy through orbital hybridizations between cations (lithium ions) and anions (MoS2) (ref. 32). Second, the intercalated lithium donates electrons to MoS2, which changes the oxidation states of Mo, and hence the electronic properties of MoS2 (refs 33, 34). Finally, intercalation drives a phase transition from the semiconductor 2H phase to the metallic 1T phase19.
The increase of electrical conductivity caused by the phase transition from the semiconductor 2H to metallic 1T phase cannot explain the changes in the in-plane thermal conductivity of bulk LixMoS2. A recent study shows the in-plane electrical conductivity of the metallic phase (1T) LiMoS2 is ≈300 S cm−1, ∼500 times that of the semiconducting phase (2H) MoS2 (ref. 35). The corresponding electronic contribution to the total thermal conductivity, predicted by the Wiedemann–Franz law, is only 0.2 W m−1 K−1 in LiMoS2. Such a small increase cannot be the predominant mechanism to account for the in-plane thermal conductivity change in bulk LixMoS2 from 45 to 80 W m−1 K−1 for x=0.34 to 0.86.
We applied the Leibfried–Schlomann (LS) equation to evaluate the effect of changes in lattice spacing, elastic constants and mass density on the thermal conductivity of LixMoS2. The LS equation only considers changes in three-phonon scattering rates and takes the form  , where
, where  is the mass of a unit cell, δ3 corresponds to atomic volume, T is temperature, γ is the Grüneisen parameter for the relevant direction of heat transfer, ωD is the Debye frequency for the relevant direction of heat transfer, and B is an amalgam of physical constants36. Using the Debye frequency defined as ωD=vDkD, where kD is the Debye cutoff vector, vD is the speed of sound, we can express the thermal conductivity
is the mass of a unit cell, δ3 corresponds to atomic volume, T is temperature, γ is the Grüneisen parameter for the relevant direction of heat transfer, ωD is the Debye frequency for the relevant direction of heat transfer, and B is an amalgam of physical constants36. Using the Debye frequency defined as ωD=vDkD, where kD is the Debye cutoff vector, vD is the speed of sound, we can express the thermal conductivity  , where B′ is a constant, Cij is the elastic constant and ρ is the density. Considering a 4% increase in atomic mass of the unit cell, 11% increase in density, 18% decrease in the effective elastic constant
, where B′ is a constant, Cij is the elastic constant and ρ is the density. Considering a 4% increase in atomic mass of the unit cell, 11% increase in density, 18% decrease in the effective elastic constant  and 0.5% increase in lattice spacing for LixMoS2 thin films from x=0 to 1, the LS equation predicts a 33% decrease in the through-plane thermal conductivity, if we assume that the change in Grüneisen parameter is negligible. Since TDTR measurement shows that through-plane thermal conductivity of thin-film LixMoS2 decreases continuously from ≈3.4 to ≈1.7 W m−1 K−1 from x=0 to 1, we conclude that the softening of the lattice is a significant contribution to the reduction in thermal conductivity in LixMoS2 thin films.
and 0.5% increase in lattice spacing for LixMoS2 thin films from x=0 to 1, the LS equation predicts a 33% decrease in the through-plane thermal conductivity, if we assume that the change in Grüneisen parameter is negligible. Since TDTR measurement shows that through-plane thermal conductivity of thin-film LixMoS2 decreases continuously from ≈3.4 to ≈1.7 W m−1 K−1 from x=0 to 1, we conclude that the softening of the lattice is a significant contribution to the reduction in thermal conductivity in LixMoS2 thin films.
Similarly for the bulk samples, if we consider the changes of elastic constants, lattice spacing, density and atomic mass in a unit cell to be 11%, 0.5%, 3.3%, 3.8%, respectively from x=0 to x=0.86, the through-plane thermal conductivity is estimated to increase by ≈14%. Under the same assumptions, the through-plane thermal conductivity of LixMoS2 should increase by ≈5% from x=0 to x=0.34. Such a small change and different trends indicate the lattice expansion and elastic constant change cannot explain the pronounced change in the through-plane thermal conductivity that we observed in bulk LixMoS2 samples.
Interestingly, Raman spectroscopy of bulk LixMoS2 samples revealed that the A1g mode peak splits into two peaks at 402 and 408 cm−1, while the E2g2 peak slightly broadens in the x=0.34 sample suggesting the co-existence of 2H and 1T phases. The peak splitting was related to the Davydov pairs of the optical phonon branches due to the splitting of intra-layer modes caused by the interlayer interaction when the lithium content is below x=0.34 (ref. 29). We do not yet have a good understanding why the split of  peak is not clearly observed in the x=0.34 sample but it may be related to the intermediate atomic structure in the not-completed phase-change process. Both high- and low-frequency Raman spectra provide evidence of increasing stacking disorder and mixture of phases during lithiation.
peak is not clearly observed in the x=0.34 sample but it may be related to the intermediate atomic structure in the not-completed phase-change process. Both high- and low-frequency Raman spectra provide evidence of increasing stacking disorder and mixture of phases during lithiation.
As a result of co-existence of two phases and increasing stacking disorder, phonon-boundary scattering increases and thermal conductivity in both through-plane and in-plane directions decrease until the largest degree of disorder is reached at x≈0.34. As intercalation proceeds, the bulk MoS2 sample becomes increasingly dominated by the 1T phase (0.34<x<0.86) and the phonon-boundary scattering rate decreases, and hence the thermal conductivity starts to increase again.
Our most striking observation is that the thermal anisotropy ratio of the bulk LixMoS2 increases from 52 (x=0) to 110 (x=0.34) with increasing disorder. This trend of thermal anisotropy ratio change with respect to the structural defects or disorder is indeed counter-intuitive and beyond any previous works. For example, a recent study of graphene oxide films by Renteria et al.14 shows an increase of thermal anisotropy ratio attributed to decreasing disorder after annealing. Luckyanova et al.13 found that the thermal anisotropy ratio decreases with interface atomic mixing in superlattices. The thermal anisotropy ratio of a disordered WSe2 crystal, ≈30, is similar to the anisotropy ratio of well-ordered WSe2 crystals37,38. Our measurements of lithiated MoS2 bulk crystal demonstrate that lithiation-induced stacking disorder and phase transition can increase the thermal anisotropy ratio.
Phonon–phonon and phonon-boundary scattering are the two possible major scattering mechanisms in bulk LixMoS2. As discussed above, we estimated the change of the intrinsic lattice thermal conductivity that is limited by phonon–phonon interactions due to the changes in elastic constants and atomic densities. The predicted change in the intrinsic phonon–phonon scattering rates is small and we therefore exclude changes in phonon–phonon scattering as the dominant mechanism in lithiated bulk LixMoS2. The combination of our Raman spectroscopy data—and the pronounced change in the thermal conductivity of bulk samples—suggest that phonon scattering in bulk LixMoS2 is dominated by phonon-boundary scattering due to stacking disorder created by the phase transition.
In highly anisotropic layered materials, boundary-limited phonon mean-free paths in the in-plane and through-plane directions can differ by orders-of-magnitude due to the combination of phonon-focusing effects and divergent length scales of disorder in the in-plane versus through-plane directions. When boundary scattering dominates the phonon mean-free paths, phonon-focusing produces anisotropic phonon mean-free path even in cubic crystals39. A recent modelling study40 demonstrates that thin films of graphite can maintain their high in-plane thermal conductivity even for film thickness as small as 10 nm. In other words, in highly anisotropic crystals, boundary scattering along the c-axis has only a minimal effect on the ab-plane thermal conductivity. Further experimental evidence of this effect comes from a recent experimental study41 of CVD-grown graphite thin films where the phonon mean-free paths are different by more than an order of magnitude: the in-plane phonon mean-free path is ≈300 nm and the through-plane mean-free path is <20 nm.
Although a sophisticated phonon transport model is needed to rigorously analyse how different phonon branches are affected by boundaries and other forms of disorder, we can estimate how the boundary-limited phonon mean-free paths in the c-axis Lc and in the ab-plane Lab change with x by comparing our measured thermal conductivities with previous studies. We compare the measured in-plane thermal conductivities of bulk LixMoS2 with the thermal conductivity of single-layer MoS2 predicted by a first-principle based Boltzmann transport equation calculation as a function of phonon-boundary scattering42. This comparison suggests Lab decreases from >1 μm to ≈200 nm for x=0–0.34.
Similarly, the comparison between our measured through-plane thermal conductivity of bulk LixMoS2 and that predicted by first-principle based Boltzmann transport equation calculations suggests Lc≈200 nm at x=0 (ref. 43). The lowest through-plane thermal conductivity in our bulk samples is comparable to that of turbostratic nano-crystalline MoS2 thin films deposited by magnetron sputtering36. In the turbostratic thin-film samples, the length of coherent stacking is unknown but should be less than the grain size ≈5 nm (ref. 44). The similar stacking disorder in our bulk samples LixMoS2 suggests the Lc<5 nm at x=0.34. A plausible explanation for this pronounced phonon mean-free path difference is that the lithium ions diffuse more easily along the in-plane direction compared with the through-plane direction. As a result, the density of disorder caused by lithium ion intercalation is less pronounced along the in-plane direction, Both Lc and Lab reach their minimum values with the maximum mixing of the two phases at x=0.34.
Finally, we noticed that the through-plane thermal conductivity of thin-film LixMoS2 sample is much lower than the in-plane thermal conductivity of the bulk LixMoS2 sample, and the trends in through-plane thermal conductivity as a function of x are different for bulk and thin-film samples. Compared with bulk MoS2, the basal planes in LixMoS2 thin films contain high density of defects, especially point defects and oxygen impurities introduced during the chemical-vapour growth process of the thin sample. Defects can significantly reduce the thermal conductivity of 2D materials by enhancing phonon scattering45,46,47. Although the semiconductor 2H to metallic 1T phase transition also occurs in the thin-film sample as indicated by the plateau in the discharge curve, unlike the bulk sample, the thermal conductivity of defective thin-film LixMoS2 is more sensitive to lattice softening than stacking disorder47. On the basis of our elastic constants measurement results and estimation by LS equation, we attribute the decreasing trend of thermal conductivity in LixMoS2 thin films with increasing lithium content x to the softening of the lattice and the increased phonon-boundary scattering at the grain or phase boundaries48.
We investigated the anisotropic thermal transport in bulk crystal and CVD-grown thin-film MoS2 samples with different amounts of lithium ion intercalation. We demonstrated that intercalation impacts thermal transport in bulk and thin-film samples differently, depending on the crystalline quality of the 2D structure. In addition, we found that lithiation tends to reduce the phonon mean-free path more along the through-plane direction in LixMoS2, rather than the in-plane direction, until the largest degree of disorder is reached at x≈0.34, leading to a significant increase in the thermal anisotropy ratio. This work provides insight on the impact of structural and compositional changes (for example, disorder, layer spacing and interfaces) on 2D materials applications, where thermal management is crucial.
Methods
Synthesis of thin-film MoS2
MoS2 thin films were grown on sapphire in a horizontal quartz tube furnace (Lindberg/Blue M 1,100 °C Tube Furnace with 1 in diameter tube). The substrate was pre-deposited with 70 nm Mo thin film, which shows electrical conductivity of about 4.8 × 105 S cm−1. The Mo film was then placed in the centre of the tube furnace and S powder (Sigma Aldrich) was loaded in a ceramic crucible on the upstream cooler zone of the tube furnace. The temperature of the S was kept between 200 and 250 °C when the centre of the tube furnace reaches 750 °C. The tube was initially purged with Ar gas (100 sccm) for 10 min to remove oxygen. During the chemical-vapour growth of MoS2 thin film, Ar gas flow rate was kept at 100 sccm, and the temperature of the tube furnace was quickly increased to 750 °C in 15 min and then held for 20 min, followed by natural cooling down.
Electrochemical intercalation of lithium
The thin-film and bulk MoS2 samples were assembled into battery configuration inside an argon-filled glovebox for lithium ion intercalation. Lithiation of thin-film MoS2 was performed in a glass vial. The thin-film MoS2 and a piece of lithium foil were used as the cathode and anode, respectively, and 1.0 M LiPF6 in 30:70 (vol%) ethylene carbonate/dimethyl carbonate (Sol-Rite) as the electrolyte. The thin-film sample was wrapped around by a piece of stainless steel foil, which was used as the electrical contact. The discharge current was 14 μA. The lithium ion intercalation of the bulk MoS2 was carried out using 2025 coin cells, with MoS2 as the cathode, lithium foil as the anode, 1.0 M LiPF6 in 30:70 (vol%) ethylene carbonate/dimethyl carbonate as electrolyte, and a Celgard 2400 separator. The discharge current used for the bulk MoS2 was 10 μA. After the discharge process, all samples were relaxed for days before they were cleaned by diethyl carbonate (anhydrous, Sigma Aldrich) inside the glovebox to remove the electrolyte left on the sample surfaces. Samples were sealed in air-tight aluminium pouches before they were transferred out of the glovebox and mailed from Ann Arbor, MI to Urbana, IL for sputtering deposition of Al or NbV for TDTR measurements.
TDTR measurements
TDTR was used to measure the thermal conductivity of bulk and thin-film intercalated MoS2. The experimental setup and model details on TDTR can be found elsewhere49,50. All the other details are shown in Supplementary Methods.
Before the TDTR measurements, metal thin films (Al or NbV) were deposited on the samples by magnetron sputtering. Samples were exposed to air for only 3–5 s before the process chamber was pumped down. We measured through-plane thermal conductivity of MoS2 at f=9.8 MHz, with a 1/e2 radius of the focused laser beams w0=11.7 μm. The thermal conductivity of MoS2 thin films reported in this work is the apparent (or effective) thermal conductivity of the thin film, including the two interfacial thermal resistances between MoS2 and the neighbouring materials, besides the intrinsic thermal resistance of the film. The sensitivity of the TDTR data to the in-plane thermal conductivity of LixMoS2 thin film is small, which makes this in-plane thermal conductivity challenging to measure.
We measured through-plane thermal conductivity of bulk MoS2 at f=9.8 MHz with w0=11.7 μm. The thermal conductivity of bulk MoS2 and the interfacial thermal conductance between Al and MoS2 were fitted. The in-plane thermal conductivity of bulk MoS2 was measured using the beam-offset TDTR method as detailed in ref. 6, at f=1.1 MHz with w0≈27 μm. NbV transducer was used in this measurement, whose thermal properties were characterized in ref. 51. The total uncertainties of the measured thermal conductivity are calculated by taking into account the systematic errors that propagate from uncertainties in the film thickness, laser spot size and thermal properties of the transducer film and substrate. We have tried to use a 65 nm-thick NbV thin film as the metal transducer to measure in-plane thermal conductivity Λ of MoS2 thin film by TDTR method. However, due to the relatively low thermal conductance of the film, that is,  , where d is the thickness of the thin film the in-plane heat flow in metal transducer and the Sapphire substrate instead of the MoS2 thin film dominates the lateral heat flow which lead to a low sensitivity to the thin film in-plane thermal conductivity in TDTR measurement. The thermal conductivity measurements are performed at different locations on our samples to confirm the homogeneous distribution of lithium.
, where d is the thickness of the thin film the in-plane heat flow in metal transducer and the Sapphire substrate instead of the MoS2 thin film dominates the lateral heat flow which lead to a low sensitivity to the thin film in-plane thermal conductivity in TDTR measurement. The thermal conductivity measurements are performed at different locations on our samples to confirm the homogeneous distribution of lithium.
Elastic constants measurement
The elastic constants of the LixMoS2 thin films were measured using pump-probe techniques. The polycrystalline MoS2 thin film with vertically aligned basal planes is transverse isotropic, which has five effective independent averaged elastic constants:  ,
,  ,
,  ,
,  and
and  . The error bars, ∼20%, are calculated by taking into account the experimental errors and the systematic errors that propagate from uncertainties in the Al film thickness, LixMoS2 film density and the input elastic constants.
. The error bars, ∼20%, are calculated by taking into account the experimental errors and the systematic errors that propagate from uncertainties in the Al film thickness, LixMoS2 film density and the input elastic constants.
Similarly, the elastic constants of bulk LixMoS2 (C33) were calculated from  , where ρ is calculated based on literature values of bulk MoS2 samples (5.06 g cm−3) and the degree of lithiation x, ρ=5.06(160+7x)/160. We deposited ≈10 nm NbV on the bulk LixMoS2 samples and used picosecond interferometry52 to determine the longitudinal speed of sound vL. In the picosecond interferometry, the Brillouin scattering frequency fB is related to the longitudinal speed of sound v by fB=2nvL/λ, where n is the index of refraction of the sample and λ is the laser wavelength. We used the literature value of n≈4.7 at λ=785 nm in this calculation53. This measurement of picosecond interferometry uses the same experiment setup as TDTR. All the other details are shown in Supplementary Methods.
, where ρ is calculated based on literature values of bulk MoS2 samples (5.06 g cm−3) and the degree of lithiation x, ρ=5.06(160+7x)/160. We deposited ≈10 nm NbV on the bulk LixMoS2 samples and used picosecond interferometry52 to determine the longitudinal speed of sound vL. In the picosecond interferometry, the Brillouin scattering frequency fB is related to the longitudinal speed of sound v by fB=2nvL/λ, where n is the index of refraction of the sample and λ is the laser wavelength. We used the literature value of n≈4.7 at λ=785 nm in this calculation53. This measurement of picosecond interferometry uses the same experiment setup as TDTR. All the other details are shown in Supplementary Methods.
Raman spectroscopy measurement
The Raman spectroscopy measurements were performed using an Acton Insight spectrometer (Princeton Instruments). The excitation wavelength is 488 nm from a Spectra-Physics Cyan (CDRH) solid-state laser. A power of ≈1 mW is used to avoid excessive sample heating. We used an optical configuration similar to that d multilayer graphene54; the laser plasma lines are removed using a BragGrate bandpass filter (OptiGrate), while the Rayleigh line is suppressed using three BragGrate notch filters (OptiGrate) in series each with an optical density 3 and a spectral bandwidth 5–10 cm−1. The backscattered signal was collected through a 20 × objective (numerical aperture=0.4) with laser spot size ≈10 μm at the sample surface and dispersed by a 1,200 g mm−1 grating with a spectral resolution ≈2 cm−1.
Additional structural analysis
TEM specimens of the thin-film MoS2 samples were prepared using a FEI FIB200 Focused Ion Beam system. The bulk TEM specimens were prepared by hand grinding and ultrasonication in ethanol. TEM was performed using a Hitachi HD 2300 STEM. X-ray diffraction was performed using a Rigaku SmartLab x-ray diffractometer.
Data availability
The data supporting the main findings of this study are available from the corresponding authors on request.
Additional information
How to cite this article: Zhu, G. et al. Tuning thermal conductivity in molybdenum disulfide by electrochemical intercalation. Nat. Commun. 7, 13211 doi: 10.1038/ncomms13211 (2016).
References
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Wang, H. et al. Integrated circuits based on bilayer MoS2 transistors. Nano. Lett. 12, 4674–4680 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 7, 490–493 (2012).
Cheng, R. et al. Few-layer molybdenum disulfide transistors and circuits for high-speed flexible electronics. Nat. Commun. 5, 5143 (2014).
Wan, C. et al. Flexible n-type thermoelectric materials by organic intercalation of layered transition metal dichalcogenide TiS2 . Nat. Mater. 14, 622–627 (2015).
Liu, J., Choi, G.-M. & Cahill, D. G. Measurement of the anisotropic thermal conductivity of molybdenum disulfide by the time-resolved magneto-optic Kerr effect. J. Appl. Phys. 116, 233107 (2014).
Jo, I., Pettes, M. T., Ou, E., Wu, W. & Shi, L. Basal-plane thermal conductivity of few-layer molybdenum disulfide. Appl. Phys. Lett. 104, 201902 (2014).
Yan, R. et al. Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent raman spectroscopy. ACS Nano 8, 986–993 (2014).
Xiong, F. et al. Li intercalation in MoS2: in situ observation of its dynamics and tuning optical and electrical properties. Nano. Lett. 15, 6777–6784 (2015).
Py, M. A. & Haering, R. R. Structural destabilization induced by lithium intercalation in MoS2 and related compounds. Can. J. Phys. 61, 76–84 (1983).
Imanishi, N., Toyoda, M., Takeda, Y. & Yamamoto, O. Study on lithium intercalation into MoS2 . Solid State Ionics 58, 333–338 (1992).
Yoo, E. et al. Large reversible Li storage of graphene nanosheet families for use in rechargeable lithium ion batteries. Nano. Lett. 8, 2277–2282 (2008).
Luckyanova, M. N. et al. Anisotropy of the thermal conductivity in GaAs/AlAs superlattices. Nano. Lett. 13, 3973–3977 (2013).
Renteria, J. D. et al. Strongly anisotropic thermal conductivity of free-standing reduced graphene oxide films annealed at high temperature. Adv. Funct. Mater. 25, 4664–4672 (2015).
Kong, D. et al. Synthesis of MoS2 and MoSe2 films with vertically aligned layers. Nano. Lett. 13, 1341–1347 (2013).
Chen, J. M. & Wang, C. S. Second order Raman spectrum of MoS2 . Solid State Commun. 14, 857–860 (1974).
Zhang, X. et al. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 44, 2757–2785 (2015).
Zhang, R., Upreti, S. & Stanley Whittingham, M. Tin-iron based nano-materials as anodes for Li-Ion batteries. J. Electrochem. Soc. 158, A1498–A1504 (2011).
Stephenson, T., Li, Z., Olsen, B. & Mitlin, D. Lithium ion battery applications of molybdenum disulfide (MoS2) nanocomposites. Energy Environ. Sci. 7, 209–231 (2014).
Cahill, D. G., Watson, S. K. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131–6140 (1992).
Cahill, D. G., Melville, A., Schlom, D. G. & Zurbuchen, M. A. Low thermal conductivity of CsBiNb2O7 epitaxial layers. Appl. Phys. Lett. 96, 121903 (2010).
Li, D., Zhao, P., Zhao, J.-C. & Cahill, D. G. Generation and detection of gigahertz surface acoustic waves using an elastomeric phase-shift mask. J. Appl. Phys. 114, 143102 (2013).
Taylor, B., Maris, H. J. & Elbaum, C. Phonon focusing in solids. Phys. Rev. Lett. 23, 416–419 (1969).
Xiao, J. et al. Electrochemically induced high capacity displacement reaction of PEO/MoS2/graphene nanocomposites with lithium. Adv. Funct. Mater. 21, 2840–2846 (2011).
Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Azhagurajan, M., Kajita, T., Itoh, T., Kim, Y.-G. & Itaya, K. In situ visualization of lithium ion intercalation into MoS2 single crystals using differential optical microscopy with atomic layer resolution. J. Am. Chem. Soc. 138, 3355–3361 (2016).
Wang, L., Xu, Z., Wang, W. & Bai, X. Atomic mechanism of dynamic electrochemical lithiation processes of MoS2 nanosheets. J. Am. Chem. Soc. 136, 6693–6697 (2014).
Wypych, F. & Schollhorn, R. 1T-MoS2, a new metallic modification of molybdenum disulfide. J. Chem. Soc. Chem. Commun. 19, 1386–1388 (1992).
Julien, C., Sekine, T. & Balkanski, M. Lattice dynamics of lithium intercalated MoS2 . Solid State Ionics 48, 225–229 (1991).
Dungey, K. E., Curtis, M. D. & Penner-Hahn, J. E. Structural characterization and thermal stability of MoS2 intercalation compounds. Chem. Mater. 10, 2152–2161 (1998).
Lukowski, M. A. et al. Enhanced hydrogen evolution catalysis from chemically exfoliated metallic MoS2 nanosheets. J. Am. Chem. Soc. 135, 10274–10277 (2013).
Ahmed, T., Modine, N. A. & Zhu, J.-X. Bonding between graphene and MoS2 monolayers without and with Li intercalation. Appl. Phys. Lett. 107, 043903 (2015).
Julien, C. M. Lithium intercalated compounds: charge transfer and related properties. Mater. Sci. Engineer. Rep. 40, 47–102 (2003).
Rocquefelte, X. et al. Mo cluster formation in the intercalation compound LiMoS2 . Phys. Rev. B 62, 2397–2400 (2000).
Xiong, F. et al. Li intercalation in MoS2: in situ observation of its dynamics and tuning optical and electrical properties. Nano. Lett. 15, 6777–6784 (2015).
Muratore, C. et al. Cross-plane thermal properties of transition metal dichalcogenides. Appl. Phys. Lett. 102, 081604 (2013).
Chiritescu, C. et al. Ultralow thermal conductivity in disordered, layered WSe2 crystals. Science 315, 351–353 (2007).
Mavrokefalos, A., Nguyen, N. T., Pettes, M. T., Johnson, D. C. & Shi, L. In-plane thermal conductivity of disordered layered WSe2 and (W)x(WSe2)y superlattice films. Appl. Phys. Lett. 91, 171912 (2007).
McCurdy, A. K., Maris, H. J. & Elbaum, C. Anisotropic heat conduction in cubic crystals in the boundary scattering regime. Phys. Rev. B 2, 4077–4083 (1970).
Minnich, A. J. Thermal phonon boundary scattering in anisotropic thin films. Appl. Phys. Lett. 107, 183106 (2015).
Zheng, Q., Braun, P. V. & Cahill, D. G. Thermal conductivity of graphite thin films grown by low temperature chemical vapor deposition on Ni (111). Adv. Mater. Interfaces 3, 1600234 (2016).
Gu, X. & Yang, R. Phonon transport in single-layer transition metal dichalcogenides: a first-principles study. Appl. Phys. Lett. 105, 131903 (2014).
Gu, X., Li, B. & Yang, R. Layer thickness-dependent phonon properties and thermal conductivity of MoS2 . J. Appl. Phys. 119, 085106 (2016).
Muratore, C. et al. Thermal anisotropy in nano-crystalline MoS2 thin films. Phys. Chem. Chem. Phys. 16, 1008–1014 (2014).
Ding, Z., Pei, Q.-X., Jiang, J.-W. & Zhang, Y.-W. Manipulating the thermal conductivity of monolayer MoS2 via lattice defect and strain engineering. J. Phys. Chem. C 119, 16358–16365 (2015).
Pop, E., Varshney, V. & Roy, A. K. Thermal properties of graphene: fundamentals and applications. MRS Bull. 37, 1273–1281 (2012).
Erhart, P., Hyldgaard, P. & Lindroth, D. O. Microscopic origin of thermal conductivity reduction in disordered van der Waals solids. Chem. Mater. 27, 5511–5518 (2015).
Guilmeau, E., Maignan, A., Wan, C. & Koumoto, K. On the effects of substitution, intercalation, non-stoichiometry and block layer concept in TiS2 based thermoelectrics. Phys. Chem. Chem. Phys. 17, 24541–24555 (2015).
Liu, J. et al. Simultaneous measurement of thermal conductivity and heat capacity of bulk and thin film materials using frequency-dependent transient thermoreflectance method. Rev. Sci. Instrum. 84, 034902 (2013).
Cahill, D. G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 75, 5119–5122 (2004).
Feser, J. P., Liu, J. & Cahill, D. G. Pump-probe measurements of the thermal conductivity tensor for materials lacking in-plane symmetry. Rev. Sci. Instrum. 85, 104903 (2014).
O’Hara, K. E., Hu, X. & Cahill, D. G. Characterization of nanostructured metal films by picosecond acoustics and interferometry. J. Appl. Phys. 90, 4852–4858 (2001).
Beal, A. R. & Hughes, H. P. Kramers-Kronig analysis of the reflectivity spectra of 2H-MoS2, 2H-MoSe2 and 2H-MoTe2 . J. Phys. C . 12, 881 (1979).
Tan, P. H. et al. The shear mode of multilayer graphene. Nat. Mater. 11, 294–300 (2012).
Wang, H. et al. MoSe2 and WSe2 Nanofilms with vertically aligned molecular layers on curved and rough surfaces. Nano. Lett. 13, 3426–3433 (2013).
Acknowledgements
We thank the analysis lab in School of Chemical Sciences in University of Illinois at Urbana-Champaign for assistance with ICP-MS analysis. TDTR and RBS measurements were done using the equipment in the Frederick Seitz Materials Research Laboratory at University of Illinois at Urbana-Champaign.
Author information
Authors and Affiliations
Contributions
G.Z., J.L. and D.G.C. conceived the samples and measurements. G.Z. and R.Z. performed electrochemical experiments and sample fabrications. J.L. performed measurements of thermal properties, elastic properties, RBS, and ICP-MS. G.Z., J.L. and Q.Z. performed structural analysis. Q.Z. carried out the Raman Spectroscopy measurements. J.L. and D.L. analysed the shear modulus. G.Z., J.L. and Q.Z. analysed data, designed figures and wrote the manuscript with comments from all co-authors. D.G.C. and D.B. coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Table 1, Supplementary Note 1, Supplementary Methods and Supplementary References (PDF 442 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhu, G., Liu, J., Zheng, Q. et al. Tuning thermal conductivity in molybdenum disulfide by electrochemical intercalation. Nat Commun 7, 13211 (2016). https://doi.org/10.1038/ncomms13211
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13211
This article is cited by
-
Observation of 2D-magnesium-intercalated gallium nitride superlattices
Nature (2024)
-
Intercalation in 2D materials and in situ studies
Nature Reviews Chemistry (2024)
-
Recent advances on liquid intercalation and exfoliation of transition metal dichalcogenides: From fundamentals to applications
Nano Research (2024)
-
Solar-driven efficient heterogeneous subminute water disinfection nanosystem assembled with fingerprint MoS2
Nature Water (2023)
-
Preparation of molybdenum disulfide microspheres and their effect on the thermal conductivity of epoxy resin
Polymer Bulletin (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.