Abstract
Magnetic and superconducting ground states can compete, cooperate and coexist. MnP provides a compelling and potentially generalizable example of a material where superconductivity and magnetism may be intertwined. Using a synchrotron-based non-resonant X-ray magnetic diffraction technique, we reveal a spiral spin order in MnP and trace its pressure evolution towards superconducting order via measurements in a diamond anvil cell. Judging from the magnetostriction, ordered moments vanish at the quantum phase transition as pressure increases the electron kinetic energy. Spins remain local in the disordered phase, and the promotion of superconductivity is likely to emerge from an enhanced coupling to residual spiral spin fluctuations and their concomitant suppression of phonon-mediated superconductivity. As the pitch of the spiral order varies across the 3d transition metal compounds in the MnP family, the magnetic ground state switches between antiferromagnet and ferromagnet, providing an additional tuning parameter in probing spin-fluctuation-induced superconductivity.
Similar content being viewed by others
Introduction
From the lodestone-based compass to modern theories of phase transitions1, magnetic materials have played an outsized role in revealing the shape of the world around us. The similarly venerable field of superconductivity serves as a prime example of emergent, collective behaviour in nature, with raised hopes of technological import with the discovery of exotic superconducting order in the cuprates. Magnetism and superconductivity often compete for preeminence as a material’s ground state, but in the right circumstances the fluctuating remains of magnetic order can induce superconducting pairing. The intertwining of the two on the microscopic level, independent of lattice excitations, is especially pronounced in heavy fermion compounds, rare earth cuprates and iron pnictides.
Here we point out that for a helical arrangement of localized spins, a variable spiral period could provide a unique tuning process from ferromagnetic to antiferromagnetic ground state in the long and short wavelength limits, respectively. Such chemical or pressure adjustable helical order naturally provides the possibility for continuous tuning between ferromagnetically and antiferromagnetically mediated superconductivity. At the same time, phonon-mediated superconductivity is suppressed because of the local ferromagnetic spin configuration2 in the low-frequency spiral fluctuation modes.
The recent discovery of a superconducting phase in the transition metal compound MnP (ref. 3) opens the possibility of investigating this scenario. MnP possesses a complex pressure–temperature (P–T) phase diagram3. At ambient pressure, there is helical spin order below the Néel temperature, TN=50 K, with a wave vector Q=(0.117, 0, 0) (ref. 4). Under pressure, the helical order is quickly replaced by ferromagnetism at ∼1 GPa, and another magnetic state, assumed to be antiferromagnetic3, emerges for P>2 GPa. Superconductivity appears after the high-pressure magnetic phase is suppressed at P∼7 GPa (ref. 3). The spin structure in the high-pressure magnetic phase remains unsettled, and is under active exploration by both X-ray and neutron5 magnetic diffraction techniques.
We employ synchrotron-based magnetic X-ray diffraction (see ‘Methods’ section) to investigate the high-pressure magnetic phases in MnP (ref. 3). This sensitive probe, suitable for 0.0002, mm3 single crystal volumes and diamond anvil cell techniques, directly reveals a reduced moment, incommensurate spin state at high pressure proximate to the superconducting state. This new magnetic order is most likely a magnetic helix with a tightened pitch in comparison to that at ambient pressure where superconductivity is absent. The extant data correlating magnetic pitch length and superconductivity is sparse but suggestive in the (V/Cr/Mn/Fe/Co/Ni)(P/As/Sb) family3,4,6,7,8,9,10,11,12,13,14,15,16,17,18,19 and, as discussed in detail below, we suggest this family of spiral magnets as a new venue for tunable, spin-fluctuation-mediated superconductivity.
Results
High-pressure spiral antiferromagnetic order
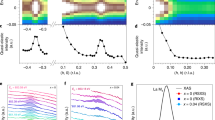
We performed non-resonant single crystal X-ray magnetic diffraction under pressure (see ‘Methods’ section)20,21,22,23,24 to elucidate the cascade of magnetic states in the P–T phase diagram of MnP (Fig. 1) and their relation to superconductivity. We discover helical magnetic order with Q′∼(0.25, 0, 0) presaging the high-pressure superconductor (Fig. 2). We observe a pair of superlattice peaks in mirror symmetry to the lattice order at three pressures, 3.17, 5.28 and 6.43 GPa, but absent at P=8.99 and 10.4 GPa. These diffraction peaks are always of single crystal nature (Fig. 3) and their pressure evolution is commensurate to that of the a axis. Here we adopt the Pbnm space group setting for MnP with a>b>c (ref. 4). The low transferred momentum of (1−Q′, 0, 0) rules out diffraction from integer lattice orders from both MnP and other components of the high-pressure cell (diamond and Ag manometer)21,22,23,24. The peak intensities lie in the range of 1–4 × 10−8 relative to the (2, 0, 0) lattice intensity, which are comparable with the estimate of non-resonant magnetic diffraction intensities (see ‘Methods’ section) and the observed diffraction signal of the low-pressure helical order under the same experimental condition (Fig. 2a). It is known that spin order can induce higher harmonics25,26. However, we did not observe a diffraction peak at (1−Q′/2, 0, 0) with commensurate sensitivity (Fig. 4). This implies that our observed pair of peaks represents the primary wave describing the spin order. We did not observe diffraction intensity at (1−2Q′, 0, 0), thereby ruling out a strong charge harmonic to the magnetic order.
The P–T phase diagram includes ferromagnetism (FM), a double-helical order (Ha-I) at low pressure4, a new helical order (Ha-II) discovered at high pressure in the current work, superconductivity (SC) and paramagnetism (PM). Phase boundary data is adapted from ref. 3 (open circles) with a reduction of pressure scale by a factor of 1.12 to match our X-ray measured Ha-II phase boundary at 4 K (filled circle). Also marked are (P, T) positions where the helical order was observed or proved null through magnetic scattering (filled squares) and where the lattice parameters are measured (crosses). The presence of multiple ferromagnetic phases44 is not distinguished here for clarity. (Inset) schematics of spin structures of three magnetic ground states, presented in a sequence of ascending pressure. The n-glide plane constraint between two helical orders in Ha-I is broken in the Ha-II phase.
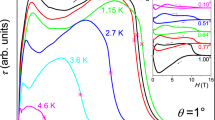
(a) Raw scans around (1, 1, 0) order at ambient pressure and T=4 K, showing both the lattice Bragg peak and a pair of non-resonant magnetic peaks associated with the helical spin order Ha-I. Solid lines are guides to the eye. (b–d) Longitudinal (θ/2θ) line shapes of (2, 0, 0) lattice, and (1±Q′, 0, 0) helical magnetic order, measured at T=4 K. We set a>b>c in the Pbnm space group for the lattice4. Lattice line shapes are instrument resolution limited for the whole pressure range, and can be fit to a Pseudo-Voigt form with a lattice coherence length exceeding 1,500 Å. The magnetic peaks are significantly broadened, indicating a shorter correlation length of the helical spin order from ∼310 Å at 3.2 GPa to ∼70 Å at 6.4 GPa, about three times the pitch length of 24 Å. All magnetic peaks are fit with a Lorentzian form on a sloped background, which could be attributed to influence from spin fluctuations in the ordered phase. However, our counting statistics are not sufficient to make a distinction from a Lorentzian-squared form, which results from disorder pinning45. The reduced background benefits from the use of a pair of wide-angle perforated diamond anvils22,24. Vertical dashed lines mark the commensurate (0.75, 0, 0) and (1.25, 0, 0) positions. Our instrument resolution is fine enough to indicate that the observed magnetic pairs are mirror symmetric to the (1, 0, 0) order, but not commensurate. The presence of mirroring peaks around (1, 0, 0) indicates the n-glide plane constraint is broken for the spin arrangement at high pressure 4, although the (1, 0, 0) lattice order is still forbidden. (e) Above Pc=6.7 GPa, magnetic diffraction is no longer observed in longitudinal scans at same positions of b–d. Vertical error bars represent 1σ s.d. counting statistics.
The single crystal nature of the magnetic order is proven by independent raw scans across the 3D reciprocal space for both (1−Q′, 0, 0) and (1+Q′, 0, 0) orders. The out-of-diffraction-plane transverse scan is dominated by the resolution function determined by the wide horizontal detector slits, while the in-plane transverse scan is intrinsic to the sample mosaic (full-width at half-maximum∼0.1°) under pressure. The longitudinal scans are of the θ/2θ type (plotted against 2θ here) and identical to those in Fig. 2c. Measurements were performed at T=4 K. Vertical error bars represent 1σ s.d. counting statistics. Solid lines are guides to the eye.
A comparison of longitudinal scans between the observed (1−Q′, 0, 0) order and null (1−Q′/2, 0, 0) position. This indicates that our observed peaks are primary waves and not higher harmonics of another wave vector. The longitudinal scan of (1−Q′, 0, 0) is identical to the data in Fig. 2b. Vertical error bars represent 1σ s.d. counting statistics.
Our limited number of observed diffraction orders and the lack of a full azimuthal study because of constrained high-pressure cell geometry make it insufficient to fully refine the high-pressure spin structure. However, in our diffraction geometry, the non-resonant magnetic cross section for orders along the (H, 0, 0) direction is only sensitive to magnetic moments projected out of the vertical diffraction plane and transverse to the wave vector Q′ (see ‘Methods’ section). With spin moments localized in Mn (see below) and an incommensurate wave vector in MnP, the magnetic order is not likely to be of a collinear, amplitude-modulated type. Thus it is reasonable to identify the magnetism in MnP as helical order with tightened pitch (Ha-II, Fig. 1 inset). This provides a consistent perspective on all three spin structures (Ha-I, FM and Ha-II). The spiral magnetism develops with a varying twist angle between neighbouring spin pairs along the wave vector direction, a subtle result due to pressure-dependent, competing exchange constants from multiple close neighbours in an anisotropic lattice27. By contrast, a recent nonpolarized neutron diffraction study at P=3.8 GPa (ref. 5) suggests spiral order along the shortest axis, b, in the Pnma space group. This result is surprising since for all other (V/Cr/Mn/Fe/Co/Ni)(P/As/Sb) family members (Table 1, refs 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19) the spiral order exists along either of the longer axes, a or c, in the Pnma space group setting.
Lattice evolution under pressure and magnetostriction
The boundary of the magnetic phase is determined most accurately by the pressure evolution of the lattice. Single crystal refinement of five to six Bragg orders of MnP at each pressure indicates that the lattice structure remains in the orthorhombic phase to 10.4 GPa. Longitudinal scans of lattice orders such as (2, 0, 0), (0, 2, 1), (2, 2, 0) and (2, 2, 2), showing instrument resolution limited profiles with no noticeable peak splitting, support this conclusion. All three lattice constants evolve nonlinearly at low pressure but linearly at high pressure, with the crossover defining the critical pressure, Pc=6.7±0.2 GPa (Fig. 5), consistent with the range where magnetic diffraction was observed directly. The lattice changes continuously under pressure to a sensitivity level of |Δl|/l∼1 × 10−3 (Fig. 5). The orthorhombic structure of MnP is considered to be a distortion from the hexagonal structure of NiAs (refs 9, 15), as the two symmetries can evolve continuously across the ratio a/c=1.732. Under pressure, the orthorhombic distortion in MnP, measured by a/c, keeps increasing from 1.85 to 1.98 and moves away from the hexagonal symmetry. While helical order in both MnSi and CrAs are suppressed by pressure through a clear first-order quantum phase transition17,18,28, the quantum phase transition in MnP at Pc is isostructural and could be continuous.
(a,b) Normalized lattice evolution at T=4 K under pressure, with a(P=0)=5.8959 Å, b(P=0)=5.2361 Å and c(P=0)=3.1807 Å in the Pbnm space group. a(P)/a(0) and b(P)/b(0) evolve slowly under pressure and are non-monotonic, while c(P)/c(0) has a strong monotonic pressure dependence. The shapes of a, b and c(P) indicate large magnetostriction. Assuming that the lattice of a non-magnetic phase should evolve linearly over this pressure range (dashed lines in a and b as a0(P)/a(P=0) and c0(P)/c(P=0)), and that the low-pressure behaviour can be modelled from extensions of the high-pressure lattice, the magnetostriction is then extracted by subtracting the estimated a0(P) and c0(P). (c) Magnetostriction, expressed as Δl/l=(l(P)−l0(P))/l0(P) in both Δc/c and Δa/a, can be scaled to magnetic phase transition temperatures TC and TN as a function of pressure. Δc and Δa are of different signs, indicating the anisotropic nature in both magnetic exchange interactions and the lattice’s response to the magnetic order. Horizontal error bars represent the full range of pressure during a measurement.
The lattice evolution with pressure indicates a significant magnetostriction, which is common to many 3d and rare-earth magnetic compounds29,30. Here in MnP, magnetostriction can be extracted from Δc and Δa of the lattice and scaled to the magnetic phase boundary of either the Curie or Néel temperatures, TC,N, as Δc/c∼Δa/a∼TC, N (Fig. 5c), regardless of whether there is underlying ferromagnetic or antiferromagnetic order. Since the staggered magnetic moment 〈m〉 is directly related to the magnetostriction, both Δl and 〈m〉 vanish at the quantum phase transition. Beyond Pc, an energy density of 7 GPa distributed over eight valence electrons in the P 3p and Mn 3d orbitals31 increases the electron kinetic energy t by ∼15 meV per electron, comparable to the magnetic exchange constants J (2.5–11 meV, ref. 32). An increasing t/J ratio reduces the ordered moment, 〈m〉, and eventually destabilizes the magnetism. While 〈m〉 drops to zero at a quantum critical point, the fate of individual local moments remains of high interest, as exemplified in heavy fermion materials33.
Local moments and fluctuation modes
Spins in MnP are deep in the local limit at ambient pressure given a Rhodes–Wohlfarth ratio of 2.2 (Fig. 6). The 15 meV per electron increase in kinetic energy sufficient to destabilize the magnetic order is not enough to fully delocalize the 3d moments, considering their 0.20 eV bandwidth31. Therefore, MnP is a system with local moments surviving beyond the quantum critical point, and spin fluctuations in the disordered state naturally raise special interest about magnetically driven superconductivity.
The magnetization M was measured in a SQUID based Magnetic Property Measurement System (Quantum Design) in a 100 Oe d.c. field, and plotted in SI units. Magnetic susceptibility χ′(T) was fit to the Currie–Weiss law above the ferromagnetic transition at 291 K to extract a moment of 2.79 μB per Mn. The measured Currie–Weiss moment is compared with the literature value of the saturated moment 1.3 μB per Mn (ref. 4) in the high field and low temperature limit to provide a Rhodes–Wohlfarth ratio of 2.2. Vertical error bars represent 1σ s.d. of measured magnetization.
In the disordered phase, the predominant spin fluctuation modes likely are still dictated by the nearby magnetic instability33,34,35. In MnSi, helical fluctuations in the form of spiral/helix paramagnons were observed for T>TC despite a weak first order transition. Those fluctuations centre at a wave vector similar in magnitude to the ordering wave vector Q, but with a random direction35, presumably because of the short range Dzyaloshinskii–Moriya interaction in a cubic lattice symmetry. In MnP and CrAs, the lattice anisotropy likely confines wave vector directions of magnetic fluctuations. The pressure evolution of Q in CrAs (ref. 19) is constant up to Pc∼0.65 GPa (refs 17, 18, 19, 36). Interpreting its behaviour for P>Pc (ref. 36) is clouded by a strong first-order phase transition and a highly strained sample condition (lattice mismatch of several per cent) in the phase coexistence region. With no significant evolution of Q in the ordered phase under pressure (Fig. 2)19, the disordered phases of MnP and CrAs should possess spin fluctuations dominated by the magnetic instability in the ordered phase, that is, spiral modes centred at Q∼(0.25, 0, 0) for MnP and (0.36, 0, 0) for CrAs.
Discussion
Fluctuation modes in spiral magnets are of particular interest in terms of the competition between spin and lattice (phonon) fluctuations and their connection to superconducting pairing of s, p, or d character. Consider a helical fluctuation at a finite wavelength. By contrast to the usual antiferromagnet, spins of nearest neighbours along the wave vector Q direction share a large ferromagnetic projection. These ferromagnetic spin fluctuations in the low frequency limit would suppress phonon-mediated superconductivity due to on-site pairing of itinerant electrons2, emphasizing magnetically mediated coupling channels. Furthermore, varying the pitch of the helical order provides a continuous tuning of local ferromagnetic order versus intermediate-range antiferromagnetic order, thus tilting the competition between the two types of magnetically mediated superconductivities.
The spin interaction between two itinerant electrons is an oscillating function in real space, with attractive regions at distance (n+1/2)λ (where n is an integer). The strongest interaction happens at a half pitch length λ/2 of the fluctuating spiral modes (Fig. 7a), which is about 12 Å in MnP. This is similar to the antiferromagnetic fluctuation-mediated interaction in the rare earth cuprates and the heavy fermion compounds37,38. There is a relatively long interaction length between itinerant charge carriers as compared with both the on-site interaction of the phonon-mediated type37 and the nearest-neighbor resonant valence bond type for underdoped cuprates39. On the other hand, the coherence lengths of Cooper pairs are typically much longer than interaction lengths in both phonon- and magnetically mediated superconductors37,39 and for MnP, the superconducting coherence length extends over 300 Å (ref. 3). This coherence length is necessarily smaller than the mean free path of itinerant electrons, thereby allowing the electron pair overlap to maintain phase coherence. The MnP samples we used have a residual resistance ratio of ∼1,000 at ambient pressure3, close to the clean limit. The issue of pairing symmetry is more tenuous, but the model of helical magnets allows certain predictions. The interaction of paring itinerant electrons at a distance r=(n+1/2)λ along the wave vector Q direction of helical spin fluctuations (Fig. 7a) mandates a preferred axial direction and suggests that the superconductivity might be of the singlet  type, especially in light of the low-symmetry lattice structures of MnP and CrAs.
type, especially in light of the low-symmetry lattice structures of MnP and CrAs.
(a) Schematic of a superconducting electron pair coupled through helical spin order in a projected planar view. The two sites of itinerant electron coupling are separated along the helical order by a half wavelength (λ/2), suggesting the possibility of singlet  -wave pairing. This scenario competes with superconductivity of a ferromagnetic type, while the nearly parallel local spin configuration always suppresses phonon-mediated superconductivity at a single site2. (b) Superconducting transition temperature Tc plotted as a function of helical wave vector Q in selected 3d intermetallic compounds. Data for MnSi (refs 28, 35), MnP (refs 3, 4) and CrAs (refs 17, 18, 19) are collected from either the literature or current work. Red solid circles represent observed superconducting transitions, which only exist in pressure-induced disordered phases beyond the helical order, and are likely antiferromagnetically mediated. The horizontal bars of the downward arrows represent the lower bounds of null searches for superconductivity. Ferromagnetically mediated superconductivity is expected to be at a lower temperature than its antiferromagnetic counterpart38,40. The pitch of the helical order represents a potential tuning method between ferromagnetically (blue region) and antiferromagnetically (red region) mediated superconductivity.
-wave pairing. This scenario competes with superconductivity of a ferromagnetic type, while the nearly parallel local spin configuration always suppresses phonon-mediated superconductivity at a single site2. (b) Superconducting transition temperature Tc plotted as a function of helical wave vector Q in selected 3d intermetallic compounds. Data for MnSi (refs 28, 35), MnP (refs 3, 4) and CrAs (refs 17, 18, 19) are collected from either the literature or current work. Red solid circles represent observed superconducting transitions, which only exist in pressure-induced disordered phases beyond the helical order, and are likely antiferromagnetically mediated. The horizontal bars of the downward arrows represent the lower bounds of null searches for superconductivity. Ferromagnetically mediated superconductivity is expected to be at a lower temperature than its antiferromagnetic counterpart38,40. The pitch of the helical order represents a potential tuning method between ferromagnetically (blue region) and antiferromagnetically (red region) mediated superconductivity.
While spiral fluctuations suppress phonon-mediated superconductivity and enhance the coupling channels for the magnetic interactions, helical fluctuations of different pitches provide the means to switch from ferromagnetic to antiferromagnetic character. With increasing spiral wavelength, the interaction strength of the antiferromagnetic coupling is reduced over an elongated r (ref. 32). Moreover, an increased spiral wavelength reduces the turning angle between neighbouring spins and thereby heightens the local ferromagnetic spin density. By varying the pitch, it is possible to tune both the ferromagnetic and antiferromagnetic spin fluctuations. Our focus on local moment helical order complements itinerant models of continuous tuning by band filling from ferromagnetic to antiferromagnetic order with a concomitant switch between magnetically mediated superconductivities of different symmetries40. Through the comparison of the cuprates and Sr2RuO4, it appears that ferromagnetically mediated superconductivity typically has an orders of magnitude lower transition temperature than its antiferromagnetic analogue of the same dimensionality40.
The dimensionality of the spin fluctuations is another interesting issue. The helical order in 3d compounds can be compared with incommensurate antiferromagnetic order in heavy fermion materials like CeCu6−xAux (ref. 33), where spin fluctuations with two-dimensional character were observed around the ordering wave vector Q (ref. 34). Even though the effective low dimensionality enhances the spin fluctuations, the extremely low-magnetic coupling strength in CeCu6−xAux (ref. 33) suppresses the possible magnetically mediated superconductivity below experimental sensitivity. Spin fluctuations in MnP are likely three-dimensional (3D) judging from the T3/2 dependence of the resistivity3, but they are matched with a large magnetic coupling strength32 and bandwidth31, so the superconducting transition temperature, Tc, could still be measurable even at a level of TN/1,000. For 3D helical magnets such as MnP and CrAs with Tc=1–2 K (Fig. 7b), the corresponding ferromagnetic type could be below the lowest range of temperatures measured to date.
Although experimental evidence is still limited, the effects of a variable spiral pitch are suggestive. We illustrate the trends in Fig. 7b for the series MnSi, MnP and CrAs as a function of their different magnetic wave vectors. With a small spiral wave vector of (0.017, 0.017, 0.017)35, MnSi does not superconduct under pressure down to at least 10 mK (ref. 28), although the lack of an inversion centre could complicate the symmetry properties of a superconducting state. For MnP at low pressure, the helical order with a wave vector of 0.117 r.l.u. (ref. 4) was replaced by ferromagnetic order at P∼1 GPa, and no superconductivity was observed down to 350 mK (ref. 3). On the other hand, both MnP at high pressure (0.25 r.l.u.) and CrAs (0.36 r.l.u.) have relatively large wave vectors (short pitches) and demonstrate superconducting ground states once the helical order is suppressed by pressure18,19. We list in Table 1 38 different intermetallic compounds with magnetic pitch varying nearly continuously from 0.07 to 0.40 r.l.u. Most of them have not been examined under pressure, neither to map the evolution of their magnetism nor to search for superconductivity. With such studies, the 3d helical magnets of the (V/Cr/Mn/Fe/Co/Ni)(P/As/Sb) family3,4,6,7,8,9,10,11,12,13,14,15,16,17,18,19 present manifest opportunities to further our understanding of the linkage between magnetism and unconventional superconductivity.
Methods
Non-resonant X-ray magnetic diffraction
The technique of non-resonant X-ray magnetic diffraction has been well established at synchrotron-based X-ray sources29,30,41,42,43. Non-resonant single crystal X-ray magnetic diffraction under pressure using 20.000 keV X-rays was carried out at beamline 4-ID-D of the Advanced Photon Source20,21,22,23,24. The X-ray energy is calibrated to the K-edge of the element Molybdenum to within a precision of 0.5 eV. The bandwidth of incident X-rays is ∼2.7 eV full-width at half-maximum, given by the use of Si (1,1,1) crystals as X-ray monochromators. Diffraction was carried out in the vertical scattering plane, with X-rays predominantly (>99%) polarized linearly in the horizontal direction perpendicular to the diffraction plane.
MnP is a 3d transition metal compound with low local symmetry at the Mn sites. Thus it is reasonable to assume that the orbital moments are quenched in this system. Spins localized at Mn sites, as suggested by our measured Rhodes–Wohlfarth ratio, are the major source of magnetism. Under the non-resonant condition and our vertical diffraction geometry, the cross section of X-ray magnetic diffraction is41,

where e and m are the electron mass and charge, respectively, ħω is the X-ray energy, 2θ is the Bragg diffraction angle and S1,2,3 are projections of the reciprocal space spin density with S2 out of the diffraction plane and S1,3 in plane41. However, the diffraction 2θ angles are all small (Fig. 3) given the need to use hard (20 keV) X-rays to penetrate the diamond anvil cell. Expanding the scattering cross section by powers of sin2(θ)∼0.005, it simplifies to  , where only the S2 perpendicular spin projection remains42,43. In our measurements (Fig. 2), the diffraction wave vectors (1±Q′, 0, 0) are parallel to the magnetic order vector (Q′, 0, 0). Hence the observed diffraction signals indicate a transverse component of antiferromagnetic order, ruling out a purely longitudinal spin wave. A spiral form is the simplest model that is consistent with our data, since localized spins also rule out an amplitude-modulated, collinear wave form.
, where only the S2 perpendicular spin projection remains42,43. In our measurements (Fig. 2), the diffraction wave vectors (1±Q′, 0, 0) are parallel to the magnetic order vector (Q′, 0, 0). Hence the observed diffraction signals indicate a transverse component of antiferromagnetic order, ruling out a purely longitudinal spin wave. A spiral form is the simplest model that is consistent with our data, since localized spins also rule out an amplitude-modulated, collinear wave form.
The magnetic diffraction cross section, σmag, can be compared with the charge diffraction cross section, σcharge, as roughly:  , where N is the total number of electrons per atom that contribute to the Thompson scattering amplitude, and fm, and f are magnetic and charge form factors, respectively. With N=25 for Mn, and a projected spin moment s⊥ about
, where N is the total number of electrons per atom that contribute to the Thompson scattering amplitude, and fm, and f are magnetic and charge form factors, respectively. With N=25 for Mn, and a projected spin moment s⊥ about  is estimated to be 2–5 × 10−8 for I(1±Q′, 0, 0)/I(2, 0, 0). This value becomes smaller as the ordered moment, 〈m〉, decreases with increasing pressure.
is estimated to be 2–5 × 10−8 for I(1±Q′, 0, 0)/I(2, 0, 0). This value becomes smaller as the ordered moment, 〈m〉, decreases with increasing pressure.
Although the non-resonant X-ray magnetic diffraction signals are typically weak, the feasibility of this technique has been demonstrated under high pressure20,22,23,24. With the development of wide-angle perforated diamond anvils22,24, it is possible to cleanly detect magnetic order with spin moments as low as 0.3 μB under pressure, with the sample volume spatially divided into six magnetic domains24. With only 0.9 mm thick diamonds and a 0.1 mm thick low-Z glassy pressure medium (methanol:ethanol 4:1 mixture) in the X-ray scattering path, in addition to the sample, the background was minimized and is devoid of sharp features across reciprocal space.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
Additional information
How to cite this article: Wang, Y. et al. Spiral magnetic order and pressure-induced superconductivity in transition metal compounds. Nat. Commun. 7, 13037 doi: 10.1038/ncomms13037 (2016).
References
Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. 65, 117–149 (1944).
Berk, N. F. & Schrieffer, J. R. Effect of ferromagnetic spin correlations on superconductivity. Phys. Rev. Lett. 17, 433–435 (1966).
Cheng, J.-G. et al. Pressure-induced superconductivity on the border of magnetic order in MnP. Phys. Rev. Lett. 114, 117001 (2015).
Felcher, G. P. Magnetic structure of MnP. J. Appl. Phys. 37, 1056–1058 (1966).
Matsuda, M. et al. Pressure dependence of the magnetic ground states in MnP. Phys. Rev. B 93, 100405 (2016).
Felcher, G. P., Smith, F. A., Bellavance, D. & Wold, A. Magnetic structure of iron monophosphide. Phys. Rev. B 3, 3046–3052 (1971).
Kallel, A., Boller, H. & Bertaut, E. F. Helimagneism in MnP-type compounds: MnP, FeP, CrAs, and CrAs1−xSbx mixed crystals. J. Phys. Chem. Solids 35, 1139–1152 (1974).
Selte, K., Kjekshus, A., Valde, G. & Andresen, A. F. Magnetic structures and properties of V1−tMntAs. Acta Chem. Scand. A30, 8–14 (1976).
Selte, K., Kjekshus, A., Valde, G. & Andresen, A. F. Magnetic structures and properties of Mn1−tCotAs. Acta Chem. Scand. A30, 468–474 (1976).
Selte, K., Kjekshus, A., Peterzéns, P. G. & Andresen, A. F. Magnetic structure of Mn0.95Fe0.05As. Acta Chem. Scand. A30, 671–672 (1976).
Haneda, S., Kazama, N., Yamaguchi, Y. & Watanabe, H. High spin-low spin transition in MnAs1−x Px (x=0.075). J. Phys. Soc. Jpn 42, 31–35 (1977).
Delphin, I. L. A., Selte, K., Kjekshus, A. & Andresen, A. F. Structural and magnetic properties of Cr1−tNitAs, Mn1−tNitAs and Fe1−tNitAs. Acta Chem. Scand. A32, 179–185 (1978).
Selte, K., Kjekshus, A., Peterzéns, P. G. & Andresen, A. F. Magnetic structures and properties of Mn1−tCrtAs(0<t≤0.40). Acta Chem. Scand. A32, 653–657 (1978).
Fjellvåg, H., Kjekshus, A., Zieba, A. & Foner, S. Magnetic properties of transition metal substituted MnP. J. Phys. Chem. Solids 45, 709–718 (1984).
Fjellvåg, H., Kjekshus, A., Stolen, S. & Andresen, A. F. Structural and magnetic properties of Mn1−tCrtAs1−xPx . Acta Chem. Scand. A42, 214–225 (1988).
Rodriguez, E. E. et al. Noncollinear spin-density-wave antiferromagnetism in FeAs. Phys. Rev. B 83, 134438 (2011).
Wu, W. et al. Superconductivity in the vicinity of antiferromagnetic order in CrAs. Nat. Commun. 5, 5508 (2014).
Kotegawa, H., Nakahara, S., Tou, H. & Sugawara, H. Superconductivity of 2.2 K under pressure in helimagnet CrAs. J. Phys. Soc. Jpn 83, 093702 (2014).
Keller, L. et al. Pressure dependence of the magnetic order in CrAs: a neutron diffraction investigation. Phys. Rev. B 91, 020409 (2015).
Feng, Y. et al. Pressure-tuned spin and charge ordering in an itinerant antiferromagnet. Phys. Rev. Lett. 99, 137201 (2007).
Feng, Y., Jaramillo, R., Wang, J., Ren, Y. & Rosenbaum, T. F. High-pressure techniques for condensed matter physics at low temperature. Rev. Sci. Instrum. 81, 041301 (2010).
Feng, Y. et al. Hidden one-dimensional spin modulation in a three-dimensional metal. Nat. Commun. 5, 4218 (2014).
Wang, J. et al. Pressure tuning of competing magnetic interactions in intermetallic CeFe2 . Phys. Rev. B 86, 014422 (2012).
Feng, Y., Palmer, A., Wang, Y., Silevitch, D. M. & Rosenbaum, T. F. Direct probe of Fermi surface evolution across a pressure-induced quantum phase transition. Phys. Rev. B 91, 155142 (2015).
McMorrow, D. F. et al. X-ray scattering study of the interplay between magnetism and structure in CeSb. J. Phys.: Condens. Matter 9, 1133–1148 (1997).
Walker, H. C. et al. Femtoscale magnetically induced lattice distortions in multiferroic TbMnO3 . Science 333, 1273–1276 (2011).
Dobrzynski, L. & Andresen, A. F. On the magnetic double helical structure in MnP- and MnAs-based alloys. J. Magn. Magn. Mater. 82, 67–76 (1989).
Doiron-Leyraud, N. et al. Fermi liquid breakdown in the paramagnetic phase of a pure metal. Nature 425, 595–599 (2003).
Chatterji, T. et al. The ground state of NaV2O5 . Solid State Commun. 108, 23–26 (1998).
Chatterji, T. et al. High-energy non-resonant X-ray magnetic scattering from EuAs3 . Solid State Commun. 131, 713–717 (2004).
Perkins, P. G., Marwaha, A. K. & Stuart, J. J. P. The band structure and magnetic properties of some transition-metal phosphides. II. Cr, V and Mn monophosphides. Theoret. Chim. Acta 59, 569–583 (1981).
Tajima, K., Ishikawa, Y. & Obara, H. Neutron scattering studies of the ferro to spiral transition in MnP. J. Magn. Magn. Mater. 15–18, 373–374 (1980).
Schröder, A. et al. Onset of antiferromagnetism in heavy-fermion metals. Nature 407, 351–355 (2000).
Stockert, O., Löhneysen, H. V., Rosch, A., Pyka, N. & Loewenhaupt, M. Two-dimensional fluctuations at the quantum-critical point of CeCu6−xAux . Phys. Rev. Lett. 80, 5627–5630 (1998).
Roessli, B., Böni, P., Fischer, W. E. & Endoh, Y. Chiral fluctuations in MnSi above the Curie temperature. Phys. Rev. Lett. 88, 237204 (2002).
Shen, Y. et al. Structural and magnetic phase diagram of CrAs and its relationship with pressure-induced superconductivity. Phys. Rev. B 93, 060503 (2016).
Sigrist, M. Introduction to unconventional superconductivity. AIP Conf. Proc. 789, 165–243 (2005).
Monthoux, P., Pines, D. & Lonzarich, G. G. Superconductivity without phonons. Nature 450, 1177–1183 (2007).
Anderson, P. W. et al. The physics behind high-temperature superconducting cuprates: the ‘plain vanilla’ version of RVB. J. Phys. Condens. Matter 16, R755–R769 (2004).
Monthoux, P. & Lonzarich, G. G. Magnetic interactions in a single-band model for the cuprates and ruthenates. Phys. Rev. B 71, 054504 (2005).
Blume, M. & Gibbs, D. Polarization dependence of magnetic X-ray scattering. Phys. Rev. B 37, 1779–1789 (1988).
Brückel, T. et al. First observation of bulk magnetic scattering using high-energy X-rays. Acta Crystallogr. A49, 679–682 (1993).
Evans, P. G., Isaacs, E. D., Aeppli, G., Cai, Z. & Lai, B. X-ray microdiffraction images of antiferromagnetic domain evolution in chromium. Science 295, 1042–1045 (2002).
Yamazaki, T. et al. Novel magnetic chiral structures and unusual temperature hysteresis in the metallic helimagnet MnP. J. Phys. Soc. Jpn 83, 054711 (2014).
Feng, Y. et al. Order parameter fluctuations at a buried quantum critical point. Proc. Natl Acad. Sci. USA 109, 7224–7229 (2012).
Acknowledgements
We thank P.B. Littlewood for helpful conversations. We are grateful to B. Fisher for assisting with the magnetization measurements. Sample preparation at the MRSEC facilities of the University of Chicago was supported by NSF Grant No. DMR-1420709. The work at the California Institute of Technology was supported by U.S. Department of Energy Basic Energy Sciences Award DE-SC0014866. The use of the Advanced Photon Source and the Center for Nanoscale Materials of Argonne National Laboratory was supported by the U.S. Department of Energy Office of Science User Facilities under contract No. DE-AC02-06CH11357. J.-G.C. and J.L.L. were supported by the MOST and NSF of China, and the Strategic Priority Research Program of the Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
Y.F. and T.F.R. designed the research. J.-G.C., W.W. and J.L.L. provided samples. Y.W. and Y.F. performed measurements and developed the theoretical framework. Y.W., Y.F. and T.F.R. prepared the manuscript. All authors commented.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, Y., Feng, Y., Cheng, JG. et al. Spiral magnetic order and pressure-induced superconductivity in transition metal compounds. Nat Commun 7, 13037 (2016). https://doi.org/10.1038/ncomms13037
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13037
This article is cited by
-
Atomic reconstruction induced by uniaxial stress in MnP
Scientific Reports (2023)
-
Strongly-coupled quantum critical point in an all-in-all-out antiferromagnet
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.