Abstract
Molecular quantum magnetism involving an isolated spin state is of particular interest due to the characteristic quantum phenomena underlying spin qubits or molecular spintronics for quantum information devices, as demonstrated in magnetic metal–organic molecular systems, the so-called molecular magnets. Here we report the molecular quantum magnetism realized in an inorganic solid Ba3Yb2Zn5O11 with spin–orbit coupled pseudospin-½ Yb3+ ions. The magnetization represents the magnetic quantum values of an isolated Yb4 tetrahedron with a total (pseudo)spin 0, 1 and 2. Inelastic neutron scattering results reveal that a large Dzyaloshinsky–Moriya interaction originating from strong spin–orbit coupling of Yb 4f is a key ingredient to explain magnetic excitations of the molecular magnet states. The Dzyaloshinsky–Moriya interaction allows a non-adiabatic quantum transition between avoided crossing energy levels, and also results in unexpected magnetic behaviours in conventional molecular magnets.
Similar content being viewed by others
Introduction
Quantum magnetism is a ubiquitous subject from the spin singlet state in non-interacting dimers to the long-range entangled state in quantum spin liquids1,2,3,4,5,6,7,8. Its nature is often described in terms of quantum values of the magnetic moments, ionic anisotropies and their coupling network9,10,11,12,13. The former two are determined by the single ionic characters, while the last one can be controlled by arrangement of the magnetic ions. Great progress in theoretical and experimental investigations on the quantum magnetism has mostly been made through variation of the coupling connectivity3,4,5,6,7,8,9,10,11,12,13. An extreme case could be the molecular magnet of an isolated magnetic cluster14,15. Meanwhile, magnetism in solids is strongly influenced by geometrical constraints such as frustration or bond alternation as well as dimensionality, and often introduces intriguing quantum phenomena1,5,6,7,8,16.
With strong spin–orbit coupling (SOC), the magnetic quantum spin is given by the total angular momentum J, rather than the spin S. The degenerate J-state is split by a crystal field (CF), and the ground-state quantum spin can be represented by a modified J, the so-called pseudospin, as discussed in lanthanide-based molecular magnets17,18,19,20,21,22. The strong 4f SOC combined with a subtle CF contributes strong magnetic anisotropy to yield a simple model Hamiltonian with Ising-like or XY-like anisotropic magnetic exchange between the molecular pseudospins. Recently, Ba3Yb2Zn5O11 was reported to be a geometrically frustrated breathing pyrochlore system with two distinct Yb–Yb distances23,24. Ba3Yb2Zn5O11 consists of two alternating main blocks of Yb4O16 and Zn10O20 (Fig. 1a). The magnetic Yb3+ ions in Yb4O16 form a tetrahedron connected with another one through corner-sharing in the three-dimensional framework. Remarkably, the inter-tetrahedron Yb–Yb distance r′=6.23 Å is much larger than the intra-tetrahedron one r=3.30 Å. Thus, the inter-magnetic exchange energy J′ becomes negligible in comparison with the intra-exchange energy J, that is, J′/J∼0 (Fig. 1b). As can be seen in the detailed ionic arrangements of the tetrahedron Yb4O16 (Fig. 1c), each Yb ion is surrounded by six oxygens to form an octahedron (YbO6) with a trigonal distortion (C3v symmetry), and the C3v symmetry axis is towards the tetrahedron center. The Yb3+ ion (4f13) effectively has a pseudospin-½ ground state of a Kramers doublet separated by the CF splitting energy of 38.2 meV (=443 K-kB) without any magnetic long-range order even below sub-Kelvin in spite of the considerable Curie–Weiss temperature ΘCW=−6.7 K (refs 24, 25), indicating possible formation of decoupled molecular spin states.
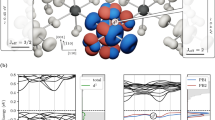
(a) Crystal structure of pyrocholre Ba3Yb2Zn5O11 with cubic space group F 3m. Green, red, blue and black spheres represent Ba, Yb, Zn and O ions, respectivley. Two main blocks of Yb4O16 and Zn10O20 are alternated and Ba ions locate in the interstices. (b) Arrays of Yb ions and Yb4 tetrahedrons with alternated Yb–Yb distances in the breathing pyrochlore structure. The inter-tetrahedron (red line) and intra-tetrahedron (grey line) Yb–Yb distances are r=3.30 Å and r′=6.23 Å, respectively. Correponding magnetic exchange couplings are denoted by J and J′. (c) Yb4 tetrahedron and YbO6 octahedron with trigonal distortion (C3v). A blue arrow denotes C3v symmetry axis pointing along the [1 1 1] direction and green arrows indicate the DM vectors d’s determined from the Moriya’s rule. (d) Field-dependent magnetization M(H) measured for upfield (magenta) and downfield (blue) sweeps with a rate of 15 mT min−1 at T=100 mK, showing the level crossing critical fields of HC1=3.5 T and HC2=8.8 T. A green solid line displays adiabatic simulation results from
3m. Green, red, blue and black spheres represent Ba, Yb, Zn and O ions, respectivley. Two main blocks of Yb4O16 and Zn10O20 are alternated and Ba ions locate in the interstices. (b) Arrays of Yb ions and Yb4 tetrahedrons with alternated Yb–Yb distances in the breathing pyrochlore structure. The inter-tetrahedron (red line) and intra-tetrahedron (grey line) Yb–Yb distances are r=3.30 Å and r′=6.23 Å, respectively. Correponding magnetic exchange couplings are denoted by J and J′. (c) Yb4 tetrahedron and YbO6 octahedron with trigonal distortion (C3v). A blue arrow denotes C3v symmetry axis pointing along the [1 1 1] direction and green arrows indicate the DM vectors d’s determined from the Moriya’s rule. (d) Field-dependent magnetization M(H) measured for upfield (magenta) and downfield (blue) sweeps with a rate of 15 mT min−1 at T=100 mK, showing the level crossing critical fields of HC1=3.5 T and HC2=8.8 T. A green solid line displays adiabatic simulation results from  with J=0.589 meV, d/J=0.27, g||=3.0 and g∥=2.4. A black dashed line displays simulation results at T=100 mK with HC1=3.7 T and HC2=7.4 T from the conventional Heisenberg magnetic exchange Hamiltonian including the Zeeman term with an exchange coupling constant J=0.554 meV and an isotropic g-factor g=2.569 reported previously24. The inset is a schematic illustration of Landau−Zener transition between two energy states of ψ0 and ψ1 as in Fig. 2d. Adiabatic and non-adiabatic processes as a function of the external magnetic field are presented with solid and dashed lines, respectivley.
with J=0.589 meV, d/J=0.27, g||=3.0 and g∥=2.4. A black dashed line displays simulation results at T=100 mK with HC1=3.7 T and HC2=7.4 T from the conventional Heisenberg magnetic exchange Hamiltonian including the Zeeman term with an exchange coupling constant J=0.554 meV and an isotropic g-factor g=2.569 reported previously24. The inset is a schematic illustration of Landau−Zener transition between two energy states of ψ0 and ψ1 as in Fig. 2d. Adiabatic and non-adiabatic processes as a function of the external magnetic field are presented with solid and dashed lines, respectivley.
In this paper, we report the molecular magnetic behaviours in magnetization and inelastic neutron scattering (INS) for inorganic polycrystalline Ba3Yb2Zn5O11 samples. The magnetization shows the hysteretic step-like jumps between Seff=0, 1 and 2 molecular magnetic states of an isolated Yb4 tetrahedron with spin–orbit coupled pseudospin-½, which reflects the non-adiabatic Landau–Zener transition. The INS measurement with external magnetic field unveils that the large Dzyaloshinsky–Moriya (DM) interaction originating from strong SOC of Yb 4f electron is essential to construct the Seff molecular magnetic states involving avoided level crossing. Our finding not only opens a possibility for qubit quantum device applications due to benefit of the regularity in the inorganic solid, but the tunable inter-tetrahedron distance also provides a playground to explore the crossover from isolated to entangled magnetic quantum systems in the presence of SOC.
Results
Magnetization and effective Hamiltonian
Figure 1d shows the field-dependent magnetization result (M versus H) at 100 mK, which displays the characteristic step-like jumps of an antiferromagnetic (AFM) coupled molecule with a total (pseudo)spin Seff formed by the four ½-pseudospins of the tetrahedron. The ground state of the AFM-coupled tetrahedron, which is the Seff=0 state at zero field, is consecutively switched to the Seff=1 and the Seff=2 state as the external magnetic field increases across corresponding critical fields. The three plateaus in M(H) represent the respective Seff=0, 1 and 2 states, and the consecutive level crossing quantum transitions are presented by the two-step feature at the critical fields HC1=3.5 T and HC2=8.8 T. It is worth to note that M(H) exhibits three distinctive features: a hysteretic behaviour near HC1, shifts of the critical fields with respect to the Heisenberg model and a non-zero slope in a lower field region 0<H<HC1, all of which are not expected in conventional molecular magnets with a simple Heisenberg AFM exchange interaction. For comparison, the simulated M(H) of the conventional molecular magnet with AFM-coupled four ½-spins, which has HC1=3.7 T and HC2=7.4 T with no slope in 0<H<HC1, is presented by the black dashed line in the figure.
Considering the pseudospin-½ with the Yb 4f strong SOC, we should adopt a generalized magnetic exchange Hamiltonian17,18,19,26,27,28 to explain the observed magnetization;

The first and second terms represent the generalized magnetic exchange and Zeeman terms, respectively. The ith site pseudospin can be represented by the Pauli spin operator Si, and the exchange coupling Jij between Si and Si is presented in a tensor form (Jμv). The Zeeman term is described with the Bohr magneton μB, external magnetic field H and a g-tensor gi reflecting the ith site single-ion magnetic anisotropy. The generalized Hamiltonian  well explains observed INS results of the breathing pyrochlore Ba3Yb2Zn5O11 with only a few none-trivial Jμv values as discussed below, and is effectively reduced to an effective exchange Hamiltonian with an additional DM interaction (antisymmetric exchange interaction) term to the conventional Heisenberg AFM Hamiltonian (Supplementary Note 1):
well explains observed INS results of the breathing pyrochlore Ba3Yb2Zn5O11 with only a few none-trivial Jμv values as discussed below, and is effectively reduced to an effective exchange Hamiltonian with an additional DM interaction (antisymmetric exchange interaction) term to the conventional Heisenberg AFM Hamiltonian (Supplementary Note 1):

The first term represents the Heisenberg exchange interaction and the second term accounts for the DM interaction, which is a result of combined effects of the SOC and the superexchange interactions. According to the Moriya’s rules28,29, the DM vector dij does not disappear in Ba3Yb2Zn5O11 (F 3m space group) with no-inversion symmetry, and its direction (green arrows in the inset of Fig. 1c) is constrained by tetrahedron symmetry (Td).
3m space group) with no-inversion symmetry, and its direction (green arrows in the inset of Fig. 1c) is constrained by tetrahedron symmetry (Td).
The step-like features in M(H) at HC1=3.5 T and HC2=8.8 T reflect the spin singlet–triplet (Seff=0–1) and triplet–quintet (Seff=1–2) level crossings, respectively. This M(H) curve can be well reproduced with the respective g-factor values g||=3.0(1) and g∥=2.4(1) for parallel and perpendicular to the symmetry axis of each YbO6, respectively (green line in Fig. 1d). These values are slightly larger than g||=2.54 and g∥=2.13, which are more accurately determined from an electron paramagnetic resonance measurement (Supplementary Note 2). It is noticed that a hysteretic behaviour appears around HC1. This behaviour reflects the Landau–Zener transition involving an avoided level crossing with an energy gap in a dissipative two-state model (inset of Fig. 1d)30,31,32,33. The level crossing energy gap hinders the adiabatic crossover between the singlet and triplet as the magnetic field increases or decreases across HC1. Evidently, we observed that the hysteresis varies with the field sweep rate (Supplementary Note 3). At HC2, the energy gap is enhanced, and the hysteretic feature becomes less effective. A finite slope in M(H) can be also noticed in the range 0<H<HC1. Due to the fact that the DM interaction admixes the singlet and triplet states, the ground state is no longer a pure Seff=0 state and the admixed triplet Seff=1 state contributes the weak field dependence to the magnetization34. While the anisotropic Zeeman term also can contribute to paramagnetic response to the applied field, its effect on M(H) is less significant than that of DM in the breathing pyrochlore Ba3Yb2Zn5O11 (Supplementary Note 3).
INS without a magnetic field
To explore magnetic excitations in this novel quantum magnet, we performed INS measurements20,21,22,35,36. Figure 2a shows the intensities I(Q,ω) as a function of momentum and energy transfer obtained from the measurements at T=200 mK and at the zero magnetic field. The I(Q, ω) exhibits four non-dispersive excitations, which correspond to the transitions from the Seff=0 ground state to the Seff=1 excited states. As temperature increases, the Seff=1 states become partially occupied due to the thermal energy, and additional transitions from the Seff=1 states become available in the INS result. Indeed, we could observe additional non-dispersive excitations at 10 K as shown in Fig. 2b.
(a,b) INS intensities I(Q, ω) as a function of momentum Q and energy transfer ħω measured using incident neutron energy E=2.27 meV (=6.0 Å) at (a) T=200 mK and (b) T=10 K. (c) Constant-ω cuts I(Q)’s obtained by integrating over ranges of 0.45 meV<ħω<0.60 meV (blue filled circle) and 0.65 meV<ħω<0.80 meV (diamond) at 200 mK. A black dashed line represents the square of the Yb3+ magnetic form factor, and a green dashed line does the model calcution for a Yb4 tetrahedron, which expresses a functional form of 1−sin(Qr)/Qr at r=3.30 Å. (d) Constant-Q cuts I(ω)’s obtained by integrating over a range of 0.8 Å−1<Q<1.8 Å−1 at T=200 mK (blue circle) and T=10 K (red circle). Solid lines present simulated I(ω)’s from the effective Hamiltonian  . (e) Schematic energy level diagram extracted from diagonalization of
. (e) Schematic energy level diagram extracted from diagonalization of  . The degeneracy of each energy level is presented in the paranthesis together with the eigenstate ψ. The excitations with indices from 1 to 10 (vertical red arrows) are observable in I(ω)’s in d. Intensity error bars are square roots of intensities.
. The degeneracy of each energy level is presented in the paranthesis together with the eigenstate ψ. The excitations with indices from 1 to 10 (vertical red arrows) are observable in I(ω)’s in d. Intensity error bars are square roots of intensities.
To confirm the molecular characteristics of the quantum spin state, we examined the Q-dependences of two dominant excitation intensities I(Q), which are integrated over 0.45–0.6 meV and 0.65–0.8 meV regions in Fig. 2a. The obtained I(Q) is compared with the calculated ones for an Yb3+ single ion (black dashed line) and an Yb4 tetrahedron molecule (green dashed line) as shown in Fig. 2c. The obtained I(Q) is obviously well explained by the molecular model rather than the ionic model35, supporting the presence of molecular quantum magnetism in Ba3Yb2Zn5O11. The Q integrated intensities I(ω) presented in Fig. 2d are also well understood in a framework of the Seff molecular magnet states. At 200 mK, we identified four excitation peaks, while seven peaks are observable at 10 K, which could be indexed with 11 excitations. The corresponding excitations (vertical arrows) are described in the energy level diagram based on the effective Hamiltonian  , which is schematically depicted in Fig. 2e.
, which is schematically depicted in Fig. 2e.
The Heisenberg exchange splits total 24 magnetic states of the Yb4 molecule, consisting of four ½ pseudospins, into doubly degenerated Seff=0, triply degenerated Seff=1 and non-degenerated Seff=2 states. Due to the DM interaction, the 3 × 3 Seff=1 states are admixed with the lowest Seff=0 states and split into four states, ψ1(1), ψ2(3), ψ3(3) and ψ4(2), with degeneracies presented in the parenthesis, while the ground state ψ0(2) is further lowered in energy. On the other hand, the Seff=2 quintet state ψ5(5) is not affected. For detailed analyses, we calculated eigenstates and eigenvalues of  using the exact diagonalization method, and estimated the magnetic scattering cross-sections. With optimized values of J=0.589 meV and d=0.158 meV (refs 37, 38), we obtained simulated I(ω) spectra at 200 mK (blue line) and 10 K (red line), which well reproduce the experimental data as shown in Fig. 2d. The obtained large DM value (d/J=0.27), which reflects the strong SOC of Yb3+ ions, is consistent with the value theoretically estimated for the Yb–O–Yb superexchange hopping (Supplementary Note 4).
using the exact diagonalization method, and estimated the magnetic scattering cross-sections. With optimized values of J=0.589 meV and d=0.158 meV (refs 37, 38), we obtained simulated I(ω) spectra at 200 mK (blue line) and 10 K (red line), which well reproduce the experimental data as shown in Fig. 2d. The obtained large DM value (d/J=0.27), which reflects the strong SOC of Yb3+ ions, is consistent with the value theoretically estimated for the Yb–O–Yb superexchange hopping (Supplementary Note 4).
INS with magnetic fields
Validity of the effective Hamiltonian can be also confirmed in the field-dependent INS results at 200 mK. Figure 3a shows I(ω), integration of I(Q,ω) over 0.8 Å−1<Q<1.8 Å−1, under various external magnetic fields in comparison with the theoretical simulations. The excitation peaks evolve with the external field. The simulated I(ω) spectra represent spherically averaged I(ω) from exactly diagonalized  . The simulations well reproduce the experiments with the g-factor values g||=2.62(2) and g∥=2.33(2), which are slightly smaller than the values obtained from the M(H) curve, likely due to an estimation error. These g-factor values are also consistent with the values estimated from the electron paramagnetic resonance spectrum and those determined from YbO6 CF analyses for reported high-energy neutron excitation spectra25 as discussed in Supplementary Notes 2 and 4, respectively.
. The simulations well reproduce the experiments with the g-factor values g||=2.62(2) and g∥=2.33(2), which are slightly smaller than the values obtained from the M(H) curve, likely due to an estimation error. These g-factor values are also consistent with the values estimated from the electron paramagnetic resonance spectrum and those determined from YbO6 CF analyses for reported high-energy neutron excitation spectra25 as discussed in Supplementary Notes 2 and 4, respectively.
(a) Constant-Q cuts I(ω)’s obtained by integrating measured I(Q,ω)’s over a range of 0.8 Å−1<Q<1.8 Å−1 at T=200 mK in external magnetic fields ranging from H=0 to H=10 T. Solid lines are obtained by fitting the experimental I(ω)’s with parameters of J, d and g-factors in  . (b) Calculated excitation energy diagrams as a function of the H-field along the three principal axes [0 0 1], [1 1 0] and [1 1 1] are overlapped on the contour map of I(ω)’s. Excitation peak positions of I(ω)’s agree well with calculations. Peak intensites are presented by the grey scale bar. Selected three excitations, related to the level crossings at HC1 and HC2 are, respectively, marked with stars, diamonds and triangles in a and b. (c) Avoided level crossing along H//[1 1 0] near H=HC1 in a low-energy region. The colour scale bar represents the magnetization value <g Sz> per Yb for the line colours in b and c. On the other hand, the avoided level crossing feature appears along H//[0 0 1] near H=HC2. Intensity error bars are square roots of intensities.
. (b) Calculated excitation energy diagrams as a function of the H-field along the three principal axes [0 0 1], [1 1 0] and [1 1 1] are overlapped on the contour map of I(ω)’s. Excitation peak positions of I(ω)’s agree well with calculations. Peak intensites are presented by the grey scale bar. Selected three excitations, related to the level crossings at HC1 and HC2 are, respectively, marked with stars, diamonds and triangles in a and b. (c) Avoided level crossing along H//[1 1 0] near H=HC1 in a low-energy region. The colour scale bar represents the magnetization value <g Sz> per Yb for the line colours in b and c. On the other hand, the avoided level crossing feature appears along H//[0 0 1] near H=HC2. Intensity error bars are square roots of intensities.
Figure 3b shows the calculated excitation energy diagrams as a function of external magnetic field H along the principle axes [0 0 1], [1 1 0] and [1 1 1] using the obtained values of the J, d and g-factors. The colour of the excitation energy line represents the magnetization value <g Sz> ranged from −g||/2 to +g||/2 as presented by a colour scale bar in Fig. 3c. One can notice that the overall energy diagram is almost identical for the three axes except minor variations in the excitation energies, which appear as peak broadenings in the observed I(ω) in Fig. 3a, and the calculated energies coincide with the peak positions. We also trace three excitation peaks as marked in Fig. 3a,b. The first excitation (diamond) corresponds to ψ0 (Seff≈0)→ψ1 (Seff≈1) for H<HC1 (≈3.5 T). For H>HC1, the Zeeman energy of ψ1 overcomes their zero-field energy difference, that is, level crossing, and the excitation is switched to the second one (star), ψ1→ψ0. As H exceeds HC2, ψ5 (Seff=2) becomes the ground state, and the third one (triangle) representing the excitation ψ1→ψ5 becomes unavailable. The avoided level crossing feature around H=HC1 is also examined in the calculated excitation. Figure 3c shows the ψ0→ψ1 to ψ1→ψ0 excitation crossover for H//[1 1 0] in a very-low-energy region. Even though H approaches HC1, the excitation energy between ψ0 and ψ1 does not vanish, confirming existence of a finite gap, that is, avoided level crossing, which originates the hysteretic behaviour of M(H) discussed above. The estimated gap energy Δ≈0.013 meV corresponds to a gigahertz range in a qubit model system.
Discussion
Our analysis demonstrates that the inorganic solid Ba3Yb2Zn5O11 realizes a novel molecular quantum magnet. By virtue of strong SOC of Yb 4f electrons, each Yb3+ ion has a spin–orbit coupled pseudospin-½, and the antisymmetric DM exchange interaction plays a crucial role in the magnetism. This quantum magnetism exhibits not only the exotic Landau–Zener transition involving avoided level crossing but also paramagnetic responses under a magnetic field that differ significantly from conventional molecular magnetism. In this inorganic material, the inter-molecular exchange coupling J′ is negligible, but as the inter-molecular spacing is reduced by the substitution of non-magnetic ions with smaller ionic sizes or by applying pressure, J′ increases to turn on the entanglement between the molecular spins. A weakly coupled alternating pyrochlore system can be considered as a protocol for quantum gates and spin manipulations by electric fields, as proposed for weakly coupled molecular spin triangles39. When J′ becomes significant, the system ends to be a typical frustrated magnet23. Therefore, this material provides a promising starting point for exploration of an uncharted crossover from molecular to entangled quantum magnetism.
Methods
Sample synthesis and magnetization
Polycrystalline Ba3Yb2Zn5O11 samples were prepared by the solid-state reaction method from a stoichiometric mixture of Ba2CO3 (99.999%), Yb2O3 (99.99%) and ZnO (99.999%) powders as in the (ref. 24). The mixture pellet was successively sintered at 1,000 °C for 24 h and at 1,120 °C for 24 h in air. The isothermal magnetization was determined for a 60 mg of pelletized sample below T=1.8 K using a conventional Faraday force magnetometer, which measures changes in the electric capacitance induced by a magnetic field gradient. To avoid any movement of grains during the measurements, we pelletized a 60 mg of powder to a cubic-shaped hard solid, and firmly mounted it on the magnetometer sample holder, and no crack was observable on the pellet after the measurements. The measurements were performed under a static magnetic field in a range from 0 to 12 T with various sweep rates from 7.5 to 30 mT min−1. The magnetization at 1.8 K, which was measured using the Quantum Design’s Magnetic Property Measurement System, was utilized as a reference to determine the magnetizations at different temperatures.
Elastic and inelastic neutron scattering
Neutron powder diffraction experiment was conducted at the high-resolution powder diffraction beamline in HANARO for the structural information (Supplementary Fig. 1; Supplementary Table 1). Powder samples of 5 g were sealed in vanadium container and placed on a closed cycle refrigerator for the diffraction measurements at 4 K. The crystal structure was determined from the Rietveld refinement using the FullProf suite software40. Time-of-flight neutron scattering experiment was carried out at the Disk Chopper Spectrometer beamline in the National Institute of Standards and Technology Center for Neutron Research. The neutron scattering data were obtained at T=200 mK and 10 K. The incident neutron energy was set to be 2.27 meV (=6 Å) with an energy resolution of 64 μeV at the elastic line. A polycrystalline sample of 10 g was sealed in a copper container, and inserted into a 10 T vertical field magnet equipped with a dilution refrigerator.
The inelastic magnetic neutron scattering intensity for isolated Yb4 tetrahedrons is given by

where I0 is a scale factor, ki and kf are initial and final neutron wave vectors, and Q and ω are the momentum and energy transfers, respectively. F(Q) is a dimensionless magnetic form factor of Yb3+, and α, β=x, y and z, and the dynamical structure factor  is defined as
is defined as

where i is the site index and  is an eigenstate
is an eigenstate  of
of  with an energy
with an energy  .
.  denotes the thermal population
denotes the thermal population  with the partition function Z, and Mi is the i-site effective magnetic moment
with the partition function Z, and Mi is the i-site effective magnetic moment  . For a powder sample with an external magnetic field H, the inelastic magnetic neutron scattering intensity is obtained by averaging I(Q, ω) over all directions of Q41 and H as
. For a powder sample with an external magnetic field H, the inelastic magnetic neutron scattering intensity is obtained by averaging I(Q, ω) over all directions of Q41 and H as

which is adopted for the INS data fitting.
Code availability
We declare that the data-simulation code supporting the findings of this study are available within article’s Supplementary Information file (Supplementary Software 1).
Data availability
The data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Park, S.-Y. et al. Spin–orbit coupled molecular quantum magnetism realized in inorganic solid. Nat. Commun. 7, 12912 doi: 10.1038/ncomms12912 (2016).
References
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Sachdev, S. Quantum magnetism and criticality. Nat. Phys. 4, 173–185 (2008).
Schollwöck, U., Richter, J., Farnell, D. J. J. & Bishop, R. F. Quantum Magnetism, (Lecture Notes in Physics) 645Springer (2004).
Affleck, I. Quantum spin chain and Haldane gap. J. Phys. Condens. Matter 1, 3047–3072 (1989).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Lee, S.-H. et al. Emergent excitations in a geometrically frustrated magnet. Nature 418, 856–858 (2002).
Sahstry, B. S. & Sutherland, B. Exact ground state of a quantum mechanical antiferromagnet. Physica 108B, 1069–1070 (1981).
Majumdar, C. K. & Ghosh, D. K. On next-nearest-neighbor interaction in linear chain. I. J. Math. Phys. 10, 1388–1398 (1969).
Blundell, S. J. & Pratt, F. L. Organic and molecular magnets. J. Phys. Condens. Matter 16, R771–R828 (2004).
Miller, J. S. Magnetically ordered molecule-based materials. Chem. Soc. Rev. 40, 3266–3296 (2011).
De Jongh, L. J. & Miedema, A. R. Experiments on simple magnetic model systems. Adv. Phys. 23, 1–260 (1974).
Dagotto, E. & Rice, T. M. Suprises on the way from one- to two-dimensional quantum magnets: the ladder materials. Science 271, 618–623 (1996).
Goddard, P. A. et al. Dimensionality selection in a molecule-based magnet. Phys. Rev. Lett. 108, 077208 (2012).
Sessoli, R., Gatteschi, D., Caneschi, A. & Novak, M. A. Magnetic bistability in a metal-ion cluster. Nautre (London) 365, 141–143 (1993).
Gatteschi, D., Caneschi, A., Pardi, L. & Sessoli, R. Large clusters of metal ions: the transition from molecular to bulk magnets. Science 265, 1054–1058 (1994).
Okamoto, Y., Nilsen, G. J., Attfield, J. P. & Hiroi, Z. Breathing pyrochlore lattice realized in a-site ordered spinel oxides LiGaCr4O8 and LiInCr4O8. Phys. Rev. Lett. 110, 097203 (2013).
Vieru, V., Iwahara, N., Ungur, L. & Chibotaru, L. F. Giant exchange interaction in mixed lanthanides. Sci. Rep. 6, 24046 (2016).
Pineda, E. M. et al. Direct measurement of dysprosium(III)·dysprosium(III) interactions in a single-molecule magnet. Nat. Commun. 5, 5243 (2014).
Pugh, T. et al. Influencing the properties of dysprosium single-molecule magnets with phosphorus donor ligands. Nat. Commun. 6, 7492 (2015).
Furrer, A., Güdel, H. U., Blank, H. & Heidemann, A. Direct observation of exchange splittings in Cs3Tb2Br9 by neutron spectroscopy. Phys. Rev. Lett. 62, 210–213 (1989).
Güdel, H. U., Furrer, A. & Blank, H. Exchange interactions in rare-erath-metal dimers. Neutron spectroscopy of Cs3Yb2Cl9 and Cs3Yb2Br9 . Inorg. Chem. 29, 4081–4084 (1990).
Aebersold, M. A., Güdel, H. U., Furrer, A. & Blank, H. Inelastic neutron scattering and optical spectroscopy of Dy3+ single ions and dimers in Cs3Y2Br9:10% Dy3+ and Cs3Dy2Br9 . Inorg. Chem. 33, 1133–1138 (1994).
Savary, L., Kee, H.-Y., Kim, Y. B. & Chen, G. Quantum spin ice on the breathing pyrochlore lattice, Preprint at http://arxiv.org/abs/1511.06972 (2015).
Kimura, K., Nakatsuji, S. & Kimura, T. Experimental realization of a quantum breathing pyrochlore antiferromagnet. Phys. Rev. B 90, 060414 (R) (2014).
Haku, T. et al. Crystal field excitations in the breathing pyrochlore antiferromagnet Ba3Yb2Zn5O11 . J. Phys. Soc. Jpn 85, 034721 (2016).
Ross, K. A., Savary, L., Gaulin, B. D. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).
McClarty, P. A., Curnoe, S. H. & Gingras, M. J. P. Energetic selection of ordered states in a model of the Er2Ti2O7 frustrated pyrochlore XY antiferromagnet. J. Phys. Conf. Ser. 145, 012032 (2009).
Canals, B., Elhajal, M. & Lacroix, C. Ising-like order by disorder in the pyrochlore antiferromagnet with Dzyaloshinskii-Moriya interactions. Phys. Rev. B 78, 214431 (2008).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev 120, 91–98 (1960).
Landau, L. D. On the theory of transfer of energy at collisions II. Phys. Z. Sowjetunion 2, 46–51 (1932).
Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. Lond. A 137, 696–702 (1932).
Chiorescu, I., Wernsdorfer, W., Müller, A., Bögge, H. & Barbara, B. Butterfly hysteresis loop and dissipative spin reversal in the S=½, V15 molecular complex. Phys. Rev. Lett. 84, 3454–3457 (2000).
Waldmann, O. et al. Butterfly hysteresis loop at nonzero bias field in antiferromagnetic molecular rings: cooling by adiabatic magnetization. Phys. Rev. Lett. 89, 246401 (2002).
Kotov, V. N., Zhitomirsky, M. E., Elhajal, M. & Mila, F. Weak antiferromagnetism and dimer order in quantum systems of coupled tetrahedra. Phys. Rev. B 70, 214401 (2004).
Furrer, A. & Waldmann, O. Magnetic cluster excitations. Rev. Mod. Phys. 85, 367–420 (2013).
Carretta, S. et al. Quantum oscillations of the total spin in a heterometallic antiferromagnetic ring: evidence from neutron spectroscopy. Phys. Rev. Lett. 98, 167401 (2007).
Rau, J. G. et al. Anisotropic exchange within decoupled tetrahedral in the quantum breathing pyrochlore Ba3Yb2Zn5O11 . Phys. Rev. Lett. 116, 257204 (2016).
Haku, T. et al. Low-energy excitations and ground state selection in quantum breathing pyrochlore antiferromagnet Ba3Yb2Zn5O11 . Phys. Rev. B 93, 220408 (R) (2016).
Carretta, S., Santini, P., Amoretti, G., Troiani, F. & Affronte, M. Spin triangles as optimal units for molecule-based quantum gates. Phys. Rev. B 76, 024408 (2007).
Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 192, 55–69 (1993).
Waldmann, O. Q dependence of the inelastic neutron scattering cross section for molecular spin clusters with high molecular symmetry. Phys. Rev. B 68, 174406 (2003).
Acknowledgements
We became aware of the experimental works by Rau et al.37 and Haku et al.38 after we have submitted this paper. They also obtained the consistent results with ours using INS without an external magnetic field and the same model Hamiltonian. In our work, we have advanced by showing that the DM interaction associated with the avoided energy level crossing plays a crucial role for unconventional quantum magnetic behaviours such as a hysteresis and paramagnetic response in magnetization, which is confirmed by INS with an external magnetic field. We are grateful to K.-B. Lee and K.-S. Park for enlightning discussions. This work is supported by the National Research Foundation (NRF) through the Ministry of Science, ICP & Future Planning (MSIP) (No. 2016K1A4A4A01922028). B.H.K. is supported by the RIKEN iTHES Project. S.-H.D. and K.-Y.C. are supported by the Korea Research Foundation grant (No. 2009-0076079) funded by the Korea government (MEST). S.L. is supported by the NRF under the contract NRF-2012M2A2A6002461.
Author information
Authors and Affiliations
Contributions
S.-Y.P., N.P.B. and S.J. performed INS measurement. J.-H.K., D.J. and M.B. carried out magnetization measurement. S.-Y.P., S.L. and S.J. performed neutron powder diffraction measurement. S.-H.D. and K.-Y.C. synthesized samples. S.-Y.P., B.-H.K., B.S. and S.J. developed the theoretical model of the effective Hamiltonian. D.-H.K., B.-H.K. and J.-H.P. performed CF and superexchange model calculations. S.-Y.P. and S.J. analysed the data. S.-Y.P., S.J. and J.-H.P. wrote the manuscript. J.-H.P. and S.J. initiated and supervised the research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Table 1, Supplementary Notes 1-4 and Supplementary References. (PDF 1242 kb)
Supplementary Software
Mathematica notebook which calculates eigenstates of a four-1/2-(pseudo)spin tetrahedron by full diagonalization of the effective Hamiltonian and simulates a magnetisation, a magnetic susceptibility and a specific heat without a directional average. (TXT 318 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Park, SY., Do, SH., Choi, KY. et al. Spin–orbit coupled molecular quantum magnetism realized in inorganic solid. Nat Commun 7, 12912 (2016). https://doi.org/10.1038/ncomms12912
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12912
This article is cited by
-
Understanding temperature-dependent SU(3) spin dynamics in the S = 1 antiferromagnet Ba2FeSi2O7
npj Quantum Materials (2023)
-
Towards understanding the magnetic properties of the breathing pyrochlore compound Ba3Yb2Zn5O11through single-crystal studies
npj Quantum Materials (2022)
-
Dichotomy in temporal and thermal spin correlations observed in the breathing pyrochlore LiGa1−xInxCr4O8
npj Quantum Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.