Abstract
Strong Coulomb repulsion and spin–orbit coupling are known to give rise to exotic physical phenomena in transition metal oxides. Initial attempts to investigate systems, where both of these fundamental interactions are comparably strong, such as 3d and 5d complex oxide superlattices, have revealed properties that only slightly differ from the bulk ones of the constituent materials. Here we observe that the interfacial coupling between the 3d antiferromagnetic insulator SrMnO3 and the 5d paramagnetic metal SrIrO3 is enormously strong, yielding an anomalous Hall response as the result of charge transfer driven interfacial ferromagnetism. These findings show that low dimensional spin–orbit entangled 3d–5d interfaces provide an avenue to uncover technologically relevant physical phenomena unattainable in bulk materials.
Similar content being viewed by others
Introduction
The strong interplay among charge, spin, orbital and lattice order parameters in transition metal oxides (TMOs) is known to produce exotic physical phenomena1, which can be significantly tuned through interfacial coupling between dissimilar materials2. Examples include enhanced superconducting critical temperature in cuprate bilayers3, formation of a two-dimensional electron gas at an interface between two band insulators4, improved transport and thermoelectric properties by fractional control of interfacial composition5,6, and conducting interfaces between transparent titanates7. Although there have been several studies of interfacial magnetism in manganite8,9,10,11,12 and ferrite13 superlattices, they exclusively involve 3d and 4d TMOs. Even though there are a few examples of successful synthesis of 3d–5d superlattices14,15,16,17, there are no examples of strong interfacial coupling between these materials as the field remains in its infancy. With the emergence of a novel insulating ground state with effective total angular momentum Jeff=1/2 that is induced by strong spin–orbit coupling (SOC), there has been enormous interest in many Ir-based 5d TMOs18,19,20,21, which have a SOC interaction strength (ξ) with an energy scale comparable to the on-site Coulomb interaction (U)22. This interest is largely due to theoretical predictions of exotic physical properties such as unconventional superconductivity23, Weyl semi-metals20 and topological insulators24,25 in 5d systems. However, these novel ground states are yet to be experimentally confirmed.
To narrow this gap between experimental and theoretical efforts, we have synthesized atomic-scale heterostructures by incorporating the antiferromagnetic insulator SrMnO3 (SMO), a 3d TMO with weak ξ (0.01–0.1 eV) strong U (5–7 eV), and the paramagnetic metal SrIrO3 (SIO), a 5d TMO with strong ξ (0.1–1 eV) and modest U (1–3 eV)22. Such a sample geometry uniquely enables the investigation of 3d–5d interfaces where collectively both U and ξ are stronger than in either parent compound. Interestingly, we find that our [(SMO)m/(SIO)n]z (MmIn) heterostructures, where m and n are, respectively, the thicknesses of SMO and SIO in unit cells, display exceptionally strong interfacial coupling between the two constituent materials, yielding a ferromagnetic ground state. Such emerging interfacial magnetism in turn results in a strong anomalous Hall effect (AHE). As the emergence of ferromagnetism and the AHE are completely absent from either parent compound, this discovery provides the first experimental evidence of strong coupling at the interface of 3d and 5d materials.
Results
Emerging magnetism
The first indication of such unique behaviour is the onset of magnetism in atomically thin superlattices. The macroscopic magnetic properties were measured with a superconducting quantum interference device (SQUID) and are shown in Fig. 1. The magnetic field (H) dependence of symmetric samples (m=n) is presented in Fig. 1 and clearly reveals the fact that samples with the thinnest layers (that is, atomically thin superlattices) have the largest magnetic response. Although this is certainly a ferromagnetic response emerging at the SIO/SMO interface, the facts that the overall magnetization (M) of M1I1 is significantly larger than twice that of M2I2 along with M4I4 having M≈0 implies that interfacial diffusion is not responsible for the magnetic properties here and the mechanism driving this induced interfacial magnetism must have a characteristic length scale of just a few unit cells. The temperature-dependent nature of the magnetization of these samples is shown in Fig. 1b. Consistent with the field sweeps, all samples with m>3 showed no magnetic order, while below this limit, the magnitude increased with decreasing m. The Curie temperature (Tc) is shown in the inset where M1I1 has the largest Tc∼190 K. Note that M1I1 has a second anomaly at ∼120 K for H⊥c that is likely associated with its electronic properties as discussed below. The magnetic anisotropy of a second M1I1 sample is presented in Fig. 1c,d. Note that, although the saturation magnetization and Tc are independent of the direction of H, both the coercive field and remnant magnetization are roughly an order of magnitude larger when H is parallel to the c axis (out of plane). This result implies that the c axis is the magnetic easy axis.
(a) M(H) of symmetric samples at T=10 K after zero-field cooling. (b) M(T) of symmetric samples at H=1 kOe after field cooling in H=1 kOe. The inset shows the SMO layer thickness (m) dependence of the Curie temperature. (c) M(H) of M1I1 at T=10 K after zero-field cooling. (d) M(T) of M1I1 at H=1 kOe after field cooling in H=1 kOe.
Elemental-specific characterization by X-rays and neutrons
To fully understand the magnetism of these superlattices, it is necessary to identify the relative contribution of Mn and Ir ions to the overall magnetic moment. Both X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD) spectra provide information rich with elemental-specific contributions regarding both the electronic and magnetic structures. Thus, we collected XAS and XMCD spectra near the L3 and L2 edges of both Mn and Ir (Fig. 2) to understand the underlying mechanism of the novel magnetism. The XAS peak position of the Mn L3 edge show that the onset of magnetism is accompanied by a shift of this peak to a lower energy, which implies that the Mn oxidation state in the heterostructures are lower than Mn4+ found in stoichiometric SMO. Similarly, the position of the Ir L3 edge shifts to a higher energy and indicates that the Ir oxidation state are enhanced relative to Ir4+ of stoichiometric SIO. It is important to note that even if the oxidation state of the constituent materials deviates from their nominal values, our data still convincingly indicate that to maintain charge balance, there is a charge transfer from the SIO to the SMO layers resulting in electron (hole)-doped SMO (SIO) layers. The average oxidation states are estimated from the peak shifts and are presented in the inset of Fig. 2, where M1I1 clearly has the largest deviation from the nominal value with a charge transfer of ∼0.5 electron/hole per perovskite unit cell. Although in absolute units these estimates of the oxidation state have a relatively large uncertainty, it is important to note that their relative uncertainties are significantly smaller than the data points. The XMCD spectra of the Mn L3 edge show that M1I1 has a large negative response, which indicates that the magnetic moment of the Mn ions (MMn) orders parallel to H. As m increases, the Mn XMCD decreases. Despite the consistency between SQUID and Mn XMCD measurements, there are surprisingly finite XMCD peaks near the Ir L edges. This XMCD result implies that there is a net magnetic moment of Ir (MIr) due to the onset of ferromagnetism or canted antiferromagnetism. The observation of net ferromagnetic order of Ir ions is quite surprising since Ir4+ and Ir5+ tend to favour antiferromagnetic26,27 and paramagnetic28,29 ground states, respectively. Thus, varying the valence state of Ir may provide a phase diagram as rich as those already known to the manganites. We were able to apply sum rules to the Ir XMCD spectra to separate the spin (S) and orbital (L) contributions of MIr and found them to be 0.013 μB and 0.057 μB, respectively, for M1I1, whereas for MMn, S and L are 0.9 μB and 0.3 μB, respectively. Combining these results, we determine the total magnetization (M=L+2S) in each material to be MIr=–0.08 μB/Ir and MMn=2.1 μB/Mn, which are in good agreement with SQUID data. Thus, we conclude that MMn is mostly driven by spin, while MIr has predominately orbital contributions due to strong SOC19. In addition, the XAS branching ratio (BR=IL3/IL2) of Mn in SMO is ∼2 and systematically increases with decreasing m. Although this qualitative behaviour can be explained by the reduction of the Mn oxidation state, it is worth noting that a BR>2 is often attributed to the presence of spin–orbit interactions30.
The data near the Mn (Ir) edges were obtained at H=50 kOe (40 kOe) with H⊥c after cooling in zero field to 15 K (10 K). Both ions display a finite XMCD signal, which indicates that both SMO and SIO are ferromagnetically active. The peak near the L3 edge of Mn (Ir) for the M1I1 sample shifts to lower (higher) energy, indicating a charge transfer from the SIO to the SMO layer. The inset shows the estimate of the oxidation state for each cation determined by a linear interpolation between known positions of Mn and Ir oxidation states, where the uncertainties were determined by propagating the instrumental energy uncertainties into oxidation state estimates.
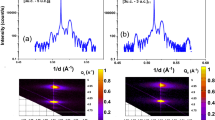
The microscopic origin of the magnetism was further investigated by polarized neutron reflectometry (PNR), which is a sensitive probe of spin asymmetry. This technique provides a detailed look at the magnetism of thin films and heterostructures as a function of depth. However, PNR of our symmetric magnetic superlattices is a formidable task since only short-period superlattices (m≤3) are magnetic and all superlattice Bragg peak positions of these samples lie at wavevector transfer (q) values unobtainable with reasonable measurement parameters. This challenge was overcome by synthesizing an asymmetric M1I10 sample, which has a larger superlattice period and an appreciable magnetic response (Supplementary Fig. 2b). As shown in Fig. 3a–c, we observed a finite spin asymmetry that is a clear indication of ferromagnetic order and, thus, M1I10 is also ferromagnetically ordered. The chemical and neutron scattering length density (SLD) profiles obtained from spin-dependent PNR measurements and X-ray SLD profile from X-ray reflectometry are shown in Fig. 3d. Note that, although it is typical, the apparent broadness of the SLDs arise from there being 13 SLDs that all differ by less than two s.d.’s (2-sigma) from the ideal fit, indicating that this model is extremely robust. From this PNR result, the magnetic depth profile is determined and presented in Fig. 3d. Notice that MMn is much larger than MIr, which is consistent with XMCD measurements. However, conversely, our PNR indicates that MIr aligns parallel to the applied magnetic field in M1I10, whereas XMCD has revealed that it aligns antiparallel for M1I1. This discrepancy suggests that there is a critical SIO thickness, in which the Ir moments realign. Confidence in this interpretation of non-zero MIr arises from the fact that if the MIr is forced to zero (dashed lines in Fig. 3a−c), the model significantly deviates from the experimental data. Moreover, if MIr is forced to align antiparallel to MMn, similar to XMCD of M1I1, this separation is exacerbated (Supplementary Fig. 2a). The thickness averaged M values for the Mn and Ir layers obtained from PNR is in excellent agreement with that obtained from SQUID measurements (Supplementary Fig. 2b)—further evidence that in-plane components of MMn and MIr for the M1I10 sample are parallel. In addition, recall that bulk SIO is paramagnetic and, even though a small ferromagnetic response has also been observed in SIO under reduced dimensionality in other studies: Sr2IrO4 (refs 31, 32) and (STO)1/(SIO)n (n≤3)15, our observation provides the first example of ferromagnetism in thick slabs of SIO that clearly arises from strong interfacial coupling between 3d and 5d TMOs.
Data were obtained from a [(SrMnO3)1/(SrIrO3)10]12 superlattice on STO after a zero-field cooling at T=10 K and H=11.5 kOe with H⊥c. (a) The spin asymmetry (SA=[R↑−R↓]/[R↑+R↓]), where solid (dotted) black lines represent models where the magnetism in the SIO layer is allowed to vary (forced to zero) for the fit. The orange and cyan rectangles represent the positions near the critical angle and first superlattice Bragg reflection shown in b and c, respectively. (d) Depth profile of X-ray (purple) and neutron (blue and pink) scattering length densities, where a schematic drawing of the sample geometry is shown above the data. (e) Magnetic depth profile obtained with fit parameters of MMn=85 emu cm−3 (0.54 μB/Mn) and MIr=9 emu cm−3 (0.06 μB/Ir).
Transport properties and Hall measurements
The electronic properties of the symmetric samples were investigated via DC transport measurements, and the temperature-dependent sheet resistance (RS) is shown in Fig. 4a. SMO (data not shown) is too resistive to measure (RS (300 K)∼1 MΩ) and SIO is semimetallic. The fact that all samples are roughly 50 nm thick and the resistance of M12I12 is approximately double that of SIO implies that the SIO layers in long-period superlattices (m≳12) dominate the overall electronic conduction. However, when the layer thicknesses are intermediately thick (3≤m≤6), the heterostructures have significantly enhanced metallicity with a weak upturn below 50 K, which is most probably due to weak localization. In this intermediate thickness region, there is minimal charge transfer, which implies that the magnitude of electron (hole) doping of the SMO (SIO) layers is quite small. Since bulk SMO is known to be insensitive to small concentrations of electron doping33, the enhanced metallicity observed in the intermediate-period superlattices likely resides within the SIO layers. This result also indicates that SIO is sensitive to small concentrations of hole doping. As the layer thickness is further reduced (m<3), the resistance increases as shown in Fig. 4a. This is somewhat counterintuitive since one would expect the onset of ferromagnetism to coincide with the enhanced metallicity. Consider the resistivity of M1I1, which displays a semimetallic behaviour with a local maximum at ∼120 K. Comparing this with comparably doped bulk La1−xSrxMnO3 (x=0.55)33, we observe a quantitatively similar temperature-dependent resistivity behaviour that is roughly an order of magnitude larger than our M1I1 superlattice. Thus, the resistivity in small-period superlattices is explained by the large electron doping concentration in atomically thin SMO layers, resulting in a finite electrical conductivity accompanied by the atomically thin SIO layers having reduced conductivity due to reduced dimensionality18, a large concentration of hole dopants34 or the finite thickness effect35,36. Therefore, the enhanced metallicity in the intermediately thick samples is due the SIO layers, while the finite conductivity for M1I1 is due to the onset of conductivity in the SMO layers.
(a) RS (T) for SMO–SIO superlattices with all samples displaying semimetallic and metallic behaviours. MR(H) =[RS (H)–RS (0)]/RS (0) × 100% with H//c for (c) M1I1 at various temperatures and (d) short-period samples (n≤6) at 2 K, where the colour scheme is identical to (a). Rxy (H) with H//c for (e) M1I1 at various temperatures and (f) short-period samples at 2 K that clearly display a nonlinear behaviour attributed to a magnetism induced anomalous Hall effect. (b) Scaling plot of σxy and σxx where they are determined using the total superlattice thickness.
The intriguing magnetic properties of these superlattices were further investigated via magnetoresistance (MR) and Hall measurements presented in Fig. 4c–f. The MR of the M1I1 sample (Fig. 4c) has a negligible response at room temperature. However, a negative linear response starts to appear near and below Tc∼190 K and increases systematically in magnitude with further decreasing temperature. Interestingly, at lower temperatures (T<75 K), a butterfly hysteresis loop appears at small H that is coupled with the coercive field as comparatively shown in Fig. 4c,e. Comparing the low-temperature MR for different samples (Fig. 4d) indicates that all superlattices have a negative MR response that increases in magnitude with the onset of magnetism, whereas the SIO film has a small positive response. These behaviours are consistent with the typical results for ferromagnets and paramagnets, respectively. Strikingly, the Hall measurements (Rxy) of our superlattices lead to an unprecedented observation. Consider the temperature-dependent Hall resistance of the M1I1 superlattice shown in Fig. 4e. Above Tc, the Hall response is linear with a negative slope, indicating n-type carriers. Below Tc, a nonlinear AHE appears, opening a large hysteresis loop at low temperatures with a shape and coercive field practically identical to M(H) sweeps obtained from SQUID measurements (Supplementary Fig. 4). In addition, it is evident from Fig. 4f that only the magnetic samples display the AHE response. Thus, it is indisputable that the AHE observed here is due to the onset of magnetism in this system.
Discussion
Since the dominant magnetic ion is Mn and the AHE is driven by magnetism, it is logical to assume the majority of AHE resides within the SMO layers. Recent advances in understanding the AHE separates such materials into three categories: (i) the dirty metal limit where intrinsic and side jump scattering leads to a scaling relationship between the transverse conductivity (σxy) and longitudinal conductivity (σxx) of σxy∝σxx1.6; (ii) the super-clean metal limit where skew scattering off extrinsic defects leads to a scaling relationship of σxy∝σxx; and (iii) the moderately dirty metal region where intrinsic scattering leads to σxy being approximately independent of σxx (refs 37, 38). The latter has been modelled theoretically utilizing Berry phases and Berry curvature to successfully bridge the dirty and super-clean limits, and has been successful in modelling 3d TMO systems within the range 3,000≤σxx≤450,000 Ω−1 cm−1 (ref. 39). Considering the scaling plot presented in Fig. 4b, we find that both M1I1 and M2I2 have σxx∼2,000 Ω−1 cm−1, which should place them in the dirty metal limit. However, fits to the low-temperature data clearly show a much weaker power law (σxy∝σxxϕ) than ϕ=1.6. Recall that, although the AHE resides in the SMO layers, the XMCD hinted that SOC substantially influences the SMO layers. Since the magnitudes of σxx that separate the three regions described above depend inversely on ξ, for 5d materials, the moderately dirty limit is roughly 45≤σxx≤6,800 Ω−1 cm−1. This remarkable agreement with our experimental results strongly suggests that SOC is instrumental in defining the novel magnetic and electronic ground states of these 3d–5d TMO heterostructures, and that they are near the moderately dirty limit that has a characteristic dissipationless AHE current40. Another observation is the magnitude of σxy observed here is significantly lower than the theoretical intrinsic scattering limit of ∼900 Ω−1 cm−1 proposed by the Thouless–Kohmoto–Nightingale–Nijs formulism41, despite the fact that σxy should scale with ξ. We attribute this discrepancy to the fact that, although the AHE resides in the SMO layers, the SIO layers still conduct appreciably well and serve as a resistive short of the voltage leads during the Hall measurements, which greatly reduce the measured values of σxy.
In summary, we have observed interfacial ferromagnetism that led to an AHE in atomic-scale SMO/SIO superlattices grown on STO by pulsed laser epitaxy. This discovery provides clear experimental evidence of strong interfacial coupling between 3d and 5d materials. Furthermore, we have shown that SOC plays an integral role in defining these unique ground states, and that this appears to be the prototypical system for investigating interfacial coupling between strong U and strong SOC, thus presenting an avenue for potential spintronics applications. In addition, despite the Mn ions being the dominant magnetic host, we observe that the spins in Ir also ferromagnetically order opening a field of investigating magnetism in multivalent Ir ions. We believe that this work will stimulate further theoretical and experimental studies that will lead to greater understanding of the role of SOC in such systems.
Methods
Sample synthesis and structural characterization
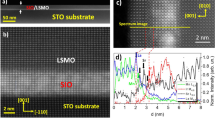
The superlattice samples of [(SrMO3)m/(SrIrO3)n]z were synthesized by pulsed laser epitaxy on atomically flat TiO2-terminated (100) SrTiO3 substrates utilizing a KrF eximer laser (λ=248 nm) with laser fluence, substrate temperature and oxygen partial pressure of 1.0 J cm−2, 700 °C and 100 mtorr, respectively. The crystal structure, orientation, phase purity and crystallinity of these superlattices were determined by X-ray diffraction and reflectivity measurements.
Magnetic and electrical measurements
The macroscopic magnetic properties were characterized with a 7 T Quantum Design MPMS3. The XAS and XMCD spectra near the Mn and Ir L edges were collected on beamlines 4-ID-C and 4-ID-D, respectively, at the Advanced Photon Source of Argonne National Laboratory. For the Mn L edge data, both electron and fluorescence yields were simultaneously monitored. The Ir L edges data were collected with a grazing incidence geometry and the fluorescence detection mode. The PNR measurements were performed on the Magnetism Reflectometer (beamline BL-4A)42 at the Spallation Neutron Source of Oak Ridge National Laboratory, and the magnetic depth profile was determined from fitting the neutron spin asymmetry that utilized the chemical model obtain from X-ray reflectometry. The DC transport measurements were performed with a 14 T Quantum Design PPMS with a home-built user bridge. Contacts were made to all superlattice layers by ultrasonic soldering of gold wires with indium solder in a Van der Pauw configuration.
Data availability
The data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Nichols, J. et al. Emerging magnetism and anomalous Hall effect in iridate–manganite heterostructures. Nat. Commun. 7:12721 doi: 10.1038/ncomms12721 (2016).
References
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Heber, J. Materials science: enter the oxides. Nature 459, 28–30 (2009).
Logvenov, G., Gozar, A. & Bozovic, I. High-temperature superconductivity in a single copper-oxygen plane. Science 326, 699–702 (2009).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Choi, W. S., Lee, S., Cooper, V. R. & Lee, H. N. Fractionally δ-doped oxide superlattices for higher carrier mobilities. Nano. Lett. 12, 4590–4594 (2012).
Choi, W. S., Ohta, H. & Lee, H. N. Thermopower enhancement by fractional layer control in 2D oxide superlattices. Adv. Mater. 26, 6701–6705 (2014).
Cooper, V. R. et al. Transparent conducting oxides: a δ-doped superlattice approach. Sci. Rep. 4, 6021–6026 (2014).
Grutter, A. J. et al. Interfacial ferromagnetism in LaNiO3/CaMnO3 superlattices. Phys. Rev. Lett. 111, 087202 (2013).
Zhai, X. et al. Correlating interfacial octahedral rotations with magnetism in (LaMnO3+δ)N/(SrTiO3)N superlattices. Nat. Commun. 5, 4283–4291 (2014).
Choi, Y. et al. Ferromagnetic Mn moments at SrRuO3/SrMnO3 interfaces. Appl. Phys. Lett. 91, 022503 (2007).
Smadici, S. et al. Electronic reconstruction at SrMnO3-LaMnO3 superlattice interfaces. Phys. Rev. Lett. 99, 196404 (2007).
Hoppler, J. et al. Giant superconductivity-induced modulation of the ferromagnetic magnetization in a cuprate-manganite superlattice. Nat. Mater. 8, 315–319 (2009).
Yu, P. et al. Interface ferromagnetism and orbital reconstruction in BiFeO3-La0.7Sr0.3MnO3 heterostructures. Phys. Rev. Lett. 105, 027201 (2010).
Kalabukhov, A., Gunnarsson, R., Claeson, T. & Winkler, D. Electrical transport properties of polar heterointerface between KTaO3 and SrTiO3. Preprint at http://arXiv:0704.1050[cond-mat.mtrl-sci] (2007).
Matsuno, J. et al. Engineering a spin-orbital magnetic insulator by tailoring superlattices. Phys. Rev. Lett. 114, 247209 (2015).
Hirai, D., Matsuno, J. & Takagi, H. Fabrication of (111)-oriented Ca0.5Sr0.5IrO3/SrTiO3 superlattices—a designed playground for honeycomb physics. APL Mater. 3, 041508 (2015).
Wei, F. & Seiji, Y. Electronic and magnetic structure under lattice distortion in SrIrO3/SrTiO3 superlattice: a first-principles study. J. Phys. Conf. Ser. 592, 012139–012145 (2015).
Moon, S. J. et al. Dimensionality-controlled insulator-metal transition and correlated metallic state in 5d transition metal oxides Srn+1IrnO3n+1 (n=1, 2, and ∞). Phys. Rev. Lett. 101, 226402–226406 (2008).
Kim, B. J. et al. Novel Jeff=1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402–076406 (2008).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101–205110 (2011).
Gegenwart, P. & Trebst, S. Spin-orbit physics: Kitaev matter. Nat. Phys. 11, 444–445 (2015).
Watanabe, H., Shirakawa, T. & Yunoki, S. Microscopic study of a spin-orbit-induced mott insulator in Ir oxides. Phys. Rev. Lett. 105, 216410 (2010).
Wang, F. & Senthil, T. Twisted Hubbard model for Sr2IrO4: magnetism and possible high temperature superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Carter, J.-M., Shankar, V. V., Zeb, M. A. & Kee, H.-Y. Semimetal and topological insulator in perovskite iridates. Phys. Rev. B 85, 115105 (2012).
Segal, N., Vente, J. F., Bush, T. S. & Battle, P. D. Structural and magnetic properties of Sr4MIrO6 (M=Ca, Zn, Cd, Li, Na). J. Mater. Chem. 6, 395–401 (1996).
Mugavero, S. J. III, Smith, M. D. & zur Loye, H.-C. Crystal growth and magnetic properties of the new iridates Ln1−xNa1+xIrO4 (Ln=Gd–Er, Y; x=0.04–0.25). Solid State Sci. 9, 555–563 (2007).
Mugavero, S. J., Smith, M. D. & zur Loye, H.-C. La9RbIr4O24: a rubidium-containing oxide with a new structure type. Inorg. Chem. 45, 946–948 (2006).
Davis, M. J., Mugavero, S. J. III, Glab, K. I., Smith, M. D. & zur Loye, H.-C. The crystal growth and characterization of the lanthanide-containing double perovskites Ln2NaIrO6 (Ln=La, Pr, Nd). Solid State Sci. 6, 413–417 (2004).
Clancy, J. P. et al. Spin-orbit coupling in iridium-based 5d compounds probed by x-ray absorption spectroscopy. Phys. Rev. B 86, 195131 (2012).
Cao, G., Bolivar, J., McCall, S., Crow, J. E. & Guertin, R. P. Weak ferromagnetism, metal-to-nonmetal transition, and negative differential resistivity in single-crystal Sr2IrO4 . Phys. Rev. B 57, 11039 (1998).
Lupascu, A. et al. Tuning magnetic coupling in Sr2IrO4 thin films with epitaxial strain. Phys. Rev. Lett. 112, 147201 (2014).
Fujishiro, H., Fukase, T. & Ikebe, M. Charge ordering and sound velocity anomaly in La1-xSrxMnO3 (x≥0.5). J. Phys. Soc. Jpn 67, 2582–2585 (1998).
Ge, M. et al. Lattice-driven magnetoresistivity and metal-insulator transition in single-layered iridates. Phys. Rev. B 84, 100402 (2011).
Son, J., LeBeau, J. M., Allen, S. J. & Stemmer, S. Conductivity enhancement of ultrathin LaNiO3 films in superlattices. Appl. Phys. Lett. 97, 202109 (2010).
Meyer, T. L., Jiang, L., Park, S., Egami, T. & Lee, H. N. Strain-relaxation and critical thickness of epitaxial La1.85Sr0.15CuO4 films. APL Mater. 3, 126102 (2015).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Onoda, S., Sugimoto, N. & Nagaosa, N. Quantum transport theory of anomalous electric, thermoelectric, and thermal Hall effects in ferromagnets. Phys. Rev. B 77, 165103 (2008).
Lee, W.-L., Watauchi, S., Miller, V. L., Cava, R. J. & Ong, N. P. Dissipationless anomalous Hall current in the ferromagnetic spinel CuCr2Se4-xBrx . Science 303, 1647–1649 (2004).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405 (1982).
Lauter, V., Ambaye, H., Goyette, R., Hal Lee, W.-T. & Parizzi, A. Highlights from the magnetism reflectometer at the SNS. Phys. B Condens. Matter 404, 2543–2546 (2009).
Acknowledgements
We thank Michael A. McGuire for his experimental assistance as well as Tae-Won Noh, Changhee Sohn, Soyeun Kim, Jun Sung Kim and Satoshi Okamoto for valuable discussions and comments. This work was supported by the US Department of Energy (DOE), Office of Science (OS), Basic Energy Sciences (BES), Materials Sciences and Engineering Division (synthesis, physical property characterization, XAS, XMCD and PNR data analysis), and the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the US DOE (PNR data fitting). The research at ORNL’s Spallation Neutron Source was sponsored by the Scientific User Facilities Division, BES, US DOE (PNR). Use of the Advanced Photon Source, an Office of Science User Facility operated for the US DOE, OS by Argonne National Laboratory, was supported by the US DOE under contract no. DE-AC02-06CH11357 (XAS/XMCD). J.L. was sponsored by the Science Alliance Joint Directed Research and Development Program at the University of Tennessee.
Author information
Authors and Affiliations
Contributions
J.N. and S.L. performed the sample synthesis. J.N., X.G., J.R.P., T.L.M., T.Z.W., G.E., D.L. and H.N.L. conducted the structural and basic physical property characterizations. J.N., T.L.M., J.W.F., D.Y., J.L. and D.H. collected and analysed the XAS and XMCD spectra. J.N., E.-J.G., A.H., V.L. and M.R.F. contributed to the PNR measurements and data analysis. H.N.L. and J.N. designed the experiment and wrote the manuscript with inputs from all authors. H.N.L. initiated the research and supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure 1-4, Supplementary Note 1 and Supplementary References (PDF 929 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nichols, J., Gao, X., Lee, S. et al. Emerging magnetism and anomalous Hall effect in iridate–manganite heterostructures. Nat Commun 7, 12721 (2016). https://doi.org/10.1038/ncomms12721
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12721
This article is cited by
-
Charge transfer driving interfacial reconstructions in perovskite oxide heterostructures
Communications Physics (2023)
-
Evolution of electronic and magnetic properties of Sr2IrO4 under strain
npj Quantum Materials (2022)
-
Interfacial effect and strain on the electrical and magnetic properties of SrRuO3/NdNiO3 bilayers with 3D island surface layer
Applied Physics A (2022)
-
Asymmetric interfaces and high-TC ferromagnetic phase in La0.67Ca0.33MnO3/SrRuO3 superlattices
Nano Research (2021)
-
Large intrinsic anomalous Hall effect in SrIrO3 induced by magnetic proximity effect
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.