Abstract
As an in-plane charge current flows in a heavy metal film with spin–orbit coupling, it produces a torque on and thereby switches the magnetization in a neighbouring ferromagnetic metal film. Such spin–orbit torque (SOT)-induced switching has been studied extensively in recent years and has shown higher efficiency than switching using conventional spin-transfer torque. Here we report the SOT-assisted switching in heavy metal/magnetic insulator systems. The experiments used a Pt/BaFe12O19 bilayer where the BaFe12O19 layer exhibits perpendicular magnetic anisotropy. As a charge current is passed through the Pt film, it produces a SOT that can control the up and down states of the remnant magnetization in the BaFe12O19 film when the film is magnetized by an in-plane magnetic field. It can reduce or increase the switching field of the BaFe12O19 film by as much as about 500 Oe when the film is switched with an out-of-plane field.
Similar content being viewed by others
Introduction
Magnetization switching in ferromagnetic materials is of both fundamental interest and technological significance. One way to switch the magnetization in a ferromagnetic film is to pass a spin-polarized electron current perpendicularly through the film. The spin-polarized current can be produced by passing a charge current through a spin polarizer, which is typically a hard magnetic layer separated from the target film by a normal metal spacer1,2,3,4. As the polarized electrons flow through the ferromagnetic film, they transfer spin angular momentum to the film and thereby produce a torque that can switch the magnetization in the film5,6. Magnetic memory based on such spin torques has already been commercialized in recent years.
The above-mentioned conventional spin-torque switching, however, has a limit, namely, that the angular momentum transferred per unit charge in the applied current usually cannot exceed a quanta of spin (ħ/2) (ref. 7). Fortunately, very recent work demonstrates that one can exceed this limit by the use of spin–orbit torque (SOT)7,8,9,10,11,12,13,14,15,16. The demonstration generally takes a non-magnetic heavy metal (HM)/ferromagnetic metal (FM) bi-layered structure, and makes use of spin–orbit coupling-produced spin Hall effect (SHE)17,18,19,20 in the HM film to convert an in-plane charge current to a pure spin current that flows across the HM thickness, produces spin accumulation at the HM/FM interface, and thereby exerts a torque on the FM. In this case, each electron in the applied current can undergo multiple spin-flip scattering at the interface, therefore enabling considerably more efficient switching than in the conventional spin-torque case.
In addition to breaking the limit of the conventional spin torque, the SOT mechanism also makes possible current-induced magnetization switching in low-damping magnetic insulators (MIs), which was impossible with the conventional spin-torque geometry. Although such a possibility has not been demonstrated so far, recent work has already demonstrated the use of SOTs from charge currents in a HM layer to either manipulate magnetic damping21,22 or induce magnetization precession22,23,24 in a neighbouring MI layer.
Here we report SOT-assisted switching in HM/MI systems. The experiments made use of Pt/BaFe12O19 bi-layered structures. Thanks to its strong spin–orbit coupling, Pt has been widely used to produce pure spin currents in previous studies22,23,24,25,26,27,28,29. BaFe12O19 is an M-type barium hexagonal ferrite and is often referred as BaM. It is one of the few MIs with strong magneto-crystalline anisotropy and shows an effective uniaxial anisotropy field of about 17 kOe30,31. It is found that the switching response in the BaM film strongly depends on the charge current applied to the Pt film. When a constant magnetic field is applied in the film plane, the charge current in the Pt film can switch the normal component of the magnetization (M⊥) in the BaM film between the up and down states. The current also dictates the up and down states of the remnant magnetization when the in-plane field is reduced to zero. When M⊥ is measured by sweeping an in-plane field, the response manifests itself as a hysteresis loop, which evolves in a completely opposite manner if the sign of the charge current is flipped. When the coercivity is measured by sweeping an out-of-plane field, its value can be reduced or increased by as much as about 500 Oe if an appropriate charge current is applied.
Results
Properties of Pt/BaM films and Hall bar structures
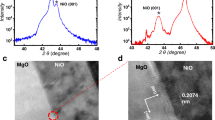
The data presented below were obtained using a Pt(5.0 nm)/BaM(3.0 nm) sample with the properties shown in Fig. 1. Figure 1a–c shows the properties of the BaM film, which was grown on a c-axis sapphire substrate by pulsed laser deposition32. The atomic force microscopy (AFM) image in Fig. 1a shows a uniform and smooth surface, and the analysis of the AFM data yielded a r.m.s. surface roughness of 0.17±0.02 nm. These results, together with other AFM data not shown, indicate that the BaM film has a reasonably good surface, which is critical for the realization of a high-quality Pt/BaM interface and a large SOT at the interface. Note that the roughness value here is an average over the measurements on nine different 1 × 1 μm areas, and the uncertainty is the corresponding s.d. The X-ray diffraction (XRD) spectrum in Fig. 1b indicates the c-axis orientation of the crystalline structure in the BaM film. The hysteresis loops in Fig. 1c were measured by a vibrating sample magnetometer with different field orientations, as indicated. The loops clearly show that the BaM film has perpendicular anisotropy, which confirms the c-axis orientation of the film. Analysis of the hysteresis data yielded an effective perpendicular anisotropy field Ha=17.6 kOe, which is very close to the bulk value (17 kOe), and a saturation induction 4πMs=4.47 kG, which is slightly smaller than the bulk value (4.70 kG)30,31. These results together indicate that the BaM film is of high quality, although it is just slightly thicker than one unit cell of BaM materials (c=2.32 nm)31. Note that the loop shown in Fig. 1c for the perpendicular field is not as square as the loops of metallic films with perpendicular anisotropy7,8, and future work is of great interest that optimizes the growth conditions for the realization of BaM films with better crystalline orientations and higher squareness.
(a) AFM surface image of the BaM film. The r.m.s. roughness is 0.17±0.02 nm. The roughness value is an average over the measurements on nine different 1 × 1 μm areas, and the uncertainty is the corresponding standard deviation. (b) XRD spectrum of the BaM film. (c) Magnetic hysteresis loops of the BaM film. (d) Optical image of the Pt(5 nm)/BaM(3 nm) Hall bar structure. Scale bar, 20 μm. (e) Anomalous Hall resistance RAHE of the Hall bar measured as a function of a magnetic field. The inset is a schematic showing the magnetic field (H) direction which is in the yz plane and 20° away from the +z axis. (f) Angle-dependent longitudinal resistance Ryy of the Hall bar. The insets show the H directions for the α, β and γ scans. α is the angle of the field relative to +z in the yz plane, β is the angle of the field relative to the +z in the xz plane and γ is the angle of the field relative to +x in the xy plane. All the measurements were done at room temperature.
Figure 1d presents a photo image of a Pt(5.0 nm)/BaM(3.0 nm) Hall bar. The Pt layer was deposited on the BaM film by sputtering at room temperature, and the Pt/BaM Hall bar structure was fabricated by photolithography and argon ion milling. The central area of the Hall bar structure is 41 μm long and 11 μm wide, and the contact leads are made of a 400-nm-thick Au film with a 3-nm-thick Ti adhesion layer. With the electrical measurement configuration shown in Fig. 1d and a field configuration shown in Fig. 1e, one can measure the Hall resistance R of the Pt layer as a function of the field H. The obtained R(H) response consists of a linear background due to the ordinary Hall effect in the Pt layer and a hysteresis component due to the anomalous Hall effect (AHE) also in the Pt layer. Figure 1e presents the AHE resistance RAHE as a function of H, which was obtained by subtracting the linear contribution from the initial R(H) data. One can see that the RAHE(H) data show a hysteresis loop response similar to the loop shown in Fig. 1c for a perpendicular field. This similarity indicates that RAHE scales with the normal component of the magnetization (M⊥) in the BaM film, and one can probe the magnetization status in the BaM film by simply measuring RAHE(H).
Three additional points should be made about the data in Fig. 1e. First, the AHE response usually occurs in FMs only, and the presence of the AHE in the paramagnetic Pt film might be interpreted by the magnetic proximity effect (MPE)33,34 or the effects of the imaginary part of the spin mixing conductance at the Pt/BaM interface35,36, as in Pt thin films grown on Y3Fe5O1237,38. Figure 1f presents the angle dependence of the longitudinal resistance Ryy measured along the Hall bar length for the field rotating in three different planes. The α dependence clearly suggests the presence of the MPE in the Pt/BaM structure33,34, while the β dependence provides an evidence for the existence of the spin mixing conductance-associated magnetoresistance in the structure35,36,37. Note that the data in Fig. 1f also indicate that the β dependence is more noticeable than the α dependence, which might suggest that in the Pt/BaM sample the spin mixing conductance-associated magnetoresistance is larger than the MPE-produced magnetoresistance. Second, the planar Hall effect39,40 also appears in the Pt/BaM structure, as shown by the experimental data in Supplementary Note 1 and Supplementary Fig. 1. However, the planar Hall effect does not invalidate the use of AHE measurements to determine the magnetization status in the BaM. This is because all of the AHE measurements in this work involved the rotation of the magnetization in the yz plane, while the planar Hall effect concerns magnetization rotation in the xy plane. Note that there has been previous work that used the planar Hall effect to probe the magnetization in Y3Fe5O12 films, where, however, the magnetization rotated in the film plane due the absence of perpendicular anisotropy and the application of an in-plane field41. Finally, the remnant magnetization Mr and coercivity Hc indicated by the loop shown in Fig. 1e are both slightly smaller than the corresponding values indicated by the data in Fig. 1c. This is because the field had a small angle with the normal direction (20°) for the data in Fig. 1e but was along the normal direction for the data in Fig. 1c. One can also see that the loop in Fig. 1e appears noisier than that in Fig. 1c, which is because the AHE is usually very strong in FMs and is relatively weak in the paramagnetic Pt.
Switching responses for out-of-plane magnetic fields
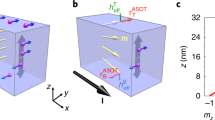
The magnetization switching indicated by the RAHE(H) data shown in Fig. 1e was driven mainly by the external field H; the currents used for the resistance measurements were low a.c. currents (0.8 mA) and their impact on the switching was negligible due to the a.c. nature of the current. However, if a large d.c. charge current is passed through the Pt layer, it can dramatically affect the switching in the BaM film. Figure 2 shows representative data that demonstrate this effect. Figure 2c,d shows the RAHE(H) responses measured for charge currents with opposite signs, as indicated. The RAHE(H) data were measured in the exact same way as described above for the data shown in Fig. 1e, but a large charge current was passed through the Hall bar right before each data point was taken. When the electrons flow in the Pt layer along the y axis, they produce a pure spin current flowing along the z axis due to the SHE17,18,19,20. For the current configuration shown in Fig. 2a, the SOT τ at the interface is along the +x direction, as indicated. This torque counters the torque produced by H and thereby hinders the switching of the magnetization M in the BaM film. This effect is clearly evident by the broadening of the RAHE(H) hysteresis loop with an increase in the current strength (I) as shown in Fig. 2c. In contrast, for the configuration shown in Fig. 2b, the SOT shares the same direction as the H-produced torque and thereby promotes the switching of M in the BaM film. This is shown by the narrowing of the RAHE(H) loop with an increase in the current strength in Fig. 2d.
(a,b) Effects of charge currents (I) in the Pt film on switching of the magnetization (M) in the BaM film under an out-of-plane field (H). The red spheres with arrows represent spin-polarized electrons deflecting toward the BaM layer. M represents the magnetization of BaM. τ represents the spin torque due to SHE. The direction of H is indicated in the insert. Note that the spin torque indicated in (a,b) is a damping-like torque (DLT). (c,d) Anomalous Hall resistance RAHE of the Hall bar measured as a function of a magnetic field for different charge currents. The field was applied 20° away from the z axis, as shown in the insets of (a,b). In (c) Grey: I=0; Blue: I=−2 mA; Olive: I=−4 mA; and Red: I=−6 mA. In (d) Grey: I=0; Blue: I=2 mA; Olive: I=4 mA; and Red: I=6 mA. (e) Measured coercivity of the BaM film as a function of the charge current density. (f,g) Coercivity versus DLT field (HDLT) estimated for three different field-like torque (FLT) fields (HFLT) through macrospin and full micromagnetic simulations, respectively. Large blue spheres: HFLT=0; small red spheres: HFLT=HDLT/2; and small olive spheres: HFLT=HDLT. The dash line in (e–g) is the Hc at I=0. All the measurements were done at room temperature.
Figure 2e plots the coercivity Hc as a function of the charge current density Jc. Note that each point in the RAHE(H) loops shown in Fig. 2c,d shows an average over 10 measurements, and the error bars in Fig. 2e show the corresponding uncertainties for the averaging. The data in Fig. 2e indicate an Hc reduction of about 460 Oe for Jc=1.09 × 107 A cm−2 and an increase of about 610 Oe for Jc=−1.09 × 107 A cm−2.
The data also show an overall linear response for the current range used. This linear behaviour indicates that one can expect even bigger changes in Hc if larger currents are applied or thinner BaM films are used. When using large currents, however, attention should be paid to the Hall bar geometry and the electrical measurement configuration so that the bar would not be damaged by the Joule heating of the currents. Figure 2f,g presents the calculated coercivities which are discussed shortly. Note that for all of the data shown in Fig. 2, the field was tilted for about 20°, the same as for the data shown in Fig. 1e. The purpose of this was to break the symmetry of the magnetization in response to the field, enabling the demonstration of the SOT effects. Note also that the anomalous behaviour of the red and olive curves at high fields shown in Fig. 2d resulted from the drifting of the resistance measurement system.
Switching responses for in-plane magnetic fields
Figure 3 presents additional RAHE data that further confirm the SOT effect demonstrated above. In contrast to the data in Fig. 2, all the data in Fig. 3 were taken with H in the film plane and along the Hall bar length. Figure 3a gives RAHE(H) loop responses measured under two charge currents with opposite signs. As indicated by the grey arrows, the two loops evolve in completely opposite manners. This result is consistent with previous switching experiments in other bi-layered systems7,11,42, and provides a strong evidence for the presence of the SOT at the interface. The physics underlying this result is as follows. When the strength of the in-plane field H is decreased gradually, the magnetic moments in the BaM film, which are initially in the film plane and along H, tend to tilt out of the film plane due to the strong perpendicular anisotropy. In the absence of charge currents, the moments do not favour tilting up or tilting down. In other words, the response of the moments to the field is symmetric about the film plane, and the normal component of the net magnetization in the film is zero, namely, M⊥=0. However, when a charge current is applied to the Pt film, the SOT (see τ in Fig. 2a,b) breaks the symmetry of the magnetization orientation in response to the field, resulting in M⊥≠0. The symmetry is broken in a different manner for the charge currents of opposite signs, and this gives rise to the opposite evolutions shown in Fig. 3a. Besides, the data in Fig. 3a also indicate that, when the in-plane field is reduced to zero, the up and down states of the net magnetization can be controlled by the charge current.
(a) Anomalous Hall resistance RAHE measured as a function of a magnetic field along the y axis for I=+6 mA and I=−6 mA, respectively. (b) RAHE measured as a function of a charge current for a fixed field (H=−17 kOe) along the y axis. (c) Switching phase diagram where the data were obtained through the switching measurements similar to those shown in (a). In (c), M⊥>0 and M⊥<0 correspond to the normal component of the magnetization in the BaM film pointing up and down, respectively. The curves define the boundaries between different magnetization states. All the measurements were done at room temperature.
Figure 3b shows a RAHE versus I response for a constant field applied along the Hall bar length direction (the −y direction). The data clearly indicate that one can use the charge current to switch between the M⊥>0 and M⊥<0 states with the assistance of an in-plane field. One can also see that RAHE almost equals to zero at I=0, indicating the absence of hysteresis responses. This is consistent with the fact that in the absence of charge currents, M almost completely aligns with the in-plane field and M⊥ is almost zero.
Figure 3c gives the switching phase diagram for in-plane fields and charge currents. The data were obtained through the switching measurements similar to those shown in Fig. 3a. The diagram tells the charge current (or the magnetic field) required to switch M in the BaM film when a constant field (or a constant current) is applied. Note that each point in Fig. 3a shows the average over 10 measurements, and the error bars in Fig. 3c show the corresponding uncertainties for the averaging. The data in Fig. 3c seem to indicate that the uncertainties are relatively large for weak charge currents. This observation can be explained in terms of SOT-caused symmetry breaking discussed above. In brief, in the presence of a small charge current, when H is reduced to 0, one has M⊥ close to 0 due to small SOT. The net effect is that the RAHE(H) response has a small slope around Hc and the uncertainty in determining Hc is larger. In contrast, in the presence of a large charge current, the SOT is strong and M⊥ has a relatively large amplitude at H=0, which results in a larger slope in the RAHE(H) response around Hc and a relatively smaller uncertainty.
There are two additional points which should be discussed about the data shown in Fig. 3a. First, one would expect M⊥≈0 and RAHE≈0 at H=15 kOe since the magnetization should be almost saturated in the presence of an in-plane field of 15 kOe, as shown by the open circles in Fig. 1c. However, the data in Fig. 3a show non-zero RAHE values at high fields. This is because the data were measured after the application of strong currents to the Pt layer, which produced a large SOT and thereby gave rise to either M⊥>0 or M⊥<0 even at high fields. Second, the two loops shown in Fig. 3a were obtained with in-plane fields, but they appear very different from the loop shown by the open circles in Fig. 1c that was also measured with in-plane fields. This is because the loop in Fig. 1c presents the in-plane component of M (M||), while the loops in Fig. 3a present the normal component of M (M⊥). One has M||=0 at H=0 for the M(H) loop measurements, and has M⊥≠0 at H=0 due to the SOT for the RAHE(H) loop measurements. These results are consistent with those observed for switching in topological insulator-based bi-layered systems42. They further confirm the presence of large SOTs at the Pt/BaM interface.
Determination of SOT fields through macrospin and micromagnetic simulations
It is believed that the SOT in the Pt/BaM structure arises from the SHE17,18,19,20 in the Pt layer, as illustrated by the diagrams in Fig. 2a,b and as discussed previously for HM/FM systems7,8,9,10,11,12,13,14,15,16. In principle, the SHE can give rise to two different torques, a damping-like torque (DLT), which is indicated by the red arrows in Fig. 2a,b, and a field-like torque (FLT), which is not shown in the figures. Taking HDLT and HFLT as the corresponding effective fields of these two torques and following the analysis in Supplementary Note 2 and Supplementary Figs 2 and 3, one can write down the total field Htotal on the normalized magnetization m in the BaM film as

where H is the external field as indicated in Figs 1 and 2 and x is the unit vector along the +x direction. Note that both HDLT and HFLT are proportional to the charge current density Jc in the Pt.
It is also possible that the SOT in the Pt/BaM structure contains a contribution associated with the MPE33,34. As discussed above, the data shown in Fig. 1f suggest the presence of the MPE in the Pt/BaM structure. If the MPE presents, the SHE and the Rashba effect in the ferromagnetic-like Pt atomic layers would also give rise to a DLT and an FLT. It is fortunate that the corresponding HDLT and HFLT fields have the exactly same symmetry as the two SOT fields in equation (1). Further, they are also proportional to Jc, as discussed in Supplementary Note 2. As a result, one can extract the strength of the SOT fields from the experimental data without having to know the relative contributions of the different mechanisms.
To determine the SOT field strength, simulations were carried out that were based on the Gilbert equation and used a macrospin model to represent the magnetization in the BaM film and the fields defined in equation (1). Ha was perpendicular to the BaM film plane. H was in the yz plane and was tilted 20° away from the +z direction initially, the same as in the experiment. The SOT fields HFLT and HDLT were obtained by comparing the experimental Hc values with those obtained from the simulations. This process involves three main steps as follows. First, one takes Jc=0 and calculates Hc. For this calculation, HFLT and HDLT are both set to zero, and the anisotropy field strength Ha is set in such a way that m flips when H is pointing in a direction opposite to its initial direction and has a strength equal to the experimentally measured Hc (1.45 kOe). Second, one considers the case of Jc≠0 but takes HFLT=0 and uses simulations to find Hc values for given HDLT values. From the point of view of the symmetry, it is clear that a flip in the direction of the HFLT field does not lead to a change in Hc because the HFLT field is orthogonal to Ha, H, and m. In contrast, a flip in the direction of the HDLT field breaks the symmetry and therefore affects Hc. For this reason, as the first stage HFLT is set to zero and Hc is calculated as a function of HDLT in this step. Third, one sets HFLT to a non-zero value and repeats the simulations to find Hc values for given HDLT and HFLT combinations. Note that the adjustment of Ha to make the Hc value comparable to the experimental value for the Jc=0 case is done for convenience of comparison of the measured and calculated results. The rate of the change of Hc with HDLT, however, remains a quantity which is independent of this approximation. Supplementary Note 3 discusses the details of the simulations.
In Fig. 2f, the blue dots show the Hc versus HDLT response calculated for HFLT=0, and the other dots are discussed shortly. One can see that the Hc versus HDLT response shows a linear dependence, the same as the experimental Hc versus Jc data. Specifically, Hc increases to about 2.0 kOe when HDLT is −400 Oe and decreases to about 0.95 kOe when HDLT is 400 Oe. The same change in the experimental Hc value is observed when Jc changes between −107 A cm−2 and 107 A cm−2. Thus, one can conclude that the strength of HDLT in the Pt/BaM is about 400 Oe at Jc=107 A cm−2. For HM/FM systems, previous work observed a HDLT field of 17 Oe for Pt(2 nm)/Co(0.6 nm)/AlOx (ref. 7), 50 Oe for Pt(3 nm)/Co(0.6 nm)/Al2O3(2 nm)43, 55–200 Oe for Pt(3 nm)/Co(0.9 nm)/Ta(0.5–4 nm)13, 50 Oe for Pt(3 nm)/Co80Fe20(0.6 nm)/MgO (ref. 9) and 200 Oe for Ta(5 nm)/Co80Fe20(0.6 nm)/MgO (ref. 9), all corresponding to the same charge current density Jc=107 A cm−2. One can see that the HDLT field in the Pt/BaM is stronger than those previously reported values.
The above-described analysis assumed HFLT=0, and similar analysis was carried out for HFLT≠0. The red and olive dots in Fig. 2f show the Hc versus HDLT responses calculated for HFLT=HDLT/2 and HFLT=HDLT, respectively. It is evident from the data in Fig. 2f that the effect of HFLT is almost negligible for HFLT=HDLT/2. For HFLT=HDLT, the Hc versus HDLT response deviates from the linear dependence for strong negative charge currents, which, however, has not been observed experimentally, indicating that HFLT is relatively small in the Pt/BaM structure.
The simulations discussed above used a macrospin to represent m in the BaM film. In the experiment, however, the switching of m may not be realized through coherent rotation, but through domain nucleation and subsequent domain wall motion, thanks to the relatively large size of the Pt/BaM Hall bar sample. In consideration of this possibility, full micromagnetic simulations were also carried out that used the well-established OOMMF code with the Oxs_SpinXferEvolve module44 to numerically solve Supplementary equation (9). The HDLT field defined by Supplementary equation (8) or (13) was taken into account by an equivalent spin torque with the polarization along the x axis. The simulated film size was set to 1 × 1 μm and the mesh size was set to 5 × 5 × 3 nm. As in the experiments, H was in the yz plane and was tilted 20° away from the +z direction initially. The procedures for the determination of the SOT fields were the same as those described above for the macrospin simulations, and the results are presented in Fig. 2g. By comparing Fig. 2f,g, one can see that the results from the two simulations are close to each other for all three different HFLT fields, confirming the accuracy of the macrospin simulation-yielded HDLT fields described above. One can also see that, for a given HDLT, Hc from the micromagnetic simulation are slightly smaller (about 4%) than that from the macrospin model. This means that, for a given Hc change, the corresponding HDLT field from the micromagnetic analysis is slightly larger than that from the macrospin analysis. Finally, it should be noted that the micromagnetic simulations indicated that the switching in the BaM was realized through domain nucleation and growth.
The numerical work presented above clearly indicates that the SOT in the Pt/BaM structure is larger than that in the HM/FM systems. This conclusion can also be obtained by direct comparisons of experimental data. For example, a reduction in Hc of about 440 Oe was observed for a Pt(3 nm)/Co(0.6 nm)/AlOx structure for an increase in Jc of 107 A cm−2 (ref. 45), while a very similar Hc reduction can be seen from the data in Fig. 2e. If one considers that the BaM layer (3 nm) in this work is five times thicker than the Co layer (0.6 nm) in the previous work, one can conclude that the SOT efficiency in the Pt/BaM structure is indeed higher than that in the Pt/Co structure. Further, in the Pt/Co structure there is always a portion of the applied current flowing in the Co layer and being wasted, which is a weakness in terms of energy efficiency.
It is important to highlight that this work may have far-reaching implications for the future development of spin-torque electronics. Specifically, the HM/MI systems offer a number of benefits in comparison with the HM/FM structures studied previously7,8,9,10,11,12,13,14,15,16. First, perpendicular anisotropy in MI films originates from bulk intrinsic anisotropy30,31 rather than surface anisotropy. This means that, when being used for actual devices, MI films have no constrains on the thickness, unlike the FM film counterpart that often relies on surface anisotropy to realize perpendicular anisotropy46. Second, the charge current flows in the HM layer only, not in the MI layer. In contrast, in a HM/FM structure the charge current also flows in the FM, resulting in certain parasitic effects. The advantage of no shunting current in the MI film becomes particularly important when the HM layer is replaced by a topological insulator layer. Recent work demonstrates that topological insulators may produce considerably larger SOT than HM materials42,47. Finally, the magnetic damping is usually significantly lower in MIs than in FMs. For example, the intrinsic Gilbert damping constant in BaM materials is 7 × 10−4 (refs 30, 31), which is at least 10 times smaller than the value in Permalloy. This advantage is significant for spin-torque oscillator applications, where the current threshold for self-oscillations decreases with the damping48 as well as for logic device applications that require low-damping, insulating spin channels49,50. As discussed above, the SOT strength in the Pt/BaM structure was found to be higher than the value reported previously for HM/FM systems7,9,13,43. This result is surprising considering the fact that there are almost no electron diffusions at the interface from the Pt layer to the BaM film, unlike in the HM/FM counterpart.
In summary, strong SOT effects have been observed in a Pt/BaM bi-layered structure. It is found that the charge current applied to the Pt film can switch the normal component of the magnetization in the BaM film between the up and down states when an in-plane magnetic field is applied. When an out-of-plane field is applied to switch the BaM film, the charge current can reduce or increase the switching field by as much as about 500 Oe. The results demonstrate the presence of large SOT in HM/MI systems in comparison to HM/FM systems and the possibility of efficient SOT-induced switching in HM/MI systems, thereby presenting potential direction for the future development of magnetic memory and logic devices for energy-efficient computing. Future work is of great interest that demonstrates current-driven, rather than current-assisted, switching in narrow BaM strips and nanoscale BaM elements. Toward this end, approaches that could be taken include replacing Pt with materials with substantially stronger spin–orbit coupling8,42,47, such as topological insulators; reducing the anisotropy in the BaM via doping, for example, scandium51; and utilizing thinner BaM films.
Methods
Material growth
The BaM film was grown on a c-axis sapphire substrate by pulsed laser deposition (PLD) techniques32. During the deposition, the oxygen pressure was 300 mTorr, the substrate temperature was 800 °C, the substrate-to-target separation was fixed at 4 cm and the energy fluence of the laser beam was set to 0.7 J cm−2. The laser pulse repetition rate was increased from 1 to 5 pulse(s) per second in five equal steps over the first 5 min and was then set to 10 pulses per second for the remaining deposition. After the deposition, the substrate was cooled down at a rate of −2 °C min−1 in 400 Torr oxygen. The sample was then annealed at 850 °C for 4 h in a standalone tube furnace, with a heating rate of 10 °C min−1 and a cooling rate of −2 °C min−1.
Device fabrication
The 5.0-nm-thick Pt film was deposited on the BaM film in an AJA magnetron sputtering system. The Pt (5.0 nm)/BaM (3.0 nm) film stack was patterned into an 11-μm-wide Hall bar with a photolithography system first and then etched in an argon ion milling system. The Hall bar contact leads were made of Ti(3.0 nm)/Au(400 nm). They were fabricated by the photolithography, thermal evaporation and lift-off processes.
Measurements
The roughness of the BaM film was measured with a Veeco Innova atomic force microscope. The crystalline structure and film thickness were measured with a Rigaku Smartlab XRD/XRR system. The hysteresis loops of the film were measured with a Microsense EV7 vibrating sample magnetometer. The electrical measurements were conducted with a Quantum Design physical property measurement system supplemented with two lock-in-amplifiers, a preamplifier and two Keithley metres.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Li, P. et al. Spin–orbit torque-assisted switching in magnetic insulator thin films with perpendicular magnetic anisotropy. Nat. Commun. 7:12688 doi: 10.1038/ncomms12688 (2016).
References
Myers, E. B., Ralph, D. C., Katine, J. A., Louie, R. N. & Buhrman, R. A. Current-induced switching of domains in magnetic multilayer devices. Science 285, 867–870 (1999).
Sun, J. Z. Current-driven magnetic switching in manganite trilayer junctions. J. Magn. Magn. Mater. 202, 157–162 (1999).
Katine, J. A., Albert, F. J., Buhrman, R. A., Myers, E. B. & Ralph, D. C. Current-driven magnetization reversal and spin-wave excitations in Co/Cu/Co pillars. Phys. Rev. Lett. 84, 3149 (2000).
Grollier, J. et al. Spin-polarized current induced switching in Co/Cu/Co pillars. Appl. Phys. Lett. 78, 3663 (2001).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996).
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996).
Liu, L., Lee, O. J., Gudmundsen, T. J., Ralph, D. C. & Buhrman, R. A. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 109, 096602 (2012).
Liu, L. Q. et al. Spin torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Emori, S., Bauer, U., Ahn, S., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Conte, R. L. et al. Spin–orbit torque-driven magnetization switching and thermal effects studied in Ta\CoFeB\MgO nanowires. Appl. Phys. Lett. 105, 122404 (2014).
Garello, K. et al. Ultrafast magnetization switching by spin-orbit torques. Appl. Phys. Lett. 105, 212402 (2014).
Cubukcu, M. et al. Spin–orbit torque magnetization switching of a three-terminal perpendicular magnetic tunnel junction. Appl. Phys. Lett. 104, 042406 (2014).
Woo, S., Mann, M., Tan, A. J., Caretta, L. & Beach, G. S. D. Enhanced spin–orbit torques in Pt/Co/Ta heterostructures. Appl. Phys. Lett. 105, 212404 (2014).
Lee, O. J. et al. Central role of domain wall depinning for perpendicular magnetization switching driven by spin torque from the spin Hall effect. Phys. Rev. B 89, 024418 (2014).
Hao, Q. & Xiao, G. Giant spin Hall effect and switching induced by spin-transfer torque in a W/Co40Fe40B20/MgO structure with perpendicular magnetic anisotropy. Phys. Rev. Appl. 3, 034009 (2015).
Hung, Y., Rehm, L., Wolf, G. & Kent, A. D. Quasistatic and pulsed current-induced switching with spin–orbit torques in ultrathin films with perpendicular magnetic anisotropy. IEEE Magn. Lett. 6, 3000504 (2014).
Dyakonov, M. I. & Perel, V. I. Possibility of orienting electron spins with current. JETP Lett. 13, 467 (1971).
Hirsch, J. E. Spin Hall effect. Phys. Rev. Lett. 83, 1834 (1999).
Day, C. Two groups observe the spin hall effect in semiconductors. Phys. Today 58, 17 (2005).
Hoffmann, A. Spin Hall effects in metals. IEEE Trans. Magn. 49, 5172–5193 (2013).
Wang, Z. et al. Electric control of magnetization relaxation in thin film magnetic insulators. Appl. Phys. Lett. 99, 162511 (2011).
Hamadeh, A. et al. Full control of the spin-wave damping in a magnetic insulator using spin–orbit torque. Phys. Rev. Lett. 113, 197203 (2014).
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262–266 (2010).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Ando, K. et al. Electric manipulation of spin relaxation using the spin hall effect. Phys. Rev. Lett. 101, 036601 (2008).
Padrón-Hernández, E., Azevedo, A. & Rezende, S. M. Amplification of spin waves in yttrium iron garnet films through the spin Hall effect. Appl. Phys. Lett. 99, 192511 (2011).
Demidov, V. et al. Magnetic nano-oscillator driven by pure spin current. Nat. Mater. 11, 1028–1031 (2012).
Liu, R. H., Lim, W. L. & Urazhdin, S. Spectral characteristics of the microwave emission by the spin hall nano-oscillator. Phys. Rev. Lett. 110, 147601 (2013).
Duan, Z. et al. Nanowire spin torque oscillator driven by spin orbit torques. Nat. Commun. 5, 5616 (2014).
Harris, V. G. Modern microwave ferrites. IEEE Trans. Magn. 48, 1075–1104 (2012).
Wu, M. in Advanced Magnetic Materials 1st edn ed. Malkinski L. Chapter 2 InTech (2012).
Li, P. et al. Generation of pure spin currents via spin Seebeck effect in self-biased hexagonal ferrite thin films. Appl. Phys. Lett. 105, 242412 (2014).
Huang, S. Y. et al. Transport magnetic proximity effects in platinum. Phys. Rev. Lett. 109, 107204 (2012).
Miao, B. F., Huang, S. Y., Qu, D. & Chien, C. L. Physical origins of the new magnetoresistance in Pt/YIG. Phys. Rev. Lett. 112, 236601 (2014).
Chen, Y. et al. Theory of spin Hall magnetoresistance. Phys. Rev. B 87, 144411 (2013).
Althammer, M. et al. Quantitative study of the spin Hall magnetoresistance in ferromagnetic insulator/normal metal hybrids. Phys. Rev. B 87, 224401 (2013).
Meyer, S. et al. Anomalous Hall effect in YIG|Pt bilayers. Appl. Phys. Lett. 106, 132402 (2015).
Zhou, X. et al. Magnetotransport in metal/insulating-ferromagnet heterostructures: spin Hall magnetoresistance or magnetic proximity effect. Phys. Rev. B 92, 060402(R) (2015).
Ky, V. D. Planar Hall effect in ferromagnetic films. Phys. Status Solidi 26, 565 (1968).
Naftalis, N. et al. Field-dependent anisotropic magnetoresistance and planar Hall effect in epitaxial magnetite thin films. Phys. Rev. B 84, 094441 (2011).
Wang, Y. et al. Electrical control of the exchange spring in antiferromagnetic metals. Adv. Mater. 27, 3196–3201 (2015).
Fan, Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).
Garello, K. et al. Symmetry and magnitude of spin–orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013).
OOMMF User’s Guide, Version 1.0. Donahue, M. J. Porter, D. G., Interagency Report NISTIR 6376 National Institute of Standards and Technology (1999).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB–MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Mellnik, A. R. et al. Spin transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Taniguchi, T., Mitani, S. & Hayashi, M. Critical current destabilizing perpendicular magnetization by the spin Hall effect. Phys. Rev. B 92, 024428 (2015).
Behin-Aein, B., Datta, D., Salahuddin, S. & Datta, S. Proposal for an all-spin logic device with built-in memory. Nat. Nanotechnol. 5, 266–270 (2010).
Papp, A., Porod, W. & Csaba, G. Hybrid yttrium iron garnet-ferromagnet structures for spin-wave devices. J. Appl. Phys. 117, 17E101 (2015).
Zuo, X. et al. Single crystal hexaferrite phase shifter at Ka band. J. Appl. Phys. 91, 7622 (2002).
Acknowledgements
This work was primarily supported by the C-SPIN, one of the SRC STARnet Centers sponsored by MARCO and DARPA. In addition, it is also supported in part by the SHINES, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award SC0012670, the U.S. National Science Foundation under Award ECCS-1231598, the U.S. Army Research Office under Award W911NF-14-1-0501 and the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award SC0008482. Work at Argonne was supported by the U.S. Department of Energy, Office of Science, Materials Science and Engineering Division. The authors also gratefully acknowledge discussions with Drs Ilya Krivorotov, Igor Barsukov, Qilin Dai, Xin Fan, Weigang Wang, Satoru Emori, Andrei Slavin, James Neilson, Kristen Buchanan, Jose de la Venta, Wanjun Jiang, Yabin Fan, David Ellsworth, and Praveen Janantha.
Author information
Authors and Affiliations
Contributions
P.L. and M.W. conceived the idea and designed the experiments. P.L., T.L. and H.C. prepared and characterized the film and device samples. D.R., G.R., H.D., J.T. and W.P. contributed to film sample characterizations. W.L., A.D., S.B.F. and M.C.M. contributed to device fabrications. P.L., T.L. and W.Z. performed the measurements and analysed the data. J.S.J. and A.H. contributed to the measurements and the data analysis. A.K., G.C. and O.M. carried out theoretical analysis and numerical modelling. M.W. supervised the study. P.L., T.L., A.K., G.C. and M.W. wrote the paper and the Supplementary Information with help from all the other co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Notes 1-3 and Supplementary References (PDF 648 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, P., Liu, T., Chang, H. et al. Spin–orbit torque-assisted switching in magnetic insulator thin films with perpendicular magnetic anisotropy. Nat Commun 7, 12688 (2016). https://doi.org/10.1038/ncomms12688
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12688
This article is cited by
-
Recent development of E-field control of interfacial magnetism in multiferroic heterostructures
Nano Research (2023)
-
Reconfigurable physical unclonable cryptographic primitives based on current-induced nanomagnets switching
Science China Information Sciences (2022)
-
Barium hexaferrite/muscovite heteroepitaxy with mechanically robust perpendicular magnetic anisotropy
npj Flexible Electronics (2021)
-
Kramers Weyl semimetals as quantum solenoids and their applications in spin-orbit torque devices
Communications Physics (2021)
-
Coercivity Enhancement and the Analysis of Asymmetric Loops in a Perpendicularly Magnetized Thin Film
Journal of Superconductivity and Novel Magnetism (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.