Abstract
Antiferromagnetic spintronics is a rapidly growing field, which actively introduces new principles of magnetic storage. Despite that, most applications have been suggested for collinear antiferromagnets. In this study, we consider an alternative mechanism based on long-range helical order, which allows for direct manipulation of the helicity vector. As the helicity of long-range homogeneous spirals is typically fixed by the Dzyaloshinskii–Moriya interactions, bi-stable spirals (left- and right-handed) are rare. Here, we report a non-collinear room-temperature antiferromagnet in the tetragonal Heusler group. Neutron diffraction reveals a long-period helix propagating along its tetragonal axis. Ab-initio analysis suggests its pure exchange origin and explains its helical character resulting from a large basal plane magnetocrystalline anisotropy. The actual energy barrier between the left- and right-handed spirals is relatively small and might be easily overcome by magnetic pulse, suggesting Pt2MnGa as a potential candidate for non-volatile magnetic memory.
Similar content being viewed by others
Introduction
Antiferromagnets (AFMs) have attracted increasing attention in state-of-the-art applied and academic research1,2,3,4. Their auxiliary role of a static support, enhancing the hardness of ferromagnetic electrodes through the exchange-bias effect in conventional microelectronics, has been broadly extended by new perspectives in spintronic applications1. For instance, by studying the magnetoresistance effects typically exploited in spintronics5, it has been demonstrated that an Ir–Mn AFM, utilized as an active medium in a tunnelling magnetoresistance device, exhibits a 160% magnetoresistance at 4 K in weak magnetic fields of 50 mT or less. AFMs also facilitate current-induced switching of their order parameter6,7,8 owing to the absence of shape anisotropy and action of spin torques through the entire volume. For example, a relatively low critical current density of 4.6 MA cm−2 was reported for the collinear AFM CuMnAs2. Additional non-trivial spintronic effects originating from a non-vanishing Berry phase might occur in non-collinear AFMs9. Non-collinear planar AFMs without mirror symmetry, such as Mn3Ir, are predicted to exhibit the anomalous Hall10,11, Kerr, magnetic circular dichroism (MCD) and other effects characterized by the same spatial tensor shape12, which were not encountered in the AFM systems so far.
Another set of specific properties, alternative to the above-mentioned, are provided by the systems with one-dimensional long-range AFM modulations, such as cycloidal q⊥(ei × ej) and screw (helical), q∥(ei × ej), with ei,j being the spin directions on i and j neighbouring atomic sites sitting along the spiral propagation vector q. These systems possess a specific order parameter κij=ei × ej, denoted as chirality or helicity. For example, in cycloidal AFM insulators, κ is coupled to the polarization vector P∼q × κ, leading to the first-order ferroelectric effect13,14,15,16. For the screw-spiral order (q × κ=0) it becomes possible only upon satisfaction of additional specific conditions, namely, the crystal structure remains invariant under inversion and rotation around κ, but non-invariant under 180° rotation of the κ-axis17,18. Information transfer in cycloidal spirals along the one-dimensional atomic chains with fixed κ stabilized by the surface Dzyaloshinskii–Moriya mechanism was demonstrated by switching their phase with an external magnetic field19. Such a scheme is inapplicable to screw spirals owing to their energy degeneracy with respect to κ reversal, even if they are deposited on a surface20. Similar to the situation with the ferroelectric effect, fixing the helicity of a screw spiral would require additional symmetry constraints on the crystal structure21. Despite the cycloidal order seeming to be more ubiquitous for applications, the aforementioned degeneracy between the left- and right-handed magnetic screws in crystals with inversion symmetry might be considered as an alternative advantage, since it allows the direct association of a bit of information with the helicity.
Here, we demonstrate such an AFM screw-spiral magnetic order in the tetragonal Pt2MnGa Heusler system, revealed by neutron diffraction experiments. Additional first-principles analysis justifies the non-relativistic exchange origin of a spiral, confirms its experimentally deduced wave vector q≈(0, 0, 1/5) in units of 2π/c, and suggests the cause of the screw-type order as a moderate hard axis (tetragonal c axis) magnetocrystalline anisotropy (MCA).
Results
Crystal structure and magnetization
There is no complete experimental information on this material in the literature. The single report on Pt2MnGa22 briefly refers to it as L21 AFM with TN=75 K, but no further details are provided. Later, Pt2MnGa was studied ab-initio by assuming ferromagnetic ordering, which revealed that the tetragonal phase is more stable23,24; therein, it was only mentioned23 that in the PtxNi2–xMnGa alloy series, the AFM correlations become stronger with increasing x. In a more recent ab-initio study25, the nearest-neighbor AFM order was found to be noticeably higher in energy compared to the ferromagnetic.
To clear the actual crystal and magnetic structure, we prepared a polycrystalline Pt2MnGa sample. The room-temperature crystal structure (Fig. 1) was deduced from the Rietveld refinement of the X-ray diffraction (XRD) data. All Bragg reflections were well indexed by assuming the tetragonal space group I4/mmm. The refined lattice parameters are a=b=4.0174(7) Å, c=7.2393(1) Å; Mn, Ga and Pt atoms occupy 2a(0, 0, 0), 2b(0, 0, 1/2) and 4d(0, 1/2, 1/4) Wyckoff sites, respectively (see the inset in Fig. 1).
Rietveld refinement of the room-temperature XRD pattern assuming a tetragonal unit cell with I4/mmm symmetry. Black, red and green lines correspond to the observed, calculated and difference patterns, respectively. The blue ticks indicate the Bragg peak positions. A sketch of the unit cell is shown in the inset: red, yellow and grey spheres indicate Mn, Ga and Pt atoms in 2a, 2b and 4d Wyckoff positions, respectively.
The low-field M(T) curves measured within the zero-field-cooled (ZFC) and field-cooled (FC) cycles are shown in Fig. 2a. The ZFC M(T) exhibits a maximum at T≈65 K, which is absent in the FC data. This observation, typical for the tetragonal polycrystalline ferrimagnetic Heusler alloys, may result from a random orientation of the anisotropic crystallites26. Overall, the amplitude of M(T) is very small in both the ZFC and FC data, even in high fields at low temperatures (Fig. 2b). The high-temperature behaviour is similar in both the ZFC and FC data and indicates magnetic ordering at 350 K. The possible presence of a small ferromagnetic component modifies the M(T) behaviour, which, at ordering temperature, exhibits a shoulder instead of the peak expected for a conventional AFM. Both isotherms M(H) at 300 K and 2 K (Fig. 2c) exhibit a non-saturating (almost linear) increase up to 7 T, similar to antiferromagnetic or paramagnetic materials. Only a narrow field hysteresis (inset of Fig. 2d) indicates a very weak ferromagnetic component at low temperature. To probe the magnetic response in a very high field, we applied magnetic pulses of 60 T amplitude. The corresponding M(H) curves measured at 257 and 1.5 K (Fig. 2d) increase monotonically and do not saturate with increasing field strength. Only a broadened step-like feature with a small hysteresis within 0<H<35 T is observed at 1.5 K indicating a metamagnetic transition close to 14 T. This hysteresis might be induced by the non-equilibrium conditions of a magnetic pulse. All these results indicate that Pt2MnGa is not ferromagnetic.
Magnetic structure determination using neutron diffraction
To determine the actual magnetic order, we have measured the powder neutron diffraction at 500 K (above the magnetic ordering), 300 K and 3 K (magnetically ordered phase). At 500 K it delivers the same crystal structure as room-temperature XRD; however, in addition, due to a higher contrast in scattering amplitudes (0.96, −3.73 and 7.29 fm for Pt, Mn and Ga, respectively), neutrons resolve a certain degree of chemical randomness (see Supplementary Note 1, Supplementary Fig. 1). A comparison of the 500, 300 and 3 K spectra within a narrow angular range (20°<2θ<35°) is shown in Fig. 3a. At 300 and 3 K, the long-range magnetic order is clearly evidenced by two additional peaks, at 2θ≈24.1° and 29.3° (indicated by the red arrows), that closely correspond to the commensurate modulation vector q=(0, 0, 1/5) in units of 2π/c. Detailed analysis reveals slightly incommensurate temperature-dependent variation: q=(0, 0, 0.207(2)·2π/c) at 300 K and (0, 0, 0.195(1)·2π/c) at 3 K.
Temperature-dependent magnetization M(T) (black line—ZFC, red line—FC regime) at (a) 0.01 T and (b) 7 T. Field-dependent magnetization M(H) hysteresis loops (c) up to 7 T at 2 (blue) and 300 K (red) and (d) up to 60 T at 1.5 K (blue) and 257 K (red). The insets in (c) show the zoomed M(H) behaviour at low magnetic field for 2 (blue) and 300 K (red).
To specify more details of the magnetic ground state, we have focused on 3 K data corresponding to the strongest magnetic peak intensities (Fig. 3b). The refinement suggests that the preferable magnetic order is a spiral (in both 2a and 2b Mn sublattices), which delivers the amplitudes of local moments close to a reasonable value for Mn in these positions (∼4 μB), whereas other variants, for example, collinear spin-wave, lead to values substantially exceeding 5 μB. In the next step, we tried to distinguish which type of spin spiral is more preferable. By assuming a spiral magnetic structure rotating in the bc plane (cycloid), we obtained the moments of 4.33(13) μB for Mn in both the 2a and 2b sites. Although these values are reasonable, they exceed those reported in the literature for Mn(2a) in Mn-based Heusler alloys. Finally, assuming the spiral rotating within the ab-plane (screw) leads to 3.93(11) μB, a value that is closer to those reported for similar structures26.
Theory
First, we determined the preferential q vector based on total energy calculations. Because in our case the basic features of a spiral are mostly controlled by the interplay of the isotropic exchange interactions, which have the largest energy scale (Dzyaloshinskii–Moriya interactions are cancelled by symmetry), it is practical to start with the non-relativistic calculations. The absence of spin–orbit coupling allows to apply the generalized Bloch theorem and study the spin spirals in the chemical unit cell without considering large supercells. The energy dispersion computed along several symmetric directions is shown in Fig. 4a. In order to plot several curves along the same coordinate axis, we use the q length in 2π/d, where d is the distance between the nearest Mn-containing atomic planes orthogonal to q. In this notation, q=0.5 corresponds to the antiparallel orientation of the nearest planes. As we see from Fig. 4a, the energy dispersion in the ab-plane ([100] and [110] directions) is monotonous, being characterized by a single minimum at q=0 (ferromagnet) and a single maximum at q=0.5 (shortest AFM order). For the out-of-ab-plane directions, one observes a formation of the local minimum within 0<q<0.5. Whereas in the direction [111] it corresponds to rather high energy, in [001], (along the c axis) it becomes global, supporting experimental conclusions. The minimum energy vector appears to be close to the experimental  (see also a more detailed plot in Fig. 4b). A complementary Monte-Carlo simulation of the classical Heisenberg model parameterized by the ab-initio exchange coupling constants (see Supplementary Note 2, Supplementary Fig. 2) reasonably reproduces the Neel temperature (TN≈350 K) and reveals that the magnetic order is set by the interplay between the strong short-range parallel and the weaker long-range (seventh shell within the Mn(2a) sublattice) antiparallel interactions along the c axis.
(see also a more detailed plot in Fig. 4b). A complementary Monte-Carlo simulation of the classical Heisenberg model parameterized by the ab-initio exchange coupling constants (see Supplementary Note 2, Supplementary Fig. 2) reasonably reproduces the Neel temperature (TN≈350 K) and reveals that the magnetic order is set by the interplay between the strong short-range parallel and the weaker long-range (seventh shell within the Mn(2a) sublattice) antiparallel interactions along the c axis.
(a) Detailed comparison of neutron diffraction patterns at 500, 300, and 3 K. Last two cases exhibit magnetic peaks, which are indicated by red arrows. (b) The observed (empty circles), calculated (red line) and difference (green line) neutron diffraction patterns at 3 K within the whole angular range. Upper vertical ticks mark the nuclear peak positions and lower vertical ticks mark the magnetic ones. Red arrows indicate the same magnetic peaks as considered in (a).
Next, we figured out the role of the relativistic effects, which determines the type of the spin spiral (screw or cycloidal). In this case, the Bloch theorem does not hold and the magnetic order can be studied only in supercells. As we can account only for commensurate modulations, the supercells must be sufficiently large to provide energies at long wavelengths, for example, a minimal supercell hosting a  modulation contains at least five standard units. As we see from Fig. 4b, the relativistic effects substantially deepen the spiral energy minimum, but almost no change in its q position was observed. The ab-plane appears to be an easy plane as the screw-type spiral has the lowest energy in the whole range of the wavelengths. The energy difference between the cycloidal and screw spirals is contributed by the MCA energy, which has a rather large magnitude for the Heusler class (as it follows from the comparison at q=0), being close to 0.65 meV atom-1 (or 2.6 meV f.u.−1). In the global minimum, this energy difference is reduced more than twice. Owing to the hard-c-axis MCA, the cycloidal spiral might be still better optimized in terms of its homogeneity (as it is distorted by the MCA); however, its energy must in any case be higher compared to the screw order. At the same time, as it follows from the energy difference between the cycloidal θ0=0° and 90° variants, which grows towards smaller q, phase optimization makes sense only for q<0.06, that is, far from the global minimum. The amplitude of the Mn moment in the screw spiral has a tendency to grow from q=0 (ferromagnetic) towards q=0.5 (shortest AFM order), though its absolute amplitude increases only slightly: from ∼3.7 to 3.8 μB, which agrees with neutron data refinement.
modulation contains at least five standard units. As we see from Fig. 4b, the relativistic effects substantially deepen the spiral energy minimum, but almost no change in its q position was observed. The ab-plane appears to be an easy plane as the screw-type spiral has the lowest energy in the whole range of the wavelengths. The energy difference between the cycloidal and screw spirals is contributed by the MCA energy, which has a rather large magnitude for the Heusler class (as it follows from the comparison at q=0), being close to 0.65 meV atom-1 (or 2.6 meV f.u.−1). In the global minimum, this energy difference is reduced more than twice. Owing to the hard-c-axis MCA, the cycloidal spiral might be still better optimized in terms of its homogeneity (as it is distorted by the MCA); however, its energy must in any case be higher compared to the screw order. At the same time, as it follows from the energy difference between the cycloidal θ0=0° and 90° variants, which grows towards smaller q, phase optimization makes sense only for q<0.06, that is, far from the global minimum. The amplitude of the Mn moment in the screw spiral has a tendency to grow from q=0 (ferromagnetic) towards q=0.5 (shortest AFM order), though its absolute amplitude increases only slightly: from ∼3.7 to 3.8 μB, which agrees with neutron data refinement.
Discussion
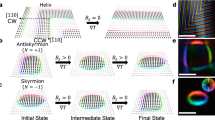
To conclude, we present a tetragonal stoichiometric (I4/mmm) Heusler compound, Pt2MnGa, exhibiting room-temperature long-range AFM spiral order, which possesses a unique combination of properties for the Heusler family of materials. Ab-initio calculations reasonably reproduce the magnetic modulation vector deduced from neutron diffraction and suggest the origin of the spiral as an interplay of the isotropic exchange interactions within the Mn sublattice. Monte-Carlo simulations of the Heisenberg model parameterized with ab-initio exchange coupling constants reasonably reproduce the Neel temperature and suggest the long-range antiparallel Mn–Mn exchange (beyond the sixth Mn shell) as a driving mechanism for the AFM order. Relativistic calculations indicate an easy-ab-plane MCA, which stabilizes the screw (proper screw or fully helical) spiral type. Owing to the inversion symmetry, the left- and right-handed spirals are equally stable. In spite of a large MCA, the energy barrier between left- and right-handed spirals can be efficiently overcome via precessional reorientation of magnetization, induced by magnetic pulses perpendicular to the spiral axis (see Fig. 5). Owing to this, the actual barrier reduces to the energy difference between the screw and cycloidal spiral orders and greatly facilitates the reorientation. In particular, this suggests Pt2MnGa as a convenient candidate for non-volatile magnetic memory based on the helicity vector as a bit of information.
Total energies ΔE calculated as functions of q (in units of 2π/d, where d is the distance between the nearest Mn-containing planes orthogonal to q). (a) Non-relativistic regime: black solid and dashed lines refer to [100] (d=a/2) and [110] ( ) directions, respectively; red dashed and solid lines—to [111]
) directions, respectively; red dashed and solid lines—to [111]  and [001] (d=c/2) directions, respectively. The energy zero is taken at q=0 (ferromagnet). (b) Detailed comparison of different regimes along [001]: red, blue and green lines/points refer to the non-relativistic (same as [001] in (a)), screw- and cycloidal-type spirals, respectively. Cycloidal order has two variants: the first one (dashed green line, open circles) at q=0 represents a hard-c-axis oriented ferromagnetic state (θ0=0) and the second one (solid green line, filled circles) at q=0 represents an easy-ab-plane oriented ferromagnetic state (θ0=90°). The energy zero corresponds to the easy-ab-plane ferromagnetic order. All lines are given for an eye guide. For several specific configurations, the Mn(2a) magnetic sublattice is shown explicitly; spin moments are coloured from red to blue according to their phase.
and [001] (d=c/2) directions, respectively. The energy zero is taken at q=0 (ferromagnet). (b) Detailed comparison of different regimes along [001]: red, blue and green lines/points refer to the non-relativistic (same as [001] in (a)), screw- and cycloidal-type spirals, respectively. Cycloidal order has two variants: the first one (dashed green line, open circles) at q=0 represents a hard-c-axis oriented ferromagnetic state (θ0=0) and the second one (solid green line, filled circles) at q=0 represents an easy-ab-plane oriented ferromagnetic state (θ0=90°). The energy zero corresponds to the easy-ab-plane ferromagnetic order. All lines are given for an eye guide. For several specific configurations, the Mn(2a) magnetic sublattice is shown explicitly; spin moments are coloured from red to blue according to their phase.
Methods
Sample preparation
The polycrystalline ingot of Pt2MnGa was prepared by melting appropriate quantities of Pt, Mn and Ga of 99.99% purity in an arc furnace under Ar atmosphere. Ingots were annealed for five days at 1273 K and then quenched in ice water.
X-ray diffraction
Crystalline quality was verified at room temperature using powder X-ray diffraction with Cu Kα radiation.
Compositional analysis
The chemical composition was justified using energy dispersive analysis of X-rays, which delivers Pt50.98Mn25.05Ga23.98 (Pt2.04Mn1.0Ga0.96); in the manuscript we refer it as Pt2MnGa.
Magnetic measurements
The temperature- (M(T)) and field-dependent (M(H)) magnetization was measured using a SQUID-VSM magnetometer. The low-field M(T) curves were measured within the ZFC and FC cycles. For the ZFC measurement, the sample was cooled in zero field down to 2 K; then, 0.1 T field was applied, and the data were recorded in the heating cycle up to 400 K. Subsequently, the data were recorded in the same field (0.1 T) by cooling from 400 K down to 2 K (FC). The magnetic isotherms M(H) have been measured at 1.2 K and 257 K in pulsed fields up to 60 T (Dresden High Magnetic Field Laboratory).
Neutron diffraction
Neutron diffraction measurements were performed at the D2B high-resolution neutron powder diffractometer (ILL, Grenoble). A vanadium cylinder was used as a sample holder. The neutron data were collected at 500 K, 300 K and 3 K using a wavelength of 1.59 Å. The refinement was done using the Fullprof software package27.
Computational details
To complement our experimental results, we computed the q-dependent total energies using the ab-initio linearized muffin-tin orbitals (LMTO) method, adopting the local spin-density approximation to the exchange-correlation28. As the method works for perfectly ordered systems, we have neglected the Mn/Ga chemical disorder indicated by neutron scattering. The unit cell parameters were taken from the present experimental refinement.
Data availability
The data that support the findings of this study are available upon request from S.S. and S.C.
Additional information
How to cite this article: Singh, S. et al. Room-temperature tetragonal non-collinear Heusler antiferromagnet Pt2MnGa. Nat. Commun. 7:12671 doi: 10.1038/ncomms12671 (2016).
Application of the external magnetic pulse Hext (indicated by the green arrow) perpendicular to the spiral wave vector q causes the precession of local moments (rotating along the dashed green curves), which changes the helicity of a spiral from left-handed screw (a), through the intermediate cycloidal state (b) and to the right-handed screw (c). In the case of the easy-plane MCA, the long period of a spiral greatly facilitates reorientation of helicity from κ↑↓q (blue) to κ↑↑q (red) or vice versa, since the top of the energy barrier between two stable screws (a,c) is a cycloid (b) κ⊥q (magenta), in which only few atomic planes with magnetic moments orthogonal to Hext acquire high energy.
References
Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 192404 (2016).
Barthem, V. M. T. S., Colin, C. V., Mayaffre, H., Julien, M.-H. & Givord, D. Revealing the properties of Mn2Au for antiferromagnetic spintronics. Nat. Commun. 4, 2892 (2013).
Wadley, P. et al. Tetragonal phase of epitaxial room-temperature antiferromagnet CuMnAs. Nat. Commun. 4, 2322 (2013).
Park, B. G. et al. A spin-valve-like magnetoresistance of an antiferromagnet-based tunnel junction. Nat. Mater. 10, 347–351 (2011).
Núñez, A. S., Duine, R. A., Haney, P. & MacDonald, A. H. Theory of spin torques and giant magnetoresistance in antiferromagnetic metals. Phys. Rev. B 73, 214426 (2006).
Gomonay, H. V. & Loktev, V. M. Spin transfer and current-induced switching in antiferromagnets. Phys. Rev. B 81, 144427 (2010).
Gomonay, E. V. & Loktev, V. M. Spintronics of antiferromagnetic systems. J. Low Temp. Phys. 40, 17 (2014).
Gomonay, O. Berry-phase effects and electronic dynamics in a noncollinear antiferromagnetic texture. Phys. Rev. B 91, 144421 (2015).
Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
Kübler, J. & Felser, C. Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014).
Seemann, M., Ködderitzsch, D., Wimmer, S. & Ebert, H. Symmetry-imposed shape of linear response tensors. Phys. Rev. B 92, 155138 (2015).
Katsura, H., Nagaosa, N. & Balatsky, A. V. Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 95, 057205 (2005).
Kenzelmann, M. et al. Magnetic inversion symmetry breaking and ferroelectricity in TbMnO3 . Phys. Rev. Lett. 95, 087206 (2005).
Mostovoy, M. Ferroelectricity in spiral magnets. Phys. Rev. Lett. 96, 067601 (2006).
Sergienko, I. A. & Dagotto, E. Role of the Dzyaloshinskii–Moriya interaction in multiferroic perovskites. Phys. Rev. B 73, 094434 (2006).
Arima, T. Ferroelectricity induced by proper-screw type magnetic order. J. Phys. Soc. Jpn 76, 073702 (2007).
Johnson, R. D. et al. Giant improper ferroelectricity in the ferroaxial magnet CaMn7O12 . Phys. Rev. Lett. 108, 067201 (2012).
Menzel, M. et al. Information transfer by vector spin chirality in finite magnetic chains. Phys. Rev. Lett. 108, 197204 (2012).
von Bergmann, K., Kubetzka, A., Pietzsch, O. & Wiesendanger, R. Interface-induced chiral domain walls, spin spirals and skyrmions revealed by spin-polarized scanning tunneling microscopy. J. Phys.: Condens. Matter 26, 394002 (2014).
Grigoriev, S. V. et al. Chiral properties of structure and magnetism in Mn1−xFexGe compounds: when the left and the right are fighting, who wins? Phys. Rev. Lett. 110, 207201 (2013).
Hames, F. A. & Crangle, J. Ferromagnetism in Heusler-type alloys based on platinum-group or palladium-group metals. J. Appl. Phys. 42, 1336–1338 (1971).
Siewert, M. et al. Designing shape-memory Heusler alloys from first-principles. Appl. Phys. Lett. 99, 191904 (2011).
Feng, L., Liu, E. K., Zhang, W. X., Wang, W. H. & Wu, G. H. First-principle investigation of electronic structure, magnetism and phase stability of Heusler-type Pt2−xMn1+xGa alloys magnetic-texture-controlled transverse spin injection. J. Magn. Magn. Mater. 377, 40–43 (2015).
Roy, T. & Chakrabarti, A. Possibility of martensite transition in Pt–Y–Ga (Y=Cr, Mn, and Fe) system: an ab-initio calculation of the bulk mechanical, electronic and magnetic properties. J. Magn. Magn. Mater. 401, 929–937 (2016).
Meshcheriakova, O. et al. Large noncollinearity and spin reorientation in the novel Mn2RhSn Heusler magnet. Phys. Rev. Lett. 113, 087203 (2014).
Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 192, 55–69 (1993).
Vosko, S. H., Wilk, L. & Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 58, 1200–1211 (1980).
Acknowledgements
S.S. thanks Alexander von Humboldt foundation for fellowship. We thank A.N. Yaresko (MPI-FKF Stuttgart) for providing his programme code and A. Chakrabarti and S.R. Barman for useful discussions. The work was financially supported by the ERC AG 291472 ‘IDEA Heusler!’ and HeuMem project within the European network M-era.net. We acknowledge the support of the HLD at HZDR, member of the European Magnetic Field Laboratory (EMFL). V.P. acknowledges the Ministry of Education, Youth and Sports National sustainability programme of Czech Republic (Project no. LO1603).
Author information
Authors and Affiliations
Contributions
C.F. supervised the project. S.S. and J.N. prepared the sample. S.S. performed structural and magnetic measurements and analysis. M.N. planned the high-magnetic-field experiment. S.S. and Y.S. performed the high-magnetic-field experiment. S.S. and E.S. performed the neutron diffraction experiment. S.S. analysed the neutron diffraction data with the help of L.C., A.S. and V.P. S.C. did the spin-spiral calculations. S.W.D. conducted the Monte-Carlo simulations. S.C. and S.S. have written the manuscript with substantial feedback from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-2, Supplementary Notes 1-2 and Supplementary References (PDF 298 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Singh, S., D’Souza, S., Nayak, J. et al. Room-temperature tetragonal non-collinear Heusler antiferromagnet Pt2MnGa. Nat Commun 7, 12671 (2016). https://doi.org/10.1038/ncomms12671
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12671
This article is cited by
-
The electronic and magnetic properties of the bulk, Sc2MnSi surfaces, and Sc2MnSi/CdTe (111) interface
Applied Physics A (2023)
-
Chiral domain wall motion in unit-cell thick perpendicularly magnetized Heusler films prepared by chemical templating
Nature Communications (2018)
-
Heusler, Weyl and Berry
Nature Reviews Materials (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.