Abstract
In contrast to the flexible rotation of magnetization direction in ferromagnets, the spontaneous polarization in ferroelectric materials is highly confined along the symmetry-allowed directions. Accordingly, chirality at ferroelectric domain walls was treated only at the theoretical level and its real appearance is still a mystery. Here we report a Néel-like domain wall imaged by atom-resolved transmission electron microscopy in Ti-rich ferroelectric Pb(Zr1−xTix)O3 crystals, where nanometre-scale monoclinic order coexists with the tetragonal order. The formation of such domain walls is interpreted in the light of polarization discontinuity and clamping effects at phase boundaries between the nesting domains. Phase-field simulation confirms that the coexistence of both phases as encountered near the morphotropic phase boundary promotes the polarization to rotate in a continuous manner. Our results provide a further insight into the complex domain configuration in ferroelectrics, and establish a foundation towards exploring chiral domain walls in ferroelectrics.
Similar content being viewed by others
Introduction
Oxide ferroelectrics, with coupling of polarization, strain, heat and electric field, are widely utilized in electronic devices such as multilayer capacitors, piezoelectric transducers, pyroelectric detectors and non-volatile high-density memories1,2. While it is well known that properties of the ferroelectrics such as piezoelectric effect and permittivity are substantially enhanced by mobile and stationary domain walls2,3,4,5, the ferroelectric domain walls themselves were found recently to possess unique properties that differ thoroughly from the bulk domains, for example, electronic conductivity6,7,8 and photovoltaic effect9. These results raise much interest10,11,12 in further exploration of the properties of domain walls and their internal structures.
As known, magnetic 180° domain walls are typically of Bloch type or Néel type13,14, across which the magnetization vector rotates continuously in a plane parallel or normal to the wall plane, respectively, while ferroelectric 180° domain walls are predominately of Ising type10. In spite of this, theoretical and computational studies predict plethora of wall structures in the oxide ferroelectrics, for example, the Bloch-type walls in rhombohedral BaTiO3 (refs 15, 16, 17) and tetragonal PbTiO3 (ref. 18), where the polarization rotation is enabled by symmetry-lowering at the walls. Driven by the flexoelectric effect19,20,21, a higher-order electromechanical coupling, a Bloch-like component combined with or without a Néel-like component19,22,23 is also predicted at the 180° domain walls. However, the chiral components are negligible in comparison with the Ising component. The recent discovery of ferroelectric monoclinic phases close to the morphotropic phase boundary (PB)24,25,26,27, for example, in Pb(Zr1−xTix)O3 (PZT), (1−x)PbMg1/3Nb2/3O3−xPbTiO3 and BiFeO3, where the polarization easily rotates within a crystallographic plane, offers new possibilities in the search of new types of domain walls.
Experimentally, direct imaging of light oxygen together with heavy cations using transmission electron microscopy (TEM) serves as the decisive basis to resolve chirality at the ferroelectric domain walls. This requirement is fulfilled by the negative spherical-aberration (CS) imaging (NCSI) technique in an aberration-corrected TEM28. In comparison with the conventional positive CS imaging technique, the NCSI technique yields an especially high image contrast29. Specifically, the robust image contrast is enhanced by superposition of the amplitude contrast because of electron diffraction channelling with the phase contrast30. As a result, atoms appear sharp and bright on a dark background31, light and heavy elements can be clearly imaged together and picometre-precision measurements of atomic positions become accessible32.
Here, by means of direct imaging of electric dipoles using the NCSI technique combined with the ultrahigh-precision measurements, we report a Néel-like rotation of polarization at monoclinic domain walls in ferroelectric PZT (x=0.54, 0.60) single crystals, where the monoclinic order coexists with the tetragonal order at the nanometre scale. The formation mechanism of the domain wall is interpreted in the light of polarization discontinuity and clamping effect at the monoclinic-tetragonal PBs.
Results
Phase and domain identification
Figure 1a shows schematically the basic axes of the monoclinic and the tetragonal unit cell structures. The relations of their lattice parameters are aM≈bM≈√2aT, cM≈cT with a small tilting angle. The spontaneous polarization (PS) is oriented along the [001]T direction in the tetragonal phase (space group P4mm), but in the monoclinic phase, it is allowed to rotate flexibly within the (110)T plane33. Our TEM studies reveal that the monoclinic phase coexists with the tetragonal phase in the PZT (x=0.54, 0.60) crystals. Figure 1b shows morphology of the x=0.60 PZT specimen oriented along the [100]T direction. The observed nanometre-scale ferroelectric domains are in agreement with earlier experimental results on the second-order nature of the ferroelectric phase transition in this composition range34 (Supplementary Note 1 and Supplementary Fig. 1). Under two-beam conditions, diffraction contrast analysis using P·g >0 relation (P is a component of PS and g is a scatting vector)35 reveals that sizes of the nesting domains are less than 20 nm and the domain boundaries cannot be clearly identified, as seen in Fig. 1c. In the selected area electron diffraction pattern shown in Fig. 1d, the reflection spots can be registered as the tetragonal phase, with a tetragonality c/a≈1.043. However, splitting of the reflection spots, which is thoroughly different from that of 90° domains36, can be found by a careful inspection, further corroborating the coexistence of the monoclinic phase with the tetragonal phase.
(a) Schematic relation of the monoclinic unit cell with respect to the tetragonal unit cells. The spontaneous polarization in the monoclinic phase (space group Cm) is allowed to rotate flexibly within the (bc)M plane as indicated by the arrow PS. (b) Bright-field TEM image illustrating morphology of the crystal specimen. Scale bar, 1 μm (c) Dark-field TEM image recorded under two-beam condition using g=( )T reflection in the [110] orientated specimen. The bright-contrast regions indicate the monoclinic domains with a polarization component along the [
)T reflection in the [110] orientated specimen. The bright-contrast regions indicate the monoclinic domains with a polarization component along the [ ]T direction. Scale bar, 20 nm. (d) The representative electron diffraction pattern recorded along the [100]T zone axis. The diffraction spots are indexed with respect to the tetragonal structure. (e) Reciprocal space mapping of the (
]T direction. Scale bar, 20 nm. (d) The representative electron diffraction pattern recorded along the [100]T zone axis. The diffraction spots are indexed with respect to the tetragonal structure. (e) Reciprocal space mapping of the ( ) reflection spot from d to show the spot splitting for the coexisting monoclinic and tetragonal phases.
) reflection spot from d to show the spot splitting for the coexisting monoclinic and tetragonal phases.
To clearly reveal the spot splitting, the area including the ( ) reflection is magnified and exemplified in Fig. 1e. Measurements yield that the c axis relating to the left- and right-side reflection spots is ∼0.415 and 0.411 nm, respectively. The good agreement of the measured results with the data from high-resolution synchrotron X-ray diffraction25 indicates that the two split spots can be indexed as the tetragonal (
) reflection is magnified and exemplified in Fig. 1e. Measurements yield that the c axis relating to the left- and right-side reflection spots is ∼0.415 and 0.411 nm, respectively. The good agreement of the measured results with the data from high-resolution synchrotron X-ray diffraction25 indicates that the two split spots can be indexed as the tetragonal ( )T and the monoclinic (
)T and the monoclinic ( )M, respectively. The (
)M, respectively. The ( )T spot is found to stretch towards the (
)T spot is found to stretch towards the ( )M spot, suggesting that lattice distortion takes place.
)M spot, suggesting that lattice distortion takes place.
Atom-resolution TEM study
To investigate details of the domain and domain wall structures, high-resolution TEM experiments were performed on the PZT crystals under the NCSI conditions. Figure 2a shows an atom-resolution image recorded along the [110]T/[100]M direction of the x=0.60 crystal. Considering the relative shifts of oxygen columns with respect to centres of the nearest neighbouring Zr/Ti columns, this image area can be divided into several different domains. Further consideration of the symmetry-allowed directions for the atomic displacements allows us to assign the domain types, either tetragonal or monoclinic, the PBs and the domain walls.
(a) The panoramic view of nesting tetragonal and monoclinic domains viewed along the [110]T direction. Yellow dotted lines trace the boundaries between the tetragonal and monoclinic phases, and white dotted lines trace the domain walls in the monoclinic phase. The phase and domain boundaries are differentiated by mapping the relative displacements of O2 columns (red arrows) with respect to centres of the nearest neighbouring Zr/Ti columns over the whole image. Scale bar, 1 nm. (b–d) Enlarged view of the relative displacements of the O2 columns in domains M-I, T-I and M-II in a. The colour circles overlapped on the images denote different column types: Pb/O1—yellow, Zr/Ti—blue and O2—red. The vertical dashed and solid lines indicate positions of the Zr/Ti columns and centres of their nearest neighbours. The relative displacements of O2 columns with respect to these centres can be directly identified in this way.
The tetragonal domains, T-I and T-II, show upward shifts of the oxygen columns (denoted by red arrows) along the [001] direction. In contrast, in the monoclinic domains, M-I and M-II, the oxygen columns shift to right-up and left-up, respectively, evidently deviating from the [001] direction. A small part of M-III domain is also detected in the right part of the image area. The displacement features of oxygen columns in the M-I, T-I and M-II domains can be directly identified from the magnified images shown in Fig. 2b–d. Yellow, blue and red circles denote Pb/O1, Zr/Ti and O2 atom columns, respectively. It is seen that the main part of the PBs lies in the (001)T, ( )T and (
)T and ( )T planes, and the rest is faceted irregularly. Particularly, the M-II, T-II and M-I domains form a flux-closure structure.
)T planes, and the rest is faceted irregularly. Particularly, the M-II, T-II and M-I domains form a flux-closure structure.
A particularly interesting feature of the atomic structure is seen in the region including the central plane of the wall between domains M-I and M-II, as denoted by a white dotted line in Fig. 2a and shown again by green arrows in Fig. 3a, where the oxygen columns exhibit vertical displacements. Meanwhile, a wall segment shifted downward by cM/2, in which the displacements of oxygen columns undergo a sharp transition, is observed at the right side of the region. Measurements of the relative displacements of oxygen columns on the left-side wall segment, extending the areas upwards and downwards from the central plane, reveal a continuous change of the oxygen displacements, that is, continuous rotation of the displacements from leftward (slightly up) in M-II through upward at central plane to rightward (slightly up) in M-I. The displacement feature of oxygen atoms forms a structure similar to the Néel wall in ferromagnets37. Quantitative measurement of the atom displacements is performed based on an iterative procedure for comparison between the experimental image and image simulated over this area (Supplementary Note 2 and Supplementary Fig. 2). The simulated image with the best fitting to the experimental image is attached to the left side of Fig. 3a.
(a) Experimental image of the monoclinic domain wall viewed along the [100]M direction. Green arrows denote the central plane of the domain wall. The inset on the left hand shows a simulated image for thickness of 4.4 nm and defocus of 5.5 nm. Scale bar, 0.5 nm. (b) Continuous rotation of the O2-displacement vectors across the domain wall compiled by δxO2-Zr/Ti and δyO2-Zr/Ti extracted from the structure model used for image simulation. Scale bar, 30 pm.
Figure 4a shows the lattice parameter changes as a function of distance away from the central plane of the Néel-like wall, which are measured from the positions of Pb to Pb atoms (blue symbols) and Zr/Ti to Zr/Ti atoms (pink symbols), respectively. It is seen that the c axis in the M-I and M-II domains is 0.415 and 0.410 nm, respectively, which decreases in a stepwise manner across the wall centre. On the contrary, the a axis in the M-I domain is ∼0.40 nm, slightly smaller than that in the M-II domain. As a result, the c/a ratio in the M-I domain is 1.038 in average, it reaches a value of 1.048 near the central plane of the wall and extends into the M-II domain by 2 unit cells. This ratio decreases to ∼1.024 in the rest part of the M-II domain as shown in Fig. 4b. Our statistical studies on both PZT crystals indicate that the c/a ratios in the M-I and M-II domains are not necessarily different from each other. It is therefore reasonable to speculate that, to a certain degree, their tetragonality values rely on conditions of the surrounding domains.
Circles and squares denote the parameters parallel and normal to the wall plane, respectively. (a) The a axis and c axis lattice parameters. Blue and pink symbols represent the values measured from the Pb to Pb and from the Zr/Ti to Zr/Ti atom positions, respectively. (b) Tetragonality c/a calculated from the a axis and c axis. (c) Relative displacements of the O2 atoms parallel and normal to the domain wall plane. The error bar is the mean s.d. measured from the experimental image and averaged along the wall plane direction.
With respect to the centres of the nearest neighbouring Ti/Zr atom columns, the rightward horizontal displacements of the O2 atoms (δxO2-Zr/Ti) undergo a smooth reduction from ∼12 pm in the M-I domain to zero at the central plane of the wall (Fig. 4c). The displacements switch to the opposite direction (leftwards) inside the M-II domain and further increase to 14 pm. Along the vertical direction, the displacements of O2 atoms gradually decay from the maximum of δyO2-Zr/Ti≈−21 pm at the central plane of the wall towards far ends of the two domains. Since the unit cell dipole moment is proportional to the relative displacement, the data in Fig. 4c represent the transition behaviour of the polarization across the domain wall. Along the horizontal wall plane direction in Fig. 3a, the parallel component of polarization smoothly decreases to zero at the central plane of the wall, and then increases when moving away from the central plane in domain M-II. Along the normal direction of the wall plane, the normal component of polarization reaches the maximum value and then gradually decays towards far ends of the two domains. The change of the relative displacements is shown as vectors in Fig. 3b, demonstrating the clear feature of the Néel-like wall. From the variation of the relative displacements, we infer that width of the domain wall is nine unit cells, four unit cells in each monoclinic domain and one unit cell at the wall centre.
Discussion
So far, structural investigations of the PZT solid solutions at ambient pressure have revealed the monoclinic (Cm) phase only, in coexistence with either the rhombohedral phases33,38,39 or the tetragonal phase40. Indeed, the coexistence of the monoclinic and the tetragonal phases is evidenced in the present study. To minimize the depolarization field energy41,42, the polarization vectors in the M-I and M-II domains are confined to lie in the same crystal plane. Therefore, the polarization observed in Fig. 3a is fully projected on the (110)T plane. The formation of the Néel-like wall configuration can be attributed to effects of polarization discontinuity at the PBs and local clamping, that is, to the local electrostatic and elastic conditions in the PZT crystals with coexistence of the two intertwining phases at the nanometre scale.
Our estimation yields a spontaneous polarization value of PS≈47 μC cm−2 for the monoclinic phase and PS=78 μC cm−2 for the tetragonal phase. Neutron diffraction refinement on x=0.60 PZT ceramics40 reported that the proportion of the two phases is ∼9:11. On the basis of this, the calculated overall polarization for the PZT (x=0.60) crystal (PS=64 μC cm−2) is in a good agreement with the macroscopic electric hysteresis loop measurement (Supplementary Note 3 and Supplementary Fig. 3). Owing to the differences in modulus and directions of the polarization with respect to the PB orientation, the polarization discontinuity inevitably results in either positive or negative charging of the PBs.
The cartoon of a single monoclinic domain positioned between the two tetragonal domains in Fig. 5a illustrates the PB charging as a source of the depolarization field Ed. The depolarization field points against the spontaneous polarization and promotes the domain splitting in order to reduce the electrostatic energy (Fig. 5b). It is qualitatively similar to the behaviour of a ferroelectric layer between two dielectric bodies, where alternate charge types on a charged plane produces in average smaller depolarization field, and hence smaller electrostatic energy than a constantly charged plane. In addition, the stray depolarization field produced by the left PBs has a component parallel to the spontaneous polarization at the wall centre. The right PBs promote the same effect with an opposite sign, but have smaller magnitude because of the multiple facets of the boundaries (Fig. 2a). Thereupon, the left-side depolarization field may contribute to drive the polarization to rotate via the [001]T direction. This is manifested by the increased c/a ratio near the wall centre, which favours the polarization to lie along the [001]T direction43. Similar effects have been reported in ferroelectric thin films44,45, where flux-closure domains and vortex nanodomains are observed near the interfaces.
(a) A monoclinic stripe domain is clamped by two tetragonal domains from both sides, where a depolarization field (Ed) is created between the electrostatically incompatible and therefore partly charged PBs (solid blue lines). (b) The clamped monoclinic domain is divided into two monoclinic domains, M-I and M-II, to reduce the electrostatic energy associated with the depolarization field in this local area. This results in presence of the domain wall (solid yellow line) in the monoclinic phase. The symbols (+ and −) denote the positive and negative bound polarization charges, respectively.
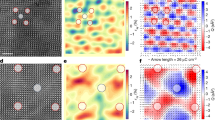
A three-dimensional (3D) phase-field simulation on a thin (110)T PZT lamella with the energy potential46 that allows the presence of a stable monoclinic phase supports the above scenario (see Methods). In addition to the effect of the electrostatic energy, the local elastic conditions are found to play a role in controlling the width of the monoclinic domain wall. When the lamella is compressed with an average strain of −0.2% for all domains in the [ ]T direction as shown in Fig. 6a, or free of external force, the monoclinic wall is very narrow (approximately one unit cell) and the polarization undergoes a sharp transition at the wall centre. However, as the compressive strain increases to −0.6% (Fig. 6b), the monoclinic wall is substantially broadened to >20 unit cells and the polarization continuously rotates across the domain wall. Together with the electric potential distribution, the polarization rotation behaviours near the monoclinic walls are illustrated in Fig. 6c,d, respectively.
]T direction as shown in Fig. 6a, or free of external force, the monoclinic wall is very narrow (approximately one unit cell) and the polarization undergoes a sharp transition at the wall centre. However, as the compressive strain increases to −0.6% (Fig. 6b), the monoclinic wall is substantially broadened to >20 unit cells and the polarization continuously rotates across the domain wall. Together with the electric potential distribution, the polarization rotation behaviours near the monoclinic walls are illustrated in Fig. 6c,d, respectively.
(a) The narrow monoclinic domain wall with a sharp polarization transition under an average compressive strain of −0.2%. Scale bar, 5 nm. (b) The wide monoclinic domain wall with a continuous rotational polarization transition under an average compressive strain of −0.6%. Scale bar, 5 nm. The colour scales the PS component distribution along the horizontal [ ]T direction. (c) The electric potential distribution in the zoomed region in a associated with the sharp polarization reorientation near the wall centre. Scale bar, 0.5 nm. (d) The electric potential distribution in the zoomed region in b associated with the continuous polarization rotation near the wall centre. Scale bar, 2 nm. The white arrows represent the spontaneous polarization PS.
]T direction. (c) The electric potential distribution in the zoomed region in a associated with the sharp polarization reorientation near the wall centre. Scale bar, 0.5 nm. (d) The electric potential distribution in the zoomed region in b associated with the continuous polarization rotation near the wall centre. Scale bar, 2 nm. The white arrows represent the spontaneous polarization PS.
It is well established that sufficiently high content of the larger Zr cations in the tetragonal PZT crystal near the morphotropic PB flattens the potential profile of the system. As a result, the monoclinic states become local minima and the presence of stable monoclinic phases are expected. Although the lower-energy phase in an idealized phase-field model would always sweep-out the higher-energy phase, even if the energy difference is very small, the realistically inhomogeneous Zr distribution, as corroborated by our phase-field simulation, enables the multiphase coexistence in the PZT crystals (Supplementary Note 4, Supplementary Fig. 4 and Supplementary Fig. 5). Facilitated by the shallow Mexican-hat-type energy potential, the energy cost of a domain wall becomes low. Polarization rotation between different stable sites46, as shown by the Néel-like rotational changes of the oxygen atoms in Fig. 3b, can therefore occupy large distance when passing through the monoclinic domain wall.
In recent years, the 180° stripe domains42,47, flux-closure domains48,49 and vortex nanodomains45 have been reported in ferroelectric PZT, BaTiO3 and BiFeO3. In contrast to these complex domain patterns, for example, the flux-closure structure consisting of consecutive 180°–90°–180° domains, the polarization transitions at these non-180° walls are sharp and the 180° walls are all Ising-like. However, the Néel-like domain walls observed in this work possesses the genuine chiral feature.
In conclusion, our results provide direct experimental evidence for the existence of Néel-like domain walls in ferroelectric materials. The findings highlight that in the low-symmetry ferroelectric phases, which widely exist in solid solutions27,33 and thin films26,50, new types of domain walls are yet to be explored both theoretically and experimentally. Extrapolating from the potential utilization of controlled chirality at magnetic Néel walls14,51 and the control of the polarization configuration by magnetic field52, we hope that our findings will stimulate explorations of ferroelectric chiral domain walls and their possible application in future electronic devices.
Methods
Material preparation
Lead zirconate titanate crystals were grown by a top-seeded solution growth technique. Optical microscopic examination showed a good optical quality of the crystals without inclusions of visible defects. The good quality of the crystals is supported also by the square-shaped saturated ferroelectric hysteresis loop and the high remnant polarization (Supplementary Fig. 3). The lamella specimens used for TEM investigations were prepared using focused ion beam system. The NanoMill Model 1040 System operated at 500 voltages was used to clean contamination on sample surfaces and mill down the lamella samples.
Imaging experiments
The TEM investigations were performed on an FEI Titan 80–300 microscope with a CS corrector for the objective lens53. The available point resolution is better than 80 pm at an operating voltage of 300 kV. Other TEM characterizations were carried out on an FEI Tecnai F20 Microscope. The experimental image was filtered to minimize the effect of contrast noise32. Structure modelling and image simulation were carried out using the CrystalKit-MacTempas Software package to determine the relative displacements between different atomic columns. The effective charges used for calculating the spontaneous polarization was inferred from the first-principles calculations43.
Phase-field simulation
The phase-field simulation results (Fig. 6 and Supplementary Fig. 4) were obtained by numerical solution of coupled 3D versions of the time-dependent Landau–Ginzburg–Devonshire equation, Poisson’s equation and equation of motion in elastic materials54 with eigthth order Landau energy polynomial46, which allows presence of the monoclinic phase. Gradient energy coefficients were used 102 times smaller those than in ref. 54 to obtain realistic domain wall widths. Ideal dielectric and compositional inhomogeneity were assumed. Equations were solved on a 2 × 15 × 60 nm3 (110)T lamella of PZT crystal. The central 40% of the lamella has x=0.5, the rest x=0.6 (Supplementary Fig. 4). The ( )T external boundaries are mechanically clamped and used to stretch and compress the lamella with sinusoidal boundary displacement in the [
)T external boundaries are mechanically clamped and used to stretch and compress the lamella with sinusoidal boundary displacement in the [ ]T direction. All other boundaries are mechanically free. The (001)T surfaces have constant potential and all remaining surfaces have zero free charge. Initial conditions were set in the proximity of the expected stationary solution. The model is numerically solved by the finite element method with a time-dependent solver in COMSOL 4.3a (COMSOL Inc., 2012) until stationary solution at each strain was reached.
]T direction. All other boundaries are mechanically free. The (001)T surfaces have constant potential and all remaining surfaces have zero free charge. Initial conditions were set in the proximity of the expected stationary solution. The model is numerically solved by the finite element method with a time-dependent solver in COMSOL 4.3a (COMSOL Inc., 2012) until stationary solution at each strain was reached.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Wei, X-K. et al. Néel-like domain walls in ferroelectric Pb(Zr,Ti)O3 single crystals. Nat. Commun. 7:12385 doi: 10.1038/ncomms12385 (2016).
References
Dawber, M., Rabe, K. M. & Scott, J. F. Physics of thin-film ferroelectric oxides. Rev. Mod. Phys. 77, 1083 (2005).
Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 61, 1267–1324 (1998).
Arlt, G. & Pertsev, N. A. Force constant and effective mass of 90° domain walls in ferroelectric ceramics. J. Appl. Phys. 70, 2283 (1991).
Nagarajan, V. et al. Dynamics of ferroelastic domains in ferroelectric thin films. Nat. Mater. 2, 43–47 (2003).
Xu, R. J., Karthik, J., Damodaran, A. R. & Martin, L. W. Stationary domain wall contribution to enhanced ferroelectric susceptibility. Nat. Commun. 5, 3120 (2014).
Seidel, J. et al. Conduction at domain walls in oxide multiferroics. Nat. Mater. 8, 229–234 (2009).
Sluka, T., Tagantsev, A. K., Bednyakov, P. & Setter, N. Free-electron gas at charged domain walls in insulating BaTiO3 . Nat. Commun. 4, 1808 (2013).
Crassous, A., Sluka, T., Tagantsev, A. K. & Setter, N. Polarization charge as a reconfigurable quasi-dopant in ferroelectric thin films. Nat. Nanotechnol. 10, 614–618 (2015).
Yang, S. Y. et al. Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 5, 143–147 (2010).
Catalan, G., Seidel, J., Ramesh, R. & Scott, J. F. Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156 (2012).
Salje, E. & Zhang, H. Domain boundary engineering. Phase Transit. 82, 452–469 (2009).
Wei, X. K. et al. Ferroelectric translational antiphase boundaries in nonpolar materials. Nat. Commun. 5, 3031 (2014).
Williams, H. J. & Goertz, M. Domain structure of perminvar having a rectangular hysteresis loop. J. Appl. Phys. 23, 316 (1952).
Emori, S., Bauer, U., Ahn, S. M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Hlinka, J. et al. Phase-field modelling of 180° “Bloch walls” in rhombohedral BaTiO3 . Phase Transit. 84, 738–746 (2011).
Taherinejad, M., Vanderbilt, D., Marton, P., Stepkova, V. & Hlinka, J. Bloch-type domain walls in rhombohedral BaTiO3 . Phys. Rev. B 86, 155138 (2012).
Marton, P., Rychetsky, I. & Hlinka, J. Domain walls of ferroelectric BaTiO3 within the Ginzburg-Landau-Devonshire phenomenological model. Phys. Rev. B 81, 144125 (2010).
Wojdeł, J. C. & Íñiguez, J. Ferroelectric transitions at ferroelectric domain walls found from first principles. Phys. Rev. Lett. 112, 247603 (2014).
Yudin, P. V., Tagantsev, A. K., Eliseev, E. A., Morozovska, A. N. & Setter, N. Bichiral structure of ferroelectric domain walls driven by flexoelectricity. Phys. Rev. B 86, 134102 (2012).
Lee, D. et al. Giant flexoelectric effect in ferroelectric epitaxial thin films. Phys. Rev. Lett. 107, 057602 (2011).
Gu, Y. et al. Flexoelectricity and ferroelectric domain wall structures: phase-field modeling and DFT calculations. Phys. Rev. B 89, 174111 (2014).
Lee, D. et al. Mixed Bloch-Néel-Ising character of 180° ferroelectric domain walls. Phys. Rev. B 80, 060102(R) (2009).
Li, M., Gu, Y., Wang, Y., Chen, L.-Q. & Duan, W. First-principles study of 180° domain walls in BaTiO3: Mixed Bloch-Néel-Ising character. Phys. Rev. B 90, 054106 (2014).
Noheda, B. et al. Tetragonal-to-monoclinic phase transition in a ferroelectric perovskite: the structure of PbZr0.52Ti0.48O3 . Phys. Rev. B 61, 8687 (2000).
Noheda, B., Cox, D. E. & Shirane, G. Stability of the monoclinic phase in the ferroelectric perovskite PbZr1-xTixO3 . Phys. Rev. B 63, 014103 (2000).
Chen, Z. et al. Low-symmetry monoclinic phases and polarization rotation path mediated by epitaxial strain in multiferroic BiFeO3 thin films. Adv. Funct. Mater. 21, 133–138 (2011).
Noheda, B., Cox, D. E., Shirane, G., Gao, J. & Ye, Z. G. Phase diagram of the ferroelectric relaxor (1-x)PbMg1/3Nb2/3O3-xPbTiO3 . Phys. Rev. B 66, 054104 (2002).
Jia, C. L., Lentzen, M. & Urban, K. Atomic-resolution imaging of oxygen in perovskite ceramics. Science 299, 870–873 (2003).
Jia, C. L., Houben, L., Thust, A. & Barthel, J. On the benefit of the negative-spherical-aberration imaging technique for quantitative HRTEM. Ultramicroscopy 110, 500–505 (2010).
Urban, K. W. et al. Negative spherical aberration ultrahigh-resolution imaging in corrected transmission electron microscopy. Phil. Trans. R Soc. A 367, 3735–3753 (2009).
Lentzen, M. et al. High-resolution imaging with an aberration-corrected transmission electron microscope. Ultramicroscopy 92, 233–242 (2002).
Jia, C.-L. et al. Atomic-scale study of electric dipoles near charged and uncharged domain walls in ferroelectric films. Nat. Mater. 7, 57–61 (2007).
Zhang, N. et al. The missing boundary in the phase diagram of PbZr1-xTixO3 . Nat. Commun. 5, 5231 (2014).
Rossetti, G. A. & Navrotsky, A. Calorimetric investigation of tricritical behavior in tetragonal Pb(ZrxTi1-x)O3 . J. Solid State Chem. 144, 188 (1999).
Asada, T. & Koyama, Y. Ferroelectric domain structures around the morphotropic phase boundary of the piezoelectric material PbZr1-xTixO3 . Phys. Rev. B 75, 214111 (2007).
Su, D. et al. Origin of 90° domain wall pinning in Pb(Zr0.2Ti0.8)O3 heteroepitaxial thin films. Appl. Phys. Lett. 99, 102902 (2011).
Chen, G. et al. Tailoring the chirality of magnetic domain walls by interface engineering. Nat. Commun. 4, 2671 (2013).
Yokota, H., Zhang, N., Taylor, A., Thomas, P. & Glazer, A. Crystal structure of the rhombohedral phase of PbZr1−xTixO3 ceramics at room temperature. Phys. Rev. B 80, 104109 (2009).
Phelan, D. et al. Single crystal study of competing rhombohedral and monoclinic order in lead zirconate titanate. Phys. Rev. Lett. 105, 027601 (2010).
Zhang, N., Yokota, H., Glazer, A. M. & Thomas, P. A. Neutron powder diffraction refinement of PbZr1-xTixO3 . Acta Crystallogr. B 67, 386–398 (2011).
Tagantsev, A. K., Courtens, E. & Arzel, L. Prediction of a low-temperature ferroelectric instability in antiphase domain boundaries of strontium titanate. Phys. Rev. B 64, 224107 (2001).
Streiffer, S. K. et al. Observation of nanoscale 180° stripe domains in ferroelectric PbTiO3 thin films. Phys. Rev. Lett. 89, 067601 (2002).
Wu, Z. & Krakauer, H. First-principles calculations of piezoelectricity and polarization rotation in Pb(Zr0.5Ti0.5)O3 . Phys. Rev. B 68, 014112 (2003).
Jia, C. L., Urban, K. W., Alexe, M., Hesse, D. & Vrejoiu, I. Direct observation of continuous electric dipole rotation in flux-closure domains in ferroelectric Pb(Zr,Ti)O3 . Science 331, 1420–1423 (2011).
Nelson, C. T. et al. Spontaneous vortex nanodomain arrays at ferroelectric heterointerfaces. Nano Lett. 11, 828–834 (2011).
Bell, A. J. Factors influencing the piezoelectric behaviour of PZT and other “morphotropic phase boundary” ferroelectrics. J. Mater. Sci. 41, 13–25 (2006).
Chen, Z. et al. 180° ferroelectric stripe nanodomains in BiFeO3 thin films. Nano Lett. 15, 6506–6513 (2015).
Tang, Y. L. et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO films. Science 348, 547 (2015).
McQuaid, R. G., McGilly, L. J., Sharma, P., Gruverman, A. & Gregg, J. M. Mesoscale flux-closure domain formation in single-crystal BaTiO3 . Nat. Commun. 2, 404 (2011).
Chen, Z. et al. Coexistence of ferroelectric triclinic phases in highly strained BiFeO3 films. Phys. Rev. B 84, 094116 (2011).
Chen, G. et al. Novel chiral magnetic domain wall structure in Fe/Ni/Cu(001) films. Phys. Rev. Lett. 110, 177204 (2013).
Leo, N. et al. Polarization control at spin-driven ferroelectric domain walls. Nat. Commun. 6, 6661 (2015).
Thust, A., Barthel, J. & Tillmann, K. FEI Titan 80-300 TEM. JLSRF 2, A41 (2016).
Stolichnov, I. et al. Bent ferroelectric domain walls as reconfigurable metallic-like channels. Nano Lett. 15, 8049–8055 (2015).
Acknowledgements
The research leading to these results has received funding from the European Research Council under the EU 7th Framework Programme (FP7/2007–2013)/ERC grant agreement no. [268058] Mobile-W and from the EU 7th Framework Programme under Grant Agreement 312483 - ESTEEM2 (Integrated Infrastructure Initiative–I3), the United States Office of Naval Research (ONR Grant No. N00014-12-1-1045) and the Natural Science and Engineering Research Council of Canada (NSERC, Grant No. 203773). We thank M. Kruth and D. Meertens for sample preparation using focused ion beam, and Y. Xie for help in crystal growth.
Author information
Authors and Affiliations
Contributions
X.-K.W. conceived and coordinated the study. X.-K.W. carried out the electron microscopy experiments, image simulation and data analysis under the supervision of C.-L.J. T.S. performed the phase-field simulation. B.-X.W. and Z.-G.Y. prepared the PZT crystals and characterized their electrical and optical properties. X.-K.W. wrote the manuscript with the help of C.-L.J. and N.S. N.S. initiated the study and was responsible for the overall direction. All authors discussed the results and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Notes 1-4 and Supplementary References (PDF 923 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wei, XK., Jia, CL., Sluka, T. et al. Néel-like domain walls in ferroelectric Pb(Zr,Ti)O3 single crystals. Nat Commun 7, 12385 (2016). https://doi.org/10.1038/ncomms12385
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12385
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.