Abstract
Applying magnetic fields has been the method of choice to magnetize non-magnetic materials, but they are difficult to focus. The magneto-electric effect and voltage-induced magnetization generate magnetization by applied electric fields, but only in special compounds or heterostructures. Here we demonstrate that a simple metal such as gold can be magnetized by a temperature gradient or magnetic resonance when in contact with a magnetic insulator by observing an anomalous Hall-like effect, which directly proves the breakdown of time-reversal symmetry. Such Hall measurements give experimental access to the spectral spin Hall conductance of the host metal, which is closely related to other spin caloritronics phenomena such as the spin Nernst effect and serves as a reference for theoretical calculation.
Similar content being viewed by others
Introduction
Generation and detection of non-equilibrium magnetization in non-magnetic conductors lie at the heart of spintronics research1,2,3. In previous studies, it was shown that spin injection can be achieved by various techniques4,5,6,7,8,9,10,11. However, the detection of the spin injection induced magnetization is more challenging because of its small magnitude. Especially, the non-equilibrium magnetization induced time-reversal symmetry breaking has been rigorously confirmed in very limited systems, which usually requires the observation of Faraday(Kerr)-type phenomena or Hall effect7,12,13,14. For some thermal spin injection methods such as the spin Seebeck effect8,15,16,17,18, the temperature-gradient-induced spin current can be detected by the inverse spin Hall effect (ISHE) while expected accompanying magnetization still lacks direct experimental evidence.
We start with considering a simple bilayer film comprising an insulator magnet such as Y3Fe5O12 (YIG) and a normal metal layer, such as Au (see Fig. 1a). Au is far from a ferromagnetic instability and the static proximity magnetization is negligibly small8,19. Perturbation, such as a temperature gradient, generates non-equilibrium magnetization dynamics in the magnet4,20,21. In such a system, non-equilibrium spin phenomena can be classified in terms of the following three regimes. First, when the spin diffusion length of the metal layer lD is much less than its thickness t, lD<<t; the normal metal properties are affected only over a thin-skin layer next to the ferromagnet, that is, the trivial class. Second, when lD∼t, the magnetization dynamics excited in the magnet injects spin angular momentum deep into the metal layer. However, the decay of the spin accumulation is steep and its average is suppressed22. Most studies that detect spin Seebeck and spin-pumping effects by the ISHE are in this regime, in which a heat current and microwave-induced magnetization dynamics are treated as a perturbation, respectively.
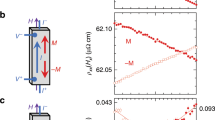
(a) In a normal metal/insulator magnet film, a non-equilibrium magnetization  can be generated in the normal metal (for example, Au) via a dynamic spin exchange by external perturbations such as a temperature-gradient (∇T). The orientation of
can be generated in the normal metal (for example, Au) via a dynamic spin exchange by external perturbations such as a temperature-gradient (∇T). The orientation of  is related to the direction of the applied ∇T. (b) In the presence of a non-equilibrium magnetization, spin-up and spin-down electrons are unequally populated. When a charge current (jc) is applied normal to
is related to the direction of the applied ∇T. (b) In the presence of a non-equilibrium magnetization, spin-up and spin-down electrons are unequally populated. When a charge current (jc) is applied normal to  , an anomalous Hall-type voltage is expected.
, an anomalous Hall-type voltage is expected.
Finally, in the regime, lD⩾t, the perturbation is able to magnetize the entire metal layer in a non-equilibrium manner as illustrated in Fig. 1a (ref. 23): non-equilibrium magnetization, which breaks time-reversal-symmetry. The created non-equilibrium magnetization  may induce a Hall electromotive force EH when a probe electric current, jc, is applied as illustrated in Fig. 1b:
may induce a Hall electromotive force EH when a probe electric current, jc, is applied as illustrated in Fig. 1b:

just as the equilibrium magnetization of ferromagnets induces the anomalous Hall effect (AHE)24,25,26,27. Observation of such a Hall effect has been considered difficult since non-equilibrium magnetization in metals is small and short-lived13.
In this article, we, nevertheless, report a non-equilibrium magnetization created by a temperature gradient observed with a lock-in Hall measurement at room temperature. In addition, we also show that the non-equilibrium magnetization generated by spin pumping can be measured by the same method. The Hall measurement method we developed enables the observation of such tiny magnetization, which highlights its high sensitivity and potential application in spintronics studies.
Results
Temperature-gradient-induced non-equilibrium magnetization
Figure 2a illustrates the experimental setup used in the present study. The first sample is a 20-nm-thick Au/5-μm-thick Y3Fe5O12 (YIG) bilayer film on a Gd3Ga5O12 substrate, where YIG is a ferrimagnetic insulator with the band gap of 2.6 eV. The YIG magnetization was aligned in the out-of-plane direction by an external magnetic field H>0.2 T (see M-H curve in Fig. 2b). The Hall effect in the Au film was measured using an in-plane current and an out-of-plane temperature-gradient ∇T, that is, a configuration that fulfills the conditions for the Hall effect anticipated above. On the other hand, a spin Seebeck voltage generated by the ISHE should vanish because of the symmetry. By simultaneously applying28 an a.c. temperature-gradient ∇T and d.c. in-plane current I, we selectively picked up the Hall voltage component VH that is proportional to ∇T (see Methods for details), while ordinary Hall components are removed by the lock-in method. We eliminated heat-induced parasitic effects that do not depend on the current direction by recording the authentic Hall response VH(+I)−VH(−I).
(a) An Illustration of the Hall measurement setup for the temperature-gradient-induced magnetization. A 20-nm-thick Au film on YIG is patterned into a Hall bar. A standard five-probe method was used for the Hall measurement. A magnetic field was applied perpendicular to the sample, which is of a 2 mm × 3 mm rectangle. A d.c. current, I, and an a.c. out-of-plane temperature gradient, ∇T, were applied simultaneously, while the Hall voltage was picked up with a lock-in amplifier. (b) Out-of-plane magnetization curve for the Au/YIG sample at 300 K. The inset shows a linear Hall response of the Au film at 300 K, indicating a negligible static magnetic proximity. (c) The Hall signal measured for |∇T|=22.2 K mm−1 (red curve) and zero (black curve) at |I|=40 mA. No magnetic-field response was observed in the latter case. Otherwise, the Hall signal shows an asymmetric magnetic-field dependence of the same saturation behaviour as the M-H curve in b. (d) Hall voltages measured for different current levels (|I|) at |∇T|=22.2 K mm−1. (e) The |I| dependence of the nAHE signal shown in d. The solid line is a linear fit. The error bar is estimated by the s.d. of the measured voltage above the saturation field. (f) The Hall voltage measured at various values of the temperature gradient. The nAHE signal vanishes when |∇T|=0 and increases with increasing |∇T|. (g) The |∇T| dependence of the nAHE signal shown in f. The solid line is a linear fit. The error bar is estimated in the same way as in e.
First, in Fig. 2c, we show the Hall voltages VH(+I)−VH(−I) measured in the absence of a temperature gradient (∇T=0). In VH(+I)−VH(−I), no field dependent signal appears, consistent with the absence of a conventional AHE that would appear in a proximity magnetized Au. For the conventional spin Seebeck measurement please see Supplementary Figs 1 and 2, and Supplementary Note 1.
Figure 2c shows the Hall voltage VH(+I)−VH(−I) measured with applying a temperature-gradient, ∇T=22.2 K mm−1 and |I|=40 mA (red curves). Importantly, the measured Hall voltage exhibits AHE-like antisymmetric field dependence and the same saturation behaviour as the M-H curve in Fig. 2b, which manifests time-reversal symmetry breaking. The field dependence of the Hall voltage similar to the M-H curve suggests that  parallel to the YIG magnetization appears in the Au layer due to the temperature gradient.
parallel to the YIG magnetization appears in the Au layer due to the temperature gradient.
Figure 2d shows a linear |I|-dependence of the Hall voltage at |∇T|=22.2 K mm−1, that vanishes at |I|→0 as shown in Fig. 2e, ruling out a contamination by the symmetry-forbidden ISHE detection of the spin Seebeck effect. Also, the observed field dependence of the Hall voltage can not be explained by the spin Hall magnetoresistance29, which has an even magnetic-field symmetry.
Figure 2f shows the temperature-gradient dependence of VH(+I)−VH(−I) at |I|=50 mA. The AHE-type signal is zero at |∇T|=0 as mentioned above and gradually emerges with increasing |∇T|. The data prove its non-equilibrium origin that distinguishes it from the AHE due to magnetic proximity30,31. Figure 2g demonstrates a linear relation between the Hall voltage and |∇T|; the temperature gradient over the Au/YIG bilayer breaks time-reversal symmetry in the Au film: an essential feature of a spin polarization. In other words, the observed Hall voltage is evidence of a temperature-gradient-induced magnetization in Au. We call this phenomenon a non-equilibrium AHE (nAHE).
Spin-pumping-induced non-equilibrium magnetization
To double check this scenario, for a similar film, we also measured nAHE induced by deterministic spin pumping, in which the magnetization dynamics is resonantly excited by microwaves as illustrated in Fig. 3a, rather than a temperature gradient. We observed nAHE as well as an ordinary Hall effect as a d.c. voltage that appears when simultaneously applying continuous microwaves and a d.c. current.
(a) An illustration of the Hall measurement setup for spin-pumping induced magnetization. The sample is a 14-nm-thick Au/YIG bilayer film without patterning. A continuous microwave and a current were applied to the sample while a d.c. Hall voltage was picked up. The sample was placed at the centre of a TE011 microwave (MW) cavity with the resonance frequency 9.45 GHz. The microwave magnetic field is along the x axis. (b) Field (H) dependence of the FMR signal (dA/dH) under 1 mW microwave excitation, A being the microwave absorption. The ferromagnetic resonance field is HFMR=5,020 Oe. (c) Field dependence of the Hall voltage at different values of the microwave power. The sensing current is fixed at 30 mA. The inset is the microwave power PMW dependence of the generated Hall voltage in the Au VnAHE. The solid line is a linear fit. (d) The Hall voltage measured with in-plane (θH=0°, 180°) and perpendicular (θH=90°, −90°) magnetic fields at 2.5 mW microwave excitation and I=30 mA. The inset shows the definition of the magnetic-field angle θH and the magnetization angle θM. (e) Current magnitude dependence of the Hall voltage measured at PMW=2.5 mW. (f) Hall voltage measured in a 24-nm-Cu95Ir5/YIG film at different values of microwave power with the same setup as in a. (g) The field angle dependence of the Hall signal in a Cu95Ir5/YIG film.
Figure 3b shows a microwave absorption spectrum near the ferromagnetic resonance (FMR) with out-of-plane magnetic fields. In Fig. 3c, the Hall voltage is measured around the FMR field HFMR at different values of microwave power for the same applied current. At zero microwave power (PMW=0), we only observe the ordinary Hall voltage that increases linearly with field.. When a microwave is applied, on the other hand, a conspicuous signal proportional to PMW emerges at HFMR on top of the normal Hall effect. The peak voltage as a function of the out-of-plane magnetic-field angle θH is shown in Fig. 3d; its sign changes by reversing the field direction and it vanishes for in-plane magnetic fields (θH=0 and 180°), consistent with the nAHE scenario.
The voltage peak is not caused by the ISHE induced by the spin pumping. By switching off the d.c. current I, the peak voltage disappears as shown by the green curve in Fig. 3e; indeed the ISHE should not appear because of the symmetry of the perpendicular magnetized configuration. The result indicates that the simultaneous application of the microwave and the current is necessary for the present Hall voltage to appear. Figure 3e shows the Hall voltage for various values of the current under the microwave irradiation. Both the normal Hall and the peak components are found to be proportional to the current amplitude and change their signs with reversing the current polarity. Thus, I-independent mechanisms such as ISHEs4 and magnetoelectric rectification32,33 are ruled out. The peak voltage is thus attributed to the nAHE, reinforcing its concept of nAHE.
We also observed nAHE signals in another paramagnetic metal: a Cu95Ir5 film on YIG, which shows a similar microwave-power and field-angle dependence, as shown in Fig. 3f,g, respectively. The nAHE appears to be universal, and it should be worthwhile to explore it in other material systems. The measurement of this effect is free of ferromagnetic electrode and does not require nanofabrication, of which the device structure is much simpler compared with previous techniques for thermal induced spin accumulation observation34,35,36,37,38.
Discussion
We formulate the nAHE in terms of the spectral spin Hall effect (SHE). The non-equilibrium magnetization in a normal metal is proportional to the spin accumulation: μs=μ↑−μ↓, while the total charge density and Fermi energy remain to leading order unmodified.  is parallel to the minority spin direction in the paramagnet. When a longitudinal electric field (E) is applied, Hall currents are induced via the spin–orbit interaction39,40:
is parallel to the minority spin direction in the paramagnet. When a longitudinal electric field (E) is applied, Hall currents are induced via the spin–orbit interaction39,40:  , where
, where  is the spin Hall conductivity for up (down) spin electrons and σ is the electron spin polarization vector. For small μs,
is the spin Hall conductivity for up (down) spin electrons and σ is the electron spin polarization vector. For small μs,  can be expanded as
can be expanded as  , in which σSHE is the ground-state spin Hall conductivity and the derivative is taken at the Fermi energy. The total Hall current reads:
, in which σSHE is the ground-state spin Hall conductivity and the derivative is taken at the Fermi energy. The total Hall current reads:

According to equation (2), the nAHE current in the linear response of μs is proportional to the energy derivative of the spin Hall conductivity (∂σSHE/∂ɛ), while the spin Hall and anomalous Hall effects scale with σSHE and σAHE, respectively41,42,43.
∂σSHE/∂ɛ can be decomposed as

where the spin Hall angle θSHE=σSHE/σ and σ is the longitudinal conductivity of a normal metal film. The second-term proportional to ∂θSHE/∂ɛ in equation (3) represents the Hall current generated by the difference between the spin Hall angles of the up- and down-spin electrons. The first term is estimated to account for only one per cent of the observed nAHE voltage (see Supplementary Fig. 3, and Supplementary Notes 2 and 3), which suggests that the ∂θSHE/∂ɛ term dominates the signal. A significant energy dependence of θSHE has recently been predicted and observed in some metals44,45,46,47,48.
In summary, we show that Au is magnetized by applying a temperature gradient or a microwave on YIG/Au bilayers. Our work also highlights the electron transport property modified by spin injection and thus offers a versatile approach for the generation and detection of non-equilibrium magnetizations in normal metals.
Methods
Sample fabrication
The single-crystaline yttrium iron garnet (YIG) films used in the present work were prepared by a liquid phase epitaxy on a gallium gadolinium garnet substrate. All samples were cut from a single 4.5-μm-thick liquid phase epitaxy YIG film. To achieve good-YIG/metal interfaces, the YIG films underwent an acid pickling process before being transferred into high vacuum where they were annealed in situ for 3 h at 500 °C. Then, the normal metal layers were sputtered at room temperature. The thickness of Au and Cu95Ir5 films was calibrated by X-ray reflectometry using control samples. The crystallographic properties of the YIG/Cu95Ir5 device were characterized by transmission electron microscopy and X-ray diffractometry, to confirm that the YIG films were high quality single crystals with a lattice constant of 12.376 Å.
Measurement setup
In the temperature-gradient-induced magnetization measurements, we used a microwave-induced heating method in off-resonance conditions. The Au/YIG sample was placed on a coplanar waveguide, and an a.c. temperature gradient was induced by applying a pulsed 20 GHz microwave with the modulation frequency 31.28 Hz. The applied magnetic-field well resided in the off-resonance range of the YIG layer. Therefore, the microwave causes no FMR, but induces heating of the Au layer via electromagnetic induction. The a.c. temperature gradient near the Au/YIG interface was confirmed by an a.c. spin Seebeck measurement and calibrated by the spin Seebeck voltages measured with a d.c. temperature gradient. Under an a.c. temperature gradient, an applied d.c. current generates a d.c. ordinary Hall signal and an a.c. nAHE signal, in which only the a.c. nAHE signal can be captured by a lock-in amplifier. For the Hall measurement, a standard five-probe method was used, in which a potentiometer is adopted to compensate the longitudinal voltage drop mixed in the Hall signal, and the out-of-plane alignment of magnetic field is confirmed in the absence of the spin Seebeck effect at saturated magnetization.
Data availability
All relevant data are available on request, which should be addressed to D.H.
Additional information
How to cite this article: Hou, D. et al. Observation of temperature-gradient-induced magnetization. Nat. Commun. 7:12265 doi: 10.1038/ncomms12265 (2016).
References
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Takahashi, S. & Maekawa, S. Spin current, spin accumulation and spin Hall effect. Sci. Technol. Adv. Mater. 9, 014105 (2008).
Zutic, I. & Dery, H. Spintronics: taming spin currents. Nat. Mater. 10, 647–648 (2011).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Valenzuela, S. O. & Tinkham, M. Direct electronic measurement of the spin Hall effect. Nature 442, 176–179 (2006).
Kimura, T., Otani, Y., Sato, T., Takahashi, S. & Maekawa, S. Room-temperature reversible spin Hall effect. Phys. Rev. Lett. 98, 156601 (2007).
Wunderlich, J. et al. Spin-injection Hall effect in a planar photovoltaic cell. Nat. Phys. 5, 675–681 (2009).
Kikkawa, T. et al. Longitudinal spin Seebeck effect free from the proximity Nernst effect. Phys. Rev. Lett. 110, 067207 (2013).
Qiu, Z. et al. All-oxide system for spin pumping. Appl. Phys. Lett. 100, 022402 (2012).
Hou, D. et al. Interface induced inverse spin Hall effect in bismuth/permalloy bilayer. Appl. Phys. Lett. 101, 042403 (2012).
Iguchi, R. et al. Spin pumping by nonreciprocal spin waves under local excitation. Appl. Phys. Lett. 102, 3 (2013).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004).
Kukreja, R. et al. X-ray detection of transient magnetic moments induced by a spin current in Cu. Phys. Rev. Lett. 115, 096601 (2015).
Li, J. et al. Direct detection of pure spin-current by x-ray pump-probe measurements. Preprint at http://arxiv.org/abs/1505.03959 (2015).
Uchida, K. et al. Observation of longitudinal spin-Seebeck effect in magnetic insulators. Appl. Phys. Lett. 97, 172505 (2010).
Uchida, K., Qiu, Z., Kikkawa, T. & Saitoh, E. Pure detection of the acoustic spin pumping in Pt/YIG/PZT structures. Solid State Commun. 198, 26–29 (2014).
Kikkawa, T. et al. Critical suppression of spin Seebeck effect by magnetic fields. Phys. Rev. B 92, 064413 (2015).
Geprägs, S. et al. Origin of the spin Seebeck effect in compensated ferrimagnets. Nat. Commun. 7, 10452 (2016).
Qu, D., Huang, S. Y., Hu, J., Wu, R. & Chien, C. L. Intrinsic spin Seebeck effect in Au/YIG. Phys. Rev. Lett. 110, 067206 (2013).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced Gilbert damping in thin ferromagnetic films. Phys. Rev. Lett. 88, 117601 (2002).
Uchida, K. et al. Spin Seebeck insulator. Nat. Mater. 9, 894–897 (2010).
Ando, K. et al. Inverse spin-Hall effect induced by spin pumping in metallic system. J. Appl. Phys. 109, 103913 (2011).
Mizukami, S., Ando, Y. & Miyazaki, T. Effect of spin diffusion on Gilbert damping for a very thin permalloy layer in Cu/permalloy/Cu/Pt films. Phys. Rev. B 66, 104413 (2002).
Hall, E. H. On the new action of magnetism on a permanent electric current. Phil. Mag. 10, 301 (1880).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Yao, Y. et al. First principles calculation of anomalous Hall conductivity in ferromagnetic bcc Fe. Phys. Rev. Lett. 92, 037204 (2004).
Hou, D. et al. Multivariable scaling for the anomalous Hall effect. Phys. Rev. Lett. 114, 217203 (2015).
Agrawal, M. et al. Microwave-induced spin currents in ferromagnetic-insulator|normal-metal bilayer system. Appl. Phys. Lett. 105, 092404 (2014).
Nakayama, H. et al. Spin Hall magnetoresistance induced by a nonequilibrium proximity effect. Phys. Rev. Lett. 110, 206601 (2013).
Huang, S. Y. et al. Transport magnetic proximity effects in platinum. Phys. Rev. Lett. 109, 107204 (2012).
Wang, Z., Tang, C., Sachs, R., Barlas, Y. & Shi, J. Proximity-induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys. Rev. Lett. 114, 016603 (2015).
Bai, L. et al. Universal method for separating spin pumping from spin rectification voltage of ferromagnetic resonance. Phys. Rev. Lett. 111, 217602 (2013).
Gui, Y. S., Mecking, N., Zhou, X., Williams, G. & Hu, C.-M. Realization of a room-temperature spin dynamo: the spin rectification effect. Phys. Rev. Lett. 98, 107602 (2007).
Slachter, A., Bakker, F. L., Adam, J. P. & van Wees, B. J. Thermally driven spin injection from a ferromagnet into a non-magnetic metal. Nat. Phys. 6, 879–882 (2010).
Hu, S. & Kimura, T. Significant modulation of electrical spin accumulation by efficient thermal spin injection. Phys. Rev. B 90, 134412 (2014).
Jin, Z. et al. Accessing the fundamentals of magnetotransport in metals with terahertz probes. Nat. Phys. 11, 761–766 (2015).
Schellekens, A. J., Kuiper, K. C., de Wit, R. & Koopmans, B. Ultrafast spin-transfer torque driven by femtosecond pulsed-laser excitation. Nat. Commun. 5, 4333 (2014).
Dankert, A. & Dash, S. P. Thermal creation of electron spin polarization in n-type silicon. Appl. Phys. Lett. 103, 242405 (2013).
Hirsch, J. E. Spin hall effect. Phys. Rev. Lett. 83, 1834–1837 (1999).
Niimi, Y. et al. Extrinsic spin hall effect induced by iridium impurities in copper. Phys. Rev. Lett. 106, 126601 (2011).
Miah, M. I. Observation of the anomalous Hall effect in GaAs. J. Phys. D 40, 1659–1663 (2007).
Wunderlich, J. et al. Spin-injection Hall effect in a planar photovoltaic cell. Nat. Phys. 5, 675–681 (2009).
Okamoto, N. et al. Electric control of the spin Hall effect by intervalley transitions. Nat. Mater. 13, 932–937 (2014).
Xu, Z., Gu, B., Mori, M., Ziman, T. & Maekawa, S. Sign change of the spin Hall effect due to electron correlation in nonmagnetic cuir alloys. Phys. Rev. Lett. 114, 017202 (2015).
Liu, L., Chen, C.-T. & Sun, J. Z. Spin Hall effect tunnelling spectroscopy. Nat. Phys. 10, 561–566 (2014).
Herschbach, C., Fedorov, D. V., Gradhand, M. & Mertig, I. Colossal spin Hall effect in ultrathin metallic films. Phys. Rev. B 90, 180406 (2014).
Gu, B. et al. Surface-assisted spin Hall effect in au films with pt impurities. Phys. Rev. Lett. 105, 216401 (2010).
Tauber, K., Fedorov, D. V., Gradhand, M. & Mertig, I. Spin Hall and spin Nernst effect in dilute ternary alloys. Phys. Rev. B 87, 161114 (2013).
Acknowledgements
We thank Zhuo Xu, Bo Gu, Qian Niu and Jana Lustikova for valuable discussions. This work was supported by ERATO ‘Spin Quantum Rectification’, PRESTO ‘Phase Interfaces for Highly Efficient Energy Utilization’, Grant-in-Aid for Scientific Research on Innovative Area, ‘Nano Spin Conversion Science’ (26103005 and 26103006), Grant-in-Aid for Scientific Research (S) (25220910), Grant-in-Aid for Scientific Research (A) (25247056 and 15H02012), Grant-in-Aid for Young Scientists (B) (26790038), Grant-in-Aid for Challenging Exploratory Research (26600067), Grant-in-Aid for Research Activity Start-up (25889003), the ImPACT program of the Council for Science, Technology and Innovation (Cabinet Office, Government of Japan) and World Premier International Research Center Initiative (WPI) all from MEXT, Japan, and NEC corporation.
Author information
Authors and Affiliations
Contributions
D.H. designed the experiment and analysed the data. E.S. supervised the study. Z.Q. and D.H. fabricated the samples and performed characterization of the sample. D.H. and E.K.V. carried out the electric measurement. G.E.W.B., D.H. and E.S. developed the explanation of the experiment. R.I. and K.S. formulated the spin accumulation in the Au film. K.U. helped the experiment. D.H., R.I., Z.Q., K.S. and E.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Notes 1-3 and Supplementary References (PDF 596 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hou, D., Qiu, Z., Iguchi, R. et al. Observation of temperature-gradient-induced magnetization. Nat Commun 7, 12265 (2016). https://doi.org/10.1038/ncomms12265
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12265
This article is cited by
-
Spin transport in antiferromagnetic insulators: progress and challenges
NPG Asia Materials (2019)
-
The valley Nernst effect in WSe2
Nature Communications (2019)
-
Magnon detection using a ferroic collinear multilayer spin valve
Nature Communications (2018)
-
Quantitative separation of the anisotropic magnetothermopower and planar Nernst effect by the rotation of an in-plane thermal gradient
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.