Abstract
The terminal Neoproterozoic Era (850–542 Ma) is characterized by the most pronounced positive sulfur isotope (34S/32S) excursions in Earth’s history, with strong variability and maximum values averaging δ34S∼+38‰. These excursions have been mostly interpreted in the framework of steady-state models, in which ocean sulfate concentrations do not fluctuate (that is, sulfate input equals sulfate output). Such models imply a large pyrite burial increase together with a dramatic fluctuation in the isotope composition of marine sulfate inputs, and/or a change in microbial sulfur metabolisms. Here, using multiple sulfur isotopes (33S/32S, 34S/32S and 36S/32S ratios) of carbonate-associated sulfate, we demonstrate that the steady-state assumption does not hold in the aftermath of the Marinoan Snowball Earth glaciation. The data attest instead to the most impressive event of oceanic sulfate drawdown in Earth’s history, driven by an increased pyrite burial, which may have contributed to the Neoproterozoic oxygenation of the oceans and atmosphere.
Similar content being viewed by others
Introduction
Sulfate represents one of the most important metabolic electron acceptors on the planet, and constraining its biogeochemical cycle is crucial for understanding the long-term redox evolution of the oceans and atmosphere1,2,3,4. Classically, the sedimentary record of sulfur cycling is probed through the sulfur isotopic composition of sedimentary pyrite, δ34Spyr, and carbonate-associated sulfate (CAS), δ34SCAS (where δ34S=103 × (34S/32Ssample/34S/32SCanyon Diablo Troilite−1), both of which may record fluctuations in past marine sulfate isotope composition5. Variations in oceanic sulfate isotope composition (δ34SSO4) are usually interpreted under steady-state assumptions6,7,8,9,10, whereby the oceanic sulfate content (MSO4), here written for 32S, remains constant:

Fin being the input flux related to weathering and Fout the output flux related to pyrite and evaporite burial. Long-term variations in δ34SSO4 therefore depend on the fraction of sulfur buried as pyrite relative to evaporite (fpyr, ranging from 0 to 1) as well as on the isotopic composition of sulfate delivered to the ocean (δ34Sin), according to the conservative isotopic mass equation:

where Δ34SSO4-pyr=δ34SSO4−δ34Spyr is the difference between the average δ34SSO4 of evaporites and/or CAS and the average δ34Spyr of sedimentary pyrite at a given time. Considering a modern δ34Sin of +3‰, a Δ34SSO4-pyr of 40‰, and a modern seawater δ34SSO4 of +21‰, the resulting present-day fpyr is close to 0.45 (ref. 11).
In a steady-state framework (equation (2)) and assuming modern δ34Sin and Δ34SSO4-pyr values, the strong positive δ34SCAS recorded in Neoproterozoic6,7,9,10,12,13, sediments would only hold for fpyr values above unity which are therefore inconsistent. A concomitant increase of both fpyr and Δ34SSO4-pyr for such excursions is thus necessary. Similarly, assuming that Δ34SSO4-pyr is constant, the high δ34SCAS values (accompanied by high δ34Spyr) need to be accounted by a concomitant increase in both fpyr and δ34Sin. For example, the δ34SCAS positive Ara anomaly (∼545 Ma)10 in Oman requires anomalously high fpyr (0.9) and δ34Sin (15‰) values for which a geological driver remains to be identified. Others have instead observed an increase in δ34SCAS values not accompanied by a change in δ34Spyr values, resulting in a Δ34SSO4-pyr increase that may reflect the advent of sulfur disproportionation (SD) metabolism7,8. An alternative possibility is that the steady-state model itself does not hold for the Neoproterozoic. This hypothesis has already been envisaged13,14 but has never really been tested so far because it increases further the number of unconstrained parameters compared with the steady-state model (for example, δ34Sin, Δ34SSO4-pyr, Fin, Fout and MSO4).
Here we use multiple sulfur isotopes (33S/32S, 34S/32S and 36S/32S ratios) of CAS and pyrite to investigate dynamic models for the Neoproterozoic sulfate reservoir evolution in the aftermath of the Marinoan glaciation. The results show that the steady-state assumption does not hold in the aftermath of the Marinoan Snowball Earth glaciation and attest to an impressive event of oceanic sulfate drawdown.
Results
Stratigraphy and age constraints
The studied sedimentary sequence corresponds to the Mirassol d’Oeste and Guia formations (Araras group, Central Brazil) and starts with a typical cap dolostone (∼635 Ma, refs 15, 16, 17) directly overlying Marinoan glacial deposits. We focus primarily on CAS as its isotopic composition is generally considered to reflect a seawater signal5, provided that diagenesis and recrystallization are limited. Samples were selected based on previous petrographic and geochemical results17 to avoid as much as possible diagenetic overprints. Selected samples were then carefully washed to avoid contamination (Methods section). It has been shown that secondary pyrite oxidation to sulfate and atmospheric sulfur contamination may lead to lower δ34SCAS values18,19. The consistent isotopic pattern displayed by the generated data set (see below) suggests that contamination was not significant in our samples.
Three slightly overlapping sections were sampled in freshly exposed quarries (Terconi, Camil and Carmelo quarries) along a basinward profile, from the innershelf to the outershelf of the Araras carbonate platform17. The base of the composite section (Fig. 1) corresponds to the post-Marinoan glaciation diamictite-dolostone contact that is globally dated at 635.5 Ma (refs 20, 21). This is further constrained by Sr and C isotopes correlations and a Pb–Pb age of 627±32 Myr (see Supplementary Information of ref. 22). The age of the top of the section is constrained by the acritarch assemblage of the overlying Nobres Formation (Cavaspina acuminata, Chlorogloeaopsis sp., Obruchevella sp., Ericiasphaera sp., Appendisphaera barbata, Tanarium irregulare, Tanarium conoideum and Micrhystridium pisinnum23), which corresponds to the ECAP biozone of Grey (2005), ref. 24, that is, to an age interval of 570–580 Myr. This estimate is coherent with recently obtained detrital zircon and mica ages at 544±7 Myr on the overlying Diamantino Formation25. We can therefore reasonably estimate a maximum depositional time (from 635 to 575 Ma) of 60 Myr for Mirassol do Oeste and Guia formations (300 m of sediments). Outcrop-based facies analysis, complemented by petrographic description of representative samples, reveals a transgressive systems tract, with the deepest part of the platform corresponding to a ramp depositional environment17.
Sulfur isotopes
We extracted sulfate from 16 micritic carbonate samples. Most CAS analyses (12 out of 16) were performed on samples from the Carmelo quarry, which contains the thickest post-glacial sedimentary sequence (Fig. 1). At the base of the section (that is, in the direct aftermath of glaciation), δ34SCAS is +14‰ (lower than that of the modern ocean, ∼+21‰) and increases steadily up to ∼+38‰, locally reaching +50.6‰ (n=2, Fig. 1 and Supplementary Table 1). Our range of values is consistent with data reported for other Marinoan post-glaciation deposits in Namibia6 and North China26.
The isotope composition of pyrite was also analysed (n=35, from Terconi, Carmelo and Camil sections). Pyrite is absent from the first 50 metres of the composite section. Above the base, its content varies between 0.01% and 3.06%. Scanning electron microscopy investigations show that pyrite is present as a mixture of framboidal aggregates (that is, early diagenetic) and euhedral crystals17 (that is, later-diagenetic). δ34Spyr increases upsection from −9.9 to +26.2‰, with strong variations in the upper part of the section that are associated with lithological variations (Fig. 1). δ34Spyr and δ34SCAS are broadly correlated (R2=0.79), yielding a mean Δ34SCAS-pyr of 33.5±5.3‰ (1σ).
Multiple sulfur isotopes
For the multiple sulfur isotopes analyses, Δ33SCAS (where Δ33S=δ33S−103 × ((δ34S/1,000+1)0.515−1), see ref. 27)) increases from −0.01‰ at the base to +0.10‰ at the top of the section (both±0.01‰, 2σ; Fig. 1). A clear positive correlation is observed between Δ33SCAS and δ34SCAS with R2=0.82 (Fig. 2). Δ36SCAS (where Δ36S=δ36S−103 × ((δ34S/1,000+1)1.89−1) varies between +0.09 and −0.46‰ (±0.1‰, 2σ) and correlates negatively with both δ34SCAS and Δ33SCAS.
Δ33S versus δ34S diagrams, best-fit line for CAS is obtained using the following parameters for the model: 34αsulfide-sulfate=0.960, 33β=0.5125 and Fin/Fout=0.3. The blue line corresponds to the evolution of the isotopic composition of the residual sulfate during a distillation. The black and green lines correspond to the isotopic evolution of the instantaneous and cumulative pyrite, respectively.
Discussion
Deviations of Δ33SCAS and Δ36SCAS from zero together with correlations of δ34SCAS−Δ33SCAS (Fig. 2), δ34SCAS−Δ36SCAS and Δ36SCAS−Δ33SCAS are observed for the first time in Neoproterozoic sections and result from mass-conservation effects27. Our results can only be produced in a non-steady-state system where Fin≠Fout, the non-zero Δ33SCAS values being a consequence of the subtle interplay of sulfate input and removal from the ocean (Methods section). Sulfate input lowers the oceanic sulfate Δ33SCAS through mixing processes (Supplementary Fig. 1), whereas sulfate removal from the ocean by hydrothermal or biological activity, the latter including bacterial sulfate-reduction (BSR) coupled to pyrite burial, increases the Δ33SCAS of the residual oceanic sulfate (Supplementary Figs 2 and 3, ref. 27).
The analytical results and observed correlations can be quantitatively modelled by combining the dynamic equations of mass balance (equation (3)) and isotopic mass balance (for example, equation (4) for 34S and 32S), which govern seawater sulfate concentrations and its isotopic compositions:

and

where 34αsulfide-sulfate is the fractionation factor between sulfur buried as pyrite and sulfur buried as evaporite at the global scale, which is usually inferred from the average sedimentary Δ34SSO4-pyr of equation (2), (ref. 10). Similar equations can be written for 33S and 36S isotope ratios. Because sulfur isotope fractionation factors 33α and 36α can be related to 34α by the 33β and 36β exponents, respectively (for example, 33β=ln(33α)/ln(34α), ref. 27), these equations can all be written as a function of 34α. Here for 33S:

33β is typically close to 0.515 for abiotic processes and varies from 0.509 to 0.516 for microbial sulfate-reduction28,29. As illustrated by equations (4 and 5), the modelled Δ33S-δ34S trend of oceanic sulfate (blue line in Fig. 2) only depends on three parameters, namely Fin/Fout-ratio, 33β and 34αsulfide-sulfate values. Most importantly, as opposed to previous approaches, in this model, 34αsulfide-sulfate is a free parameter that we can explore to determine the best-fit scenario, that is, it is not deduced from the Δ34SSO4-pyr values. The model does not depend on strong temporal constraints; therefore no a priori assumption was made on the initial sulfate residence time. Equally, no attempt was made to fit the isotope trend in Fig. 1, which would require a well-constrained deposition rate. However, we emphasize that the observed increase in δ34SCAS-values (and also Δ33SCAS, and δ34Spyr) through time is consistent with our model.
To better address the origin of the 34S-enriched signatures of oceanic sulfate, we investigated the variations in multiple sulfur isotope compositions for various combinations of Fin/Fout, 33β and 34αsulfide-sulfate solving simultaneously equations (3, 4, 5). All parameters, namely 33β− and 36β− factors, Fin/Fout, 34αsulfide-sulfate and S-isotope compositions of inputs were considered constant with time. Initial oceanic sulfate-sulfur isotope values were chosen from the data at the base of the sequence, which correspond to the onset of the observed excursion with δ34Sinitial∼+12‰, Δ33Sinitial=−0.016‰ and Δ36Sinitial=−0.1‰ (Fig. 2). The initial values may in fact have been lower and, in this respect, our approach is conservative. Note that they are consistent with the few other available Neoproterozoic sulfate multi-isotopic values obtained on Amadeus Basin (Australia), MacKenzie Fold Belt (Canada) and Oman (refs 14, 30). We explored the space of solutions for different combinations of Fin/Fout-ratio, 33β−factor and 34αsulfide-sulfate by calculating the Fin/Fout-ratio that best fits the δ34S−Δ33S slope defined by our data for a given set of 34α and 33β values. For that, we used 51 values of 33β (from 0.511 to 0.516) and 231 values of 34α (expressed as 1,000ln(34α) from −17‰ to −60‰). A total of 11,781 combinations of 33β, 34α and Fin/Fout values compatible with the observed δ34S−Δ33S slope were produced (Fig. 3). We can restrict step by step the space of solution of our model using constraints available for δ34SCASfinal−δ34SCASinitial, which describes the range of δ34SCAS variation during the excursion, and 36β, which is the exponent linking 34α and 36α-values [36β=ln(36α)/ln(34α)]. Each step is described below and the successive restrictions of the space of solution are shown in the 1,000ln(34α) versus 33β-exponent diagram of Fig. 3a–c.
The results show the combinations of 33β, 34α and Fin/Fout that fit our data in 1,000ln(34α) versus 33β−exponents diagrams. (a) illustrates the δ34SCAS-range (that is, δ34SCASfinal−δ34SCASinitial) compatible with our data. The curve #2 delimitates the field below which the difference between δ34SCASfinal and δ34SCASinitial values (+38‰ and +12‰, respectively) is too low (that is, δ34SCASfinal−δ34SCASinitial<26‰) to account for the high δ34SCAS-values measured in our section. (b) illustrates the Fin/Fout-ratios that fit the observed δ34SCAS versus Δ33SCAS slope for each pair of 33β, 34α. The white curve #3 highlights the steady-state conditions, where Fin=Fout. (c) represents the combinations of 33β and 34α compatible with our data for different 36β values. The intercept between the modelled space of solution and results from BSR experiments allows restricting further the space of solution. The grey polygon represents the final solution space.
Valid combinations of 33β, 34α and Fin/Fout are restricted to the coloured, lower half-right of each panel of Fig. 3, which is delimited by curve #1. There are no viable solutions above curve #1 because the corresponding 33β and 34α-values would produce Δ33S too close to zero compared with our data (Fig. 2). The first constraint used here is the δ34SCASfinal−δ34SCASinitial parameter. Combinations of 33β, and 34α compatible with our data for different δ34SCASfinal−δ34SCASinitial values are shown in Fig. 3a. Curve #2 delimitates the field below which the difference between δ34SCASfinal and δ34SCASinitial values (+38‰ and +12‰, respectively) is too low (that is, δ34SCASfinal−δ34SCASinitial<26‰) to account for the high δ34SCAS-values measured in our section. Therefore, only results above curve #2 (that is, δ34SCASfinal−δ34SCASinitial>26‰) are valid. This further constrains the space of solution to between curves #1 and #2, with 33β-exponent <0.514 and 1,000ln(34α)<−30‰, as defined by the intercept between curves #1 and #2 (Fig. 3a).
Figure 3b represents the range of Fin/Fout-ratios compatible with our model. It illustrates the calculated Fin/Fout-ratios that fit the observed δ34SCAS versus Δ33SCAS slope for each pair of 33β and 34α. The white curve #3 highlights steady-state conditions, where Fin=Fout. This figure clearly shows that for the field defined by curves #1 and #2, Fin/Fout-ratios are always below unity (Fin<Fout), pointing to a decrease in oceanic sulfate concentration through time. This demonstrates that whatever the input parameters, the observed trends between δ34SCAS versus Δ33SCAS cannot be reproduced in a steady-state model (Supplementary Fig. 4). Taken together, Fig. 3a and Fig. 3b constrain the solution space to Fin<Fout and 33β<0.514 (between curves #1 and #2). Another interesting outcome of the model is that β33-values are distinct from those expected for sulfate-reduction to hydrogen sulfide under thermodynamic equilibrium (green curve in Fig. 3a), a result consistent with previous studies31,32,33.
The space of solution can be further restricted taking into account the fact that 36β must also fit the observed Δ33S versus Δ36S correlation (Fig. 4a). Figure 3c represents the combinations of 33β and 34α compatible with our data for different 36β-values. Our space of solutions (between curves #1 and #2) is compared with 34αsulfide-sulfate data and their respective 33β and 36β exponents estimated from batch culture experiments for the two main sulfur metabolisms, namely SD and BSR (refs 28, 29). Our space of solutions intersects only the field delimited by the BSR data set while SD data (red dots in Fig. 3c) plot outside. This allows us to assume that BSR is the main mechanism leading to sulfate drawdown and to further restrict our space of solutions to its intersection with the BSR cultures data set. It is worth noting, however, that available data from culture experiments are still limited and present significant variability. In Fig. 5, all available 34αsulfide-sulfate, 33β and 36β-values data for culture experiments28,29,34,35,36,37 are plotted together with our modelled values (full grey circle). Although available data most clearly relate to BSR, one cannot rule out that part of the signal may reflect a mixed signature between SD and BSR organisms (Fig. 5).
(a) The Δ36SCAS versus Δ33SCAS diagram and (b) the Δ33SCAS versus δ34SCAS diagram. Changes in Fin/Fout of ±5% (green line), in 1,000ln(34α) of ±7‰ (grey line) and in 33β of ±0.3‰ are tested. The blue line corresponds to the best-fit model and the dashed to the straight line passing through the data. This figure highlights the high sensitivity of the model to all considered parameters (that is, Fin/Fout, 34α and 33β). Based on duplicate and triplicate analyses, uncertainties of Δ33S and Δ36S values by the SF6 technique are estimated at 0.01‰ and 0.2‰ in 2σ, respectively.
(a) 33β versus 36β diagram. (b) 33β versus 1,000ln(34αsulfide-sulfate) diagram. Blue circles are data from BSR culture experiments, (refs 28, 29, 34, 35, 36, 37). Red squares are data from SD culture experiments, ref. 29. The grey circle represents the results from our model (with the associated error bars, corresponding to the intersect between the solution space-Fig. 3a,b, and the field defined by culture experiments-Fig. 3c).
The final space of solutions in Fig. 3 is represented by a grey polygon which corresponds to the following combination of values: 34αsulfide-sulfate∼0.960±0.005, 33β∼0.5125±0.0005 and Fin/Fout=0.30±0.25. The high sensitivity of the model allow to have precise values for the best-fit scenario, indeed slight modifications of each modelled parameter (34αsulfide-sulfate, 33β and Fin/Fout) shows significant effects on the δ34SCAS versus Δ33SCAS slope (Fig. 4b).
This multi-isotopic approach allows us, using the best-fit values deduced above for 33β, 34α and Fin/Fout in equations (4 and 5), to quantify the contraction of the sulfate reservoir responsible for the observed increase in both δ34SCAS and Δ33SCAS (blue line in Fig. 2). For the strong increase in δ34S-value from +12‰ at the base of the section to +38‰ at the top, the model indicates that water column sulfate concentrations decreased dramatically by nearly 50%. In other words, at the end of deposition of the Guia Formation, sulfate concentration would be only half its initial value (Fig. 1). A single extreme δ34SCAS value of +50‰ is observed in a typical event bed at the top of the section17, characterized by hummocky cross stratification. Given its sedimentary characteristics, it is unclear whether this single extreme value should be considered; if representative, it would indicate a 60% decrease compared with the sulfate concentration observed at the base of the Araras composite section. The high δ34S values reported in post-Marinoan glacial deposits from Namibia7 and North China26 can also be accounted for by a drawdown of oceanic sulfate in a dynamic non steady-state sulfur cycle, without invoking the extreme modifications in both fpyr and δ34Sin needed in a steady-state model approach.
The model also provides fundamental constraints on the lower limit of marine sulfate concentration during the Neoproterozoic. For sulfate concentrations below 1 mM, the sulfur isotope fractionation associated with BSR decreases, reaching 0‰ below 200 μM (ref. 38) or lower39. The results showing 34α sulfide-sulfate close to 0.960 (Δ34S=−40‰) without significant changes throughout the sequence, suggests that sulfate concentrations remained well above 200 μM even by the end of the sulfate reservoir drawdown. The fractionation factor would otherwise have decreased significantly38. This constrains the lower limit of marine sulfate concentration in the immediate aftermath of the glaciation to well above 400 μM. These estimates are consistent with the work of Kah et al.13, who constrained the upper limits of Neoproterozoic marine sulfate concentrations to between 7 and 10 mM using a completely independent approach.
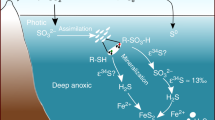
The post-glacial marine environment recorded in the Snowball aftermath deposits is thought to be characterized by an enhanced delivery of phosphate40 and bioavailable iron41. The resulting planktonic bloom suggested by Elie et al.42 accompanying the Snowball deglaciation may have increased the organic matter flux to the sediment exhausting its dissolved O2 content and enhancing anaerobic respiration of organic matter. We thus suggest here that post-glacial conditions were adequate for anaerobic sulfate-reduction metabolism triggering significant sulfate removal from the water column. If widespread, such a sulfate drawdown by BSR and pyrite burial would have important consequences for other biogeochemical cycles including the global oxygen budget during the end of the Neoproterozoic Era2,43. Pyrite burial plays a key role in the long-term sources of atmospheric O2 and its transient increase may have contributed to the accumulation of O2 in the oceans and atmosphere44,45. While burial of organic matter is generally considered to be the most important driver of O2 production on geological timescales (present-day value 10 × 1012 mol O2 per year), refs 44, 45, today pyrite burial contribution to this long-term redox balance is of the same order of magnitude44,45.
We therefore estimated a minimum range of O2 fluxes produced by the post-glacial intense BSR activity and pyrite burial implied by our model. Because the flux of sulfate delivery to the ocean (Fin) is unknown for this period, we only calculate the net O2 flux due to a 50% decrease of the ocean sulfate concentration without continuous sulfate inputs to the ocean. In that sense the fluxes in the following calculation has to be taken as minimum values. From a global perspective and assuming the modern ocean volume46, the combined results of our study and others13,46,47,48 constrain the total marine sulfate reservoir of the late Neoproterozoic to between 5 × 1017 mol and 13 × 1018 mol (SO42− concentrations of 0.4–10 mM, respectively). Considering the stoichiometry of BSR coupled to pyrite precipitation, where reduction of 1 mol SO42− and burial as pyrite equates the release of 2 mol O2, ref. 49, a 50% decrease in the late Neoproterozoic sulfate reservoir by BSR coupled to pyrite burial is equivalent to the net total production of 0.5–13 × 1018 mol of O2.
To express this number as a flux of O2, one needs tight temporal constraints that are lacking for the Araras Group (see above). Figure 6 presents the flux of O2 produced from pyrite buried per year as a function of the duration of the δ34SCAS increase episode. Using the conservative deposition time of 60 Myr, the decrease in sulfate concentration observed would lead to an O2 production comprised between 0.1 and 1.2 × 1012 mol per year (Fig. 6). These values correspond respectively to 0.1 and 3.2% of the modern production of O2 attributed to pyrite burial per year (Fig. 6)49,50. If the increase in δ34S-values has occurred over a shorter interval of time, which is supported by the fact that the observed increase in δ34S-values occurs within the first 175 m of the section, the O2 flux is then higher. For a depositional time period of 10 Myr, the O2 production flux would rise to between 1.5 and 20% of the present O2 production by BSR activity (Fig. 6). We conclude, therefore, that in the aftermath of the Marinoan glaciation enhanced BSR and pyrite burial represents a viable mechanism contributing to the Neoproterozoic oxygenation event of the ocean-atmosphere system.
O2 fluxes produced by a 50% distillation of the oceanic sulfate reservoir by sulfate-reduction and pyrite burial as a function of the duration of the sulfur isotopic excursion. For the bottom curve the starting concentration of sulfate was of 0.4 mM, for the top one it was of 10 mM. The y axis to the right corresponds to the proportion of O2 produced compared with the present production of O2 attributed to pyrite burial per year (PPO/yr), estimated at 7 Tmol per year by Holland et al.44
Methods
Sample preparation
Five to 100 g of carbonate samples (with carbonate contents typical >70 wt% of the total rock) were powdered, leached of soluble sulfates in a 5% NaCl solution, followed by four rinses in deionized (DI) water. This step was repeated three times, then the powder was dissolved in 4 N HCl (12 h). The acidified samples were filtered, on a 0.45-μm nitrocellulose paper and an excess of 250 g l−1 of BaCl2 was added to the filtrate to precipitate BaSO4.
Multiple sulfur analyses
The samples were prepared and analysed for their multiple sulfur isotope compositions at the Stable Isotope Laboratory of the Institut de Physique du Globe de Paris.The barium sulfate was subsequently reacted with Thode reagent51 in a helium atmosphere extraction line. The released H2S was converted to silver sulfide (Ag2S) by reaction with a silver nitrate solution and silver sulfide was fluorinated to produce SF6. The δ34S values are presented in the standard delta notation against V-CDT with an analytical reproducibility of≤0.1‰. We report these values against an assumed Δ33S and Δ36S for Vienna Cañon Diablo troilite (V-CDT) that yields δ34S, Δ33S and Δ36S values for IAEA S-2 (n=23) of 5.224‰, 0.030 and −0.203‰, respectively. Based on duplicate and triplicate analyses, uncertainties of Δ33S and Δ36S values by the SF6 technique are estimated at 0.01 and 0.2‰ in 2σ, respectively.
Model and concepts associated with non-zero Δ33S and Δ36S
The plot of 33S/32S and 34S/32S fractionations displays a slight curvature expressed by:

The β-exponent is not arbitrary and can be deduced from the high-temperature approximation of the reduced partition function, from the mass (in atomic mass unit) of the considered isotopes, for example, ref. 52. Thus, for 33S/32S and 34S/32S fractionation 33β corresponds to:

Exception made of a few molecules showing little relevance in the present study27,53, and discussion in ref. 54, equilibrium isotope fractionation at any temperature show β-values close to the high-temperature approximation27,53. Using δ notation one can write:

A mixing between two isotopically different pools (A and B) will fall along a mixing line (equations (9); ref. 55) that deviates from the theoretical equilibrium curve:

where X denotes for the fraction of A. In other words, two sulfur reservoirs at isotope equilibrium will lie on the same fractionation line, with the same Δ33S. In contrast mixing will be expressed along a secondary fractionation line with negative Δ33S. The resulting Δ33S-anomaly is maximum for 50% mixing being approximately −0.05‰ for two pools differing by 40‰ in δ34S.
Given that the mixing of two pools leads to negative Δ33S, the formation of two sulfur pools at isotope equilibrium will move them along a secondary fractionation line above that of the starting composition. These effects can be enhanced by Rayleigh distillation (that is, open system fractionation) and can be demonstrated starting from the well-known equation56:

With δA the isotopic composition of the residual component of A and and δA(0) being the starting isotope composition, f is the residual sulfate concentration in our case, and α is the isotopic fractionation corresponding to the given system studied (bacterial sulfato-reduction in our study).
Data availability
All results that support the findings of this study are available in Supplementary Table 1.
Additional information
How to cite this article: Sansjofre, P. et al. Multiple sulfur isotope evidence for massive oceanic sulfate depletion in the aftermath of Snowball Earth. Nat. Commun. 7:12192 doi: 10.1038/ncomms12192 (2016).
References
Kump, L. R. & Garrels, R. M. Modeling atmospheric O2 in the global sedimentary redox cycle. Am. J. Sci. 286, 337–360 (1986).
Berner, R. A., Beerling, D. J., Dudley, R., Robinson, J. M. & Wildman, R. A. Jr Phanerozoic atmospheric oxygen. Annu. Rev. Earth Planet. Sci. 31, 105–134 (2003).
Garrels, R. M. & Lerman, A. Coupling of the sedimentary sulfur and carbon cycles; an improved model. Am. J. Sci. 284, 989–1007 (1984).
Holser, W. T., Maynard, J. B. & Cruikshank, K. M. Evolution of the Global Biogeochemical Sulphur Cycle 21–56Wiley (1989).
Kampschulte, A. & Strauss, H. The sulfur isotopic evolution of Phanerozoic seawater based on the analysis of structurally substituted sulfate in carbonates. Chem. Geol. 204, 255–286 (2004).
Hurtgen, M. T., Halverson, G. P., Arthur, M. A. & Hoffman, P. F. Sulfur cycling in the aftermath of a 635-Ma snowball glaciation: Evidence for a syn-glacial sulfidic deep ocean. Earth Planet. Sci. Lett. 245, 551–570 (2006).
Hurtgen, M. T., Arthur, M. A. & Halverson, G. P. Neoproterozoic sulfur isotopes, the evolution of microbial sulfur species, and the burial efficiency of sulfide as sedimentary pyrite. Geology 33, 41–44 (2005).
Canfield, D. E. & Teske, A. Late Proterozoic rise in atmospheric oxygen concentration inferred from phylogenetic and sulphur-isotope studies. Nature 382, 127–132 (1996).
Strauss, H., Banerjee, D. M. & Kumar, V. The sulphur isotopic composition of Neoproterozoic to early Cambrian seawater – evidence from the cyclic Hanseran evaporates, NW India. Chem. Geol. 175, 17–28 (2001).
Fike, D. A. & Grotzinger, J. P. A paired sulfate-pyrite d34S approach to understanding the evolution of the Ediacaran-Cambrian sulfur cycle. Geochim. Cosmochim. Acta 72, 2636–2648 (2008).
Strauss, H. Geological evolution from isotope proxy signals - sulfur. Chem. Geol. 161, 89–101 (1999).
Shields-Zhou, G. & Och, L. The case for a Neoproterozoic Oxygenation Event: geochemical evidence and biological consequences. Geol. Soc. Am. 21, 4–11 (2011).
Kah, L. C., Lyons, T. W. & Franck, T. D. Low marine sulphate and protracted oxygenation of the Proterozoic biosphere. Nature 431, 834–838 (2004).
Wu, N., Farquhar, J. & Strauss, H. δ34S and Δ33S records of Paleozoic seawater sulfate based on the analysis of carbonate associated sulphate. Earth Planet. Sci. Lett. 399, 44–51 (2014).
Romero, J. A. S., Lafon, J. M., Nogueira, A. C. R. & Soares, J. L. Sr isotope geochemistry and Pb-Pb geochronology of the Neoproterozoic cap carbonates, Tangara da Serra, Brazil. Intern. Geol. Rev. 1, 1–19 (2012).
Nogueira, A. C. R., Riccomini, C., Sial, A. N., Moura, C. A. V. & Fairchild, T. R. Soft-sediment deformation at the base of the Neoproterozoic Puga cap carbonate (southwestern Amazon craton, Brazil): Confirmation of rapid icehouse to greenhouse transition in snowball Earth. Geology 31, 613–616 (2003).
Sansjofre, P. et al. Paleoenvironmental reconstruction of the Ediacaran Araras platform (Western Brazil) from the sedimentary and trace metals record. Precambr. Res. 241, 185–202 (2014).
Gill, B. C., Lyons, T. W. & Frank, T. D. Behavior of carbonate-associated sulfate during meteoric diagenesis and implicationsfor the sulfur isotope paleoproxy. Geochim. Cosmochim. Acta 72, 4699–4711 (2008).
Peng, Y. et al. Widespread contamination of carbonate-associated sulfate by present-day secondary atmospheric sulfate: evidence from triple oxygen isotopes. Geology 42, 815–818 (2014).
Condon, D. et al. U-Pb ages from the neoproterozoic Doushantuo Formation, China. Science 308, 95–98 (2005).
Hoffmann, K. H., Condon, D. J., Bowring, S. A. & Crowley, J. L. U-Pb zircon date from the Neoproterozoic Ghaub Formation, Namibia: constraints on Marinoan glaciation. Geology 32, 817–820 (2004).
Sansjofre, P. et al. A carbon isotope challenge to the snowball Earth. Nature 478, 93–96 (2011).
Hidalgo, R. L. Vida após as glaciações globais neoproterozoicas: um estudo microfossilífero de capas carbonáticas dos Crátons do São Francisco e Amazônico PhD thesis 195Sao Paulo University (2007).
Grey, K. Ediacaran palynolog of Australia. Association of Australasian Palaeontologists. Geological Survey of Western Australia, Canberra, memoir 1 31, 439 (2005).
McGee, B., Collins, A. S., Trindade, R. I. & Payne, J. Age and provenance of the Cryogenian to Cambrian passive margin to foreland basin sequence of the northern Paraguay Belt, Brazil. Geol. Soc. Am. Bull. 127, 76–86 (2015).
Shen, B. et al. Stratification and mixing of a post-glacial Neoproterozoic ocean: evidence from carbon and sulfur isotopes in a cap dolostone from northwest China. Earth Planet. Sci. Lett. 265, 209–228 (2008).
Farquhar, J., Johnston, D. T. & Wing, B. A. Implications of conservation of mass effects on mass-dependent isotope fractionations: influence of network structure on sulfur isotope phase space of dissimilatory sulfate reduction. Geochim. Cosmochim. Acta 71, 5862–5875 (2007).
Johnston, D. T. Multiple sulfur isotopes and the evolution of Earth's surface sulfur cycle. Earth Sci. Rev. 106, 161–183 (2011).
Johnston, D. T. et al. Multiple sulfur isotope fractionations in biological systems: a case study with sulfate reducers and sulfur disproportionators. Am. J. Sci. 305, 645–660 (2005).
Johnston, D. T. et al. Active microbial sulfur disproportionation in the Mesoproterozoic. Science 310, 1477–1479 (2005).
Ono, S., Shanks, W. C., Rouxel, O. J. & Rumble, D. S-33 constraints on the seawater sulfate contribution in modern seafloor hydrothermal vent sulfides. Geochim. Cosmochim. Acta 71, 1170–1182 (2007).
Ono, S., Keller, N. S., Rouxel, O. & Alt, J. C. Sulfur-33 constraints on the origin of secondary pyrite in altered oceanic basement. Geochim. Cosmochim. Acta 87, 323–340 (2012).
Turchyn, A. V. & Schrag, D. Oxygen isotope constraints on the sulfur cycle over the past 10 million years. Science 303, 2004–2007 (2004).
Farquhar, J. et al. Multiple sulphur isotopic interpretations of biosynthetic pathways: implications for biological signatures in the sulphur isotope record. Geobiology 1, 27–36 (2003).
Johnston, David T., James, Farquhar & Canfield, Donald E. Sulfur isotope insights into microbial sulfate reduction: when microbes meet models. Geochim. Cosmochim. Acta 71, 3929–3947 (2007).
Leavitt, William D. et al. Influence of sulfate reduction rates on the Phanerozoic sulfur isotope record.. Proc. Natl Acad. Sci. USA 110, 11244–11249 (2013).
Sim, M. S. Physiology of multiple sulfur isotope fractionation during microbial sulfate reduction. Doctoral dissertation, Massachusetts Institute of Technology ((2012).
Habicht, K. S., Gade, M., Thamdrup, B., Berg, P. & Canfield, D. E. Calibration of sulfate levels in the Archean Ocean. Science 298, 2372–2374 (2002).
Crowe, S. A. et al. Sulfate was a trace constituent of Archean seawater. Science 346, 735–739 (2014).
Planavsky, N. J. et al. The evolution of the marine phosphate reservoir. Nature 467, 1088–1090 (2010).
Raiswell, R. Iron transport from the continents to the open ocean: the aging–rejuvenation cycle. Elements 7, 101–106 (2011).
Elie, M., Nogueira, A. C. R., Nédélec, A., Trindade, R. I. F. & Kenig, F. A red algal bloom in the aftermath of the Marinoan Snowball Earth. Terra Nova 19, 303–308 (2007).
Logan, G. A., Hayes, J. M., Hieshima, G. B. & Summons, R. E. Terminal Proterozoic reorganization of biogeochemical cycles. Nature 376, 53–56 (1995).
Holland, H. D. Volcanic gases, black smokers, and the Great Oxidation Event. Geochim. Cosmochim. Acta 66, 3811–3826 (2002).
Catling, D. C. Encyclopedia of Astrobiology 1200–1208Springer (2011).
Costello, M. J., Cheung, A. & De Hauwere, N. Surface area and the seabed area, volume, depth, slope, and topographic variation for the world’s seas, oceans, and countries. Environ. Sci. Technol. 44, 8821–8828 (2010).
Kurtz, A., Kump, L. R., Arthur, M. A., Zachos, J. C. & Paytan, A. Early Cenozoic decoupling of the global carbon and sulfur cycles. Paleoceanography 18, 1–14 (2003).
Hurtgen, M. T., Pruss, S. B. & Knoll, A. H. Evaluating the relationship between the carbon and sulfur cycles in the later Cambrian ocean: an example from the Port au Port Group, western Newfoundland, Canada. Earth Planet. Sci. Lett. 281, 288–297 (2009).
Berner, R. A. The Phanerozoic carbon cycle: CO2 and O2 158Oxford University Press (2004).
Lalonde, S. V. & Konhauser, K. O. Benthic perspective on Earth’s oldest evidence for oxygenic photosynthesis. Proc. Natl Acad. Sci. 112, 995–1000 (2015).
Thode, H. G., Monster, J. & Dunford, H. B. Sulphur isotope geochemistry. Geochim. Cosmochim. Acta 25, 159–174 (1961).
Young, E. D., Galy, A. & Nagahara, H. Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochim. Cosmochim. Acta 66, 1095–1104 (2002).
Otake, T., Lasaga, A. C. & Ohmoto, H. Ab initio calculations for equilibrium fractionations in multiple sulfur isotope systems. Chem. Geol. 249, 357–376 (2008).
Thomassot, E. et al. Metasomatic diamond growth: A multi-isotope study (13 C, 15N, 33S, 34S) of sulphide inclusions and their host diamonds from Jwaneng (Botswana). Earth Planet. Sci. Lett. 282, 79–90 (2009).
Miller, M. F. et al. Mass-independent fractionation of oxygen isotopes during thermal decomposition of carbonates. Proc. Natl Acad. Sci. USA 99, 10988–10993 (2002).
Mariotti, A. et al. Experimental determination of nitrogen kinetic isotope fractionation: some principles; illustration for the denitrification and nitrification processes. Plant Soil 62, 413–430 (1981).
Acknowledgements
We are extremely grateful to Stefan Lalonde for scientific discussion and English edition. We thank David Johnston and James Farquhar for their data compilation. Research was supported by a French MRT doctoral fellowship and a SETSI grant to P.S., two INSU (SYSTER) grants to M.A. R.I.F.T. and A.C.R.N. were supported by the INCT-Geociam programme, and by FAPESP and CNPq grants (grant 2005/53521-1, São Paulo Research Foundation (FAPESP)). This work was supported by a grant from Agence Nationale de la Recherche (ANR eLIFE2) by the Labex UnivEarths programme of Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02) and the Labex Mer (ANR-10-LABX-0019). This is Institut de Physique du Globe de Paris contribution number 3749.
Author information
Authors and Affiliations
Contributions
P.C., M.A., R.I.F. and P.S. conceived the work. P.S., A.C.R.N., R.I.F.T. and M.A. did the sampling. P.S. carried out sulfur isotopic analyses. P.C., P.S. and P.A. performed the sulfur isotope modelling. P.S., P.C., R.I.F.T. and M.A. wrote the paper and most of the Supplementary Information. All authors discussed the interpretation of the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Table 1 and Supplementary References. (PDF 497 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sansjofre, P., Cartigny, P., Trindade, R. et al. Multiple sulfur isotope evidence for massive oceanic sulfate depletion in the aftermath of Snowball Earth. Nat Commun 7, 12192 (2016). https://doi.org/10.1038/ncomms12192
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12192
This article is cited by
-
Bisnorgammacerane traces predatory pressure and the persistent rise of algal ecosystems after Snowball Earth
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.