Abstract
Finding alternative optoelectronic mechanisms that overcome the limitations of conventional semiconductor devices is paramount for detecting and harvesting low-energy photons. A highly promising approach is to drive a current from the thermal energy added to the free-electron bath as a result of light absorption. Successful implementation of this strategy requires a broadband absorber where carriers interact among themselves more strongly than with phonons, as well as energy-selective contacts to extract the excess electronic heat. Here we show that graphene-WSe2-graphene heterostructure devices offer this possibility through the photo-thermionic effect: the absorbed photon energy in graphene is efficiently transferred to the electron bath leading to a thermalized hot carrier distribution. Carriers with energy higher than the Schottky barrier between graphene and WSe2 can be emitted over the barrier, thus creating photocurrent. We experimentally demonstrate that the photo-thermionic effect enables detection of sub-bandgap photons, while being size-scalable, electrically tunable, broadband and ultrafast.
Similar content being viewed by others
Introduction
Since the discovery of the photoelectric effect in the late nineteenth century1, a great number of photodetectors that rely on the emission of photoexcited charge carriers have been proposed. These carriers—sometimes referred to as hot carriers, although they are not thermalized with the electron bath—are typically injected over a Schottky barrier between a metal and a semiconductor, allowing detection of photons with energy lower than the semiconductor bandgap (see Fig. 1a). This process, called internal photoemission, has led to the development of visible and near-infrared photodetectors2,3, which have recently been combined with plasmonic enhancement schemes4,5,6,7,8. However, the efficiency of this mechanism drops for photon energy lower than the Schottky barrier height ΦB (ref. 9) and is limited by the ability to extract the carriers before they lose their initial energy, which in metals typically occurs on a timescale of ∼100 fs (ref. 10).
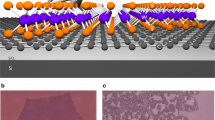
(a) Simplified band diagram illustrating the internal photoemission process taking place at a metal–semiconductor interface. Non-thermalized photoexcited carriers in metal with sufficient energy to overcome the Schottky barrier ΦB can be injected into the semiconductor before they lose their initial energy (within 100 fs for conventional metals10). The portion of the energy band filled by electrons and the bandgap of the semiconductor are shaded in blue and pale orange, respectively. Low (high) energy photon and the electronic transition following their absorption are represented by red (green) sinusoidal and vertical arrows. The out-of-equilibrium electron distributions n(E) resulting from these processes are illustrated on the left-hand side with the corresponding colours. Photoexcited electrons are depicted by blue dots and their possible transfer path is represented by blue dashed arrows. (b) Simplified band diagram of the PTI effect at a G/WSe2 interface. The ultrafast thermalization of photoexcited carriers in graphene gives rise to a hot-electron distribution n(E) with a lifetime longer than 1 ps. As the number of electrons in the hot tail (yellow shaded area) of n(E) increases, more electrons are emitted over the Schottky barrier ΦB, which generates a larger thermionic current (represented by the horizontal arrow). The colour gradient from blue to yellow illustrates the heat contained in the electron distribution. The offset between the graphene neutrality point and WSe2 conduction edge is denoted by Φ0 and was experimentally determined to be 0.54 eV (ref. 28). (c) Schematic representation of the heterostructure on a 285-nm-thick SiO2/Si substrate, to which a gate voltage (VG) is applied to modify the Fermi-level μ of the bottom graphene. An interlayer bias voltage (VB) between the top (GT) and bottom (GB) graphene flakes can be applied, and current or photocurrent flowing through GB is measured. (d) Optical image of a heterostructure composed of a 28-nm-thick WSe2 flake. The top and bottom hBN flakes are 10 and 70 nm thick, respectively. For clarity, graphene flakes are shaded in grey and outlined by a black dashed line, whereas WSe2 is coloured in orange and outlined by an orange line. Scale bar, 5 μm.
A promising way to overcome these limitations is to make use of the excess thermal energy contained in the electron bath. This energy arises from the thermalization of photoexcited carriers with other carriers, which results in a hot carrier distribution with a well-defined temperature Te. For increasing Te, a larger fraction of carriers can overcome the Schottky barrier, creating a current via thermionic emission (Fig. 1b). In this scheme, even photons with energies below ΦB can lead to an increase in Te and subsequently to carrier emission. However, in order to reach high Te, the hot carriers must be weakly coupled to the surrounding phonon bath11.
Graphene, which has recently emerged as an excellent platform for converting photons into hot carriers12, has the ideal properties to implement this scheme. Graphene presents strong electron–electron interactions leading to carrier thermalization within ∼50 fs (refs 13, 14), where a large fraction (>50%) of the initial energy of photoexcited carriers is transferred to the electronic system15. This efficient carrier heating creates a thermalized hot carrier state that is relatively long-lived (longer than 1 ps)16, owing to weak coupling to the lattice and the environment. These thermalized carriers can thus reach temperatures significantly higher than the phonon bath temperature (Te>Tph) even under continuous-wave (CW) excitation17 (see Supplementary Note 1 and Supplementary Fig. 1). Moreover, the tunability of the graphene Fermi energy gives control over the height of the Schottky barrier. For these reasons, graphene was recently proposed as a promising material for efficient and tunable thermionic emission of hot carriers18,19,20.
Here, we use graphene/WSe2/graphene van der Waals heterostructures to detect low-energy photons (with a wavelength up to 1.5 μm) through photo-thermionic (PTI) emission. Figure 1b shows in detail how the PTI photocurrent is generated: photons are absorbed by graphene, creating electron–hole pairs, which then rapidly equilibrate into a thermalized carrier distribution with an elevated electron temperature Te compared with the temperature of the lattice Tph and the environment T0; carriers within this distribution with an energy larger than the Schottky barrier height ΦB at the graphene/WSe2 interface can be injected into the WSe2 and travel to the other graphene layer. The number of carriers with sufficient energy scales with  , where kB is the Boltzmann constant.
, where kB is the Boltzmann constant.
Results
Device structure
In our device, WSe2—a transition metal dichalcogenide with a bandgap Eg∼1.3 eV—provides an energy barrier between the two graphene sheets with low interfacial defects and reduced Fermi-level pinning. The active device (depicted schematically in Fig. 1c) is encapsulated between layers of hexagonal boron nitride (hBN) which provides a clean, charge-free environment for the graphene and WSe2 flakes21. The device is equipped with an electrostatic bottom gate (VG) that enables control of the Fermi energy μ and thereby ΦB of (mainly) the bottom graphene. All measurements presented in the main text are obtained from one particular device comprising a 28-nm-thick WSe2 flake (see Fig. 1d) and are performed at room temperature with a quasi-CW laser source, unless otherwise mentioned (see Methods). We have studied devices with WSe2 flakes of various thicknesses (L=2.2–40 nm) and obtained similar results, consistent with the PTI effect (see Supplementary Note 2 and Supplementary Figs 2 and 3).
Photocurrent measurements
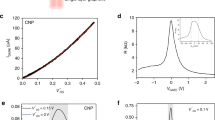
The PTI process is driven by the light-induced increase of the thermal energy of the electron gas (kBTe). Signatures of this mechanism are readily visible in the data presented in Fig. 2. First, the photocurrent spectrum of Fig. 2a shows a sizable, spectrally flat response for photon energies well below the bandgap of WSe2 (Ephoton<Eg). That is expected from a thermally driven photocurrent, given the uniform absorption of graphene in the visible, near-infrared range and the fact that kBTe is independent of Ephoton for constant power15,22. Furthermore, the photocurrent generated in this sub-bandgap regime exhibits a striking superlinear dependence on laser power P (Fig. 2b,c). This is a direct consequence of the thermal activation of carriers over the Schottky barrier, which, in first approximation, scales exponentially with P (see Methods). In contrast, the photocurrent in the above-bandgap regime (Ephoton>Eg) varies strongly with Ephoton and scales linearly with P. This photoresponse is characteristic of light absorption in WSe2 and transfer of photoexcited carriers to the graphene electrodes, a process driven by the potential drop across the WSe2 layer23,24,25.
(a) Photocurrent (PC) spectrum measured at room temperature in the G/WSe2/G region with laser power P=90 μW, VB=0.6 V and VG=0 V (same conditions for b,c). The insets illustrate the absorption process taking place in the different photoresponse regimes: absorption in WSe2 for Ephoton>Eg and absorption in graphene for Ephoton<Eg. The transition between these two regimes is represented by the background colour gradient, where red (blue) corresponds to the graphene (WSe2) absorption regimes. The vertical orange dashed line corresponds to the energy of the bulk WSe2 bandgap. (b) Power dependence of the photocurrent for various values of photon energy Ephoton. The dots represent experimental data and the solid lines are power law fits (PC∝Pα) obtained with a fit range P=70–120 μW. (c) Fitted power law index α versus photon energy, showing the transition from linear to superlinear power dependence. This transition occurs around Ephoton=Eg, the indirect bandgap of WSe2. The error bars correspond to the s.d. obtained from the linear fit. (d) Time-resolved photocurrent change ΔPC(Δt)=PC(Δt)−PC(Δt→∞), measured using the setup and technique described in ref. 24 with an average laser power of 260 μW (wavelength 800 nm), at low temperature (30 K) and bias (VB=0.04 V) in order to suppress the contribution of the photocurrent originating from WSe2 absorption. Experimental data are represented by orange dots and the solid black line is a decaying exponential fit with time constant τcool=1.3 ps. Inset: same data and fit in logarithmic scale.
Alternative photocurrent generation mechanisms are less likely to contribute to the observed sub-bandgap photocurrent. To verify this, we measured a device with a Au/WSe2 interface, where photocurrent is generated by internal photoemission of non-thermalized photoexcited carriers (see Supplementary Note 3 and Supplementary Fig. 4). This device shows a strong dependence on Ephoton along with a cutoff energy at Ephoton=ΦB, and a linear power dependence—clearly at odds with our observations for G/WSe2/G (where G stands for graphene) devices. We note that multi-photon absorption followed by charge transfer could also lead to a superlinear power dependence, but the laser intensity required to induce significant two-photon absorption in either graphene or WSe2 is at least 1–2 orders of magnitude higher than the one used in our experiment (smaller than 1 GWcm−2) (refs 26, 27). Similarly, the photo-thermoelectric and bolometric effects could generate sub-bandgap photocurrent, but both would have a sublinear—rather than the observed superlinear—power dependence16,28.
To further verify that the sub-bandgap photocurrent stems from the PTI effect, we perform time-resolved photocurrent measurements by varying the time delay Δt between two sub-picosecond laser pulses generated by a Ti:sapphire laser (see Supplementary Note 4 and Supplementary Fig. 5). From the dynamics of the positive correlation signal (due to the superlinear power dependence) in Fig. 2d, we extract a characteristic decay time τcool of 1.3 ps, which is on the order of the cooling time of hot carriers in graphene16,22. All together the observations presented in Fig. 2 suggest that the sub-bandgap, superlinear, picosecond photocurrent is governed by the PTI effect.
Electrical tuning of the PTI effect
In contrast to bulk metal–semiconductor systems, this graphene-based heterostructure offers the possibility to tune the Schottky barrier, and therefore the magnitude of the PTI photocurrent, using the interlayer bias voltage (VB) and gate voltage (VG). Applying these voltages is necessary in order to generate a finite photocurrent, as it breaks the symmetry of our device, which is composed of two G/WSe2 Schottky barriers with opposite polarity. As the infrared photocurrent maps (Ephoton=0.8 eV) in Fig. 3a,b indicate, the interlayer voltage VB essentially controls over which of the two Schottky barriers hot carriers are injected: for VB=−0.6 V (Fig. 3a), the photoactive region corresponds to the area where the top graphene overlaps with the WSe2 layer (GT/WSe2), whereas the interface with the bottom graphene (GB/WSe2) is photoactive for VB=+0.6 V (Fig. 3b). In Fig. 3c,d, we examine the photocurrent originating from regions containing a single G/WSe2 interface, thus allowing us to assess each Schottky barrier individually. To create a current, hot carriers need to be emitted over the G/WSe2 interface and subsequently transported along the WSe2 layer and collected by the other graphene electrode, as illustrated in the insets of Fig. 3c,d. When the interlayer bias VB makes this process energetically favourable, each Schottky barrier gives rise to a photocurrent with a specific sign. The photocurrent generated in the G/WSe2/G region (Fig. 3e) exhibits both signs as it stems from charge injection over both top and bottom Schottky barriers. From the photocurrent sign associated with each layer, we deduce that hot electrons, rather than holes, are predominantly emitted over both Schottky barriers. This is expected given the work functions of graphene and electron affinity of WSe2 (ref. 29).
(a,b) PC maps of the device shown in Fig. 1d measured with an interlayer bias voltage VB of (a) −0.6 V and (b) 0.6 V, and VG=0 V. The graphene flakes are outlined by black dotted lines and the WSe2 flake by solid orange lines, as in Fig. 1d. Scale bar, 3 μm. (c–e) PC versus VB and VG measured on single Schottky barriers formed by (c) top or (d) bottom graphene and WSe2, as well as (e) double G/WSe2/G interfaces. The coloured circle (green, red and blue) in the upper right corner of each measurement corresponds to the position of the focused laser beam which are indicated on the PC maps (a,b). The black dashed line in e indicates where PC is null. All measurements are scaled to the same colour bar. Insets of c,d: side view of the heterostructure illustrating the generation and transport of hot carriers from one graphene flake to the other. Insets of e: band diagrams depicting the PTI effect in G/WSe2/G for VB<0 (left) and VB>0 (right). (f) PC versus VG taken from (e) at VB=0.6 V. Inset: band diagrams of the GB/WSe2 Schottky barrier at low (bottom) and high (top) VG illustrating the increase of PTI emission resulting from the lowering of ΦB. All measurements are performed at room temperature, with Ephoton=0.8 eV and P=110 μW.
One of the hallmarks of thermionic emission is its exponential dependence on the Schottky barrier height. In our device, the gate voltage VG provides a crucial way of enhancing the photocurrent by controlling the height of the GB/WSe2 Schottky barrier via the tuning of the Fermi energy of GB. As Fig. 3f demonstrates, doping the bottom graphene layer with electrons by applying a positive gate voltage VG effectively lowers ΦB and results in a strong increase in photocurrent. At high VG (low ΦB), the device reaches a responsivity of up to 0.12 mAW−1 at wavelength λ=1,500 nm, which, for 0.5% light absorption in graphene30, translates into an internal quantum efficiency (IQE) of 2%. These figures of merit are similar to those obtained in devices using the in-plane photo-thermoelectric effect31 and can be further improved by adjusting the relevant physical parameters as discussed below.
Theoretical model of the PTI effect
The gate tunability of the PTI process and its distinct power dependence allow for a quantitative comparison of our measurements with a Schottky barrier model based on the Landauer transport formalism32 (see Methods). In this model, the photocurrent depends on the fraction of carriers with enough energy to overcome the barrier, governed by Te and ΦB, and on the carrier injection time τinj. The values for ΦB(VG) are extracted from temperature-dependent dark current measurements (Fig. 4a) and are consistent with a band offset Φ0 of 0.54 eV (ref. 29). For simplicity, we assume that heat in the electronic system dissipates through a single, rate-limiting cooling pathway characterized by a thermal conductance Γ, such that under steady-state conditions the increase in temperature is proportional to P/Γ (see Supplementary Note 1).
(a) Schottky barrier height ΦB versus VG extracted from the temperature-dependence of dark current measurements. Inset: Arrhenius plot of the dark current at different VG and VB=0.36 V. Experimental data are represented by blue dots and the solid black lines are linear fits. The error bars in the main panel correspond to the standard deviation obtained from these fits. (b) PC versus ΦB and laser power P, measured (left plot) and according to our PTI model (right plot). PC is measured at room temperature, with Ephoton=0.8 eV and VB=0.36 V. (c) PC versus ΦB for different values of P and (d) PC versus P for various values of ΦB taken from b. The data points correspond to the experiment and the solid black lines to the model. The upper horizontal axis shows the rise in electronic temperature ΔT=Te−T0 (extracted from the fit of the model to the experiment). Insets of c,d: same experimental data and theoretical curves in logarithmic scale.
Figure 4b compares the measured and fitted PC as a function of ΦB(VG) and laser power. This two-dimensional fit yields a carrier injection time τinj=47±10 ps and a thermal conductance Γ=0.5±0.3 MWm−2 K−1. This value of τinj is almost identical to the one found for ideal G/Si Schottky barriers32, while the one obtained for Γ matches the predicted thermal conductance of G/hBN interfaces due to electron coupling with SPP phonons33 and is also consistent with disorder-enhanced supercollisions with acoustic phonons16 (see Supplementary Note 1). The excellent agreement between model and experiment is clearly visible in Fig. 4c,d. We note that the same measurements were performed at other ambient temperatures (T0=230 and 330 K) and the analysis yields very similar results (see Supplementary Note 5 and Supplementary Fig. 6).
Discussion
The device modelling and extracted physical parameters provide important insights into how to improve the efficiency of the PTI process. They also explain why this mechanism dominates the photoresponse of graphene/semiconductor heterostructures, while being absent for metal/semiconductor devices. The reason is that the thermal conductance Γ of our graphene-based device is more than 2 orders of magnitude smaller than the thermal conductance due to electron–phonon coupling in thin (∼10 nm) metal films10 (see Supplementary Note 3). Hence, thermalized hot carriers in metals do not reach a sufficiently high temperature to generate significant PTI photocurrent. Strategies to substantially increase the device efficiency include further reduction of the thermal conductance in graphene-based devices, for example, by using a nonpolar encapsulating material33. Likewise, the efficiency of the process can be readily improved by lowering ΦB. Indeed, we find that the PTI efficiency increases by one order of magnitude (up to 20%) by extrapolating the IQE to higher Te (∼1,000 K) or lower ΦB (∼0.06 eV, see Supplementary Note 6 and Supplementary Fig. 7). Moreover, our model suggests that the efficiency can be greatly enhanced by reducing the carrier injection time τinj, which is related to the coupling energy between adjacent layers. The long τinj obtained from our fit appears to be one of the main factors limiting the observed IQE and is presumably due to momentum mismatch between electronic states in the two adjacent materials. The interlayer transfer of charge carriers and heat in van der Waals heterostructures is currently not well understood and further studies are needed in order to unveil the limits of the PTI efficiency.
We finally note that the PTI effect shows some similarities to photon-enhanced thermionic emission (PETE), with the important differences that for PETE the photoexcited carriers are in thermal equilibrium with the lattice of a hot semiconductor and are emitted over a vacuum energy barrier34,35. There are also important resemblances between the PTI mechanism and the concept of hot carrier solar cells, since both require decoupling of the electron and phonon baths and energy-selective contacts11,36. Both PETE devices and hot-solar cells have an interesting potential for power conversion, but harvesting low-energy photons is limited by the bandgap of the semiconducting absorber. Interestingly, in our PTI device, which has a very simple geometry and operates at room temperature, we also find a gate-dependent open-circuit voltage (of the photocurrent) of up to 0.17 V with a fill factor of 38%. This effect, observable in Fig. 3e, opens up a promising avenue for infrared energy harvesting using graphene as the active material37. Furthermore, the PTI mechanism should work over an extremely broad wavelength range, including the mid-infrared and far-infrared (terahertz) regions and can be used for ultrafast photodetection, given that the signal recovery time is on the order of picoseconds. Finally, these vertical thermionic devices have a scalable active area and can be easily integrated with conventional and flexible solid-state devices. These features make the photo-thermionic effect a highly promising mechanism for a plethora of optoelectronic applications38.
Methods
Device fabrication and optoelectronics measurements
The heterostructures are fabricated the same way as described in ref. 24. Photocurrent is generated by focusing a supercontinuum laser (NKT Photonics SuperK extreme, repetition rate f=40 MHz and pulse duration dt=100 ps) with a microscope objective (Olympus LCPlanN × 50) on the device. The photocurrent is measured using a preamplifier and a lock-in amplifier synchronized with a mechanical chopper at 117 Hz.
PTI emission model
In the reverse-bias regime, the Schottky barrier model based on the Landauer transport formalism32 (see Supplementary Note 7) predicts that the current density J thermionically emitted over a Schottky barrier of height ΦB at temperature T is

where e0 is the elementary charge, kB is the Boltzmann’s constant, ħ is the reduced Planck’s constant, vF is the graphene Fermi velocity, Φ0 is the band offset at the G/WSe2 interface (0.54 eV) and τinj is the charge injection time. In our experiment, the thermionic photocurrent (PC) we measure is produced by the increase of electronic temperature ΔT=Te−T0 upon illumination of the device with a quasi-CW laser at λ=1,500 nm. Hence, it follows that the photocurrent is  , where A is the area of the laser beam (laser spot size of 1.75 μm), D is the duty cycle (D=dt·f=0.04%) and T0 is the ambient temperature. Using these equations and assuming T0≫ΔT, one can show that
, where A is the area of the laser beam (laser spot size of 1.75 μm), D is the duty cycle (D=dt·f=0.04%) and T0 is the ambient temperature. Using these equations and assuming T0≫ΔT, one can show that  , which makes evident the superlinear behaviour of the photocurrent. Finally, we assume that the rise in electronic temperature created by each pulse is
, which makes evident the superlinear behaviour of the photocurrent. Finally, we assume that the rise in electronic temperature created by each pulse is  , where α is the light absorption in graphene (0.5%), ηheat is the fraction of absorbed energy that is transferred to the electron bath (∼70%) (ref. 15), P is the average power of the laser and Γ is the thermal conductance of the rate-limiting thermal dissipation step (see Supplementary Note 1).
, where α is the light absorption in graphene (0.5%), ηheat is the fraction of absorbed energy that is transferred to the electron bath (∼70%) (ref. 15), P is the average power of the laser and Γ is the thermal conductance of the rate-limiting thermal dissipation step (see Supplementary Note 1).
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Massicotte, M. et al. Photo-thermionic effect in vertical graphene heterostructures. Nat. Commun. 7:12174 doi: 10.1038/ncomms12174 (2016).
References
Hertz, H. Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung. Ann. Phys. Chem. 267, 983–1000 (1887).
Peters, D. W. An infrared detector utilizing internal photoemission. Proc. IEEE 55, 704–705 (1967).
Scales, C. & Berini, P. Thin-film Schottky barrier photodetector models. Quantum Electron. IEEE J. 46, 633–643 (2010).
Brongersma, M. L., Halas, N. J. & Nordlander, P. Plasmon-induced hot carrier science and technology. Nat. Nanotechnol. 10, 25–34 (2015).
Clavero, C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat. Photon. 8, 95–103 (2014).
Goykhman, I., Desiatov, B., Khurgin, J., Shappir, J. & Levy, U. Locally oxidized silicon surface-plasmon schottky detector for telecom regime. Nano Lett. 11, 2219–2224 (2011).
Knight, M. W., Sobhani, H., Nordlander, P. & Halas, N. J. Photodetection with active optical antennas. Science 332, 702–704 (2011).
Goykhman, I. et al. On-chip integrated, silicon–graphene plasmonic Schottky photodetector with high responsivity and avalanche photogain. Nano Lett. 16, 3005–3013 (2016).
Fowler, R. H. The analysis of photoelectric sensitivity curves for clean metals at various temperatures. Phys. Rev. 38, 45–56 (1931).
Qiu, T. Q. & Tien, C. L. Heat transfer mechanisms during short-pulse laser heating of metals. J. Heat Transfer 115, 835–841 (1993).
Ross, R. T. & Nozik, A. J. Efficiency of hot-carrier solar energy converters. J. Appl. Phys. 53, 3813–3818 (1982).
Voisin, C. & Plaçais, B. Hot carriers in graphene. J. Phys. Condens. Matter 27, 160301 (2015).
Breusing, M. et al. Ultrafast nonequilibrium carrier dynamics in a single graphene layer. Phys. Rev. B 83, 153410 (2011).
Brida, D. et al. Ultrafast collinear scattering and carrier multiplication in graphene. Nat. Commun. 4, 1987 (2013).
Tielrooij, K. J. et al. Photoexcitation cascade and multiple hot-carrier generation in graphene. Nat. Phys. 9, 248–252 (2013).
Graham, M. W., Shi, S.-F., Ralph, D. C., Park, J. & McEuen, P. L. Photocurrent measurements of supercollision cooling in graphene. Nat. Phys. 9, 103–108 (2012).
Gabor, N. M. et al. Hot carrier-assisted intrinsic photoresponse in graphene. Science 334, 648–652 (2011).
Liang, S.-J. & Ang, L. K. Electron thermionic emission from graphene and a thermionic energy converter. Phys. Rev. Appl. 3, 014002 (2015).
Rodriguez-Nieva, J. F., Dresselhaus, M. S. & Levitov, L. S. Thermionic emission and negative dI/dV in photoactive graphene heterostructures. Nano Lett. 15, 1451–1456 (2015).
Rodriguez-Nieva, J. F., Dresselhaus, M. S. & Song, J. C. W. Hot-carrier convection in graphene Schottky junctions, Preprint at http://arxiv.org/abs/1504.0721 (2015).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Tielrooij, K. J. et al. Generation of photovoltage in graphene on a femtosecond timescale through efficient carrier heating. Nat. Nanotechnol. 10, 437–443 (2015).
Britnell, L. et al. Strong light-matter interactions in heterostructures of atomically thin films. Science 340, 1311–1314 (2013).
Yu, W. J. et al. Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nat. Nanotechnol. 8, 952–958 (2013).
Massicotte, M. et al. Picosecond photoresponse in van der Waals heterostructures. Nat. Nanotechnol. 11, 42–46 (2015).
Chen, W., Wang, Y. & Ji, W. Two-photon absorption in graphene enhanced by the excitonic fano resonance. J. Phys. Chem. C 119, 16954–16961 (2015).
Zhang, S. et al. Direct observation of degenerate two-photon absorption and its saturation in WS2 and MoS2 monolayer and few-layer films. ACS Nano 9, 7142–7150 (2015).
Yan, J. et al. Dual-gated bilayer graphene hot-electron bolometer. Nat. Nanotechnol. 7, 472–478 (2012).
Kim, K. et al. Band alignment in WSe2–graphene heterostructures. ACS Nano 9, 4527–4532 (2015).
Stauber, T., Peres, N. M. R. & Geim, A. K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 78, 085432 (2008).
Freitag, M., Low, T. & Avouris, P. Increased responsivity of suspended graphene photodetectors. Nano Lett. 13, 1644–1648 (2013).
Sinha, D. & Lee, J. U. Ideal graphene/silicon schottky junction diodes. Nano Lett. 14, 4660–4664 (2014).
Low, T., Perebeinos, V., Kim, R., Freitag, M. & Avouris, P. Cooling of photoexcited carriers in graphene by internal and substrate phonons. Phys. Rev. B 86, 045413 (2012).
Schwede, J. W. et al. Photon-enhanced thermionic emission for solar concentrator systems. Nat. Mater. 9, 762–767 (2010).
Schwede, J. W. et al. Photon-enhanced thermionic emission from heterostructures with low interface recombination. Nat. Commun. 4, 1576 (2013).
Würfel, P. Solar energy conversion with hot electrons from impact ionisation. Sol. Energy Mater. Sol. Cells 46, 43–52 (1997).
Nelson, C. a., Monahan, N. R. & Zhu, X.-Y. Exceeding the Shockley–Queisser limit in solar energy conversion. Energy Environ. Sci. 6, 3508 (2013).
Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Acknowledgements
We are grateful to Qiong Ma, Pablo Jarillo-Herrero, Mark Lundeberg and Ilya Goykhman for valuable discussions. M.M. thanks the Natural Sciences and Engineering Research Council of Canada (PGSD3-426325-2012). P.S. acknowledges financial support by a scholarship from the ‘la Caixa’ Banking Foundation. F.V. acknowledges the financial support from Marie-Curie International Fellowship COFUND and ICFOnest program. K.J.T. acknowledges the financial support from Mineco (FIS2014-59639-JIN). F.H.L.K. acknowledges support by Fundacio Cellex Barcelona, the ERC Career integration grant (294056, GRANOP), the ERC starting grant (307806, CarbonLight), the Mineco grants RYC-2012-12281 and FIS2013-47161-P and support by the EC under the Graphene Flagship (contract no. CNECT-ICT-604391).
Author information
Authors and Affiliations
Contributions
M.M. and F.H.L.K. conceived and designed the experiments. M.M., P.S. and F.V. fabricated the samples, carried out the experiments and M.M. performed the data analysis. K.W. and T.T provided boron nitride crystals. M.M., F.V., K.J.T., P.S. and F.H.L.K discussed the results and co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-7, Supplementary Notes 1-7 and Supplementary References (PDF 1626 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Massicotte, M., Schmidt, P., Vialla, F. et al. Photo-thermionic effect in vertical graphene heterostructures. Nat Commun 7, 12174 (2016). https://doi.org/10.1038/ncomms12174
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12174
This article is cited by
-
Solution-processed nitrogen-doped graphene quantum dots/perovskite composite heterojunction for boosting performance of anatase titanium dioxide (TiO2)-based UV photodetector
Advanced Composites and Hybrid Materials (2023)
-
Light trapping enhanced broadband photodetection and imaging based on MoSe2/pyramid Si vdW heterojunction
Nano Research (2023)
-
High-performance and stable hybrid photodetector based on a monolayer molybdenum disulfide (MoS2)/nitrogen doped graphene quantum dots (NH2 GQDs)/all-inorganic (CsPbBr3) perovskite nanocrystals triple junction
Advanced Composites and Hybrid Materials (2023)
-
Observation of ultrafast interfacial Meitner-Auger energy transfer in a Van der Waals heterostructure
Nature Communications (2023)
-
Graphene charge-injection photodetectors
Nature Electronics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.