Abstract
Weyl fermions that emerge at band crossings in momentum space caused by the spin–orbit interaction act as magnetic monopoles of the Berry curvature and contribute to a variety of novel transport phenomena such as anomalous Hall effect and magnetoresistance. However, their roles in other physical properties remain mostly unexplored. Here, we provide evidence by neutron Brillouin scattering that the spin dynamics of the metallic ferromagnet SrRuO3 in the very low energy range of milli-electron volts is closely relevant to Weyl fermions near Fermi energy. Although the observed spin wave dispersion is well described by the quadratic momentum dependence, the temperature dependence of the spin wave gap shows a nonmonotonous behaviour, which can be related to that of the anomalous Hall conductivity. This shows that the spin dynamics directly reflects the crucial role of Weyl fermions in the metallic ferromagnet.
Similar content being viewed by others
Introduction
The spin dynamics in magnets is an important subject studied for many decades. Early studies are based on the spin Hamiltonians where the electronic states are indirectly reflected in the magnetic parameters1. Recently, microscopic understanding starting from the electronic band structures has become a realistic target with the help of advanced first-principles calculations2,3,4.
In ferromagnets, repulsive Coulomb interaction between electrons results in an exchange splitting Jex between bands with up () and down () spins, which produces spontaneous magnetization, as shown in Fig. 1a. Therefore, the band crossings ɛn(k)=ɛm(k) (n m) between the different bands (nth and mth bands), where ɛn(k) and ɛm(k) are the momentum (k) dependence of the energy bands of the corresponding states, occur on two-dimensional surface in the three-dimensional momentum space. In the presence of spin–orbit interactions, λ1(k) and λ2(k), that mix different spin components and give the off-diagonal matrix elements, the band crossings turn into anti-crossings with the gap as indicated by the red curve in Fig. 1a. More explicitly, the effective Hamiltonian reads
(a) The energy (ɛ) dispersions of up () and down () spin bands with the exchange splitting Jex. ɛF is the Fermi energy. The band crossings ɛn(k)=ɛm(k) occur when the overlap of the up and down spin bands are finite. In the presence of the spin–orbit interaction, which mixes the up and down spins, the band crossings turn into the anti-crossings with the gap opening (red curve). (b) Band structure near the Weyl point k0. The band dispersions with fixed kz are shown in the kx–ky plane. The gap closes at the Weyl point k=k0. (c) Distribution of the emergent magnetic field b(k) near a Weyl point. The flux penetrating the area S is given by the solid angle subtended by S, and the total flux is 2πη. Therefore, Weyl fermion acts as a monopole or anti-monopole of the emergent magnetic field depending on the chirality η=±1.

with 2 × 2 Pauli matrices σ=(σ1,σ2,σ3), and the gap is given by  . This gap closes when the three coefficients of the Pauli matrices σ’s are zero in equation (1), which can be satisfied by tuning the three components of the momentum k at some k0 in three dimensions. Figure 1b shows this situation, where the energy dispersions at each fixed kz and the gap closes at k=k0. Expanding equation (1) with respect to k–k0, one obtains H=ηv(k–k0)·σ with the momentum k being appropriately redefined. Here v is the velocity and η=±1 determines the chirality. This is nothing but the Weyl fermion and k0 is called Weyl point, which is ubiquitous in magnets as long as the band overlaps of both spin components are finite.
. This gap closes when the three coefficients of the Pauli matrices σ’s are zero in equation (1), which can be satisfied by tuning the three components of the momentum k at some k0 in three dimensions. Figure 1b shows this situation, where the energy dispersions at each fixed kz and the gap closes at k=k0. Expanding equation (1) with respect to k–k0, one obtains H=ηv(k–k0)·σ with the momentum k being appropriately redefined. Here v is the velocity and η=±1 determines the chirality. This is nothing but the Weyl fermion and k0 is called Weyl point, which is ubiquitous in magnets as long as the band overlaps of both spin components are finite.
It has been pointed out that the band crossing of the form in equation (1) is of crucial importance for the Berry curvature; it acts as a source or sink (monopole) of the emergent magnetic field b(k). More explicitly,  as shown in Fig. 1c, and the flux integral over the surface enclosing k0 is 2πη. This emergent magnetic field gives the anomalous velocity and Hall current in the presence of the external electric field, which is the origin of the intrinsic anomalous Hall effect in ferromagnets: that is, σxy can be written as the integral of the Berry phase curvature (the gauge field) over the occupied electronic states5,6,7,8. The anomalous Hall effect emerging in the ferromagnetic phase of SrRuO3 has been analysed from this viewpoint, where σxy shows nonmonotonous dependence on the magnetization. We note that this anomalous Hall effect can be well reproduced by a first-principles calculation. In the ferromagnetic phase of SrRuO3, also a tight-binding model reveals that a number of Weyl points are produced in the first Brillouin zone by the above-mentioned process9. Therefore, the origin of the Berry curvature resulting in the nonmonotonous σxy in SrRuO3 is Weyl fermions as magnetic monopoles6,7,8,9,10. The optical Hall conductivity σxy(ω) in the terahertz region also supports the presence of Weyl fermion within the range of 5 meV near the Fermi energy11.
as shown in Fig. 1c, and the flux integral over the surface enclosing k0 is 2πη. This emergent magnetic field gives the anomalous velocity and Hall current in the presence of the external electric field, which is the origin of the intrinsic anomalous Hall effect in ferromagnets: that is, σxy can be written as the integral of the Berry phase curvature (the gauge field) over the occupied electronic states5,6,7,8. The anomalous Hall effect emerging in the ferromagnetic phase of SrRuO3 has been analysed from this viewpoint, where σxy shows nonmonotonous dependence on the magnetization. We note that this anomalous Hall effect can be well reproduced by a first-principles calculation. In the ferromagnetic phase of SrRuO3, also a tight-binding model reveals that a number of Weyl points are produced in the first Brillouin zone by the above-mentioned process9. Therefore, the origin of the Berry curvature resulting in the nonmonotonous σxy in SrRuO3 is Weyl fermions as magnetic monopoles6,7,8,9,10. The optical Hall conductivity σxy(ω) in the terahertz region also supports the presence of Weyl fermion within the range of 5 meV near the Fermi energy11.
Recently, several materials have been theoretically proposed and experimentally studied, where Weyl fermions are located exactly at the Fermi energy and govern the transport phenomena, that is, Weyl semimetals12,13,14,15,16,17,18. For example, the large magnetoresistance is discussed from the viewpoint of chiral anomaly. We note that the previous studies are, however, restricted mostly to the transport properties, and the influence of Weyl fermions on other phenomena are unexplored.
In this paper, we report the fingerprint of Weyl fermions and magnetic monopoles in the spin dynamics of SrRuO3. It has been recognized that SrRuO3 is a rare example of 4d band ferromagnetic metal with a pseudo-cubic perovskite crystal structure, and the ferromagnetism has been extensively studied19,20,21. Recently, a large spin wave gap was observed in SrRuO3 (ref. 22), whereas La0.8Sr0.2MnO3, a ferromagnet having a similar pseudo-cubic structure, showed no spin wave gap22. Although the large magnetic anisotropy in SrRuO3 is one of remarkable features, no anomaly in the temperature dependence of the magnetic anisotropy has been found in the static properties19,20,21,23. We show that Weyl fermions play a crucial role in the spin dynamics by measuring the temperature dependence of spin waves in SrRuO3.
Results
Spin waves observed by neutron Brillouin scattering (NBS)
We have measured small momentum magnetic excitations in a polycrystalline sample of SrRuO3 by NBS experiments, namely inelastic neutron scattering (INS) experiments near the forward direction. In case that a sizable single crystal is not available, NBS is the most appropriate magnetic INS method for studying the spin dynamics. The state-of-the-art instrument (High-Resolution Chopper Spectrometer, HRC) at intense pulsed neutron scattering facilities like J-PARC (Japan Proton Accelerator Research Complex) has provided an opportunity for the present study approaching the kinematical constraint of the neutron scattering by providing high-energy neutrons of sub eV region. Typical data of the observed INS spectra are shown in Fig. 2, and were analysed by using the scattering functions I(Q,E) expressed as follows:
Observed spectra are displayed as a function of E at several Q values (0.2, 0.25, 0.3 Å−1) for selected T (a: 4 K, b: 38 K, c: 86 K, d: 115 K, e: 147 K, f: 165 K). Spectra are shifted by a constant to aid the eye. The vertical bars represent statistical errors determined from the square root of neutron counts. The solid lines are fitted curves to the observed spectra, and the shaded areas are magnetic components.


where E and Q is the energy and momentum transfers of neutrons, respectively. Equation (2) presents the spectrum for the spin waves with energy ES at temperature T below the ferromagnetic transition temperature TC (=165 K), and equation (3) corresponds to the paramagnetic scattering with the energy width Γ at T=TC. The magnetic form factor of spin component can be approximated to be F(Q)=1 in the present small Q range. AS(Q) and AC(Q) represent the other Q dependence in the scattering intensity. The thermal population factor is given by n+1=[1–exp(−E/kBT)]−1 with the Boltzmann constant kB. Each scattering function is the form convoluted with the instrumental resolution, and contains the elastic scattering component B(Q,E). ΔE is the energy resolution and W is the energy width of spin waves determined from the instrumental resolution. ΔE and B(Q,E) are determined experimentally. The quantities, AS, AC, ES and Γ, are determined by the standard least square fitting procedure, as shown in Figs 2 and 3.
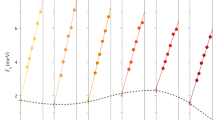
(a–f) Spin wave energy ES and (h) intensity AS(Q) are plotted in Q for selected T below TC=165 K. The lines in (a–f) are fitted to the quadratic dispersion relation, and the open circles at Q=0 Å−1 are the spin wave gap Eg obtained by the fit. (g) Energy width Γ and (i) intensity AC(Q) of the paramagnetic scattering at T=TC are plotted in Q. The lines in g and i are the fitted curves to the dynamical scaling law. The vertical bars represent statistical errors, some of them are smaller than the sizes of the marks.
The spin wave energies ES can be well fitted to the simple dispersion relation for ferromagnetic spin waves ES(Q)=Eg+DQ2, which is clearly extrapolated to the finite spin wave gap Eg∼2 meV, as shown in Fig. 3a–f. The peak intensities AS(Q) in Fig. 3h increase as Q gets reduced, which suggests that the magnetic excitations contain another component, that is, orbital moment, other than spin. The large Eg emerges due to the spin–orbit interaction as described below. We note that the increase in AS(Q) at low Q can be in accord with the spreading of the orbital component in real space. As shown in Fig. 4a, D decreases as T increases, that is a normal behaviour observed in both localized electron systems and itinerant electron systems24. On the other hand, Eg shows nonmonotonous thermal evolution. The finite value of Eg indicates an internal magnetic field acting on the system.
(a) Stiffness constant D, (b) anomalous Hall conductivity σxy/σ0 with σ0=9.9 × 102 Ω−1 cm−1, (c) spin wave gap Eg as a function of T/TC and (d) Eg as a function of M(T)/M0. The vertical bars in a and c represent the statistical errors of the measured values. The solid line in a is the measured curve of M(T)/M0. The experimental data of σxy(T) for the bulk sample and those for the film sample scaled to the bulk samples are plotted with an empirical curve (solid line) to express σxy(T) for both samples in b, where the vertical bars represent experimental errors. The solid lines in c and d are the fit to equation (4) with a=3.2 meV and b=−9.5, and the dashed lines in c and d are the calculated curves with a=3.2 meV and b=0, by using the empirical curve for σxy. It should be noted that D(T) and Eg(T) are proportional to magnetization M(T) in the strong correlation limit.
Discussion
The T dependence of Eg is nonmonotonous and clearly differs from that of the spontaneous magnetization M. A magneto-optical measurements showed the ferromagnetic resonance (FMR) frequency at 250 GHz almost independent of T at T<80 K (ref. 23); this also differs from M(T). Both Eg and the FMR frequency show the anomalous T dependence. The observed Eg=1.5–2.1 meV at low T including the error bars is of the comparable magnitude as Eg∼1 meV estimated by the FMR frequency of 250 GHz. The anisotropy energy of K∼12 T estimated by the bulk magnetization21 is comparable to these values. At zero temperature,  is given both in the strong and weak correlation cases; if we use the value
is given both in the strong and weak correlation cases; if we use the value  for a powder sample25, we obtain Eg∼1 meV. The dipole interaction can also contribute to the spin wave gap at the zone centre, which is directly observed by the FMR and Brillouin light scattering. Such gap is 0.03 meV for yttrium iron garnet film26, and we anticipate it to be smaller for SrRuO3 having smaller magnetic moment than the yttrium iron garnet film. It should be noted that, in the NBS using a polycrystalline sample, Eg is extrapolated from the dispersion observed at finite Q by mapping onto the simple spin Hamiltonian neglecting such a small dipole interaction.
for a powder sample25, we obtain Eg∼1 meV. The dipole interaction can also contribute to the spin wave gap at the zone centre, which is directly observed by the FMR and Brillouin light scattering. Such gap is 0.03 meV for yttrium iron garnet film26, and we anticipate it to be smaller for SrRuO3 having smaller magnetic moment than the yttrium iron garnet film. It should be noted that, in the NBS using a polycrystalline sample, Eg is extrapolated from the dispersion observed at finite Q by mapping onto the simple spin Hamiltonian neglecting such a small dipole interaction.
The nonmonotonous T dependence of the anomalous Hall conductivity σxy of SrRuO3 was discussed from the viewpoint of Weyl fermions, that is, magnetic monopoles in the momentum space6,8,10. Similarly, Weyl fermions are expected to produce the nonmonotonous T dependence of the spin dynamics as well. As discussed below, Eg is expected to be fitted by the following formula;

Here, σ0=e2/ha0=9.9 × 102 Ω−1 cm−1 (a0 being the lattice constant of SrRuO3) is used as a normalization factor for σxy. As shown in Fig. 4c,d, the nonmonotonous T dependence of Eg can be well reproduced by using the parameter of a=3.2 meV and b=−9.5. For M(T)/M0 and σxy(T)/σ0, we used the experimental results (see the Methods for details).
Now we sketch the theoretical background of equation (4) (see the Methods for details). The spin wave at the zero momentum is described by the action obtained by integrating over the electrons as (ref. 27)

where the first term with the coefficient α is the integrand represent of the Berry phase, whereas the second term is the spin anisotropy energy. Then spin wave gap Eg(T) is given by the ratio K/α. The main idea is that the Weyl fermions contribute resonantly to α as in the case of σxy because of the small energy denominator, although the former takes the finite value α0 even without the spin–orbit interaction, whereas the latter comes solely from the spin–orbit interaction (see the Methods for details). Assuming a single Weyl fermion near the Fermi energy, as suggested by the terahertz optical spectroscopy11, there is a one-to-one correspondence between the spin operators and current operators. Therefore, the contribution α1 to the coefficient α from the Weyl fermion is given by λσxy with λ being a constant. Since  (see the Methods for details), we obtain
(see the Methods for details), we obtain  , which is equivalent to equation (4). Here the temperature-independent anisotropy energy K is assumed, which is justified down to T∼40 K by the magnetization curve measurement28.
, which is equivalent to equation (4). Here the temperature-independent anisotropy energy K is assumed, which is justified down to T∼40 K by the magnetization curve measurement28.
To conclude, the nonmonotonous temperature dependence of the spin wave gap is unveiled by NBS in SrRuO3, which is related to its nonmonotonous anomalous Hall effect through the Weyl fermions near the Fermi energy. This result has revealed the connection between the transport and dynamical magnetic properties through the enhanced spin-orbit coupling effect. NBS employed here has the large potentiality. It can provide the detailed information of the generalized magnetic susceptibility in the small Q-region in addition to the energy of the magnetic excitations, which we focused in the present paper. NBS will thus provide a powerful method to solve unsettled issues in dynamical magnetism, including a role of orbital component in the magnetic fluctuation.
Methods
Materials
The sizable single crystals of SrRuO3 necessary for INS experiments have never been synthesized so that the spectroscopic studies must be performed using powder (polycrystalline) samples. We prepared polycrystals of SrRuO3 (73 g) by the well-established method of synthesis25, and the high quality of the sample was confirmed by our subsequent bulk measurements. The crystal structure with a single phase was confirmed by the X-ray diffraction. The magnetization measurement under the low magnetic field (H=10 Oe) is well fitted to m(T)=m0(1–(T/TC)a)b, as shown in the inset of Fig. 5a, and the ferromagnetic transition temperature was determined to be TC=165 K. This value of TC is the highest in the powder forms and comparable to that of the single-crystal forms.
(a) The ferromagnetic transition temperature TC (=165 K) is estimated from the temperature dependence of the low-field magnetization. (b) The temperature dependence of magnetic Bragg scattering at (100) is well fitted to IM(T)=IM0(1–T/TC)2β, and the critical exponent is determined to be β=0.25±0.01 by using TC=165 K.
The elastic neutron scattering from the magnetic Bragg reflection at (100) was observed on the HRC (see below) with Ei=12.5 meV. The observed intensity is the sum of the T-dependent magnetic component IM and the constant nuclear component IN, and thus, well fitted to I(T)=IM+IN=IM0(1–T/TC)2β+IN with the above-obtained value of TC=165 K by parameterizing β, IM0 and IN, as shown in Fig. 5b, where IM/IM0=(I(T)–IN)/IM0 is plotted. The obtained critical exponent β=0.25±0.01 agrees well with that from the early neutron diffraction experiment29. Therefore, we used the T dependence of the saturation magnetization, M(T)/M0=(1–T/TC)β with these values of TC and β for the analysis of D(T) and Eg(T). The stiffness constant D(T) at T=4–130 K was fitted with D0(1–T/TC)β and D0 was obtained to be 62 meV.
For the transport measurement, the powder sample of SrRuO3 obtained in the same batch as that for the INS experiments was sintered by high-pressure spark plasma sintering and patterned in Hall bar geometry using conventional photo-lithography and Ar ion dry-etching. The Hall resistivity ρH was measured together with the longitudinal and transverse resistivities, ρxx and ρyx, as a function of T under an applied magnetic field. The anomalous resistivity ρyx was determined after subtracting the ordinary Hall contribution from the measured ρH, and the transverse conductivity σxy was determined as ρyx/(ρxx2+ρyx2)≅ρyx/ρxx2, and plotted in Fig. 4b as the bulk sample. The error bars of σxy for the bulk sample are large at low temperatures because of very small values of resistance. On the other hand, the error bars of σxy for the film sample are relatively small because of high resistance and well-defined shape of the Hall bar10. We also plotted σxy for the film sample10, which was scaled to the bulk data by a factor of 0.61. The reduction factor of 0.61 was determined by minimizing the difference (χ2) between the bulk data and the film data. An empirical formula was established to express σxy(T) for both the film and the bulk samples, as indicated with the solid line in Fig. 4b. For the analysis of Eg(T), we used the empirical formula for σxy(T)/σ0, where σ0=e2/ha0=9.9 × 102 Ω−1 cm−1 with a0=3.9 Å being the atomic distance, e being the elementary charge and h being the Planck’s constant.
NBS and data analysis
To observe ferromagnetic excitations in a polycrystalline sample, we have applied the NBS method by using the HRC installed at the Materials and Life Science Experimental Facility, J-PARC30. On the HRC, neutron beams extracted from the pulsed neutron source are monochromatized by a Fermi chopper (the incident neutron energy (Ei) is selected) and are incident upon the sample. Scattered neurons, of which energy transfer (E) is determined from the time-of-flight, are collected with a detector system covering the scattering angles continuously. By utilizing high-energy (sub eV) neutrons with the short pulses realizing the high-energy resolution of ΔE/Ei∼2% on the HRC, one can perform NBS experiments, that is, INS experiments near to the forward direction like the conventional optical Brillouin scattering method22,30. Normally, a sizable single crystal is required for INS experiments. However, excitations near to the zone centre, where scattering intensities remain even by the powder average of the dynamical structure factor, can be detected by the NBS.
To measure the spin wave dispersion relation for SrRuO3, we selected Ei=100 meV. Then, the transferred energy E reaches to higher than 10 meV with the energy resolution ΔE=2 and 3.4 meV and the transferred momentum Q approaches down to ∼0.15 and 0.175 Å−1, respectively, by using the detecting system that covers the scattering angles down to 0.6°. The condition with ΔE=3.4 meV provides the peak intensity of the excitation spectrum twice that with ΔE=2 meV. Several experimental improvements have made the NBS methods feasible in the practical level for our studies: they include the short-pulse and the high-energy neutrons with higher flux provided by the intense pulsed neutron source as well as the lower background at low angles. Using this new state-of-the-art instrument HRC, we could achieve the data quality equivalent to that by INS measurements with single crystals22. These improvements in the instrumentation made it possible for us to get access to the current (Q,E) space, which is essential for this study. The HRC provides the highest resolution of its class in the (Q,E) space for the present study.
We measured the INS spectra at T=4, 20, 38, 61, 86, 115 and 147 K with the ΔE=3.4 meV condition, and at T=4, 100, 130 and 165 K with the ΔE=2.0 meV condition. It should be noted that the spin wave dispersion relation obtained at T=4 K with the ΔE=3.4 meV condition was identical to that with the ΔE=2.0 meV condition. The scanned data without the sample was defined as the background, which was subtracted from the raw data after normalizing by the exposure time of the data acquisition. The E dependence of the background-subtracted intensities were well fitted with equation (2) or (3).
The functional form of the elastic scattering B(Q,E) in equations (2) and (3) is almost described by a Gaussian function centred at E=0 meV with ΔE being the full-width at half-maximum, however, it has a tiny tail at the negative E side. The neutrons are emitted from the neutron source with a time distribution, and the tail originates from the neutrons with higher energies than Ei emitted later than the time origin of the time-of-flight and transmitted through the time window of the Fermi chopper. The value of ΔE and the shape of the tail in B(Q,E) were determined by measuring the shape of the incoherent elastic scattering at low T and higher Q, where the elastic peak is well separated from the spin wave peaks. As the elastic component consists of the incoherent elastic scattering and the Bragg scattering at the zone centre, B(Q,E) decreases as Q increases and becomes constant. The peak value of B(Q,E) can be determined as the peak intensity of the Gaussian component in each spectrum. It should be noted that ΔE is independent of Q.
The spin wave components could be described by the Gaussian function with the width W in equation (2), which was estimated from ΔE and the influence of the Q resolution via the spin wave dispersion as follows22,31,

where dES/dQ=2DQ, and ΔQ=0.12 Å−1 is estimated from the instrumental geometry22. The value of D in Fig. 4a was used after some iterations. The excitation energy width finer than W cannot be determined experimentally. As the tail in B(Q,E) is much smaller than the peak intensity of B(Q,E), the resolution-limited scattering can be approximated to a Gaussian scattering function with the width W determined by the instrumental resolution, neglecting the small contribution of the tail. Similar to this, the resolution function with which the Lorentzian component is convoluted for the spectrum at T=TC can be approximated to a Gaussian scattering function with ΔE, as shown in equation (3).
The spin wave energies ES decrease upon heating and eventually go to zero at TC. The spectra also change their nature from the Gaussian function for spin waves to the Lorentzian function centred at E=0 meV for the paramagnetic spin fluctuations, as shown in Fig. 2. The scattering function at T=TC is typical of the critical scattering observed in metallic ferromagnets32: the power law Γ=γQ2.5 clearly holds with γ=76 meV Å2.5, and the Q dependence of intensity AC(Q) is well fitted to the functional form of the critical scattering (Q−2) convoluted with the instrumental resolution, as shown in Fig. 3g,i. This indicates that the spectra observed at T<TC are of spin waves.
In the case of ferromagnetic spin waves, the dispersion relation normally follows the Q2 law (ES(Q)=DQ2+Eg) independently of the crystalline orientation in a small Q region for cubic or isotropic lattices. In fact, spin waves in the single crystalline sample of the nearly cubic perovskite La0.8Sr0.2MnO3 show the isotropic Q2 law (Eg=0 meV) at Q≤0.3 Å−1, although the dispersion curve along [001] bends down to lower energies than the [111] curve at Q>0.3 Å−1 (ref. 33). The dispersion relation at Q≤0.3 Å−1 observed by the NBS on the HRC using a polycrystalline sample of La0.8Sr0.2MnO3 was identical to that obtained by using the single crystalline sample22. Although the crystal structure of SrRuO3 is orthorhombic, similar to La0.8Sr0.2MnO3, it can be approximated to be cubic with the lattice constant of 3.9 Å within the present instrumental resolution. We applied this established experimental technique to the present study of the spin dynamics in SrRuO3. Figure 6 shows the INS spectra in SrRuO3 observed on the HRC at Q=0.175–0.5 Å−1 at a step of 0.025 Å−1. The spin wave peak positions for SrRuO3 were well defined and described by the Q2 law at Q≤0.3 Å−1, however, deviated from the Q2 law at Q>0.3 Å−1. Furthermore, the spectra became much broader at Q⩾0.375 Å−1 and the peak positions could not be accurately determined. Therefore, we confirmed that the spin wave dispersion can be approximated to the Q2 law by using data for Q≤0.3 Å−1. All our analyses reported here are based on the data collected for Q≤0.3 Å−1.
INS spectra are plotted at Q=0.175–0.5 Å−1 at a step of 0.025 Å−1, which are indicated with small solid circles with vertical bars presenting the statistical errors. Each spectrum was fitted with equation (2) by using the calculated resolution width W for Q≤0.3 Å−1 and by parameterizing W for Q>0.3 Å−1. The solid lines are the fitted curve to the spectrum, and the shaded areas are the spin wave components obtained by the fit. The determined spin wave peak positions are plotted with large circles. The different colours correspond to the different Q values. The red line indicates the spin wave dispersion with the Q2 law determined for Q≤0.3 Å−1.
Theoretical analysis
The basic facts about theories of spin wave dispersion and the effects of the Weyl fermions are summarized here.
First, the T dependence of the stiffness constant D without the spin–orbit interaction has been studied theoretically both in the strong and weak correlation limits. In the strong correlation case, the spin wave is discussed in terms of the Heisenberg spin Hamiltonian  . The linearized equation of motion with respect to S+=Sx+iSy reads
. The linearized equation of motion with respect to S+=Sx+iSy reads

which results in  , where Q=|q| for small q=(qx, qy, qz) (Q≤0.3 Å−1 in the present case). On the other hand, in the weak correlation limit, although random phase approximation predicts the diverging D(T) towards TC (ref. 34), the self-consistent renormalization theory predicts the vanishing D(T) as T→TC (refs 35, 36). Experimentally, D(T) for a metallic ferromagnet Ni3Al, for instance, decreases to zero as T increases to the transition temperature TC. This behaviour is consistent with both the self-consistent renormalization theory35,36, and also the Heisenberg model24.
, where Q=|q| for small q=(qx, qy, qz) (Q≤0.3 Å−1 in the present case). On the other hand, in the weak correlation limit, although random phase approximation predicts the diverging D(T) towards TC (ref. 34), the self-consistent renormalization theory predicts the vanishing D(T) as T→TC (refs 35, 36). Experimentally, D(T) for a metallic ferromagnet Ni3Al, for instance, decreases to zero as T increases to the transition temperature TC. This behaviour is consistent with both the self-consistent renormalization theory35,36, and also the Heisenberg model24.
In the weak correlation limit, the spin wave dispersion is determined by the generalized spin susceptibility χ+−(q,ω) of electrons as given as follows34,

with

where  is the generalized spin susceptibility without the electron–electron interaction, f(ɛ) is the Fermi distribution function and
is the generalized spin susceptibility without the electron–electron interaction, f(ɛ) is the Fermi distribution function and  is the energy dispersion of up (down) spin with U being the electron–electron interaction. By solving the equation
is the energy dispersion of up (down) spin with U being the electron–electron interaction. By solving the equation  , one can obtain the spin wave dispersion ω(q). Although the detailed form depends on ɛ(k), one can consider the expansion of χ+−(q,ω) with respect to ω and q. The coefficient α0 of ω is
, one can obtain the spin wave dispersion ω(q). Although the detailed form depends on ɛ(k), one can consider the expansion of χ+−(q,ω) with respect to ω and q. The coefficient α0 of ω is  , whereas that of q2 is
, whereas that of q2 is  near the transition temperature TC (ref. 34).
near the transition temperature TC (ref. 34).
Next, we consider the effects of the spin–orbit interaction. In the strong correlation limit, it introduces the spin anisotropy term  , which adds the gap
, which adds the gap  to the spin wave dispersion ω(q). Although experiments determining the spin wave gap have been often reported, the reports on its temperature dependence are very few. In the case of ferromagnets, the temperature dependence of the spin wave gap is hardly detected, because a ferromagnet having a crystal structure with high symmetry normally shows gapless spin wave. In the case of antiferromagnets, spin wave gap can be enhanced by the exchange interaction J as
to the spin wave dispersion ω(q). Although experiments determining the spin wave gap have been often reported, the reports on its temperature dependence are very few. In the case of ferromagnets, the temperature dependence of the spin wave gap is hardly detected, because a ferromagnet having a crystal structure with high symmetry normally shows gapless spin wave. In the case of antiferromagnets, spin wave gap can be enhanced by the exchange interaction J as  . The antiferromagnetic resonance frequency, that is a spin wave gap in antiferromagnet and is also proportional to
. The antiferromagnetic resonance frequency, that is a spin wave gap in antiferromagnet and is also proportional to  , shows a monotonous temperature dependence as a function of the magnetization for insulating antiferromagnets such as MnF2 (ref. 37) and MnO (ref. 38). The spin wave gap shows a monotonous temperature dependence as a function of the magnetization even for a metallic antiferromagnet γFeMn (ref. 39).
, shows a monotonous temperature dependence as a function of the magnetization for insulating antiferromagnets such as MnF2 (ref. 37) and MnO (ref. 38). The spin wave gap shows a monotonous temperature dependence as a function of the magnetization even for a metallic antiferromagnet γFeMn (ref. 39).
Equation (9) should be generalized to include the spin–orbit interaction in the electronic band structure,

where n,m are the band indices including the pseudospin. Equation (10) usually has a complex form, but one can consider the expansion with respect to ω and q as discussed above. The zero-th order term χ+−(0,0)–χzz(0,0) determines the anisotropy K, which is basically independent of T near TC, that is, it can be defined even in the normal phase. On the other hand, when we expand with respect to ω as

the linear order term in ω contains the square of the energy denominator, and is hence sensitive to the Weyl fermions27.
Now we discuss how equation (4) is derived theoretically based on the Weyl fermion. The spin dynamics is described by the effective action A for the spin fluctuation field Sα obtained by integrating over the electronic degrees of freedom as27

Where  is the correlation function of the conduction electron spin σα. We are interested in the action A0 for the uniform component (q=0), which is given by equation (5), where the coefficient α of the Berry phase term is given by
is the correlation function of the conduction electron spin σα. We are interested in the action A0 for the uniform component (q=0), which is given by equation (5), where the coefficient α of the Berry phase term is given by  , and K represents the spin anisotropy energy. Most of the contribution to α comes from the bands not largely influenced by the spin–orbit interaction, that is, α0, and nontrivial contribution α1 comes from Weyl fermions. As described above,
, and K represents the spin anisotropy energy. Most of the contribution to α comes from the bands not largely influenced by the spin–orbit interaction, that is, α0, and nontrivial contribution α1 comes from Weyl fermions. As described above,  . The contribution α1 from the Weyl fermion is proportional to σxy, as shown below. The Hamiltonian in equation (1) is rewritten as
. The contribution α1 from the Weyl fermion is proportional to σxy, as shown below. The Hamiltonian in equation (1) is rewritten as  , where fa(k) is expanded near the band crossing point k0 as
, where fa(k) is expanded near the band crossing point k0 as  . One can relate the current operator ja and the spin operator σb as
. One can relate the current operator ja and the spin operator σb as  as ja is obtained by replacing k with k+e A and taking derivative of the Hamiltonian with the vector potential A. By using the above relation between σb and ja,
as ja is obtained by replacing k with k+e A and taking derivative of the Hamiltonian with the vector potential A. By using the above relation between σb and ja,  is equal to λσxy with the coefficient
is equal to λσxy with the coefficient  . By taking the variational derivative of A0 in equation (5) with respect to Sx and Sy, one can derive the equation of motion and obtain the spin wave gap as
. By taking the variational derivative of A0 in equation (5) with respect to Sx and Sy, one can derive the equation of motion and obtain the spin wave gap as  , which is equivalent to equation (4) used to fit the data. Thus, the correspondence between Eg and σxy is expected from the fact that the band crossings act as the magnetic monopoles in momentum space. Here we need to assume that K is independent of T to justify the fitting by equation (4). This fact is consistent with the expectation that the Weyl fermion does not resonantly contribute to K, as the energy denominator is ɛn(k)–ɛm(k) in equation (10) for K, whereas the expression of α in equation (11) contains the energy denominator (ɛn(k)–ɛm(k))2.
, which is equivalent to equation (4) used to fit the data. Thus, the correspondence between Eg and σxy is expected from the fact that the band crossings act as the magnetic monopoles in momentum space. Here we need to assume that K is independent of T to justify the fitting by equation (4). This fact is consistent with the expectation that the Weyl fermion does not resonantly contribute to K, as the energy denominator is ɛn(k)–ɛm(k) in equation (10) for K, whereas the expression of α in equation (11) contains the energy denominator (ɛn(k)–ɛm(k))2.
Data availability
The authors declare that the data supporting the findings of this study are available within the article.
Additional information
How to cite this article: Itoh, S. et al. Weyl fermions and spin dynamics of metallic ferromagnet SrRuO3. Nat. Commun. 7:11788 doi: 10.1038/ncomms11788 (2016).
References
Rado, G. T. & Suhl, H. Magnetism, A Treatise on Modern Theory and Materials Academic (1963).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Sandratskii, L. M. Noncollinear magnetism in itinerant-electron systems: theory and applications. Adv. Phys. 47, 91–160 (1998).
Sato, K. et al. First-principles theory of dilute magnetic semiconductors. Rev. Mod. Phys. 82, 1633–1690 (2010).
Nagaosa, N., Sinova, J., Onoda, S., McDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Onoda, M. & Nagaosa, N. Topological nature of anomalous Hall effect in ferromagnets. J. Phys. Soc. Jpn. 71, 19–22 (2002).
Onoda, S., Sugimoto, N. & Nagaosa, N. Intrinsic versus extrinsic anomalous Hall effect in ferromagnets. Phys. Rev. Lett. 97, 126602 (2006).
Chen, Y., Bergman, D. L. & Burkov, A. A. Weyl fermions and the anomalous Hall effect in metallic ferromagnets. Phys. Rev. B 88, 125110 (2013).
Mathieu, R. et al. Scaling of the anomalous Hall effect in Sr1-xCaxRuO3 . Phys. Rev. Lett 93, 016602 (2004).
Shimano, R., Ikebe, Y., Takahashi, K. S., Kawasaki, M., Nagaosa, N. & Tokura, Y. Terahertz Faraday rotation induced by an anomalous Hall effect in the itinerant ferromagnet SrRuO3 . EPL 95, 17002 (2011).
Burkov, A. A. Chiral anomaly and transport in Weyl metals. J. Phys. Condens. Matter 27, 113201 (2015).
Witczak-Krempa, W. & Kim, Y. B. Topological and magnetic phases of interacting electrons in the pyrochlore iridates. Phys. Rev. B 85, 045124 (2012).
Wan, X., Vishwanath, A. & Savrasov, S. Y. Computational design of axion insulators based on 5d spinel compounds. Phys. Rev. Lett. 108, 146601 (2012).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4 . Phys. Rev. Lett. 107, 186806 (2011).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun 6, 7373 (2015).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Halàsz, G. B. & Balents, L. Time-reversal invariant realization of the Weyl semimetal phase. Phys. Rev. B 85, 035103 (2012).
Koster, G. et al. Structure, physical properties, and applications of SrRuO3 thin films. Rev. Mod. Phys. 84, 253–298 (2012).
Cao, G., McCall, S., Shepard, M., Crow, J. E. & Guertin, R. P. Thermal, magnetic, and transport properties of single-crystal Sr1-xCaxRuO3 (0≤x≤1.0). Phys. Rev. B 56, 321–329 (1997).
Kats, Y., Genish, I., Klein, L., Reiner, J. W. & Beasley, M. R. Large anisotropy in the paramagnetic susceptibility of SrRuO3 films. Phys. Rev. B 71, 100403 (2005).
Itoh, S. et al. Neutron Brillouin scattering with pulsed spallation neutron source—spin-wave excitations from ferromagnetic powder samples. J. Phys. Soc. Jpn. 82, 043001 (2013).
Langner, M. C. et al. Observation of ferromagnetic resonance in SrRuO3 by the time-resolved magneto-optical Kerr effect. Phys. Rev. Lett. 102, 177601 (2009).
Semadeni, F., Roessli, B., Böni, P., Vorderwisch, P. & Chatterji, T. Critical fluctuations in the weak itinerant ferromagnet Ni3Al: a comparison between self-consistent renormalization and mode-mode coupling theory. Phys. Rev. B 62, 1083–1088 (2000).
Lee, S. et al. Large in-plane deformation of RuO6 octahedron and ferromagnetism of bulk SrRuO3 . J. Phys. Condens. Matter 25, 465601 (2013).
Serga, A. A., Sandweg, C. W., Vasyuchka, V. I., Jungfleisch, M. B. & Hillebrands, B. Brillouin light scattering spectroscopy of parametrically excited dipole-exchange magnons. Phys. Rev. B 86, 134403 (2012).
Onoda, M., Mishchenko, A. S. & Nagaosa, N. Left-handed spin wave excitation in ferromagnet. J. Phys. Soc. Jpn. 77, 013702 (2008).
Kanbayasi, A. Magnetocrystalline anisotropy of SrRuO3 . J. Phys. Soc. Jpn. 41, 1879–1883 (1976).
Bushmeleva, S. N., Pomjakushin, V. Y., Pomjakushina, E. V., Sheptyakov, D. V. & Balagurov, A. M. Evidence for the band ferromagnetism in SrRuO3 from neutron diffraction. J. Magn. Magn. Matter 305, 491–496 (2006).
Itoh, S. et al. High Resolution Chopper Spectrometer (HRC) at J-PARC. Nucl. Instr. Meth. Phys. Res. A 631, 90–97 (2011).
Crevecoeur, R., de Schepper, I., de Graaf, L., Montfrooij, W., Svensson, E. & Carlile, C. Angular and time resolution of neutron time of flight spectrometers. Nucl. Instr. Meth. Phys. Res. A 356, 415–421 (1995).
Endoh, Y. & Böni, P. Magnetic excitations in metallic ferro- and antiferromagnets. J. Phys. Soc. Jpn. 75, 111002 (2006).
Moussa, F. et al. Spin waves in the ferromagnetic metallic manganites La1-x(Ca1-ySry)xMnO3 . Phys. Rev. B 76, 064403 (2007).
Izuyama, T., Kim, D. J. & Kubo, R. Band theoretical interpretation of neutron diffraction phenomena in ferromagnetic metals. J. Phys. Soc. Jpn 18, 1025–1042 (1963).
Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism Springer (1985).
Lonzarich, G. G. & Taillefer, L. Effect of spin fluctuations on the magnetic equation of state of ferromagnetic or nearly ferromagnetic metals. J. Phys. C 18, 4339–4372 (1985).
Johnson, F. M. & Nethercot, A. H. Jr Antiferromagnetic resonance in MnF2 . Phys. Rev 114, 705–716 (1959).
Keffer, F., Sievers, A. J. III & Tinkham, M. Infrared antiferromagnetic resonance in MnO. J. Appl. Phys. 32, 65S–66S (1961).
Tajima, K., Ishikawa, Y., Endoh, Y. & Noda, Y. Spin dynamics in itinerant antiferromagnetic γFeMn alloys. J. Phys. Soc. Jpn. 41, 1195–1203 (1976).
Acknowledgements
NBS experiments were performed at spectrometers, PHAROS in Los Alamos Neutron Science Center and BRISP in Institut Laue Langevin, in the early stage of this work. We acknowledge F. Trouw, A. Llobet, A. Orecchini, A. De Francesco, C. Petrillo, Jaehong Jeong for their early contributions. With this experience, we were encouraged to develop the NBS method at the HRC at J-PARC. The neutron scattering experiment was approved by the Neutron Scattering Program Advisory Committee of the Institute of Materials Structure Science, High Energy Accelerator Research Organization (Nos. 2012S01, 2013S01, 2014S01, 2015S01 and 2016S01). This research was partly supported by Grants-in-Aid for Scientific Research (Nos. 23244068, 24224009, 26103006 and 26400376) and for Challenging Exploratory Research from the MEXT, and by Institute for Basic Science in Korea (IBS-R009-G1).
Author information
Authors and Affiliations
Contributions
S.It., Y.E., J.-G.P., N.N. and Y.T. conceived the study. S.It., Y.E., T.Y., S.Ib. and J.-G.P. performed the neutron scattering experiments. Y.K. prepared the sample. K.S.T. performed the transport experiment. N.N. provided theoretical insight. All the authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Itoh, S., Endoh, Y., Yokoo, T. et al. Weyl fermions and spin dynamics of metallic ferromagnet SrRuO3. Nat Commun 7, 11788 (2016). https://doi.org/10.1038/ncomms11788
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11788
This article is cited by
-
Magnetism and berry phase manipulation in an emergent structure of perovskite ruthenate by (111) strain engineering
npj Quantum Materials (2023)
-
The thickness dependence of quantum oscillations in ferromagnetic Weyl metal SrRuO3
npj Quantum Materials (2023)
-
Strain engineering of electronic properties and anomalous valley hall conductivity of transition metal dichalcogenide nanoribbons
Scientific Reports (2022)
-
Challenges in identifying chiral spin textures via the topological Hall effect
Communications Materials (2022)
-
Spin structure and dynamics of the topological semimetal Co3Sn2-xInxS2
npj Quantum Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.