Abstract
Metallic transition-metal dichalcogenides (TMDCs) are benchmark systems for studying and controlling intertwined electronic orders in solids, with superconductivity developing from a charge-density wave state. The interplay between such phases is thought to play a critical role in the unconventional superconductivity of cuprates, Fe-based and heavy-fermion systems, yet even for the more moderately-correlated TMDCs, their nature and origins have proved controversial. Here, we study a prototypical example, 2H-NbSe2, by spin- and angle-resolved photoemission and first-principles theory. We find that the normal state, from which its hallmark collective phases emerge, is characterized by quasiparticles whose spin is locked to their valley pseudospin. This results from a combination of strong spin–orbit interactions and local inversion symmetry breaking, while interlayer coupling further drives a rich three-dimensional momentum dependence of the underlying Fermi-surface spin texture. These findings necessitate a re-investigation of the nature of charge order and superconducting pairing in NbSe2 and related TMDCs.
Similar content being viewed by others
Introduction
In combination with broken structural inversion symmetry, spin–orbit coupling (SOC) provides a powerful route to stabilize spin-polarized electronic states without magnetism. This can give rise to electrically-tuneable spin splittings via the Rashba effect, promising new technological developments in spintronics1, and underpins the formation of spin-helical Dirac cones at the surfaces of topological insulators2. It is strongly desired to realize similar effects in systems where more pronounced electronic interactions drive the emergence of collective phases. In non-centrosymmetric superconductors, for example, spin-splitting driven by strong SOC is expected to induce a mixing of spin-triplet and singlet superconducting order parameters3, and offers potential for stabilizing topological superconductors4. Yet, identifying suitable candidate materials has proved a major challenge to date. Partly this is driven by a relative dearth of non-centrosymmetric metals, while for non-magnetic systems in which the centre of inversion is maintained, robust-spin degeneracies of their electronic states would typically be expected due to the dual constraints of time-reversal and inversion symmetry.
In contrast, we show here from spin- and angle-resolved photoemission (ARPES) measurements that the normal state of the centrosymmetric TMDC superconductor 2H-NbSe2 (hereafter denoted NbSe2) hosts a strong layer-resolved and momentum-dependent spin polarization of its electronic states at and in the vicinity of the Fermi level. We attribute this as a consequence of a recently-realized form of spin polarization that can emerge in globally centrosymmetric materials in which constituent structural units nonetheless break inversion symmetry5,6,7. Together with first-principles calculations, we show how this drives a critical and complex interplay of interlayer interactions and SOC in NbSe2. This yields a rich underlying spin-polarized electronic landscape from which charge order and superconductivity emerge upon cooling.
Results
Bulk electronic properties of NbSe2
We consider here exclusively the layered 2H polymorph (Fig. 1a). Each layer forms a graphene-like honeycomb structure with Nb occupying the A sublattice and two Se atoms situated on the B sublattice. These lie out of the basel plane, equidistant above and below the transition metal. The unit cell contains two such layers, stacked along the c-axis with 180° in-plane rotation. Our resistivity measurements (Fig. 1b) from single-crystal NbSe2 samples show a metallic temperature-dependence. They additionally exhibit a pronounced hump at a temperature of TCDW≈33 K indicative of charge-density wave (CDW) formation8, as well as a sharp superconducting transition at Tc≈7 K. The corresponding normal-state Fermi surface is shown in Fig. 1c, as measured by ARPES. There are two barrels centred around each zone-corner  point, which are strongly trigonally-warped. Two further barrels are centred at the
point, which are strongly trigonally-warped. Two further barrels are centred at the  point, the inner of which is hexagonal, while the outer exhibits additional warping. From our first-principles density-functional theory (DFT) calculations, and consistent with previous studies9,10,11, we assign all four of these Fermi surface sheets as being predominantly derived from Nb 4d orbitals. Additional spectral weight at the zone centre is evident in our ARPES measurements for selected photon energies, which we attribute as a fifth, highly three-dimensional, Fermi surface sheet of predominantly Se pz orbital character.
point, the inner of which is hexagonal, while the outer exhibits additional warping. From our first-principles density-functional theory (DFT) calculations, and consistent with previous studies9,10,11, we assign all four of these Fermi surface sheets as being predominantly derived from Nb 4d orbitals. Additional spectral weight at the zone centre is evident in our ARPES measurements for selected photon energies, which we attribute as a fifth, highly three-dimensional, Fermi surface sheet of predominantly Se pz orbital character.
(a) Centrosymmetric bulk crystal structure (side view) of 2H-NbSe2. This is formed by stacking non-centrosymmetric layers of D3h symmetry with 180° relative rotations, restoring the bulk inversion centre. (b) Resistivity measurements show clear signatures of charge-density wave formation at TCDW≈33 K and superconductivity at Tc≈7 K (magnified in the insets). (c) Normal-state Fermi surface measured by ARPES with hν=100 eV (left-hand-side) and hν=106 eV (right-hand-side); EF±20 meV. This consists of two Nb-derived barrels centred around the zone-corner  points, two Nb-derived barrels at the Brillouin zone centre and an additional central diffuse pocket (most visible at hν=106 eV) predominantly derived from Se pz orbitals.
points, two Nb-derived barrels at the Brillouin zone centre and an additional central diffuse pocket (most visible at hν=106 eV) predominantly derived from Se pz orbitals.
This sheet also contributes diffuse filled-in intensity, due to the finite out-of-plane momentum (kz) resolution of ARPES, close to the zone centre in measurements of the electronic dispersions along in-plane high-symmetry directions (Fig. 2a). The Nb-dominated states, on the other hand, yield clear spectral features close to their Fermi crossings. Kinks in their measured dispersion and a decrease in linewidth near the Fermi-level point to relatively strong electron–phonon coupling in this system11,12,13. It is these Nb-derived states that are known to host the largest energy gaps at the Fermi level arising from the CDW and superconducting instabilities in this system13,14,15,16, although the origins of these have proved highly controversial8,10,11,13,14,15,16,17,18,19,20,21,22. To the best of our knowledge, all prior theoretical treatments assume these orders emerge from an electronic liquid of trivially spin-degenerate character. Indeed, standard expectations of group theory would say this must be the case for the centrosymmetric space group (P63/mmc) of 2H-NbSe2.
In contrast, we directly observe pronounced spin polarizations of the underlying electronic states in spin-resolved energy distribution curves (spin-EDCs, see Methods) measured along the  direction, shown in Fig. 2c–f. Close to the saddle point of these bands (Fig. 2d), two clearly-separated peaks can be observed in spin-EDCs. The measured spin polarization is almost entirely out-of-plane (Fig. 2d and Supplementary Fig. 1), with a sign that reverses between the two bands. We attribute this as arising from local inversion symmetry breaking within the individual layers that make up the bulk crystal structure5,6,23. For sufficiently weak interlayer interactions (a point we return to below), pronounced SOC characteristic of the 4d transition metal can lift the spin degeneracy of the states localized within each layer, that thus strongly feel the local inversion asymmetry. A layer-dependent sign change of this spin polarization, mediated by the rotated-layer stacking of the bulk crystal structure, would act to restore overall spin degeneracy as required by global inversion and time-reversal symmetries. Nonetheless, the electronic states retain strong layer-resolved spin polarizations. Depth-averaging probes would largely be insensitive to these, but photoemission is a surface sensitive technique. Incoherent superposition of photoelectrons emitted from neighbouring layers of the unit cell would lead to some suppression of the measured spin polarization, while interference effects can further complicate this picture5. Nonetheless, the extreme surface sensitivity at the photon energies used here, with an inelastic mean free path on the order of the interlayer separation, renders us predominantly sensitive to the spin texture of the top-most layer of the unit cell.
direction, shown in Fig. 2c–f. Close to the saddle point of these bands (Fig. 2d), two clearly-separated peaks can be observed in spin-EDCs. The measured spin polarization is almost entirely out-of-plane (Fig. 2d and Supplementary Fig. 1), with a sign that reverses between the two bands. We attribute this as arising from local inversion symmetry breaking within the individual layers that make up the bulk crystal structure5,6,23. For sufficiently weak interlayer interactions (a point we return to below), pronounced SOC characteristic of the 4d transition metal can lift the spin degeneracy of the states localized within each layer, that thus strongly feel the local inversion asymmetry. A layer-dependent sign change of this spin polarization, mediated by the rotated-layer stacking of the bulk crystal structure, would act to restore overall spin degeneracy as required by global inversion and time-reversal symmetries. Nonetheless, the electronic states retain strong layer-resolved spin polarizations. Depth-averaging probes would largely be insensitive to these, but photoemission is a surface sensitive technique. Incoherent superposition of photoelectrons emitted from neighbouring layers of the unit cell would lead to some suppression of the measured spin polarization, while interference effects can further complicate this picture5. Nonetheless, the extreme surface sensitivity at the photon energies used here, with an inelastic mean free path on the order of the interlayer separation, renders us predominantly sensitive to the spin texture of the top-most layer of the unit cell.
Spin–valley locking
Our measurements show how such spin textures in NbSe2 persist up to the Fermi level. This is evident in spin-resolved EDCs along the  direction (Fig. 2c–f) as well as the spin polarization of EDCs and a Fermi-level momentum-distribution curve along the
direction (Fig. 2c–f) as well as the spin polarization of EDCs and a Fermi-level momentum-distribution curve along the  direction (Fig. 3). The latter clearly reveals how the spin polarization reverses sign for each pair of Fermi surface sheets centred on neighbouring
direction (Fig. 3). The latter clearly reveals how the spin polarization reverses sign for each pair of Fermi surface sheets centred on neighbouring  and
and  points. This is a natural consequence of time-reversal symmetry. Here, this results in a coupling of the spin to the so-called valley index, the quantum number which distinguishes
points. This is a natural consequence of time-reversal symmetry. Here, this results in a coupling of the spin to the so-called valley index, the quantum number which distinguishes  - and
- and  -centred Fermi surfaces in NbSe2 (Fig. 3e). Such spin–valley coupling has recently been extensively investigated for the band extrema in monolayers of semiconducting TMDCs24,25,26, where it has not only been shown to lead to new physics, such as a valley Hall effect27, but also to offer potential for devices exploiting the valley pseudospin28,29. Our observations here point to a pronounced role of spin–valley coupling also for the low-energy quasiparticle excitations of the metallic 2H-structured TMDCs.
-centred Fermi surfaces in NbSe2 (Fig. 3e). Such spin–valley coupling has recently been extensively investigated for the band extrema in monolayers of semiconducting TMDCs24,25,26, where it has not only been shown to lead to new physics, such as a valley Hall effect27, but also to offer potential for devices exploiting the valley pseudospin28,29. Our observations here point to a pronounced role of spin–valley coupling also for the low-energy quasiparticle excitations of the metallic 2H-structured TMDCs.
(a) Dispersion measured (hν=22 eV) along the  direction, together with the corresponding spin polarisation of a momentum distribution curve at the Fermi level and (b–d) EDCs at the momenta marked in a. These reveal how the sign of the spin polarization for each zone-corner Fermi surface sheet becomes locked to the valley degree of freedom, as shown schematically in e.
direction, together with the corresponding spin polarisation of a momentum distribution curve at the Fermi level and (b–d) EDCs at the momenta marked in a. These reveal how the sign of the spin polarization for each zone-corner Fermi surface sheet becomes locked to the valley degree of freedom, as shown schematically in e.
Critically, it is from this spin-polarized Fermi sea that electron–hole and electron–electron pairing interactions drive the formation of CDW order and superconductivity. The largest CDW gaps in NbSe2 are located on the zone-corner spin–valley-locked Fermi surfaces13. The CDW wave vector is entirely in-plane30, making the hidden layer-dependent spin polarizations relevant. The underlying spin textures can also be expected to have important implications for superconductivity. Recent measurements on electrically gated MoS2, which is known to host a strong spin–valley locking in its band structure25,26, have found evidence for unconventional so-called Ising superconductivity31,32. In this, the pronounced spin–orbit field that induces the underlying spin texture of the electronic states pins the spin of Cooper pair electrons in the out-of-plane direction. This leads to upper critical fields dramatically exceeding the Pauli paramagnetic limit for a magnetic field applied within the ab-plane. Similar phenomenology has recently been reported for mono- and few-layer NbSe2 (ref. 33), entirely consistent with our direct observation of spin–valley locking in this compound.
In bulk NbSe2, the spin-layer locking, and also multi-band nature as compared to gated MoS2, raises further prospects for stabilizing a delicate balance between different pairing states. In the normal state, we find that the  -centred Fermi surface barrels, which are known to support a modulated superconducting gap in the bulk13,34, are also strongly spin-polarized along the
-centred Fermi surface barrels, which are known to support a modulated superconducting gap in the bulk13,34, are also strongly spin-polarized along the  direction (Fig. 2c). Their spin polarization, however, is completely suppressed along
direction (Fig. 2c). Their spin polarization, however, is completely suppressed along  (Fig. 2b). Intriguingly, the largest superconducting gaps of this Fermi surface determined in Rahn et al.13 are located at the regions of strongest spin polarization evident here. Pronounced superconducting gaps are also known to occur on the zone-corner Fermi surfaces13,15,34, which as demonstrated above, host strong spin–valley locking even in the bulk. Given the pronounced influence of SOC, a mixing of spin-triplet and spin-singlet order parameters could potentially be expected3. Forming even pseudospin-singlet Cooper pairs from the strongly spin-polarized Fermi surfaces could necessitate a phase locking between the order parameter of neighbouring Fermi surface sheets. Moreover, the c-axis coherence length in NbSe2 is much greater than the interlayer separation35,36. This raises the tantalizing prospect that the inherent coupling between the spin and layer pseudospins reported here could be tuned to drive an instability to an odd-parity pair density-wave state, where the sign of the superconducting gap becomes tied to the layer index7,37. The proximity of bulk NbSe2 and similar compounds to such phases requires further theoretical exploration, and will depend sensitively on the relative importance of inter- and intra-band as well as interlayer pairing interactions.
(Fig. 2b). Intriguingly, the largest superconducting gaps of this Fermi surface determined in Rahn et al.13 are located at the regions of strongest spin polarization evident here. Pronounced superconducting gaps are also known to occur on the zone-corner Fermi surfaces13,15,34, which as demonstrated above, host strong spin–valley locking even in the bulk. Given the pronounced influence of SOC, a mixing of spin-triplet and spin-singlet order parameters could potentially be expected3. Forming even pseudospin-singlet Cooper pairs from the strongly spin-polarized Fermi surfaces could necessitate a phase locking between the order parameter of neighbouring Fermi surface sheets. Moreover, the c-axis coherence length in NbSe2 is much greater than the interlayer separation35,36. This raises the tantalizing prospect that the inherent coupling between the spin and layer pseudospins reported here could be tuned to drive an instability to an odd-parity pair density-wave state, where the sign of the superconducting gap becomes tied to the layer index7,37. The proximity of bulk NbSe2 and similar compounds to such phases requires further theoretical exploration, and will depend sensitively on the relative importance of inter- and intra-band as well as interlayer pairing interactions.
Three-dimensional spin structure
Our DFT calculations (Fig. 4) already reveal a key role of interlayer interactions in mediating and controlling the underlying spin texture of the normal-state bulk Fermi surface. The calculated spin polarization projected onto the first layer of the unit cell is shown throughout the full three-dimensional Brillouin zone in Fig. 4a,b. The momentum-dependent spin polarizations are determined by the effective spin–orbit field, Bso=β(∇V × k), where β is a momentum-dependent scaling factor, ∇V is the net electrostatic potential gradient and k is the crystal momentum. The horizontal mirror symmetry of each NbSe2 structural unit about the transition-metal plane (σh of the D3h point group; Fig. 1a) ensures that ∇V is entirely within the xy plane. Due to the 180° relative rotation of neighbouring NbSe2 monolayers in the bulk crystal structure, ∇V, and thus Bso, has opposite sign for successive layers in the unit cell. This causes the sign of the spin polarization to reverse at each momentum-space point when projected onto layer 2 versus layer 1 of the unit cell (Supplementary Fig. 3). This confirms that local inversion asymmetry within each NbSe2 layer drives the formation of the spin-polarized states observed here.
(a,b) DFT calculations of the (a) out-of-plane and (b) in-plane spin polarization of the three-dimensional Fermi surface of NbSe2 projected onto the first layer of the unit cell. (c,d) Calculated electronic structure along (c) A-L-H-A (kz=π/c) and (d) Γ-M-K-Γ (kz=0) with and without SOC. (e) Corresponding influence of SOC on the Fermi surface contours in the Γ-K-H-A and Γ-M-L-A planes (shown throughout the full three-dimensional Brillouin zone in Supplementary Fig. 2). (f) Our experimental ARPES measurements of such kz-dependent Fermi surfaces (hν=60–130 eV) are in good general agreement with the theoretical calculations including SOC, supporting a SOC-mediated suppression of interlayer hopping in the Γ-K-H-A plane.
For electronic states whose wavefunctions are completely delocalized over both layers of the unit cell, the spin–orbit field from each layer cancels. Such states are consequently unpolarized, restoring the conventional expectations for a centrosymmetric space group. This can be observed for the highly three-dimensional pancake-like Fermi surface at the Brillouin zone centre here. In contrast, for electronic states predominantly localized within individual layers of the unit cell, strong layer-dependent spin–orbit fields mediate large layer-resolved spin polarizations. This is ideally realized at the three-dimensional Brillouin zone boundary along kz (kz=π/c). In a tight-binding picture, for this kz, interlayer hoppings within a unit cell and between neighbouring unit cells are out of phase with each other and thus cancel10. This can be directly visualized by comparing the dispersion of the electronic states along the Γ-M-K-Γ and A-L-H-A directions: neglecting SOC, a single fourfold degenerate band crosses the Fermi level in the kz=π/c plane (Fig. 4c), whereas this is split into a pair of twofold degenerate bands by interlayer interactions for |kz|<π/c, as evident in Fig. 4d.
With its forbidden interlayer coupling, the electronic structure for the kz=π/c plane is thus formally equivalent to that of an isolated monolayer. The spin–orbit field is consequently maximized, driving the largest (>90%) layer-dependent spin-polarizations. These are purely out-of-plane (Fig. 4a,b), as (∇V × k) must lie entirely along z at the Brillouin zone boundary along kz. Along the A-L direction, however, a vertical mirror plane in the crystal structure forbids any out-of-plane component of (∇V × k). The spin–orbit field must therefore be strictly zero along A-L. This enforces a touching, and hence spin degeneracy, of the zone-centre Fermi surface barrels along this direction, which are otherwise strongly spin-polarized throughout the kz=π/c plane.
For other kz through the Brillouin zone, the spin–orbit field strength can be partially suppressed by finite interlayer coupling. Moreover, the z-component of the momentum induces a non-zero component of (∇V × k) in the xy plane. Together, this causes not only the magnitude of the Fermi surface spin polarization, but also its vectorial spin texture, to develop a strong dependence on both the in- and out-of-plane momentum (Fig. 4a,b). Within the Γ-M-L-A plane, the calculated Fermi surface crossings are relatively strongly dispersive in kz (Fig. 4e). This is consistent with our experimental measurements of the kz-dependent Fermi surface (Fig. 4f) and points to significant interlayer coupling. Even away from kz=π/c, where there are strict spin degeneracies along A-L as discussed above, the Fermi surface spin polarizations therefore become strongly suppressed in the entire vicinity of the Γ-M-L-A plane.
For the Γ-K-H-A plane, on the other hand, we find that the kz dispersion of the Fermi surface crossings are significantly reduced by the inclusion of spin–orbit coupling in the calculations (Fig. 4e), in keeping with our experimental measurements of more two-dimensional Fermi contours for this plane (Fig. 4f). This reduction in kz dispersion is achieved by a lifting, via SOC, of the fourfold degeneracy that would otherwise be present along the A-H line, and is accompanied by the emergence of strong spin polarization of the Fermi surface crossings for kz=π/c. This is in contrast to the A-L line, where the energetic degeneracy of the Fermi crossings is protected by their symmetry-enforced spin degeneracy. The reduction of kz dispersion within the Γ-K-H-A plane is equivalent to a spin–orbit-mediated suppression of interlayer hopping here28. This allows relatively strong spin polarizations to be maintained in the vicinity of this plane, with only a moderate suppression of the spin–orbit field strength away from kz=π/c.
For momenta close to the K-H line, the in-plane momentum is always much larger than the out-of-plane component. This causes (∇V × k) to remain predominately aligned along z. The spin polarizations of the zone-corner Fermi surfaces are thus largely out-of-plane throughout the full Brillouin zone (Fig. 4a). For the Nb-derived zone-centre Fermi surface barrels, however, much stronger (up to ∼25%) in-plane components develop (Fig. 4b). The in-plane spin texture is largely radial to the Fermi surface (Supplementary Fig. 4), and switches sign about the kz=0 plane. This indicates a non-zero component of (∇V × k) within the plane, with a direction that is tied to the sign of kz. It thus confirms that an in-plane component of the spin texture arises due to finite out-of-plane momentum, where no symmetry constraint exists to cancel the in-plane component of the spin–orbit field for low-symmetry momenta with 0<|kz|<π/c. The existence of such hidden in-plane spin textures is a unique property of the bulk compound. Indeed, the in-plane spin component goes strictly to zero at the Brillouin zone boundary along kz, enforced by symmetry, and recovering a monolayer-like purely out-of-plane spin texture for kz=±π/c. The bulk system thus hosts a rich intertwining of spin, orbital and layer degrees of freedom, mediating a three-dimensional nature of its spin texture that can be expected to further modulate its pairing interactions31.
Discussion
Taken together, our results show how the combination of interlayer hopping and intralayer inversion symmetry breaking can lead to particularly rich momentum-dependent spin textures of metallic TMDCs. Suppression of Fermi-surface spin polarization away from the Brillouin zone boundary along kz will be reduced with decreased interlayer interactions. Indeed, upper critical fields, already known to exceed the Pauli limit for bulk NbSe2 (ref. 38), are dramatically enhanced in other 2H-TMDC superconductors as a function of increasing interlayer separation39. This points to a susceptibility of the bulk systems to Ising superconductivity similar to that recently observed in isolated monolayers33. The delicate balance between interlayer hopping and SOC strength in NbSe2 makes this an ideal material for understanding, and ultimately controlling the role of layer-dependent spin polarizations on the collective states and phases of transition-metal dichalcogenides.
Methods
ARPES
Spin-resolved ARPES measurements were performed at the I3 beamline of MAX IV Laboratory, Sweden, and ARPES measurements were performed using the I05 beamline of Diamond Light Source, UK. Measurements were performed at temperatures of 50–80 K using p-polarized synchrotron light. Scienta R4000 hemispherical electron analyzers were utilized for all measurements. This was additionally fitted with a mini-Mott detector scheme for the spin-ARPES measurements, configured to simultaneously probe the out-of-plane and in-plane (along the analyzer slit direction) component of the photoelectron spin40. The finite spin-detection efficiency was corrected using a Sherman function of S=0.17 (ref. 40), and the spin-resolved EDCs determined according to

with  ,
,  the measured intensity on the individual detectors in the Mott scattering chamber, corrected by a relative detector efficiency calibration, and the total spin polarization,
the measured intensity on the individual detectors in the Mott scattering chamber, corrected by a relative detector efficiency calibration, and the total spin polarization,

Calculations
DFT calculations including SOC were performed using the modified Becke–Johnson exchange potential and Perdew–Burke–Ernzerhof correlation functional implemented in the WIEN2K programme41. A 20 × 20 × 10 k-mesh was employed. The DFT results were downfolded using maximally localized Wannier functions42,43,44, employing Nb 4d orbitals and Se 5p orbitals as basis functions. The resulting tight-binding Hamiltonian allows a direct extraction of the spin and layer projections of the electronic structure.
Data availability
Data underpinning this publication can be accessed at http://dx.doi.org/10.17630/edd53357-41e3-4313-9e5e-a0e7780ef4be.
Additional information
How to cite this article: Bawden, L. et al. Spin–valley locking in the normal state of a transition-metal dichalcogenide superconductor. Nat. Commun. 7:11711 doi: 10.1038/ncomms11711 (2016).
References
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin–orbit coupling. Nat. Mater. 14, 871–882 (2015).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 85, 3045 (2010).
Gor’kov, L. P. & Rashba, E. I. Superconducting 2D system with lifted spin degeneracy: mixed singlet-triplet state. Phys. Rev. Lett. 87, 037004 (2001).
Sato, M. & Fujimoto, S. Topological phases of noncentrosymmetric superconductors: edge states, Majorana fermions, and non-Abelian statistics. Phys. Rev. B 79, 094504 (2009).
Riley, J. M. et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nat. Phys 10, 835–839 (2014).
Zhang, X., Liu, Q., Luo, J.-W., Freeman, A. J. & Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387–393 (2014).
Sigrist, M. et al. Superconductors with staggered non-centrosymmetricity. J. Phys. Soc. Jpn. 83, 061014 (2014).
Wilson, J. A., Di Salvo, F. J. & Mahajan, S. Charge-density waves in metallic, layered, transition-metal dichalcogenides. Phys. Rev. Lett. 32, 882 (1974).
Rossnagel, K. et al. Fermi surface of 2H-NbSe2 and its implications on the charge-density-wave mechanism. Phys. Rev. B 64, 235119 (2001).
Johannes, M. D., Mazin, I. I. & Howells, C. A. Fermi-surface nesting and the origin of the charge-density wave in 2H-NbSe2 . Phys. Rev. B 73, 205102 (2006).
Flicker, F. & van Wezel, J. Charge order from orbital-dependent coupling evidenced by NbSe2 . Nat. Commun. 6, 7034 (2015).
Weber, F. et al. Electron–phonon coupling and the soft phonon mode in TiSe2 . Phys. Rev. Lett. 107, 107403 (2011).
Rahn, D. J. et al. Gaps and kinks in the electronic structure of the superconductor 2H-NbSe2 from angle-resolved photoemission at 1 K. Phys. Rev. B 85, 224532 (2012).
Kiss, T. et al. Charge-order-maximized momentum-dependent superconductivity. Nat. Phys. 3, 720–725 (2007).
Yokoya, T. et al. Fermi surface sheet-dependent superconductivity in 2H-NbSe2 . Science 294, 2518–2520 (2001).
Borisenko, S. V. et al. Two energy gaps and Fermi-surface ‘arcs’ in NbSe2 . Phys. Rev. Lett. 102, 166402 (2009).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2 . Nat. Nano 10, 765–769 (2015).
Rice, T. M. & Scott, G. K. New mechanism for a charge-density-wave instability. Phys. Rev. Lett. 35, 120 (1975).
Shen, D. W. et al. Primary role of the barely occupied states in the charge density wave formation of NbSe2 . Phys. Rev. Lett. 101, 226406 (2008).
Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Cond. Matter. 23, 21 (2011).
Soumyanarayanan, A. et al. Quantum phase transition from triangular to stripe charge order in NbSe2 . P. Natl Acad. Sci. USA 110, 1623–1627 (2013).
Laverock, J. et al. k-resolved susceptibility function of 2H-TaSe2 from angle-resolved photoemission. Phys. Rev. B 88, 035108 (2013).
Riley, J. M. et al. Negative electronic compressibility and tunable spin splitting in WSe2 . Nat. Nano 10, 1043–1047 (2015).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nano 7, 494–498 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nano 7, 490–493 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Gong, Z. et al. Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers. Nat. Commun. 4, 2053 (2013).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Moncton, D. E. et al. Neutron scattering study of the charge-density wave transitions in 2H-TaSe2 and 2H-NbSe2 . Phys. Rev. B 16, 801 (1977).
Saito, Y. et al. Superconductivity protected by spin–valley locking in gate-tuned MoS2 . Nat. Phys. 12, 144–149 (2016).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2 . Science 350, 1353–1357 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Huang, C. L. et al. Experimental evidence for a two-gap structure of superconducting NbSe2: a specific-heat study in external magnetic fields. Phys. Rev. B 76, 212504 (2007).
Sanchez, D., Junod, A., Muller, J., Berger, H. & Lévy, F. Specific heat of 2H-NbSe2 in high magnetic fields. Phys. B 204, 167–175 (1995).
Nader, A. & Monceau, P. Critical field of 2H-NbSe2 down to 50 mK. SpringerPlus 3, 16 (2014).
Yoshida, T., Sigrist, M. & Yanase, Y. Pair-density wave states through spin–orbit coupling in multilayer superconductors. Phys. Rev. B 86, 134514 (2012).
Foner, S. & McNiff, E. J. Jr Upper critical fields of layered superconducting NbSe2 at low temperature. Phys. Lett. A 45, 429–430 (1973).
Klemm, R. A. Pristine and intercalated transition metal dichalcogenide superconductors. Phys. C 514, 86–94 (2015).
Berntsen, M. H. et al. A spin- and angle-resolving photoelectron spectrometer. Rev. Sci. Instrum. 81, 035104 (2010).
Blaha, P. et al. WIEN2K package, version 10.1. Available at http://www.wien2k.at (2010).
Souza, I. et al. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally localised Wannier functions. Comp. Phys. Commun. 178, 685699 (2008).
Kuneš, J. et al. WIEN2WANNIER: from linearized augmented plane waves to maximally localized Wannier functions. Comp. Phys. Commun. 181, 1888–1895 (2010).
Acknowledgements
We thank M.R. Lees for assistance with the transport measurements and C. Hooley, P. Wahl, A.P. Mackenzie, S. Lee and B. Braunecker for useful discussions. We gratefully acknowledge support from the Engineering and Physical Sciences Research Council, UK (work at St Andrews under Grant No. EP/I031014/1 and work at Warwick under Grant No. EP/M028771/1) and the International Max Planck partnership. P.D.C.K. acknowledges support from the Royal Society through a University Research Fellowship. M.S.B. was supported by the Grant-in-Aid for Scientific Research (S) (No. 24224009) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. L.B., J.M.R. and V.S. acknowledge studentship funding from EPSRC through Grant Nos. EP/G03673X/1, EP/L505079/1 and EP/L015110/1, respectively. The experiments at MAX IV Laboratory were made possible through funding from the Swedish Research Council and the Knut and Alice Wallenberg Foundation. We also thank Diamond Light Source for access to beamline I05 (Proposal No. SI11383) that contributed to the results presented here.
Author information
Authors and Affiliations
Contributions
The experimental data were measured by L.B., S.P.C., F.M., J.M.R., L.J.C-M., V.S., K.W.B.H., C.M.P., J.W.W. and P.D.C.K., and analyzed by L.B.; theoretical calculations were performed by M.S.B; G.B. synthesized the samples used in this study; M.L., C.M.P., T.B., T.K.K. and M.H. maintained the synchrotron ARPES end stations and provided experimental support; P.D.C.K., M.S.B. and L.B. wrote the manuscript, with input and discussions from all co-authors; P.D.C.K. conceived the study and was responsible for overall project planning and direction.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4 (PDF 3319 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Bawden, L., Cooil, S., Mazzola, F. et al. Spin–valley locking in the normal state of a transition-metal dichalcogenide superconductor. Nat Commun 7, 11711 (2016). https://doi.org/10.1038/ncomms11711
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11711
This article is cited by
-
Every-other-layer dipolar excitons in a spin-valley locked superlattice
Nature Nanotechnology (2023)
-
A magnetic field for each electron
Nature Materials (2023)
-
Giant valley-Zeeman coupling in the surface layer of an intercalated transition metal dichalcogenide
Nature Materials (2023)
-
Fermi surface chirality induced in a TaSe2 monosheet formed by a Ta/Bi2Se3 interface reaction
Nature Communications (2022)
-
Hidden spin-orbital texture at the \(\overline{{{\Gamma }}}\)-located valence band maximum of a transition metal dichalcogenide semiconductor
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

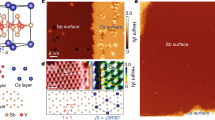



 direction. (b–f) Spin-resolved EDCs at the momenta marked in a, revealing a strong spin polarization of these electronic states along
direction. (b–f) Spin-resolved EDCs at the momenta marked in a, revealing a strong spin polarization of these electronic states along  . The horizontal axis tick marks denote the zero of each EDC.
. The horizontal axis tick marks denote the zero of each EDC.
