Abstract
The random walk formalism is used across a wide range of applications, from modelling share prices to predicting population genetics. Likewise, quantum walks have shown much potential as a framework for developing new quantum algorithms. Here we present explicit efficient quantum circuits for implementing continuous-time quantum walks on the circulant class of graphs. These circuits allow us to sample from the output probability distributions of quantum walks on circulant graphs efficiently. We also show that solving the same sampling problem for arbitrary circulant quantum circuits is intractable for a classical computer, assuming conjectures from computational complexity theory. This is a new link between continuous-time quantum walks and computational complexity theory and it indicates a family of tasks that could ultimately demonstrate quantum supremacy over classical computers. As a proof of principle, we experimentally implement the proposed quantum circuit on an example circulant graph using a two-qubit photonics quantum processor.
Similar content being viewed by others
Introduction
Quantum walks are the quantum mechanical analogue of the well-known classical random walk and they have established roles in quantum information processing1,2,3. In particular, they are central to quantum algorithms created to tackle database search4, graph isomorphism5,6,7, network analysis and navigation8,9, and quantum simulation10,11,12, as well as modelling biological processes13,14. Meanwhile, physical properties of quantum walks have been demonstrated in a variety of systems, such as nuclear magnetic resonance15,16, bulk17 and fibre18 optics, trapped ions19,20,21, trapped neutral atoms22 and photonics23,24. Almost all physical implementations of quantum walk so far followed an analogue approach as for quantum simulation25, whereby the apparatus is dedicated to implement specific instances of Hamiltonians without translation onto quantum logic. However, there is no existing method to implement analogue quantum simulations with error correction or fault tolerance, and they do not scale efficiently in resources when simulating broad classes of large graphs. Some exceptions of demonstrations of quantum walks, such as ref. 15, adopted the qubit model, but did not discuss potentially efficient implementation of quantum walks.
Efficient quantum circuit implementations of continuous-time quantum walks (CTQWs) have been presented for sparse and efficiently row-computable graphs26,27, and specific non-sparse graphs28,29. However, the design of quantum circuits for implementing CTQWs is in general difficult, since the time-evolution operator is time dependent and non-local1. A subset of circulant graphs have the property that their eigenvalues and eigenvectors can be classically computed efficiently30,31. This enables construction of a scheme that efficiently outputs the quantum state  , which corresponds to the time-evolution state of a CTQW on corresponding graphs. One can then either implement further quantum circuit operations or perform direct measurements on
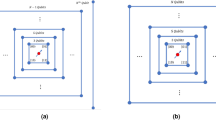
, which corresponds to the time-evolution state of a CTQW on corresponding graphs. One can then either implement further quantum circuit operations or perform direct measurements on  to extract physically meaningful information. For example the ‘SWAP test’32 can be used to estimate the similarity of dynamical behaviours of two circulant Hamiltonians operating on two different initial states, as shown in Fig. 1a. This procedure can also be adapted to study the stability of quantum dynamics of circulant molecules (for example, the DNA Möbius strips33) in a perturbational environment34,35. When measuring
to extract physically meaningful information. For example the ‘SWAP test’32 can be used to estimate the similarity of dynamical behaviours of two circulant Hamiltonians operating on two different initial states, as shown in Fig. 1a. This procedure can also be adapted to study the stability of quantum dynamics of circulant molecules (for example, the DNA Möbius strips33) in a perturbational environment34,35. When measuring  in the computational basis we can sample the probability distribution
in the computational basis we can sample the probability distribution
(a) The SWAP test32 can be used to estimate the similarity of two evolution states of two similar circulant systems, or when one of the Hamiltonians is non-circulant but efficiently implementable. In brief, an ancillary qubit is entangled with the output states  and
and  of two compared processes according to
of two compared processes according to  . On measuring the ancillary qubit we obtain outcome ‘1’ with probability
. On measuring the ancillary qubit we obtain outcome ‘1’ with probability  —the probability of observing ‘1’ indicates the similarity of dynamical behaviours of the two processes. See its complexity analysis in Supplementary Note 1. (b) Probability distributions are sampled by measuring the evolution state in a complete basis, such as the computational basis. (c) An example of the quantum circuit for implementing diagonal unitary operator D=exp(−itΛ), where the circulant Hamiltonian has 5 non-zero eigenvalues. The open and solid circles represent the control qubits as ‘if
—the probability of observing ‘1’ indicates the similarity of dynamical behaviours of the two processes. See its complexity analysis in Supplementary Note 1. (b) Probability distributions are sampled by measuring the evolution state in a complete basis, such as the computational basis. (c) An example of the quantum circuit for implementing diagonal unitary operator D=exp(−itΛ), where the circulant Hamiltonian has 5 non-zero eigenvalues. The open and solid circles represent the control qubits as ‘if  ’ and ‘if
’ and ‘if  ’, respectively.
’, respectively.  , where
, where  is the corresponding eigenvalue.
is the corresponding eigenvalue.

that describes the probability of observing the quantum walker at position x∈{0, 1}n—an n-bit string, labelling one of the 2n vertices of the given graph, as shown in Fig. 1b. Sampling of this form is sufficient to solve various search and characterization problems4,9, and can be used to deduce critical parameters of the quantum walk, such as mixing time2.
Here we present efficient quantum circuits for implementing CTQWs on circulant graphs with an eigenvalue spectrum that can be classically computed efficiently. These quantum circuits provide the time-evolution states of CTQWs on circulant graphs exponentially faster than best previously known methods30. We report a proof-of-principle experiment, where we implement CTQWs on an example circulant graph (namely the complete graph of four vertices) using a two-qubit photonics quantum processor to sample the probability distributions and perform state tomography on the output state of a CTQW. We also provide evidence from computational complexity theory that the probability distributions p(x) that are output from the circuits of this circulant form are in general hard to sample from using a classical computer, implying our scheme also provides an exponential speedup for sampling. We adapt the methodology of refs 36, 37, 38 to show that if there did exist a classical sampler for a somewhat more general class of circuits, then this would have the following unlikely complexity-theoretic implication: the infinite tower of complexity classes known as the polynomial hierarchy would collapse. This evidence of hardness exists despite the classical efficiency with which properties of the CTQW, such as the eigenvalues of circulant graphs, can be computed on a classical machine.
Results
Quantum circuit for CTQW on circulant graph
For an undirected graph G of N vertices, a quantum particle (or ‘quantum walker’) placed on G evolves into a superposition  of states in the orthonormal basis
of states in the orthonormal basis  that correspond to vertices of G. The exact evolution of the CTQW is governed by connections between the vertices of
that correspond to vertices of G. The exact evolution of the CTQW is governed by connections between the vertices of  where the Hamiltonian is given by
where the Hamiltonian is given by  for hopping rate per edge per unit time
for hopping rate per edge per unit time  and where A is the N-by-N symmetric adjacency matrix, whose entries are Ajk=1, if vertices j and k are connected by an edge in G, and Ajk=0 otherwise1. The dynamics of a CTQW on a graph with N vertices can be evaluated in time poly(N) on a classical computer. When a CTQW takes place on a graph G of exponential size, that is, N=2n for an input of size n, it becomes interesting to use quantum processors to simulate dynamics.
and where A is the N-by-N symmetric adjacency matrix, whose entries are Ajk=1, if vertices j and k are connected by an edge in G, and Ajk=0 otherwise1. The dynamics of a CTQW on a graph with N vertices can be evaluated in time poly(N) on a classical computer. When a CTQW takes place on a graph G of exponential size, that is, N=2n for an input of size n, it becomes interesting to use quantum processors to simulate dynamics.
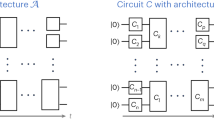
Circulant graphs are defined by symmetric circulant adjacency matrices for which each row j when right rotated by one element, equals the next row j+1—for example, complete graphs, cycle graphs and Mobius ladder graphs are all subclasses of circulant graphs, and further examples are shown in Supplementary Note 2. It follows that Hamiltonians for CTQWs on any circulant graph have a symmetric circulant matrix representation, which can be diagonalized by the unitary Fourier transform31, that is, H=Q†ΛQ, where

and Λ is a diagonal matrix containing eigenvalues of H, which are all real and whose order is determined by the order of the eigenvectors in Q. Consequently, we have exp(−itH)=Q†exp(−itΛ)Q, where the time dependence of exp(−itH) is confined to the diagonal unitary operator D=exp(−itΛ).
The Fourier transformation Q can be implemented efficiently by the well-known QFT quantum circuit39. For a circulant graph that has N=2n vertices, the required QFT of N dimensions can be implemented with O((logN)2)=O(n2) quantum gates acting on O(n) qubits. To implement the inverse QFT, the same circuit is used in reverse order with phase gates of opposite sign. D can in general be implemented using at most N=2n controlled-phase gates with phase values being a linear function of t, because an arbitrary phase can be applied to an arbitrary basis state, conditional on at most n–1 qubits. However, given a circulant graph that has O(poly(n)) non-zero eigenvalues, only O(poly(n)) controlled-phase gates are needed to implement D. If the given circulant graph has O(2n) distinct eigenvalues, which can be characterized efficiently (such as the cycle graphs and Mobius ladder graphs), then we are still able to implement the diagonal unitary operator D using polynomial quantum resources. A general construction of efficient quantum circuits for D was given by Childs40, and is shown in Supplementary Fig. 1 and Supplementary Note 3 for completeness. Thus, the quantum circuit implementations of CTQWs on circulant graphs can be constructed, which have an overall complexity of O(poly(n)), and act on at most O(n) qubits. Compared with the best-known classical algorithm based on fast Fourier transform, that has the computational complexity of O(n2n) (ref. 30), the proposed quantum circuit implementation generates the evolution state  with an exponential advantage in speed.
with an exponential advantage in speed.
Experimental demonstration
To demonstrate implementation of our scheme with two qubits, we have built photonic quantum logic to simulate CTQWs on the K4 graph—a complete graph with self loops on four vertices (Fig. 2a). The family of complete graphs KN are a special kind of circulant graph, with an adjacency matrix A where Ajk=1 for all j, k. Their Hamiltonian has only 2 distinct eigenvalues, 0 and  . Therefore, the diagonal matrix of eigenvalues of K4 is
. Therefore, the diagonal matrix of eigenvalues of K4 is  . We can readily construct the quantum circuit for implementing CTQWs on K4 based on diagonalization, using the QFT matrix. However, the choice of using the QFT matrix as the eigenbasis of Hamiltonian is not strictly necessary—any equivalent eigenbasis can be selected. Through the diagonalization using Hadamard eigenbasis, an alternative efficient quantum circuit for implementing CTQWs on K4 is shown in Fig. 2b, which can be easily extended to KN.
. We can readily construct the quantum circuit for implementing CTQWs on K4 based on diagonalization, using the QFT matrix. However, the choice of using the QFT matrix as the eigenbasis of Hamiltonian is not strictly necessary—any equivalent eigenbasis can be selected. Through the diagonalization using Hadamard eigenbasis, an alternative efficient quantum circuit for implementing CTQWs on K4 is shown in Fig. 2b, which can be easily extended to KN.
(a) The K4 graph. (b) The quantum circuit for implementing CTQW on the K4 graph. This can also be used to implement CTQW on the K4 graph without self-loops, up to a global phase factor  . H and X represent the Hadamard and Pauli-X gate, respectively.
. H and X represent the Hadamard and Pauli-X gate, respectively.  is a phase gate. (c) The experimental set-up for a reconfigurable two-qubit photonics quantum processor, consisting of a polarization-entangled photon source using paired type-I BiBO crystal in the sandwich configuration and displaced Sagnac interferometers. See further details in Methods.
is a phase gate. (c) The experimental set-up for a reconfigurable two-qubit photonics quantum processor, consisting of a polarization-entangled photon source using paired type-I BiBO crystal in the sandwich configuration and displaced Sagnac interferometers. See further details in Methods.
We built a configurable two-qubit photonics quantum processor (Fig. 2c), adapting the entanglement-based technique presented in ref. 41, and implemented CTQWs on K4 graph with various evolving times and initial states. Specifically, we prepared two different initial states  and
and  , which represent the quantum walker starting from vertex 1, and the superposition of vertices 1 and 2, respectively. We chose the evolution time following the list
, which represent the quantum walker starting from vertex 1, and the superposition of vertices 1 and 2, respectively. We chose the evolution time following the list  , which covers the whole periodical characteristics of CTQWs on K4 graph. For each evolution, we sampled the corresponding probability distribution with fixed integration time, shown in Fig. 3a,b. To measure how close the experimental and ideal probability distributions are, we calculated the average fidelities defined as
, which covers the whole periodical characteristics of CTQWs on K4 graph. For each evolution, we sampled the corresponding probability distribution with fixed integration time, shown in Fig. 3a,b. To measure how close the experimental and ideal probability distributions are, we calculated the average fidelities defined as  . The achieved average fidelities for the samplings with two distinct initial states are 96.68±0.27% and 95.82±0.25%, respectively. Through the proposed circuit implementation, we are also able to examine the evolution states using quantum state tomography, which is generally difficult for the analogue simulations. For two specific evolution states
. The achieved average fidelities for the samplings with two distinct initial states are 96.68±0.27% and 95.82±0.25%, respectively. Through the proposed circuit implementation, we are also able to examine the evolution states using quantum state tomography, which is generally difficult for the analogue simulations. For two specific evolution states  and
and  , we performed quantum state tomography and reconstructed the density matrices using the maximum likelihood estimation technique. The two reconstructed density matrices achieve fidelities of 85.81±1.08% and 88.44±0.97%, respectively, shown in Fig. 3c,d.
, we performed quantum state tomography and reconstructed the density matrices using the maximum likelihood estimation technique. The two reconstructed density matrices achieve fidelities of 85.81±1.08% and 88.44±0.97%, respectively, shown in Fig. 3c,d.
(a,b) The experimental sampled probability distributions with ideal theoretical distributions overlaid, for CTQWs on K4 graph with initial states  and
and  . The s.d. of each individual probability is also plotted, which is calculated by propagating error assuming Poissonian statistics. (c,d) The ideal theoretical and experimentally reconstructed density matrices for the states
. The s.d. of each individual probability is also plotted, which is calculated by propagating error assuming Poissonian statistics. (c,d) The ideal theoretical and experimentally reconstructed density matrices for the states  (corresponding to ρ1) and
(corresponding to ρ1) and  (corresponding to ρ2). Both of the real and imaginary parts of the density matrices are obtained through the maximum likelihood estimation technique, and is shown as Re(ρ) and Im(ρ), respectively. Further results are shown in Supplementary Table 1, Supplementary Fig. 2 and Supplementary Note 4.
(corresponding to ρ2). Both of the real and imaginary parts of the density matrices are obtained through the maximum likelihood estimation technique, and is shown as Re(ρ) and Im(ρ), respectively. Further results are shown in Supplementary Table 1, Supplementary Fig. 2 and Supplementary Note 4.
Here we have chosen to use K4 in our experiment because it is simple enough to be implementable with state of the art photonics capability, while it provides an example to demonstrate our protocol for simulating CTQW on a circulant graph with controlled quantum logic. As the size of graph increases, the simplicity of KN implies that CTQWs on this family of graphs can easily be simulated classically for arbitrary N—for CTQW on a complete graph of size N, an arbitrary output probability amplitude  can be readily obtained as
can be readily obtained as  if x=y, and
if x=y, and  otherwise, where
otherwise, where  and
and  represent the initial state and evolution state, respectively. However, our outlined quantum circuit implementation (Fig. 1) extends to implement CTQW on far more complicated circulant graphs.
represent the initial state and evolution state, respectively. However, our outlined quantum circuit implementation (Fig. 1) extends to implement CTQW on far more complicated circulant graphs.
Hardness of the sampling problem
To provide evidence that simulating CTQW on general circulant graphs is likely to be hard classically, we consider a circuit of the form Q†DQ, where D is a diagonal matrix made up of poly(n) controlled-phase gates and Q is the quantum Fourier transform. Define pD to be the probability of measuring all qubits to be 0 in the computational basis after Q†DQ is applied to the input state  . It is readily shown that
. It is readily shown that

This implies that pD can also be obtained through a circuit of form H⊗nDH⊗n with D unchanged—this represents a class of circuits known as instantaneous quantum polynomial time (IQP), which has the following structure: each qubit line begins and ends with a Hadamard (H) gate, and, in between, every gate is diagonal in the computational basis37,42. As such, pD is a probability that is classically hard to compute—it is known that computing pD for arbitrary diagonal unitaries D made up of circuits of poly(n) gates, even if each acts on O(1) qubits, is #P-hard38,43,44. This hardness result even holds for approximating pD up to any relative error strictly less than 1/2 (refs 38, 43, 44), where  is said to approximate pD up to relative error ɛ if
is said to approximate pD up to relative error ɛ if

Note that other output probabilities p(x) cannot be achieved using IQP circuits since a general circulant graph cannot be diagonalized by Hadamard matrices but rather by more heterogeneous Fourier matrices.
Towards a contradiction, assume that there exists a polynomial-time randomized classical algorithm, which samples from p, as defined in equation (1). Then a classic result of Stockmeyer45 states that there is an algorithm in the complexity class FBPPNP, which can approximate any desired probability p(x) to within relative error O(1/poly(n)). This complexity class FBPPNP—described as polynomial-time randomized classical computation equipped with an oracle to solve arbitrary NP problems—sits within the infinite tower of complexity classes known as the polynomial(-time) hierarchy46. Combining with the above hardness result of approximating pD, we find that the assumption implies that an FBPPNP algorithm solves a #P-hard problem, so P#P would be contained within FBPPNP, and therefore the polynomial hierarchy would collapse to its third level. This consequence is considered very unlikely in computational complexity theory46. A similar methodology has been used to prove the hardness of IQP and boson sampling36,37,38.
We therefore conclude that, in general, a polynomial-time randomized classical sampler from the distribution p is unlikely to exist. Further, this even holds for classical algorithms which sample from any distribution  which approximates p up to relative error strictly <1/2 in each probability p(x). It is worth noting that if the output distribution results from measurements on only O(poly(log n)) qubits47, or obeys the sparsity promise that only a poly(n)-sized, and a priori unknown, subset of the measurement probabilities are non-zero48, it could be classically efficiently sampled. It was shown in ref. 38 that assuming certain conjectures in complexity theory, it is classically hard to sample from distributions that are close in total variation distance to arbitrary IQP probability distributions. The differences between circulant and IQP circuits imply that this result does not go through immediately in our setting. Therefore, it remains open to prove hardness of approximate simulation of CTQWs on circulant graphs, which specifically requires to show that computing most of the output probabilities of circulant circuits is hard, assuming some conjectures in complexity theory.
which approximates p up to relative error strictly <1/2 in each probability p(x). It is worth noting that if the output distribution results from measurements on only O(poly(log n)) qubits47, or obeys the sparsity promise that only a poly(n)-sized, and a priori unknown, subset of the measurement probabilities are non-zero48, it could be classically efficiently sampled. It was shown in ref. 38 that assuming certain conjectures in complexity theory, it is classically hard to sample from distributions that are close in total variation distance to arbitrary IQP probability distributions. The differences between circulant and IQP circuits imply that this result does not go through immediately in our setting. Therefore, it remains open to prove hardness of approximate simulation of CTQWs on circulant graphs, which specifically requires to show that computing most of the output probabilities of circulant circuits is hard, assuming some conjectures in complexity theory.
Discussion
In this paper, we have described how CTQWs on circulant graphs can be efficiently implemented on a quantum computer, if the eigenvalues of the graphs can be characterized efficiently classically. In fact, we can construct an efficient quantum circuit to implement CTQWs on any graph whose adjacency matrix is efficiently diagonalisable, in other words, as long as the matrix of column eigenvectors Q and the diagonal matrix of the eigenvalue exponentials D can be implemented efficiently. To demonstrate our implementation scheme, we simulated CTQWs on an example 4-vertex circulant graph, K4, using a two-qubit photonic quantum logic circuit. We have shown that the problem of sampling from the output probability distributions of quantum circuits of the form Q†DQ is hard for classical computers, based on a highly plausible conjecture that the polynomial hierarchy does not collapse. This observation is particularly interesting from both perspectives of CTQW and computational complexity theory, as it provides new insights into the CTQW framework and also helps to classify and identify new problems in computational complexity theory. For the CTQWs on the circulant graphs of poly(n) non-zero eigenvalues, the proposed quantum circuit implementations do not need a fully universal quantum computer, and thus can be viewed as an intermediate model of quantum computation. Meanwhile, the evidence we provided for hardness of the sampling problem indicates a promising candidate for experimentally establishing quantum supremacy over classical computers, and further evidence against the extended Church–Turing thesis. To claim in an experiment super-classical performance based on the conjecture outlined in this work, future demonstrations would need to consider circulant graphs that are more general than KN and that are of sufficient size to be outside the capabilities of a classical computer. For photonics, the biggest challenges remain increasing the number of indistinguishable photons and controlled gate operations. For any platform, quantum circuit implementation of CTQWs could be more appealing due to available methods in fault tolerance and error correction, which are difficult to implement for other intermediate models like boson sampling49 and for analogue quantum simulation. Our results may also lead to other practical applications through the use of CTQWs for quantum algorithm design.
Methods
Experimental set-up
A diagonally polarized, 120 mW, continuous-wave laser beam with central wavelength of 404 nm is focused at the centre of paired type-I BiBO crystals with their optical axes orthogonally aligned to each other, to create the polarization entangled photon-pairs50. Through the spontaneous parametric downconversion process, the photon pairs are generated in the state of  , where H and V represent horizontal and vertical polarization, respectively. The photons pass through the polarization beam-splitter (PBS) part of the dual PBS/beam-splitter cubes on both arms to generate two-photon four-mode state of the form
, where H and V represent horizontal and vertical polarization, respectively. The photons pass through the polarization beam-splitter (PBS) part of the dual PBS/beam-splitter cubes on both arms to generate two-photon four-mode state of the form  (where r and b labels the red and blue paths shown in Fig. 2c, respectively). Rotations T1 and T2 on each path, consisting of half wave-plate (HWP) and quarter wave plate (QWP), convert the state into
(where r and b labels the red and blue paths shown in Fig. 2c, respectively). Rotations T1 and T2 on each path, consisting of half wave-plate (HWP) and quarter wave plate (QWP), convert the state into  , where
, where  and
and  can be arbitrary single-qubit states. The four spatial modes 1b, 2b, 1r and 2r pass through four single-qubit quantum gates P1, P2, Q1 and Q2, respectively, where each of the four gates is implemented through three wave plates: QWP, HWP and QWP. The spatial modes 1b and 1r (2b and 2r) are then mixed on the beam-splitter part of the cube. By post-selecting the case where the two photons exit at ports 1 and 2, we obtain the state
can be arbitrary single-qubit states. The four spatial modes 1b, 2b, 1r and 2r pass through four single-qubit quantum gates P1, P2, Q1 and Q2, respectively, where each of the four gates is implemented through three wave plates: QWP, HWP and QWP. The spatial modes 1b and 1r (2b and 2r) are then mixed on the beam-splitter part of the cube. By post-selecting the case where the two photons exit at ports 1 and 2, we obtain the state  . In this way, we implement a two-qubit quantum operation of the form P1⊗P2+Q1⊗Q2 on the initialized state
. In this way, we implement a two-qubit quantum operation of the form P1⊗P2+Q1⊗Q2 on the initialized state  .
.
As shown in Fig. 2b, the quantum circuit for implementing CTQW on the K4 graph consists of Hadamard gates (H), Pauli-X gates (X) and controlled-phase gate (CP). CP is implemented by configuring  , P2=I,
, P2=I,  ,
,  , where P1 and Q1 are implemented by polarizers. Altogether with combining the operation (H·X)⊗(H·X) before CP with state preparation and the operation (X·H)⊗X·H after CP with measurement setting, we implement the whole-quantum circuit on the experimental set-up. The evolution time of CTQW is controlled by the phase value of R, which is determined by setting the three wave plates of Q2 in Fig. 2c to
, where P1 and Q1 are implemented by polarizers. Altogether with combining the operation (H·X)⊗(H·X) before CP with state preparation and the operation (X·H)⊗X·H after CP with measurement setting, we implement the whole-quantum circuit on the experimental set-up. The evolution time of CTQW is controlled by the phase value of R, which is determined by setting the three wave plates of Q2 in Fig. 2c to  ,
,  ,
,  , where the angle
, where the angle  of HWP equals to the phase of R:−4γ t. The evolution time t is then given by
of HWP equals to the phase of R:−4γ t. The evolution time t is then given by  .
.
Additional information
How to cite this article: Qiang, X. et al. Efficient quantum walk on a quantum processor. Nat. Commun. 7:11511 doi: 10.1038/ncomms11511 (2016).
References
Farhi, E. & Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 58, 915 (1998).
Kempe, J. Quantum random walks: an introductory overview. Contemp. Phys. 44, 307–327 (2003).
Childs, A. M., Gosset, D. & Webb, Z. Universal computation by multiparticle quantum walk. Science 339, 791–794 (2013).
Childs, A. M. & Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 70, 022314 (2004).
Douglas, B. L. & Wang, J. B. A classical approach to the graph isomorphism problem using quantum walks. J. Phys. A 41, 075303 (2008).
Gamble, J. K., Friesen, M., Zhou, D., Joynt, R. & Coppersmith, S. N. Two-particle quantum walks applied to the graph isomorphism problem. Phys. Rev. A 81, 052313 (2010).
Berry, S. D. & Wang, J. B. Two-particle quantum walks: entanglement and graph isomorphism testing. Phys. Rev. A 83, 042317 (2011).
Berry, S. D. & Wang, J. B. Quantum-walk-based search and centrality. Phys. Rev. A 82, 042333 (2010).
Sánchez-Burillo, E., Duch, J., Gómez-Gardeñes, J. & Zueco, D. Quantum navigation and ranking in complex networks. Sci. Rep. 2, 605 (2012).
Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996).
Berry, D. W. & Childs, A. M. Black-box hamiltonian simulation and unitary implementation. Quantum Inf. Comput. 12, 29–62 (2012).
Schreiber, A. et al. A 2D quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786 (2007).
Rebentrost, P. et al. Environment-assisted quantum transport. New J. Phys. 11, 033003 (2009).
Du, J. et al. Experimental implementation of the quantum random-walk algorithm. Phys. Rev. A 67, 042316 (2003).
Ryan, C. A. et al. Experimental implementation of a discrete-time quantum random walk on an NMR quantum-information processor. Phys. Rev. A 72, 062317 (2005).
Do, B. et al. Experimental realization of a quantum quincunx by use of linear optical elements. J. Opt. Soc. Am. B 22, 499–504 (2005).
Schreiber, A. et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Xue, P., Sanders, B. C. & Leibfried, D. Quantum walk on a line for a trapped ion. Phys. Rev. Lett. 103, 183602 (2009).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504 (2009).
Zähringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503 (2010).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177 (2009).
Perets, H. B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).
Carolan, J. et al. On the experimental verification of quantum complexity in linear optics. Nat. Photon. 8, 621 (2014).
Manouchehri, K. & Wang, J. B. Physical Implementation of Quantum Walks Springer-Verlag (2014).
Aharonov, D. & Ta-Shma, A. in Proceedings of the 35th Annual ACM Symposium on Theory of Computing 20–29 (ACM, New York, NY, USA, 2003).
Berry, D. W., Ahokas, G., Cleve, R. & Sanders, B. C. Efficient quantum algorithms for simulating sparse hamiltonians. Commun. Math. Phys. 270, 359–371 (2007).
Childs, A. M. & Kothari, R. Limitations on the simulation of non-sparse hamiltonians. Quantum Inf. Comput. 10, 669–684 (2009).
Childs, A. M. On the relationship between continuous-and discrete-time quantum walk. Commun. Math. Phys. 294, 581–603 (2010).
Ng, M. K. Iterative Methods for Toeplitz Systems Oxford Univ. Press (2004).
Gray, R. M. Toeplitz and Circulant Matrices: A Review Now Publishers Inc. (2006).
Buhrman, H., Cleve, R., Watrous, J. & De Wolf, R. Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001).
Han, D. et al. Folding and cutting DNA into reconfigurable topological nanostructures. Nat. Nanotechnol. 5, 712–717 (2010).
Peres, A. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 30, 1610 (1984).
Prosen, T. & Znidaric, M. Stability of quantum motion and correlation decay. J. Phys. A Math. Gen. 35, 1455 (2002).
Aaronson, S. & Arkhipov, A. in Proceedings of the 43rd Annual ACM Symposium on Theory of Computing 333-342 (ACM Press, New York, NY, USA, 2011).
Bremner, M. J., Jozsa, R. & Shepherd, D. J. Classical simulation of commuting quantum computations implies collapse of the polynomial hierarchy. Proc. R. Soc. A Math. Phys. Engineering Science 467, 459–472 (2010).
Bremner, M. J., Montanaro, A. & Shepherd, D. J. Average-case complexity versus approximate simulation of commuting quantum computations. Preprint at http://arxiv.org/abs/1504.07999 (2015).
Nielsen, N. A. & Chuang, I. L. Quantum Computation and Quantum Information Cambridge Univ. Press (2010).
Childs, A. M. Quantum Information Processing in Continuous Time (PhD thesis, Massachusetts Institute of Technology (2004).
Zhou, X. Q. et al. Adding control to arbitrary unknown quantum operations. Nat. Commun. 2, 413 (2011).
Shepherd, D. & Bremner, M. J. Temporally unstructured quantum computation. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science 465, 1413–1439 (2009).
Fujii, K. & Morimae, T. Quantum commuting circuits and complexity of Ising partition functions. Preprint at http://arxiv.org/abs/1311.2128 (2013).
Goldberg, L. A. & Guo, H. The complexity of approximating complex-valued Ising and Tutte partition functions. Preprint at http://arxiv.org/abs/1409.5627 (2014).
Stockmeyer, L. J. On approximation algorithms for #P. SIAM J. Comput. 14, 849–861 (1985).
Papadimitriou, C. Computational Complexity Addison-Wesley (1994).
Nest, M. Simulating quantum computers with probabilistic methods. Quantum Inf. Comput. 11, 784–812 (2011).
Schwarz, M. & Nest, M. Simulating quantum circuits with sparse output distributions. Preprint at http://arxiv.org/abs/1310.6749 (2013).
Rohde, P. P. & Ralph, T. C. Error tolerance of the boson-sampling model for linear optics quantum computing. Phys. Rev. A 85, 022332 (2012).
Rangarajan, R., Goggin, M. & Kwiat, P. Optimizing type-I polarization-entangled photons. Opt. Express 17, 18920–18933 (2009).
Acknowledgements
We thank Anthony Laing and Peter J. Shadbolt for helpful discussions. We acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC), the European Research Council (ERC)—including BBOI, QUCHIP (H2020-FETPROACT-3-2014: Quantum simulation) and PIQUE (FP7-PEOPLE-2013-ITN)—the Centre for Nanoscience and Quantum Information (NSQI), the US Army Research Office (ARO) grant W911NF-14-1-0133. X.Q. acknowledges support from University of Bristol and China Scholarship Council. T.L. is supported by an International Postgraduate Research Scholarship, Australian Postgraduate Award and the Bruce and Betty Green Postgraduate Research Top-Up Scholarship. J.L.O.B. acknowledges a Royal Society Wolfson Merit Award and a Royal Academy of Engineering Chair in Emerging Technologies. J.B.W. acknowledges the Benjamin Meaker visiting professorship provided by IAS at University of Bristol. J.C.F.M. was supported by a Leverhulme Trust Early Career Fellowship and an EPSRC Early Career Fellowship.
Author information
Authors and Affiliations
Contributions
X.Q., T.L., J.L.O.B., J.B.W. and J.C.F.M. conceived and designed the project. T.L. and J.B.W. proposed the circuit construction scheme. X.Q., K.A. and X.Z. built the experiment set-up. X.Q. performed the experiments and analysed the data. A.M. provided the complexity theory proofs. X.Q., T.L., A.M., J.L.O.B., J.B.W. and J.C.F.M. wrote the manuscript. J.L.O.B., J.B.W. and J.C.F.M. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-2, Supplementary Table 1, Supplementary Notes 1-4 and Supplementary References (PDF 573 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Qiang, X., Loke, T., Montanaro, A. et al. Efficient quantum walk on a quantum processor. Nat Commun 7, 11511 (2016). https://doi.org/10.1038/ncomms11511
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11511
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.