Abstract
Designing new materials with novel topological properties and reduced dimensionality is always desirable for material innovation. Here we report the design of a two-dimensional material, namely Be5C2 monolayer on the basis of density functional theory computations. In Be5C2 monolayer, each carbon atom binds with five beryllium atoms in almost the same plane, forming a quasi-planar pentacoordinate carbon moiety. Be5C2 monolayer appears to have good stability as revealed by its moderate cohesive energy, positive phonon modes and high melting point. It is the lowest-energy structure with the Be5C2 stoichiometry in two-dimensional space and therefore holds some promise to be realized experimentally. Be5C2 monolayer is a gapless semiconductor with a Dirac-like point in the band structure and also has an unusual negative Poisson’s ratio. If synthesized, Be5C2 monolayer may find applications in electronics and mechanics.
Similar content being viewed by others
Introduction
Carbon in known molecules and materials typically has tetrahedral tetracoordination (for example, diamond), planar tricoordination (for example, graphite) or linear dicoordination (for example, ethyne) arrangements. Especially, the tetrahedral preference of tetracoordinate carbon compounds, which was deduced by van’t Hoff1 and Lebel2 more than a century ago, is one of the major foundations of organic chemistry. In 1968, Monkhorst3 first discussed an exceptional bonding pattern of carbon, namely planar tetracoordinate carbon (ptC), by proposing a planar methane (D4h), which is actually not a minimum energy structure. Later in 1970, by insightful analysis of ptC bonding in the hypothetical planar methane, Hoffman et al.4 suggested that ptCs can be stabilized electronically by replacing H atoms in planar methane by σ donors (to facilitate electron transfer to electron-deficient σ bonds) or π acceptors (to delocalize the unfavourable lone pair of ptC). Along this line, in 1976 Collins et al.5 theoretically devised the first ptC-containing molecule 1, 1-dilithiocyclopropane. One year later Cotton and Millar6 synthesized the first ptC-containing molecule, although the unique ptC configuration was not recognized at that time. Ever since, ptC chemistry has been a subject of extensive studies7,8,9. Numerous ptC species have been designed theoretically10,11,12,13,14,15 and some global minimum structures, such as CAl4+ (ref. 16), CAl42+ (ref. 17) and CAl3Si− (ref. 18) have been observed experimentally. More excitingly, besides ptC, many molecules containing planar pentacoordinate carbon (ppC)19,20,21,22 and hexacoordinate carbon (phC)23,24,25 have been designed computationally. The rule-breaking chemical bonding in these planar hypercoordinate carbons can lead to completely new molecules and materials, which are of fundamental importance to chemistry and materials science.
The unique topology and dimensionality may lead to exceptional properties of materials. It is not a surprise to witness the growing interest in designing ptC-containing solids and nanostructures in recent years26,27,28,29,30. Especially, stimulated by the extensive studies of graphene31,32 and inorganic layered materials33,34, many two-dimensional (2D) materials with rule-breaking chemical bonding have been designed computationally35,36,37,38,39,40,41,42. For example, on the basis of ptC molecule CB4 (ref. 43), Wu et al.35 designed the first ptC-containing 2D material, namely B2C graphene, which was later confirmed to be only a local minimum44. Li et al.36 and Dai et al.37 predicted that Al2C monolayer in its lowest-energy configuration have all C atoms being ideal ptC. More interestingly, Li et al.45 demonstrated recently that one C atom can bind to six beryllium (Be) atoms in an almost planar manner, yielding a phC-featuring 2D material with a Be2C stoichiometry. With intriguing structural and electronic properties, these 2D materials are expected to have important applications in some specific fields.
In contrast to ptC and phC, no attempt exists for extending ppC into solids until now. Motivated by the successful design of ptC- and phC-containing materials, we are quite curious whether it is possible to extend ppC into solids. Addressing this issue would deliver not only unique structures but also some fantastic properties, which is of both theoretical and practical importance.
In this work, by means of density functional theory (DFT) computations, we first confirm that the ppC molecule Be9C24− is a local minimum on the potential energy surface. Based on the structural characters of Be9C24−, we design a ppC-containing 2D material, namely Be5C2 monolayer, in which each C atom binds to five Be atoms to form a quasi-planar pentacoordinate moiety. Our Be5C2 monolayer has rather good thermal and kinetic stabilities and is energetically the most favourable isomer in 2D space. Dramatically, the electronic band structure of Be5C2 monolayer has a Dirac-like point at the Fermi level, endowing an intriguing semimetallic feature. More interestingly, Be5C2 monolayer possesses a negative Poisson’s ratio, which is rather rare in nanostructures. These fascinating properties make Be5C2 monolayer a promising candidate for future applications in electronics and mechanics.
Results
Be9C24− as the inspiring ppC species for 2D monolayer
Our design of periodic 2D Be5C2 monolayer is initially inspired by our finding of the ppC molecule, namely Be9C24−, which has singlet ground state and D2h symmetry (Fig. 1a). Computed at B3LYP level of theory with 6–311+G*(d, p) basis set, Be9C24− is a local minimum with the lowest vibrational frequency of 158.5 cm−1. In this molecule, each C atom binds to five Be atoms to form a ppC moiety of Be5C, which has been shown to be a local minima20. Structurally, Be9C24− can be viewed as two Be5C moieties fused by sharing one Be atom. The C–Be bond lengths are in the range of 1.70–1.76 Å, whereas the Be–Be bond lengths are in the range of 2.02–2.39 Å.
(a) Optimized geometric structure of Be9C24− molecule. The black and green balls represent C and Be atoms, respectively. The red and black numbers are the Wiberg bond index (WBI) and lengths (in angstroms) of the representative chemical bonds, respectively. (b) The canonical molecular orbitals of Be9C24−.
According to the natural population analysis, each ppC of Be9C24− possesses a 2.18 |e| negative charge (−0.40 |e| according to the Hirshfeld charge population analysis) and the natural electron configuration is 2s1.422px1.472py1.662pz1.60, indicating that ppCs in Be9C24− are essentially stabilized through Be σ-donation and delocalization of carbon 2pz electrons. The computed Wiberg bond index for C–Be bonds are 0.52 and 0.61, respectively, resulting in a total Wiberg bond index of 2.81 for each ppC. Moreover, we also scrutinized the molecular orbitals of Be9C24− to get more information on its stabilization mechanism. As shown in Fig. 1b, the highly delocalized π (for example, HOMO-7 and HOMO-8) and σ (for example, HOMO-3, HOMO-4 and HOMO-5) orbitals can help maintain the planar configuration.
Geometric properties of Be5C2 monolayer
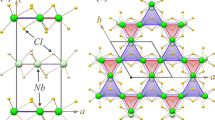
The fusing of two Be5C moieties to Be9C24− reminds us of the roadmap of fusing benzene rings to polycyclic aromatic hydrocarbons (for example, naphthalene and anthracene) and then to 2D infinite graphene. Inspired by the ppC-containing Be9C24−, we designed a new 2D inorganic material, namely Be5C2 monolayer by generalizing the structural characters of Be9C24−. As shown in Fig. 2a, 1 unit cell of Be5C2 monolayer consists of 8 C atoms and 20 Be atoms with the optimized lattice parameters being a=8.92 Å and b=9.21 Å, respectively. Similar to Be9C24−, in Be5C2 monolayer each C atom binds to five Be atoms to form a ppC moiety of Be5C and two neighbouring Be5C moieties share one Be atom (Be1) to form a Be9C2 moiety in the a (Be9C2-I) or b (Be9C2-II) direction. Especially, one Be9C2-I moiety is fused with four neighbouring Be9C2-II moieties by sharing the peripheral Be atoms (Be2) and vice versa, leading to the formation of a 2D network with four Be9C2 moieties in one unit cell. The optimized coordinates of Be5C2 monolayer are presented in Supplementary Table 1. It is noteworthy that the Be5C2 monolayer is remarkably buckled rather than an exactly planar structure (Fig. 2b). The buckling, measured by the vertical distance between the bottommost Be atoms and the uppermost Be atom, is as high as 2.14 Å. Even so, the ppCs in Be5C2 monolayer still have a good planarity (Supplementary Fig. 1). According to our computations, the total degrees of five Be–C–Be angles for ppCs in Be9C2-I and Be9C2-II moieties are 371.44° and 364.84°, respectively, which are a little higher than the ideal 360°. Interestingly, when Be9C24− is neutralized by four protons (H+), the obtained Be9C2H4 molecule is also severely buckled (Supplementary Fig. 2). In Be5C2 monolayer, the length of C–Be1 bonds (1.66 Å, 1.68 Å) is much shorter than that of C–Be2 bonds (1.73 Å, 1.74 Å). Moreover, our computations revealed that Be5C2 monolayer has a non-magnetic ground state, indicating that there are no unpaired electrons in Be5C2 monolayer.
(a) Top and (b) side views of geometric structure of Be5C2 monolayer. The blue dashed lines denote a unit cell; a and b represent the lattice vectors, 1 and 2 denote the different Be atoms, I and II represent the different Be9C2 moieties. (c) Deformation charge density of 2D Be5C2 monolayer. Red and yellow refer to electron accumulation and depletion regions, respectively.
We then computed the deformation electronic density of Be5C2 monolayer to elucidate its bonding nature. The deformation electronic density is defined as the total electronic density excluding those of isolated atoms. As clearly shown in Fig. 2c, some electrons are extracted from the 2s orbitals of Be atoms and well delocalized over C–Be bonds, indicating that C atoms form multicentre covalent bonds with neighbouring Be atoms, which is crucial for stabilizing the ppC moieties. The similar stabilizing mechanism has been found in ptC- and phC-containing 2D materials35,36,37,38,39,40,45. According to the Hirshfeld charge popular analysis, C, Be1 and Be2 atoms in Be5C2 monolayer possess a −0.32, +0.16 and +0.12 |e| charge, respectively. The buckling of Be5C2 monolayer stretches the Be–Be distances and probably helps reduce the otherwise even stronger repulsive interactions between Be atoms.
We also used the recently developed Solid State Adaptive Natural Density Partitioning (SSAdNDP) method46 to better understand the unique chemical bonding of Be5C2 monolayer. According to our results (Supplementary Fig. 3), there is no classical two-centre–two-electron (2c–2e) C–Be bond in Be5C2 monolayer. For one unit cell of Be5C2 monolayer, the SSAdNDP search revealed twenty-four 3c–2e Be–C–Be σ-bonds (responsible for the bonding within the Be5C units), four 4c–2e σ-bonds on four Be squares and eight 6c–2e π-bonds over eight Be5C units, accounting for 72 electrons per unit cell. This bonding pattern is consistent with the symmetry of Be5C2 monolayer. Especially, the existence of delocalized σ- and π-bonds could essentially stabilize the ppCs in Be5C2 monolayer.
Stability of Be5C2 monolayer
Although Be5C2 monolayer has rather intriguing structural properties, we are unclear whether it is a stable structure. To assess the stability, we first computed the cohesive energy of Be5C2 monolayer, which is defined as: Ecoh=(nEC+mEBe−E)/(n+m), in which EC, EBe and E are the total energies of a single C atom, a single Be atom and Be2C monolayer, respectively; n and m are the number of C and Be atoms in the supercell, respectively. According to our computations, Be5C2 monolayer has a cohesive energy of 4.58 eV per atom. As a reference, the cohesive energies of the experimentally realized 2D silicene47,48 and phosphorene49,50 are 3.71 and 3.61 eV per atom, respectively. As silicene and phosphorene are composed of covalent bonds, the even higher cohesive energy can ensure that Be5C2 monolayer is a strongly connected network.
The stability of Be5C2 monolayer can be further confirmed by its phonon dispersion curves. As shown in Fig. 3a, no appreciable imaginary phonon mode is present, suggesting the good kinetic stability of Be5C2 monolayer. Remarkably, the highest frequency of Be5C2 monolayer reaches up to 1,120 cm−1, which is higher than those of MoS2 monolayer (473 cm−1)51, silicene (580 cm−1)52 and our recently designed phC-containing Be2C monolayer (1,020 cm−1)45, indicating robust C–Be bonds in Be5C2 monolayer. The analysis of partial phonon density of states (DOS; Fig. 3b) revealed that the highest frequency of Be5C2 monolayer is mainly contributed by C–Be1 bonds.
Moreover, to examine the thermal stability of Be5C2 monolayer, we performed first-principles molecular dynamic (FPMD) simulations using a 2 × 2 supercell. Our three simulations at temperature of 1,000, 1,500 and 2,000 K show that Be5C2 monolayer can maintain its structural integrity throughout a 10-ps FPMD simulation up to 1,500 K, but is seriously disrupted at 2,000 K, suggesting that Be5C2 monolayer has a melting point between 1,500 and 2,000 K (Supplementary Fig. 4). We also performed optimizations for the distorted structures from MD simulations. After full atomic relaxation, those structures from MD simulations at 1,000 and 1,500 K can recover the initial configuration of Be5C2 monolayer. The above results demonstrate that Be5C2 monolayer has a remarkable thermal stability.
The moderate cohesive energy, all positive phonon modes and good thermal stability can ensure that Be5C2 monolayer is at least a local minimum structure on the potential energy surface. However, is the ppC-containing Be5C2 monolayer a global minimum? It is noteworthy that the global minimum structure is more likely to be achieved than the local minimum structures experimentally. For example, many isomers of graphene, such as Haeckelite graphene53, T-graphene54 and penta-graphene55 have been designed computationally, but none of them has been realized experimentally. Therefore, we performed a global search for the lowest-energy structure of Be5C2 monolayer in the 2D space using first-principles-based particle-swarm optimization (PSO) method as implemented in CALYPSO code. After a comprehensive search, we obtained three stable isomers of 2D Be5C2, which are labelled as Be2C5-I, Be2C5-II and Be2C5-III, respectively. As shown in Fig. 4a, Be2C5-I is actually the above discussed ppC-featuring Be5C2 monolayer. Interestingly, in Be2C5-II (Fig. 4b) and Be2C5-III (Fig. 4c), each C atom binds to five Be atoms to form a ppC moiety of Be5C and the Be9C2 moieties also can be found in these two isomers. Be2C5-I is 50 and 101 meV per atom lower in energy than Be2C5-II and Be2C5-III, respectively, indicating that Be2C5-I is the global minimum structure in the 2D space. Therefore, the ppC-featuring Be5C2 monolayer holds great potential to be realized experimentally.
Electronic properties of Be5C2 monolayer
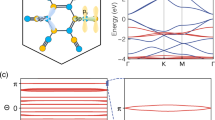
With such interesting structural characteristics, does Be5C2 monolayer also have intriguing properties? To address this issue, we computed the band structure of the lowest-energy Be5C2 monolayer. As shown in Fig. 5a, Be5C2 monolayer is gapless or semi-metallic with the conduction band minimum (CBM) and valence band maximum (VBM) meeting at the Fermi level, which is quite similar to that of graphene. However, the meeting point of Be5C2 monolayer is located on the path from G (0, 0, 0) point to Y (0, 0.5, 0) point rather than on a high-symmetry point as for graphene. Especially, the conduction and valence bands around the Fermi level exhibit a linear dispersion relation, suggesting that the meeting point of Be5C2 monolayer is also Dirac-like. Considering that the PBE functional tend to underestimate the band gap, we recomputed the band structure of Be5C2 monolayer using the hybrid HSE06 functional56 and found that the dispersion of the valence and conduction bands at the Fermi level is similar to that predicted by PBE and no appreciable band gap can be identified (Supplementary Fig. 5). Thus, the gapless property of Be5C2 monolayer is solid.
To obtain deeper insight into the electronic properties of Be5C2 monolayer, we analysed its DOS. As shown in Fig. 5b, the DOS is zero at the Fermi level, which further supports the presence of the Dirac cone. The partial DOS analysis shows that the VBM and CBM are contributed by both Be-2p and C-2p states, and the contribution from Be-2p states is much more than that from C-2p states. Moreover, we plotted the partial charge densities of the VBM and CBM. As shown in Fig. 5c,d, both VBM and CBM are mainly originated from the delocalized orbitals of Be atoms and partially from the multicentre bonding between C and Be atoms.
Mechanical properties of Be5C2 monolayer
Besides the electronic properties, we also investigated the mechanical properties of Be5C2 monolayer by examining its elastic constants. As a validation, the computed elastic constants of graphene are C11=C22=342.93 GPa and C12=C21=62.23 GPa respectively, which achieve good agreements with experimental measurements57 and previous computations58. For Be5C2 monolayer, its elastic constants were computed to be C11=32.90 GPa, C22=130.89 GPa, C12=C21=−5.32 GPa and C66=48.32 GPa, which are in agreement with the mechanical stability criteria for a tetragonal 2D sheet (C11C22−C122>0, C66>0)55. The in-plane Young’s modules along a (Ya) and b (Yb) directions, which can be deduced from the elastic constants by Ya=(C11C22−C12C21)/C22 and Yb=(C11C22−C12C21)/C11, were computed to be 32.68 and 130.03 N m−1, respectively. As Ya is not equal to Yb, Be5C2 monolayer is mechanically anisotropic. Moreover, computed at the same level of theory, the in-plane Young’s modules of Be5C2 monolayer are less than those of graphene (Ya=Yb=331.63 N m−1) but higher than those of phosphorene (Ya=25.50 N m−1 and Yb=91.61 N m−1), suggesting that Be5C2 monolayer has good mechanical properties.
Remarkably, we noted that Be5C2 monolayer has a negative C12, which results in negative Poisson’s ratios of −0.041 (C12/C22) and −0.16 (C12/C11) for a and b directions, respectively. It is noteworthy that the Poisson’s ratio is defined as the negative ratio of transverse to axial strain. The negative Poisson’s ratio indicates that Be5C2 monolayer can be compressed or stretched in both two directions at the same time. For a validation, we applied a uniaxial strain of 5% in a and b directions of Be5C2 monolayer, respectively. Just as expected, the equilibrium lattice parameters of b and a directions are elongated by ∼0.2 and ∼0.8%, respectively, confirming that Be5C2 monolayer indeed has negative Poisson’s ratios.
Discussion
The unusual negative Poisson’s ratio may endow Be5C2 monolayer with enhanced toughness and shear resistance, as well as enhanced sound and vibration adsorption. Correspondingly, Be5C2 monolayer could find some important applications in the fields of mechanics, tissue engineering and national security. It is worth noting that the negative Poisson’s ratio is rather peculiar, as in nature nearly all materials have a positive Poisson’s ratio, except some so-called auxetic materials59. Recently, Jiang et al.60 demonstrated theoretically that single-layer black phosphorus has a negative Poisson’s ratio due to the unique puckered configuration. However, the negative Poisson’s ratio of phosphorene was observed in the out-of-plane direction, which is different from that of Be5C2 monolayer. Remarkably, the Poisson’s ratio of Be5C2 monolayer in the b direction (−0.16) is much higher than that of phosphorene (−0.027)60, rendering Be5C2 monolayer a more promising candidate for specific application in mechanical devices. No doubt, the negative Poisson’s ratio of Be5C2 monolayer should be originated from its intriguing structural properties, especially the uniquely oriented chemical bonds. Our results could provide some guidelines for designing materials with a negative Poisson ’s ratio.
With so many fascinating properties, it is desirable to synthesize Be5C2 monolayer in the laboratory. Considering that there is no layered structure of Be5C2 in nature, a promising approach is to grow Be5C2 monolayer on the surface of metal or metal oxide via chemical vapour deposition with accurately controlled Be/C ratio, just similar to the growth of silicene47,48. It is noteworthy that Be has toxic properties and the chemical vapour deposition synthesis usually requires high temperature; hence, special caution should be given during the experimental realization.
To summarize, inspired by the bonding characters of a ppC-containing molecule, Be9C24−, we designed a ppC-containing 2D inorganic material with a Be5C2 stoichiometry. Our DFT computations demonstrated that ppCs in Be5C2 monolayer are essentially stabilized by the charge transfer from Be ligands. The moderate cohesive energy, absence of imaginary modes in phonon spectrum and high melting point evaluated from FPMD simulations indicated that Be5C2 monolayer is experimentally viable. Especially, a global minimum search revealed that Be5C2 monolayer is the lowest-energy structure for the Be5C2 stoichiometry in 2D space, which endows Be5C2 monolayer great possibility to be realized experimentally. Our computations demonstrated that Be5C2 monolayer is semi-metallic with a zero band gap in the electronic band structure. More interestingly, Be5C2 monolayer has rather intriguing mechanical properties featured with a negative Poisson’s ratio. Therefore, Be5C2 monolayer is expected to have wide applications in electronics and mechanics. We hope our theoretical studies will promote the experimental realization of this novel material and attract more attentions on investigating nanomaterials with novel chemical bonding.
Methods
DFT computations
For the Be9C24− molecule, geometry optimizations, frequency analyses and electronic structure computations were performed at the B3LYP61,62 level of theory with the 6–311+G*(d, p) basis set as implemented in Gaussian 03 package63. For 2D Be5C2 monolayer, DFT computations were performed using the plane-wave technique implemented in Vienna ab initio simulation package64. The ion–electron interaction was described using the projector-augmented plane wave approach65,66. The generalized gradient approximation expressed by PBE functional67 and a 500-eV cutoff for the plane-wave basis set were adopted in all the computations. The convergence threshold was set as 10−4 eV in energy and 10−3 eV Å−1 in force. We set the x and y directions parallel and the z direction perpendicular to the layer plane, and adopted a supercell length of 15 Å in the z direction. The Brillouin zones was sampled with an 8 × 6 × 1 Γ centred k points grid. The phonon spectrum was computed using finite displacement method as implemented in CASTEP code68. The elastic constants were also computed using the CASTEP code. The chemical bonding analysis of Be5C2 monolayer was done using the SSAdNDP method46, which can well interpret the chemical bonding in terms of classical lone pairs, two-centre bonds, as well as multi-centre delocalized bonds in bulk solids, surfaces and nanostructures.
Molecular dynamics simulations
The thermal stability of Be5C2 monolayer was evaluated by means of first-principles molecular dynamics simulations. The ground-state structure of Be2C monolayer was annealed at different temperatures. At each temperature, MD simulation in NVT ensemble lasts for 10 ps with a time step of 1.0 fs. The temperature was controlled by using the Nosé-Hoover method69.
Global minimum structure searches
The PSO method within the evolutionary scheme as implemented in the CALYPSO code70 was employed to find the low-energy structures of 2D Be5C2 monolayer. In our PSO simulation, the number of generation was maintained at 30. Unit cells containing total atoms of 7, 14 and 28 were considered. The structure relaxations during the PSO simulation were performed using Vienna ab initio simulation package at PBE level of theory.
Data availability
All relevant data are available from the authors.
Additional information
How to cite this article: Wang, Y. et al. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat. Commun. 7:11488 doi: 10.1038/ncomms11488 (2016).
References
van’tHoff, J. H. On the structure formulas in three-dimensional space. Arch. Neerl. Sci. Exactes Nat. 445–454 (1874).
LeBel, J. A. Sur les relations qui existent entre les formules atomiques des coprs organique et le pouvoir de leurs dissolutions. Bull. Soc. Chim. Fr. 22, 337–347 (1874).
Monkhorst, H. J. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1111–1112 (1968).
Hoffmann, R., Alder, R. W. & Wilcox, C. F. Jr Planar tetracoordinate carbon. J. Am. Chem. Soc. 92, 4992–4993 (1970).
Collins, J. B. et al. Stabilization of planar tetracoordinate carbon. J. Am. Chem. Soc. 98, 5419–5427 (1976).
Cotton, F. A. & Millar, M. The probable existence of a triple bond between two vanadium atoms. J. Am. Chem. Soc. 99, 7886–7891 (1977).
Keese, R. Carbon flatland: planar tetracoordinate carbon and fenestranes. Chem. Rev. 106, 4787–4808 (2006).
Merino, G., Mendez-Rojas, M. A., Vela, A. & Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 28, 362–372 (2007).
Yang, L.-M., Ganz, E., Chen, Z., Wang, Z.-X. & Schleyer, P. v. R. Four decades of the chemistry of planar hypercoordinate compounds. Angew. Chem. Int. Ed. 54, 9468–9501 (2015).
Krogh-Jespersen, M.-B., Chandrasekhar, J., Wuerthwein, E.-U., Collins, J. B. & Schleyer, P. v. R. Molecular orbital study of tetrahedral, planar, and pyramidal structures of the isoelectronic series BH4−, CH4, NH4+, AlH4−, SiH4, and PH4+. J. Am. Chem. Soc. 102, 2263–2268 (1980).
Boldyrev, A. I. & Simons, J. Tetracoordinated planar carbon in pentaatomic molecules. J. Am. Chem. Soc. 120, 7967–7972 (1998).
Merino, G., Méndez-Rojas, M. A. & Vela, A. (C5M2-n)n− (M=Li, Na, K, and n=0, 1, 2). A new family of molecules containing planar tetracoordinate carbons. J. Am. Chem. Soc. 125, 6026–6027 (2003).
Merino, G. et al. Theoretical analysis of the smallest carbon cluster containing a planar tetracoordinate carbon. J. Am. Chem. Soc. 126, 16160–16169 (2004).
Wang, Z. X., Zhang, C. G., Chen, Z. F. & Schleyer, P. v. R. Planar tetracoordinate carbon species involving beryllium substituents. Inorg. Chem. 47, 1332–1336 (2008).
Wu, Y. B., Lu, H. G., Li, S. D. & Wang, Z. X. Simplest neutral singlet C2E4 (E=Al, Ga, In, and Tl) global minima with double planar tetracoordinate carbons: equivalence of C2 moieties in C2E4 to carbon centers in CAl42− and CAl5+. J. Phys. Chem. A 113, 3395–3402 (2009).
Li, X., Zhang, H.-F., Wang, L.-S., Boldyrev, A. I. & Simons, J. Tetracoordinated planar carbon in the Al4C−Anion: a combined photoelectron spectroscopy and ab initio study. J. Am. Chem. Soc. 121, 6033–6038 (1999).
Li, X., Zhang, H.-F., Wang, L.-S., Geske, G. D. & Boldyrev, A. I. Pentaatomic tetracoordinate planar carbon, [CAl4]2−: a new structural unit and its salt complexes. Angew. Chem. Int. Ed. 39, 3630–3632 (2000).
Wang, L.-S., Boldyrev, A. I., Li, X. & Simons, J. Experimental observation of pentaatomic tetracoordinate planar carbon-containing molecules. J. Am. Chem. Soc. 122, 7681–7687 (2000).
Wang, Z.-X. & Schleyer, P. v. R. Construction principles of “hyparenes”: families of molecules with planar pentacoordinate carbons. Science 292, 2465–2469 (2001).
Pei, Y., An, W., Ito, K., Schleyer, P. v. R. & Zeng, X. C. Planar pentacoordinate carbon in CAl5+: a global minimum. J. Am. Chem. Soc. 130, 10394–10400 (2008).
Jimenez-Halla, J. O. et al. CAl4Be and CAl3Be2−: global minima with a planar pentacoordinate carbon atom. Chem. Commun. 46, 8776–8778 (2010).
Grande-Aztatzi, R. et al. Planar pentacoordinate carbons in CBe54− derivatives. Phys. Chem. Chem. Phys. 17, 4620–4624 (2015).
Exner, K. & Schleyer, P. v. R. Planar hexacoordinate carbon: a viable possibility. Science 290, 1937–1940 (2000).
Ito, K. et al. Myriad planar hexacoordinate carbon molecules inviting synthesis. J. Am. Chem. Soc. 129, 1510–1511 (2007).
Wang, Z.-X. & Schleyer, P. v. R. Planar hypercoordinate carbons joined: wheel-shaped molecules with C–C axles. Angew. Chem. Int. Ed. 41, 4082–4085 (2002).
Pancharatna, P. D., Méndez-Rojas, M. A., Merino, G., Vela, A. & Hoffmann, R. Planar tetracoordinate carbon in extended systems. J. Am. Chem. Soc. 126, 15309–15315 (2004).
Yang, L. M., Ding, Y. H. & Sun, C. C. Design of sandwich-like complexes based on the planar tetracoordinate carbon unit CAl42−. J. Am. Chem. Soc. 129, 658–665 (2007).
Zhang, C. J., Sun, W. X. & Cao, Z. X. Zigzag boron-carbon nanotubes with quasi-planar tetracoordinate carbons. J. Am. Chem. Soc. 130, 5638–5639 (2008).
Wu, M.-H., Pei, Y. & Zeng, X. C. Planar tetracoordinate carbon strips in edge decorated graphene nanoribbon. J. Am. Chem. Soc. 132, 5554–5555 (2010).
Wu, Y. B., Jiang, J. L., Zhang, E. W. & Wang, Z. X. Computationally designed families of flat, tubular, and cage molecules assembled with “starbenzene” building blocks through hydrogen-bridge bonds. Chem. Eur. J. 16, 1271–1280 (2010).
Novoselov, K. S. et al. A roadmap for graphene. Nature 490, 192–200 (2012).
Tang, Q., Zhou, Z. & Chen, Z. Graphene-related nanomaterials: tuning properties by functionalization. Nanoscale 5, 4541–4583 (2013).
Xu, M. S., Liang, T., Shi, M. & Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 113, 3766–3798 (2013).
Tang, Q., Zhou, Z. & Chen, Z. Innovation and discovery of graphene-like materials via density functional theory computations. WIREs Comput. Mol. Sci. 5, 360–379 (2015).
Wu, X. J., Pei, Y. & Zeng, X. C. B2C graphene, nanotubes, and nanoribbons. Nano Lett. 9, 1577–1582 (2009).
Li, Y., Liao, Y., Schleyer, P. v. R. & Chen, Z. Al2C monolayer: the planar tetracoordinate carbon global minimum. Nanoscale 6, 10784–10791 (2014).
Dai, J., Wu, X., Yang, J. & Zeng, X. AlxC monolayer sheets: two-dimensional networks with planar tetracoordinate carbon and potential applications as donor materials in solar cell. J. Phys. Chem. Lett. 5, 2058–2065 (2014).
Zhang, Z., Liu, X., Yakobson, B. I. & Guo, W. Two-dimensional tetragonal TiC monolayer sheet and nanoribbons. J. Am. Chem. Soc. 133, 19326–19329 (2012).
Li, Y., Li, F., Zhou, Z. & Chen, Z. SiC2 silagraphene and its one-dimensional derivatives: where planar tetracoordinate silicon happens. J. Am. Chem. Soc. 133, 900–908 (2011).
Yang, L.-M. et al. Two-dimensional Cu2Si monolayer with planar hexacoordinate copper and silicon bonding. J. Am. Chem. Soc. 137, 2757–2762 (2015).
Yang, L.-M. et al. Revealing unusual chemical bonding in planar hyper-coordinate Ni2Ge and quasi-planar Ni2Si two-dimensional crystals. Phys. Chem. Chem. Phys. 17, 26043–26048 (2015).
Yang, L.-M. et al. Post-anti-van’t Hoff-Le Bel motif in atomically thin germanium ally film. Phys. Chem. Chem. Phys. 17, 17545–17551 (2015).
Pei, Y. & Zeng, X. C. Probing the planar tetra-, penta-, and hexacoordinate Carbon in carbon-boron mixed clusters. J. Am. Chem. Soc. 130, 2580–2592 (2008).
Luo, X. et al. Predicting two-dimensional boron-barbon compounds by the global optimization method. J. Am. Chem. Soc. 133, 16285–16290 (2011).
Li, Y., Liao, Y. & Chen, Z. Be2C monolayer with quasi-planar hexacoordinate carbons: a global minimum structure. Angew. Chem. Int. Ed. 53, 7248–7252 (2014).
Galeev, T. R., Dunnington, B. D., Schmidt, J. R. & Boldyrev, A. I. Solid state adaptive natural density partitioning: a tool for deciphering multi-center bonding in periodic systems. Phys. Chem. Chem. Phys. 15, 5022–5029 (2013).
Feng, B. J. et al. Evidence of silicene in honeycomb structures of silicon on Ag (111). Nano. Lett. 12, 3507–3511 (2012).
Fleurence, A. et al. Experimental evidence for epitaxial silicene on diboride thin films. Phys. Rev. Lett. 108, 245501 (2012).
Li, L. et al. Black phosphorus field-effect transistors. Nat. Nanotechnol. 9, 372–377 (2014).
Liu, H., Neal, A. T., Zhu, Z., Tomanek, D. & Ye, P. D. Phosphorene: an unexplored 2D semiconductor with a high hole mobility. ACS Nano 8, 4033–4041 (2014).
Molina-Sánchez, A. & Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2 . Phys. Rev. B 84, 155413 (2011).
Cahangirov, S., Topsakal, M., Akturk, E., Sahin, H. & Ciraci, S. Two-and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 102, 236804 (2009).
Terrones, H. et al. New metallic allotropes of planar and tubular carbon. Phys. Rev. Lett. 84, 1716 (2000).
Liu, Y., Wang, G., Huang, Q., Guo, L. & Chen, X. Structural and electronic properties of t graphene: a two-dimensional carbon allotrope with tetrarings. Phys. Rev. Lett. 108, 225505 (2012).
Zhang, S. et al. Penta-graphene: a new carbon allotrope. Proc. Natl Acad. Sci. USA 112, 2372–2377 (2015).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential”. J. Chem. Phys. 124, 219906 (2006).
Lee, C. G., Wei, X. D., Kysar, J. W. & Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008).
Li, X., Zhang, Q. & Wang, Q. Stability and physical properties of a tri-ring based porous gC4N3 sheet. Phys. Chem. Chem. Phys. 15, 7142–7146 (2013).
Lakes, R. S. Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040 (1987).
Jiang, J.-W. & Park, H. S. Negative Poisson’s ratio in single-layer black phosphorus. Nat. Commun. 5, 4727 (2014).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Lee, C., Yang, W. & Parr, R. G. Development of the colle-salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Mater. Phys. 37, 785 (1988).
Frisch, M. J. et al. GAUSSIAN 03, Revision E.02 Gaussian, Inc. (2004).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, L. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Segall, M. D. et al. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 14, 2717 (2002).
Martyna, G. J., Klein, M. L. & Tuckerman, M. E. Nosé-Hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97, 2635–2643 (1992).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Acknowledgements
Support in China by Natural Science Foundation of China (numbers 21403115 and 21522305) and the NSF of Jiangsu Province of China (number BK20150045), and in the United States by National Science Foundation (Grant EPS-1010094) and Department of Defense (Grant W911NF-12-1-0083) is gratefully acknowledged. The computational resources used in this research were provided by Shanghai Supercomputer Center.
Author information
Authors and Affiliations
Contributions
Y.L. and Z.C. conceived the initial idea of this research. Y.W. and F.L. demonstrated the initial idea and collected all the data. Y.W., Y.L. and Z.C. wrote the paper and all authors commented on it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5 and Supplementary Table 1 (PDF 1598 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, Y., Li, F., Li, Y. et al. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat Commun 7, 11488 (2016). https://doi.org/10.1038/ncomms11488
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11488
This article is cited by
-
Auxetic α-Li2O: A Novel 2D Materials with Negative Possion's Ratio
JOM (2024)
-
Theoretical Predition of Two-dimensional SiGeP2 by the Global Optimization Method
Journal of Wuhan University of Technology-Mater. Sci. Ed. (2023)
-
Structure search of two-dimensional systems using CALYPSO methodology
Frontiers of Physics (2022)
-
Ternary CE2Ba2 (E = As, Sb) Clusters: New Pentaatomic Planar Tetracoordinate Carbon Species with 18 Valence Electrons
Journal of Molecular Modeling (2022)
-
A first principles investigation on the structural, mechanical, electronic, and catalytic properties of biphenylene
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.