Abstract
Sodium-ion batteries are attractive energy storage media owing to the abundance of sodium, but the low capacities of available cathode materials make them impractical. Sodium-excess metal oxides Na2MO3 (M: transition metal) are appealing cathode materials that may realize large capacities through additional oxygen redox reaction. However, the general strategies for enhancing the capacity of Na2MO3 are poorly established. Here using two polymorphs of Na2RuO3, we demonstrate the critical role of honeycomb-type cation ordering in Na2MO3. Ordered Na2RuO3 with honeycomb-ordered [Na1/3Ru2/3]O2 slabs delivers a capacity of 180 mAh g−1 (1.3-electron reaction), whereas disordered Na2RuO3 only delivers 135 mAh g−1 (1.0-electron reaction). We clarify that the large extra capacity of ordered Na2RuO3 is enabled by a spontaneously ordered intermediate Na1RuO3 phase with ilmenite O1 structure, which induces frontier orbital reorganization to trigger the oxygen redox reaction, unveiling a general requisite for the stable oxygen redox reaction in high-capacity Na2MO3 cathodes.
Similar content being viewed by others
Introduction
Li-ion batteries power almost all of today’s portable electronics and their ability to store energy is increasingly important for large-scale applications such as electric vehicles and power grids. However, Li resources are limited and unevenly distributed geographically; hence, alternatives need to be found. Na-ion batteries have garnered great attention as candidates for large-scale applications owing to the abundance and low cost of sodium. Accordingly, Na-ion (de)intercalation compounds have been explored intensively1,2,3,4,5,6,7,8.
Among the various positive electrode materials that have been investigated, layered transition metal oxides NaMO2 (M=transition metal) are considered to be the most promising3,9,10,11,12,13, in part owing to their large theoretical capacities and the simple analogies from the successful application of LiMO2 in Li-ion battery systems. However, the stably cyclable capacity of NaMO2 is too small for practical use because deintercalation of a large amount of Na ions from the Na layer between the MO2 slabs usually causes irreversible structural changes14,15.
Replacing M atoms in the MO2 slab with Na (for example, Na[Na1/3M2/3]O2 or Na2MO3) is an appealing strategy to suppress these structural changes over a wider compositional range. The [Na1/3M2/3]O2 slabs supply additional Na ions, thereby increasing the reversible capacity while suppressing the over-deintercalation of Na ions from the Na layer. This ‘A2−xMO3’ strategy has already been adopted in many lithium systems such as Li2MnO3–LiMO2 and Li2RuO3, in which enhanced capacities exceeding a M4+/M3+ one-electron reaction have been achieved through additional oxygen redox contribution16,17,18.
In our previous work, we applied this strategy to sodium systems, using a model compound, Na2RuO3 (Na[Na1/3Ru2/3]O2)19. However, despite the presence of [Na1/3Ru2/3]O2 slabs, Na2RuO3 delivered a modest capacity of 135 mAh g−1, limited to the Ru5+/Ru4+ one-electron reaction. In contrast, Rozier et al.20 very recently reported that Na2RuO3 can deliver a capacity greatly exceeding that of the Ru5+/Ru4+ one-electron reaction. At present, the discrepancy between the reported electrochemical properties is an open question. More generally, the requisite conditions for successful application of the ‘A2−xMO3’ strategy for large-capacity sodium systems are poorly understood.
Here we demonstrate that a highly stabilized intermediate phase with honeycomb-type cation ordering in the [Na1/3M2/3]O2 slab is critical for the effective use of the ‘A2−xMO3’ strategy, by comparing two polymorphs of Na2RuO3; namely, ‘ordered’ Na2RuO3 with honeycomb-ordered [Na1/3M2/3]O2 slabs and ‘disordered’ Na2RuO3 with randomly distributed [Na1/3M2/3]O2 slabs (Fig. 1).
Results
Structural characterization of Na2RuO3
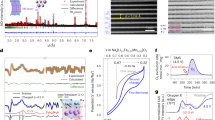
Ordered Na2RuO3 (hereafter denoted O-Na2RuO3) was synthesized by a thermal decomposition method, in which Na2RuO4 was annealed at 850 °C for 48 h under an Ar atmosphere21. Disordered Na2RuO3 (hereafter denoted D-Na2RuO3) was synthesized for comparison according to our previously reported procedure19. The 99Ru Mössbauer spectra of both compounds (insets in Fig. 2a,b) show a singlet absorption peak with an isomer shift around −0.3 mm s−1, which is a typical value for Ru4+ (for example, −0.25 mm s−1 for Y2Ru2O7 and −0.33 mm s−1 for SrRuO3)22, suggesting successful formation of stoichiometric Na2RuO3 compositions from both syntheses. The synchrotron X-ray diffraction (XRD) pattern of D-Na2RuO3 (Fig. 2a) is fully indexed to the O3 structure (R\(\overline{3}\)m space group, a=3.0969(3) Å and c=15.970(2) Å); all diffraction peaks are well-fitted by Rietveld refinement with a structural model in which Na and Ru are randomly distributed in the [Na1/3Ru2/3]O2 slabs (Fig. 1 and Supplementary Table 1). Na in the Na layer occupies octahedral sites and the oxide ions are stacked in an ABCABC arrangement (O3 structure)23. The selected area electron diffraction (SAED) pattern along the [001]hex zone axis (Fig. 2c) shows diffraction spots fully indexed by the R\(\overline{3}\)m model with disordered [Na1/3Ru2/3]O2 slabs.
Observed and calculated (Rietveld method) synchrotron X-ray diffraction patterns for (a) disordered and (b) ordered Na2RuO3. Red crosses: experimental, black line: calculated, blue line: difference and green bars: Bragg positions. The black arrows in b indicate the superstructure peaks that were not considered for the refinement. Insets of a,b correspond to the 99Ru Mössbauer spectra recorded at 4.2 K for both pristine materials. Vertical error bars represent 1σ s.d. of counting statistics. Selected area electron diffraction (SAED) patterns in the (c) [001]hex zone axes of disordered Na2RuO3, and in the (d) [001]hex and (e) [110]hex zone axes of ordered Na2RuO3. The red circles and arrows, respectively, indicate the central and fundamental diffraction spots, which are common to disordered Na2RuO3. Un-marked diffraction spots in between correspond to superstructure peaks. Scale bars, 10 nm−1.
The synchrotron XRD pattern of O-Na2RuO3 (Fig. 2b and Supplementary Table 1) is similar to that of D-Na2RuO3 and is almost fitted by Rietveld refinement in the R\(\overline{3}\)m space group (a=3.1195(5) Å and c=15.989(4) Å) assuming disordered [Na1/3Ru2/3]O2 slabs. However, diffuse scatterings remain, as highlighted by the black arrows in Fig. 2b. Similar characteristics have been reported for many A2MO3 (A=Li, Na and M=transition metal(s)) materials, and usually arise from honeycomb ordering in the MO2 slabs16,17,20. Indeed, the SAED pattern along the [001]hex zone axis (Fig. 2d) shows many extra diffraction spots, which are not predicted using the standard R\(\overline{3}\)m model with disordered [Na1/3Ru2/3]O2 slabs. These spots can be indexed to a  supercell arising from the honeycomb ordering of Na and Ru in the [Na1/3Ru2/3]O2 slabs (Fig. 1). In contrast, the SAED pattern along the [110]hex zone axis (Fig. 2e) shows extra streaks along [001]hex. This feature is characteristic of stacking faults in honeycomb-ordered [A1/3M2/3]O2 slabs along the chex direction, explaining the diffusive nature of the superstructure reflections in Fig. 2b (ref. 24).
supercell arising from the honeycomb ordering of Na and Ru in the [Na1/3Ru2/3]O2 slabs (Fig. 1). In contrast, the SAED pattern along the [110]hex zone axis (Fig. 2e) shows extra streaks along [001]hex. This feature is characteristic of stacking faults in honeycomb-ordered [A1/3M2/3]O2 slabs along the chex direction, explaining the diffusive nature of the superstructure reflections in Fig. 2b (ref. 24).
Electrochemical properties of Na2RuO3
Having demonstrated the differences between O- and D-Na2RuO3 in terms of the in-plane ordering and stacking sequences of the [Na1/3Ru2/3]O2 slabs, the Na+ (de)intercalation properties of both materials were studied to clarify the influence of the honeycomb ordering. Figure 3a,b shows the charge–discharge curves measured between 1.5 and 4.0 V versus Na/Na+ at 30 mA g−1 (a rate of ∼C/5). Here charging is an anodic process (Na deintercalation) and discharging is a cathodic process (Na intercalation). D-Na2RuO3 (Fig. 3a) delivers a reversible capacity of 135 mAh g−1, corresponding to (de)intercalation of 1.0 Na+, which is consistent with our previous report19. In contrast, the reversible capacity of O-Na2RuO3 exceeds 180 mAh g−1, indicating reversible (de)intercalation of 1.3 Na+, beyond a Ru5+/Ru4+ one-electron redox process. This behaviour is in agreement with that of Na2RuO3 reported by Rozier et al.20. Importantly, the voltage profile of O-Na2RuO3 significantly differs from the S-shaped voltage profile of D-Na2RuO3. O-NaxRuO3 (0.7≤x≤2) exhibits a staircase-like charge profile with a first voltage plateau around 2.5 V for 1.0≤x≤2.0 and a second voltage plateau around 3.6 V for 0.7≤x≤1.0; the second voltage plateau is related to the extra capacity of O-Na2RuO3, which exceeds that of the Ru5+/Ru4+ one-electron reaction. Although the plateau at 3.6 V shows gradual narrowing with repeating the cycles presumably due to slight loss of the crystallinity (Supplementary Fig. 1a,b), O-Na2RuO3 shows excellent capacity retention of 160 mAh g−1 after 50 cycles (Fig. 3c), which indicates the remarkable stability of the redox processes that contribute to the increased capacity. Indeed, the voltage plateau around 3.6 V is clearly observed for every charge process, suggesting occurrence of the accumulative oxygen redox reaction (Supplementary Fig. 1c,d)18. Therefore, the available capacity significantly exceeds one-electron redox reaction for O-Na2RuO3 even after 50 cycles. It is surprising that the in-plane honeycomb-type cation ordering in O-Na2RuO3 is solely responsible for the drastic changes in the electrochemical properties that results in 30% higher capacity. To the best of our knowledge, this is the first demonstration of the critical role of honeycomb-type cation ordering in [A1/3M2/3]O2 slabs in determining the primary electrochemical properties.
Structural change during (de)sodiation
To clarify the reaction mechanisms in Na2RuO3, we studied the structural changes of D-Na2RuO3 and O-Na2RuO3 during cycling (Fig. 4a–d). As reported previously19 and further supported by ex situ XRD patterns (Supplementary Fig. 2), D-NaxRuO3 undergoes a structural change from O3 to P3 (with Na in prismatic sites owing to the ABBCCA oxide-ion stacking) on charging23. This O3→P3 transition is commonly observed in O3-NaMO2 materials through gliding of the [Na1/3Ru2/3]O2 slabs from ABCABC (O3) to ABBCCA (P3) stacking9,25. The synchrotron XRD pattern of the charged state (D-Na1RuO3; Supplementary Fig. 3 and Supplementary Table 2) is fully fitted by the Rietveld refinement assuming a P3 structure (R\(\overline{3}\)m space group, a=2.927(2) Å and c=16.774(12) Å), in which Na ions in the Na layer are located in prismatic sites (inset in Fig. 3a). The interlayer distance is significantly increased from 5.323(1) Å (x=2) to 5.591(4) Å (x=1) because of the high aspect ratio of the prismatic Na sites in the P3 structure (Fig. 4a).
(a) Interlayer distance of the different phases involved on desodiation as a function of x in disordered and ordered NaxRuO3. (b) Crystal structure of ilmenite-type Na1RuO3. All Na ions displace cooperatively towards Na vacancies in the honeycomb planes. (c) Observed and calculated (Rietveld method) synchrotron X-ray diffraction patterns for ordered Na1RuO3. Red crosses: experimental, black line: calculated, blue line: difference and green bars: Bragg positions. The inset shows the selected area electron diffraction (SAED) pattern for ilmenite-type Na1RuO3. Scale bar, 10 nm−1 (d) Ex situ XRD patterns showing the evolution of the superstructure peaks for ordered NaxRuO3 on charge.
It should be emphasized that O-Na2RuO3 exhibits a completely different structural evolution from D-Na2RuO3 on charging. The in situ and ex situ XRD patterns of O-Na2RuO3 (Supplementary Figs 4 and 5) at the first plateau show that an intermediate phase ‘X’ with an unknown structure (presumably a P-type phase based on the interlayer distance of around 5.5 Å) appears during the initial stages of the desodiation, and that the O3 phase is eventually transformed to a new phase at x=1 with an extremely short interlayer distance of around 5.2 Å (Fig. 4a). These complex equilibria among the O3, X and O1 phases are responsible for the long voltage plateau observed in the 1≤x≤2 composition range of O-NaxRuO3. On charging, the diffuse scatterings of the superstructure gradually disappear, while new, well-resolved peaks appear (Fig. 4d). The well-resolved character of the new superstructure reflections suggest that the disordered stacking of the honeycomb lattice is spontaneously adjusted towards the ordered state during electrochemical desodiation. The Rietveld refinement and SAED pattern of O-Na1RuO3 (Fig. 4b,c and Supplementary Tables 2 and 3) confirm that the [Na1/3Ru2/3]O2 layers maintain the original honeycomb-type in-plane ordering. As shown in Fig. 4b, the ABCABC stacking sequence of oxygen is transformed to an ABAB sequence, in which Na in the Na layer occupies octahedral sites (O1 structure; inset in Fig. 3b). This ordered structure is isomorphic with the ilmenite FeTiO3-type structure26.
In the refined structure of O-Na1RuO3 (R\(\overline{3}\) space group, a=5.2492(1) Å and c=15.6201(6) Å), the Na site in the [Na1/3Ru2/3]O2 slabs is vacant, which means Na was extracted from the [Na1/3Ru2/3]O2 slabs prior to the Na layers. In this very unique, stable intermediate ilmenite-type Na1RuO3, all NaO6 octahedra in the Na layer share faces with a RuO6 octahedron and a ‘□O6’ octahedron of the adjacent [□1/3Ru2/3]O2 slabs (□: Na vacancy). As shown in Fig. 4a, the interlayer distance of O-Na1RuO3 (5.2067(2) Å) is much shorter than that of D-Na1RuO3 (5.591(4) Å) as a result of substantial displacement of Na in the Na layer towards □O6 octahedra by Coulombic attraction (Fig. 4b). Importantly, the RuO6 octahedron is strongly distorted: the shortest neighbouring O–O distance is 2.580(4) Å, whereas the longest is 3.080(6) Å (Fig. 5 and Supplementary Table 3).
Schematic representation of the structural changes during charge–discharge for disordered Na2RuO3 and ordered Na2RuO3. Ordered Na2RuO3 can distort cooperatively to raise the energy level of the antibonding σ* orbital of the O–O bond, leading to the oxygen redox reaction. Disordered Na1RuO3 cannot accommodate the RuO6 distortion due to strain frustration, which prevents the oxygen redox reaction.
The ilmenite structure of O-Na1RuO3 is stabilized by the following mechanisms: (1) the ordered Na arrangement minimizes Na+–Na+ repulsion; (2) the Na vacancy □ in the [□1/3Ru2/3]O2 slab strongly attracts Na ions in the face-sharing octahedra in adjacent Na layers; (3) the ordered and displaced arrangement of Na ions minimizes Ru5+–Na+ repulsive interactions; and (4) the cooperative distortion of the RuO6 octahedra can minimize the total strain energy in the ordered honeycomb lattice. All these mechanisms lead to the formation of the ilmenite phase with well-ordered stacking of the honeycomb lattices.
On discharge, in situ XRD patterns (Supplementary Fig. 4) prove that the phase transformation is almost reversible except for a small asymmetry, that is, the appearance of the X phase only at charge. Presumably, this parasitic asymmetric behaviour is observed under non-equilibrium conditions such as the microscale heterogeneity.
Electronic structure of Na2−xRuO3
After the O3→O1 transition, O-Na2RuO3 delivers additional capacity, exceeding that of the Ru5+/Ru4+ one-electron reaction at the higher voltage plateau of around 3.7 V. To clarify the overall redox mechanism in O-Na2RuO3, we conducted Ru L3-edge and oxygen K-edge X-ray absorption spectroscopy (XAS) in the partial fluorescence yield mode at various charge depths (Fig. 6, Supplementary Figs 6 and 7). The Ru L3-edge XAS directly probes the 4d orbitals through the Laporte-allowed 2p→4d transition27. Furthermore, because the O 2p orbital strongly hybridizes with the Ru 4d orbital, oxygen K-edge XAS can be used to monitor the hole created on the O 2p and Ru 4d orbitals on charging28. Note that the probing depth of the partial fluorescence yield mode is about 100 nm; hence, the spectra are bulk sensitive29.
(a) States of charge of the samples for X-ray absorption spectroscopy. (b) Ruthenium L3-edge and (c) oxygen K-edge X-ray absorption spectra for various O-NaxRuO3 compositions: (i) x=2.0 (black), (ii) x=1.5 (blue), (iii) x=1.0 (green) and (iv) x=0.62 (red). The asterisked peak corresponds to O 2p-Na 3p. The calculated oxygen K-edge spectra for ordered Na2RuO3 (black) and ilmenite-type NaRuO3 (green) are also shown.
The Ru L3-edge spectrum for pristine O-Na2RuO3 (t2g4eg0, neglecting the trigonal distortion of Ru for clarity), Fig. 6b, shows two absorption peaks corresponding to the excitation from the 2p orbital to the unoccupied t2g and eg orbitals. The peak position for the 2p→eg absorption (2841.5 eV) is similar to that reported for Ru4+ (2841.6 eV) in SrRuO3 and RuO2 (ref. 27), confirming Ru4+ in pristine O-Na2RuO3. On charging to ilmenite-type Na1RuO3, two absorption peaks shift to higher energy. Since the peak position of the 2p→eg absorption for ilmenite-type Na1RuO3 (2,843 eV) agrees with that of Ru5+ in Sr4Ru2O9 (ref. 27), oxidation from Ru4+ to Ru5+ occurs at the first potential plateau. However, further desodiation at the second plateau does not shift the 2p→eg absorption peak, suggesting no substantial change in the valence state of Ru.
The O K-edge spectrum of pristine O-Na2RuO3 (t2g4eg0) shows a large peak at 534 eV, which is ascribed to the unoccupied hybridized orbital of O 2p–Na 3p, and its peak intensity simply reflects the amount of Na in the lattice30. The calculated density of states for O-Na2RuO3 (Fig. 7a) also indicates that the O 2p–Na 3p hybridized orbital exists in this energy range. For the lower energy region that represents the redox reaction, the calculated oxygen K-edge spectrum agrees well with the spectra from 528 to 533 eV. Thus, the peaks around 529 eV and 532 eV can be ascribed to the unoccupied hybridized orbitals of O 2p–Ru t2g and O 2p–Ru eg, respectively31,32. At the voltage plateau of 2.5 V, desodiation diminishes the O 2p–Na 3p signal, whereas the peak intensity of O 2p–Ru t2g (around 529 eV) increases on charging, indicating hole generation on the O 2p–Ru t2g orbital. The increase in the peak intensity around 529 eV is also in good agreement with the calculated oxygen K-edge spectrum for ilmenite-type Na1RuO3.
On further charging at the second plateau (around 3.6 V), the peak intensity of the O 2p–Ru t2g is almost constant, whereas the peak around 532 eV broadens as a result of the new absorption band emerging around 533 eV. This spectral change cannot be explained by Ru5+→Ru6+ oxidation (hole generation on O 2p–Ru t2g). One possible explanation is the formation of a new chemical bond involving oxygen. For example, formation of an O–O bond (that is, peroxo/superoxo-like groups O2n− (1≤n≤3)) has been proposed as the oxygen redox mechanism for many Li2(M,M′)O3 cathode materials (M,M′=Fe, Ru, Sb, Sn or Ir)18,33,34. Here the hole generated by further charging is stabilized on the antibonding σ* orbital of the O–O bond which is covalently bonded to the transition metal. It should be noted that the 99Ru Mössbauer spectrum of O–Na0.62RuO3 (Supplementary Fig. 8) shows absorption with an isomer shift of δ=+0.21 mm s−1, which is a typical value for Ru5+ (+0.11 mm s−1 for Na3RuO4 and +0.19 mm s−1 for Ca2EuRuO6)22, supporting that no further Ru5+→Ru6+ oxidation occurs.
On discharge, while the 2p→t2g and 2p→eg signals in the Ru L3-edge spectra shift to the initial lower energy region, the O–O bond and O 2p–Ru t2g signals in the O K-edge spectra decrease reversibly (Supplementary Figs 6 and 7). Furthermore, although the diffraction peaks of the ex situ XRD pattern after cycling exhibit weak broadening due to the slight loss of the crystallinity, O-Na2RuO3 still shows characteristic diffuse scatterings similar to the pristine compound (Supplementary Fig. 1b), which suggests that the honeycomb-type in-plane ordering is maintained during the charge–discharge cycles for all Na compositions, where 0.7≤x≤2. Importantly, this is the first simultaneous achievement of extra oxygen redox capacity and structural integrity leading to totally reversible oxygen participation. All other A2−xMO3-type electrodes suffer from severe structural rearrangement on the first charge and from lowering of the operating voltage during subsequent cycles16,17,34,35,36. This structural rearrangement occurs because M migrates from octahedral sites in the M layer to face-sharing tetrahedral sites in the adjacent A layer35. Presumably, this inter-site migration of Ru is suppressed in Na2RuO3 because of incompatibility of large Ru with the tetrahedral site. Furthermore, the interlayer O–O bond formation, which is predicted theoretically for delithiated Li2MnO3 to destabilize the oxygen redox reaction37, should be inhibited by the large interlayer distance in NaxRuO3 (for example, 5.2−5.5 Å for NaxRuO3 and 4.7−4.8 Å for LixRu0.75Mn0.25O3)36. As shown in Supplementary Fig. 9, the initial Coulombic efficiency of O-Na2RuO3 is higher (95%) than that of other A2−xMO3 (for example, 70% for Li2MnO3 and 90% for Li2RuO3)17,36,38,39.
Discussion
The critical role of honeycomb ordering in Na2RuO3 based on the aforementioned original observations is summarized in Fig. 5. The ordered [□1/3Ru2/3]O2 slabs in ilmenite O-Na1RuO3 accommodate the distortion of the RuO6 octahedra cooperatively, whereby the shortest O–O distance is 2.580(4) Å. Because the short O–O distance raises the energy level of the antibonding σ* orbital of the O–O bond to the Fermi level, the oxygen redox reaction is triggered. Indeed, the calculated density of states for ilmenite O-Na1RuO3 (Fig. 7b) shows that the occupied antibonding orbitals of the O–O bond exist near the Fermi level. The naturally derived scenario is that, once the hole is generated on the antibonding σ* orbital of the O–O bond, the O–O distance becomes shorter40. This short distance leads to the higher energy level of the antibonding σ* orbital of the oxygen–oxygen bond and an acceleration of the oxygen redox reaction. This hypothesis was recently reinforced by McCalla et al.34: scanning transmission electron microscopy and neutron diffraction on fully delithiated Li2IrO3 (Li0.5IrO3) determined the shorter O–O distance (2.45 Å) after the oxygen oxidation. However, as demonstrated in this work, the short O–O distance is required before the oxygen oxidation to achieve the extra capacity. For example, the disordered [Na1/3Ru2/3]O2 slabs in D-Na1RuO3 cannot accommodate the cooperative distortion of the RuO6 octahedra owing to strain frustration. Thus, the O–O distances in D-Na1RuO3 are long enough (2.751(6) and 2.927(1) Å) so that the energy level of the antibonding σ* orbital of the O–O bond is well below the Fermi level, which inhibits the extra oxygen redox process within the electrolyte stability window. Therefore, honeycomb-type cation ordering in the [Na1/3M2/3]O2 slab is a structural requisite condition to trigger the stable oxygen redox capacity in Na2MO3.
Finally, we mention the role of Ru in the oxygen redox reaction. Very recently, Saubanère et al.37 theoretically demonstrated that the covalent bond between the peroxo-like (O2)n− 2p and Ru 4d orbitals in Li2RuO3 (reductive coupling mechanism) is essential to facilitate the oxygen redox reaction and to suppress the oxygen gas release, whereas the M(3d)-O(2p) overlap is too small to enable this mechanism. For O-Na2RuO3, in addition to the stable structural nature inherent in the Na system by suppressing both the inter-site Ru migration and the interlayer O–O bond formation as discussed above, the similar reductive coupling mechanism through the large orbital overlap between the Ru 4d and O 2p orbitals should suppress the oxygen gas release, which explains the high cycle stability of O-Na2RuO3 compared with that of any other Li excess materials (Supplementary Fig. 9).
In conclusion, the present work demonstrates the critical role of honeycomb-type cation ordering in Na2MO3 to achieve enhanced reversible capacity based on the oxygen redox process. In comparison to its disordered polymorph, O-Na2RuO3 with in-plane honeycomb ordering exhibits a significantly different voltage profile, leading to a 30% extra capacity, spurred by the electrochemically driven, further ordered intermediate, NaRuO3, which accommodates cooperative distortion of the RuO6 octahedra. The short O–O distance in distorted RuO6 induces frontier orbital reorganization, triggering the oxygen redox reaction.
To the best of our knowledge, this is the first report that clarifies the underlying structural requirement to trigger the oxygen redox reaction in A2−xMO3. By further exploiting the compositional versatility of A2MO3 while meeting this requirement, there is great potential to develop oxygen redox electrodes for superior batteries. Considering the impact of the stable intermediate on the overall electrode properties, the peculiar phenomena and concepts demonstrated here may give general implications for a deeper understanding and improved utilization of intercalation materials.
Methods
Synthesis of Na2RuO3
Ordered Na2RuO3 was synthesized by the thermal decomposition method according to the literature where Na2RuO4 was annealed at 850 °C for 48 h under Ar atmosphere21. Disordered Na2RuO3 was synthesized according to the procedure we previously reported19. The NaHCO3 and RuO2 precursors were calcined at 850 °C for 12 h under Ar atmosphere. Both compounds were handled in a globe box filled with Ar (dew point below −110 °C).
Materials characterization
Powder X-ray diffraction patterns were recorded on a Rigaku TTR-III diffractometer equipped with Cu Kα radiation in 0.02° steps over the 2θ range of 10–80°. XRD patterns were measured at SPring-8 BL02B2 and Photon Factory BL-8B. The samples were handled without air exposure throughout the experiments. Rietveld refinements were carried out using Jana2006 (ref. 41) or TOPAS-Academic software. The profile of Na1RuO3 was better described using independent crystallite size for 00l reflections, Popa’s sphere harmonics for h0l and hkl reflections and different crystallite sizes for (h0k)=3n as implemented in TOPAS in order to take into account the stacking faults affecting part of the diffraction peaks. The crystal structures were drawn using VESTA42. SAED patterns were recorded using an electron microscope (HF-3000S; Hitachi Ltd.) operated at 300 kV and an imaging plate system (FDL-5000; Fujifilm). The camera length was calibrated with a Si crystal. 99Ru Mössbauer spectroscopy was carried out with the 99Rh source (T1/2=15 days), which was prepared by the 99Ru(p,n)99Rh reaction at the RIKEN AVF cyclotron. The 99Ru(p,n)99Rh reaction was conducted with a 99Ru (95% enriched) target under 12 MeV proton irradiation. Both the source and the samples were cooled in liquid He during the measurements. The samples were transferred into the liquid He cryostat without air exposure. The Doppler velocity was calibrated by measuring a 57Fe Mossbauer spectrum of α-Fe, and the zero velocity was determined by the isomer shift of Ru metal at 4.2 K.
Electrochemical measurement
For the electrochemical measurements, 80 wt% of Na2RuO3 was mixed with 10 wt% of acetylene black and 10 wt% of polyvinylidene in N-methyl pyrrolidone to make a slurry, which was then coated onto Al foil. The dried films were used as a cathode in the 2,032-type coin cells with Na metal as an anode. NaPF6 (1 M) in ethylene carbonate/diethyl carbonate (1:1 v/v) was used as an electrolyte. The charge–discharge experiments were conducted at 30 mA g−1 between 1.5−4.0 V versus Na/Na+, within the electrolyte stability window.
Samples for ex situ characterization
The electrodes for ex situ XRD, XAS and 99Ru Mossbauer spectroscopy were prepared as described above. O-Na1RuO3 samples for synchrotron XRD and TEM studies were prepared following the same method except that the positive electrode consisted in a pellet (Ø 10 mm, 50 mg) of O-Na2RuO3 that was sintered at 850 °C for 12 h. The batteries were then cycled to a designated voltage that was maintained for a few hours (Na1RuO3) or until a given current has been applied. After cycling, the batteries were introduced into an Ar-filled glovebox and the collected electrodes were washed three to five times with anhydrous dimethyl carbonate.
In situ XRD
In situ XRD (operando mode) was carried out using an in situ cell purchased from Rigaku on a D8 ADVANCE powder diffractometer equipped with Co Kα radiation in 0.02° steps over the 2θ range of 17−25° (1.37 s per step, one pattern recorded every ≈12 min). The electrochemical part of the cell is similar to the one described above. The only exception lies in the preparation of the electrode whose slurry was coated on plastic films to be peeled off after drying. The current rate was C/20 (full (dis)charge theoretically achieved in 20 h), allowing us to record an XRD pattern every Δx=0.02. Only selected patterns are shown in Supplementary Fig. 4 for clarity concerns. Electrochemistry was controlled and recorded using a Biologic VMP3.
X-ray absorption
O K-edge XAS was carried out at BL07LSU of SPring-8. The samples were transferred to a vacuum chamber without air exposure. Bulk-sensitive partial-fluorescence yield (PFY) mode was used for the O K-edge XAS. Energy resolution was approximately 100 meV. All the spectra were recorded using a silicon drift detector at room temperature. The spectra were normalized by the peak intensity at 532 eV, because the peak at 532 eV corresponding to O 2p-Ru eg may not be affected by the redox of Ru5+/Ru4+. Ru L3-edge XAS was carried out at BL27SU of SPring-8. The samples were transferred to a vacuum chamber without exposure to air. The spectra were recorded in the bulk-sensitive PFY mode using a silicon drift detector at room temperature.
Ab initio calculation
Spin-polarized DFT+U calculations were performed using the VASP code43 with Ueff for Ru ranging from 0.5 to 4.5 eV. Van der Waals density functional optPBE44 was employed. The plane-wave energy cut-off was set to 520 eV and the Brillouin zone integration was done in a k-point grid chosen to converge the energy to 10−4 eV. Atomic coordinates and lattice parameters were relaxed using conjugate gradient method until the maximum force on atoms is <2 × 10−3 eV Å−1. Initial geometry of Na2RuO3 in the C2/m symmetry was taken from the literature45 while the initial geometry for NaRuO3 in the R\(\overline{3}\) symmetry is from the present work. Antiferromagnetic ordering of spin on Ru was assumed, the pattern was set to be Néel type. The oxygen K-edge X-ray absorption pattern was calculated by the WIEN2k code46 employing the full potential linear augmented plane-wave method, dipole approximation to the golden rule for the transition probability was assumed.
Additional information
How to cite this article: Mortemard de Boisse, B. et al. Intermediate honeycomb ordering to trigger oxygen redox chemistry in layered battery electrode. Nat. Commun. 7:11397 doi: 10.1038/ncomms11397 (2016).
References
Yabuuchi, N., Kubota, K., Dahbi, M. & Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 114, 11636–11682 (2014).
Kundu, D., Talaie, E., Duffort, V. & Nazar, L. F. The emerging chemistry of sodium ion batteries for electrochemical energy storage. Angew. Chem. Int. Ed. 54, 3431–3448 (2015).
Yabuuchi, N. et al. P2-type Nax[Fe1/2Mn1/2]O2 made from earth-abundant elements for rechargeable Na batteries. Nat. Mater. 11, 512–517 (2012).
Barpanda, P., Oyama, G., Nishimura, S., Chung, S. C. & Yamada, A. A 3.8 V Earth-abundant sodium battery electrode. Nat. Commun. 5, 4358 (2014).
Billaud, J. et al. β-NaMnO2: a high-performance cathode for sodium-ion batteries. J. Am. Chem. Soc. 136, 17243–17248 (2014).
Wang, X. et al. Pseudocapacitance of MXene nanosheets for high-power sodium-ion hybrid capacitors. Nat. Commun. 6, 6544 (2015).
Qian, J., Wu, X., Cao, Y., Ai, X. & Yang, H. High capacity and rate capability of amorphous phosphorous for sodium-ion batteries. Angew. Chem. Int. Ed. 52, 4633–4636 (2013).
Wang, Y. et al. A zero-strain layered metal oxide as the negative electrode for long-life sodium-ion batteries. Nat. Commun. 3, 2365 (2013).
Komaba, S. et al. Study on the reversible electrode reaction of Na1−xNi0.5Mn0.5O2 for a rechargeable sodium-ion battery. Inorg. Chem. 51, 6211–6220 (2012).
Wang, X., Liu, G., Iwao, T., Okubo, M. & Yamada, A. Role of ligand-to-metal charge transfer in O3-Type NaFeO2-NaNiO2 solid solution for enhanced electrochemical properties. J. Phys. Chem. C 118, 2970–2976 (2014).
Mortemard de Boisse, B., Carlier, D., Guignard, M., Bourgeois, L. & Delmas, C. P2-NaxMn1/2Fe1/2O2 phase used as positive electrode in Na Batteries; structural changes induced by the electrochemical (De)intercalation process. Inorg. Chem. 53, 11197–11205 (2014).
Li, X. et al. Direct visualization of the Jahn-Teller effect coupled to Na ordering in Na5/8MnO2 . Nat. Mater. 13, 586–592 (2014).
Billaud, J. et al. Na0.67Mn1−xMgxO2 (0≤x≤0.2): a high capacity cathode for sodium-ion batteries. Energy Environ. Sci. 7, 1387–1391 (2014).
Ma, X., Chen, H. & Ceder, G. Electrochemical properties of monoclinic NaMnO2 . J. Electrochem. Soc. 158, A1307–A1312 (2015).
Yabuuchi, N., Yano, M., Yoshida, H., Kuze, S. & Komaba, S. Synthesis and electrode performance of O3-type NaFeO2-NaNi1/2Mn1/2O2 solid solution for rechargeable sodium batteries. J. Electrochem. Soc. 160, A3131–A3137 (2013).
Thackeray, M. M., Johnson, C. S., Vaughey, J. T., Li, N. & Hackney, S. A. Advances in manganese-oxide ‘composite’ electrodes for lithium-ion batteries. J. Mater. Chem. 15, 2257–2267 (2005).
Sathiya, M. et al. Reversible anionic redox chemistry in high-capacity layered-oxide electrodes. Nat. Mater. 12, 827–835 (2013).
Sathiya, M. et al. Electron paramagnetic resonance imaging for real time monitoring of Li-ion batteries. Nat. Commun. 6, 6276 (2015).
Tamaru, M., Wang, X., Okubo, M. & Yamada, A. Layered Na2RuO3 as a cathode material for Na-ion batteries. Electrochem. Commun. 33, 23–26 (2013).
Rozier, P. et al. Anionic redox chemistry in Na-rich Na2Ru1−ySnyO3 positive electrode materials for Na-ion batteries. Electrochem. Commun. 53, 29–32 (2015).
Mogare, K. M., Friese, K., Klein, W. & Jansen, M. Synthesis and crystal structures of two sodium ruthenate: Na2RuO4 and Na2RuO3 . Z. Anorg. Chem. 630, 547–552 (2004).
Gütlich, P., Bill, E. & Trautwein, A. X. in Mössbauer Spectroscopy and Transition Metal Chemistry Springer-Verlag (2011).
Delmas, C., Fouassier, C. & Hagenmuller, P. Structural classification and properties of the layered oxides. Phys. B 99, 81–85 (1980).
Meng, Y. S. et al. Cation ordering in layered O3 Li[NixLi1/3−2x/3Mn2/3−x/3]O2 (0≤x≤1/2) compounds. Chem. Mater. 17, 2386–2394 (2005).
Mortemard de Boisse, B. et al. O3-NaxMn1/3Fe2/3O2 as a positive electrode materials for Na-ion batteries: structural evolutions and redox mechanisms upon Na+ (de)intercalation. J. Mater. Chem. A 3, 10976–10989 (2015).
Barth, T. F. W. & Posnjak, E. The crystal structure of ilmenite. Z. Kristallogr. 88, 265–270 (1934).
Manoharan, S. S. & Sahu, R. K. Evidence for an anomalous redox ionic pair between Ru and Mn in SrRu0.5Mn0.5O3: an X-ray absorption spectroscopy approach. Chem. Commun. 21, 3068–3069 (2002).
de Groot, F. & Kotani, A. Core Level Spectroscopy of Solids; Advances in Condensed Matter Science CRC Press (2008).
Achkar, A. J. et al. Bulk sensitive X-ray absorption spectroscopy free of self-absorption effects. Phys. Rev. B 83, 081106 (R) (2011).
Kroll, T. et al. X-ray absorption spectroscopy of NaxCoO2 layered cobaltates. Phys. Rev. B 74, 115123 (2006).
Han, S. W. et al. Electronic structure of RuSr2EuCu2O8 studied by X-ray absorption and photoemission spectroscopies. Phys. Rev. B 85, 014506 (2012).
Pchelkina, Z. V. et al. Electronic structure of Li2RuO3 studied by LDA and LDA+DMFT calculations and soft X-ray spectroscopy. Phys. Rev. B 91, 115138 (2015).
McCalla, E. et al. Understanding the roles of anionic redox and oxygen release during electrochemical cycling of lithium-rich layered Li4FeSbO6 . J. Am. Chem. Soc. 137, 4804–4814 (2015).
McCalla, E. et al. Visualization of O-O peroxo-like dimers in high-capacity layered oxides for Li-ion batteries. Science 350, 1516–1521 (2015).
Sathiya, M. et al. Origin of voltage decay in high-capacity layered oxide electrodes. Nat. Mater. 14, 230–238 (2015).
Sathiya, M. et al. High performance Li2Ru1−yMnyO3 (0.2≤x≤0.8) cathode materials for rechargeable lithium-ion batteries: their understanding. Chem. Mater. 25, 1121–1131 (2013).
Saubanère, et al. The intriguing question of anionic redox in high-energy density cathodes for Li-ion batteries. Energy Environ. Sci. 9, 984–991 (2016).
Yu, D. Y. W., Tanagida, K., Kato, Y. & Nakamura, H. Electrochemical activities in Li2MnO3 . J. Electrochem. Soc. 156, A417–A424 (2009).
Koga, H. et al. Different oxygen redox participation for bulk and surface: a possible global explanation for the cycling mechanism of Li1.20Mn0.54Co0.13Ni0.13O2 . J. Power Sources 236, 250–258 (2013).
Tarascon, J. M. et al. In situ structural and electrochemical study of Ni1−xCoxO2 metastable oxides prepared by soft chemistry. J. Solid State Chem. 147, 410–420 (1999).
Petřiček, V., Dušek, M. & Palatinus, L. Jana2006—the crystallographic computing system: General features. Z. Kristallogr. 229, 345–352 (2014).
Monma, K. & Izumi, F. VESTA 3 for Three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 44, 1272–1276 (2011).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 6, 15–50 (1996).
Klimes, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der waals density functional. J. Phys. Condens. Matter 22, 022201 (2010).
Wang, J. C. et al. Lattice-tuned magnetism of Ru4+ (4d4) ions in single crystals of tshe layered honeycomb ruthenates Li2RuO3 and Na2RuO3 . Phys. Rev. B 90, 161110 (2014).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties Karlheinz Schwarz, Techn. Univ. Wien, Austria (2001).
Acknowledgements
This work was financially supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan; Grant-in-Aid for Specially Promoted Research No. 15H05701. This work was also supported by MEXT, Japan under the ‘Elemental Strategy Initiative for Catalysis and Batteries (ESICB)’. M.O. was financially supported by MEXT, Japan; Grant-in-Aid for Challenging Exploratory Research No. 15K13798. M.O. was also supported by the Hattori Hokokai Foundation. The synchrotron XRD experiment was performed under approval of Photon Factory Program Advisory Committee (Proposal No.2013G670) and the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2015A1503, 2014A1196 and 2013A1665). The SAED patterns were recorded at Nanotechnology Platform of MEXT (No. A-14-NM-0064). The synchrotron X-ray absorption experiments at SPring-8 were performed with the approval of the Japan Synchrotron Radiation Research Institute (Proposal No. 2015B1471) and by the joint research in the Synchrotron Radiation Research Organization and the Institute for Solid State Physics, the University of Tokyo (Proposal No. 2015A7403).
Author information
Authors and Affiliations
Contributions
M.O. and A.Y. conceived and directed the project. B.M.d.B., G.L. and J.M. synthesized Na2RuO3. B.M.d.B., G.L. and J.M. evaluated the electrochemical properties of Na2RuO3. B.M.d.B., G.L. and S.N. analysed the XRD patterns of NaxRuO3. M.O., H.K. and Y.H. measured and analysed the XAS spectra. J.K. measured and analysed the TEM and electron diffraction micrographs. Y.K. measured and analysed the 99Ru Mössbauer spectra. S.-C.C calculated the oxygen K-edge spectra and the density of states. B.M.d.B., S.N., M.O. and A.Y. wrote the manuscript. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-9 and Supplementary Tables 1-3. (PDF 1071 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mortemard de Boisse, B., Liu, G., Ma, J. et al. Intermediate honeycomb ordering to trigger oxygen redox chemistry in layered battery electrode. Nat Commun 7, 11397 (2016). https://doi.org/10.1038/ncomms11397
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11397
This article is cited by
-
Understanding voltage hysteresis and decay during anionic redox reaction in layered transition metal oxide cathodes: A critical review
Nano Research (2023)
-
Correlating ligand-to-metal charge transfer with voltage hysteresis in a Li-rich rock-salt compound exhibiting anionic redox
Nature Chemistry (2021)
-
Nonpolarizing oxygen-redox capacity without O-O dimerization in Na2Mn3O7
Nature Communications (2021)
-
Covalency does not suppress O2 formation in 4d and 5d Li-rich O-redox cathodes
Nature Communications (2021)
-
Topologically protected oxygen redox in a layered manganese oxide cathode for sustainable batteries
Nature Sustainability (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.