Abstract
Semiconductor-based quantum structures integrated into mechanical resonators have emerged as a unique platform for generating entanglement between macroscopic phononic and mesocopic electronic degrees of freedom. A key challenge to realizing this is the ability to create and control the coupling between two vastly dissimilar systems. Here, such coupling is demonstrated in a hybrid device composed of a gate-defined quantum dot integrated into a piezoelectricity-based mechanical resonator enabling milli-Kelvin phonon states to be detected via charge fluctuations in the quantum dot. Conversely, the single electron transport in the quantum dot can induce a backaction onto the mechanics where appropriate bias of the quantum dot can enable damping and even current-driven amplification of the mechanical motion. Such electron transport induced control of the mechanical resonator dynamics paves the way towards a new class of hybrid semiconductor devices including a current injected phonon laser and an on-demand single phonon emitter.
Similar content being viewed by others
Introduction
Mechanical resonators are one of the most ideal realization of harmonic oscillators with excellent quality factors of >106 and high operation frequencies that can be >1 GHz, and they have emerged as an important platform for both scientific studies and new device applications1. The key to further functionalizing the resonator is its hybridization with other physical systems, where the resonator motion can be not only detected but also manipulated by the auxiliary system using backaction from the coupling. One of the most successful platforms for this concept are cavity optomechanics where the mechanical resonator forms one of the mirrors in an optical cavity and the resultant backaction force from the confined photons can damp and amplify its harmonic motion2,3. This reversible feature plays an essential role in many applications, especially in the generation of non-classical phonon states4,5, where cooling and the subsequent parametric amplification allow preparation of entangled states superposing both phonons and photons6,7.
Compared with optomechanical systems, the hybridization of a mechanical resonator with a quantum low-dimensional system has been barely developed despite its importance for many electromechanical applications8,9,10,11,12,13,14,15,16,17. This is principally due to the integration of an electron cavity, that is, a quantum dot (QD), into the resonator with perfectly controlled coupling proving technologically challenging. Previously, such hybrid devices have been studied using primarily metal-based single electron transistors (SETs), in which the tunnel barriers and the electron energies lack the wide tunability required for creating and harnessing the precisely controlled electron backaction onto the mechanics18,19,20,21,22,23,24.
In this study, we have employed a gate-controlled QD based on the GaAs/AlGaAs system, which enables superior control of the confined electron states, and the intrinsic piezoelectricity of this material system allows highly efficient electron-to-mechanics coupling. With the aid of this QD-resonator platform, precise control of the backaction polarity and magnitude is demonstrated by only adjusting the operation point of the QD gate bias.
Results
Hybrid mechanical resonator QD system
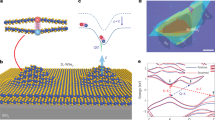
The GaAs/AlGaAs modulation-doped heterostructure used in this study sustains a two-dimensional electron gas (2DEG) 90 nm below the surface and Au-Schottky gate electrodes are lithographically defined on the surface (see Methods and Supplementary Fig. 1). The two gate electrodes that are fabricated on the left clamping point of the resonator, as shown in Fig. 1a, are used to actuate and detect the mechanical motion of the resonator14,25. Figure 1d shows the measured frequency response of the fundamental flexural motion, where AC actuation voltage Vd=150 μV is applied to the upper gate, while the generated piezovoltage is detected by the lower gate. From Lorentzian fitting, a resonance frequency f0=1.664699 MHz and quality factor Q0=2.4 × 105 are determined. The QD is electrostatically defined using the Schottky gate electrodes on the right clamping point of the mechanical resonator as shown in Fig. 1b. The charge states in the QD can be controlled via the gate-voltage Vg and the source-drain bias Vsd applied across the QD, and are monitored via the resultant current through the QD. Figure 1e shows a grayscale plot of the differential conductance G as a function of Vg and Vsd showing a typical Coulomb diamond structure. In what follows, we mainly focus on the Coulomb peak around Vg=−0.465 V (≡Vg0) as indicated by the square in Fig. 1e.
(a) False-colour scanning electron microscope (FCSEM) image of the hybrid device along with the measurement setup (scale bar, 20 μm). A doubly clamped electromechanical resonator of 50 μm length, 6 μm width and 1 μm thickness is fabricated along the  crystal axis of GaAs. (b) FCSEM image of the Schottky gate electrodes defining the quantum dot at the right clamping point of the mechanical resonator (scale bar, 1 μm). Application of negative bias voltage to these gates depletes the underlying two-dimensional electrons and confines a few electrons within a small spacial area of <300 × 300 nm2 (red circle in b). (c) Finite element method simulation of the mechanical strain associated with the fundamental flexural mode’s motion, showing the maximum strain at the clamping points. (d) The frequency response voltage power spectrum SV of the electromechanical transducer around the centre frequency f0=1664699.2 Hz of the fundamental flexural mode along with a Lorentzian fit (solid line). (e) A plot of the differential conductance of the quantum dot as a function of Vg and Vsd showing typical Coulomb diamonds as indicated by the red dashed lines. In each diamond, the number of electrons N in the QD are changed. In this study, we focus on the Coulomb peak enclosed by the blue square. (f) A Coulomb peak with the mechanical resonator under three different actuation conditions; α, no actuation; β, off-mechanical resonance actuation with Vd=150 μV at f=f0−100 Hz; γ, on-mechanical resonance actuation with Vd=150 μV.
crystal axis of GaAs. (b) FCSEM image of the Schottky gate electrodes defining the quantum dot at the right clamping point of the mechanical resonator (scale bar, 1 μm). Application of negative bias voltage to these gates depletes the underlying two-dimensional electrons and confines a few electrons within a small spacial area of <300 × 300 nm2 (red circle in b). (c) Finite element method simulation of the mechanical strain associated with the fundamental flexural mode’s motion, showing the maximum strain at the clamping points. (d) The frequency response voltage power spectrum SV of the electromechanical transducer around the centre frequency f0=1664699.2 Hz of the fundamental flexural mode along with a Lorentzian fit (solid line). (e) A plot of the differential conductance of the quantum dot as a function of Vg and Vsd showing typical Coulomb diamonds as indicated by the red dashed lines. In each diamond, the number of electrons N in the QD are changed. In this study, we focus on the Coulomb peak enclosed by the blue square. (f) A Coulomb peak with the mechanical resonator under three different actuation conditions; α, no actuation; β, off-mechanical resonance actuation with Vd=150 μV at f=f0−100 Hz; γ, on-mechanical resonance actuation with Vd=150 μV.
The coupling between the QD and the resonator arises from piezoelectricity in GaAs. The elastic strain associated with the mechanical motion induces a piezoelectric field that can serve as an effective gate voltage acting on the QD. To maximize this effect, the position of the QD is designed with reference to finite element method simulation of the corresponding mechanical strain. The results (shown in Fig. 1c) suggest that the maximum strain appears at the clamping points and thus we locate the QD at this point. To confirm the mechanical coupling in this device, a Coulomb peak is measured at different mechanical actuation conditions (as shown in Fig. 1f). This figure reveals that the Coulomb peak is clearly distorted from its intrinsic shape when the resonator is actuated on mechanical resonance that is f=f0. This behaviour is in contrast to the case of off-mechanical resonance actuation, that is, f=f0−100 Hz, where the Coulomb peak shows no distortion, thus ensuring that the coupling is purely mechanical and not electric between the left and right clamping points.
In this configuration, the hybrid electromechanical system can be modelled by the Jaynes–Cummings Hamiltonian:

where ħ is the reduced Plank constant. The first term describes the mechanical resonator as a harmonic oscillator with frequency ω0=2πf0 where  and
and  are its creation and annihilation operators. The second term describes the Pauli operator
are its creation and annihilation operators. The second term describes the Pauli operator  mapped onto the two-level system composed of a higher
mapped onto the two-level system composed of a higher  and a lower
and a lower  energy state in the QD with energy difference ΔE. The coupling between the mechanics and the QD is captured by the third term, which describes the energy shift in the two level system from the mechanical motion. This coupling can be quantified by the single phonon coupling constant ħg0=xzp(d(ΔE)/dx) where the mechanical displacement
energy state in the QD with energy difference ΔE. The coupling between the mechanics and the QD is captured by the third term, which describes the energy shift in the two level system from the mechanical motion. This coupling can be quantified by the single phonon coupling constant ħg0=xzp(d(ΔE)/dx) where the mechanical displacement  in terms of its zero-point fluctuation xzp. Indeed, to completely define this hybrid system, equation (1) should also include terms corresponding to the conduction electrons in the source-drain leads and the tunnel coupling between the leads and the QD. These additional terms describe the situation when a finite bias voltage is applied to the source-drain leads, leading to non-equilibrium transport across the QD. Consequently, when the mechanical motion changes ΔE in the QD, the response of the charge transport across the QD can induce piezoelectric stress, which can act as a backaction force on to the resonator.
in terms of its zero-point fluctuation xzp. Indeed, to completely define this hybrid system, equation (1) should also include terms corresponding to the conduction electrons in the source-drain leads and the tunnel coupling between the leads and the QD. These additional terms describe the situation when a finite bias voltage is applied to the source-drain leads, leading to non-equilibrium transport across the QD. Consequently, when the mechanical motion changes ΔE in the QD, the response of the charge transport across the QD can induce piezoelectric stress, which can act as a backaction force on to the resonator.
Determination of the coupling constant
To quantitatively characterize the QD resonator coupling, the thermomechanical motion of the resonator was detected via the current fluctuation through the QD using the setup in Fig. 2a. Figure 2b–d show the power spectrum density at three different temperatures (100, 200 and 400 mK). The high-temperature spectrum shows a larger peak area compared with the low-temperature spectrum, reflecting the correspondingly larger thermal motion. According to the energy equipartition theorem, the squared displacement 〈x2〉 of the thermal motion is proportional to the temperature25. Consequently, measuring the temperature dependence of the power spectra enables the QD current to be converted into a displacement, thus yielding a responsivity. Figure 2f shows the temperature dependence of the peak area normalized by the square of the transconductance gm, which is shown in Fig. 2e. The normalized peak area linearly depends on temperature, which yields a responsivity of 1.82 × 106 Vm−1, and this calibration enables conversion of the current noise spectra SI into the desired displacement noise spectra. From this analysis, the minimum detectable displacement of 63 fm Hz−0.5 and position resolution of 170 fm are extracted. This performance is comparable to values reported using metal-based SET detectors18,19, as well as being three orders of magnitude more sensitive than a pure piezovoltage measurement from the Schottky electrode (Fig. 1d), which typically performs on the order of 10–100 pm Hz−0.5 as reported elsewhere26,27.
(a) A schematic of the experimental setup for measuring thermal motion of the mechanical resonator. The potential fluctuation Δϕ induced by the piezoelectric field associated with the mechanical thermal motion results in current fluctuations, which are fed into a load resistor RL=1 kΩ and the voltage drop across the load is amplified by cryogenic (G1) and room-temperature (G2) amplifiers (see Methods). The resultant amplified signal is measured with a spectrum analyser. (b–d) The current power spectral density SI around f0 at three different temperature. The bold solid line shows a Lorenzian fit, from which the peak area A corresponding to the squared amplitude of the mechanical motion is obtained. (e,f) Temperature dependence of the transconductance gm≡dI/dVsd (e) and A normalized by gm (f) along with a linear fit (solid line).
Finally, this responsivity (η) enables the single phonon coupling rate to be extracted from ħg0=(Δϕ/ΔVg)ηΔxzp, where the transfer coefficient Δϕ/ΔVg defines the change in the electrostatic potential Δϕ in the QD induced by the effective gate voltage ΔVg associated with the mechanical motion. In this QD, Δϕ/ΔVg=0.14 eVV−1 is determined from the Coulomb diamond detailed in Fig. 1e, which yields g0/2π=150 kHz. To evaluate the potency of this coupling16, g0 is normalized by ω0, yielding a value of ∼0.09, which is comparable to superconducting qubit-based hybrid mechanical systems where values in the range of 0.005–0.125 have been achieved28,29. Indeed, in this regime backaction from the superconducting qubit’s charge states has been observed, thus suggesting the availability backaction effects in our semiconducting QD-based hybrid mechanical system.
Backaction from the QD
The presence of backaction emerges as a perturbation of the resonance frequency f=f0+ΔfB and the quality factor Q=Q0+ΔQB from their intrinsic values, where a positive (negative) value of ΔQB indicates amplification (damping) of the mechanical motion from the backaction force. In standard models, this amplification and damping can be described in terms of a backaction force, which is characterized by a delay time  . In this system,
. In this system,  is the time for the local charges in the QD to produce a mechanical force after the mechanical motion modulates the charge distribution in the QD2,30. The resultant shift in ω and Q are approximately given by
is the time for the local charges in the QD to produce a mechanical force after the mechanical motion modulates the charge distribution in the QD2,30. The resultant shift in ω and Q are approximately given by


where KB and K0 are the backaction and intrinsic force constants, respectively, with  and
and  . Both suppression and enhancement of Q-factor can then be obtained depending on the sign of KB.
. Both suppression and enhancement of Q-factor can then be obtained depending on the sign of KB.
Figure 3a–c show the measured f-shift, Q, and G as a function of Vg and Vsd, where f and Q are determined by Lorentzian fits to the frequency response at each Vg and Vsd by actuating the resonator at Vd=150 μV and measuring the resultant motion via the detection circuit on the left clamping point as shown in Fig. 1a. Both f and Q deviate from their intrinsic values around the Coulomb peak, indicating the presence of backaction in this regime. Figure 3d–i show characteristic traces measured at Vsd=0 and Vsd=0.48 mV, highlighting the clear difference between equilibrium and non-equilibrium conditions, respectively. In Fig. 3d (Vsd=0), the measured f shows a linear Vg dependence as indicated by the dashed line and a dip at Vg=Vg0, which is in contrast to the Q-value shown in Fig. 3e, which keeps its intrinsic value throughout the measured Vg range. The linear f-shift is caused by Vg-induced piezoelectric strain, which linearly modifies the spring constant that in turn tunes the resonance frequency as widely observed in GaAs-based electromechanical resonators14,31. The additional dip structure at Vg=Vg0 is caused by a softening of the spring constant due to single-electron charge fluctuation in the QD as seen previously22,23. Specifically, the alignment of the single electron state in the QD with the electrochemical potential of the unbiased source-drain leads yields stochastic charge fluctuations whose piezoelectric backaction onto the mechanics causes a redshift in the resonance frequency.
(a–c) Colour plots of frequency shift f−f0, quality factor Q and differential conductance G as a function of Vsd and Vg. These plots correspond to the Vsd and Vg region as indicated by the blue square in Fig. 1e and Vg0=−0.465 V is the gate voltage at which the Coulomb peak is positioned, where the dashed lines indicate the Coulomb diamond. (d–i) Comparison of the mechanical backaction effects between Vsd=0 mV (d–f) and Vsd=0.48 mV (g–i). In Vsd=0 mV, a linear f-shift, as indicated by the dashed line, as well as a f-dip at Vg=Vg0 is observed, whereas no deviation is found in the corresponding Q-factor as I=0. At finite Vsd, both frequency and Q-factor are modulated around the Coulomb peak, indicating the presence of a backaction force from the local charge state in the QD. Red (blue) area in h highlights the enhancement (suppression) of Q-factor. Schematics in (f,i) depict the corresponding energy diagram in the QD and the leads. In f, the relevant single electron level is above (below) the unbiased electrochemical potential when Vg<Vg0 (Vg>Vg0). In i, the electron energy level moves across the electrochemical potential in the source (drain) electrode when Vg<Vg0 (Vg>Vg0).
More striking features are observed in non-equilibrium conditions with a finite Vsd=0.48 mV where both f and Q nonlinearly vary around the Coulomb peak as shown in Fig. 3g–i. The sign and the magnitude of the resultant deviations depend on Vg, so that the polarity and the efficiency of backaction is electrically tunable depending on the QD’s energy states. As the Q-factor characterizes the mechanical damping properties of the resonator, the observed enhancement (suppression) of Q indicates an amplification (damping) of the mechanical motion driven by the single electron transport in the QD.
Discussion
This asymmetrically oscillating perturbation feature centred at the Coulomb peak has not been observed previously in other electromechanical resonator hybrid systems. More usually, only the suppression of Q due to enhanced energy dissipation from single-electron fluctuations is observed in both biased metal- and carbon-nanotube-based SETs22,23,24,32. These latter observations are well explained by standard models where a single electron state in the SET is assumed to be incoherently tunnel coupled to the lead electrodes and the delay is determined by the electron tunnelling process, which is generally much faster than the resonator motion. In fact, the estimated delay time  =290 ns for this semiconductor-based QD electromechanical system, obtained by substituting the observed deviations in f and Q into
=290 ns for this semiconductor-based QD electromechanical system, obtained by substituting the observed deviations in f and Q into  , derived from equations (2) and (3), is long when compared with the typical time scales relevant to transport in QDs such as tunnelling, which is of the order of a picosecond.
, derived from equations (2) and (3), is long when compared with the typical time scales relevant to transport in QDs such as tunnelling, which is of the order of a picosecond.
Very recently, a new model was proposed assuming an additional delay time in the system, which can describe the asymmetrical oscillation of the Q-factor around the Coulomb peak30. If this time delay, T12 satisfies the condition ω0T12≈1, the timescale for mechanics and the electronic states in the QD enable the efficient manifestation of backaction effects. The possible mechanism that could lead to the additional delay process include coherent electron transfer across the QD21,33 and excitation/relaxation processes between, for instance, the first two levels in the QD30.
The relevance of this model to our experiment is further supported by comparing it with the backaction induced by a quantum point contact (QPC), which eliminates the energy-level structure that is suggested as being essential to the asymmetric oscillation in the Q-factor in the delayed backaction model. Indeed, in the QPC case f and Q shifts are also observed when finite Vsd is applied to the QPC (Supplementary Figs 2 and 3); however, their features are radically different to those observed with the QD, both qualitatively and quantitatively (see Supplemental Note 1). In particular, f- and Q-shifts show clear dependence on the power P=IVsd, suggesting that the observed behaviour in the QPC case originates from Joule heating (Supplementary Fig. 3d). In contrast for the QD, no P dependence is found as shown in Supplementary Fig. 4, thus demonstrating that the observed backaction in this case (Fig. 3g,h) stems from a mechanism other than Joule heating. Consequently, the fact that the QPC has no backaction effect (other than Joule heating) on the mechanics verifies the central role played by the excitation/relaxation process in the energy-level structure confined by the QD.
In conclusion, highly tunable backaction effects are demonstrated in a QD-mechanical resonator hybrid system integrating a gate-defined GaAs/AlGaAs QD into a piezoelectric beam resonator. Depending on the applied gate voltage, both damped and amplified mechanical motion can be activated by the single electron transport in the QD. The unique feature of this system is that the backaction polarity and the magnitude can be precisely controlled by simply tuning the operating point of the QD transport. In practice, the current-driven phonon amplification offers a key breakthrough to realizing current injection phonon lasers12,13,34. More fundamentally, the turnstile operation of the QD current could be harnessed in an electrically controlled single phonon emitter. Furthermore, the switchable operation from backaction cooling to parametric amplification paves the way to generating non-classical phonon states, which transfer the microscopic quantum phenomena uniquely observed in low-dimensional electron systems into macroscopic mechanical objects.
Methods
Sample fabrication
The hybrid QD mechanical resonator system was fabricated from a GaAs/AlGaAs modulation doped heterostructure (see Supplementary Fig. 1) sustaining a 2DEG. A single hetero junction is located 90 nm below the surface, where a 2DEG with a sheet density of 3 × 1011 cm−2 is formed. The lithographic steps employed to fabricate the hybrid device are as follows: (1) a shallow mesa containing the 2DEG was defined by photolithography and wet-etched using an H2O:H2O2:H2SO4 (25:1:5) solution at 10 °C for 40 s. The mesa height was 200 nm. (2) Ohmic contacts to the 2DEG were defined by means of photolithography and deposition of 200-nm-thick AuGeNi. The sample was then annealed in H2 ambient at 430 °C for 60 s, to alloy the AuGeNi to the 2DEG. (3) Cross-marks used as alignment markers for the electron beam (e-beam) lithography were defined by e-beam lithography and were deposited with Cr/Au (1/100 nm). (4) The fine mesa pattern near the electromechanical resonator (purple area in Fig. 1a) was defined by e-beam lithography and wet-etched as in step (1). (5) Again, using e-beam lithography, the fine Schottky electrodes at the resonators clamping point were defined and then deposited with Cr/Au (1/25 nm). (6) Photolithography was then used to define the metal lines connecting the fine Schottky gate electrodes to the bonding pads, which were deposited with 200-nm-thick Au. (7) The final photolithography step defined the doubly clamped mechanical resonator, which was wet-etched using H2O:H2O2:H2SO4 (25:1:5) solution at 10 °C for 5 min, to expose the Al0.65Ga0.35As sacrificial layer. The resonator was then released from the substrate by selectively etching the sacrificial layer using hydrofluoric acid (HF) solution (10 wt%) for 4 min at room temperature. After rinsing the sample in water, acetone and ethanol, the sample was gently dried in air.
Measurement setup
All measurements were carried out inside a high-vacuum chamber (<10−5 Pa) on a dilution refrigerator with a base temperature of 80 mK. The thermal motion measurement of the resonator through the QD current (data shown in Fig. 2) was carried out using the setup shown in Fig. 2a, where a bias voltage Vsd is applied to the source contact and the drain is shunted to the ground by a load resistor RL=1 kΩ. A voltage drop across the load is amplified by a home-made HEMT amplifier cooled at 4 K and is followed by a commercially available amplifier (NF SA-220F5) at room temperature. The total voltage power gain factor F of this two-stage setup was F=7.32 × 106 in units of V2 V−2. The amplified voltage signal is fed to a digital spectrum analyser and is converted to a frequency-domain spectrum. The measured power spectrum Sout of the amplified voltage signal is related to the power spectrum of the QD current SI via  . The mechanical motion measurements shown in Figs 1d and 3d–i were carried out by measuring the piezovoltage generated on the electrodes at the left-clamping point (Fig. 1a) using a two-stage amplification setup similar to that detailed above.
. The mechanical motion measurements shown in Figs 1d and 3d–i were carried out by measuring the piezovoltage generated on the electrodes at the left-clamping point (Fig. 1a) using a two-stage amplification setup similar to that detailed above.
Thermal motion analysis
The power spectrum density of the QD current SI is related to the displacement spectra Sx of the resonator via  . Here, η is the responsivity, which is the transfer coefficient from the displacement of the mechanical resonator to the piezoelectric gate voltage that appears on the QD, and gm≡dI/dVg is the transconductance, that is, the transfer coefficient from the piezoelectric gate voltage to the QD current. According to the energy equipartition theorem19, the squared displacement 〈x2〉 of the thermal motion is proportional to T as Ks〈x2〉=kBT with two known parameters; Ks being the spring constant and kB being the Boltzmann constant. In this resonator, Ks=128.4 Nm−1 was deduced from Ks=Meff(2πf0)2 with Meff=1.174 × 10−12 kg being the effective mass of the resonator. Here Meff=0.73M and M is the total mass of the beam; the coefficient 0.73 normalizes the fundamental flexural mode of the doubly clamped beam resonator to a harmonic oscillator35. Care was exercised in calibrating the net responsivity η from the T dependence of the thermal motion spectra (Fig. 2b–d), because thermal broadening of the Coulomb peak also reduces the transconductance gm (Fig. 2e). To correct for this reduction, gm was measured as a function of temperature with a small AC voltage modulation of 10 μV at 13 Hz superposed to the DC gate voltage Vg, which yielded a modulated current that was detected in a lock-in amplifier. Next, the reduced gm was accounted for by normalizing the peak area A by
. Here, η is the responsivity, which is the transfer coefficient from the displacement of the mechanical resonator to the piezoelectric gate voltage that appears on the QD, and gm≡dI/dVg is the transconductance, that is, the transfer coefficient from the piezoelectric gate voltage to the QD current. According to the energy equipartition theorem19, the squared displacement 〈x2〉 of the thermal motion is proportional to T as Ks〈x2〉=kBT with two known parameters; Ks being the spring constant and kB being the Boltzmann constant. In this resonator, Ks=128.4 Nm−1 was deduced from Ks=Meff(2πf0)2 with Meff=1.174 × 10−12 kg being the effective mass of the resonator. Here Meff=0.73M and M is the total mass of the beam; the coefficient 0.73 normalizes the fundamental flexural mode of the doubly clamped beam resonator to a harmonic oscillator35. Care was exercised in calibrating the net responsivity η from the T dependence of the thermal motion spectra (Fig. 2b–d), because thermal broadening of the Coulomb peak also reduces the transconductance gm (Fig. 2e). To correct for this reduction, gm was measured as a function of temperature with a small AC voltage modulation of 10 μV at 13 Hz superposed to the DC gate voltage Vg, which yielded a modulated current that was detected in a lock-in amplifier. Next, the reduced gm was accounted for by normalizing the peak area A by  . Figure 2f shows that
. Figure 2f shows that  depends linearly on T, reflecting the linear T dependence of the thermal motion. The slope of the linear fit, combined with the equipartition theorem, namely
depends linearly on T, reflecting the linear T dependence of the thermal motion. The slope of the linear fit, combined with the equipartition theorem, namely  , allows the responsivity η=1.82 × 106 Vm−1 to be deduced. From this, the current power spectrum SI in the thermal motion spectra (Fig. 2b–d) can be converted to the corresponding displacement Sx using
, allows the responsivity η=1.82 × 106 Vm−1 to be deduced. From this, the current power spectrum SI in the thermal motion spectra (Fig. 2b–d) can be converted to the corresponding displacement Sx using  .
.
The lowest noise floor observed at T=80 mK corresponds to  fm Hz−0.5, which is the minimum detectable displacement sensitivity in the present setup. The position resolution δx is also estimated to be δx=170 fm, using (δx)2=Sx × Δf with Δf=f0/Q being the bandwidth of the resonator. This optimum position resolution is ∼70 times the zero-point fluctuation
fm Hz−0.5, which is the minimum detectable displacement sensitivity in the present setup. The position resolution δx is also estimated to be δx=170 fm, using (δx)2=Sx × Δf with Δf=f0/Q being the bandwidth of the resonator. This optimum position resolution is ∼70 times the zero-point fluctuation  fm for this resonator.
fm for this resonator.
Additional information
How to cite this article: Okazaki, Y. et al. Gate-controlled electromechanical backaction induced by a quantum dot. Nat. Commun. 7:11132 doi: 10.1038/ncomms11132 (2016).
References
Cleland, A. N. Foundations of Nanomechanics Springer (2003).
Metzger, C. H. & Karrai, K. Cavity cooling of a microlever. Nature 432, 1002–1005 (2004).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Cohen, J. D. et al. Phonon counting and intensity interferometry of a nanomechanical resonator. Nature 520, 522–525 (2015).
Verhagen, E., Deléglise, S., Weis, S., Schliesser, A. & Kippenberg, T. J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 482, 63–67 (2012).
Palomaki, T. A., Teufel, J. D., Simmonds, R. W. & Lehnert, K. W. Entangling mechanical motion with microwave fields. Science 342, 710–713 (2013).
Stettenheim, J. et al. A macroscopic mechanical resonator driven by mesoscopic electrical backaction. Nature 466, 86–90 (2010).
Grudinin, I. S., Lee, H., Painter, O. & Vahala, K. J. Phonon laser action in a tunable two-level system. Phys. Rev. Lett. 104, 083901 (2010).
Beardsley, R. P., Akimov, A. V., Henini, M. & Kent, A. J. Coherent terahertz sound amplification and spectral line narrowing in a stark ladder superlattice. Phys. Rev. Lett. 104, 085501 (2010).
Gardner, J., Bennett, S. D. & Clerk, A. A. Mechanically probing coherent tunneling in a double quantum dot. Phys. Rev. B 84, 205316 (2011).
Okuyama, R., Eto, M. & Brandes, T. Optical phonon lasing in semiconductor double quantum dots. J. Phys. Soc. Jpn 82, 013704 (2013).
Khaetskii, A., Golovach, V. N., Hu, X. & Žutić, I. Proposal for a phonon laser utilizing quantum-dot spin states. Phys. Rev. Lett. 111, 186601 (2013).
Mahboob, I., Nishiguchi, K., Fujiwara, A. & Yamaguchi, H. Phonon lasing in an electromechanical resonator. Phys. Rev. Lett. 110, 127202 (2013).
Kabuss, J., Carmele, A., Brandes, T. & Knorr, A. Optically driven quantum dots as source of coherent cavity phonons: a proposal for a phonon laser scheme. Phys. Rev. Lett. 109, 054301 (2012).
Yeo, I. et al. Strain-mediated coupling in a quantum dot-mechanical oscillator hybrid system. Nat. Nanotechnol. 9, 106–110 (2014).
Montinaro, M. et al. Quantum dot opto-mechanics in a fully self-assembled nanowire. Nano Lett. 14, 4454–4460 (2014).
Knobel, R. G. & Cleland, A. N. Nanometre-scale displacement sensing using a single electron transistor. Nature 424, 291–293 (2003).
LaHaye, M. D., Buu, O., Camarota, B. & Schwab, K. C. Approaching the quantum limit of a nanomechanical resonator. Science 304, 74–77 (2004).
Weig, E. M. et al. Single-electron-phonon interaction in a suspended quantum dot phonon cavity. Phys. Rev. Lett. 92, 046804 (2004).
Naik, A. et al. Cooling a nanomechanical resonator with quantum backaction. Nature 443, 193–196 (2006).
Steele, G. A. et al. Strong coupling between single-electron tunneling and nanomechanical motion. Science 325, 1103–1107 (2009).
Lassagne, B., Tarakanov, Y., Kinaret, J., Garcia-Sanchez, D. & Bachtold, A. Coupling mechanics to charge transport in carbon nanotube mechanical resonators. Science 325, 1107–1110 (2009).
Benyamini, A., Hamo, A., Kusminskiy, S. V., von Oppen, F. & Ilani, S. Real-space tailoring of the electron-phonon coupling in ultraclean nanotube mechanical resonators. Nat. Phys. 10, 151–156 (2014).
Okazaki, Y., Mahboob, I., Onomitsu, K., Sasaki, S. & Yamaguchi, H. Quantum point contact displacement transducer for a mechanical resonator at sub-Kelvin temperatures. Appl. Phys. Lett. 103, 192105 (2013).
Mahboob, I. & Yamaguchi, H. Bit storage and bit flip operations in an electromechanical oscillator. Nat. Nanotechnol. 3, 275–279 (2008).
Mahboob, I., Flurin, E., Nishiguchi, K., Fujiwara, S. & Yamaguchi, H. Enhanced force sensitivity and noise squeezing in an electromechanical resonator coupled to a nanotransistor. Appl. Phys. Lett. 97, 253105 (2010).
LaHaye, M. D., Suh, J., Echternach, P. M., Schwab, K. C. & Roukes, M. L. Nanomechanical measurements of a superconducting qubit. Nature 459, 960–964 (2009).
Pirkkalainen, J.-M. et al. Hybrid circuit cavity quantum electrodynamics with a micromechanical resonator. Nature 494, 211–215 (2013).
Shevchenko, S. N., Rubanov, D. G. & Nori, F. Delayed-response quantum back action in nanoelectromechanical systems. Phys. Rev. B 91, 165422 (2015).
Masmanidis, S. C. et al. Multifunctional nanomechanical systems via tunably coupled piezoelectric actuation. Science 317, 780–783 (2007).
Armour, A. D., Blencowe, M. P. & Zhang, Y. Classical dynamics of a nanomechanical resonator coupled to a single-electron transistor. Phys. Rev. B 69, 125313 (2004).
Blencowe, M. P., Imbers, J. & Armour, A. D. Dynamics of a nanomechanical resonator coupled to a superconducting single-electron transistor. New J. Phys. 7, 236 (2005).
Liu, Y.-Y. et al. Semiconductor double quantum dot micromaser. Science 347, 285–287 (2015).
Ekinci, K. L. & Roukes, M. L. Nanoelectromechanical systems. Rev. Sci. Instrum. 76, 061101 (2005).
Acknowledgements
We thank R. Okuyama, M. Eto, N. Lambert, Y. Tokura, S. Shevchenko, W.J. Munro and G.J. Milburn for fruitful discussions. This work was partly supported by JSPS KAKENHI Grant Number 23241046 and Grant-in-Aid for Scientific Research on Innovative Areas Number 15H05869.
Author information
Authors and Affiliations
Contributions
Y.O. fabricated the device, performed the measurements and analysed the data. K.O. grew the GaAs heterostructure. S.S. supported the device fabrication. Y.O., I.M. and H.Y. wrote the paper. H.Y. planned the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4 and Supplementary Note 1 (PDF 206 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Okazaki, Y., Mahboob, I., Onomitsu, K. et al. Gate-controlled electromechanical backaction induced by a quantum dot. Nat Commun 7, 11132 (2016). https://doi.org/10.1038/ncomms11132
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11132
This article is cited by
-
Nonlinear nanomechanical resonators approaching the quantum ground state
Nature Physics (2023)
-
Hermitian and non-Hermitian normal-mode splitting in an optically-levitated nanoparticle
Quantum Frontiers (2022)
-
Cooling and self-oscillation in a nanotube electromechanical resonator
Nature Physics (2020)
-
Nanomechanical pump–probe measurements of insulating electronic states in a carbon nanotube
Nature Nanotechnology (2019)
-
Dynamical coupling between a nuclear spin ensemble and electromechanical phonons
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.