Abstract
Ocean tides are the oscillatory motions of seawater forced by the gravitational attraction of the Moon and Sun with periods of a half to a day and wavelengths of the semi-Pacific to Pacific scale. Ocean infragravity (IG) waves are sea-surface gravity waves with periods of several minutes and wavelengths of several dozen kilometres. Here we report the first evidence of the resonance between these two ubiquitous phenomena, mutually very different in period and wavelength, in deep oceans. The evidence comes from long-term, large-scale observations with arrays of broadband ocean-bottom seismometers located at depths of more than 4,000 m in the Pacific Ocean. This observational evidence is substantiated by a theoretical argument that IG waves and the tide can resonantly couple and that such coupling occurs over unexpectedly wide areas of the Pacific Ocean. Through this resonant coupling, some of ocean tidal energy is transferred in deep oceans to IG wave energy.
Similar content being viewed by others
Introduction
Infragravity (IG) waves are surface waves that are observed in deep1 and coastal2 oceans. IG waves are strongest near the shoreline3, where they cause harbour oscillations and near-shore processes such as sediment transport4. Disturbances due to IG waves make it difficult to interpret long-period seismograms at the ocean bottom5,6. Forcing of IG waves is believed to be a major source of Earth's background free oscillations (also known as Earth's hum)7,8,9,10,11,12,13,14. IG waves are mainly generated through nonlinear interactions between high-frequency (period: 20–5 s) wind waves15,16. There are a few reports on the tidal modulation of IG waves in coastal oceans (water depth: 10–30 m)17,18,19 and that on the 1,000-m-deep shelf6, where the IG wave energy is reduced at low tide. The suggested mechanisms for tidal modulation emphasize the influence of the tide on the generation or decay of IG waves in shallow seas19,20. No tidal modulation has been reported for IG waves in open seas or deep oceans. Here we present the first evidence of the resonance between IG waves and the tide in deep oceans, and show that such resonance can occur over wide areas of the Pacific Ocean.
Results
Modulation of IG waves by ocean tide
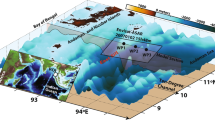
We analysed the continuous vertical component records obtained from two broadband ocean-bottom seismometer (BBOBS; sensor: Guralp CMG-3T) arrays: one (1 February 2003–31 January 2004) with 7 stations (FP array), deployed in French Polynesia21 and the other (1 December 2006–30 November 2007) with 11 stations (PS array), deployed in the northern Philippine Sea22. Figure 1 shows the geographical distributions of the stations in these two arrays, which are mostly located at depths of 4,000–5,000 m. Details of the observations are provided in the Methods section. Figure 2a shows two examples of seafloor noise spectra, one obtained from the FP array and the other obtained from the PS array. It has been reported that the spectral peak appearing at ∼10 mHz is a signature of the seafloor disturbance caused by IG waves1,5. This interpretation is supported by Figure 2b, which shows that the depth dependence of the peak frequency in the IG band can be attributed to the hydrodynamic filtering of IG waves. Figure 3 shows the FP array records that are bandpass-filtered between 4 and 20 mHz; in this frequency range, the signal due to the IG waves is dominant. The IG wave trains show temporal variations on a semidiurnal to diurnal scale; however, visual inspection does not reveal any unique periodicity in time coherent through the array. In order to detect any semidiurnal or diurnal periodicity in the IG wave activity coherent across the stations, we divided the 1-year record obtained from a station into ∼30-day (2.8 × 106 s)-long segments with an overlap of ∼10 days (1.0 × 106 s). Each of the 30-day-long segments was bandpass filtered between 4 and 20 mHz to extract the IG signals. The negative IG signals were reversed in sign in order to obtain an absolute-value time series, which was used as a measure of the IG wave activity. The persistency of temporal periodicity among different stations in the same sampling period was examined by normalizing the maximum amplitude of each 30-days long record and by calculating a cross-spectrum Qij(f) between stations i and j(≠i). The temporal persistence of the periodicity was examined by constructing cross-spectrograms. The cross-spectrogram for a station pair i and j is a plot of the cross-spectral power |Qij(f)| against time. For ease of illustration, we define the stacked cross-spectrogram for the ith station as a stack of the cross-spectrograms obtained for all pairs of the ith station and the other stations in the same seismic array. Figure 4 shows the stacked cross-spectrograms so defined. The frequency (period: 23.93 h) of the principal solar tide K1, frequency 2 (period: 12.42 h) of the principal lunar tide M2, and its double frequency 2 are indicated by arrows along the frequency axis of each stacked cross-spectrogram. Note that the intervals between and and between and 2 are not equal to each other. The spectral peaks at these three frequencies can be recognized in the spectrograms for almost all time periods and across all the stations. The M2 signal is much stronger in the FP spectrograms than in the PS spectrograms, whereas the intensity of the K1 signal is almost the same in the FP and PS spectrograms. The second harmonic of the M2 signal is considerably weaker than the first harmonic in both the FP and PS spectrograms.
Geographical distributions of the stations in the French Polynesia (FP) array21 (close-up in b) and Philippine Sea (PS) array22 (close-up in c). These stations are mostly located at depths of 4,000–5,000 m. We analysed the continuous vertical records at 7 FP-array stations (red circles) available between 1 February 2003 and 31 January 2004 and those at 11 PS-array stations (orange circles) available between 1 December 2006 and 30 November 2007. For the PS array, only the results obtained for the seven western stations are shown in Figure 4. The stations of the PS array not considered in the analysis are shown by orange dots. The BBOBS stations not belonging to the FP and PS arrays are shown by white circles in a.
(a) Seafloor noise spectra at station FP5 for the period 14 January 2003 and 14 January 2004 and those at T05 for the period 11 November 2006–11 November 2007. Each of the power spectra is calculated using the standard procedure followed in seismology29, for a record-section length of 4,096 s and sampling rate of 100 Hz. The 10 spectral lines with the lowest noise amplitudes in the frequency range 0.02–0.05 Hz are blackened to show the noise spectra typical to quiet days. The spectral peak ∼0.01 Hz (indicated by the arrow) represents the disturbance due to infragravity (IG) waves. The two red curves indicate the New Low Noise Model (NLNM) and New High Noise Model (NHNM) of Peterson29. (b) Plot of the peak frequency f0 (in Hz) in the infragravity band against seafloor depth H (in m). Data are obtained from all the BBOBS stations shown in Figure 1. The plots are approximated by the relation f0=(2H)−1/2. This relation is understood as k0H≈1.4, which can be expected if the hydrodynamic filtering of IG waves1 is responsible for the peak.
Example of the FP array records (18–25 September 2003) bandpass filtered between 4 and 20 mHz. The dominant signal in this band is the seafloor disturbance due to IG waves. The IG wave trains show temporal variations on a semidiurnal to diurnal scale. The theoretical tidal sea level changes are shown below each record25.
Stacked cross-spectrogram for each of the stations of the (a) FP and (b) PS arrays. The stacked cross-spectrogram for a station is a stack of the cross-spectrograms for all the pairs of that station and the other stations in the same seismic array. Each record is normalized by its maximum amplitude. The arrows along the frequency axis indicate the principal solar tide K1, the principal lunar tide M2 and the second harmonic of M2, respectively, in the order of increasing frequency.
A theory of the resonance between IG waves and the ocean tide
A theory was developed for the coupling of IG waves with the tide in a long-wave approximation. Details of this theory are provided in the Methods section. The wave field is assumed to be a random, homogeneous superposition of free IG waves of the form  where
where  is the horizontal wavenumber vector and
is the horizontal wavenumber vector and  (ref. 23). This assumption is justified by observations made in the deep ocean1. The angular frequency ω is related to k as
(ref. 23). This assumption is justified by observations made in the deep ocean1. The angular frequency ω is related to k as  , where c is the frequency-independent propagation speed; g, the gravitational acceleration; and H, the water depth. The tidal motion in the local coordinates can be expressed as
, where c is the frequency-independent propagation speed; g, the gravitational acceleration; and H, the water depth. The tidal motion in the local coordinates can be expressed as  so that the co-phase line of the ocean tide with an angular frequency Ω moves in the direction given by the wavenumber vector
so that the co-phase line of the ocean tide with an angular frequency Ω moves in the direction given by the wavenumber vector  and with a speed defined by C≡Ω/K. The fluid-dynamic equation of motion including the advection term has a solution of the form
and with a speed defined by C≡Ω/K. The fluid-dynamic equation of motion including the advection term has a solution of the form  showing the tide-modulated IG waves, where the amplification factor R is proportional to
showing the tide-modulated IG waves, where the amplification factor R is proportional to  In a homogenous random wave field, there is always a wavenumber vector
In a homogenous random wave field, there is always a wavenumber vector  such that
such that  with which R undergoes resonant divergence, if
with which R undergoes resonant divergence, if

Comparison of the observations and theory
We calculated R for the Pacific Ocean by using the global bathymetry model of ETOPO224 and an ocean tidal model developed by Matsumoto et al.25 We set the ω value to the peak frequency in the IG wave band of the seafloor noise at each observational site, as shown by the arrow in Figure 2a. Figure 5a,b show the maps of R for the M2 and K1 tides, respectively. The area coloured in red is essentially in resonant state, as defined by inequality (1), which may be approximated as c≥C. For a 4,000-m ocean depth, c≈200 m s−1, whereas the tidal co-phase line at latitude ϑ is expected to move westward with a speed C≈450×cosϑ m s−1, if a laterally uniform ocean covers a laterally uniform Earth. This implies that for a 4,000-m-deep uniform ocean, resonance is expected only at high latitudes (ϑ≳65°). Figure 5 demonstrates how different the resonance in the real ocean is from that in the uniform model ocean. In Figure 5, the white area is understood to be in a near-resonance state, where the precise value of R is not calculable according to our first-order perturbation theory. We can see that unexpectedly wide areas of the Pacific Ocean are in the resonant or near-resonant state. A major part of the FP array is within the resonant area for the M2 tide, whereas a major part of the PS array is outside the resonant area; this would be the reason for the M2 signal being stronger in the FP array than in the PS array (Fig. 4). On the other hand, a major part of either array is within the resonant area for the K1 tide, explaining that the K1 signal intensities in the FP and PS arrays are not very different (Fig. 4).
R is a measure of how large the coupled-wave amplitude is relative to the amplitude of the undisturbed wave. The area that is practically in a resonant state is coloured in red. The whitish area may be understood to be in a near-resonant state. The tidal co-phase lines are contoured. White dots indicate the amphidromic points. Map (a) for the M2 tide and (b) for the K1 tide.
Discussion
Although the above-mentioned observations clearly indicate that IG waves in the deep ocean recorded by the BBOBSs are persistently modulated by tidal disturbances, there is a possibility of these waves being apparently modulated by the tide-related sensitivity change of the instrument. Such a sensitivity change may be caused by tilting of the sensor axis due either to the tidal currents or to the solid Earth tide. Either possibility, however, is unlikely, as will be explained below. Figure 6a,b shows comparisons of the theoretical tides with the tidal-band records of the FP array corrected for the instrumental response. In Figure 6a, the comparison is made for the gravity component (corresponding approximately to the vertical displacement) of the theoretical solid Earth tide25. In Figure 6b, the comparison is made for the sea level change (corresponding approximately to the horizontal velocity) of the theoretical ocean tide25. The value attached to each pair of the observed and theoretical traces is a lag-time τ to obtain the best waveform match. In Figure 6a, the observed and theoretical traces are in almost in phase (τ always <0.4 h), indicating that the observed traces are almost π/2 out of phase with the tilt component of the solid tide. In Figure 6b, the observed and theoretical traces are not in phase, where τ increases systematically (from −3.3 to +1.2 h) as we move southwestward through the array (from FP2 to FP8, Fig. 1). Clearly, the vertical records in the tidal band are dominated by the gravity signal due to the solid Earth tide. There is no indication for the vertical records being affected by tilting of the instrument due either to the seafloor tilt or to the tidal current at the BBOBS site. The observed tidal modulation of IG waves should be an actual process occurring in the ocean, rather than an apparent phenomenon caused by the instrumental tilting.
(a, b) Example of the FP array records (31 July–31 August 2003) filtered through the tidal band and corrected for the instrumental response. Comparison is made with (a) the gravity component (or vertical displacement) of the theoretical solid Earth tide25 and (b) the sea level change (or horizontal velocity) of the theoretical ocean tide25. The value attached to each paired trace indicates the relative time shift that yields the best waveform match. (c) Plots of theoretical cross-spectral phases for the tilt of the solid Earth tide and for the sea level change of the ocean tide against the observed cross-spectral phase for the IG wave activity at the M2 tidal frequency. Plots are made for every station pair in the FP array if the observed cross-spectral power at the M2 tidal frequency is >0.95 times the maximum cross-spectral power. A phase in the range 0–2π is reduced to that in the range 0–π by appropriately subtracting π. If the observed and theoretical cross-spectral phases coincide with each other, the plots should lie on the dotted straight line.
This is further confirmed in Figure 6c, which compares the phase  of the observed cross-spectrum
of the observed cross-spectrum  with
with  and
and  in the same sampling period. Here,
in the same sampling period. Here,  and
and  are the cross-spectral phases of the tilt component of the theoretical solid Earth tide and the sea surface elevation of the theoretical ocean tide25, respectively. The cross-correlation function of the observed time series takes only positive values, whereas the cross-correlation functions of the theoretical tides take both positive and negative values. To account for this difference, a phase in the range 0–2π is reduced to that in the range 0–π. In Figure 6c, the values of
are the cross-spectral phases of the tilt component of the theoretical solid Earth tide and the sea surface elevation of the theoretical ocean tide25, respectively. The cross-correlation function of the observed time series takes only positive values, whereas the cross-correlation functions of the theoretical tides take both positive and negative values. To account for this difference, a phase in the range 0–2π is reduced to that in the range 0–π. In Figure 6c, the values of  and
and  are plotted against
are plotted against  for the FP array for the cases where
for the FP array for the cases where  is very large (more than 0.95 times the maximum of
is very large (more than 0.95 times the maximum of  over the frequency range shown in Fig. 4). It is apparent that
over the frequency range shown in Fig. 4). It is apparent that  is in better agreement with
is in better agreement with  than with
than with  The agreement of
The agreement of  with
with  and the absence of ocean tide signals on the records in the tidal band (Fig. 6c) indicate that tidal modulation occurs by coupling between IG waves and the ocean tide in the deep ocean, and not by tide-induced tilting of the sensor axis. If this is the case, the propagation of IG waves may not be perfectly isotropic1, but preferentially parallel to the direction of the co-phase lines. This hypothesis can be tested by carrying out long-term, dense-array observations of the pressure changes at the sea bottom.
and the absence of ocean tide signals on the records in the tidal band (Fig. 6c) indicate that tidal modulation occurs by coupling between IG waves and the ocean tide in the deep ocean, and not by tide-induced tilting of the sensor axis. If this is the case, the propagation of IG waves may not be perfectly isotropic1, but preferentially parallel to the direction of the co-phase lines. This hypothesis can be tested by carrying out long-term, dense-array observations of the pressure changes at the sea bottom.
We have shown that free IG waves in the deep ocean are amplified by the resonance with ocean tides and that such resonance can occur over wide areas of the Pacific Ocean. This implies that ocean tides dissipate a certain amount of energy through resonant coupling with IG waves. Our findings suggest the existence of a possible driving force for IG waves in deep oceans and a possible dissipation mechanism of ocean tidal energy in deep oceans26,27.
Methods
A theory of the resonance between IG waves and the ocean tide
Herein, we present a theory of the resonant coupling between IG waves and the ocean tide. In a long-wave approximation, the two-dimensional equation of motion and the equation for conservation of mass are written as

where  is the horizontal velocity vector; ξ, the sea surface elevation; g, the gravitational acceleration; φ, the tidal potential; and H, the water depth28. When H=const and ζ≪H,
is the horizontal velocity vector; ξ, the sea surface elevation; g, the gravitational acceleration; φ, the tidal potential; and H, the water depth28. When H=const and ζ≪H,

To obtain the first-order solution, we ignore the nonlinear advection term in (2):

Under the assumption that the wave field is random and homogeneous23, the free-wave solution can be given as

where

and  The free-wave (IG wave) propagates in the direction defined by the wavenumber vector
The free-wave (IG wave) propagates in the direction defined by the wavenumber vector  with a frequency-independent speed c. We express the free-wave-induced sea surface elevation as
with a frequency-independent speed c. We express the free-wave-induced sea surface elevation as

Substituting this expression in the linearized second equation in (1), we obtain

Without taking into account the detailed form of the tidal potential, we assume that the tidal response can be locally expressed in terms of the horizontal velocity as follows:

so that the co-phase line of the tide moves in the direction defined by the wavenumber vector with a speed defined by
with a speed defined by

The height variation associated with (8) is

with

The first-order solution  is then written as
is then written as

In a more general case, we assume that the fluid velocity can be expanded in a perturbation series  where the first-order term is given by (12)23. To determine
where the first-order term is given by (12)23. To determine  we must make allowance for the nonlinear term. The solution can be obtained by solving the following equation:
we must make allowance for the nonlinear term. The solution can be obtained by solving the following equation:

When (12) is introduced on the right-hand side of (13) and only the interaction terms between free waves and the tide are retained, (13) reduces to

The particular solution of (14) is given by

where

and

Condition for the resonance between IG waves and the ocean tide:
If

there is a wavenumber vector  , such that
, such that

in a homogeneous random wave field. With such a  value, either
value, either  or
or  becomes infinite in (15), and hence, the IG wave resonates with the tide. The resonance area in the Pacific Ocean, as defined by (17), is shown for the M2 tide in Figure 5a and for the K1 mode in Figure 5b.
becomes infinite in (15), and hence, the IG wave resonates with the tide. The resonance area in the Pacific Ocean, as defined by (17), is shown for the M2 tide in Figure 5a and for the K1 mode in Figure 5b.
No resonance occurs if

where the sine–sine modulation term dominates the cosine–cosine term in (15). The amplitude of the IG wave becomes maximum when the wavenumber vectors  and
and  are in the same direction, so that
are in the same direction, so that

where

Thus, in the case of (19), the interaction of an IG wave packet with the tide results in a tide-modulated IG wave packet whose amplitude is R times that of the original wave packet. This amplification factor R may be rewritten as follows, by using (5) and (11):

For the non-resonant area in the Pacific Ocean, as defined by (19), R is plotted for the M2 tide in Figure 5a and for the K1 mode in Figure 5b. Note that the plane-wave approximations, as in (8) and (10), may not be valid near the amphidromic point around which the tidal system rotates28. The behaviour near the amphidromic point is beyond the scope of our theory.
Broadband seismic observation at sea bottoms
The BBOBS system has been developed by the Earthquake Research Institute of the University of Tokyo since the 1990s. A BBOBS unit is a self-pop-up type, designed to rise from the seafloor after receipt of an acoustic command. The BBOBS with a three-component CMG-3 T broadband sensor (Guralp Systems) senses ground motions at periods from 0.02 to 360 s with a sampling rate of 100 Hz at 24-bit resolution. All of the seismic instrument components, including the sensor, data logger, transponder and batteries, are packed into a 65-cm diameter titanium alloy pressure housing, which allows for a maximum operating depth of 6,000 m. The system runs for as long as 500 days to ensure long-term seismic observations. We have practiced more than 50 long-term BBOBS experiments since 1999, including several array observations at the Pacific Ocean seafloor. The locations of all the BBOBS stations are shown in Figure 1.
Additional information
How to cite this article: Sugioka, H. et al. Evidence for infragravity wave-tide resonance in deep oceans. Nat. Commun. 1:84 doi: 10.1038/ncomms1083 (2010).
References
Webb, S. C., Zhang, X. & Crawford, W. Infragravity waves in the deep ocean. J. Geophys. Res. 96, 2723–2736 (1991).
Tucker, M. J. Surf beat: sea waves of 1–5 min period. Proc. R. Soc. Lond. A 202, 565–573 (1950).
Elgar, S., Herbers, T. H. C., Okihiro, M., Oltman-Shay, J. & Guza, R. T. Observations of infragravity waves. J. Geophys. Res. 97, 15573–15577 (1992).
Holman, R. A. & Bowen, A. J. Bars, bumps, and holes: models for the generation of complex beach topography. J. Geophys. Res. 87, 457–468 (1982).
Webb, S. C. Broadband seismology and noise under the ocean. Rev. Geophys. 36, 105–142 (1998).
Dolenc, D., Romanowicz, B., Stakes, D., McGill, P. & Neuhauser, D. Observations of infragravity waves at the Monterey ocean bottom broadband station (MOBB). Geochem. Geophys. Geosyst. 6, Q09002 (2005).
Rhie, J. & Romanowicz, B. Excitation of Earth's continuous free oscillations by atmosphere-ocean-seafloor coupling. Nature 431, 552–556 (2004).
Rhie, J. & Romanowicz, B. A study of the relation between ocean storms and the Earth's hum. Geochem. Geophys. Geosyst. 7, Q10004 (2006).
Tanimoto, T. The oceanic excitation hypothesis for the continuous oscillations of the Earth. Geophys. J. Int. 160, 276–288 (2005).
Kurrle, D. & Widmer-Schnidrig, R. The horizontal hum, of the Earth: a global background of spheroidal and toroidal modes. Geophys. Res. Lett. 35, L06304 (2008).
Webb, S. C. The Earth's 'hum' is driven by ocean waves over the continental shelves. Nature 445, 754–756 (2007).
Bromirski, P. D. & Gerstoft, P. Dominant source regions of the Earth's 'hum' are coastal. Geophys. Res. Lett. 36, L13303 (2009).
Nishida, K., Kawakatsu, H., Fukao, Y. & Obara, K. Background Love and Rayleigh waves simultaneously generated at the Pacific Ocean floors. Geophys. Res. Lett. 35, L16307 (2008).
Fukao, Y., Nishida, K. & Kobayashi, N. Seafloor topography, ocean infragravity waves and background Love and Rayleigh waves. J. Geophys. Res. 115, B04302 (2009).
Longuet-Higgins, M. S. & Stewart, R. W. Radiation stress and mass transport in gravity waves, with application to 'surf beats'. J. Fluid Mech. 13, 481–504 (1962).
Herbers, T. H. C., Elgar, S. & Guza, R. T. Generation and propagation of infragravity waves. J. Geophys. Res. 100, 24863–24872 (1995).
Guza, R. T. & Thornton, E. B. Swash oscillations on a natural beach. J. Geophys. Res. 87, 483–491 (1982).
Okihiro, M. & Guza, R. T. Infragravity energy modulation by tides. J. Geophys. Res. 100, 16143–16148 (1995).
Thomson, J., Elgar, S., Raubenheimer, B., Herbers, T. H. C. & Guza, R. T. Tidal modulation of infragravity waves via nonlinear energy losses in the surfzone. Geophys. Res. Lett. 33, L05601 (2006).
Dolenc, D., Romanowicz, B., McGill, P. & Wilcock, W. Observations of infragravity waves at the ocean-bottom broadband seismic stations Endeavour (KEBB) and Explorer (KXBB). Geochem. Geophys. Geosyst. 9, Q05007 (2008).
Suetsugu, D. et al. Probing south Pacific mantle plumes with ocean bottom seismographs. EOS Trans. Am. Geophys. Union 86, 429–435 (2005).
Shiobara, H., Baba, K. & Utada, H. Ocean bottom array probes stagnant slab beneath the Philippine Sea. EOS Trans. Am. Geophys. Union 90, 70–71 (2009).
Hasselmann, K. A statistical analysis of the generation of microseisms. Rev. Geophys. 1, 177–210 (1963).
Smith, W. H. F. & Sandwell, D. T. Global sea floor topography from satellite altimetry and ship depth soundings. Science 277, 1956–1962 (1997).
Matsumoto, K., Takanezawa, T. & Ooe, M. Ocean tide models developed by assimilating TOPEX/POSEIDON altimeter data into hydrodynamical model: a global model and a regional model around Japan. J. Oceanography 56, 567–581 (2000).
Munk, W. H. & Macdonald, G. J. F. The Rotation of the Earth (Cambridge University Press, 1960).
Munk, W. H. & Wunsch, C. Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. 45, 1977–2010 (1998).
Apel, J. R. Principles of Ocean Physics (Academic, 1987).
Peterson, J. Observations and modelling of seismic background noise. USGS Open-File Report 93–322 (1993).
Acknowledgements
We thank Hajime Shiobara, Earthquake Research Institute, University of Tokyo, and Daisuke Suetsugu, Japan Agency for Marine-Earth Technology (JAMSTEC), for organizing the BBOBS observation experiments. We are also thankful to the captains and crew of the research vessels and the Shinkai-6500 operation team of JAMSTEC for their valuable support during the cruises. This study was supported by a Grant-in-Aid for Scientific Research from the Japan Society for the Promotion of Science (19740282).
Author information
Authors and Affiliations
Contributions
H.S. carried out observations and analysed the obtained data; Y.F. proposed the theory; and T.K. developed the observation system.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Sugioka, H., Fukao, Y. & Kanazawa, T. Evidence for infragravity wave-tide resonance in deep oceans. Nat Commun 1, 84 (2010). https://doi.org/10.1038/ncomms1083
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1083
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.