Abstract
Mantle plumes are thought to play a key role in transferring heat from the core–mantle boundary to the lithosphere, where it can significantly influence plate tectonics. On impinging on the lithosphere at spreading ridges or in intra-plate settings, mantle plumes may generate hotspots, large igneous provinces and hence considerable dynamic topography. However, the active role of mantle plumes on subducting slabs remains poorly understood. Here we show that the stagnation at 660 km and fastest trench retreat of the Tonga slab in Southwestern Pacific are consistent with an interaction with the Samoan plume and the Hikurangi plateau. Our findings are based on comparisons between 3D anisotropic tomography images and 3D petrological-thermo-mechanical models, which self-consistently explain several unique features of the Fiji–Tonga region. We identify four possible slip systems of bridgmanite in the lower mantle that reconcile the observed seismic anisotropy beneath the Tonga slab (VSH>VSV) with thermo-mechanical calculations.
Similar content being viewed by others
Introduction
The Fiji–Tonga area in the Southwest Pacific shows many unique features. First, the Tonga slab is not only the fastest subducting slab on Earth, at a speed of 24 cm per year, but also accommodates the fastest back-arc opening within the Lau Back-arc Basin at a rate of 17 cm per year (ref. 1) (Fig. 1). Second, it shows intense seismicity, with the number of reported deep earthquakes in the transition zone being 10-fold larger than in any other subduction zone2. Third, anomalous Ocean Island Basalt (OIB) signatures such as very high 3He/4He ratios and latitudinal gradients in trace element and isotopic (Sr–Nd–Pb) enrichment are found in the northwestern corner of the Lau Basin and nearby regions (Fig. 1) (refs 3, 4, 5, 6, 7, 8, 9, 10), which appear to originate from the Samoan plume. A final distinctive feature is the strong upward deflection of the 660 km mantle discontinuity beneath the region11 that may indicate plume-related upwelling of hot materials from the lower mantle. Other studies12,13 also support high temperature in the upper mantle beneath the North Fiji Basin and the Lau Basin from geological, geochemical and geophysical evidence. Recent seismic tomographic models14,15 reveal a complex subduction slab morphology in the region, with a stagnant slab above the 660-km discontinuity in the northernmost Tonga region and a penetrating slab below the 660-km discontinuity further south, where the Hikurangi plateau is entrained into the subduction zone (Fig. 1). However, the spatial distribution, extent and direction of mantle flow from the Samoan plume and its effect on the slabs still remain enigmatic.
Seismicity with depth deeper than 60 km is obtained from Engdahl et al.58 and indicated by coloured circles according to the focal depth. Plate boundaries are depicted by solid lines: orange and cyan lines represent ridges and trenches, respectively. Magenta lines indicate transform faults. Regions where Ocean Island Basalts (OIB; high He3/He4 ratio) with a signature of the Samoan plume are found3,4,5 are indicated by enclosed solid magenta lines. Other possible signatures of the Samoan plume are found in the regions represented by yellow enclosed lines6,7,8,9,10. Relative velocity of the Pacific plate to the Australian plate is depicted by the thick white arrow based on MORVEL by DeMets et al.59 and velocities from GPS stations in an Australia-fixed reference frame are indicated by thin white arrows60.
Here we suggest a self-consistent hypothesis to explain all the aforementioned phenomena by comparing results from three-dimensional (3D) anisotropic tomography and 3D geodynamic modelling. To constrain the region’s dynamical processes, it is necessary to image not only the isotropic structure (for example, Vs and Vp in three dimensions, which do not give direct insight into mantle flow), but also the anisotropic structure, since anisotropy can be a proxy for deformation and the pattern of mantle flow. Because uncertainties in corrections for crustal structure can have a dramatic effect on the imaging of radial anisotropy16, we recently built a new global anisotropic tomography model that is able to overcome this problem by incorporating crustal thickness perturbations as model parameters along with a massive seismic data set (Methods)17,18.
Results
Seismic tomography
Our isotropic structure model (Figs 2a,c and 3a; Supplementary Fig. 1a), shows the Kermadec and Tonga slabs as high-velocity anomalies (blue colour), while a large continuous low-velocity anomaly upwelling (red colour) from the core–mantle boundary reaches the Tonga slab in the uppermost lower mantle. This upwelling appears to originate from the location of a reported mega-sized ultra-low-velocity zone (ULVZ)19 in the large low shear-wave velocity province beneath the Pacific. The Tonga slab, which is in contact with the mantle plume upwelling, is stagnant in the mantle transition zone, while further south the Kermadec slab penetrates into the lower mantle (Supplementary Fig. 1a; Supplementary Movie 1), consistent with other recent studies14,15.
(a,c) Cross sections from the Voigt average model ( ) in the direction of SW–NE and NW–SE, respectively. (b,d) Cross sections from the anisotropic model (
) in the direction of SW–NE and NW–SE, respectively. (b,d) Cross sections from the anisotropic model ( in the direction of SW–NE and NW–SE, respectively, down to 1,400 km depth, from where the resolution of the anisotropic structure is limited18. Focal depths from EHB data58 with an upper bound of 60 km are superimposed in the cross sections as grey circles. The mantle discontinuity at 660 km is indicated by black-dashed lines in cross sections. Hot spots are represented as triangles in the in-maps. (e,f) Isotropic dVs and radial anisotropy from the geodynamic modelling shown in Fig. 4d. The vertical cross-section is taken at Z=1,300 km. In e the anomalies are due to (1) variations of temperature and (2) topography of major mantle phase transitions occurring approximately at 410, 520 and 660 km depth. In f radial anisotropy in the lower mantle results from the strain-induced fabric of bridgmanite calculated with easy [100](001) system five times weaker than all other slip systems (Supplementary Fig. 8).
in the direction of SW–NE and NW–SE, respectively, down to 1,400 km depth, from where the resolution of the anisotropic structure is limited18. Focal depths from EHB data58 with an upper bound of 60 km are superimposed in the cross sections as grey circles. The mantle discontinuity at 660 km is indicated by black-dashed lines in cross sections. Hot spots are represented as triangles in the in-maps. (e,f) Isotropic dVs and radial anisotropy from the geodynamic modelling shown in Fig. 4d. The vertical cross-section is taken at Z=1,300 km. In e the anomalies are due to (1) variations of temperature and (2) topography of major mantle phase transitions occurring approximately at 410, 520 and 660 km depth. In f radial anisotropy in the lower mantle results from the strain-induced fabric of bridgmanite calculated with easy [100](001) system five times weaker than all other slip systems (Supplementary Fig. 8).
As for the anisotropic structure (Figs 2b,d and 3b; Supplementary Fig. 1b; Supplementary Movie 2), a faster SH velocity anomaly of ∼2% (blue colour) is observed behind the Tonga slab and reaches down to ∼1,400 km depth. Below this depth the resolution of the anisotropic structure is limited and hence the anomaly is not resolvable18. An anisotropy anomaly (VSH>VSV) in this region has been previously suggested20, but we have been able to better constrain its extent both vertically and laterally with our global tomography approach. Unlike previous interpretations of a thin anomaly (∼100 km) (ref. 20), we find the anomaly to be thick (∼1,000 km). In the transition zone (at ∼410–660-km depth) a region with faster SV velocity is observed near the slabs. Extensive resolution tests show that these observed features are robust (Supplementary Figs 2–4). We observe anomalies of faster SH velocity beneath other stagnant slabs as well18. For example, a faster SH anomaly reaches down to around 1,200 km beneath the Japan trench where no plume activity exists (Supplementary Fig. 5). Given the good resolution beneath the Japan trench, this may indicate that the faster SH velocity beneath the stagnant slab may be caused by subduction-induced shear deformation21, which is reproduced in the geodynamic modelling in Supplementary Fig. 6. However, the anomaly beneath the Tonga slab is deeper and stronger than in other regions (Supplementary Fig. 5), strongly suggesting a contribution of the Samoan plume to this anomaly.
Geodynamic modelling
Geodynamic modelling offers a unique tool to investigate mantle dynamics during plume–slab interaction. Using the modelling strategy of ref. 21 (Methods), we find that both the recent tectonic evolution and the present-day seismological observations of the Tonga–Kermadec subduction zone can be reproduced when an upwelling plume hits the bottom of a subducting oceanic plate in the transition zone (Fig. 4; Supplementary Movies 3 and 4). We chose a relatively large plume, based on the extent (∼1,000 km) of the deflection of the 660-km discontinuity11 and the resolving power of our model, which is confirmed in another recent waveform tomography study22. On the one hand, the upwelling plume favours stagnation in the transition zone of the overlying slab segment (Fig. 4c,d) and increases trench retreat at the opposite side of the subduction system23 (Supplementary Fig. 7c). It is worth noting that slab stagnation is found also in models where the plume is upwelling beneath the centre of the plate. On the other hand, the entrainment of the Hikurangi plateau arrests trench motion and decreases the rate of subduction on the Kermadec slab23,24,25, while promoting fast (up to >9 cm per year) trench retreat on the Tonga slab (Figs 4b,d and 5; Supplementary Fig. 7 for the trench position with time). The fast trench rollback, in turn, increases the subduction velocity and the tendency of the slab to stagnate in the transition zone by decreasing the slab dip angle26, and induces strong toroidal mantle flow patterns around the edge of the Tonga slab, which bring hot plume materials into the mantle wedge. Near the edge of the subduction zone, the upper mantle and upper transition zone are characterized by mostly positive and negative radial anisotropy, respectively, due to toroidal flow-related deformation (Fig. 2f). In the uppermost lower mantle, a broad and thick radial anisotropy anomaly is associated with the hot plume due to plume–plate interaction. This anomaly is juxtaposed with a ribbon-like radial anisotropy anomaly located beneath the flat slab segment and which is due to subduction-induced deformation (for example, refs 21, 27). By systematically investigating several potential bridgmanite fabrics (Methods), a positive radial anisotropy (VSH>VSV) anomaly is associated with the plume when the dominant slip system is either [100](010), [100](001),  or <110>
or <110> (Fig. 2f; Supplementary Fig. 8). These slip systems are consistent with those identified in high-pressure deformational experiments on bridgmanite28,29. Consequently, the results from geodynamic modelling support our view that the unusually large and strong upwelling seen in the seismological model may account for the intense deformation beneath the Tonga slab, hampering the penetration of the Tonga slab into the lower mantle, unlike the Kermadec slab.
(Fig. 2f; Supplementary Fig. 8). These slip systems are consistent with those identified in high-pressure deformational experiments on bridgmanite28,29. Consequently, the results from geodynamic modelling support our view that the unusually large and strong upwelling seen in the seismological model may account for the intense deformation beneath the Tonga slab, hampering the penetration of the Tonga slab into the lower mantle, unlike the Kermadec slab.
Comparison of four different models at 32 Myr characterized by: (a) oceanic plate only; (b) oceanic plate and plateau (transparent light green); (c) oceanic plate and plume (red); (d) oceanic plate, plateau and plume. The transparent grey plane in d indicates the position of the dVs and radial anisotropy cross sections displayed in Fig. 2e,f and Supplementary Fig. 8. The oceanic plate is coloured according to the depth of the material. To avoid colour-coding confusion, the core material at the bottom of the domain is not visualized.
(a) oceanic plate only (velocities taken only at the centre of the symmetric plate); (b) oceanic plate and plateau; (c) oceanic plate and plume; (d) oceanic plate, plateau and plume. The purple, green and red lines mark the arrival of slab at the 660-km discontinuity (decreasing both velocities), the arrival of the plateau at the trench (causing trench advance and strong trench retreat on the opposite side of the trench, see Supplementary Fig. 7), and beginning of the interaction slab–plume in the transition zone (which increases shortly, and then slows down the velocities where it impinges, while accelerating the kinematics on the opposite side of the plate).
Discussion
After colliding with the Tonga slab, the Samoan plume seems to change its upward direction to parallel to the slab (Figs 2a,c and 4d). In the upper mantle, plume materials migrate into the mantle wedge around the northern tip of the Tonga slab30 (white arrow in Supplementary Fig. 1c), consistent with our 3D thermal–mechanical simulations and with results from laboratory experiments31. Corresponding anisotropy shows faster SH than SV velocity (Supplementary Fig. 1d), which may indicate the horizontal flow in the upper mantle assuming the presence of A-type fabric in olivine. The plume material’s migration is responsible for OIB signatures in the Rochambeau Rift in the northwestern corner of the Lau Basin and nearby regions3,4,5,6,7,8,9,10, being pervasive throughout the Lau and North Fiji Basins.
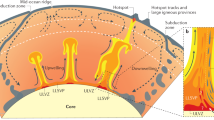
In Fig. 6, we summarize our interpretation of the main features of the mantle flow around the Tonga–Kermadec slabs and their interaction with the Samoan plume. A mega ULVZ at the core–mantle boundary seems to generate an unusually large mantle plume, which ascends through the transition zone (Fig. 6a). The plume collided with the Tonga slab at the bottom of the mantle transition zone at ∼10 Myr, since the likely location of the Tonga slab at that time15 coincides with that of the Samoan plume in our model. This collision caused intense deformation and buoyancy (Fig. 6b), contributing to slab stagnation and probably leading to the significant observed seismicity. During the past 10 Myr, the length of the stagnant slab is thought to have increased to about 700–800 km (refs 14, 15), which is consistent with a probable subduction rate of 7.2–14.2 cm per year (ref. 15), considering slab buckling and compression (Fig. 6c). The plume–slab collision time of 10 Myr is consistent with the beginning of the fast slab retreat32, which has caused the migration of plume materials into the mantle wedge, around the edge of the Tonga slab (Fig. 6d). However, the fast retreat of the northern Tonga–Kermadec trench margin is mostly ascribable to the entrainment at depth of the Hikurangi plateau, which, together with the adjacent Chatham Rise–plate boundary interaction, provides a regional impediment to subduction of the Pacific plate.
(a) The Samoan plume is generated at the Mega ULVZ19 at the core–mantle boundary and is ascending to the surface. (b) The Samoan plume collided with the Tonga slab at the transition zone at about 10 Myr. (c) The upward stress by the collision has caused the stagnant slab and intense seismicity (cross marks), which is further enhanced by fast slab retreat (red arrow) due to the subduction of the Hikurangi plateau. (d) A schematic diagram illustrating the slab–plume interaction beneath the Tonga–Kermadec arc. Cyan lines on the surface show trenches, as shown in Fig. 1. HP, Hikurangi Plateau; KT, Kermadec Trench; NHT, New Hebrides Trench; TT, Tonga Trench; VT, Vitiaz Trench. The Samoan plume originates from a Mega ULVZ at the core–mantle boundary (CMB). The buoyancy caused by large stress from the plume at the bottom of the Tonga slab may contribute to the slab stagnation within the mantle transition zone, while the Kermadec slab is penetrating into the lower mantle directly. At the northern end of the Tonga slab, plume materials migrate into the mantle wedge, facilitated by strong toroidal flow around the slab edge induced by fast slab retreat.
Our high-resolution isotropic and radially anisotropic models interpreted together with 3D petrological-thermo-mechanical numerical simulations provide the clearest picture so far of how mantle plumes can interact with subducting slabs from the mid mantle to the Earth’s surface. Our detection of the large and very active Samoan plume ties together many different previous observations1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,27,30,31,32 providing observational evidence that mantle plumes can be big and strong, able to contribute to slab stagnation and possibly to intense deep seismicity, and the coupled plume-fast slab retreat effect can further enhance slab stagnation and deformation. Since retreating slabs seem to dominate the Earth’s subduction system1, significant interactions between fast retreating slabs and upwellings may be more common on Earth than previously thought23. Up to now, such interactions may have remained largely undetected due to limited seismic resolution and to the lack of fully concerted seismic and geodynamical interpretations. Our models open the way to hunt for possible hidden plumes beneath other slabs stagnating in the mid-mantle, to predict their geochemical and subduction kinematics signature in the geological record and to unravel their role on slab deformation, with potential strong implications in terms of the nature of material exchange between the Earth’s upper and lower mantle. Our unique approach combining for the first time constraints from seismic tomography and the dynamical modelling of anisotropy in a systematic way also promises to reveal unprecedented details about the evolution of other regional settings.
Methods
Radially anisotropic mantle model
The novelty of our strategy is to use a massive and diverse data set, and to incorporate Moho perturbations to the inversions to address crustal effects consistently17,18 . We use the same inversion scheme as in ref. 16, with body-wave travel times added to the modelling using the theoretical developments of Woodhouse and his colleagues33,34. The models are parameterized horizontally using spherical harmonic basis functions expanded up to degree 35 (nominal lateral resolution of ∼600 km), and 21 spline functions are used for variations in the radial direction (see, for example, Fig. 4 in ref. 35). Horizontal norm damping is applied for regularization, and we adopt PREM36 as the reference model. We applied 1.3 times more damping to the anisotropic parameters than to the isotropic parameters to avoid over-interpretation, because of weaker sensitivity of the data to the anisotropic structure and consequently poorer resolution. Since we do not invert for seismic velocity in the crust, before the inversions we correct all the data using crustal corrections from the model CRUST2.0 (ref. 37). Therefore, our strategy to deal with the crust is a hybrid one; first, we carry out crustal corrections using CRUST2.0 taking into account crustal velocity and crustal thickness. Then, in our inversions, we estimate crustal thickness perturbations from CRUST2.0 using our data sets, which include group velocity data. The crustal thickness perturbations are estimated simultaneously to variations in 3D shear-wave velocity and radial anisotropy in the whole mantle.
Isotropic and anisotropic parameters are represented respectively as follows:

To keep the problem tractable, we scale perturbations of VP and density to perturbations of VS using the scaling relations  and
and  , respectively38,39.
, respectively38,39.
Since the model parameters in this study consist of perturbations of isotropic S velocity, S radial anisotropy and crustal thickness, the inverse problem can be written as follows:

where δe is a measure of misfit between the data and theoretical calculations for a given reference model, r is the Earth’s radius parameter, a is the total radius at the Earth’s surface, and δνS, δζS and δd indicate perturbations of isotropic S velocity, S radial anisotropy and discontinuities with respect to the reference model.  ,
,  and Kd are depth sensitivity kernels with respect to isotropic S velocity, S anisotropy and discontinuities, respectively. For comparison with other models, we convert the parameters to the Voigt average isotropy (
and Kd are depth sensitivity kernels with respect to isotropic S velocity, S anisotropy and discontinuities, respectively. For comparison with other models, we convert the parameters to the Voigt average isotropy ( ) and radial anisotropy (
) and radial anisotropy ( ) in the main paper.
) in the main paper.
Depth sensitivity kernels with respect to phase velocities are calculated using the approach of ref. 40, while the formulation of ref. 41 is used to compute group velocity kernels. Sensitivity kernels with respect to crustal thickness are calculated by following ref. 42 for phase velocity data and numerical differentiation for group velocity data. The great circle approximation is used to linearly relate the various datasets to Earth’s structure43.
3D petrological-thermo-mechanical modelling
We used I3MG, a 3D geodynamic framework based on a mixed Eulerian–Lagrangian finite difference scheme44. The numerical domain (X–Y–Z: 5,000 × 2,000 × 4,000 km) is discretized with 245 × 197 × 101 Eulerian nodes, while the material properties are defined on and advected by ∼40 millions Lagrangian particles. The initial model set-up is characterized by a 3,300 × 80 × 2,000 km oceanic plate connected to a gently dipping, 335 km long slab, which drives subduction self-consistently (Supplementary Fig. 9a; Supplementary Table 1). Depending on the type of model, a relatively buoyant (2,950 kg m−3) 1,000 × 30 × 500 km plateau is prescribed on the left side of the plate, and a thermally buoyant plume is defined at the bottom of the mantle through a two-dimensional Gaussian function centered at (X=1,600 km; Z=1,500 km; that is, on the front right side of the plate) with height and width of 500 km (plume volume is 7.854 × 108 km3, ∼2% of the domain volume). A 100-km thick, low viscosity, high-density layer at the bottom of the computational domain simulates the liquid core. Free slip is imposed on all boundaries.
The shallow thermal structure is calculated according to the half-space cooling model45 down to 90 km, then a constant thermal gradient of 0.5 K km−1 is assigned. The 70-Myr-old oceanic plate is juxtaposed with a 20-Myr-old mantle and a weak background crust, which produce moderate lateral friction on the plate. The plume has an initial constant temperature of 2,055 K, which is also the initial temperature at the simulated core–mantle boundary (Y=1,900 km). Consequently, the thermally induced buoyancy of the plume decreases towards such boundary.
A composite visco-plastic rheology based on deformation invariants has been used for the oceanic plate crust, as well as for the mantle and the overlying 30 km thick background crust surrounding the oceanic plate. The effective viscosity ηeff is the result of combined dislocation and diffusion creep mechanisms:

Power-law creep is given by:

where AD, E, V, n are experimentally determined flow-law parameters and τII is the second invariant of the deviatoric stress tensor. For simplicity, the flow law of Dry Olivine46 is used for the whole mantle (Supplementary Table 1).
At low deviatoric stresses, thermally activated diffusion becomes the dominant creep mechanism. Following ref. 45, transition from dislocation to diffusion creep is prescribed at a given deviatoric stress, τII_trans, implying that:


A low-transition stress value favouring dislocation creep is used for the upper mantle and transition zone, while for the lower mantle and the plume τII_trans=30 MPa. Such rheological change across the transition zone—lower mantle boundary is implemented by varying τII_trans as the density of the mantle Lagrangian particles cross the arbitrary value of 4,150 kg m−3.
The strength of the material is limited by:

τyield is determined with a plastic Drucker–Prager criterion46:

where CDP=Ccos φ and μ=sin φ are the cohesion and coefficient of friction, φ is the friction angle.
The oceanic plate is made of a strong, 20-km-thick core with constant viscosity (1024 Pa·s) embedded in between two weaker layers 30-km thick. The lower layer has a constant viscosity of 3 × 1022 Pa·s, while the crust is visco-plastic. In such layer, brittle weakening is implemented as (Supplementary Table 1):

where μ0 and μ1 are the coefficient of friction at zero deformation and at strain ɛ1. Brittle weakening is needed to prevent subduction on the side of the slab and to ensure lubrication at the plates contact after bending-related deformation. Note also that because of the relatively low resolution, very low values of μ0, μ1 and ɛ1 are needed to ensure an efficient lubrication on the top boundary of the subducting slab. Although simplified, such layered rheological structure captures the essential characteristic of the lithosphere yielding profile (for example, ref. 47) producing realistic subduction patterns while preventing slab breakoff48,49,50.
The dynamics of subduction through the mid mantle is affected by several phase transitions that may favour or hinder the sinking of the slab/upwelling of the plume via buoyancy forces. These phase transitions are included by using P–T-dependent density and enthalpy maps generated with PERPLE_X51 for a pyrolitic mantle composition (Supplementary Fig. 9b).
Mantle fabric modelling
The method for computing the lattice preferred orientation (LPO) of mantle polycrystalline aggregates is accurately described in refs 21, 50. The Lagrangian aggregates are homogeneously distributed (initial spacing is 50 × 30 × 50 km) within the computational domain and are passively advected by means of the Eulerian velocity field obtained by the macro-flow modelling. At each time-step, the fabric development of each aggregate is calculated according to the Eulerian velocity gradient field using D-Rex52, modified to account for non-steady-state deformation and deformation history50,53, combined diffusion–dislocation creep mechanisms and strain-induced LPO of mid-mantle aggregates21.
The modal abundances of the aggregates composed by 1,000 crystals reflect a pyrolitic mantle composition (Wd:Grt=60:40 for the upper transition zone, 410–520 km; Rw:Grt=60:40 for the lower transition zone, 520–660 km; Brd:MgO=80:20 for the lower mantle, 660–1,900 km), with the exception of the upper mantle where a more appropriate harzburgitic composition is chosen (Ol:Ens=70:30, 0–410 km) (ref. 54). Phase transition of the whole crystal aggregate is set to occur at arbitrary density crossovers that are assumed to represent the (sharp) boundary between two different rock types (Ol:Ens→Wd:Grt=3,650 kg m−3; Wd:Grt→Rw:Grt=3,870 kg m−3; Rw:Grt→Brd:MgO=4,150 kg m−3). Although part of the LPO can be inherited by aggregates during phase transformation55, when a given density boundary is crossed, the composition of the crystal aggregate is changed and its LPO is reset by randomizing the crystal orientation.
Fabric development is computed only for the fraction of viscous deformation accommodated by dislocation creep and only for phases such as olivine, enstatite, wadsleyite and bridgmanite, which display significant single-crystal visco-elastic anisotropy. Conversely, because aggregates of cubic phases such as ringwoodite, garnet and MgO-periclase are mostly isotropic in the mid mantle56, their crystal orientation is maintained random through the model run. As a result, the lower transition zone will appear as isotropic. The strain-induced LPOs of olivine, enstatite and wadsleyite are obtained by comparison with available experimental data (Supplementary Table 2). In contrast, very little is known about the mechanical properties and deformation mechanisms of bridgmanite at lower mantle P–T conditions. Nevertheless, several potential slip systems have been identified through ab initio simulations57 and high-pressure, low-strain deformational experiments28,29. Dominant slip systems in the uppermost lower mantle appear to be [100](010), [100](001), [010](100), [010](001), [001](100), [001](010), [001]{10}, <10>(001), <110>{110}. Consequently, we have tested different lower mantle LPOs. To understand the pattern of radial anisotropy associated with a given dominant slip system, most fabrics are characterized by an easy slip system much weaker than the others (Supplementary Fig. 10). An additional fabric has been obtained with normalized critical resolved shear stresses from static (0 K) ab initio atomic scale modelling run at pressure typical of the uppermost lower mantle56,57 (Supplementary Table 2). The different radial anisotropy patterns in the lower mantle resulting from these fabrics are reported in Supplementary Fig. 8.
The elastic properties of the aggregates are obtained by Voigt-averaging the crystal elastic properties (scaled by the local P–T conditions through P–T derivatives of the elastic moduli21) according to their volume and orientation. Interpolating the elastic moduli from the Lagrangian aggregates throughout the model domain allows us to calculate, for example, the radial anisotropy and isotropic Vp and Vs anywhere in the model (Fig. 2e,f; Supplementary Figs 8 and 9c).
Additional information
How to cite this article: Chang, S. J. et al. Upper- and mid-mantle interaction between the Samoan plume and the Tonga–Kermadec slabs. Nat. Commun. 7:10799 doi: 10.1038/ncomms10799 (2016).
References
Schellart, W. P., Freeman, J., Stegman, D. R., Moresi, L. & May, D. Evolution and diversity of subduction zones controlled by slab width. Nature 446, 308–311 (2007).
Gurnis, M., Ritsema, J., Van Heijst, H. J. & Zhong, S. Tonga slab deformation: the influence of a lower mantle upwelling on a slab in a young subduction zone. Geophys. Res. Lett. 27, 2373–2376 (2000).
Volpe, A. M., Macdougall, J. D. & Hawkins, J. W. Lau Basin basalts (LBB): trace element and Sr-Nd isotopic evidence for heterogeneity in backarc basin mantle. Earth Planet. Sci. Lett. 90, 174–186 (1988).
Poreda, R. J. & Craig, H. He and Sr isotopes in the Lau Basin mantle: depleted and primitive mantle components. Earth Planet. Sci. Lett. 113, 487–493 (1992).
Lupton, J. E., Arculus, R. J., Greene, R. R., Evans, L. J. & Goddard, C. I. Helium isotope variations in seafloor basalts from the Northwest Lau Backarc Basin: mapping the influence of the Samoan hotspot. Geophys. Res. Lett. 36, L17313 (2009).
Gill, J. & Whelan, P. Postsubduction ocean island alkali basalts in Fiji. J. Geophys. Res. 94, 4579–4588 (1989).
Hart, S. R. et al. Genesis of the Western Samoa seamount province: age, geochemical fingerprint and tectonics. Earth Planet. Sci. Lett. 227, 37–56 (2004).
Jackson, M. G. et al. Samoan hot spot track on a “hot spot highway”: Implications for mantle plumes and a deep Samoan mantle source. Geochem. Geophys. Geosyst. 11, Q12009 (2010).
Lytle, M. L., Kelley, K. A., Hauri, E. H., Gill, J. B., Papia, D. & Arculus, R. J. Tracing mantle sources and Samoan influence in the northwestern Lau back-arc basin. Geochem. Geophys. Geosyst. 13, Q10019 (2012).
Price, A. A. et al. Evidence for a broadly distributed Samoan-plume signature in the northern Lau and North Fiji Basins. Geochem. Geophys. Geosyst. 15, doi:10.1002/2013GC005061 (2014).
Schmerr, N., Garnero, E. J. & McNamara, A. K. Deep mantle plumes and convective upwelling beneath the Pacific Ocean. Earth Planet. Sci. Lett. 294, 143–151 (2010).
Lagabrielle, Y., Goslin, J., Martin, H., Thirot, J.-L. & Auzende, J.-M. Multiple active spreading centres in the hot North Fiji Basin (Southwest Pacific): a possible model for Archaean seafloor dynamics? Earth Planet. Sci. Lett. 149, 1–13 (1997).
Zhao, D. et al. Depth extent of the Lau Back-arc spreading center and its relation to subduction processes. Science 278, 254–257 (1997).
Fukao, Y. & Obayashi, M. Subducted slabs stagnant above, penetrating through, and trapped below the 660 km discontinuity. J. Geophys. Res. 118, 1–19 (2013).
Schellart, W. P. & Spakman, W. Mantle constraints on the plate tectonic evolution of the Tonga-Kermadec-Hikurangi subduction zone and the South Fiji Basin region. Austral. J. Earth Sci. 59, 933–952 (2012).
Ferreira, A. M. G., Woodhouse, J. H., Visser, K. & Trampert, J. On the robustness of global radially anisotropic surface wave tomography. J. Geophys. Res. 115, B04313 (2010).
Chang, S.-J., Ferreira, A. M. G., Ritsema, J., van Heijst, H. J. & Woodhouse, J. H. Global radially anisotropic mantle structure from multiple datasets: a review, current challenges, and outlook. Tectonophysics 617, 1–19 (2014).
Chang, S.-J., Ferreira, A. M. G., Ritsema, J., van Heijst, H. J. & Woodhouse, J. H. Joint inversion for global isotropic and radially anisotropic mantle structure including crustal thickness perturbations. J. Geophys. Res. 120, 4278–4300 (2015).
Thorne, M. S., Garnero, E. J., Jahnke, G., Igel, H. & McNamara, A. K. Mega ultra low velocity zone and mantle flow. Earth Planet. Sci. Lett. 364, 59–67 (2013).
Wookey, J., Kendall, J.-M. & Barruol, G. Mid-mantle deformation inferred from seismic anisotropy. Nature 415, 777–780 (2002).
Faccenda, M. Mid mantle seismic anisotropy around subduction zones. Phys. Earth Planet. Inter. 227, 1–19 (2014).
French, S. W. & Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 525, 95–99 (2015).
Betts, P. G., Mason, W. G. & Moresi, L. The influence of a mantle plume head on the dynamics of a retreating subduction zone. Geology 40, 739–742 (2012).
Mason, W. G., Moresi, L., Betts, P. G. & Miller, M. S. Three-dimensional numerical models of the influence of a buoyant oceanic plateau on subduction zones. Earth Planet. Sci. Lett. 483, 71–79 (2010).
Betts, P. G., Moresi, L., Miller, M. S. & Willis, D. Geodynamics of oceanic plateau and plume head accretion and their role in Phanerozoic orogenic systems of China. Geosci. Front. 6, 49–59 (2015).
Christensen, U. R. The influence of trench migration on slab penetration into the lower mantle. Earth Planet. Sci. Lett. 140, 27–39 (1996).
Chen, W.-P. & Brudzinski, M. R. Evidence for a large-scale remnant of subducted lithosphere beneath Fiji. Science 292, 2475–2479 (2001).
Wenk, H.-R. et al. In situ observation of texture development in olivine, ringwoodite, magnesiowuestite and silicate perovskite at high pressure. Earth Planet. Sci. Lett. 226, 507–519 (2004).
Cordier, P., Ungar, T., Zsoldos, L. & Tichy, G. Dislocation creep in MgSiO3 perovskite at conditions of the Earth’s uppermost lower mantle. Nature 428, 837–840 (2004).
Turner, S. & Hawkesworth, C. Using geochemistry to map mantle flow beneath the Lau Basin. Geology 26, 1019–1022 (1998).
Druken, K. A., Kincaid, C., Griffiths, R. W., Stegman, D. R. & Hart, S. R. Plume-slab interaction: the Samoa-Tonga system. Phys. Earth Planet. Inter. 232, 1–14 (2014).
Hall, R. & Spakman, W. Subducted slabs beneath the eastern Indonesia-Tonga region: insights from tomography. Earth Planet. Sci. Lett. 201, 321 (2002).
Woodhouse, J. H. A note on the calculation of travel times in a transversely isotropic Earth model. Phys. Earth Planet. Inter. 25, 357–359 (1981).
Woodhouse, J. H. & Girnius, T. P. In Seismic Discrimination, Semiannual Technical Summary Report to the Defense Advanced Research Projects Agency 61–65MIT Lincoln Laboratory (1982).
Ritsema, J., Deuss, A., van Heijst, H. J. & Woodhouse, J. H. S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 184, 1223–1236 (2011).
Dziewoński, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Bassin, C., Laske, G. & Masters, G. The current limits of resolution for surface wave tomography in North America. EOS Trans. AGU. Fall Meet. Suppl., Abstract 81, S12A–03 (2000).
Robertson, G. S. & Woodhouse, J. H. Evidence for proportionality of P and S heterogeneity in the lower mantle. Geophys. J. Int. 123, 85–116 (1995).
Anderson, O. L., Schreiber, E., Liebermann, R. C. & Soga, N. Some elastic constant data on minerals relevant to geophysics. Rev. Geophys. 6, 491–524 (1968).
Takeuchi, H. & Saito, M. in Methods of Computational Physics Vol. 11, ed. Bolt B. A. 217–295Academic Press (1972).
Rodi, W., Glover, P., Li, T. & Alexander, S. A fast, accurate method for computing group-velocity partial derivatives for Rayleigh and Love modes. Bull. Seism. Soc. Am. 65, 1105–1114 (1975).
Woodhouse, J. H. & Dahlen, F. A. The effect of a general aspherical perturbation on the free oscillations of the Earth. Geophys. J. Royal Astro. Soc. 53, 335–354 (1978).
Woodhouse, J. H. & Dziewonski, A. M. Mapping the upper mantle: Three dimensional modeling of earth structure by inversion of waveforms. J. Geophys. Res. 89, 5953–5986 (1984).
Gerya, T. V. Introduction to Numerical Geodynamic Modelling 358Cambridge University Press (2009).
Turcotte, D. & Schubert, G. Geodynamics 456Cambridge University Press (2002).
Ranalli, G. Rheology of the Earth 413Chapman and Hall (1995).
Kohlstedt, D. L., Evans, B. & Mackwell, S. J. Strength of the lithosphere: Constrains imposedby laboratory experiments. J. Geophys Res. 100, 17,587–17,602 (1995).
Morra, G., Regenauer-Lieb, K. & Giardini, D. Curvature of oceanic arcs. Geology 34, 877–880 (2006).
Capitanio, F. A., Morra, G. & Goes, S. Dynamics of plate bending at the trench and slab-plate coupling. Geochem. Geophys. Geosys 10, Q04002 (2009).
Faccenda, M. & Capitanio, F. A. Seismic anisotropy around subduction zones: Insights from three-dimensional modeling of upper mantle deformation and SKS splitting calculations. Geochem. Geophys. Geosyst. 14, 243–262 (2013).
Connolly, J. A. D. Computation of phase equilibria by linear programming: a tool for geodynamic modeling and its application to subduction zone decarbonation. Earth Planet. Sci. Lett. 236, 524–541 (2005).
Kaminski, E., Ribe, N. M. & Browaeys, J. T. D-Rex, a program for calculation of seismic anisotropy due to crystal lattice preferred orientation in the convective upper mantle. Geophys. J. Int. 158, 744–752 (2004).
Faccenda, M. & Capitanio, F. A. Development of mantle seismic anisotropy during subduction-induced 3-D flow. Geophys. Res. Lett. 39, L11305 (2012).
Mainprice, D. in Treatise on Geophysics Vol. 2, ed. Schubert G. 437–492Elsevier (2007).
Mainprice, D. Phase transformation and inherited lattice preferred orientations: implications for seismic properties. Tectonophysics 180, 213–228 (1990).
Carrez, P., Ferré, D. & Cordier, P. Implications for plastic flow in the deep mantle from modelling dislocations in MgSiO3 minerals. Nature 446, 68––70 (2007).
Mainprice, D., Tommasi, A., Ferré, D., Carrez, P. & Cordier, P. Predicted glide systems and crystal preferred orientations of polycrystalline silicate Mg-Perovskite at high pressure: Implications for the seismic anisotropy in the lower mantle. Earth Planet. Sci. Lett. 271, 135–144 (2008).
Engdahl, E. R., Van der Hilst, R. D. & Buland, R. Global teleseismic earthquake relocation with improved travel times and procedures for depth determination. Bull. Seism. Soc. Am 88, 722–743 (1998).
DeMets, C., Gordon, R. G. & Argus, D. F. Geologically current plate motions. Geophys. J. Int. 181, 1–80 (2010).
Bevis, M. et al. Geodetic observations of very rapid convergence and back-arc extension at the Tonga arc. Nature 374, 249–251 (1995).
Acknowledgements
This research was initially supported by the Leverhulme Trust (project F/00 204/AS), followed by support by NERC project NE/K005669/1 and the Korea Meteorological Administration Research and Development Program under grant KMIPA 2015-7030. A.M.G.F. also thanks the European Commission's Initial Training Network project QUEST (contract FP7- PEOPLE-ITN-2008-238007, www.quest-itn.org) for the funding. M.F. was supported by the Progetto di Ateneo FACCPTRAT12 granted by the Universite di Padova. We gratefully acknowledge the availability of global seismograms from the IRIS/IDA/USGS, GEOSCOPE and GEOFON networks and the IRIS DATA Centre. The inversions were carried out initially on the High Performance Computing Cluster supported by the Research and Specialist Computing Support services at the University of East Anglia followed by the national UK supercomputing facilities HECToR and Archer. Geodynamic simulations were performed on Galileo Computing Cluster, CINECA, Italy. We thank our colleagues John Brodholt, David Dobson, Carolina Lithgow-Bertelloni, Phil Meredith, Alex Song and Lars Stixrude for fruitful discussions. We also thank the comments of three reviewers that helped to improve this manuscript.
Author information
Authors and Affiliations
Contributions
S.J.C. carried out all the final inversions and built some parts of the inversion codes. A.M.G.F. built all the initial modelling codes and carried out initial test inversions. M.F. carried out all the geodynamical simulations. S.J.C., A.M.G.F. and M.F. carried out the interpretation and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-10, Supplementary Tables 1-2 and Supplementary References. (PDF 3938 kb)
Supplementary Movie 1
Three-dimensional isosurfaces from the Voigt average models from 60 km to 2800 km beneath the study region. Red and blue isosurfaces indicate -1 and +1 % perturbations, respectively. Cyan lines on the surface show trenches. (MOV 13329 kb)
Supplementary Movie 2
Three-dimensional isosurfaces from the anisotropic models from 60 km to 2800 km beneath the study region. Red and blue isosurfaces indicate -1 and +1 % perturbations, respectively. Cyan lines on the surface show trenches. (MOV 13135 kb)
Supplementary Movie 3
Self-consistent evolution of a numerical model characterized by a subducting oceanic plate with a relatively buoyant plateau and upwelling mantle plume (same as in Fig. 4d). Color scale as in Fig. 4 in the main text. View is toward the X axis. (MOV 7498 kb)
Supplementary Movie 4
Self-consistent evolution of a numerical model characterized by a subducting oceanic plate with a relatively buoyant plateau and upwelling mantle plume (same as in Fig. 4d). Color scale as in Fig. 4 in the main text. View is from the left side of the numerical domain. (MOV 1842 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chang, SJ., Ferreira, A. & Faccenda, M. Upper- and mid-mantle interaction between the Samoan plume and the Tonga–Kermadec slabs. Nat Commun 7, 10799 (2016). https://doi.org/10.1038/ncomms10799
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10799
This article is cited by
-
Onset of double subduction controls plate motion reorganisation
Nature Communications (2024)
-
Contact of the Samoan Plume with the Tonga Subduction from Intermediate and Deep-Focus Earthquakes
Surveys in Geophysics (2021)
-
Ubiquitous lower-mantle anisotropy beneath subduction zones
Nature Geoscience (2019)
-
Mantle temperature anomaly in southern Kermadec speculated by three-dimensional numerical subduction modeling
Geo-Marine Letters (2018)
-
Persistence of strong silica-enriched domains in the Earth’s lower mantle
Nature Geoscience (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 and from the anisotropic model (
and from the anisotropic model ( at depths of 400, 500, 600, 700, 800, 1,000, 1,200 and 1,400 km, respectively. Plate boundaries are indicated by grey lines.
at depths of 400, 500, 600, 700, 800, 1,000, 1,200 and 1,400 km, respectively. Plate boundaries are indicated by grey lines.

