Abstract
In submerged microcavities there is a tradeoff between resonant enhancement for spatial water and light overlap. Why not transform the continuously resonating optical mode to be fully contained in a water microdroplet per se? Here we demonstrate a sustainable 30-μm-pure water device, bounded almost completely by free surfaces, enabling >1,000,000 re-circulations of light. The droplets survive for >16 h using a technique that is based on a nano-water bridge from the droplet to a distant reservoir to compensate for evaporation. More than enabling a nearly-perfect optical overlap with water, atomic-level surface smoothness that minimizes scattering loss, and ∼99% coupling efficiency from a standard fibre. Surface tension in our droplet is 8,000 times stronger than gravity, suggesting a new class of devices with water-made walls, for new fields of study including opto-capillaries.
Similar content being viewed by others
Introduction
Liquids have served microcavity research from Ashkin’s studies on optical resonances in levitating droplets1 to recent optofluidic2 resonators3. Droplets can provide an optical quality factor (Q) in proximity to the limit restricted by water absorption and radiation loss4. However, water microdrops5 quickly vaporize due to their large area/volume ratio.
The current state of the art in optofluidic resonators3,6,7 includes single-use droplets in experiments with a pulse laser5, water in pipettes8, toroids in water9,10,11,12, submerged spheres in water13, a stream of microdroplet dye lasers14, water droplets in oil15 and water glycerol on a hydrophobic surface12 and microfluidic optomechanics16. Modern techniques used to perform measurements on solid resonators can be utilized for these resonators as well. Among them are cancelling frequency drifts in the resonator10 and in the pump11, cavity-enhanced spectroscopy7,14,17, broad-band spectroscopy using frequency combs18, and recently, exploiting ring-up for ultrafast spectroscopy19. In their inherent essence, microcavities confine multiple optical passes. Accordingly, and with several close descriptions encountered in literature, the major goodness-of-fit parameters of such resonators are their smallness, 1/Vm (ref. 20), where Vm is the volume of the optical mode, their optical quality factor, Q, and the optical intensity at the region of interest20. Water walls are used in various applications21 including reactions at a gas-liquid interface22.
Here we fabricate a stable spheroidal shape water-walled droplet around a cylindrical stem (Fig. 1). Light can circulate in this droplet near its interface, and when the circumference is an integer number of wavelengths, an optical resonance known as a whispering-gallery mode is formed. There are many advantages to water-walled devices enveloped in air. A maximal contrast between air and the water-core results in a minimal radiation loss, allowing for tight confinement (1/Vm; ref. 4). In addition, air is so transparent that the droplet’s Q can be limited by water absorption only. Last, optical intensity is almost totally contained in the water near the interface with air. Therefore, thermal capillary waves23 can interact with resonantly enhanced light near the interface24.
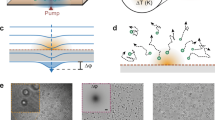
(a) A silica stem is plasma treated to modify its hydrophilicity. A water microdroplet is then formed near the stem’s end ((b) right) while in fluidic contact with a water reservoir ((b) left) via a nano water bridge covering the stem ((b) centre). (c) Micrograph of the drop together with its calculated mode (inset). (d) The bridged droplet maintained its shape for 16 h. (e) Control group: evaporation of a non-bridged droplet on a plate. Vertical and horizontal configurations were equivalent here, since gravity is negligible when compared with surface tension.
Results
Fabrication of the droplet sustainer
We will now describe our method for sustaining the water walls of a microfluidic device (Supplementary Movie 1). As one can see in Fig. 1b,c, a nanoscale water bridge extends from the droplet all the way to a practically unlimited reservoir that replenishes it. Total compensation for evaporation is achieved by designing the hydrophilicity and geometry of our solid surfaces, to enable this bridge; while bearing in mind that water, from energy consideration, prefers to minimize the product of interfacial-tension and area. As will be explained in more details in (Supplementary Fig. 1, Supplementary Methods, Supplementary note 1-2), a wet-plasma treated25 (Fig. 1a) cylindrical stem holds the microdroplet (Fig. 1b,c) while in fluidic contact with the water bridge (Fig. 1b centre). The micrograph of our sustainer presents a droplet (Fig. 1c), where light can circumferentially circulate along an equatorial line and may form an optical whispering-gallery resonance. On need, water can surround the full length of the stem (Fig. 1c) including the formation of a droplet at its end. The existence of the water bridge is confirmed by touching it with a dry object, and watching the object absorb liquid.
The droplet endures perturbations such as holding it (with its sustainer) in a hand and walking with it to another set-up. The droplet also survives touch by a 1-μm tapered fibre. In fact, the taper broke in such tests while the droplet lived on. This is expected since surface tension governs at small scales. To put it into perspective, surface tension in our device is >8,000 times stronger than gravity as defined by its Eötvös number (Supplementary Note 3), meaning that such droplets might even withstand high accelerations. While regular droplets at these scales quickly vaporize (Fig. 1e and Supplementary Movie 2), our microfluidic device was sustained for >16 h (Fig. 1d); when we had to interfere and cut the experiment, to continue to the next study.
Characterization of water droplet resonator
In the following, we will demonstrate our claim to high-Q optical resonances in this sustainable water droplet. We use a tapered fibre12,15,26,27 to evanescently couple light in and out of the droplet (Fig. 2a). We scan the laser wavelength over a region that contains one or more of its resonances. We then deduce the optical quality factor of our micro-droplet resonator from the measured optical linewidth (Δλ) with the formula Q=λ/Δλ.
(a) Experimental set-up (b–e) Monitoring resonator transmission while scanning the wavelength through resonance provides the linewidth. (f) Coupling efficiency close to 99% was measured at critical coupling conditions. (g) Thermal asymmetry of the resonance linewidth measured from two consequented scans. The droplet’s diameter was between 20 and 40 μm. The water is high-purity deionized water (18 MΩ cm−1) and the heavy water is deuterium oxide 99.9 atom % D (item# 151882–100G from Sigma-Aldrich). The taper to resonator distance is 900 nm at the under-coupled regime (Fig. 3b–e) and 700 nm at the critically coupled regime (f). This distance between the taper and resonator was estimated based on the input from the droplet positioning system (P-611.3 NanoCube, Physik Instrumente, PI).
The quality factor was tested on heavy and distilled water droplets at the red and near infrared as shown in Fig. 2b–e. Both distilled and heavy water supports an optical finesse over a million at 780 nm. As seen when diving in the ocean, blue light penetrates water much deeper than red. Thus, 480 nm light will enable one, or maybe even two, orders of magnitude improvement in our measured finesse. Still, even at 780 nm, with an almost complete optical mode overlap with water, the product of finesse and mode penetration in water in our system is >1,000 times higher than other devices. This said, finesse higher than ours was demonstrated using solid devices28. Our quality factors (Fig. 2c,e) suggest an upper limit for scattering losses in our system. Scattering, including from Brownian capillary waves24, might occur in our system; yet, they attenuate light by <0.0001, cm−1.
By bringing the taper closer to the droplet we establish critical coupling. As a result, transmission at resonance drops to almost zero (Fig. 2f), indicating that the coupling efficiency to our devise is ∼99% (ref. 27). Contrary to common solids, the thermal broadening29 is seen here (Fig. 2g) while scanning towards the shorter wavelengths. This is expected since the thermal coefficient of refractive index for water is negative. Linewidth narrowing (Fig. 2g) was observed when scanning toward the longer wavelength exhibiting thermal asymmetry similar to what is readily seen in solid-state resonators29. Increasing the optical input power up to 1 mW results no changes in the resonator and its modal properties when compared with a solid-state resonator.
Characterization of the resonance stability and tenability
Too measure the stability of the resonance during evaporation and subsequent replenishment, we perpetually scan our laser frequency through resonance while monitoring transmission and tracking the resonance (Fig. 3a). We find deviation of 0.3 Å in radius and 0.6 GHz in resonance frequency as calculated from the s.d. of 16 measurements that span over a 0.08-s period. We again monitor the resonance; however, this time we apply voltage to the droplet. As one can see in Fig. 3b, a 10 GHz frequency drift (corresponding to a 5 Å increase in the droplet radius) was observed on increasing the voltage by 10 V. In this regard, it was suggested that hydration shells, including droplets, prefer negative charges30, which can explain the pulling of the droplet toward the positive electrode.
(a) Monitoring the droplet size through its resonance frequency reveals a s.d. of 0.3 Å in radius during a 0.08 s period. Parameters here are similar with the ones in Fig. 2c where the resonance frequency is revealed from the centre of the best-fitting Lorentzian (red line, Fig. 2c). (b) Controlling the water-droplet size and its resonance frequency by applying an external voltage. Parameters are similar to (a) except for an electrode here that was located 300 μm from the droplet. The error bars in (b) represents the s.d. when voltage was not applied (a). We note that the water reservoir is always grounded.
As for Q variation, we monitored no Q degradation over time, even after using the same set-up for a few days without washing it. Our method worked with every type of water that we tried. This includes the purest water that we could find, as well as the dirtiest water that exhibited a quality factor near 10,000. Applicability of liquid-walled resonators to other fluids is evident by the fact that we could successfully excite similar resonances in non-evaporating liquids such as silicone oil and paraffin. Organic liquids (such as acetone) that we tested benefitted from a very-good adhesion to the stem. However, at this preliminary stage we could not find an organophobic material for the reservoir.
In conclusion, devices bounded by water-air interfaces can host optical resonances at their edges. Until today, the fast evaporation of the entire device challenged such experiments. This technology stopper is mitigated here by establishing a nano water bridge that feeds the device. This enables water walls almost all-over microfluidic devices at room pressure and temperature, with no controller, no feedback loop and no additives to the water.
Additional information
How to cite this article: Maayani, S. et al. Water-walled microfluidics for high optical finesse cavities. Nat. Commun. 7:10435 doi: 10.1038/ncomms10435 (2016).
References
Ashkin, A. & Dziedzic, J. Observation of resonances in the radiation pressure on dielectric spheres. Phys. Rev. Lett. 38, 1351 (1977).
Psaltis, D., Quake, S. R. & Yang, C. Developing optofluidic technology through the fusion of microfluidics and optics. Nature 442, 381–386 (2006).
Vollmer, F. & Arnold, S. Whispering-gallery-mode biosensing: label-free detection down to single molecules. Nat. Methods 5, 591–596 (2008).
Weinstein, L. Open Resonators and Open Waveguides The Golem Press (1969).
Zhang, J.-Z. & Chang, R. K. Generation and suppression of stimulated Brillouin scattering in single liquid droplets. JOSA B 6, 151–153 (1989).
Fan, X. & White, I. M. Optofluidic microsystems for chemical and biological analysis. Nat. Photon. 5, 591–597 (2011).
Vollmer, F. & Yang, L. Review Label-free detection with high-Q microcavities: a review of biosensing mechanisms for integrated devices. Nanophotonics 1, 267–291 (2012).
Suter, J. D. et al. Label-free quantitative DNA detection using the liquid core optical ring resonator. Biosens. Bioelectron. 23, 1003–1009 (2008).
Armani, A., Armani, D., Min, B., Vahala, K. & Spillane, S. Ultra-high-Q microcavity operation in H2O and D2O. Appl. Phys. Lett. 87, 151118 (2005).
He, L., Özdemir, Ş. K., Zhu, J., Kim, W. & Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat. Nanotechnol. 6, 428–432 (2011).
Lu, T. et al. High sensitivity nanoparticle detection using optical microcavities. Proc.Natl Acad. Sci. 108, 5976–5979 (2011).
Jonáš, A., Karadag, Y., Mestre, M. & Kiraz, A. Probing of ultrahigh optical Q-factors of individual liquid microdroplets on superhydrophobic surfaces using tapered optical fiber waveguides. JOSA B 29, 3240–3247 (2012).
Arnold, S., Khoshsima, M., Teraoka, I., Holler, S. & Vollmer, F. Shift of whispering-gallery modes in microspheres by protein adsorption. Opt. Lett. 28, 272–274 (2003).
Li, Z. & Psaltis, D. Optofluidic dye lasers. Microfluid Nanofluid 4, 145–158 (2008).
Hossein-Zadeh, M. & Vahala, K. J. Fiber-taper coupling to Whispering-Gallery modes of fluidic resonators embedded in a liquid medium. Opt. Express 14, 10800–10810 (2006).
Bahl, G. et al. Brillouin cavity optomechanics with microfluidic devices. Nat. Commun. 4, 1994 (2013).
Symes, R., Sayer, R. M. & Reid, J. P. Cavity enhanced droplet spectroscopy: Principles, perspectives and prospects. Phys. Chem. Chem. Phys. 6, 474–487 (2004).
Avino, S. et al. Evanescent-wave comb spectroscopy of liquids with strongly dispersive optical fiber cavities. Appl. Phys. Lett. 102, 201116 (2013).
Serge Rosenblum, Y. L., Lior, A., Frank, V. & Barak, D. Cavity ring-up spectroscopy for ultrafast sensing with optical microresonators. Nat. Commun. 6, 6788 (2015).
Mazzei, A. et al. Controlled coupling of counterpropagating whispering-gallery modes by a single Rayleigh scatterer: a classical problem in a quantum optical light. Phys. Rev. Lett. 99, 173603 (2007).
Atencia, J. & Beebe, D. J. Controlled microfluidic interfaces. Nature 437, 648–655 (2005).
Zhao, B., Moore, J. S. & Beebe, D. J. Surface-directed liquid flow inside microchannels. Science 291, 1023–1026 (2001).
Aarts, D. G., Schmidt, M. & Lekkerkerker, H. N. Direct visual observation of thermal capillary waves. Science 304, 847–850 (2004).
Vrij, A. Light scattering from liquid interfaces. Adv. Colloid. Interface. Sci. 2, 39–64 (1968).
Sumner, A. L. et al. The nature of water on surfaces of laboratory systems and implications for heterogeneous chemistry in the troposphere. Phys.l Chem. Chem. Phys. 6, 604–613 (2004).
Knight, J., Cheung, G., Jacques, F. & Birks, T. Phase-matched excitation of whispering-gallery-mode resonances by a fiber taper. Opt. Lett. 22, 1129–1131 (1997).
Spillane, S., Kippenberg, T., Painter, O. & Vahala, K. Ideality in a fiber-taper-coupled microresonator system for application to cavity quantum electrodynamics. Phys. Rev. Lett. 91, 043902 (2003).
Savchenkov, A. A., Matsko, A. B., Ilchenko, V. S. & Maleki, L. Optical resonators with ten million finesse. Opt. Express. 15, 6768–6773 (2007).
Carmon, T., Yang, L. & Vahala, K. Dynamical thermal behavior and thermal self-stability of microcavities. Opt. Express. 12, 4742–4750 (2004).
Scheu, R. et al. Charge asymmetry at aqueous hydrophobic interfaces and hydration shells. Angew. Chem. 126, 9714–9717 (2014).
Acknowledgements
This research was supported by ICore: the Israeli Excellence center ‘Circle of Light’ and by the Israeli Science Foundation grant no. 2013/15.
Author information
Authors and Affiliations
Contributions
S.M. fabricatede devices and performed the experiments. L.L.M. and T.C. supervised the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure 1, Supplementary Notes 1-3, Supplementary Methods and Supplementary References. (PDF 374 kb)
Supplementary Movie 1
Fabrication of a water-walled microfluidic (slowed down by a factor of 8) (MOV 4515 kb)
Supplementary Movie 2
Vaporization of control-group water droplets that are sprayed on a resolution target (real time). (MOV 1725 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Maayani, S., Martin, L. & Carmon, T. Water-walled microfluidics for high-optical finesse cavities. Nat Commun 7, 10435 (2016). https://doi.org/10.1038/ncomms10435
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10435
This article is cited by
-
Review of biosensing with whispering-gallery mode lasers
Light: Science & Applications (2021)
-
Fundamental limits in high-Q droplet microresonators
Scientific Reports (2017)
-
Light and Capillary Waves Propagation in Water Fibers
Scientific Reports (2017)
-
Ripplon laser through stimulated emission mediated by water waves
Nature Photonics (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.