Abstract
The Josephson effect describes the generic appearance of a supercurrent in a weak link between two superconductors. Its exact physical nature deeply influences the properties of the supercurrent. In recent years, considerable efforts have focused on the coupling of superconductors to the surface states of a three-dimensional topological insulator. In such a material, an unconventional induced p-wave superconductivity should occur, with a doublet of topologically protected gapless Andreev bound states, whose energies vary 4π-periodically with the superconducting phase difference across the junction. In this article, we report the observation of an anomalous response to rf irradiation in a Josephson junction made of a HgTe weak link. The response is understood as due to a 4π-periodic contribution to the supercurrent, and its amplitude is compatible with the expected contribution of a gapless Andreev doublet. Our work opens the way to more elaborate experiments to investigate the induced superconductivity in a three-dimensional insulator.
Similar content being viewed by others
Introduction
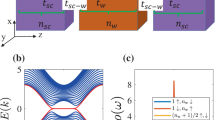
The helical nature of the topological surface states, where the spin is locked perpendicular to the momentum1, is predicted to give rise to exotic superconductivity when coupled to the conventional pairing potential of a s-type superconductor. The broken spin rotation symmetry allows the appearance of triplet p-wave correlations and of gapless Andreev bound states, regardless of the microscopic details of the theoretical model2,3,4,5. In a three-dimensional (3D) topological insulator (TI)-based Josephson junction (JJ), in which superconductivity is induced by the proximity effect of a s-wave superconductor (Fig. 1a), Andreev-bound states appear in the induced gap Δi. They can be pictured as (Fig. 1b) a single topological Andreev doublet (depicted in blue) that occurs at transverse momentum ky=0 and is immune to back-scattering (thus has perfect transmission), and non-topological oblique modes (ky≠0, depicted in red) that are expected to have lower transmissions. The topological protection of the zero mode constitutes a superconducting analogue to Klein tunnelling5. As depicted in Fig. 1b, the peculiarity of this topological doublet is its 4π-periodicity (or equivalently a contribution I4π sin φ/2 to the supercurrent) with respect to the superconducting phase difference φ across the junction4,6,7. The non-ambiguous observation of such gapless states is regarded as an important experimental signature of the unconventional superconductivity in TIs, but no robust evidence has been reported yet8,9,10,11,12,13. A major hindrance could be the coexistence of residual bulk conductance or of a large number of gapped conventional modes12,13. Furthermore, the finite lifetime of the positive energy branch prevents observation of a 4π-periodic Josephson effect in stationary measurements as various relaxation mechanisms can restore a 2π-periodicity for the current–phase relation (CPR)14,15,16,17. The 4π-periodic Josephson effect can therefore be unveiled more easily by the dynamics of the junction. To reveal the periodicity of the Josephson supercurrent, an rf driving current Irf is added to the dc drive to induce the so-called Shapiro steps18. When the dynamics of a conventional JJ is phase-locked to the rf drive, steps of constant voltage appear in the I–V characteristic of the junction for voltages Vn=nhf/2e where  is the step index. However, for a purely 4π-periodic supercurrent, only a sequence of even steps should be observed. In the case of nanowires19, signs of the disappearance of the first step (n=1) have been reported and attributed to a theoretically expected topological phase transition driven by a magnetic field along the axis of the nanowire, although the topological state in the nanowires has yet to be identified in the normal transport regime. Even though it is known that other systems (JJ between p/d-wave superconductors14,20) could lead to similar effects without the need for topological protection, such effects have yet to be observed.
is the step index. However, for a purely 4π-periodic supercurrent, only a sequence of even steps should be observed. In the case of nanowires19, signs of the disappearance of the first step (n=1) have been reported and attributed to a theoretically expected topological phase transition driven by a magnetic field along the axis of the nanowire, although the topological state in the nanowires has yet to be identified in the normal transport regime. Even though it is known that other systems (JJ between p/d-wave superconductors14,20) could lead to similar effects without the need for topological protection, such effects have yet to be observed.
(a) Artist view of the Josephson junction. Mesa stripes of HgTe (represented in mauve) are patterned on the CdTe substrate (blue), with a width W=2 μm. Nb contacts (in yellow) are added at the surface, with a width of 1–4 μm, separated by a variable distance L. (b) Typical energy spectra ɛ(φ) of the Andreev bound states in a 3D TI-based junction, as a function of the phase difference φ in the JJ, with Δi. The gapless 4π-periodic topological mode is depicted as a blue line, corresponding to transverse momentum ky=0 and contributing to the 4π-periodic supercurrent I4π sin φ/2. Gapped modes depicted in red correspond to ky≠0 and contribute to the 2π-periodic supercurrent I2π (containing sin φ and higher order harmonics).
In this article, we study HgTe, a genuine 3D TI whose topological properties have been established independently21,22, and observe an anomalous doubled Shapiro step appearing at low frequency (equivalently a missing n=1 step). While several other mechanisms (non-linearities, capacitance effects, higher harmonics in the CPR23,24) are known to cause the appearance of additional subharmonic steps in the Shapiro response, to our knowledge, only the existence of a 4π-periodic contribution I4π sin φ/2 in the total supercurrent can be responsible for the disappearance of odd steps25.
Results
Device characterization
Our devices are fabricated from coherently strained undoped HgTe layers of 65–90 nm thickness, epitaxially grown on a CdTe substrate. The band inversion of HgTe enforces the existence of topological surface states, while strain opens a gap (≃22 meV) in the bulk of the material26. Previous work has highlighted the high quality of the topological states in this material9,21,22. Quantized Hall plateaus are routinely observed, which demonstrate that transport occurs exclusively through the surface states, without any detectable parallel conductance from the bulk. The mobility and charge density, relevant for our experiments, are evaluated from a Hall bar produced separately from the same wafer as the junctions, and yield typically μ=1–3 × 104 cm2 V−1 s−1, and ne=3−7 × 1011 cm−2. From these values, we extract a mean free path of  nm. The JJs are fabricated by depositing niobium contacts at the surface of a HgTe mesa, using standard sputtering and lift-off techniques (see Methods section and Supplementary Fig. 1). The geometry is shown in Fig. 1a. Each superconducting contact has a width of 1–4 μm, the HgTe weak link has a width of W=2 μm (corresponding to the width of the mesa stripe) and a variable length L ranging from 150 to 600 nm. From the electron density ne, we evaluate the number of transport modes
nm. The JJs are fabricated by depositing niobium contacts at the surface of a HgTe mesa, using standard sputtering and lift-off techniques (see Methods section and Supplementary Fig. 1). The geometry is shown in Fig. 1a. Each superconducting contact has a width of 1–4 μm, the HgTe weak link has a width of W=2 μm (corresponding to the width of the mesa stripe) and a variable length L ranging from 150 to 600 nm. From the electron density ne, we evaluate the number of transport modes  . The niobium of the contacts has a critical temperature of Tc≃8 K, slightly lower than that of bulk Nb (9.2 K). A typical I–V curve obtained at 30 mK is presented in Fig. 2a and exhibits hysteresis, as commonly reported9,27. We find that the critical current of devices with the same dimensions varies by about 30%, which underlines the reproducibility and quality of the fabrication process. A recurring feature in all devices is the presence of an excess current in the I–V curve (Fig. 2a, Supplementary Note 1 and Fig. 2). For high biases, the I–V curves become linear with an asymptote that does not go through the origin but is shifted towards higher currents. This excess current is understood as due to the fact that electrons in an energy window near the superconducting gap carry twice as much current due to Andreev reflections28,29. It thus illustrates the presence of Andreev reflections at both S–TI interfaces. Such an excess current has been previously observed for superconducting point-contacts30,31, but is not commonly reported in thin film structures presumably due to the presence of elastic scattering. This emphasizes the high quality and reproducibility of our devices in agreement with our previous observations9,10,32.
. The niobium of the contacts has a critical temperature of Tc≃8 K, slightly lower than that of bulk Nb (9.2 K). A typical I–V curve obtained at 30 mK is presented in Fig. 2a and exhibits hysteresis, as commonly reported9,27. We find that the critical current of devices with the same dimensions varies by about 30%, which underlines the reproducibility and quality of the fabrication process. A recurring feature in all devices is the presence of an excess current in the I–V curve (Fig. 2a, Supplementary Note 1 and Fig. 2). For high biases, the I–V curves become linear with an asymptote that does not go through the origin but is shifted towards higher currents. This excess current is understood as due to the fact that electrons in an energy window near the superconducting gap carry twice as much current due to Andreev reflections28,29. It thus illustrates the presence of Andreev reflections at both S–TI interfaces. Such an excess current has been previously observed for superconducting point-contacts30,31, but is not commonly reported in thin film structures presumably due to the presence of elastic scattering. This emphasizes the high quality and reproducibility of our devices in agreement with our previous observations9,10,32.
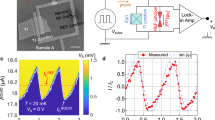
(a) I–V curve in the absence of rf irradiation for the two sweep directions, taken at base temperature T≃30 mK. The asymptotes (grey solid lines) do not cross the origin, emphasizing the presence of an excess current. (Inset) Detailed view of the I–V curve, that exhibits hysteresis between the upward and downward sweep direction. (b) Shapiro steps for three different frequencies measured at T≃800 mK. The plotted voltage scale is in normalized units hf/2e to highlight the formation of Shapiro steps in the I–V curve in the presence of rf irradiation. For a high-frequency f=11.2 GHz (blue line), all steps are clearly visible for voltages  (up to |n|>12, but only the first three are shown for the sake of clarity). For an intermediate frequency (f=5.3 GHz, blue line), the first step (n=1) is noticeably reduced. At low frequency (f=2.7 GHz, red line), the first step is fully suppressed, while all other steps remain visible. (c) Bar plots obtained by binning the measurement data according to voltage, for f=2.7 GHz and 11.2 GHz. The Shapiro steps appear as peaks in the bin counts for
(up to |n|>12, but only the first three are shown for the sake of clarity). For an intermediate frequency (f=5.3 GHz, blue line), the first step (n=1) is noticeably reduced. At low frequency (f=2.7 GHz, red line), the first step is fully suppressed, while all other steps remain visible. (c) Bar plots obtained by binning the measurement data according to voltage, for f=2.7 GHz and 11.2 GHz. The Shapiro steps appear as peaks in the bin counts for  . While all steps are visible for f=11.2 GHz, the first Shapiro step (n=1) is absent at f=2.7 GHz.
. While all steps are visible for f=11.2 GHz, the first Shapiro step (n=1) is absent at f=2.7 GHz.
AC response
We now turn to the study of the response of these devices to rf irradiation and highlight the existence of a 4π-periodic supercurrent. To this end, we focus on three devices produced from the same wafer, for which the width of the junction is set to W=2 μm, for nominal lengths of L=150, 400 and 600 nm. The experiment described below has been repeated on more than 10 devices, made out of three different wafers with similar characteristics, in three different measurement setups, all yielded similar results (Supplementary Fig 3 to 10 and Note 2).
To observe the Shapiro steps, the sample is irradiated with a radio-frequency excitation via a coaxial line, the open end of which is adjusted to be around 1 mm from the sample. In this geometry, frequencies in the range of 2–12 GHz are easily accessible, but the rf power supplied to the sample is not calibrated. Under rf irradiation, we observe the appearance of Shapiro steps in the I–V characteristic at quantized voltages Vn=nhf/2e, where  is the step index18. In contrast to the standard JJ response, with steps at each n, we find at lower frequency that the n=1 step is missing. To illustrate this anomalous Shapiro response of our junctions, we present three I–V curves corresponding to three different excitation frequencies in Fig. 2b (for the junction with L=150 nm). The applied rf power is chosen such that all curves display similar critical currents, the full range of rf power will be discussed later. For a high-frequency f=11.2 GHz, one typical I–V curve is plotted as a blue line (with voltage normalized to hf/2e). Several steps are clearly visible with step height hf/2e. At lower frequencies f=5.3 GHz (green line), higher order steps are visible but a clear reduction of the amplitude of the n=1 step occurs. For a frequency of f=2.7 GHz (red line), this first odd step is fully suppressed, showing an anomalous first step at hf/e. The presence or absence of the n=1 can be conveniently detected by binning the measurement data according to the voltage (with a
is the step index18. In contrast to the standard JJ response, with steps at each n, we find at lower frequency that the n=1 step is missing. To illustrate this anomalous Shapiro response of our junctions, we present three I–V curves corresponding to three different excitation frequencies in Fig. 2b (for the junction with L=150 nm). The applied rf power is chosen such that all curves display similar critical currents, the full range of rf power will be discussed later. For a high-frequency f=11.2 GHz, one typical I–V curve is plotted as a blue line (with voltage normalized to hf/2e). Several steps are clearly visible with step height hf/2e. At lower frequencies f=5.3 GHz (green line), higher order steps are visible but a clear reduction of the amplitude of the n=1 step occurs. For a frequency of f=2.7 GHz (red line), this first odd step is fully suppressed, showing an anomalous first step at hf/e. The presence or absence of the n=1 can be conveniently detected by binning the measurement data according to the voltage (with a  bin size). The resulting histograms of the voltage V are presented as bar plots in Fig. 2c. For Vn=nhf/2e with n integer, Shapiro steps appear as peaks in the bin counts, the amplitude of which then reflects the length of the current step (in nA). For f=11.2 GHz, all steps emerge clearly from the background. For f=2.7 GHz, the peak at V=hf/2e is absent, reflecting the suppression of the n=1 Shapiro step. This anomalous behaviour of the Shapiro steps constitutes the main finding of this article. Below, we carefully analyse its origin and conclude that it indicates the existence of a 4π-periodic contribution to the supercurrent.
bin size). The resulting histograms of the voltage V are presented as bar plots in Fig. 2c. For Vn=nhf/2e with n integer, Shapiro steps appear as peaks in the bin counts, the amplitude of which then reflects the length of the current step (in nA). For f=11.2 GHz, all steps emerge clearly from the background. For f=2.7 GHz, the peak at V=hf/2e is absent, reflecting the suppression of the n=1 Shapiro step. This anomalous behaviour of the Shapiro steps constitutes the main finding of this article. Below, we carefully analyse its origin and conclude that it indicates the existence of a 4π-periodic contribution to the supercurrent.
Dependence on rf power
We now examine the crossover from high to low frequency, for which the first odd Shapiro step n=1 progressively disappears. To this end, we scan the presence of Shapiro steps for a range of rf powers at fixed frequencies and generate two-dimensional colour plots of the bin counts at the voltage V (which indicates the current height of the Shapiro step when present) as a function of the voltage V and rf current Irf. As shown in Fig. 3 (for the junction with L=150 nm), such plots reveal the presence of Shapiro steps as maxima at constant quantized voltages (horizontal lines). Let us first examine measurements taken at f=11.2 GHz. (Fig. 3c). At Irf=0, a single maximum at V=0 reflects the presence of a supercurrent. As Irf increases, Shapiro steps progressively appear, starting from low values of n, while the amplitude of the supercurrent (n=0) decreases and eventually vanishes. At higher powers, the steps show an oscillatory pattern, reminiscent of Bessel functions occurring in the voltage bias case33,34. Horizontal linecuts at constant voltages give access to the amplitude of the first steps (n=0, 1, 2, 3 and 4), presented in the lower panels of Fig. 3 as a function of rf current Irf. For high frequencies such as f=11.2 GHz, our device exhibits the conventional behaviour that is seen in various other systems (carbon nanotubes35, graphene36 or Bi2Se3 (ref. 12) weak links), that always (regardless of frequency) show a clear presence of the n=1 step. The case of atomic contacts (with a few ballistic highly transparent modes) is particularly well understood, and also exhibits a strong n=1 Shapiro resonance in excellent agreement with theoretical models37,38. In the Supplementary Note 3 and Figs 11 and 12, we provide additional measurements on graphene-based devices (another example of two-dimensional Dirac material), that also show this standard behaviour in all accessible regimes.
(a–c) 2D map of the bin counts for frequencies f=2.7, 5.3 and 11.2 GHz, respectively. Shapiro steps are identified as maxima for constant voltages Vn (white dashed lines emphasize n=0, 1 and 2). For f=11.2 GHz, all steps are visible. When frequency is lowered (f=5.3 GHz), the first odd step (n=1) is absent up to a rf excitation indicated by the red arrow. Finally, at f=2.7 GHz, the first step is completely invisible up to the crossing point that marks the beginning of the oscillatory regime at high rf currents. A dark fringe (indicated by a dark grey arrow) is observed at finite voltages in the oscillating pattern concomitant with the missing n=1 step. (d–f) Horizontal linecuts through the previous colormaps (frequencies f=2.7, 5.3 and 11.2 GHz) that give access to the amplitudes of steps 0–4. While all Shapiro steps are clearly visible at high frequencies, the step n=1 progressively disappears as f decreases. From these plots, we access the maximum widths wn of each step (see the example of w4 at f=2.7 GHz). For clarity, the different curves are offset by 0.4, 0.6 and 1.7 μA for d–f, respectively.
In contrast to the conventional Shapiro features commonly reported, our HgTe-based junctions exhibit a very clear vanishing of the first step n=1 when the excitation frequency f is decreased. Measurements at f=5.3 GHz show that the first step is suppressed below a certain value of Irf (indicated by the red arrow), and that it is completely absent at f=2.7 GHz. In the oscillatory regime at higher rf currents, a suppressed first oscillation (dark fringe indicated by the dark grey arrow) becomes clearly visible at low frequency, demonstrating the range of influence of the vanishing first step on the rest of the pattern. In the lower panels, a complete suppression of the first step or disturbances in the oscillations at higher rf currents can similarly be observed. This crossover has been observed on all working devices, up to 800 mK, which is the highest stable temperature accessible in our fridge. In some cases, hysteretic behaviour at low temperatures hinders the observation of low-index steps (Supplementary Fig. 8 and Note 2). However, importantly, biasing instabilities and sudden current switches (such as the ones observed in the hysteretic regime) can be excluded as a mechanism for the missing n=1 step, as the same features are seen in measurements of a junction in which bistability is suppressed by a shunt resistor (Supplementary Fig. 9 and Note 3).
In opposition to a missing n=1 step, additional subharmonic steps (for n=p/q fractional value) are often observed37,39 as a consequence of non-linearities, capacitance effects or higher harmonics in the CPR. Such higher harmonics have been predicted5 and detected32 in our junctions. At higher frequencies, we indeed observe half-integer steps (n=1/2, 3/2 and so on, Supplementary Note 3 and Fig. 6) but they clearly appear in a different regime from where we observe the missing n=1 step.
Analysis and amplitude of the 4π-periodic supercurrent
The presence of a 4π-periodic contribution in the supercurrent I4π sin φ/2 is the only known mechanism to result in the observed doubling of the Shapiro step size. As already mentioned, microscopic models based on Bogoliubov-de Gennes equations have predicted such a 4π-periodic contribution in the CPR2,3,4,5, which originates from the presence of a gapless topological Andreev doublet. This anomalous CPR can then be supplemented with the Josephson equation on the time-evolution of the phase difference to simulate the dynamics of such a system (see Methods section). This dynamics is captured in the extended Resistively Shunted Junction (RSJ) model of Dominguez et al.25 It takes into account the presence of a sin φ/2 contribution in the supercurrent and explains the crossover between the two frequency regimes by the highly non-linear dynamics of the junction. When a small 4π-periodic contribution I4π sin φ/2 is superposed on a large 2π-periodic supercurrent I2π sin φ in the CPR, the latter dominates the high-frequency Shapiro response, but the weak 4π-periodic contribution is revealed at low frequencies by doubled Shapiro steps (Supplementary Note 4 and Figs 13, 14, 15). Doubled Shapiro steps are observed only when the driving frequency f becomes smaller than the characteristic frequency  (with Rn the normal state resistance of the device). This frequency scale based on the amplitude of the 4π-periodic supercurrent is expected to be much smaller than the typical Josephson frequency scale
(with Rn the normal state resistance of the device). This frequency scale based on the amplitude of the 4π-periodic supercurrent is expected to be much smaller than the typical Josephson frequency scale  (fJ≃53 GHz for the 150 nm long junction), as
(fJ≃53 GHz for the 150 nm long junction), as  . To estimate I4π, we introduce two indicators Q12 and Q34 as follows. From the maximum amplitude of the first lobe of each step, denoted by
. To estimate I4π, we introduce two indicators Q12 and Q34 as follows. From the maximum amplitude of the first lobe of each step, denoted by  , (see Fig. 3a where the measurement is indicated for the n=4 step), we define and compute the ratios Q12=w1/w2, Q34=w3/w4, and plot them as a function of the rf excitation frequency (Fig. 4). Despite some scattering, we observe a clear decrease of Q12 towards 0 with decreasing frequency, while Q34 remains constant around 1, for all lengths. For the shortest junction (150 nm) Q12 reaches a value of 0.05 around 2 GHz, and the first step n=1 is invisible. For comparison, we have also plotted the boundaries (grey dashed lines) between which the ratios Q12 and Q34 vary in the standard RSJ model34,40 (with only a sin φ component in the supercurrent). While the ratio Q34 remains close to the grey region, the behaviour of Q12 is not properly described. Assuming the validity of the above criterion, one can evaluate the number of 4π-periodic channels. We estimate f4π=4.5–5 GHz and I4π=250–300 nA for the 150-nm junction, and f4π=4 GHz and I4π=50–70 nA for the longer junctions (400 and 600 nm). One can compare these values with the maximum supercurrent carried by one channel41, given by eΔi/ħ per channel where Δi can be estimated from the decay of Ic with temperature (Supplementary Figs 2 and 3 and Note 2). With Δi=0.35 meV (150 nm) and Δi=0.1–0.15 meV (400 and 600 nm), we estimate that the 4π-periodic contribution amounts to that of 1–3 channels that is compatible with the presence of one topological mode in our system, despite uncertainties on the exact value of f4π and Δi. Results on three other junctions with different parameters have been compiled (Supplementary Table 1) and are consistent with this estimate.
, (see Fig. 3a where the measurement is indicated for the n=4 step), we define and compute the ratios Q12=w1/w2, Q34=w3/w4, and plot them as a function of the rf excitation frequency (Fig. 4). Despite some scattering, we observe a clear decrease of Q12 towards 0 with decreasing frequency, while Q34 remains constant around 1, for all lengths. For the shortest junction (150 nm) Q12 reaches a value of 0.05 around 2 GHz, and the first step n=1 is invisible. For comparison, we have also plotted the boundaries (grey dashed lines) between which the ratios Q12 and Q34 vary in the standard RSJ model34,40 (with only a sin φ component in the supercurrent). While the ratio Q34 remains close to the grey region, the behaviour of Q12 is not properly described. Assuming the validity of the above criterion, one can evaluate the number of 4π-periodic channels. We estimate f4π=4.5–5 GHz and I4π=250–300 nA for the 150-nm junction, and f4π=4 GHz and I4π=50–70 nA for the longer junctions (400 and 600 nm). One can compare these values with the maximum supercurrent carried by one channel41, given by eΔi/ħ per channel where Δi can be estimated from the decay of Ic with temperature (Supplementary Figs 2 and 3 and Note 2). With Δi=0.35 meV (150 nm) and Δi=0.1–0.15 meV (400 and 600 nm), we estimate that the 4π-periodic contribution amounts to that of 1–3 channels that is compatible with the presence of one topological mode in our system, despite uncertainties on the exact value of f4π and Δi. Results on three other junctions with different parameters have been compiled (Supplementary Table 1) and are consistent with this estimate.
For each length L of the JJ, we calculate the ratios of step amplitudes Q12=w1/w2 (a) and Q34=w3/w4 (b) and plot them as a function of the rf frequency. Q12 shows a very clear decrease as frequency f is lowered. A minimum around 0.05 is obtained for the 150-nm junction, but we observe that this minimum tends to increase with the length L of the junction. In contrast, even if the measurements show some scattering, the ratio of higher order steps Q34 does not show significant variation. For comparisons, we evaluated Q12 and Q34 from a conventional RSJ model, and show the results as a grey area.
Finally, one might also suspect that the 4π-periodic contribution stems from Landau–Zener transitions occurring at the anticrossing (for φ=π[2π]), causing some highly transparent 2π-periodic states to behave effectively as 4π-periodic, in the absence of truly 4π-periodic modes. In a single mode model25, one can numerically show that the quantization of the Shapiro steps is lost when the Landau–Zener tunnelling probability is <1: the Shapiro steps split in two and depart from their quantized values Vn, (n even), and eventually disappear for probabilities below 0.7. We do not experimentally observe such effects in any accessible regime. Assuming the validity of this specific model, an upper bound on the possible energy splitting 2δ between positive and negative energy branches can be evaluated from the Landau–Zener transition probability. Given our experimental resolution, we obtain the upper-bound δ≤9 μeV for the 400 and 600 nm junctions, and δ≤18 μeV for the 150 nm one (Supplementary Note 4 and Figs 16 and 17). This is much smaller than the energy scale given by the temperature (70 μeV at 800 mK) and corresponds in both cases to a transmission ≥0.994. Besides, there are no reports of missing odd Shapiro steps due to Landau–Zener transitions in highly ballistic junctions to date.
Interestingly, only the first step n=1 is missing (similarly to that reported for etched InSb nanowire devices19), and not the following odd steps n=3, 5 and so on. This feature is not well understood, but one can also speculate that the frequency f has to be lowered further for other odd steps to vanish, in a range that is not accessible in this experiment. An alternative explanation is given by enhanced relaxation (due, for example, to coupling to the continuum of states above the superconducting gap), with a characteristic time scale that decreases as voltage increases15,42. However, most models assume a voltage bias of the junction and a more detailed analysis of the current bias case is needed.
To conclude, we have presented robust evidence for a 4π-periodic contribution to the supercurrent flowing in JJs based on the 3D TI HgTe. The consistency of the measurements in Hall bars and JJs signals that our devices are well-controlled, with well-defined proximity-induced superconducting HgTe contacts connected via a ballistic HgTe surface. Under rf irradiation, a suppression of the first Shapiro step is observed at low frequencies and low magnetic fields, for a wide range of temperatures (up to 800 mK), which we attribute to the existence of a 4π-periodic component in the supercurrent. The study of its order of magnitude and of Landau–Zener transitions reveal that these experimental observations are compatible with the presence of a few 4π-periodic gapless Andreev bound states. The topologically non-trivial behaviour of HgTe has been established in the previous work, so that such states would likely stem from the topologically protected gapless Andreev doublet. However, our current observations cannot exclude the presence of trivial ballistic states. Further investigations are required to conclusively demonstrate the relationship of these observations to Majorana physics4,43. Besides, these observations with a 3D TI of strained HgTe are very encouraging for future experiments in which the weak link would consist of narrow HgTe quantum wells that exhibit the quantum spin Hall effect44, in which the total number of transport modes should be reduced to a few.
Methods
Sample preparation and layer characterization
Bulk HgTe layers are grown by molecular beam epitaxy on a CdTe substrate. Before the fabrication of the JJs, the transport properties of each layer are characterized by the measurement of longitudinal and transverse (Hall) resistance in a Hall bar geometry. From the longitudinal resistance at zero magnetic field, one can extract the mobility of the layer, while the density is obtained from a linear fit of the Hall resistance between 0 and 500 mT. The layers being very similar to the ones presented in refs 21, 22, we refer the interested reader to these references where the measurements are discussed in detail.
Using a Ti/SiO2 etch mask, the samples are patterned via Ar+ ion beam milling to obtain 2-μm wide HgTe stripes. The Nb contacts (60 nm Nb+Al/Ru cap) are sputtered on top of the HgTe layer, after a short Ar+-milling step to remove any adsorbant or reaction product left on the HgTe mesa after exposure to air. The top-layer of HgTe below the contact may be disordered due to the deposition of the Nb contacts. We assume that this top surface is proximitized by interaction with the Nb, but that the HgTe weak link between the contacts remains in the ballistic regime as highlighted in the main text.
In Supplementary Fig. 1, scanning electron microscopy pictures of a typical junction are shown. From these scanning electron microscopy pictures, it is observed that the nominal length (used in the article) probably overestimates the physical length of the JJs. We evaluate the physical length to be 60–70 nm smaller than the nominal length.
Simulations using RSJ equations
The 4π-periodic contribution to the supercurrent has been theoretically investigated using microscopic models, in particular Bogoliubov-de Gennes hamiltonians2,3,5. However, difficulties arise when dynamics have to be taken into account. The RSJ model is to our knowledge the only way to define the time-averaged voltage measured in a current bias experiment like ours. The CPR derived from microscopic model can then be supplemented with the universally valid time-evolution of the phase difference of the Josephson effect, dφ/dt=2eV/ħ. In this framework, the junction is modelled together with a resistive shunt to capture the impedance of the environment (that plays an essential role in the dynamics of the junction). The total current through the system I can be written as the sum I=IR+IS where  is the current through the resistor Rn and IS the supercurrent through the junction. The geometrical capacitance is small, and we neglect it here9. Combining the first Josephson equation dφ/dt=2eV/ħ, and the current bias I=Idc+ Irf sin 2πft obtains a first-order ordinary differential equation:
is the current through the resistor Rn and IS the supercurrent through the junction. The geometrical capacitance is small, and we neglect it here9. Combining the first Josephson equation dφ/dt=2eV/ħ, and the current bias I=Idc+ Irf sin 2πft obtains a first-order ordinary differential equation:

This model does not take into account all microscopic details (for example, the normal state resistance Rn, which is assumed to be independent of voltage, which in reality will not be true). It has nonetheless the key aspects to capture the essential features of the dynamic Josephson current relevant to our observations. Simulations based on a standard RSJ model34 have been carried out to compare our results with a simple and well-understood model. The rf excitation is here represented as a current Irf instead of a voltage Vrf in agreement with most of the literature on Shapiro steps. It assumes that the characteristic field impedance of the radiation field is high compared with the junction impedance34. In our case (low capacitance), the typical impedance of the junction is given by its resistance (typically between 30 and 150 Ω), smaller than the free space impedance (in which the rf excitation signal propagates before the junction) given by  . This approximation is probably a bit crude, but it is further justified by the overall agreement of the effect of frequency on the Shapiro response (Fig. 3 and Supplementary Figs 5, 13, 14.), which is a characteristic feature of the current bias model developed by Russer34. We simulate the results of this equation using a simple Runge-Kutta algorithm (RK4) to obtain the I–V curve, realize a binning of the voltage V and finally compute the ratios Q12, Q34 for comparison with experimental results.
. This approximation is probably a bit crude, but it is further justified by the overall agreement of the effect of frequency on the Shapiro response (Fig. 3 and Supplementary Figs 5, 13, 14.), which is a characteristic feature of the current bias model developed by Russer34. We simulate the results of this equation using a simple Runge-Kutta algorithm (RK4) to obtain the I–V curve, realize a binning of the voltage V and finally compute the ratios Q12, Q34 for comparison with experimental results.
Additional information
How to cite this article: Wiedenmann, J. et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 7:10303 doi: 10.1038/ncomms10303 (2016).
References
Fu, L., Kane, C. & Mele., E. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Fu, L. & Kane, C. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Olund, C. T. & Zhao, E. Current-phase relation for Josephson effect through helical metal. Phys. Rev. B 86, 214515 (2012).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Conden. Matter Phys. 4, 113–136 (2013).
Tkachov, G. & Hankiewicz, E. M. Helical Andreev bound states and superconducting Klein tunneling in topological insulator Josephson junctions. Phys. Rev. B 88, 075401 (2013).
Kitaev, A. Unpaired Majorana fermions in quantum wires. Physics Uspekhi 44, 131 (2001).
Zhang, F. & Kane, C. L. Anomalous topological pumps and fractional Josephson effects. Phys. Rev. B 90, 020501 (2014).
Veldhorst, M. et al. Josephson supercurrent through a topological insulator surface state. Nat. Mater. 11, 417–421 (2012).
Oostinga, J. B. et al. Josephson Supercurrent through the Topological Surface States of Strained Bulk HgTe. Phys. Rev. X 3, 021007 (2013).
Maier, L. et al. Phase-sensitive SQUIDs based on the 3D topological insulator HgTe. Phys. Scr. T164, 014002 (2015).
Kurter, C., Finck, A. D. K., Ghaemi, P., Hor, Y. S. & Van Harlingen, D. J. Dynamical gate-tunable supercurrents in topological Josephson junctions. Phys. Rev. B 90, 014501 (2014).
Galletti, L. et al. Influence of topological edge states on the properties of Bi2Se3/Al hybrid Josephson devices. Phys. Rev. B 89, 134512 (2014).
Finck, A. D. K., Kurter, C., Hor, Y. S. & Van Harlingen., D. J. Phase coherence and andreev reflection in topological insulator devices. Phys. Rev. X 4, 041022 (2014).
Kwon, H.-J., Yakovenko, V. M. & Sengupta, K. Fractional ac Josephson effect in unconventional superconductors. Low Temp. Phys. 30, 613 (2004).
San-Jose, P., Prada, E. & Aguado, R. Ac Josephson effect in finite-length nanowire junctions with Majorana modes. Phys. Rev. Lett. 108, 257001 (2012).
Pikulin, D. I. & Nazarov, Y. V. Phenomenology and dynamics of a Majorana Josephson junction. Phys. Rev. B 86, 140504 (2012).
Badiane, D. M., Glazman, L. I., Houzet, M. & Meyer., J. S. Ac Josephson effect in topological Josephson junctions. C. R. Phys. 14, 840–856 (2013).
Shapiro., S. Josephson currents in superconducting tunneling: the effect of microwaves and other observations. Phys. Rev. Lett. 11, 80–82 (1963).
Rokhinson, L. P., Liu, X. & Furdyna., J. K. The fractional a.c. Josephson effect in a semiconductor/superconductor nanowire as a signature of Majorana particles. Nat. Phys. 8, 795–799 (2012).
Tanaka, Y. & Kashiwaya, S. Theory of Josephson effects in anisotropic superconductors. Phys. Rev. B 56, 892–912 (1997).
Brüne, C. et al. Quantum Hall Effect from the Topological Surface States of Strained Bulk HgTe. Phys. Rev. Lett. 106, 126803 (2011).
Brüne, C. et al. Dirac-screening stabilized surface-state transport in a topological insulator. Phys. Rev. X 4, 041045 (2014).
Renne, M. J. & Polder, D. Some analytical results for the resistively shunted Josephson junction. Revue de Physique Appliquée 9, 25–28 (1974).
Valizadeh, A., Kolahchi, M. R. & Straley, J. P. On the origin of fractional shapiro steps in systems of josephson junctions with few degrees of freedom. J. Nonlinear Math. Phys. 15, 407–416 (2008).
Domínguez, F., Hassler, F. & Platero, G. Dynamical detection of Majorana fermions in current-biased nanowires. Phys. Rev. B 86, 140503 (2012).
Fu, L. & Kane., C. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Courtois, H., Meschke, M., Peltonen, J. & Pekola, J. Origin of hysteresis in a proximity Josephson junction. Phys. Rev. Lett. 101, 067002 (2008).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting microconstrictions: excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 25, 4515–4532 (1982).
Klapwijk, T. M., Blonder, G. E. & Tinkham, M. Explanation of subharmonic energy gap structure in superconducting contacts. Physica B+C 109-110, 1657–1664 (1982).
Scheer, E. et al. Proximity effect and multiple andreev reflections in gold atomic contacts. Phys. Rev. Lett. 86, 284–287 (2001).
Weitz, D. A., Skocpol, W. J. & Tinkham, M. Characterization of niobium point contacts showing Josephson effects in the far infrared. J. Appl. Phys. 49, 4873 (1978).
Sochnikov, I. et al. Nonsinusoidal current-phase relationship in Josephson junctions from the 3D topological insulator HgTe. Phys. Rev. Lett. 114, 066801 (2015).
Tinkham., M. Introduction to Superconductivity Dover Publications (2004).
Russer, P. Influence of microwave radiation on current-voltage characteristic of superconducting weak links. J. Appl. Phys. 43, 2008 (1972).
Cleuziou, J.-P. et al. Gate-tuned high frequency response of carbon nanotube Josephson junctions. Phys. Rev. Lett. 99, 117001 (2007).
Heersche, H. B., Jarillo-Herrero, P., Oostinga, J. B., Vandersypen, L. M. K. & Morpurgo, A. F. Bipolar supercurrent in graphene. Nature 446, 56–59 (2007).
Chauvin, M. et al. Superconducting atomic contacts under microwave irradiation. Phys. Rev. Lett. 97, 1–4 (2006).
Cuevas, J. C., Heurich, J., Martn-Rodero, A., Levy Yeyati, A. & Schön, G. Subharmonic shapiro steps and assisted tunneling in superconducting point contacts. Phys. Rev. Lett. 88, 157001 (2002).
Dubos, P., Courtois, H., Buisson, O. & Pannetier, B. Coherent low-energy charge transport in a diffusive S-N-S junction. Phys. Rev. Lett. 87, 206801 (2001).
McCumber, D. E. Effect of ac Impedance on dc Voltage-Current Characteristics of Superconductor Weak-Link Junctions. J. Appl. Phys. 39, 3113 (1968).
Beenakker, C. W. J. & van Houten, H. Josephson current through a superconducting quantum point contact shorter than the coherence length. Phys. Rev. Lett. 66, 3056–3059 (1991).
Houzet, M., Meyer, J. S., Badiane, D. M. & Glazman, L. I. Dynamics of Majorana States in a Topological Josephson Junction. Phys. Rev. Lett. 111, 046401 (2013).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
König, M. et al. Quantum spin hall insulator state in HgTe quantum wells. Science 318, 766 (2007).
Acknowledgements
We gratefully acknowledge G. Fève and B. Plaçais for the loan of amplifiers, as well as M. Houzet, J. Meyer, H. Pothier, F. Hassler, A. Brinkman, C.W.J. Beenakker, A. Akhmerov, P. Burset, E.M. Hankiewicz, G. Tkachov and B. Trauzettel for enlightening discussions. This work is supported by German Research Foundation (DFG-JST joint research project ‘Topological Electronics’, Leibniz Program, DFG-Sonderforschungsbereich 1170 ‘Tocotronics’ and DFG-Schwerpunktprogramme 1459 and 1666), the EU ERC-AG program (Project 3-TOP), the Elitenetzwerk Bayern program Topologische Isolatoren and the DARPA MESO project. R.S.D. acknowledges support from Grants-in-Aid for Young Scientists B (No. 26790008). T.M.K. is financially supported by the European Research Council Advanced grant No.339306 (METIQUM) and by the Ministry of Education and Science of the Russian Federation under Contract No.14.B25.31.007. S.T. acknowledges financial support from Grants-in-Aid for Scientific Research S (No. 26220710), MEXT project for Developing Innovation, JST Strategic International Cooperative Program (DFG-JST) and ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan). E.B., T.M.K. and L.W.M. gratefully thank the Alexander von Humboldt foundation for its support.
Author information
Authors and Affiliations
Contributions
E.B., R.S.D, K.I., C.G., A.O, S.T., H.B. and L.W.M. planned the project and design of the experiment. C.A., C.B., L.M and J.W. grew the material and prepared the HgTe samples. J.W., R.S.D, S.H. and E.B. performed the experiments. E.B. realized the numerical simulations. O.H. prepared the graphene samples, O.H., J.W. S.H. and E.B. measured them. All authors participated in the analysis of the data led by J.W., E.B, R.S.D. and T.M.K. All authors jointly wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-17, Supplementary Table 1, Supplementary Notes 1-4 and Supplementary References (PDF 5849 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wiedenmann, J., Bocquillon, E., Deacon, R. et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat Commun 7, 10303 (2016). https://doi.org/10.1038/ncomms10303
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10303
This article is cited by
-
Supercurrent mediated by helical edge modes in bilayer graphene
Nature Communications (2024)
-
Symmetry-broken Josephson junctions and superconducting diodes in magic-angle twisted bilayer graphene
Nature Communications (2023)
-
Recent progress on Majorana in semiconductor-superconductor heterostructures—engineering and detection
Science China Physics, Mechanics & Astronomy (2023)
-
Nonreciprocal charge transport in topological superconductor candidate Bi2Te3/PdTe2 heterostructure
npj Quantum Materials (2022)
-
Proximity-induced superconductivity in (Bi1−xSbx)2Te3 topological-insulator nanowires
Communications Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.