Abstract
Iridium oxides with a honeycomb lattice have been identified as platforms for the much anticipated Kitaev topological spin liquid: the spin-orbit entangled states of Ir4+ in principle generate precisely the required type of anisotropic exchange. However, other magnetic couplings can drive the system away from the spin-liquid phase. With this in mind, here we disentangle the different magnetic interactions in Li2IrO3, a honeycomb iridate with two crystallographically inequivalent sets of adjacent Ir sites. Our ab initio many-body calculations show that, while both Heisenberg and Kitaev nearest-neighbour couplings are present, on one set of Ir–Ir bonds the former dominates, resulting in the formation of spin-triplet dimers. The triplet dimers frame a strongly frustrated triangular lattice and by exact cluster diagonalization we show that they remain protected in a wide region of the phase diagram.
Similar content being viewed by others
Introduction
As early as in the 1970s it was suggested that quantum spins in a solid can, instead of ordering in a certain pattern, form a fluid type of ground state—a quantum spin liquid1,2. Theory predicts a remarkable set of collective phenomena to occur in spin liquids3. In the honeycomb lattice Kitaev spin model4, for instance, a spin-liquid state that has different topological phases with elementary excitations displaying Majorana statistics has been anticipated. This has been argued to be relevant for applications in topological quantum computing5,6,7,8,9.
The essential feature of the Kitaev model is that there is a different type of spin coupling for each of the three magnetic bonds originating from a given S=1/2 spin site,  ,
,  and
and  , where j, k and l are S=1/2 nearest neighbours (NN’s) of the reference site i and K is the Kitaev coupling strength. However, finding materials in which the Kitaev spin model and the spin-liquid ground state are realized has proven to be very challenging3. In this respect the strongly spin-orbit coupled honeycomb iridates have recently been brought to the fore10,11. These compounds have the chemical formula A2IrO3, with A=Na or Li, and contain Ir4+ ions in the centre of oxygen octahedra that form a planar hexagonal network. Each Ir4+ ion has five electrons in the 5d shell which the crystal field splits into a t2g and an eg manifold. Since the crystal field splitting is large, the lowest-energy electron configuration is
, where j, k and l are S=1/2 nearest neighbours (NN’s) of the reference site i and K is the Kitaev coupling strength. However, finding materials in which the Kitaev spin model and the spin-liquid ground state are realized has proven to be very challenging3. In this respect the strongly spin-orbit coupled honeycomb iridates have recently been brought to the fore10,11. These compounds have the chemical formula A2IrO3, with A=Na or Li, and contain Ir4+ ions in the centre of oxygen octahedra that form a planar hexagonal network. Each Ir4+ ion has five electrons in the 5d shell which the crystal field splits into a t2g and an eg manifold. Since the crystal field splitting is large, the lowest-energy electron configuration is  . This is equivalent to the t2g shell containing a single hole with spin S=1/2. However, the
. This is equivalent to the t2g shell containing a single hole with spin S=1/2. However, the  state additionally bears a finite effective angular moment Leff=1. The strong spin-orbit coupling for 5d electrons therefore splits up the
state additionally bears a finite effective angular moment Leff=1. The strong spin-orbit coupling for 5d electrons therefore splits up the  manifold into an effective total angular momentum
manifold into an effective total angular momentum  quartet and a
quartet and a  doublet. As for the hole the latter is lowest in energy, an effective spin
doublet. As for the hole the latter is lowest in energy, an effective spin  doublet (often referred to as a pseudospin
doublet (often referred to as a pseudospin  ) defines to first approximation the local ground state of the Ir4+ ion.
) defines to first approximation the local ground state of the Ir4+ ion.
Whereas the formation of such a local  doublet is well-known for Ir4+ ions inside an undistorted oxygen octahedron12, the remarkable insight of refs 10, 11 is that when two such octahedra share an edge, the magnetic superexchange interactions between the
doublet is well-known for Ir4+ ions inside an undistorted oxygen octahedron12, the remarkable insight of refs 10, 11 is that when two such octahedra share an edge, the magnetic superexchange interactions between the  sites are in principle precisely of Kitaev type. This observation has made the A2IrO3 honeycomb iridates prime candidate materials in the search for Kitaev spin-liquid ground states.
sites are in principle precisely of Kitaev type. This observation has made the A2IrO3 honeycomb iridates prime candidate materials in the search for Kitaev spin-liquid ground states.
Experimentally, however, both Na2IrO3 and Li2IrO3 have been found to order magnetically below 15 K (refs 13, 14). While inelastic neutron scattering15, X-ray diffraction16 and resonant inelastic X-ray scattering experiments17 indicate an antiferromagnetic (AF) zigzag ordering pattern in Na2IrO3, the nature of the magnetic order of Li2IrO3 is to date unknown13,14. The questions that arise are therefore, (i) which magnetic instability preempts the formation of the spin-liquid state, and how close does the system remains to that state.
To answer these fundamental questions it is essential to quantify the relative strengths of the NN magnetic interactions in Li2IrO3, which are already known to be not only of Kitaev, but also of Heisenberg type. The observed zigzag order in its counterpart system Na2IrO3 has indeed been rationalized on the basis of ferromagnetic (FM) Heisenberg J and AF Kitaev K couplings18,19,20, but also interpreted in terms of an AF J and FM K (refs 13, 15, 21, 22). Recent ab initio many-body calculations favour the latter scenario, with a relatively large FM Kitaev exchange and significantly weaker AF NN Heisenberg interactions in this material23. This scenario is also supported by investigations of model Hamiltonians derived by downfolding schemes based on density functional theory calculations24. Besides the NN terms, strongly frustrating longer range exchange couplings involving the second (J2) and third (J3) iridium coordination shells were also shown to be relevant13,15,20, resulting in very rich magnetic phase diagrams13,23,25.
On the basis of the similarity in crystal structure, one might naively expect that the magnetic interactions in A=Li are similar to the ones in A=Na. Here we show that this is not at all the case. The strengths of the NN interactions J and K turn out to crucially depend on the Ir–O–Ir bond angles and distances. Employing ab initio wave-function quantum chemistry methods, we find in particular that in contrast to Na2IrO3 (ref. 23) the Heisenberg coupling J in Li2IrO3 even has opposite signs for the two crystallographically inequivalent sets of adjacent Ir sites. This behaviour follows a general trend of J and K as functions of bond angles and interatomic distances that we have established through a larger, additional set of quantum chemistry calculations. The latter show that the NN Heisenberg J has a parabolic dependence on the Ir–O–Ir bond angle and at around 98° changes sign. This explains why in Na2IrO3, with Ir–O–Ir angles in the range of 98–100° (ref. 15), all J′s are positive, while in Li2IrO3, which has significantly smaller bond angles ∼95°(ref. 26), the FM component to the NN Heisenberg exchange is much stronger. The large FM coupling  meV on one set of Ir–Ir links in Li2IrO3 gives rise to an effective picture of triplet dimers composing a triangular lattice. To determine the magnetic phase diagram as a function of the strength of the second and third neighbour exchange interactions (J2 and J3) we use for this effective triplet-dimer model a semiclassical approach, which we further confront to the magnetic phase diagram for the original honeycomb Hamiltonian calculated by exact cluster diagonalization. This comparison shows that indeed the triplet dimers act as rigid objects in a wide range of the J2–J3 parameter space. We localize Li2IrO3 in a parameter range where the phase diagram has incommensurate magnetic order, the nature of which goes beyond the standard flat helix modulation scenario, owing to the Kitaev exchange anisotropy.
meV on one set of Ir–Ir links in Li2IrO3 gives rise to an effective picture of triplet dimers composing a triangular lattice. To determine the magnetic phase diagram as a function of the strength of the second and third neighbour exchange interactions (J2 and J3) we use for this effective triplet-dimer model a semiclassical approach, which we further confront to the magnetic phase diagram for the original honeycomb Hamiltonian calculated by exact cluster diagonalization. This comparison shows that indeed the triplet dimers act as rigid objects in a wide range of the J2–J3 parameter space. We localize Li2IrO3 in a parameter range where the phase diagram has incommensurate magnetic order, the nature of which goes beyond the standard flat helix modulation scenario, owing to the Kitaev exchange anisotropy.
Results
Heisenberg–Kitaev Hamiltonian
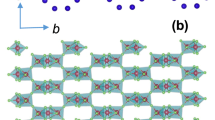
The experimental data reported in ref. 26 indicate C2h point-group symmetry for one set of NN IrO6 octahedra, denoted as B1 in Fig. 1, and slight distortions of the Ir2O2 plaquettes that lower the symmetry to Ci for the other type of adjacent octahedra, labelled B2 and B3. The most general, symmetry allowed form of the effective spin Hamiltonian for a pair of NN Ir d5 sites, as discussed in Methods and Supplementary Note 1, is then
(a) The two distinct sets of NN links26 are labelled as B1 (along the crystallographic b axis) and B2/B3. (b) The large FM interaction J=−19.2 meV on B1 bonds stabilizes rigid T=1 triplets that frame an effective triangular lattice. The triplet dimers remain protected in a wide region of the phase diagram, including the incommensurate ICx and (c) diagonal-zigzag phase, see text. (d) Representative exchange couplings for B1 (J, K), B2/B3 (J′, K′), second neighbour (J2) and third neighbour (J3) paths on the original hexagonal grid are shown. Jδ (δ∈{a, b, a−2b}) are isotropic exchange interactions on the effective triangular net.

The b index refers to the type of Ir–Ir link (b∈{B1,B2,B3}). Whereas the Hamiltonians  on the Ir–Ir links B2 and B3 are related by symmetry, the bond B1 is distinct from a symmetry point of view. Further,
on the Ir–Ir links B2 and B3 are related by symmetry, the bond B1 is distinct from a symmetry point of view. Further,  and
and  denote pseudospin-1/2 operators, Jb is the isotropic Heisenberg interaction and Kb the Kitaev coupling. The latter plus the off-diagonal coefficients
denote pseudospin-1/2 operators, Jb is the isotropic Heisenberg interaction and Kb the Kitaev coupling. The latter plus the off-diagonal coefficients  define the symmetric anisotropic exchange tensor. It is shown below that these
define the symmetric anisotropic exchange tensor. It is shown below that these  elements are not at all negligible, as assumed in the plain Kitaev–Heisenberg Hamiltonian.
elements are not at all negligible, as assumed in the plain Kitaev–Heisenberg Hamiltonian.
In equation (1), α and β stand for components in the local, Kitaev bond reference frame {xb, yb, zb}10. The zb axis is perpendicular to the Ir2O2 plaquette (Methods section, Supplementary Note 2 and Supplementary Fig. 1). In the following, we denote JB1=J, JB2=JB3=J′, KB1=K, KB2=KB3=K′ and similarly for the  elements.
elements.
NN exchange interactions
To make reliable predictions for the signs and strengths of the exchange coupling parameters we rely on many-body quantum chemistry machinery, in particular, multireference configuration interaction (MRCI) computations27 on properly embedded clusters. Multiconfiguration reference wave functions were first generated by complete active space self-consistent field (CASSCF) calculations. For two NN IrO6 octahedra, the finite set of Slater determinants was defined in the CASSCF treatment in terms of ten electrons and six (Ir t2g) orbitals. The self-consistent field optimization was carried out for an average of the lowest nine singlet and nine triplet states associated with this manifold. All these states entered the spin-orbit calculations, both at the CASSCF and MRCI levels. On top of the CASSCF reference, the MRCI expansion additionally includes single and double excitations from the Ir t2g shells and the 2p orbitals of the bridging ligands. Results in good agreement with the experimental data were recently obtained with this computational approach for related 5d5 iridates displaying corner-sharing IrO6 octahedra28,29,30.
Relative energies for the four low-lying states describing the magnetic spectrum of two NN octahedra and the resulting effective coupling constants are provided in Table 1. To derive the latter, we map the quantum chemically computed eigenvalues listed in the table to the eigenvalues of the effective magnetic Hamiltonian in equation (1). For the effective picture of  pseudospins assumed in equation (1), the set of four eigenfunctions contains the singlet
pseudospins assumed in equation (1), the set of four eigenfunctions contains the singlet  and the triplet components
and the triplet components  ,
,  ,
,  . In C2h symmetry, the ‘full’ spin-orbit wave functions associated to
. In C2h symmetry, the ‘full’ spin-orbit wave functions associated to  ,
,  ,
,  and
and  transform according to the Ag, Bu, Bu and Au irreducible representations, respectively. Since two of the triplet terms may interact, the most compact way to express the eigenstates of the effective Hamiltonian in equation (1) is then
transform according to the Ag, Bu, Bu and Au irreducible representations, respectively. Since two of the triplet terms may interact, the most compact way to express the eigenstates of the effective Hamiltonian in equation (1) is then  ,
,  ,
,  and
and  . The angle αb parametrizes the amount of
. The angle αb parametrizes the amount of  mixing, related to finite off-diagonal
mixing, related to finite off-diagonal  couplings. This degree of admixture is determined by analysis of the full quantum chemistry spin-orbit wave functions. The effective parameters provided in Table 1 are obtained for each type of Ir–Ir link by using the
couplings. This degree of admixture is determined by analysis of the full quantum chemistry spin-orbit wave functions. The effective parameters provided in Table 1 are obtained for each type of Ir–Ir link by using the  ,
,  ,
,  ,
,  MRCI relative energies and the
MRCI relative energies and the  mixing coefficients (see Methods and Supplementary Note 1). For a comparison of the effective parameters derived from CASSCF and MRCI relative energies, see Supplementary Tables 1 and 2.
mixing coefficients (see Methods and Supplementary Note 1). For a comparison of the effective parameters derived from CASSCF and MRCI relative energies, see Supplementary Tables 1 and 2.
For the B1 links in Li2IrO3 (Li213) we find that both J and K are FM, in contrast to Na2IrO3 (Na213) where J is AF for all pairs of Ir NN’s23. Insights into this difference between the Li and Na iridates are provided by the curves plotted in Fig. 2, displaying the dependence of the NN J on the amount of trigonal distortion for simplified structural models of both Li213 and Na213. The trigonal compression of the O octahedra translates into Ir–O–Ir bond angles >90°. Additional distortions giving rise to unequal Ir–O bond lengths, see the footnotes in Table 1, were not considered in these idealized lattice configurations. Interestingly, we find that for 90° bond angle—the case for which most of the superexchange models are constructed10,11,18,22—both J and K are very small,  .
.
Results of spin-orbit MRCI calculations are shown, for NN Ir–Ir links in both Li213 (continuous lines) and Na213 (dashed). For each system, the NN Ir–Ir distances are set to the average value in the experimental crystal structure15,26 and the Ir–O bond lengths are all the same. Consequently, J=J′ and K=K′. The variation of the Ir–O–Ir angles is the result of gradual trigonal compression. Note that  ,
,  meV at 90°. Inset: dependence of the NN J in Li213 when the bridging O’s are gradually shifted in opposite senses parallel to the Ir–Ir axis.
meV at 90°. Inset: dependence of the NN J in Li213 when the bridging O’s are gradually shifted in opposite senses parallel to the Ir–Ir axis.
In Fig. 2, while |K| monotonously increases with the Ir–O–Ir bond angle, J displays a parabolic behaviour and with a minimum at ∼94°. Indeed on the basis of simplified superexchange models one expects J to be minimal at around a bond angle close to 90°. However, from superexchange models it is at the same time expected that K is substantial for such bond angles. The difference between the ab initio results for 90° Ir–O–Ir angles and the predictions of simplified superexchange models originates from assuming in the latter perfectly degenerate Ir 5d and O 2p orbitals and from the subsequent cancellation of particular intersite d–p–d exchange paths. The quantum chemistry calculations show that the Ir 5d levels are not degenerate (nor the O 2p functions at a given site); the symmetry lowering at the Ir/O sites and this degeneracy lifting are related to the strongly anisotropic, layered crystal structure. For the actual honeycomb lattice with trigonal distortions of oxygen cages, one should develop a superexchange theory using the trigonal 5d orbital basis, as well as the correspondingly oriented oxygen orbitals. This produces a more general anisotropy than the Kitaev one. This is the essential reason we find at 90° for Na213 (Ir–Ir average distances of 3.133 Å): J=0.32, K=−0.43, Γxy=2.6, Γzx=−1.3, Γyz=1.3 and for Li213 (Ir–Ir average distances of 2.980 Å): J=0.40, K=−1.60, Γxy=5.4, Γzx=−2.8, Γyz=2.8 meV. For both materials K actually turns out to be the smallest of the anisotropic exchange constants at 90°. The small value of K may give the impression that only a weak uniaxial anisotropy is active (Supplementary Table 3). However, if one diagonalizes the full Γ matrix to obtain its principal axes (which in general are distinct from any crystallographic directions) and corresponding anisotropies, one finds sizable anisotropic exchange constants as large as few meV.
Our investigation also shows that the large FM J value obtained for the B1 Ir–Ir links in Li213 is the superposition of three different effects (Fig. 2): (i) an Ir–O–Ir bond angle smaller than the value of ≈98° where J changes sign which in contrast to Na213 takes us into the FM regime, (ii) the shift to lower values of the minimum of the nearly parabolic J curve in Li213 as compared with Na213 and further (iii) the additional distortions giving rise to three different sets of Ir–O bond lengths for each IrO6 octahedron. The latter are significantly stronger in Li213, remove the degeneracy of the Ir t2g levels and make that the NN B1 J is even lower than the minimum of the parabola displayed in Fig. 2. It is also interesting that the off-diagonal Γyz and Γzx couplings on B1 have about the same strength with the Kitaev K (Table 1). Our ab initio results justify more detailed model Hamiltonian investigations of such off-diagonal couplings along the lines of refs 21, 22, 24.
For the B2 and B3 links, the Ir–O bonds on the Ir–O2–Ir plaquette have different lengths and the symmetry of the two-octahedra block is lowered to Ci (ref. 26). The ab initio data show that consequently the FM exchange is here disfavoured such that J′ turns AF. This is illustrated in the inset of Fig. 2, where we plot the evolution of the NN Heisenberg coupling when in addition to trigonal distortions the bridging ligands on the Ir–O2–Ir plaquette are gradually shifted in opposite senses parallel to the Ir–Ir axis. For the reference equilateral plaquette, the Ir–O–Ir bond angle is set to the average value in the experimental structure, 95° (ref. 26). It is seen that such additional distortions indeed enhance the AF contribution to the Heisenberg superexchange. Although the bond symmetry is lower for the B2/B3 links, the analysis of the spin-orbit wave functions shows however negligible additional mixing effects and the ab initio results were still mapped onto a C2h model with  .
.
Longer range interactions
Having established the dominant NN couplings we now turn to the magnetic phase diagram of Li213 including the effect of second and third neighbour Heisenberg interactions J2 and J3. The latter are known to be sizable22 and to significantly influence certain properties13,15,23,25. However, since correlated quantum chemistry calculations for these longer range interaction terms are computationally much too demanding, we investigate their effect by computations for extended effective Hamiltonians that use the ab initio NN magnetic interactions listed in Table 1 and adjustable isotropic J2, J3 exchange couplings.
Triplet dimers
With strong FM exchange on the B1 bonds, a natural description of the system consists in replacing all B1 pairs of Ir 1/2 pseudospins by rigid triplet degrees of freedom. This mapping leads to an effective model of spin T=1 entities on a triangular lattice, captured by the Hamiltonian

where δ∈{a, b, a−2b} (Fig. 1d and Supplementary Fig. 2). It includes both on-site (Γ1) and intersite (Jδ, Γ2,δ) effective interaction terms. While the explicit expressions of these terms are given in Methods, the essential features of the model are as follows. First, among the few different contributions to Γ1, there is an effective coupling of the form  . Since K<0, this term selects the two triplet components with Tz=±1 and therefore acts as an easy-axis anisotropy. Second, there are two different types of effective exchange couplings between NN triplets, see Fig. 1d. This asymmetry reflects the constitutive difference between bonds B1 and B2/B3. Finally, there is also an effective longer range exchange driven by the J3 interaction in the original hexagonal model.
. Since K<0, this term selects the two triplet components with Tz=±1 and therefore acts as an easy-axis anisotropy. Second, there are two different types of effective exchange couplings between NN triplets, see Fig. 1d. This asymmetry reflects the constitutive difference between bonds B1 and B2/B3. Finally, there is also an effective longer range exchange driven by the J3 interaction in the original hexagonal model.
According to our ab initio results, the on-site anisotropy splitting is  meV, about twice the ordering temperature in Li213. Naively, this may suggest a truncation of the local Hilbert space such that it includes only the Tz=±1 components, which would lead to an effective doublet instead of a triplet description. However, such a truncation would not properly account for transverse spin fluctuations driven by intersite exchange (which may even exceed the on-site splitting, depending on the values of J2 and J3) or for the coupling to the Tz=0 component via off-diagonal terms in Γ1. Lacking a priori a clear separation of energy scales, one is thus left with a description in terms of T=1 triplets.
meV, about twice the ordering temperature in Li213. Naively, this may suggest a truncation of the local Hilbert space such that it includes only the Tz=±1 components, which would lead to an effective doublet instead of a triplet description. However, such a truncation would not properly account for transverse spin fluctuations driven by intersite exchange (which may even exceed the on-site splitting, depending on the values of J2 and J3) or for the coupling to the Tz=0 component via off-diagonal terms in Γ1. Lacking a priori a clear separation of energy scales, one is thus left with a description in terms of T=1 triplets.
In momentum space, the effective model takes the form

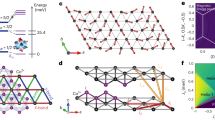
where  , N is the number of B1 bonds and Λ(k) is a symmetric 3 × 3 matrix (Supplementary Note 3). Since T=1, the classical limit is expected to yield a rather accurate overall description of the phase diagram. The minimum eigenvalue λQ of Λ(k) over the Brillouin zone provides a lower bound for the classical ground-state energy31,32,33,34. As shown in Fig. 3a, there exist five different regions for
, N is the number of B1 bonds and Λ(k) is a symmetric 3 × 3 matrix (Supplementary Note 3). Since T=1, the classical limit is expected to yield a rather accurate overall description of the phase diagram. The minimum eigenvalue λQ of Λ(k) over the Brillouin zone provides a lower bound for the classical ground-state energy31,32,33,34. As shown in Fig. 3a, there exist five different regions for  meV, three with commensurate (FM, diagonal zigzag and stripy) and two with incommensurate (IC) Q (we call them ICx and ICy, with Q=(q, 0) and (0, q), respectively). In all commensurate regions, the state
meV, three with commensurate (FM, diagonal zigzag and stripy) and two with incommensurate (IC) Q (we call them ICx and ICy, with Q=(q, 0) and (0, q), respectively). In all commensurate regions, the state  (where vQ is the eigenvector associated with λQ) saturates the above lower energy bound and in addition satisfies the spin length constraint |TR|=1 for all R. We note in particular that compared to the more symmetric case of Na213 (ref. 23), only the diagonal-zigzag configurations are favoured in Li213, with FM correlations along the two diagonal directions of the lattice. The third, horizontal zigzag configuration is penalized by the strong FM Heisenberg coupling on the B1 links. Correspondingly, we expect Bragg peaks only at two out of the three M points of the Brillouin zone, namely
(where vQ is the eigenvector associated with λQ) saturates the above lower energy bound and in addition satisfies the spin length constraint |TR|=1 for all R. We note in particular that compared to the more symmetric case of Na213 (ref. 23), only the diagonal-zigzag configurations are favoured in Li213, with FM correlations along the two diagonal directions of the lattice. The third, horizontal zigzag configuration is penalized by the strong FM Heisenberg coupling on the B1 links. Correspondingly, we expect Bragg peaks only at two out of the three M points of the Brillouin zone, namely  (see
(see  in Fig. 3c and Supplementary Fig. 3). Turning to the incommensurate regions ICx and ICy, the minimum eigenvalue λQ is nondegenerate, which implies that one cannot form a flat helical modulation that saturates the low energy bound and satisfies the spin length constraint for all R. Especially for ICx that is the most likely candidate for Li213 (see below), this opens the possibility for nontrivial nonplanar modulations of the magnetization.
in Fig. 3c and Supplementary Fig. 3). Turning to the incommensurate regions ICx and ICy, the minimum eigenvalue λQ is nondegenerate, which implies that one cannot form a flat helical modulation that saturates the low energy bound and satisfies the spin length constraint for all R. Especially for ICx that is the most likely candidate for Li213 (see below), this opens the possibility for nontrivial nonplanar modulations of the magnetization.
Phase diagram of Li213 in the J2–J3 plane with the NN couplings listed in Table 1, along with schematic spin configurations and Bragg peak positions (red circles) for each phase. (a) Classical phase diagram of the effective spin T=1 model on the triangular lattice, found by a numerical minimization of the interaction matrix Λ(k) in the Brillouin zone (BZ). The actual ground-state configurations in the incommensurate regions ICx and ICy can be much richer than the standard coplanar helix states owing to anisotropy, see text. (b) Quantum mechanical phase diagram for the original spin-1/2 model. (c) Structure factor  for representative momenta in different phases. Note that in the ICx phase, the peak position (±Qa, 0) takes values between 0<Qa≤2π/a, depending on J2 and J3. (d) Long range spin–spin correlation profiles
for representative momenta in different phases. Note that in the ICx phase, the peak position (±Qa, 0) takes values between 0<Qa≤2π/a, depending on J2 and J3. (d) Long range spin–spin correlation profiles  at J2=J3=3 (that is, inside the diagonal-zigzag phase), as obtained by exact diagonalization (ED) calculations. The reference Ir site is shown as a black square rectangle, positive (negative) correlations are denoted by filled blue (open red) circles whose radii scale with
at J2=J3=3 (that is, inside the diagonal-zigzag phase), as obtained by exact diagonalization (ED) calculations. The reference Ir site is shown as a black square rectangle, positive (negative) correlations are denoted by filled blue (open red) circles whose radii scale with  . We also show explicitly the actual values for the NN correlations.
. We also show explicitly the actual values for the NN correlations.
Exact diagonalization calculations
To establish the effect of quantum fluctuations and further test the triplet-dimer picture, we additionally carried out exact diagonalization calculations on 24-site clusters for the original honeycomb spin-1/2 model including the effect of J2 and J3. Periodic boundary conditions were applied, as in previous studies18,23. We calculated the static spin-structure factor  as a function of J2 and J3 while fixing the NN magnetic couplings to the ones in Table 1. For a given set of J2 and J3 values, the dominant order is determined according to the wave number Q=Qmax providing a maximum of
as a function of J2 and J3 while fixing the NN magnetic couplings to the ones in Table 1. For a given set of J2 and J3 values, the dominant order is determined according to the wave number Q=Qmax providing a maximum of  . The resulting phase diagram is given in Fig. 3b. For each phase, the real-space spin configuration and the reciprocal-space Bragg peak positions are shown. In the absence of J2 and J3, the system is in a spin-liquid phase characterized by a structureless
. The resulting phase diagram is given in Fig. 3b. For each phase, the real-space spin configuration and the reciprocal-space Bragg peak positions are shown. In the absence of J2 and J3, the system is in a spin-liquid phase characterized by a structureless  (Fig. 3c) that is adiabatically connected to the Kitaev liquid phase for
(Fig. 3c) that is adiabatically connected to the Kitaev liquid phase for  (ref. 10). By switching on J2 and J3, we recover most of the classical phases of the effective spin-1 model, including the ICx phase, albeit with a smaller stability region due to finite-size effects. That the 24-site cluster correlations do not show the ICy phase may well be an intrinsic effect, given that the classical ICy region is very narrow. We also find an AF Néel state region, which is now shifted to larger J3’s as compared with Na213 (ref. 23), due to the large negative J on B1 bonds.
(ref. 10). By switching on J2 and J3, we recover most of the classical phases of the effective spin-1 model, including the ICx phase, albeit with a smaller stability region due to finite-size effects. That the 24-site cluster correlations do not show the ICy phase may well be an intrinsic effect, given that the classical ICy region is very narrow. We also find an AF Néel state region, which is now shifted to larger J3’s as compared with Na213 (ref. 23), due to the large negative J on B1 bonds.
We note that detecting the diagonal-zigzag phase by exact diagonalization calculations requires large-size setups of lattice sites. This is related to the proximity of this phase to the special point Γ=0 where the model is highly frustrated. Indeed, in this limit the classical ground-state manifold consists of a one-parameter family of states with two sublattices of spins with arbitrary relative orientation angle. This situation is common in various well-known frustrated models, such as the J1–J2 model on the square lattice35,36,37. The lifting of the accidental degeneracy, either by quantum fluctuations or due to a finite Γ (Supplementary Note 4, Supplementary Figs 4 and 5), and the associated locking mechanism between the two sublattices involve a very large length scale38,39. This explains why our exact spin–spin correlation profiles provided in Fig. 3d show that the two sublattices are nearly decoupled from each other.
Except for the Néel and the spin-liquid phase, all other phases feature rigid triplets on the B1 bonds. This is shown in Fig. 3d for the diagonal-zigzag phase at J2=J3=3, where the NN correlation function on the B1 bonds,  , almost saturates to the full spin-triplet value of 1/4. This shows that the effective triplet picture is quite robust.
, almost saturates to the full spin-triplet value of 1/4. This shows that the effective triplet picture is quite robust.
Comparison to experiment
Our result for rigid triplet degrees of freedom finds support in recent fits of the magnetic susceptibility data, which yield effective moments of 2.22 μB for Li213 (ref. 40), much larger than the value of 1.74 μB expected for an isotropic 1/2 spin system. Triplet dimerization was earlier suggested to occur in the chain-like compound In2VO5 (ref. 41). FM, quintet dimers were also proposed to form in ZnV2O4 (ref. 42).
Turning finally to the nature of the actual magnetic ground state of Li213, we first note that the longer range couplings J2 and J3 are expected to be both AF13,15 and to feature values not larger than 5–6 meV (ref. 15) in honeycomb iridates, which suggests that Li213 orders either with a diagonal-zigzag or ICx pattern. Recent magnetic susceptibility and specific heat measurements indeed show indications (ref. 14) that the magnetic ground state of Li213 could be different from AF zigzag, while powder diffraction and inelastic neutron scattering data (R. Coldea, personal communication) show signatures of incommensurate magnetic order. These experimental findings are consistent with the ICx spin configuration. As explained above, the actual nature of this phase goes beyond the standard flat helical modulations because the latter are penalized by the anisotropic exchange terms in the Hamiltonian. It should be noted that the incommensurate type of magnetic order in Li2IrO3 has also been rationalized with model Hamiltonian calculations by including additional long range anisotropic Kitaev couplings on the honeycomb lattice43.
Conclusions
To summarize, we have established a microscopic spin model and zero-temperature phase diagram for the layered honeycomb iridate Li2IrO3, one of the proposed realizations of the spin-1/2 Kitaev–Heisenberg model with strongly spin-orbit coupled Ir4+ magnetic ions. Ab initio quantum chemistry electronic-structure calculations show that, in contrast to Na2IrO3, the structural inequivalence between the two types of Ir–Ir links has a striking influence on the effective spin Hamiltonian, leading in particular to two very different nearest-neighbour superexchange pathways, one weakly antiferromagnetic  and another strongly ferromagnetic (−19 meV). The latter gives rise to rigid spin-1 triplets on a triangular lattice that remain well protected in a large parameter regime of the phase diagram, including a diagonal zigzag and an incommensurate ICx phase. In view of these theoretical findings and the experimental observation of an incommensurate magnetic propagation vector in neutron diffraction (R. Coldea, personal communication), we propose that the magnetic ground state of Li2IrO3 lies in the incommensurate ICx phase. Settling its detailed nature and properties calls for further, dedicated experimental and theoretical investigations.
and another strongly ferromagnetic (−19 meV). The latter gives rise to rigid spin-1 triplets on a triangular lattice that remain well protected in a large parameter regime of the phase diagram, including a diagonal zigzag and an incommensurate ICx phase. In view of these theoretical findings and the experimental observation of an incommensurate magnetic propagation vector in neutron diffraction (R. Coldea, personal communication), we propose that the magnetic ground state of Li2IrO3 lies in the incommensurate ICx phase. Settling its detailed nature and properties calls for further, dedicated experimental and theoretical investigations.
Methods
Embedded-cluster quantum chemistry calculations
All ab initio calculations were carried out with the quantum chemistry package Molpro44. Embedded clusters consisting of two NN edge-sharing IrO6 octahedra were considered. To accurately describe the charge distribution at sites in the immediate neighbourhood45,46, the four adjacent Ir4+ ions and the closest 22 Li+ neighbours were also explicitly included in the actual cluster. The surrounding solid-state matrix was modeled as a finite array of point charges fitted to reproduce the crystal Madelung field in the cluster region. The spin-orbit treatment was carried out according to the procedure described in ref. 47, using spin-orbit pseudopotentials for Ir (Supplementary Note 1).
Even with trigonal distortions of the oxygen cages, the point-group symmetry of a given block of two NN IrO6 octahedra is C2h. Since the C2 axis lies here along the Ir–Ir bond, the effective magnetic Hamiltonian for two adjacent Ir sites is most conveniently expressed in a local reference system {Xb, Yb, Zb} with Xb along the Ir–Ir link (Zb is always perpendicular to the Ir2O2 plaquette). It reads

where b∈{B1,B2,B3}. The diagonal elements in the second term on the right hand side sum up to 0 to give a traceless symmetric anisotropic exchange tensor. If Xb is C2 axis, only one off-diagonal element is nonzero.
In the local Kitaev reference frame {xb, yb, zb}, that is rotated from {Xb, Yb, Zb} by 45o about the Zb=zb axis (Supplementary Note 2, Supplementary Fig. 1 and refs 10, 23), the Hamiltonian shown above in equation (4) is transformed to the Hamiltonian in equation (1). For the latter, the effective exchange couplings are obtained for each type of Ir–Ir link as

where the connection to the quantum chemically computed eigenvalues provided in Table 1 (and Supplementary Tables 1 and 2) is

 ,
,  ,
,  ,
,  are the ab initio eigenvalues,
are the ab initio eigenvalues,  and ζb=sinαb, where αb is the mixing parameter.
and ζb=sinαb, where αb is the mixing parameter.
Effective spin T=1 description
To find the effective interactions between the B1 triplet dimers, we begin by deriving the equivalent operators in the TR=1 manifold for a B1 bond at position R, where TR=SR,1+SR,2 and SR,1, SR,2 are the ionic Ir pseudospins defining the B1 bond. If the projector in the TR=1 manifold is tagged as PT, we obtain for the dipolar channel  , while for the quadrupolar channel
, while for the quadrupolar channel

 is here the quadrupolar operator for a spin-1 degree of freedom and ξ=1/2. Using equivalent operators we then find the first-order effective Hamiltonian
is here the quadrupolar operator for a spin-1 degree of freedom and ξ=1/2. Using equivalent operators we then find the first-order effective Hamiltonian  of equation (2). The only non-zero elements of the symmetric on-site tensor Γ1 are
of equation (2). The only non-zero elements of the symmetric on-site tensor Γ1 are  ,
,  and
and  , while those of Γ2,δ are
, while those of Γ2,δ are  ,
,  ,
,  and
and  . Finally, the intersite isotropic exchange interactions are Ja=(J2+J3)/2, Ja−2b=J3/4, Jb=Ja−b=J2/2+J′/4. We here employed the global coordinate system {x, y, z} corresponding to the Kitaev-like frame {xb, yb, zb} with b=B1 (Supplementary Figure 1). J′, K′, A′, B′ and C′ are effective coupling constants on the bonds B2 and B3, as also mentioned in the main text. We stress that the on-site quadrupolar term
. Finally, the intersite isotropic exchange interactions are Ja=(J2+J3)/2, Ja−2b=J3/4, Jb=Ja−b=J2/2+J′/4. We here employed the global coordinate system {x, y, z} corresponding to the Kitaev-like frame {xb, yb, zb} with b=B1 (Supplementary Figure 1). J′, K′, A′, B′ and C′ are effective coupling constants on the bonds B2 and B3, as also mentioned in the main text. We stress that the on-site quadrupolar term  scales with K/2, while in the classical treatment of the original spin-1/2 model such a term would scale with K/4. We can trace this back to the value of ξ=1/2 found above, which in the classical treatment is ξclas=1/4. This means that the quantum mechanical correlations strongly enhance the effect of the ‘on-site’ anisotropy term K. The latter favours alignment along the z axis, against the effect of K′ which favours alignment within the xy plane. This point is further discussed in Supplementary Note 3 and 4, where we compare the classical treatment of the original spin-1/2 hexagonal model with the effective spin-1 triangular model.
scales with K/2, while in the classical treatment of the original spin-1/2 model such a term would scale with K/4. We can trace this back to the value of ξ=1/2 found above, which in the classical treatment is ξclas=1/4. This means that the quantum mechanical correlations strongly enhance the effect of the ‘on-site’ anisotropy term K. The latter favours alignment along the z axis, against the effect of K′ which favours alignment within the xy plane. This point is further discussed in Supplementary Note 3 and 4, where we compare the classical treatment of the original spin-1/2 hexagonal model with the effective spin-1 triangular model.
Additional information
How to cite this article: Nishimoto, S. et al. Strongly frustrated triangular spin lattice emerging from triplet dimer formation in honeycomb Li2IrO3. Nat. Commun. 7:10273 doi: 10.1038/ncomms10273 (2016).
References
Anderson, P. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 8, 153–160 (1973) .
Fazekas, P. & Anderson, P. W. On the ground state properties of the anisotropic triangular antiferromagnet. Philos. Mag. 30, 423–440 (1974) .
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010) .
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006) .
Baskaran, G., Mandal, S. & Shankar, R. Exact Results for Spin Dynamics and Fractionalization in the Kitaev Model. Phys. Rev. Lett. 98, 247201 (2007) .
Chen, H.-D. & Nussinov, Z. Exact results of the Kitaev model on a hexagonal lattice: spin states, string and brane correlators, and anyonic excitations. J. Phys. A 41, 075001 (2008) .
Vidal, J., Schmidt, K. P. & Dusuel, S. Perturbative approach to an exactly solved problem: Kitaev honeycomb model. Phys. Rev. B 78, 245121 (2008) .
Tikhonov, K. S., Feigel’man, M. V. & Kitaev, A. Y. Power-law spin correlations in a perturbed spin model on a honeycomb lattice. Phys. Rev. Lett. 106, 067203 (2011) .
Nussinov, Z. & van den Brink, J. Compass models: theory and physical motivations. Rev. Mod. Phys. 87, 1–59 (2015) .
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009) .
Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a honeycomb lattice: possible exotic phases in iridium oxides A2IrO3 . Phys. Rev. Lett. 105, 027204 (2010) .
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions Clarendon Press (1970) .
Singh, Y. et al. Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A2IrO3 . Phys. Rev. Lett. 108, 127203 (2012) .
Cao, G. et al. Evolution of magnetism in the single-crystal honeycomb iridates (Na1−xLix)2IrO3 . Phys. Rev. B 88, 220414 (2013) .
Choi, S. K. et al. Spin waves and revised crystal structure of honeycomb iridate Na2IrO3 . Phys. Rev. Lett. 108, 127204 (2012) .
Ye, F. et al. Direct evidence of a zigzag spin-chain structure in the honeycomb lattice: A neutron and x-ray diffraction investigation of single-crystal Na2IrO3 . Phys. Rev. B 85, 180403 (2012) .
Liu, X. et al. Long-range magnetic ordering in Na2IrO3 . Phys. Rev. B 83, 220403 (2011) .
Chaloupka, J., Jackeli, G. & Khaliullin, G. Zigzag magnetic order in the iridium oxide Na2IrO3 . Phys. Rev. Lett. 110, 097204 (2013) .
Andrade, E. C. & Vojta, M. Magnetism in spin models for depleted honeycomb-lattice iridates: spin-glass order towards percolation. Phys. Rev. B 90, 205112 (2014) .
Rau, J. G., Lee, E. K.-H. & Kee, H.-Y. Generic spin model for the honeycomb iridates beyond the Kitaev limit. Phys. Rev. Lett. 112, 077204 (2014) .
Sela, E., Jiang, H.-C., Gerlach, M. H. & Trebst, S. Order-by-disorder and spin-orbital liquids in a distorted Heisenberg-Kitaev model. Phys. Rev. B 90, 035113 (2014) .
Foyevtsova, K., Jeschke, H. O., Mazin, I. I., Khomskii, D. I. & Valent, R. Ab initio analysis of the tight-binding parameters and magnetic interactions in Na2IrO3 . Phys. Rev. B 88, 035107 (2013) .
Katukuri, V. M. et al. Kitaev interactions between j=1/2 moments in honeycomb Na2IrO3 are large and ferromagnetic: insights from ab initio quantum chemistry calculations. New J. Phys. 16, 013056 (2014) .
Yamaji, Y., Nomura, Y., Kurita, M., Arita, R. & Imada, M. First-principles study of the honeycomb-lattice iridates Na2IrO3 in the presence of strong spin-orbit interaction and electron correlations. Phys. Rev. Lett. 113, 107201 (2014) .
Kimchi, I. & You, Y.-Z. Kitaev-Heisenberg-J2-J3 model for the iridates A2IrO3 . Phys. Rev. B 84, 180407 (2011) .
O’Malley, M. J., Verweij, H. & Woodward, P. M. Structure and properties of ordered Li2IrO3 and Li2PtO3 . J. Solid State Chem. 181, 1803–1809 (2008) .
Helgaker, T., Jørgensen, P. & Olsen, J. Molecular Electronic-Structure Theory Wiley (2000) .
Bogdanov, N. A., Katukuri, V. M., Stoll, H., van den Brink, J. & Hozoi, L. Post-perovskite CaIrO3: A j=1/2 quasi-one-dimensional antiferromagnet. Phys. Rev. B 85, 235147 (2012) .
Katukuri, V. M., Stoll, H., van den Brink, J. & Hozoi, L. Ab initio determination of excitation energies and magnetic couplings in correlated quasi-two-dimensional iridates. Phys. Rev. B 85, 220402 (2012) .
Katukuri, V. M. et al. Mechanism of basal-plane antiferromagnetism in the spin-orbit driven iridate Ba2IrO4 . Phys. Rev. X 4, 021051 (2014) .
Luttinger, J. M. & Tisza, L. Theory of dipole interaction in crystals. Phys. Rev 70, 954–964 (1946) .
Bertaut, E. F. Configurations magnétiques. méthode de Fourier. J. Phys. Chem. Solids 21, 256–279 (1961) .
Litvin, D. B. The Luttinger-Tisza method. Physica 77, 205–219 (1974) .
Kaplan, T. A. & Menyuk, N. Spin ordering in three-dimensional crystals with strong competing exchange interactions. Philos. Mag. 87, 3711–2785 (2007) .
Chandra, P. & Doucot, B. Possible spin-liquid state at large S for the frustrated square Heisenberg lattice. Phys. Rev. B 38, 9335–9338 (1988) .
Schulz, H. J., Ziman, T. A. L. & Poilblanc, D. Magnetic order and disorder in the frustrated quantum Heisenberg antiferromagnet in two dimensions. J. Phys. I France 6, 675–703 (1996) .
Bishop, R. F., Farnell, D. J. J. & Parkinson, J. B. Phase transitions in the spin-half J1 –J2 model. Phys. Rev. B 58, 6394–6402 (1998) .
Chandra, P., Coleman, P. & Larkin, A. I. Ising transition in frustrated Heisenberg models. Phys. Rev. Lett. 64, 88–91 (1990) .
Weber, C. et al. Ising transition driven by frustration in a 2D classical model with continuous symmetry. Phys. Rev. Lett. 91, 177202 (2003) .
Lei, H., Yin, W.-G., Zhong, Z. & Hosono, H. Structural, magnetic, and electrical properties of Li2Ir1−xRuxO3 . Phys. Rev. B 89, 020409 (2014) .
Kimber, S. A. J., de Vries, M. A., Sanchez-Benitez, J., Kamenev, K. V. & Attfield, J. P. Triplet dimerization crossover driven by magnetic frustration in In2VO5 . Phys. Rev. B 77, 014428 (2008) .
Pardo, V. et al. Homopolar bond formation in ZnV2O4 close to a metal-insulator transition. Phys. Rev. Lett. 101, 256403 (2008) .
Reuther, J., Thomale, R. & Rachel, S. Spiral order in the honeycomb iridate Li2IrO3 . Phys. Rev. B 90, 100405 (2014) .
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2, 242–253 (2012) .
Hozoi, L., Siurakshina, L., Fulde, P. & van den Brink, J. Ab initio determination of Cu 3d orbital energies in layered copper oxides. Sci. Rep. 1, 65 (2011) .
de Graaf, C., Sousa, C. & Broer, R. Ionization and excitation energies in CuCl and NiO within different embedding schemes. J. Mol. Struct. (Theochem) 458, 53–60 (1999) .
Berning, A., Schweizer, M., Werner, H.-J., Knowles, P. J. & Palmieri, P. Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 98, 1823–1833 (2000) .
Acknowledgements
We thank R. Coldea, Y. Singh, N. A. Bogdanov and D. I. Khomskii for insightful discussions. The computations were partially performed at the High Performance Computing Center (ZIH) at the Technical University Dresden. Partial financial support from the German Research Foundation (HO-4427 and SFB 1143) is gratefuly acknowledged.
Author information
Authors and Affiliations
Contributions
V.M.K. carried out the ab initio calculations and subsequent mapping of the ab initio data onto the effective spin Hamiltonian, with assistance from L.H., H.S., V.Y. and I.R. S.N. performed the exact diagonalization calculations. I.R. performed the triplet-dimer mapping and analysis, with assistance from S.N. and U.K.R. L.H. and J.v.d.B. designed the project. S.N., V.M.K., L.H., I.R. and J.v.d.B. wrote the paper, with contributions from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Tables 1-3, Supplementary Notes 1-4 and Supplementary References (PDF 1319 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nishimoto, S., Katukuri, V., Yushankhai, V. et al. Strongly frustrated triangular spin lattice emerging from triplet dimer formation in honeycomb Li2IrO3. Nat Commun 7, 10273 (2016). https://doi.org/10.1038/ncomms10273
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10273
This article is cited by
-
Local Moment Instability of Os in Honeycomb Li2.15Os0.85O3
Scientific Reports (2018)
-
Kitaev exchange and field-induced quantum spin-liquid states in honeycomb α-RuCl3
Scientific Reports (2016)
-
Iridates from the molecular side
Nature Communications (2016)
-
Atomic-scale observation of structural and electronic orders in the layered compound α-RuCl3
Nature Communications (2016)
-
The vicinity of hyper-honeycomb β-Li2IrO3 to a three-dimensional Kitaev spin liquid state
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.