Abstract
The miniaturization of future electronic devices is intimately connected to the ability to control electric fields on the atomic scale. In a nanoscopic system defined by a limited number of charges, the combined dynamics of bound and free charges become important. Here we present a model system based on the electrostatic interaction between a metallic tip of a scanning tunnelling microscope and a GaAs(110) semiconductor surface. The system is driven out of equilibrium by optical excitation, which provides ambipolar free charge carriers, and by an optically induced unipolar tunnel current. This combination enables the active control of the density and spatial distribution of free and bound charge in the space-charge region, that is, modifying the screening processes. Temporal fluctuations of single dopants are modified, meaning we are able to control the noise of the system. It is found that free charge carriers suppress the noise level in field-controlled, nanoscopic systems.
Similar content being viewed by others
Introduction
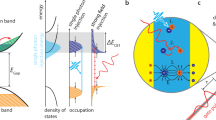
Nowadays, semiconductor-based electronic devices have already reached the nanometre size1,2,3. At this scale, the discreteness of charge, given by, for example, charged single impurities, has already become visible4,5. The latter are the natural limit of the miniaturization process of future electronic applications. Processes, which define the equilibrium charge state of such a nanoscopic device, are shown in Fig. 1a. A gate voltage ionizes dopant atoms to build up the local space charge region (SCR). A current of free minority charge carriers IH towards the field region sets in (Fig. 1a, α). Recombination of carriers inside the SCR results in spatial and temporal fluctuating charges. All this depends on the charge density, the emission (Fig. 1a, β) and capture rate (Fig. 1a, δ) of dopants and the dynamics of the minority charge carriers.
(a) The geometry and spatial extend of a SCR is very sensitive to the charge distribution. Besides ionized dopants, a current of minority charge carriers IH towards the surface is found (α). This charge replaces the function of the ionized dopants. Doping atoms charge (β) and discharge (δ) by capturing free holes or electrons depending on the hole density at the surface. (b) The STM tip-induced potential is used as a local gate electrode to create a SCR of ionized dopants reaching several nanometres into the sample. (c) By generating photoexcited electrons and holes, the free charge is separated by the tip-induced field resulting in a hole accumulation at the surface and thereby to a more efficient screening of the potential drop. (d) Tunnelling electrons address the hole gas, driving the system out of its equilibrium state. By changing the tunnel current, the hole density and, thus, the screening length of the SCR is controlled.
In the following, we describe an approach in which the sharp tip of a scanning tunnelling microscope (STM) serves as the very local gate4,5,6,7,8,9,10. Free charge generation by optical excitation and carrier injection by the tunnel current allows driving the system out of equilibrium. We are able to actively control the charge configuration at the surface and thereby establish different screening processes. Values like the carrier flow inside the SCR for different tunnel currents, optical excitation powers and bias voltages can be extracted. Moreover, it is possible to characterize the charge dynamics using a noise analysis of the tunnel current for different charge configurations at the surface.
Results
STM on the GaAs(110) surface under optical excitation
Positioned only a few Ångstrom above a surface with a low carrier density, the metallic tip induces a nanoscopic SCR inside the sample (Fig. 1b). At an n-doped (3 × 1018 cm−3) GaAs(110) surface with a positive sample voltage of 2.5 V applied, a depleting charge layer is induced extending ∼20 nm into the sample surface with only ∼10 ionized dopants involved4.
To get access to the dynamics of this nanoscaled system, we have combined STM with optical excitation (Fig. 1c). Photogenerated electron–hole pairs will be separated by the electric field. In equilibrium, this current of positive minority charge carriers IH (n-doped) towards the surface is balanced by recombination and thermionic emission. The SCR is modified by the hole accumulation, screening the potential between tip and sample more efficiently. Originally ionized dopants partly discharge, which results in a shift of the surface potential, by default described as a surface photovoltage11.
The photogenerated charge accumulation at the surface results in an additional current channel12,13,14,15. Carrier injection via the tunnel current IT into the valence band distorts the balance of free charge given by optical excitation and locally fixed charge of ionized dopants inside the SCR (Fig. 1d), modifying the non-equilibrium conditions. Surprisingly within the framework of locally resolved surface photovoltage experiments, this carrier injection has been widely neglected up to now16,17,18. The influence of IT on the screening process of the SCR has been subject to studies before13,19,20,21. Cahill et al.19 describes this effect as a consequence of a ‘charging’ due to high tunnel currents leading to an electron accumulation at the surface and counteracting the photogenerated holes. Similar observations were made by Terada et al.21 discussed as an increase of hole recombination at increased tunnel currents. Chen et al.20 describe the change in the SCR as a result of a leakage current modifying the concentration of the free, photogenerated charge and is treated as a parasitic side effect. More sophisticated is the work of Sommerhalter et al.13. By observing direct tunnelling into minority carriers, they succeeded to develop a model considering the influence of the charge injection by IT.
In our experiment, IT is used as a control parameter for the charge distribution inside the SCR. Unlike previous studies, we keep the tip–sample potential constant when changing the tunnel current. This allows us to study the balance of free and bound charge at the surface by actively tuning the screening process of the SCR and to disentangle and control the dynamics of the system by only changing IT. At weak photoillumination, we are able to investigate the full range of carrier injection going from low to high currents and thereby at the same time testing and modifying the screening process in three regimes.
Valence band tunnelling visible in STM topographies
In Fig. 2a,b constant current topographies of the optically excited GaAs(110) for positive bias voltages visualize the contribution of tunnelling into photogenerated minority carriers for the first time locally resolved. Different atomic corrugations are observed, which can be attributed to specific resonant surface states positioned energetically inside the valence band (Fig. 2a) and conduction band (Fig. 2b)22,23 (Supplementary Note 1; Supplementary Fig. 1). The visibility of the valence band corrugation (Fig. 2a) at positive bias voltage is, in contrast to spectroscopic measurements, a direct evidence that tunnelling into photogenerated holes via valence band tunnelling IV is possible. Under dark conditions at 0.3 V bias voltage, the conduction band cannot be addressed due to the tip-induced band bending. With optical excitation, it is a priori open which tunnel channel (valence or conduction band) is dominant and depends strongly on the density of states and the transmission probability (for details see Supplementary Note 2).
(a) The topography at 0.3 V (400 pA) shows the atomic corrugation characteristic for valence band tunnelling. (b) At 0.7 V (400 pA), the corrugation originating from conduction band states is visible. (c–e) Optical excitation-dependent I(z) spectroscopies (set point: 2.5 V/10 pA). A plateau appears in the curves, which moves in position for increasing optical power. The black-dashed line shows the I(z) characteristics without optical excitation. (f) Hole field-induced mHF and dopant field-induced mDF capture rate of holes at the surface. The error bars stem from the fitting quality of the model (for details see the Supplementary Notes 4 and 5). (g–i) A model including both tunnel channels attributes different charge configurations to the three regimes in the I(z) characteristics. Model calculations are shown as red-dotted lines in c–e.
Accessing different tunneling regimes with I(z) spectroscopy
Using I(z) spectroscopy as a function of low optical excitation power PL and at fixed bias voltage, we are able to exclusively monitor the influence of IT on the screening process inside the surface. The change in the surface potential when decreasing the tip–sample distance by 3 Å is about 5% of the whole SCR and hence is negligible. Figure 2c–e shows a set of I(z) curves taken at a set point of 2.5 V and 10 pA. It is important to note that this set point allows to directly compare the curves acquired at different PL (Supplementary Note 1; Supplementary Fig. 2). A plateau-like signature can be identified in the experimental data, moving in position when changing PL and bias voltage (the latter not shown here). In standard tunnel theory, the current dependency I(z) on the tip–sample distance z is described by an exponential relation I(z)∝exp(−αz) with  and Φ as the apparent barrier height of the tunnel junction24. A closer look on the I(z) spectra in Fig. 2c–e strongly suggests to divide the curve into three electronic configurations, indicated by the blue shadings in Fig. 2c–e and labelled as I, II and III. In I and III, the I(z) curves follow the expected exponential dependency. We extract a barrier height Φ for the tunnelling electrons of 2.5 eV (see Supplementary Note 3 and Supplementary Fig. 3 for more details), the same value obtained for the I(z) characteristics under dark conditions (dotted line in Fig. 2c). Analogous to the topographic analysis, we conclude that conduction band tunnelling is the predominant process at higher bias voltages. Nevertheless, the topography in Fig. 2a demonstrates that the tunnelling into photogenerated holes is possible.
and Φ as the apparent barrier height of the tunnel junction24. A closer look on the I(z) spectra in Fig. 2c–e strongly suggests to divide the curve into three electronic configurations, indicated by the blue shadings in Fig. 2c–e and labelled as I, II and III. In I and III, the I(z) curves follow the expected exponential dependency. We extract a barrier height Φ for the tunnelling electrons of 2.5 eV (see Supplementary Note 3 and Supplementary Fig. 3 for more details), the same value obtained for the I(z) characteristics under dark conditions (dotted line in Fig. 2c). Analogous to the topographic analysis, we conclude that conduction band tunnelling is the predominant process at higher bias voltages. Nevertheless, the topography in Fig. 2a demonstrates that the tunnelling into photogenerated holes is possible.
Modelling the tunnelling into photogenerated minority carriers
To describe the complex I(z) characteristics under optical excitation, we present a two-channel tunnelling model (Fig. 2g–i), which includes both the current into the valence band IV and into the conduction band IC.
In regime I (Fig. 2e), the valence band tunnelling IV is as low that it is not significantly influencing the charge density nH at the surface. The electrostatic potential between tip and sample is completely screened by the photogenerated charge, leading to flat band conditions for all optical power ratings PL. The tunnelling into the valence band IV is balanced by a hole current  . This current can be regarded as a field-driven current induced by the distortion of the hole gas-screening process (hole gas-induced field (HF), see Supplementary Note 4 and Supplementary Fig. 4). In this regime, the transmission probability and not the density of final states of the tunnelling process is the limiting factor for valence band tunnelling IV. Therefore, nH defined by the potential between tip and sample and also the SCR is constant as a function of the tunnel current IT.
. This current can be regarded as a field-driven current induced by the distortion of the hole gas-screening process (hole gas-induced field (HF), see Supplementary Note 4 and Supplementary Fig. 4). In this regime, the transmission probability and not the density of final states of the tunnelling process is the limiting factor for valence band tunnelling IV. Therefore, nH defined by the potential between tip and sample and also the SCR is constant as a function of the tunnel current IT.
For higher currents, IV overcomes  resulting in a filling of final states for tunnelling electrons. Consequently, the hole concentration at the surface decreases (Fig. 2h). At the crossover from I to II (at z1), valence band tunnelling IV and the hole current
resulting in a filling of final states for tunnelling electrons. Consequently, the hole concentration at the surface decreases (Fig. 2h). At the crossover from I to II (at z1), valence band tunnelling IV and the hole current  have equalized. In this transition regime II, the hole density nH can be actively tuned by adjusting the tunnel current. As this value defines the screening length of the induced field, the controlled decrease of nH at the surface leads to an IV-dependent rebuilding of the SCR (Fig. 2h). As a consequence, two counteracting processes set in. First, due to the rebuilding of the SCR, the conduction band tunnelling IC decreases, as a fraction of the bias voltage drops inside the sample. Second, the longer spatial extend of the resulting SCR changes the current of photogenerated holes towards the surface. The holes are accelerated by the tip-induced field, partly screened by ionized dopants, resulting in a more pronounced field-driven hole current
have equalized. In this transition regime II, the hole density nH can be actively tuned by adjusting the tunnel current. As this value defines the screening length of the induced field, the controlled decrease of nH at the surface leads to an IV-dependent rebuilding of the SCR (Fig. 2h). As a consequence, two counteracting processes set in. First, due to the rebuilding of the SCR, the conduction band tunnelling IC decreases, as a fraction of the bias voltage drops inside the sample. Second, the longer spatial extend of the resulting SCR changes the current of photogenerated holes towards the surface. The holes are accelerated by the tip-induced field, partly screened by ionized dopants, resulting in a more pronounced field-driven hole current  (dopant-induced field (DF), see Supplementary Note 5 and Supplementary Fig. 8). Consequently, IH and as a result the valence band tunnelling IV increases. Nevertheless, the plateau in the I(z) curves in II shows that the decrease of the conduction band tunnelling due to the change of the SCR is the dominant effect. At the end of regime II (at z2), the SCR found without optical excitation is re-established.
(dopant-induced field (DF), see Supplementary Note 5 and Supplementary Fig. 8). Consequently, IH and as a result the valence band tunnelling IV increases. Nevertheless, the plateau in the I(z) curves in II shows that the decrease of the conduction band tunnelling due to the change of the SCR is the dominant effect. At the end of regime II (at z2), the SCR found without optical excitation is re-established.
Regime III (Fig. 2i) is defined by the lowest hole density at the surface (nH≈0). The tunnelling into the valence band has even exceeded  . This corresponds to an instant annihilation of all holes participating in the screening process of the potential between tip and sample. The charge is solely provided by ionized, locally fixed dopants. The tunnelling current I(z) can be described by the sum of the exponential IC(z) characteristics of conduction band tunnelling plus the valence band tunnelling IV balancing the field-driven current of holes towards the surface. A further increase of the tunnelling current IT does not change nH and thereby the SCR. IV, being limited by
. This corresponds to an instant annihilation of all holes participating in the screening process of the potential between tip and sample. The charge is solely provided by ionized, locally fixed dopants. The tunnelling current I(z) can be described by the sum of the exponential IC(z) characteristics of conduction band tunnelling plus the valence band tunnelling IV balancing the field-driven current of holes towards the surface. A further increase of the tunnelling current IT does not change nH and thereby the SCR. IV, being limited by  , becomes a constant, tunnel current-independent contribution, only dependent on the bias voltage.
, becomes a constant, tunnel current-independent contribution, only dependent on the bias voltage.
To quantify this model, we describe the overall current I(z) as the sum of valence band IV(z) and conduction band tunnelling IC(z) in the three different current regimes. Our model is able to accurately reproduce the observation (red lines in Fig. 2c–e, Supplementary Note 6). A detailed analysis (Supplementary Notes 4 and 5; Supplementary Figs 5,6,7,9 and 10) shows that both, the hole gas-induced field-driven current  and the dopant-induced field-driven current
and the dopant-induced field-driven current  , depend linearly on the optical excitation power PL (
, depend linearly on the optical excitation power PL ( and
and  ). According to the model at z1 or z2, the valence band tunnelling has equalized
). According to the model at z1 or z2, the valence band tunnelling has equalized  or
or  , respectively, allowing us to extract the charge generation inside the SCR. The capture rate mDF(z2) is eight to nine times higher in comparison to mHF (Fig. 2f). The model allows us to calculate and to separate valence and conduction band tunnelling (Supplementary Note 6; Supplementary Fig. 11). At an optical power of 100 μW, valence band tunnelling contributes 4% at z1, whereas at z2 the valence band tunnelling accounts for over 30% of the overall tunnel current. The latter corresponds to an annihilation of 2.5 × 108 holes per second. With a focus diameter of 50 μm and a penetration depth of about 1 μm of the laser light25, holes in an excitation volume of (40 nm)3 are collected. This volume has the same magnitude as the spatial extends of the SCR under dark conditions, suggesting that in regime III all holes in the tip-induced electric field are depopulated. Both values, mHF and mDF, show a significant bias voltage dependency, which is correlated to the potential drop between STM tip and sample that is needed to be screened (for more details see Supplementary Notes 4 and 5).
, respectively, allowing us to extract the charge generation inside the SCR. The capture rate mDF(z2) is eight to nine times higher in comparison to mHF (Fig. 2f). The model allows us to calculate and to separate valence and conduction band tunnelling (Supplementary Note 6; Supplementary Fig. 11). At an optical power of 100 μW, valence band tunnelling contributes 4% at z1, whereas at z2 the valence band tunnelling accounts for over 30% of the overall tunnel current. The latter corresponds to an annihilation of 2.5 × 108 holes per second. With a focus diameter of 50 μm and a penetration depth of about 1 μm of the laser light25, holes in an excitation volume of (40 nm)3 are collected. This volume has the same magnitude as the spatial extends of the SCR under dark conditions, suggesting that in regime III all holes in the tip-induced electric field are depopulated. Both values, mHF and mDF, show a significant bias voltage dependency, which is correlated to the potential drop between STM tip and sample that is needed to be screened (for more details see Supplementary Notes 4 and 5).
To sum up this section, we compare our results and the model to previous studies13,19,20,21. Contrary to refs 19, 21, we can exclude the effect of increased electron injection into the conduction band for high tunnel currents leading to a change in the SCR, as the topographic analysis in Fig. 2a,b is able to clearly show additional valence band tunnelling into minority carriers. This mechanism, also discussed in refs 13, 20, reacts very sensitive to the size of the SCR, dependent on the STM tip geometry, the potential between tip and sample and the density of optical excitation. By keeping the bias voltage fixed and applying low optical excitation the I(z) spectroscopy allows us to develop a quantitative two-channel tunnelling model. An advantage of our experimental conditions in comparison to previous work13 is the combination of conduction band IC and valence band tunnelling IV enabling us to monitor the change of the SCR, having a major influence on IC, and the behaviour of the tunnelling into photogenerated minority carriers, giving the position of the plateau region in the I(z) curves, simultaneously. Also, by having a defined SCR in regime I (flat band conditions) and III (TIBB under dark conditions), an extensive computational effort of the tip-induced potential can be avoided.
Noise analysis of the nanoscaled space charge region
Concluding, it is obvious that different charge configurations have to be considered in the discussed three regimes. To extract the corresponding dynamic properties, we analyse the noise characteristics of the tunnel current. By subtracting a low-frequency filtered I(z) curve from the raw data, the signal in a frequency range between 10 Hz and 1.5 kHz is isolated (Fig. 3a). In comparison to the noise without optical excitation, we observe a spontaneous increase in noise in regime II in spectra taken at the photoexcited surface. The standard deviation σRMS in current is plotted against the average current for an optical excitation of 37, 75 and 134 μW compared to the values under dark conditions in Fig. 3b–d. The behaviour of the noise level in the excited case is unequivocally connected to the previously discussed tunnelling regimes, indicated by the blue shadings in Fig. 3b–d.
At 37 μW optical excitation (Fig. 3b), the noise in the tunnel regime I shows the same trend compared to the non-excited case. For regime II, σRMS increases. We attribute this to a non-equilibrium charging and discharging process of dopants4,5,9,26 inside the SCR (Fig. 1a,d) due to the carrier injection. By disturbing the hole density at the surface by valence band tunnelling IV drives the SCR in metastable configurations. We expect subtle but frequent changes in the geometry of the SCR leading to variations in the tunnelling current, and thereby to additional noise.
In regime III, we observe a saturation of σRMS, yielding σRMS (37 μW)<σRMS (0). Previous studies5,27 have shown that under dark conditions bistable charging processes of doping atoms have to be taken into account. Assuming that these processes define the noise level of the spectra without optical excitation, our results suggest that the presence of free electron–hole pairs suppresses this charge switching in the photoexcited case9,26. We like to point out that the decrease in noise in comparison to the noise under dark conditions is not the result of a simple decrease of the SCR. Our analysis suggests that in regime III the SCR, normally found under dark conditions, has been rebuilt. Here the charge of the SCR is solely defined by ionized dopants. But even though no more hole accumulation is expected at the surface in the tip-induced field, it is conceivable that the electron–hole pairs, present in the bulk material, cause an additional screening of the SCR. The geometry of the SCR, normally given by the rather stochastic distribution of donors, is smoothed and thereby the charge state of the dopants is stabilized.
By analysing the evolution of the noise level for higher optical power steps at 74 μW (Fig. 3c) and 134 μW (Fig. 3d), this free charge stabilization in the bulk material can actually reduce the noise induced by space charge dynamics even in I and II. In this z-range, σRMS decreases monotonically for increasing PL. In particular for an optical power of 134 μW (Fig. 3d), the noise level is below the values without optical excitation showing that charge switching of bistable dopants is reduced.
From previous studies, the noise level is expected to increase linearly with the tunnel current up to a tunnelling regime close to the point contact of the STM tip28. In contrast, in regime III, a saturation in IT of σRMS can be observed (Fig. 3b–d), indicating that the resulting σRMS is defined by processes independent of the tunnel current for the optically excited surface. Regarding the dependency on the optical excitation power, we observe a slight increase of σRMS with increasing PL. Nevertheless, the saturation behaviour for increasing tunnel currents implies that in the frequency range up to 1 kHz charge fluctuations are the dominant contributions to the noise characteristic.
Discussion
In summary, our results show that tunnelling into minority charge carriers at the surface allows to actively tune the screening process and thereby to decouple the SCR from parameters such as the gate voltage or gate geometry. By controlling the density of minority charge carriers, we are able to suppress the noise in this field determined, nanoscopic system considerably.
For a more detailed analysis of the dynamics, a resolution beyond the kHz bandwidth of the STM is required. This can be achieved using pulsed optical excitation14,21, which gives the possibility to gain deeper insight into the time scales of the interplay of the tunnel current IT and the minority carrier current IH.
Methods
Experimental set-up
The experiments are performed in a custom-built, low-temperature STM working under UHV condition (6 K at a base pressure of P<3 × 10−11 mbar). For optical excitation, a stabilized continuous wave diode laser at a wavelength of 785 nm and a maximum power of 100 mW is used. The focus diameter of the laser is about 50 μm. With an illumination angle of roughly 30° this results in an optical excited area of 1.57 × 10−8 m2. The tips are electrochemically etched from a polycrystalline tungsten wire. The typical tip radius is about 10–40 nm. I(V,z) spectroscopy is used to study the effect of the tunnelling process on the photogenerated charge.
Additional information
How to cite this article: Kloth, P. et al. Controlling the screening process of a nanoscaled space charge region by minority carriers. Nat. Commun. 7:10108 doi: 10.1038/ncomms10108 (2016).
References
Peercy, P. The drive to miniaturization. Nature 406, 1023–1026 (2000).
Lee, D. H. & Gupta, J. A. Tunable field control over the binding energy of single dopants by a charged vacancy in GaAs. Science 330, 1807–1810 (2010).
Koenraad, P. M. & Flatté, M. E. Single dopants in semiconductors. Nat. Mater. 10, 91–100 (2011).
Teichmann, K. et al. Controlled charge switching on a single donor with a scanning tunneling microscope. Phys. Rev. Lett. 101, 76103 (2008).
Teichmann, K. et al. Bistable charge configuration of donor systems near the GaAs(110) surfaces. Nano Lett. 11, 3538–3542 (2011).
Feenstra, R. M. & Stroscio, J. A. Tunneling spectroscopy of the GaAs(110) surface. J. Vac. Sci. Technol. B. 5, 923 (1987).
Zheng, H., Weismann, A. & Berndt, R. Tuning the electron transport at single donors in zinc oxide with a scanning tunnelling microscope. Nat. Commun. 5, 2992 (2014).
Fernández-Torrente, I., Kreikemeyer-Lorenzo, D., Stróżecka, A., Franke, K. J. & Pascual, J. I. Gating the charge state of single molecules by local electric fields. Phys. Rev. Lett. 108, 036801 (2012).
Smakman, E. P., Helgers, P. L. J., Verheyen, J., Koenraad, P. M. & Möller, R. Tunable switching dynamics of a single Si dopant in GaAs (110). Phys. Rev. B 90, 041410 (2014).
Heinrich, B. W., Braun, L., Pascual, J. I. & Franke, K. J. Protection of excited spin states by a superconducting energy gap. Nat. Phys. 9, 765–768 (2013).
Garett, C. G. B. & Brattain, W. H. Physical theory of semiconductor surfaced. Phys. Rev 99, 376–387 (1955).
Akari, S., Lux-Steiner, M. C., Vögt, M., Stachel, M. & Dransfeld, K. Photoassisted tunneling spectroscopy: preliminary results on tungsten diselenide. J. Vac. Sci. Technol. B 9, 561–563 (1991).
Sommerhalter, C., Matthes, T. W., Boneberg, J. & Leiderer, P. Tunneling spectroscopy on semiconductor with a low surface state density. J. Vac. Sci. Technol. B 15, 1876 (1997).
Yoshida, S. & Terada, Y. Direct probing of transient photocurrent dynamics in p-wse2 by time-resolved scanning tunneling microscopy. Appl. Phys.Express 6, 1–4 (2013).
Schnedler, M., Portz, V., Weidlich, P. H., Dunin-Borkowski, R. E. & Ebert, P. Quantitative description of photoexcited scanning tunneling spectroscopy and its application to the GaAs(110) surface. Phys. Rev. B 91, 1–13 (2015).
Hamers, R. J. & Markert, K. Atomically resolved carrier recombination at Si(111)-(7 × 7) surfaces. Phys. Rev. Lett. 64, 1051–1054 (1990).
Aloni, S., Nevo, I. & Haase, G. Local Fermi-level pinning at a single adatom (Cs) or vacancy (As) on a GaAs(110) surface. Phys. Rev. B 60, R2165–R2168 (1999).
Takeuchi, O., Yoshida, S. & Shigekawa, H. Light-modulated scanning tunneling spectroscopy for nanoscale imaging of surface photovoltage. Appl. Phys. Lett. 84, 3645 (2004).
Cahill, D. G. & Feenstra, R. M. Carrier injection and scanning microscopy at the Si(111)-2 × 1 surface. J. Vac. Sci. Technol. A 11, 792–796 (1993).
Chen, T., Fung, S. & Beling, C. Leakage current induced drop in Ef in PES studies of Schottky Barrier Formation. Solid State Commun. 89, 779–781 (1994).
Terada, Y., Yoshida, S., Takeuchi, O. & Shigekawa, H. Real-space imaging of transient carrier dynamics by nanoscale pump–probe microscopy. Nat. Photon. 4, 869–874 (2010).
Chelikowsky, J. J. R. & Cohen, M. M. L. Self-consistent pseudopotential calculation for the relaxed (110) surface of GaAs. Phys. Rev. B 20, 4150–4159 (1979).
Ebert, P. et al. Contribution of surface resonances to scanning tunneling microscopy images: (110) surfaces of III-V semiconductors. Phys. Rev. Lett. 77, 2997–3000 (1996).
Binnig, G. & Rohrer, H. Scanning tunneling microscopy. Surf. Sci. 126, 236–244 (1983).
Sturge, M. D. Optical absorption of gallium arsenide between 0.6 and 2.75 eV. Phys. Rev. 127, 768–773 (1962).
Smakman, E. P., van Bree, J. & Koenraad, P. M. Laser and voltage manipulation of bistable Si dopants in the GaAs (110) surface. Phys. Rev. B 87, 85414 (2013).
Ralls, K. S. et al. Discrete resistance switching in submicrometer silicon inversion layers: individual interface traps and low-frequency (1 f□?) noise. Phys. Rev. Lett. 52, 228–231 (1984).
Schneider, N. L., Schull, G. & Berndt, R. Optical probe of quantum shot-noise reduction at a single-atom contact. Phys. Rev. Lett. 105, 026601 (2010).
Acknowledgements
This work was supported by the CRC1073 project C4.
Author information
Authors and Affiliations
Contributions
M.W. and P.K. planned the experiment. P.K. and K.K. conducted the experiment and the data analysis. P.K. and M.W. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-11 and Supplementary Notes 1-6, Supplementary Reference. (PDF 1061 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kloth, P., Kaiser, K. & Wenderoth, M. Controlling the screening process of a nanoscaled space charge region by minority carriers. Nat Commun 7, 10108 (2016). https://doi.org/10.1038/ncomms10108
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10108
This article is cited by
-
Scanning probe microscopy
Nature Reviews Methods Primers (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.