Abstract
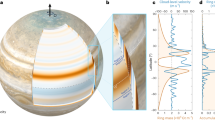
The depth to which Jupiter’s observed east–west jet streams extend has been a long-standing question1,2. Resolving this puzzle has been a primary goal for the Juno spacecraft3,4, which has been in orbit around the gas giant since July 2016. Juno’s gravitational measurements have revealed that Jupiter’s gravitational field is north–south asymmetric5, which is a signature of the planet’s atmospheric and interior flows6. Here we report that the measured odd gravitational harmonics J3, J5, J7 and J9 indicate that the observed jet streams, as they appear at the cloud level, extend down to depths of thousands of kilometres beneath the cloud level, probably to the region of magnetic dissipation at a depth of about 3,000 kilometres7,8. By inverting the measured gravity values into a wind field9, we calculate the most likely vertical profile of the deep atmospheric and interior flow, and the latitudinal dependence of its depth. Furthermore, the even gravity harmonics J8 and J10 resulting from this flow profile also match the measurements, when taking into account the contribution of the interior structure10. These results indicate that the mass of the dynamical atmosphere is about one per cent of Jupiter’s total mass.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Dowling, T. E. Dynamics of Jovian atmospheres. Annu. Rev. Fluid Mech. 27, 293–334 (1995)
Vasavada, A. R. & Showman, A. P. Jovian atmospheric dynamics: an update after Galileo and Cassini. Rep. Prog. Phys. 68, 1935–1996 (2005)
Hubbard, W. B. Gravitational signature of Jupiter’s deep zonal flows. Icarus 137, 357–359 (1999)
Bolton, S. J. Juno Final Concept Study Report. Technical Report AO-03-OSS-03 (New Frontiers, NASA, 2005)
Iess, L. et al. Measurement of Jupiter’s asymmetric gravity field. Nature 555, https://doi.org/10.1038/nature25776 (2018)
Kaspi, Y. Inferring the depth of the zonal jets on Jupiter and Saturn from odd gravity harmonics. Geophys. Res. Lett. 40, 676–680 (2013)
Liu, J., Goldreich, P. M. & Stevenson, D. J. Constraints on deep-seated zonal winds inside Jupiter and Saturn. Icarus 196, 653–664 (2008)
Cao, H. & Stevenson, D. J. Zonal flow magnetic field interaction in the semi-conducting region of giant planets. Icarus 296, 59–72 (2017)
Galanti, E. & Kaspi, Y. An adjoint based method for the inversion of the Juno and Cassini gravity measurements into wind fields. Astrophys. J. 820, 91 (2016)
Guillot, T. et al. A suppression of differential rotation in Jupiter’s deep interior. Nature 555, https://doi.org/10.1038/nature25775 (2018)
Bolton, S. J. et al. Jupiter’s interior and deep atmosphere: the initial pole-to-pole passes with the Juno spacecraft. Science 356, 821–825 (2017)
Hubbard, W. B. High-precision Maclaurin-based models of rotating liquid planets. Astrophys. J. 756, L15 (2012)
Kaspi, Y. et al. The effect of differential rotation on Jupiter’s low-degree even gravity moments. Geophys. Res. Lett. 44, 5960–5968 (2017)
Kaspi, Y., Flierl, G. R. & Showman, A. P. The deep wind structure of the giant planets: results from an anelastic general circulation model. Icarus 202, 525–542 (2009)
Zhang, K., Kong, D. & Schubert, G. Thermal-gravitational wind equation for the wind-induced gravitational signature of giant gaseous planets: mathematical derivation, numerical method and illustrative solutions. Astrophys. J. 806, 270–279 (2015)
Cao, H. & Stevenson, D. J. Gravity and zonal flows of giant planets: from the Euler equation to the thermal wind equation. J. Geophys. Res. Planets 122, 686–700 (2017)
Galanti, E., Kaspi, Y. & Tziperman, E. A full, self-consistent, treatment of thermal wind balance on fluid planets. J. Comput. Phys. 810, 175–195 (2017)
Schneider, T. & Liu, J. Formation of jets and equatorial superrotation on Jupiter. J. Atmos. Sci. 66, 579–601 (2009)
Kaspi, Y., Hubbard, W. B., Showman, A. P. & Flierl, G. R. Gravitational signature of Jupiter’s internal dynamics. Geophys. Res. Lett. 37, L01204 (2010)
Atkinson, D. H., Pollack, J. B. & Seiff, A. The Galileo probe Doppler wind experiment: measurement of the deep zonal winds on Jupiter. J. Geophys. Res. 103, 22911–22928 (1998)
Liu, J. & Schneider, T. Mechanisms of jet formation on the giant planets. J. Atmos. Sci. 67, 3652–3672 (2010)
Liu, J., Schneider, T. & Kaspi, Y. Predictions of thermal and gravitational signals of Jupiter’s deep zonal winds. Icarus 224, 114–125 (2013)
Galanti, E. & Kaspi, Y. Deciphering Jupiter’s deep flow dynamics using the upcoming Juno gravity measurements and a dynamical inverse model. Icarus 286, 46–55 (2017)
Salyk, C., Ingersoll, A. P., Lorre, J., Vasavada, A. & Del Genio, A. D. Interaction between eddies and mean flow in Jupiter’s atmosphere: analysis of Cassini imaging data. Icarus 185, 430–442 (2006)
Busse, F. H. A simple model of convection in the Jovian atmosphere. Icarus 29, 255–260 (1976)
Lian, Y. & Showman, A. P. Generation of equatorial jets by large-scale latent heating on the giant planets. Icarus 207, 373–393 (2010)
Wahl, S. et al. Comparing Jupiter interior structure models to Juno gravity measurements and the role of an expanded core. Geophys. Res. Lett. 44, 4649–4659 (2017)
Li, C. et al. The distribution of ammonia on Jupiter from a preliminary inversion of Juno microwave radiometer data. Geophys. Res. Lett. 44, 5317–5325 (2017)
Janssen, M. A. et al. Microwave remote sensing of Jupiter’s atmosphere from an orbiting spacecraft. Icarus 173, 447–453 (2005)
Tollefson, J. et al. Changes in Jupiter’s zonal wind profile preceding and during the Juno mission. Icarus 296, 163–178 (2017)
Hubbard, W. B. Planetary Interiors (Van Nostrand Reinhold, 1984)
Guillot, T. & Morel, P. CEPAM: a code for modeling the interiors of giant planets. Astron. Astrophys. Suppl. Ser. 109, 109–123 (1995)
Militzer, B., Soubiran, F., Wahl, S. M. & Hubbard, W. B. Understanding Jupiter’s interior. J. Geophys. Res. Planets 121, 1552–1572 (2016)
Miguel, Y., Guillot, T. & Fayon, L. Jupiter internal structure: the effect of different equations of state. Astron. Astrophys. 596, A114 (2016)
Helled, R. & Stevenson, D. J. The fuzziness of giant planets’ cores. Astrophys. J. Lett. 840, L4 (2017)
Wisdom, J. & Hubbard, W. B. Differential rotation in Jupiter: a comparison of methods. Icarus 267, 315–322 (2016)
Pedlosky, J. Geophysical Fluid Dynamics (Springer, 1987)
Vallis, G. K. Atmospheric and Oceanic Fluid Dynamics (Cambridge Univ. Press, 2006)
Hubbard, W. B. Conventric Maclaurian spheroid models of rotating liquid planets. Astrophys. J. 768, 43 (2013)
Kong, D., Zhang, K. & Schubert, G. Odd gravitational harmonics of Jupiter: effects of spherical versus nonspherical geometry and mathematical smoothing of the equatorially antisymmetric zonal winds across the equatorial plane. Icarus 277, 416–423 (2016)
Folkner, W. M. et al. Jupiter gravity field from first two orbits by Juno. Geophys. Res. Lett. 44, 4694–4700 (2017)
Porco, C. C. et al. Cassini imaging of Jupiter’s atmosphere, satellites and rings. Science 299, 1541–1547 (2003)
Kaspi, Y., Showman, A. P., Hubbard, W. B., Aharonson, O. & Helled, R. Atmospheric confinement of jet-streams on Uranus and Neptune. Nature 497, 344–347 (2013)
Kong, D., Zhang, K. & Schubert, G. Wind-induced odd gravitational harmonics of Jupiter. Mon. Not. R. Astron. Soc. 450, L11–L15 (2015)
Dowling, T. E. Estimate of Jupiter’s deep zonal-wind profile from Shoemaker-Levy 9 data and Arnold’s second stability criterion. Icarus 117, 439–442 (1995)
Acknowledgements
We thank M. Allison and A. Showman for discussions. The research described here was carried out in part at the Weizmann Institute of Science (WIS) under the sponsorship of the Israeli Space Agency, the Helen Kimmel Center for Planetary Science at the WIS and the WIS Center for Scientific Excellence (Y.K. and E.G.); at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA (W.M.F., M.P. and S.M.L.); at the Southwest Research Institute under contract with NASA (S.J.B.); at the Université Côte d’Azur under the sponsorship of Centre National d’Etudes Spatiales (T.G. and Y.M.); and at La Sapienza University under contract with Agenzia Spaziale Italiana (L.I. and D.D.). All authors acknowledge support from the Juno project.
Author information
Authors and Affiliations
Contributions
Y.K. and E.G. designed the study. Y.K. wrote the paper. E.G. developed the gravity inversion model. D.J.S. led the working group within the Juno Science Team and provided theoretical support. W.B.H. initiated the Juno gravity experiment and provided theoretical support. W.B.H., T.G., Y.M., R.H., B.M. and S.L.W. provided interior models and tested the implications of the results. L.I., D.D., W.M.F. and M.P. carried out the analysis of the Juno gravity data. H.C., D.J.S. and J.B. supported the interpretation regarding the magnetic field. J.I.L. and A.P.I. provided theoretical support. S.J.B., S.M.L. and J.E.P.C. supervised the planning, execution and definition of the Juno gravity experiment. All authors contributed to the discussion and interpretation of the results within the Juno Interiors Working Group.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks J. Fortney and N. Nettelmann for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 The vorticity balance.
Solution to equation (6). a, Left-hand-side term with the wind profile from Fig. 3. b, Total of the right-hand side. c–h, The six terms on the right-hand side of equation (6), showing that the thermal wind balance (a and d) is the leading-order balance. Note that the different panels have different colour scales.
Extended Data Figure 2 Jupiter’s mass distribution.
The percentage of Jupiter’s mass as a function of depth beneath the 1-bar level. The grey line shows that roughly 1% of the mass is contained above a depth of 3,000 km.
Extended Data Figure 3 Example of wind profiles used for the statistical significance test.
The observed cloud-level wind (black), together with a sample of ten randomly generated wind profiles.
Extended Data Figure 4 Optimized solutions for the odd harmonics using random zonal wind profiles.
a–f, Optimized solutions (blue) for J3, J5, J7 and J9 for flows with 1,000 different artificial meridional profiles of the zonal wind (as in Extended Data Fig. 3). The Juno measurements are shown in red with their corresponding uncertainty ellipse. The optimized solution corresponding to Jupiter’s observed cloud-level zonal wind profile (Fig. 3) is shown in black with the corresponding uncertainty ellipse. g, The cost function for all different meridional profiles explored, with the red line corresponding to the solution with the Jupiter zonal wind profile. Fewer than 1% of the solutions have lower cost functions (green).
Extended Data Figure 5 Solutions for the odd harmonics using random zonal wind profiles and a fixed vertical profile.
a–f, Solutions (blue) for J3, J5, J7 and J9 for flows with 1,000 different artificial meridional profiles of the zonal wind (as in Extended Data Fig. 3), and the vertical profile held fixed with H = 2,000 km, ΔH = 1,500 km and α = 1. The Juno measurements are shown in red with their corresponding uncertainty ellipse. The solution with these parameters and using Jupiter’s observed cloud-level zonal wind profile is shown in black with the corresponding uncertainty ellipse. g, The cost function for all different meridional profiles explored, with the red line corresponding to the solution with the Jupiter zonal wind profile. This shows that when no optimization is done (which takes into consideration the relative measurement error of the different harmonics), the solutions are spread equally over all four quadrants in these phase spaces (unlike in Extended Data Fig. 4). Only one solution has a lower cost function (green).
Rights and permissions
About this article
Cite this article
Kaspi, Y., Galanti, E., Hubbard, W. et al. Jupiter’s atmospheric jet streams extend thousands of kilometres deep. Nature 555, 223–226 (2018). https://doi.org/10.1038/nature25793
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature25793
This article is cited by
-
Observational evidence for cylindrically oriented zonal flows on Jupiter
Nature Astronomy (2023)
-
The deep winds of Jupiter
Nature Astronomy (2023)
-
Jupiter’s cloud-level variability triggered by torsional oscillations in the interior
Nature Astronomy (2023)
-
An intense narrow equatorial jet in Jupiter’s lower stratosphere observed by JWST
Nature Astronomy (2023)
-
Jupiter Science Enabled by ESA’s Jupiter Icy Moons Explorer
Space Science Reviews (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.