Abstract
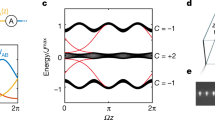
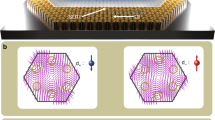
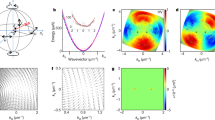
When a two-dimensional (2D) electron gas is placed in a perpendicular magnetic field, its in-plane transverse conductance becomes quantized; this is known as the quantum Hall effect1. It arises from the non-trivial topology of the electronic band structure of the system, where an integer topological invariant (the first Chern number) leads to quantized Hall conductance. It has been shown theoretically that the quantum Hall effect can be generalized to four spatial dimensions2,3,4, but so far this has not been realized experimentally because experimental systems are limited to three spatial dimensions. Here we use tunable 2D arrays of photonic waveguides to realize a dynamically generated four-dimensional (4D) quantum Hall system experimentally. The inter-waveguide separation in the array is constructed in such a way that the propagation of light through the device samples over momenta in two additional synthetic dimensions, thus realizing a 2D topological pump5,6,7,8. As a result, the band structure has 4D topological invariants (known as second Chern numbers) that support a quantized bulk Hall response with 4D symmetry7. In a finite-sized system, the 4D topological bulk response is carried by localized edge modes that cross the sample when the synthetic momenta are modulated. We observe this crossing directly through photon pumping of our system from edge to edge and corner to corner. These crossings are equivalent to charge pumping across a 4D system from one three-dimensional hypersurface to the spatially opposite one and from one 2D hyperedge to another. Our results provide a platform for the study of higher-dimensional topological physics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Klitzing, K. v., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980)
Avron, J. E., Sadun, L., Segert, J. & Simon, B. Chern numbers, quaternions, and Berry’s phases in Fermi systems. Commun. Math. Phys. 124, 595–627 (1989)
Fröhlich, J. & Perdini, B. in Mathematical Physics 2000 9−47 (Imperial College Press, 2000)
Zhang, S.-C. & Hu, J. A four-dimensional generalization of the quantum Hall effect. Science 294, 823–828 (2001)
Thouless, D. J. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983)
Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012)
Kraus, Y. E., Ringel, Z. & Zilberberg, O. Four-dimensional quantum Hall effect in a two-dimensional quasicrystal. Phys. Rev. Lett. 111, 226401 (2013)
Verbin, M., Zilberberg, O., Lahini, Y., Kraus, Y. E. & Silberberg, Y. Topological pumping over a photonic Fibonacci quasicrystal. Phys. Rev. B 91, 064201 (2015)
Haldane, F. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008)
Wang, Z., Chong, Y., Joannopoulos, J. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009)
Rechtsman, M. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013)
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013)
Cheng, X. et al. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 15, 542–548 (2016)
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013)
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014)
Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350–354 (2016)
Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016)
Slobozhanyuk, A. et al. Three-dimensional all-dielectric photonic topological insulator. Nat. Photon. 11, 130–136 (2017)
Lu, L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015)
Noh, J. et al. Experimental observation of optical Weyl points and Fermi arc-like surface states. Nat. Phys. 13, 611–617 (2017)
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008)
Sugawa, S., Salces-Carcoba, F., Perry, A. R., Yue, Y. & Spielman, I. B. Observation of a non-Abelian Yang monopole: from new Chern numbers to a topological transition. Preprint at https://arxiv.org/abs/1610.06228 (2016)
Lu, L. & Wang, Z. Topological one-way fiber of second Chern number. Preprint at https://arxiv.org/abs/1611.01998 (2016)
Prodan, E., Leung, B. & Bellissard, J. The noncommutative nth-Chern number (n ≥ 1). J. Phys. A 46, 485202 (2013)
Boada, O., Celi, A., Latorre, J. & Lewenstein, M. Quantum simulation of an extra dimension. Phys. Rev. Lett. 108, 133001 (2012)
Jukić, D. & Buljan, H. Four-dimensional photonic lattices and discrete tesseract solitons. Phys. Rev. A 87, 013814 (2013)
Price, H. M., Zilberberg, O., Ozawa, T., Carusotto, I. & Goldman, N. Four-dimensional quantum Hall effect with ultracold atoms. Phys. Rev. Lett. 115, 195303 (2015)
Ozawa, T., Price, H. M., Goldman, N., Zilberberg, O. & Carusotto, I. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum Hall physics. Phys. Rev. A 93, 043827 (2016)
Price, H., Zilberberg, O., Ozawa, T., Carusotto, I. & Goldman, N. Measurement of Chern numbers through center-of-mass responses. Phys. Rev. B 93, 245113 (2016)
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. At. Mol. Opt. Phys. 43, 163001 (2010)
Szameit, A. et al. Control of directional evanescent coupling in fs laser written waveguides. Opt. Express 15, 1579–1587 (2007)
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017)
Noh, J. et al. Topological protection of photonic mid-gap cavity modes. Preprint at https://arxiv.org/abs/1611.02373 (2016)
Lohse, M., Schweizer, C., Price, H. M., Zilberberg, O. & Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 553, https://doi.org/10.1038/nature25000 (2018)
Fleischer, J. W., Segev, M., Efremidis, N. K. & Christodoulides, D. N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 422, 147–150 (2003)
Harper, P. G. Single band motion of conduction electrons in a uniform magnetic field. Proc. Phys. Soc. A 68, 874–878 (1955)
Kraus, Y. E. & Zilberberg, O. Topological equivalence between the Fibonacci quasicrystal and the Harper model. Phys. Rev. Lett. 109, 116404 (2012)
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976)
Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 71, 3697–3700 (1993)
Středa, P. Theory of quantised Hall conductivity in two dimensions. J. Phys. Chem. 15, L717–L721 (1982)
Acknowledgements
We thank H. M. Price, M. Lohse, C.-X. Liu, W. Benalcazar, E. Prodan and T. Ozawa for their comments and feedback on the manuscript. O.Z. thanks the Swiss National Science Foundation for financial support. M.C.R. acknowledges the National Science Foundation under award number ECCS-1509546, the Charles E. Kaufman Foundation, a supporting organization of the Pittsburgh Foundation, and the Alfred P. Sloan Foundation under fellowship number FG-2016-6418. K.P.C. acknowledges the National Science Foundation under award numbers ECCS-1509199 and DMS-1620218.
Author information
Authors and Affiliations
Contributions
O.Z., J.G., Y.E.K. and M.C.R. performed the theoretical analysis; S.H. developed the laser fabrication process and characterized the samples with the assistance of J.G. and M.W., under the supervision of K.P.C. and M.C.R.; O.Z. and M.C.R. designed the experiment, wrote the manuscript and supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 Waveguide coupling parameters and illustration of a 1D pump.
a, The overall scale A (dashed red line) and exponential decay prefactor γ (solid orange line) that describe the inter-waveguide coupling as a function of their separation s: t(s) = Aexp(−γs). The parameters were obtained using a thorough calibration procedure (see Methods) and are plotted as a function of wavelength. b, An additional illustration of the waveguide spacing used to implement our topological pump. To simplify the diagram, we show a 1D waveguide array, which corresponds to an implementation of a 1D pump. This configuration can be thought of as resulting from a constant y slice through the full 2D waveguide array.
Extended Data Figure 2 Nearest-neighbour band structure obtained from two decoupled models.
See equation (2). a, Finite-sample band structure (energy E versus pump parameter) for a single Harper model aligned along the x direction. Boundary modes highlighted in orange (red) are localized on the left (right) end of the 1D sample. The first Chern number associated with each bulk band is also shown. b, Band structure for the fully separable 2D pump taken along the path ϕx = ϕy for a system that decomposes into two independent Harper models. Each band in b is obtained by summing a pair of bands from a. The resulting bands can be classified by the types of state that appear in the sum: bulk–bulk (2D bulk), bulk–boundary (2D edge) or boundary–boundary (2D corner). These types are respectively coloured grey, red or orange, and black. As a function of ϕi, the edge modes form ‘dispersive’ bands that thread through the 2D bulk gaps. The corner modes thread between the edge bands and are therefore forced to cross 2D bulk bands along their ϕi trajectory.
Rights and permissions
About this article
Cite this article
Zilberberg, O., Huang, S., Guglielmon, J. et al. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 553, 59–62 (2018). https://doi.org/10.1038/nature25011
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature25011
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.