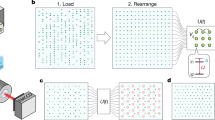
Abstract
Controllable, coherent many-body systems can provide insights into the fundamental properties of quantum matter, enable the realization of new quantum phases and could ultimately lead to computational systems that outperform existing computers based on classical approaches. Here we demonstrate a method for creating controlled many-body quantum matter that combines deterministically prepared, reconfigurable arrays of individually trapped cold atoms with strong, coherent interactions enabled by excitation to Rydberg states. We realize a programmable Ising-type quantum spin model with tunable interactions and system sizes of up to 51 qubits. Within this model, we observe phase transitions into spatially ordered states that break various discrete symmetries, verify the high-fidelity preparation of these states and investigate the dynamics across the phase transition in large arrays of atoms. In particular, we observe robust many-body dynamics corresponding to persistent oscillations of the order after a rapid quantum quench that results from a sudden transition across the phase boundary. Our method provides a way of exploring many-body phenomena on a programmable quantum simulator and could enable realizations of new quantum algorithms.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Bloch, I., Dalibard, J. & Nascimbène, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267–276 (2012)
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010)
Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013)
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013)
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013)
Monz, T. 14-qubit entanglement: creation and coherence. Phys. Rev. Lett. 106, 130506 (2011)
Islam, R. et al. Emergence and frustration of magnetism with variable-range interactions in a quantum simulator. Science 340, 583–587 (2013)
Song, C. et al. 10-qubit entanglement and parallel logic operations with a superconducting circuit. Phys. Rev. Lett. 119, 180511 (2017)
Gärttner, M. et al. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 13, 781–786 (2017)
Kuhr, S. Quantum-gas microscopes: a new tool for cold-atom quantum simulators. Natl Sci. Rev. 3, 170–172 (2016)
Trotzky, S. et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 8, 325–330 (2012)
Mazurenko, A. et al. A cold-atom Fermi-Hubbard antiferromagnet. Nature 545, 462–466 (2017)
Rønnow, T. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014)
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016)
Jaksch, D. et al. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211 (2000)
Weimer, H., Müller, M., Lesanovsky, I., Zoller, P. & Büchler, H. P. A Rydberg quantum simulator. Nat. Phys. 6, 382–388 (2010)
Wilk, T. et al. Entanglement of two individual neutral atoms using Rydberg blockade. Phys. Rev. Lett. 104, 010502 (2010)
Isenhower, L. et al. Demonstration of a neutral atom controlled-NOT quantum gate. Phys. Rev. Lett. 104, 010503 (2010)
Saffman, M. Quantum computing with atomic qubits and Rydberg interactions: progress and challenges. J. Phys. B 49, 202001 (2016)
Pritchard, J. D. et al. Cooperative atom-light interaction in a blockaded Rydberg ensemble. Phys. Rev. Lett. 105, 193603 (2010)
Schauß, P. et al. Observation of spatially ordered structures in a two-dimensional Rydberg gas. Nature 491, 87–91 (2012)
Schauß, P. et al. Crystallization in Ising quantum magnets. Science 347, 1455–1458 (2015)
Zeiher, J. et al. Coherent many-body spin dynamics in a long-range interacting Ising chain. Preprint at https://arxiv.org/abs/1705.08372 (2017)
Labuhn, H. et al. Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models. Nature 534, 667–670 (2016)
Barredo, D., de Léséleuc, S., Lienhard, V., Lahaye, T. & Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 354, 1021–1023 (2016)
Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 354, 1024–1027 (2016)
Kim, H. et al. In situ single-atom array synthesis using dynamic holographic optical tweezers. Nat. Commun. 7, 13317 (2016)
Dudin, Y. O., Li, L., Bariani, F. & Kuzmich, A. Observation of coherent many-body Rabi oscillations. Nat. Phys. 8, 790–794 (2012)
Zeiher, J. et al. Microscopic characterization of scalable coherent Rydberg superatoms. Phys. Rev. X 5, 031015 (2015)
Fendley, P., Sengupta, K. & Sachdev, S. Competing density-wave orders in a one-dimensional hard-boson model. Phys. Rev. B 69, 075106 (2004)
Pohl, T., Demler, E. & Lukin, M. D. Dynamical crystallization in the dipole blockade of ultracold atoms. Phys. Rev. Lett. 104, 043002 (2010)
Petrosyan, D., Mølmer, K. & Fleischhauer, M. On the adiabatic preparation of spatially-ordered Rydberg excitations of atoms in a one-dimensional optical lattice by laser frequency sweeps. J. Phys. B 49, 084003 (2016)
Schachenmayer, J., Lesanovsky, I., Micheli, A. & Daley, A. J. Dynamical crystal creation with polar molecules or Rydberg atoms in optical lattices. New J. Phys. 12, 103044 (2010)
Richerme, P. et al. Experimental performance of a quantum simulator: Optimizing adiabatic evolution and identifying many-body ground states. Phys. Rev. A 88, 012334 (2013)
Sachdev, S. Quantum Phase Transitions 2nd edn (Cambridge Univ. Press, 2009)
Sachdev, S., Sengupta, K. & Girvin, S. M. Mott insulators in strong electric fields. Phys. Rev. B 66, 075128 (2002)
Zurek, W. H., Dorner, U. & Zoller, P. Dynamics of a quantum phase transition. Phys. Rev. Lett. 95, 105701 (2005)
D’Alessio, L., Kafri, Y., Polkovnikov, A. & Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 65, 239–362 (2016)
Abanin, D., De Roeck, W., Ho, W. W. & Huveneers, F. A rigorous theory of many-body prethermalization for periodically driven and closed quantum systems. Commun. Math. Phys. 354, 809–827 (2017)
Feiguin, A. et al. Interacting anyons in topological quantum liquids: the golden chain. Phys. Rev. Lett. 98, 160409 (2007)
Lesanovsky, I. & Katsura, H. Interacting Fibonacci anyons in a Rydberg gas. Phys. Rev. A 86, 041601 (2012)
Moessner, R. & Raman, K. S. in Introduction to Frustrated Magnetism (eds Lacroix, C. et al.) 437–479 (Springer, 2011)
Lester, B. J., Luick, N., Kaufman, A. M., Reynolds, C. M. & Regal, C. A. Rapid production of uniformly filled arrays of neutral atoms. Phys. Rev. Lett. 115, 073003 (2015)
Pichler, H., Zhu, G., Seif, A., Zoller, P. & Hafezi, M. Measurement protocol for the entanglement spectrum of cold atoms. Phys. Rev. X 6, 041033 (2016)
Schiulaz, M., Silva, A. & Müller, M. Dynamics in many-body localized quantum systems without disorder. Phys. Rev. B 91, 184202 (2015)
Swingle, B., Bentsen, G., Schleier-Smith, M. & Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 94, 040302(R) (2016)
Chandran, A., Schulz, M. D. & Burnell, F. J. The eigenstate thermalization hypothesis in constrained Hilbert spaces: a case study in non-abelian anyon chains. Phys. Rev. B 94, 235122 (2016)
Huse, D. A. & Fisher, M. E. Commensurate melting, domain walls, and dislocations. Phys. Rev. B 29, 239–270 (1984)
Lechner, W., Hauke, P. & Zoller, P. A quantum annealing architecture with all-to-all connectivity from local interactions. Sci. Adv. 1, e1500838 (2015)
Farhi, E. & Harrow, A. W. Quantum supremacy through the quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1602.07674 (2016)
Singer, K., Stanojevic, J., Weidemüller, M. & Côté, R. Long-range interactions between alkali Rydberg atom pairs correlated to the ns–ns, np–np and nd–nd asymptotes. J. Phys. B 38, S295 (2005)
Hall, J. L. & Zhu, M. in Laser Manipulation of Atoms and Ions (eds Arimondo, E. et al.) 671–702 (Elsevier, 1993)
Fox, R. W., Oates, C. W. & Hollberg, L. W. in Cavity-Enhanced Spectroscopies (eds van Zee, R. D. & Looney, J. P. ) 1–46 (Elsevier, 2003)
Beterov, I. I., Ryabtsev, I. I., Tretyakov, D. B. & Entin, V. M. Quasiclassical calculations of blackbody-radiation-induced depopulation rates and effective lifetimes of Rydberg nS, nP, and nD alkali-metal atoms with n ≤ 80. Phys. Rev. A 79, 052504 (2009)
Glaz, J. & Sison, C. P. Simultaneous confidence intervals for multinomial proportions. J. Stat. Plan. Inference 82, 251–262 (1999)
Johansson, J. R., Nation, P. D. & Nori, F. QuTiP: an open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 183, 1760–1772 (2012)
Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Preprint at https://arxiv.org/abs/1608.00263 (2016)
Baxter, R. J. Exactly Solved Models in Statistical Mechanics (Courier Corporation, 2007)
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192 (2011)
Haegeman, J. Time-dependent variational principle for quantum lattices. Phys. Rev. Lett. 107, 070601 (2011)
Vidal, G. Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004)
Daley, A. J., Kollath, C., Schollwöck, U. & Vidal, G. Time-dependent density-matrix renormalization-group using adaptive effective Hilbert spaces. J. Stat. Mech. 2004, P04005 (2004)
Acknowledgements
We thank E. Demler, A. Chandran, S. Sachdev, A. Vishwanath, P. Zoller, P. Silvi, T. Pohl, M. Knap, M. Fleischhauer, S. Hofferberth and A. Harrow for discussions. This work was supported by NSF, CUA, ARO, and a Vannevar Bush Faculty Fellowship. H.B. acknowledges support by a Rubicon Grant of the Netherlands Organization for Scientific Research (NWO). A.O. acknowledges support by a research fellowship from the German Research Foundation (DFG). S.S. acknowledges funding from the European Union under the Marie Skłodowska Curie Individual Fellowship Programme H2020-MSCA-IF-2014 (project number 658253). H.P. acknowledges support by the National Science Foundation (NSF) through a grant at the Institute for Theoretical Atomic Molecular and Optical Physics (ITAMP) at Harvard University and the Smithsonian Astrophysical Observatory. H.L. acknowledges support by the National Defense Science and Engineering Graduate (NDSEG) Fellowship.
Author information
Authors and Affiliations
Contributions
The experiments and data analysis were carried out by H.B., S.S., A.K., H.L., A.O., A.S.Z. and M.E. Theoretical analysis was performed by H.P. and S.C. All work was supervised by M.G., V.V. and M.D.L. All authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
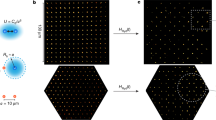
Extended Data Figure 1 Experimental sequence and Rydberg laser set-up.
a, The tweezer array is initially loaded from a magneto-optical trap (MOT). A single-site-resolved fluorescence image taken with an electron-multiplying CCD camera (EMCCD) is used to identify the loaded traps. Using this information, a feedback protocol rearranges the loaded atoms into a preprogrammed configuration, which is verified by the second EMCCD image. After that, all atoms are optically pumped into the |F = 2, mF = −2〉 state, the tweezers are turned off and the Rydberg lasers are pulsed. After the traps are turned back on, a third EMCCD image is taken to detect Rydberg excitations with single-site resolution. b, Schematic representation of the Rydberg laser set-up, which is used to stabilize two external cavity diode lasers to a reference optical cavity with a fast Pound–Drever–Hall lock. TA, tapered amplifier; AOM, acousto-optic modulator; EOM, electo-optic modulator; PD, photodetector; PBS, polarizing beam splitter; QWP, quarter-wave plate.
Extended Data Figure 2 Drop-recapture curve.
Measurements of atom loss probability as a function of trap-off time. For short times of up to 4 μs, the loss is dominated by finite trap lifetime (1% plateau). At larger trap-off times, the atomic motion away from the tweezer introduces additional losses. The solid line is a Monte Carlo simulation for a temperature of 11.8 μK.
Extended Data Figure 3 Typical Rabi oscillation, homogeneity and coherence for non-interacting atoms.
a = 23 μm,  . a, Rabi oscillations. We observe a typical decay time of about 6 μs, which is limited mainly by intensity fluctuations from shot to shot. b, The fitted Rabi frequency for each atom across the array (spatial extent of about 300 μm) is homogeneous to within 3%. c, Measurement of the population in the Rydberg state after a spin echo pulse sequence (inset). We find no decay of coherence over typical measurement periods of several microseconds, thereby ruling out fast sources of decoherence. Error bars in a–c denote 68% confidence intervals.
. a, Rabi oscillations. We observe a typical decay time of about 6 μs, which is limited mainly by intensity fluctuations from shot to shot. b, The fitted Rabi frequency for each atom across the array (spatial extent of about 300 μm) is homogeneous to within 3%. c, Measurement of the population in the Rydberg state after a spin echo pulse sequence (inset). We find no decay of coherence over typical measurement periods of several microseconds, thereby ruling out fast sources of decoherence. Error bars in a–c denote 68% confidence intervals.
Extended Data Figure 4 Spectroscopic measurement of Rydberg interactions.
Spectroscopy on pairs of atoms separated by approximately 5.74 μm is shown. a, For single-atom losses, we observe a single peak at Δ = 0 corresponding to the two-photon coupling from |g, g〉 to |W〉. b, For two-atom losses, we observe an additional peak at Δ = 2π × 12.2 MHz. This corresponds to the four-photon coupling from |g, g〉 to |r, r〉 through the intermediate state |W〉, detuned by Δ. The interaction energy is then V = 2Δ. This four-photon resonance is broadened as a result of random atom positions within the optical tweezers that result in fluctuations in interaction strengths from shot to shot of the experiment. Solid lines are fits with a single Lorentzian (a) and the sum of two Lorentzians (b). Error bars denote 68% confidence intervals.
Extended Data Figure 5 Ground-state preparation probability.
We compare the ground-state preparation probability obtained here (measured, red circles; corrected for detection infidelity, blue circles) with the most complete previous observations of a Z2-symmetry breaking transition in a system of trapped ions (green circles)34. We note that the interaction Hamiltonians for the two systems are not identical, owing to the finite interaction range. In particular, the long-range interactions tend to frustrate adiabatic transitions into Z2-ordered states in ref. 34 and, to lesser extent, in this work. Error bars denote 68% confidence intervals.
Extended Data Figure 6 State preparation with 51-atom clusters.
a, Average position-dependent Rydberg probability in a 51-atom cluster after the adiabatic sweep. The Z2 order is visible at the edges of the system, whereas the presence of domain walls leads to an apparently featureless bulk throughout the centre of the system. Inset, average Rydberg probabilities in a 13-atom chain, in which the Z2 order is visible throughout the system, but the small system size prevents the study of bulk properties. b, Variance of the domain-wall distribution during Z2 state preparation. Points and error bars represent measured values. The solid red line corresponds to a full numerical simulation of the dynamics using a matrix product state ansatz (see text and Fig. 5). Error bars in a and b denote 68% confidence intervals.
Extended Data Figure 7 State reconstruction.
a, Reconstructed parent distribution. b, Comparison of measured domain-wall distribution (red) and predicted observation given the parent distribution in a (blue). c, Difference between the two distributions in b.
Extended Data Figure 8 Comparison to a thermal state.
a, Domain-wall density for thermal states at different entropy per atom s/kB. The lower line corresponds to the actual number of domain walls in a system of the corresponding temperature; the upper line gives the domain-wall density that would be measured at this temperature, given the finite detection fidelity. The horizontal dashed line denotes the experimentally measured domain-wall density, from which we infer a corresponding entropy per atom, and equivalently temperature, in a thermal ensemble. b, Entropy per atoms for a thermal state at given inverse temperature β = 1/(kBT) in a 51-atom array. c, Expected distribution of the number of domain walls for the thermal ensemble at β = 3.44/Δ, with (red) and without (blue) taking into account finite detection fidelity. d, Experimentally measured correlation function g(2)(d) (blue) and correlation function corresponding to a thermal ensemble at β = 3.44/Δ (grey). The inset shows the rectified correlation function on a logarithmic scale, indicating that the measured correlation function decays exponentially, but with a different correlation length from that obtained from a thermal state with the measured number of domain walls.
Extended Data Figure 9 Oscillations in domain-wall density using a variational matrix product state ansatz.
The dynamics of the domain-wall density in the bulk of the array under the constrained Hamiltonian ℋc at Δ = 0 is shown. The blue line shows the evolution of the domain-wall density obtained by integrating the variational equations of motion (equation (5)) with initial conditions θa = π/2, θb = 0, that is, the crystalline initial state. The red line shows the exact dynamics of the domain-wall density at the centre of a system of 25 atoms initially in the crystalline state under the constrained Hamiltonian ℋc.
Extended Data Figure 10 Decay of oscillations after a quench and entropy growth.
a, Dynamics of the domain-wall density under the constrained Hamiltonian ℋc for different initial states. The red line shows the domain-wall density for a system of 25 atoms initially prepared in the electronic ground state. In this case, the domain-wall density relaxes quickly to a steady value corresponding to thermalization. In contrast, the blue line shows the dynamics if the system is initialized in the Z2-ordered state. In this case, the domain-wall density oscillates over several periods and even for very long times does not relax fully to a steady value. b, Same as in a, but taking into account the full 1/R6 interactions. While the dynamics for an initial state |g〉⊗N is very similar to the one obtained in the constrained case, for the crystalline initial state the decay of the oscillations is faster than in the constrained model. c, Growth of entanglement entropy in a bipartite splitting of the 25-atom array for the different cases displayed in a and b. The entropy is defined as the von Neumann entropy of the reduced state of the first 13 atoms of the array. The dashed lines correspond to dynamics under the constrained Hamiltonian, neglecting the 1/R6 tail, whereas the solid lines take the full interactions into account. Red lines correspond to the initial state |g〉⊗N, whereas blue lines correspond to crystalline initial states. In all panels we chose Ω = 2π × 2 MHz and, where applicable, interaction parameters such that the nearest-neighbour interaction evaluates to Vi,i+1 = 2π × 25.6 MHz.
Rights and permissions
About this article
Cite this article
Bernien, H., Schwartz, S., Keesling, A. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017). https://doi.org/10.1038/nature24622
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature24622
This article is cited by
-
Controllable quantum scars induced by spin–orbit couplings in quantum dots
Discover Nano (2024)
-
An optical tweezer array of ultracold polyatomic molecules
Nature (2024)
-
Hidden orders and phase transitions for the fully packed quantum loop model on the triangular lattice
Communications Physics (2024)
-
Quantum many-body simulations on digital quantum computers: State-of-the-art and future challenges
Nature Communications (2024)
-
Programmable Heisenberg interactions between Floquet qubits
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.