Abstract
Precise comparisons of the fundamental properties of matter–antimatter conjugates provide sensitive tests of charge–parity–time (CPT) invariance1, which is an important symmetry that rests on basic assumptions of the standard model of particle physics. Experiments on mesons2, leptons3,4 and baryons5,6 have compared different properties of matter–antimatter conjugates with fractional uncertainties at the parts-per-billion level or better. One specific quantity, however, has so far only been known to a fractional uncertainty at the parts-per-million level7,8: the magnetic moment of the antiproton,  . The extraordinary difficulty in measuring
. The extraordinary difficulty in measuring  with high precision is caused by its intrinsic smallness; for example, it is 660 times smaller than the magnetic moment of the positron3. Here we report a high-precision measurement of
with high precision is caused by its intrinsic smallness; for example, it is 660 times smaller than the magnetic moment of the positron3. Here we report a high-precision measurement of  in units of the nuclear magneton μN with a fractional precision of 1.5 parts per billion (68% confidence level). We use a two-particle spectroscopy method in an advanced cryogenic multi-Penning trap system. Our result
in units of the nuclear magneton μN with a fractional precision of 1.5 parts per billion (68% confidence level). We use a two-particle spectroscopy method in an advanced cryogenic multi-Penning trap system. Our result  = −2.7928473441(42)μN (where the number in parentheses represents the 68% confidence interval on the last digits of the value) improves the precision of the previous best
= −2.7928473441(42)μN (where the number in parentheses represents the 68% confidence interval on the last digits of the value) improves the precision of the previous best  measurement8 by a factor of approximately 350. The measured value is consistent with the proton magnetic moment9, μp = 2.792847350(9)μN, and is in agreement with CPT invariance. Consequently, this measurement constrains the magnitude of certain CPT-violating effects10 to below 1.8 × 10−24 gigaelectronvolts, and a possible splitting of the proton–antiproton magnetic moments by CPT-odd dimension-five interactions to below 6 × 10−12 Bohr magnetons11.
measurement8 by a factor of approximately 350. The measured value is consistent with the proton magnetic moment9, μp = 2.792847350(9)μN, and is in agreement with CPT invariance. Consequently, this measurement constrains the magnitude of certain CPT-violating effects10 to below 1.8 × 10−24 gigaelectronvolts, and a possible splitting of the proton–antiproton magnetic moments by CPT-odd dimension-five interactions to below 6 × 10−12 Bohr magnetons11.
Similar content being viewed by others
Main
Within the physics programme at the Antiproton Decelerator of CERN, the properties of protons and antiprotons5,6, antiprotons and electrons12, and hydrogen13 and antihydrogen14,15 are compared with high precision. Such experiments, including those described here, provide stringent tests of CPT invariance. Our presented antiproton magnetic moment measurement reaches a fractional precision of 1.5 parts per billion (p.p.b.) at 68% confidence level, enabled by our new measurement scheme. Compared to the double-Penning trap technique16 used in the measurement of the proton magnetic moment9, this new method eliminates the need for cyclotron cooling in each measurement cycle and increases the sampling rate.
Our technique uses a hot cyclotron antiproton for measurements of the cyclotron frequency νc, and a cold Larmor antiproton to determine the Larmor frequency νL. By evaluating the ratio of the frequencies measured in the same magnetic field, the magnetic moment of the antiproton (in units of the nuclear magneton, the g-factor)  is obtained. With this new technique we have improved the precision of the previous best antiproton magnetic moment measurement8 by a factor of approximately 350 (Fig. 1a).
is obtained. With this new technique we have improved the precision of the previous best antiproton magnetic moment measurement8 by a factor of approximately 350 (Fig. 1a).
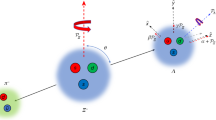
a, Historical overview of antiproton magnetic moment measurements. b, The relevant part of the Penning trap assembly used in this experiment. In the homogeneous magnetic field of the precision trap, the cyclotron frequency of the cyclotron particle is measured and spin transitions of the Larmor particle are induced. In the inhomogeneous magnetic field of the analysis trap, the spin state is first initialized and then analysed after each spin-flip attempt in the precision trap. c, Single spin-flip sequence recorded in the analysis trap. The resolution of the experiment is sufficient to clearly identify the spin eigenstate.
Our experiment17 is located in the Antiproton Decelerator facility, which provides bunches of 30 million antiprotons at a kinetic energy of 5.3 MeV. These particles can be captured and cooled in Penning traps by using degrader foils, a well timed high-voltage pulse and electron cooling17. The core of our experiment is formed by two central devices; a superconducting magnet operating at a magnetic field of B0 = 1.945 T, and an assembly of cylindrical Penning-trap electrodes18 (partly shown in Fig. 1b) that is mounted inside the horizontal bore of the magnet. A part of the electrode assembly forms a spin-state analysis trap with an inhomogeneous magnetic field Bz,AT(z) = B0,AT + B2,ATz2, at B0,AT = 1.23 T and B2,AT = 272(12) kT m−2, and a precision trap with magnetic field B0 that is a factor of approximately 105 more homogeneous. Here, z is the axial coordinate parallel to the magnetic field axis. The distance between the central electrodes of the analysis trap and the precision trap is 48.6 mm. The application of voltage ramps to electrodes that interconnect the traps allows adiabatic shuttling of the particles between the traps. The electrode assembly is placed inside an indium-sealed trap can in which the low pressure enables antiprotons to be stored for years19,29. Each of the traps is equipped with a sensitive tuned circuit for non-destructive image current detection of the particles’ axial oscillation frequencies at νz ≈ 675 kHz (ref. 20). In addition, a detector with tunable resonance frequency (νr ≈ 30.0 ± 0.4 MHz) for detection and resistive cooling of the modified cyclotron frequency at ν+,PT ≈ 29.656 MHz is connected to a segmented electrode of the precision trap. The trapped antiprotons are manipulated by radio-frequency drives applied to the trap electrodes, or spin-flip coils mounted in close proximity to the trap (Fig. 1b). Quadrupolar drives21 at frequencies νrf = ν+ − νz and νrf = νz + ν− allow the measurement of the modified cyclotron frequency ν+,PT as well as the magnetron frequency  by coupling the axial and the radial modes. This enables the cyclotron frequency to be determined using the invariance theorem22
by coupling the axial and the radial modes. This enables the cyclotron frequency to be determined using the invariance theorem22  .
.
The analysis trap with its strong superimposed magnetic bottle B2,AT is essential for non-destructively determining the spin state of the antiproton. The inhomogeneity couples the spin magnetic moment of the particle to its axial oscillation frequency νz,AT. A spin transition induces an axial frequency shift of

where  is the antiproton mass and h is the Planck constant. Consequently, the measurement of the axial frequency νz,AT = νz,0 ± Δνz,SF/2 in the analysis trap allows the non-destructive identification of the spin state of the single trapped antiproton23. The unambiguous detection of these 0.2 parts per million (p.p.m.) changes in νz,AT is the major challenge in measuring the antiproton magnetic moment. Only antiprotons with a cyclotron energy E+/kB below the threshold energy (E+/kB)TH = 0.2 K, where kB is the Boltzmann constant, have axial frequency fluctuations that are sufficiently small to clearly resolve single antiproton spin transitions23,24 (Fig. 1c).
is the antiproton mass and h is the Planck constant. Consequently, the measurement of the axial frequency νz,AT = νz,0 ± Δνz,SF/2 in the analysis trap allows the non-destructive identification of the spin state of the single trapped antiproton23. The unambiguous detection of these 0.2 parts per million (p.p.m.) changes in νz,AT is the major challenge in measuring the antiproton magnetic moment. Only antiprotons with a cyclotron energy E+/kB below the threshold energy (E+/kB)TH = 0.2 K, where kB is the Boltzmann constant, have axial frequency fluctuations that are sufficiently small to clearly resolve single antiproton spin transitions23,24 (Fig. 1c).
To perform experiments, we load the precision trap with a single antiproton and remove contaminants such as electrons and negatively charged ions with kick-out and high power radio-frequency pulses. Subsequently, the magnetron and the modified cyclotron modes of the particle are cooled by sideband drives and direct resistive cooling, respectively. To this end, the resonance frequency of the cyclotron detector is adjusted to ν+,PT, which couples the antiproton to the thermal bath of the detector with Td ≈ 12.8(8) K. The energy E+,L/kB of the modified cyclotron mode after such a thermalization cycle is analysed by measuring the axial frequency in the magnetic bottle B2,AT of the analysis trap8. Once an antiproton with E+,L/kB < 0.05 K has been prepared, we keep it in the analysis trap and detune the resonance frequency of the cyclotron detector by approximately 800 kHz. This is of utmost importance to prevent heating of the modified cyclotron mode of the cold antiproton by interaction with the detector when it later returns to the precision trap. In the next step, another single antiproton is loaded into the precision trap and cleaned from contaminants. Both radial modes are coupled to the axial detector using sideband drives, which cools the radial modes to the sideband limit22  , corresponding to E+,c/kB ≈ 350 K and |E−,c|/kB ≈ 90 mK. This configuration, a cold Larmor particle in the analysis trap and a hot cyclotron particle in the precision trap, constitutes the initial condition of an experiment cycle, which is illustrated in Fig. 2a.
, corresponding to E+,c/kB ≈ 350 K and |E−,c|/kB ≈ 90 mK. This configuration, a cold Larmor particle in the analysis trap and a hot cyclotron particle in the precision trap, constitutes the initial condition of an experiment cycle, which is illustrated in Fig. 2a.
a, Schematic illustration of the two-particle-based g-factor measurement scheme. b, Fluctuations in the cyclotron-mode energy induced by the particle transport. Blue dots, fluctuations between subsequent measurements. Green dots, average root-mean-square fluctuation of bins with 10 mK width. Red line, fit to the green dots. For illustrative purposes, the red line and green dots have been duplicated with negative sign. c, Distribution of measured cyclotron energies E+,L/kB throughout the measurement campaign.
The first step of an actual g-factor measurement cycle k starts with the initialization of the spin state of the Larmor particle in the analysis trap. For this purpose we alternate axial frequency measurements νz,k,j and spin-flip drives and evaluate Δ = νz,k,j+1 − νz,k,j. Here, j is the index of axial frequency measurements of the spin-state identification sequence, which is repeated until |Δ| > ΔTH = 190 mHz is observed. At our root-mean-square-background axial frequency fluctuation of approximately 65 mHz this corresponds to an identification of the spin state with an initialization fidelity23 of >98%. Each of these spin-state initialization attempts requires about 25 min. Afterwards, the cyclotron frequency νc,k,j of the cyclotron particle in the precision trap is measured three times, j ∈ {1, 2, 3}. Subsequently, this particle is shuttled to a park electrode located upstream (Fig. 1b), and the Larmor particle is moved to the precision trap. Here, a radio-frequency field at drive frequency νrf,k and spin-transition Rabi frequency ΩR is applied for 8 s using the spin-flip coil, slightly saturating the Larmor resonance (see Methods). Then the Larmor particle is transported back to the analysis trap and the cyclotron particle to the precision trap, where we perform three additional measurements of the cyclotron frequency νc,k,j, where j ∈ {4, 5, 6}. Finally, the spin state of the Larmor particle in the analysis trap is identified and compared to the previously identified spin state. With a total of 122 s per cyclotron frequency measurement, and about 8 s and 79 s for the spin-flip drive and each individual transport, respectively, a frequency measurement cycle k requires, on average, about 890 s. Together with the initialization of the spin state, an entire experiment cycle takes about 40 min, which is about three times faster than in our 2014 proton magnetic moment measurement9.
By repeating this scheme for different spin-flip drive frequencies νrf,k and normalizing to the measured cyclotron frequencies νc,k, we obtain a g-factor resonance, which is the spin-flip probability as a function of the frequency ratio Γk = νrf,k/νc,k. Here, νc,k is the average of the six recorded cyclotron frequency measurements νc,k,j,PT taken in cycle k. Averaging is used to account for the temporal drift 
 in the field of the superconducting magnet, and to reduce the impact of fluctuations induced by residual magnetic field inhomogeneities.
in the field of the superconducting magnet, and to reduce the impact of fluctuations induced by residual magnetic field inhomogeneities.
To apply this two-particle measurement scheme routinely, it is crucial to keep the energy of the Larmor particle below (E+,L/kB)TH = 0.2 K. Consequently, we minimize parasitic heating of the ν+-mode by disconnecting all radio-frequency supplies whenever possible. Multiple-order filter stages are connected to the high power spin-flip drive lines. After optimization of our particle manipulation radio-frequency networks, we achieved the cycle-to-cycle heating rate of the modified cyclotron mode that is shown in Fig. 2b. As expected for quantum oscillators, the heating rate per cycle scales linearly with the mode energy E+,L (refs 24, 25), but remains below 22 mK per cycle for (E+,L/kB) < (E+,L/kB)TH. The mean heating rate averaged over the entire measurement campaign is less than 17 mK per cycle, which enables us to conduct about 75 measurement cycles before re-cooling of the cyclotron mode is required. Figure 2c displays a histogram of energies E+,L/kB measured during the entire measurement campaign. The total mean energy is E+,L/kB = 120 mK, corresponding to an average axial frequency stability of 65 mHz and a final spin-state identification fidelity between 80% and 90% (see ref. 23 and Methods).
The recorded g-factor resonance is shown in Fig. 3. A maximum-likelihood estimate of an appropriate lineshape function  to the data, in which we convolve the shape function
to the data, in which we convolve the shape function  derived in ref. 26 with measurement and magnetic-field fluctuations, yields an experimental antiproton g-factor of
derived in ref. 26 with measurement and magnetic-field fluctuations, yields an experimental antiproton g-factor of  , the number in brackets representing the 68% confidence interval of our maximum-likelihood estimate. The linewidth of 13.3(1.0) p.p.b. results from drive saturation (12.7(1.0) p.p.b.) and magnetic field fluctuations (3.9(1) p.p.b.).
, the number in brackets representing the 68% confidence interval of our maximum-likelihood estimate. The linewidth of 13.3(1.0) p.p.b. results from drive saturation (12.7(1.0) p.p.b.) and magnetic field fluctuations (3.9(1) p.p.b.).
Spin-flip probability as a function of the irradiated frequency ratio νrf/νc. The red line is the result of a direct likelihood estimation of  and ΩR. The grey area indicates the 68% error band. The black data points are binned averages of the measured PSF(Γ ) displayed with error bars corresponding to 1 s.d.
and ΩR. The grey area indicates the 68% error band. The black data points are binned averages of the measured PSF(Γ ) displayed with error bars corresponding to 1 s.d.
Compared to ref. 8, in this work the frequencies νL and νc are measured in the 85,000 times more homogeneous magnetic field of the precision trap. This greatly reduces the width of the g-factor resonance and thus enables measurements at a higher precision. In comparison to the double Penning-trap method16, which is performed with a single particle, and in which each measurement of νc heats the modified cyclotron energy E+, the two-particle technique does not require cooling of the cyclotron mode in each measurement attempt, which improves the data accumulation rate. However, the two particles are at different mode energies E+,c ≠ E+,L and E−,c ≠E−,L, which induces systematic frequency shifts that need to be corrected.
The dominant systematic uncertainty arises from the uncertainty in the axial temperature during the high-precision frequency measurements. We cannot exclude the possibility that the spin-flip drive in the precision trap increases the axial temperature of the Larmor particle by up to 0.68(7) K while the spin-flip drive is applied, compared to the axial temperature during the sideband drive of the cyclotron particle. As a consequence, the magnetic field experienced by the Larmor particle while the spin-flip drive is applied in the precision trap would be slightly different. Based on measured constraints, we account for this effect by adding a systematic uncertainty of (Δg/g)drive = 0.97 p.p.b. The leading systematic shifts arise from the cyclotron energy difference of the cyclotron and the Larmor particle (E+,c − E+,L)/kB ≈ 356(27) K, which induces g-factor shifts of  p.p.b. and
p.p.b. and  p.p.b., owing to the linear and quadratic residual magnetic field gradients in the precision trap, B1,PT = 71.2(4) mT m−1 and B2,PT = 2.7(3) mT m−1, respectively. All systematic corrections, including contributions of less than 0.1 p.p.b., are summarized in Table 1. For an extended discussion, see Methods.
p.p.b., owing to the linear and quadratic residual magnetic field gradients in the precision trap, B1,PT = 71.2(4) mT m−1 and B2,PT = 2.7(3) mT m−1, respectively. All systematic corrections, including contributions of less than 0.1 p.p.b., are summarized in Table 1. For an extended discussion, see Methods.
The corrections to the measured result add up to −0.4(1.0) p.p.b., which leads to the final result for the antiproton g-factor:  = 2.7928473441(42) (68% confidence level, CL).
= 2.7928473441(42) (68% confidence level, CL).
The result has a fractional precision of  = 1.5 × 10−9. The 95% confidence interval determined from the analysis of our statistical and systematic uncertainties is
= 1.5 × 10−9. The 95% confidence interval determined from the analysis of our statistical and systematic uncertainties is  = 2.6 × 10−9 (95% CL).
= 2.6 × 10−9 (95% CL).
The result is consistent with our previously measured value for the proton magnetic moment μ p = 2.792847350(9)μN and supports CPT invariance in this system. By combining both results, we obtain:

with a (95% CL). The uncertainty of this g-factor difference enables us to set new constraints to CPT-odd b coefficients of the non-minimal standard model extension10, which considers the sensitivity of different experiments with respect to CPT-violating cosmic fields27. With the experiment geometry described in ref. 8 and following the evaluation approach described in ref. 10, we obtain  GeV,
GeV,  GeV−1 and
GeV−1 and  GeV−1 for the proton coefficients, and
GeV−1 for the proton coefficients, and  GeV,
GeV, 
 GeV−1 and
GeV−1 and  GeV−1 for the antiproton coefficients. This improves the previous best limits8 by more than two orders of magnitude. The energy resolution in the b coefficients for protons/antiprotons reaches a comparable magnitude to the limits for muon4 <10−23 GeV to <10−24 GeV and electron/positron <7 × 10−24 GeV to <6 × 10−25 GeV b coefficients28. Furthermore, our measurement enables us to derive new limits on a possible magnetic moment splitting for protons/antiprotons
GeV−1 for the antiproton coefficients. This improves the previous best limits8 by more than two orders of magnitude. The energy resolution in the b coefficients for protons/antiprotons reaches a comparable magnitude to the limits for muon4 <10−23 GeV to <10−24 GeV and electron/positron <7 × 10−24 GeV to <6 × 10−25 GeV b coefficients28. Furthermore, our measurement enables us to derive new limits on a possible magnetic moment splitting for protons/antiprotons  , which has been discussed in a recent analysis of CPT-odd physics based on dimension-five interactions11. Using 95% confidence limit on the g-factor difference of the value presented here, we obtain:
, which has been discussed in a recent analysis of CPT-odd physics based on dimension-five interactions11. Using 95% confidence limit on the g-factor difference of the value presented here, we obtain:

where μB is the Bohr magneton. Our measurement improves on the limit reported in ref. 11 by three orders of magnitude.
Further improvements in the measurement precision of the antiproton magnetic moment using our method are possible. We expect that with a technically revised apparatus, including improved magnetic shielding, an improved resistive cooling system for the cyclotron mode with lower temperature, and a precision trap with a more homogeneous magnetic field, it will be possible to achieve a tenfold improvement in the limit on CPT-odd interactions from proton/antiproton magnetic moment comparisons in the future.
Methods
Uncertainties and confidence levels
We chose to use the 68% CL of the measured data as the quoted experimental uncertainty, to facilitate the comparison to our previous proton magnetic moment measurement9, where we also used 68% CL. Our recent statistical antiproton g-factor measurement is quoted at a relative precision of δg/g = 820 p.p.b. (95% CL), and for the 68% CL we reported δg/g = 520 p.p.b.8. The improvement factor quoted in the text compares the 68% confidence levels of the two measurements. Constraints on standard model extension coefficients are usually quoted with 95% confidence levels10, so we quote both values in the text and use the 95% CL to calculate the limits on CPT-odd interactions.
Systematic effects in the precision trap
Imperfections of the electric quadrupole potential and the residual magnetic field inhomogeneity in the precision trap give rise to small amplitude-dependent frequency shifts of the antiproton’s eigenfrequencies and thereby of the determined g-factor. A comprehensive analysis of amplitude-dependent systematic effects can be found in the references22,30. In our case, the dominant systematic uncertainties scale all with the residual magnetic bottle B2,PT and the axial temperature Tz.
Determination of the magnetic field gradients
The magnetic field around the centre of the precision trap can be approximated as Bz,PT(z) = B0,PT + B1,PTz + B2,PTz2. The magnetic field gradients in the precision trap result mainly from the magnetic ring electrode of the analysis trap. The linear gradient B1,PT can be determined by measuring the cyclotron frequency as a function of the position in the trap. The position of the particle is changed by applying offset voltages dV to one of the correction electrodes, and the particle shift dz/dV is extracted from potential calculations. From several independent measurements carried out during the experiment run, we extracted B1,PT = 71.2(4) mT m−1. The magnetic bottle parameter B2,PT is accessible by measuring the axial frequency νz,i−1 and νz,i before and after a sideband drive. From the distribution of the values δi = {νz,i − νz,i−1}, we obtain the parameter B1,PTT+,PT = B2,PT(ν+,PT/νz,PT)Tz = 976(23) T m−2 K. With Tz = 8.12(61) K from the temperature measurement discussed below, this yields B2,PT = 2.74(22) T m−2. Within error bars, this result is consistent with the B2 parameter extracted from finite-element-method simulations, B2,PT,F = 3.1(4) T m−2, which calculates the magnetic field in the precision trap caused by the magnetic bottle in the analysis trap.
Axial temperature determination
We determine Tz in the precision trap from the lineshape model of the dip signal on the axial detector. The lineshape χD of the dip in the frequency spectrum of the axial detector’s signal is given as:

where χ(ν,νz,Δνz) denotes the dip lineshape function for a constant axial frequency31,32 νz + Δνz. νz denotes the unperturbed axial frequency, Tz is the temperature of the axial detection system, C4 and C6 characterize potential perturbations in the trap and give rise to an amplitude-dependent axial frequency shift22,30 Δνz(Ez,C4,C6). A variation of the voltage ratio that is applied to the correction electrodes Vce and the ring electrode Vring—the tuning ratio TR = Vce/Vring—changes C4 and C6 and thereby the signal-to-noise ratio of the dip. By measuring the change in the signal-to-noise ratio of the dip as a function of the tuning ratio, the axial temperature Tz can be obtained.
This approach reduces the determination of Tz to the knowledge of the trap specific parameter D4 = dC4/dTR, which is robust with respect to typical machining errors and offset voltages, and can be reproduced by calculations within an uncertainty of <10%. The scaling dSNR/dTR (SNR, signal-to-noise ratio) as a function of temperature is shown in Extended Data Fig. 1. We have measured a scaling of dSNR/dTR = 11.5(4) dB per mUnit in the precision trap (mUnit expresses changes in the tuning ratio; a change by 1 mUnit corresponds to a change of 0.001 in the tuning ratio), and extract an axial temperature Tz = 8.12(61) K. The value can be backed up by measurements of the detector signal-to-noise ratio and comparisons to the width σ(νz) of the axial frequency scatter after cyclotron sideband coupling. All obtained values are consistent within errors.
Axial temperature during spin-flip and sideband drives
To compare the axial temperature while the spin-flip and sideband drives are applied, we have compared fast Fourier transform spectra of the axial detection system in the precision trap without any applied external drive signal and while spin-flip and sideband drives were irradiated. The noise level of the detector can be used to calculate the effective temperature of the detection system with the known impedance using the Johnson–Nyquist formula.
Measurements taken while the spin-flip drive was applied show an increase of 0.355(36) dB in the detector’s noise signal. On the basis of the available data, we cannot conclude whether the additional noise was added at the input or the output stage of our cryogenic detector. Thus, we cannot exclude the possibility that the increased signal level affected the particle temperature while the spin-flip drive was applied. Once coupled to the detector via the input stage, the observed increase in the signal level would correspond to an effective temperature increase of ΔTz = 0.68(7) K. As a consequence, the frequencies νL and νc were potentially probed at different axial mean-square amplitudes z2 and consequently at different average magnetic fields.
The most conservative approach to considering the potential change in Tz in the g-factor evaluation assumes that the related temperature increase occurs only when the spin flip drive is applied, while the sideband drive in cyclotron frequency measurements did not affect Tz. From this assumption we extract the dominant systematic uncertainty to the g-factor with (δg/g)drive = 0.97(7) p.p.b. (68% CL). For the 95% CL, the limit on the g-factor shift is calculated on the basis of the noise level shift increased by two s.d., which results in (δg/g)drive = 1.06(8) p.p.b. (95% CL).
Summary of g-factor shifts in the precision trap
In our measurement, we need to consider frequency shifts caused by the octupole perturbation in the trapping potential C4, which affects the cyclotron frequency determined by the invariance theorem, but not the Larmor frequency. The major contribution to the cyclotron frequency shift comes from the axial frequency shift Δνz,C4 = 32 × ΔTR × Tz mHz per mUnit K (0.032 × ΔTR × Tz mHz K−1), where ΔTR = −5 × 10−5 is the tuning ratio offset from the optimum working point. This results in a g-factor shift of (δg/g)Φ = −10(1) parts per trillion (p.p.t.). Higher-order perturbations contribute less than 0.1 p.p.t.
The residual magnetic field inhomogeneity B2,PT changes the magnetic field experienced by the antiprotons depending on their axial amplitudes. The frequency shifts in both frequencies νL and νc are considered in the g-factor lineshape function, and compensate each other in the frequency ratio.
The second effect that needs to be considered is the temperature difference in the cyclotron mode of the two particles (E+,c − E+,L)/kB = 356(27) K. Owing to the magnetic-field gradients in our trap, the cyclotron frequency is effectively measured at a lower magnetic field. This results in shifts of the measured g-factor of (δg/g)B1 = +0.22(2) p.p.b. owing to the change in the axial equilibrium position, and (δg/g)B2 = +0.12(2) p.p.b. owing to the difference in the radial orbit. Further, the cyclotron energy difference causes a relativistic shift of the measured cyclotron frequency, which changes the measured g-factor by (δg/g)rel = +0.033(3) p.p.b. All other amplitude-dependent systematic shifts are negligible.
The image charge induced by the antiproton in the trap electrodes interacts back with the particle and modifies cyclotron frequency determined via the invariance theorem. This causes another systematic deviation of the extracted cyclotron frequency and modifies the measured g-factor by (δg/g)im = +0.04 p.p.b., the error of this value being on the sub-p.p.t. level33,34.
Asymmetric voltage relaxation drifts after the particle transport in the precision trap also affect our measurements. The first measurement of the sideband particle’s axial frequency after the spin-flip drive in the precision trap is effectively measured at a lower trapping potential than the sideband frequencies. The required correction of 0.15(2) p.p.b. was included in the determination of Γk, and is contained in the statistical g-factor evaluation. The voltage drift also means that the axial equilibrium position spin-flip particle drifts in the magnetic field gradient B1,PT during the Larmor drive. This systematically shifts the measured g-factor by (δg/g)V = +0.04(2) p.p.b.
Two-particle comparisons
To ensure that no contaminants were co-trapped with one of the antiprotons, which would induce systematic g-factor shifts, we compared the charge-to-mass ratios of the two particles6 and confirmed that the cyclotron frequencies of the two antiprotons were identical within an uncertainty of 0.28 p.p.b., the value being limited by the statistics of the comparison measurement.
Lineshape of the g-factor resonance
The basic mechanisms giving rise to the lineshape of the Larmor resonance in Penning trap measurements have been discussed26. The residual magnetic bottle in the precision trap and the interaction of the particle’s axial mode with the image-current detector generate a lineshape that is a convolution of the unperturbed Rabi resonance and the Boltzmann distribution of the axial energy. The spin-flip probability in the precision trap can be expressed as:

with  being the angular Rabi frequency of the spin-flip drive, where brf is the magnetic field amplitude of the spin-flip drive in the perpendicular direction to the z-axis. trf = 8 s is the Larmor drive duration,
being the angular Rabi frequency of the spin-flip drive, where brf is the magnetic field amplitude of the spin-flip drive in the perpendicular direction to the z-axis. trf = 8 s is the Larmor drive duration,  is the probed g/2-factor ratio,
is the probed g/2-factor ratio,  is the antiproton g-factor, and
is the antiproton g-factor, and  is the Larmor lineshape function. The latter is obtained from χL(ωL,B0) derived in the analysis in ref. 26 as:
is the Larmor lineshape function. The latter is obtained from χL(ωL,B0) derived in the analysis in ref. 26 as:

with the parameters  ,
,  . ΔωL = 2π0.440(49) s−1 is the Larmor linewidth parameter, and γPT = 1.75 Hz is the damping constant of the axial detector in the precision trap. Δνc is the cyclotron-frequency shift, which is composed of the difference in magnetic field obtained from the cyclotron-frequency measurements to the average magnetic field during the spin-flip drive, and the measurement fluctuations caused by the sideband method. The distribution of Δνc is analysed below. The line-shape function used in the g-factor evaluation is the convolution of the cyclotron-frequency shift distribution ρ(ν) and the lineshape function
. ΔωL = 2π0.440(49) s−1 is the Larmor linewidth parameter, and γPT = 1.75 Hz is the damping constant of the axial detector in the precision trap. Δνc is the cyclotron-frequency shift, which is composed of the difference in magnetic field obtained from the cyclotron-frequency measurements to the average magnetic field during the spin-flip drive, and the measurement fluctuations caused by the sideband method. The distribution of Δνc is analysed below. The line-shape function used in the g-factor evaluation is the convolution of the cyclotron-frequency shift distribution ρ(ν) and the lineshape function  :
:

Magnetic field model
The average cyclotron frequency shift Δνc and the cyclotron frequency shift distribution ρ(ν) in  define the location of the resonance relative to the
define the location of the resonance relative to the  -factor and contribute to the width of the resonance. Therefore, these parameters require a detailed analysis.
-factor and contribute to the width of the resonance. Therefore, these parameters require a detailed analysis.
The measurement of both frequencies νL and νc is carried out in the residual magnetic field inhomogeneity of the precision trap B2,PT. The axial amplitude z2 shifts the measured cyclotron frequency by  155(4) mHz compared to the frequency in the trap centre. We consider this effect by adding Δνc,B2 to Δνc in the lineshape function
155(4) mHz compared to the frequency in the trap centre. We consider this effect by adding Δνc,B2 to Δνc in the lineshape function  . For the Larmor frequency, the detector–particle interaction of the axial motion in the presence of B2,PT is inherently contained in the lineshape function.
. For the Larmor frequency, the detector–particle interaction of the axial motion in the presence of B2,PT is inherently contained in the lineshape function.
Further, the sideband method for the measurement of the modified cyclotron frequency ν+ induces fluctuations on νc because the sideband drive couples the modified cyclotron mode to the axial detector. This results in a measurement of the sideband frequencies νl and νr in thermal equilibrium with T+ = ν+/νz × Tz and a measurement of the axial frequency with a different energy E+ after each drive. Therefore, the measured modified cyclotron frequency is:

where (E+/kB) is a state of the Boltzmann distribution of the cyclotron energy with temperature T+. The dominant resulting fluctuation is:

which has an expectation value of zero. The contribution of this effect to the cyclotron frequency shift distribution ρ(ν) with six averaged cyclotron frequency measurements is approximated by a normal distribution with a standard deviation of σ(νc,SB)/νc = 2.17(6) p.p.b.
External magnetic field fluctuations caused by the imperfectly shielded periodic ramps of the antiproton decelerator magnets and random-walk magnetic-field fluctuations of the superconducting magnet cause a magnetic-field difference from the one obtained by the cyclotron frequency measurements and the real magnetic field during the spin-flip drive. To analyse this effect, we construct a magnetic-field model based on our cyclotron-frequency measurements. The model consists of the sideband fluctuations described above, a magnetic-field white-noise component Δνc,W with standard deviation σW, and a random-walk component Δνc,RW with standard deviation  , with Δt being the time difference between two measurements. Extended Data Fig. 2 shows the measured standard deviations of the cyclotron frequency shifts as function of Δt and the total fluctuations predicted by our magnetic field model. Based on this, we simulate the evolution of the magnetic field for 1,000 measurement cycles, which reproduce the observation shown in Extended Data Fig. 2 within uncertainties. To analyse the impact on the ratios Γk, we determine the standard deviation of the magnetic-field difference that the spin-flip particle experiences during the Larmor drive and the effective magnetic field determined from six averaged cyclotron frequencies. From these Monte-Carlo simulations, we obtain σB,c/B0 = 3.9(1) p.p.b.
, with Δt being the time difference between two measurements. Extended Data Fig. 2 shows the measured standard deviations of the cyclotron frequency shifts as function of Δt and the total fluctuations predicted by our magnetic field model. Based on this, we simulate the evolution of the magnetic field for 1,000 measurement cycles, which reproduce the observation shown in Extended Data Fig. 2 within uncertainties. To analyse the impact on the ratios Γk, we determine the standard deviation of the magnetic-field difference that the spin-flip particle experiences during the Larmor drive and the effective magnetic field determined from six averaged cyclotron frequencies. From these Monte-Carlo simulations, we obtain σB,c/B0 = 3.9(1) p.p.b.
On the basis of the calibration of our external flux gate sensors, we contribute 1.8(4) p.p.b. to stem from imperfectly shielded external magnetic field ramps from the deceleration cycle of the antiproton decelerator.
In total, the magnetic-field fluctuations are dominated by white noise, therefore we approximate the cyclotron-frequency shift distribution ρ(ν) by a normal distribution with standard deviation σc = 3.9(1) p.p.b. In the evaluation, the convolution of the lineshape function with this cyclotron frequency shift distribution is used.
Larmor drive amplitude and saturation
The magnetic field fluctuations σc smear out the Larmor resonance and reduce the maximum spin-flip probability for measurements with unsaturated Larmor drive. Therefore, we deliberately applied a drive amplitude that slightly saturates the Larmor transition to keep the contrast in spin-flip probability, that is, the difference in spin-flip probability for on-resonance to off-resonance data pointes, at a stable maximum. Thereby, we avoided an increase in the measurement statistics required to resolve the g-factor resonance. Our choice of the drive amplitude leads to the saturated resonance shown in Fig. 3. The drive saturation is included in our line-shape model and its effect is considered in the statistical evaluation.
Optimization of the spin-transition identification procedure
The observation of the spin transitions in the precision trap requires the identification of the initial and the final state of each spin-flip attempt in the analysis trap. For this purpose, we drive spin-transitions in the analysis trap and analyse the axial frequency shift caused by each drive to identify the spin state23,25. In contrast to the discussion in ref. 23, we determine the probabilities for spin up  for the initial state and final state of each spin-flip attempt individually based on a recursive formula23, which is reproduced here for convenience:
for the initial state and final state of each spin-flip attempt individually based on a recursive formula23, which is reproduced here for convenience:

where  is a set of measured axial frequency shifts, h0 and h+ are normal distributions with standard deviation
is a set of measured axial frequency shifts, h0 and h+ are normal distributions with standard deviation  describing the axial frequency shift distributions for spin-flip drives, where the spin state remains unchanged and changes to spin up, respectively. PSF,AT ≈ 50% is the spin-flip probability of the spin-flip drive in the analysis trap. The recursion is initialized with maximum ignorance
describing the axial frequency shift distributions for spin-flip drives, where the spin state remains unchanged and changes to spin up, respectively. PSF,AT ≈ 50% is the spin-flip probability of the spin-flip drive in the analysis trap. The recursion is initialized with maximum ignorance  = 0.5. Note that the order of the set
= 0.5. Note that the order of the set  can be reversed to determine the starting state of the sequence.
can be reversed to determine the starting state of the sequence.
The fidelity of the spin-state identification, that is, the mean probability to assign the correct spin state, is limited by the axial frequency fluctuations  65 mHz, which are not negligible compared to the frequency shift induced by a spin transition ΔνSF ≈ 172 mHz. To increase the contrast of the g-factor resonance, we define the initial state of the precision trap spin transition with high fidelity. For this purpose, we deliberately wait until we drive a spin transition, where the spin-flip frequency shift ±ΔνSF and the axial frequency shift add up so that |νz| > 190 mHz. Depending on the cyclotron energy and the associated frequency fluctuation
65 mHz, which are not negligible compared to the frequency shift induced by a spin transition ΔνSF ≈ 172 mHz. To increase the contrast of the g-factor resonance, we define the initial state of the precision trap spin transition with high fidelity. For this purpose, we deliberately wait until we drive a spin transition, where the spin-flip frequency shift ±ΔνSF and the axial frequency shift add up so that |νz| > 190 mHz. Depending on the cyclotron energy and the associated frequency fluctuation  , this defines the initial spin state with a fidelity higher than 98%.
, this defines the initial spin state with a fidelity higher than 98%.
The determination of the final state requires us to determine the spin state at the beginning of the spin-state identification sequence. Owing to the limited fidelity, information on the spin state at the beginning is lost with each spin-flip attempt. The probability to extract the correct spin state from the sequence is defined by the random values of the axial frequency fluctuations and the occurrence of spin-transitions during the first spin-flip drives in the sequence. This reduces the average final spin-state fidelity to a value between about 80% and about 90%, depending on the cyclotron energy of the antiproton.
Maximum likelihood estimation of the g-factor
The data analysed in the statistical evaluation were recorded in the time period from 5 September 2016 to 28 November 2016. In total, 1,008 measurement sequences with Larmor drive at a fixed amplitude, three preceding and three subsequent cyclotron frequency measurements, spin state initialization and final spin state determination have been carried out. Seventy-five of these measurement sequences are disregarded in the evaluation, as they were perturbed by external magnetic field shifts caused by operations on the overhead crane or other magnets in the environment of our apparatus. These measurement cycles have been identified using our magnetic-field monitoring system based on flux-gate, GMR and Hall sensors, which are placed in our experiment zone.
In our analysis procedure, we determine  from a direct maximum likelihood estimation based on the frequency ratios Γk and the preceding and subsequent series of axial frequency shifts
from a direct maximum likelihood estimation based on the frequency ratios Γk and the preceding and subsequent series of axial frequency shifts  and
and  , respectively. These are recorded during the spin-state determination in the analysis trap. The likelihood function can be expressed as:
, respectively. These are recorded during the spin-state determination in the analysis trap. The likelihood function can be expressed as:

Where PSF,PT is the lineshape function including the convolution with the cyclotron frequency shift distribution. 
 is the probability that a spin-flip has occurred in the precision trap based on the axial frequency information in the analysis trap. The spin-up probabilities for the initial and final states are given by
is the probability that a spin-flip has occurred in the precision trap based on the axial frequency information in the analysis trap. The spin-up probabilities for the initial and final states are given by  and
and  , respectively.
, respectively.
The likelihood function in the plane of σc is shown in Extended Data Fig. 3 as function of the Rabi frequency ΩR/(2π) and the relative difference between the antiproton and proton g-factors,  . We determine the confidence intervals for the antiproton g-factor as described35. As a result, we obtain
. We determine the confidence intervals for the antiproton g-factor as described35. As a result, we obtain

ΩR/(2π) = 1.11(14) Hz, which is a relative uncertainty of (δg/g)stat = 1.1 p.p.b. in  with 68% CL, and (δg/g)stat = 2.3 p.p.b. for the 95% CL.
with 68% CL, and (δg/g)stat = 2.3 p.p.b. for the 95% CL.
Fluctuation model dependence
The determination of  and
and  require the spin-flip probability in the analysis trap PSF,AT, the frequency shift caused by a spin transition ΔνSF, and the axial frequency fluctuation without drive
require the spin-flip probability in the analysis trap PSF,AT, the frequency shift caused by a spin transition ΔνSF, and the axial frequency fluctuation without drive  as input parameters23. The first two parameters are extracted from an maximum likelihood estimation using all measured frequency shifts with spin-flip drive in the analysis trap during the measurement sequence. We obtain ΔνSF = 170.4(2.0) mHz, and PSF,AT = 47.29(0.68)%. The variations in the g-factor when changing ΔνSF and PSF,AT within their uncertainties are only 12 p.p.t. and 15 p.p.t., respectively. The major contribution of uncertainty from the spin-state analysis comes from the values of the axial frequency fluctuations
as input parameters23. The first two parameters are extracted from an maximum likelihood estimation using all measured frequency shifts with spin-flip drive in the analysis trap during the measurement sequence. We obtain ΔνSF = 170.4(2.0) mHz, and PSF,AT = 47.29(0.68)%. The variations in the g-factor when changing ΔνSF and PSF,AT within their uncertainties are only 12 p.p.t. and 15 p.p.t., respectively. The major contribution of uncertainty from the spin-state analysis comes from the values of the axial frequency fluctuations  , which need to be determined for each measurement sequence k individually, since the cyclotron energy E+,k changes for each data point owing to the residual heating effect during the particle transport. At a fixed averaging time, the axial frequency fluctuation scales as:
, which need to be determined for each measurement sequence k individually, since the cyclotron energy E+,k changes for each data point owing to the residual heating effect during the particle transport. At a fixed averaging time, the axial frequency fluctuation scales as:

where  summarizes the cyclotron-energy independent axial frequency fluctuations, for example, owing to voltage fluctuations and fast Fourier transform averaging, and
summarizes the cyclotron-energy independent axial frequency fluctuations, for example, owing to voltage fluctuations and fast Fourier transform averaging, and  is the contribution due to cyclotron quantum transitions driven by spurious noise in the analysis trap25,36. We determine E+ for each data point, based on the axial frequency
is the contribution due to cyclotron quantum transitions driven by spurious noise in the analysis trap25,36. We determine E+ for each data point, based on the axial frequency  , the analysis trap ring voltage
, the analysis trap ring voltage  , and on the frequency information from the last cyclotron cooling procedure. Each spin-state determination is accompanied by measurements of frequency fluctuations without spin-flip drive. The combined information of E+,k and the measured frequency fluctuations is used to determine the parameters of
, and on the frequency information from the last cyclotron cooling procedure. Each spin-state determination is accompanied by measurements of frequency fluctuations without spin-flip drive. The combined information of E+,k and the measured frequency fluctuations is used to determine the parameters of  . We account in our model for a slow drift of the voltage reference of our analysis trap ring voltage power supply. This requires us to adjust the values of (E+/kB) at constant ring voltage by 2.7 mK per day. Changing the model parameters and the cyclotron energy E+ within their confidence intervals causes a g-factor variation of 133 p.p.t. and 238 p.p.t. for the 68% CL and the 95% CL, respectively. We add the uncertainties of all three parameters in quadrature to the uncertainty of the determined g-factor.
. We account in our model for a slow drift of the voltage reference of our analysis trap ring voltage power supply. This requires us to adjust the values of (E+/kB) at constant ring voltage by 2.7 mK per day. Changing the model parameters and the cyclotron energy E+ within their confidence intervals causes a g-factor variation of 133 p.p.t. and 238 p.p.t. for the 68% CL and the 95% CL, respectively. We add the uncertainties of all three parameters in quadrature to the uncertainty of the determined g-factor.
Data availability
The datasets generated during and/or analysed during this study are available from the corresponding authors on reasonable request.
Change history
20 October 2017
This Letter should have contained an associated Creative Commons statement in the Author Information section; this has been corrected in the online version.
References
Lüders, G. Proof of the TCP theorem. Ann. Phys. 2, 1–15 (1957)
Schwingenheuer, B. et al. CPT tests in the neutral Kaon system. Phys. Rev. Lett. 74, 4376–4379 (1995)
Van Dyck, R. S., Schwinberg, P. B. & Dehmelt, H. G. New high-precision comparison of electron and positron g-factors. Phys. Rev. Lett. 59, 26–29 (1987)
Bennett, G. W. et al. Final report of the E821 muon anomalous magnetic moment measurement at BNL. Phys. Rev. D 73, 072003 (2006)
Gabrielse, G. et al. Precision mass spectroscopy of the antiproton and proton using simultaneously trapped particles. Phys. Rev. Lett. 82, 3198–3201 (1999)
Ulmer, S. et al. High-precision comparison of the antiproton-to-proton charge-to-mass ratio. Nature 524, 196 (2015)
DiSciacca, J. et al. One-particle measurement of the antiproton magnetic moment. Phys. Rev. Lett. 110, 130801 (2013)
Nagahama, H. et al. Six-fold improved single particle measurement of the magnetic moment of the antiproton. Nat. Commun. 8, 14084 (2017)
Mooser, A. et al. High-precision measurement of the magnetic moment of the proton. Nature 509, 596 (2014)
Ding, Y. & Kostelecky, V. A. Lorentz-violating spinor electrodynamics and Penning traps. Phys. Rev. D 94, 056008 (2016)
Stadnik, Y. V., Roberts, B. M. & Flambaum, V. V. Tests of CPT and Lorentz symmetry from muon anomalous magnetic dipole moment. Phys. Rev. D 90, 045035 (2014)
Hori, M. et al. Buffer-gas cooling of antiprotonic helium to 1.5 to 1.7 K, and antiproton-to-electron mass ratio. Science 354, 610 (2016)
Parthey, C. G. et al. Improved measurement of the hydrogen 1S–2S transition frequency. Phys. Rev. Lett. 107, 203001 (2011)
Kuroda, N. et al. A source of antihydrogen atoms for in flight hyperfine spectroscopy. Nat. Commun. 5, 3089–3092 (2014)
Amole, C. et al. Resonant quantum transitions in trapped antihydrogen atoms. Nature 483, 439–443 (2012)
Häffner, H. et al. Double Penning trap technique for precise g-factor determinations in highly charged ions. Eur. Phys. J. D 22, 163–182 (2003)
Smorra, C. et al. The BASE Experiment. Eur. Phys. J. Spec. Top. 224, 3055 (2015)
Gabrielse, G., Haarsma, L. & Rolston, L. S. Open-endcap Penning traps for high precision experiments. Int. J. Mass Spectrom. 88, 319–332 (1989)
Smorra, C. et al. A reservoir trap for antiprotons. Int. J. Mass Spectrom. 389, 10 (2015)
Nagahama, H. et al. Highly sensitive superconducting circuits at 700 kHz with tunable quality factors for image-current detection of single trapped antiprotons. Rev. Sci. Instrum. 87, 113305 (2016)
Cornell, E. A., Weisskoff, R. M., Boyce, K. R. & Pritchard, D. E. Mode coupling in a Penning trap: Pi- pulses and a classical avoided crossing. Phys. Rev. A 41, 312 (1990)
Brown, L. S. & Gabrielse, G. Geonium theory: physics of a single electron or ion in a Penning trap. Rev. Mod. Phys. 58, 233–311 (1986)
Smorra, C. et al. Observation of individual spin quantum transitions of a single antiproton. Phys. Lett. B 769, 1 (2017)
Ulmer, S. et al. Observation of spin flips with a single trapped proton. Phys. Rev. Lett. 106, 253001 (2011)
Mooser, A. et al. Resolution of single spin flips of a single proton. Phys. Rev. Lett. 110, 140405 (2013)
Brown, L. S. Geonium lineshape. Ann. Phys. 159, 62–98 (1985)
Kostelecký, V. A. & Russell, N. Data table for Lorentz and CPT violation. Rev. Mod. Phys. 83, 11 (2011)
Mittleman, R. K., Ioannou, I. I., Dehmelt, H. G. & Russell, N. Bound on CPT and Lorentz symmetry with a trapped electron. Phys. Rev. Lett. 83, 2116–2119 (1999)
Sellner, S. et al. Improved limit on the directly measured antiproton lifetime. New J. Phys. 19, 083023 (2017)
Ketter, J. et al. First-order perturbative calculation of the frequency-shifts caused by static cylindrically-symmetric electric and magnetic imperfections of a Penning trap. Int. J. Mass Spectrom. 358, 1–16 (2014)
Wineland, D. J. & Dehmelt, H. G. Stored ion calorimeter. J. Appl. Phys. 46, 919 (1975)
Feng, X. et al. Tank circuit model applied to particles in a Penning trap. J. Appl. Phys. 79, 8 (1996)
Porto, J. V. Series solution for the image charge fields in arbitrary cylindrically symmetric Penning traps. Phys. Rev. A 64, 023403 (2001)
Köhler, F. et al. Isotope dependence of the Zeeman effect in lithium-like calcium. Nat. Commun. 7, 10246 (2016)
Patrignani, C. et al. Review of particle physics. Chin. Phys. C 40, 100001 (2016)
Mooser, A. et al. Demonstration of the double Penning Trap technique with a single proton. Phys. Lett. B 723, 78–81 (2013)
Acknowledgements
We acknowledge technical support from the Antiproton Decelerator group, CERN’s cryolab team, and all other CERN groups which provide support to Antiproton Decelerator experiments. We acknowledge financial support from the RIKEN Initiative Research Unit Program, RIKEN President Funding, RIKEN Pioneering Project Funding, RIKEN FPR Funding, the RIKEN JRA Program, the Grant-in-Aid for Specially Promoted Research (no. 24000008) of MEXT, the Max-Planck Society, the EU (ERC Advanced Grant No. 290870-MEFUCO), the Helmholtz-Gemeinschaft, and the CERN Fellowship program.
Author information
Authors and Affiliations
Contributions
The two-particle method was invented by S.U. and implemented by C.S. The measurement routine was commissioned by C.S., S.S. and S.U. The data analysis was performed by C.S. and S.U. M.J.B., J.A.H., T.H., H.N., T.T., S.S., C.S. and S.U. contributed to experiment maintenance during the 2015/2016 antiproton run. The manuscript was written by S.U., C.S., A.M. and K.B. and discussed among and approved by all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks N. Guise, H. Haeffner and K. Jungmann for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 Axial temperature determination.
Scaling of the parameter dSNR/dTR as a function of detector temperature is shown. The blue filled circles represent results based on electrostatic potential calculations, the red line is the measured value, dSNR/dTR = 11.5(4) dB per mUnit, and the green lines indicate standard uncertainty (68% CL).
Extended Data Figure 2 Parameter determination of the magnetic field model.
The standard deviation of the cyclotron frequency difference of two measurements is shown as function of their time difference. The data points shown with 1 s.d. error bars are based on the cyclotron frequency data of the g-factor measurement, and the curve shows the prediction of our magnetic field model based on these data.
Extended Data Figure 3 Result of the statistical g-factor resonance evaluation.
The likelihood function was calculated for σc = 3.9 p.p.b. as function of the Rabi frequency ΩR/(2π) and the antiproton g-factor  . The white cross marks the point with the maximum likelihood. The areas including points ΩR/(2π),
. The white cross marks the point with the maximum likelihood. The areas including points ΩR/(2π),  within the 68.3%, 95.5% and 99.7% confidence levels are shown in light grey, grey and dark grey, respectively, and the black area marks points outside these limits. gp is the proton g-factor from ref. 9: gp/2 = 2.792847350(9).
within the 68.3%, 95.5% and 99.7% confidence levels are shown in light grey, grey and dark grey, respectively, and the black area marks points outside these limits. gp is the proton g-factor from ref. 9: gp/2 = 2.792847350(9).
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) licence. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons licence, users will need to obtain permission from the licence holder to reproduce the material. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smorra, C., Sellner, S., Borchert, M. et al. A parts-per-billion measurement of the antiproton magnetic moment. Nature 550, 371–374 (2017). https://doi.org/10.1038/nature24048
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature24048
This article is cited by
-
A way forward for fundamental physics in space
npj Microgravity (2022)
-
Direct measurement of the 3He+ magnetic moments
Nature (2022)
-
A 16-parts-per-trillion measurement of the antiproton-to-proton charge–mass ratio
Nature (2022)
-
Sympathetic cooling of a trapped proton mediated by an LC circuit
Nature (2021)
-
Fundamental symmetry tested using antihydrogen
Nature (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.