Abstract
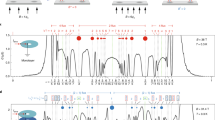
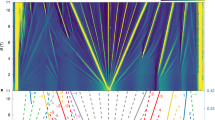
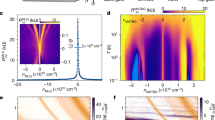
Non-Abelian anyons are a type of quasiparticle with the potential to encode quantum information in topological qubits protected from decoherence1. Experimental systems that are predicted to harbour non-Abelian anyons include p-wave superfluids, superconducting systems with strong spin–orbit coupling, and paired states of interacting composite fermions that emerge at even denominators in the fractional quantum Hall (FQH) regime. Although even-denominator FQH states have been observed in several two-dimensional systems2,3,4, small energy gaps and limited tunability have stymied definitive experimental probes of their non-Abelian nature. Here we report the observation of robust even-denominator FQH phases at half-integer Landau-level filling in van der Waals heterostructures consisting of dual-gated, hexagonal-boron-nitride-encapsulated bilayer graphene. The measured energy gap is three times larger than observed previously3,4. We compare these FQH phases with numerical and theoretical models while simultaneously controlling the carrier density, layer polarization and magnetic field, and find evidence for the paired Pfaffian phase5 that is predicted to host non-Abelian anyons. Electric-field-controlled level crossings between states with different Landau-level indices reveal a cascade of FQH phase transitions, including a continuous phase transition between the even-denominator FQH state and a compressible composite fermion liquid. Our results establish graphene as a pristine and tunable experimental platform for studying the interplay between topology and quantum criticality, and for detecting non-Abelian qubits.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

 state.
state.

Similar content being viewed by others
References
Kitaev, A. Yu. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003)
Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987)
Ki, D.-K., Fal’ko, V. I., Abanin, D. A. & Morpurgo, A. F. Observation of even denominator fractional quantum Hall effect in suspended bilayer graphene. Nano Lett. 14, 2135–2139 (2014)
Falson, J. et al. Even-denominator fractional quantum Hall physics in ZnO. Nat. Phys. 11, 347–351 (2015)
Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991)
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989)
Halperin, B. I., Lee, P. A. & Read, N. Theory of the half-filled Landau level. Phys. Rev. B 47, 7312–7343 (1993)
Willett, R. L., Ruel, R. R., West, K. W. & Pfeiffer, L. N. Experimental demonstration of a Fermi surface at one-half filling of the lowest Landau level. Phys. Rev. Lett. 71, 3846–3849 (1993)
Kang, W., Stormer, H. L., Pfeiffer, L. N., Baldwin, K. W. & West, K. W. How real are composite fermions? Phys. Rev. Lett. 71, 3850–3853 (1993)
Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297 (2000)
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008)
Papic´, Z. & Abanin, D. A. Topological phases in the zeroth Landau level of bilayer graphene. Phys. Rev. Lett. 112, 046602 (2014)
Lee, K. et al. Chemical potential and quantum Hall ferromagnetism in bilayer graphene. Science 345, 58–61 (2014)
Maher, P. et al. Tunable fractional quantum Hall phases in bilayer graphene. Science 345, 61–64 (2014)
Hunt, B. M. et al. Direct measurement of discrete valley and orbital quantum numbers in bilayer graphene. Nat. Commun. (in the press)
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Compressibility of the two-dimensional electron gas: measurements of the zero-field exchange energy and fractional quantum Hall gap. Phys. Rev. B 50, 1760–1778 (1994)
Levin, M., Halperin, B. I. & Rosenow, B. Particle-hole symmetry and the Pfaffian state. Phys. Rev. Lett. 99, 236806 (2007)
Lee, S.-S., Ryu, S., Nayak, C. & Fisher, M. P. A. Particle-hole symmetry and the ν = 5/2 quantum Hall state. Phys. Rev. Lett. 99, 236807 (2007)
Halperin, B. I. Theory of the quantized Hall conductance. Helv. Phys. Acta 56, 75–102 (1983)
Kumar, A., Csáthy, G. A., Manfra, M. J., Pfeiffer, L. N. & West, K. W. Nonconventional odd-denominator fractional quantum Hall states in the second Landau level. Phys. Rev. Lett. 105, 246808 (2010)
Apalkov, V. M. & Chakraborty, T. Stable Pfaffian state in bilayer graphene. Phys. Rev. Lett. 107, 186803 (2011)
Metlitski, M. A., Mross, D. F., Sachdev, S. & Senthil, T. Cooper pairing in non-Fermi liquids. Phys. Rev. B 91, 115111 (2015)
Rezayi, H. R. & Simon, S. H. Breaking of particle-hole symmetry by Landau level mixing in the ν = 5/2 quantized Hall State. Phys. Rev. Lett. 106, 116801 (2011)
Zaletel, M. P., Mong, R. S. K., Pollmann, F. & Rezayi, E. H. Infinite density matrix renormalization group for multicomponent quantum Hall systems. Phys. Rev. B 91, 045115 (2015)
Rezayi, E. H. Landau level mixing and the ground state of the ν = 5/2 quantum Hall effect. Phys. Rev. Lett. 119, 026801 (2017)
Levin, M. & Halperin, B. I. Collective states of non-Abelian quasiparticles in a magnetic field. Phys. Rev. B 79, 205301 (2009)
von Keyserlingk, C. W., Simon, S. H. & Rosenow, B. Enhanced bulk-edge Coulomb coupling in fractional Fabry–Perot interferometers. Phys. Rev. Lett. 115, 126807 (2015)
Wei, D. S. Mach–Zehnder interferometry using spin- and valley-polarized quantum Hall edge states in graphene. Sci. Adv. 3, e1700600 (2017)
Cooper, N. R. & Stern, A. Observable bulk signatures of non-Abelian quantum Hall states. Phys. Rev. Lett. 102, 176807 (2009)
Barkeshli, M., Nayak, C., Papic, Z., Young, A. & Zaletel, M. Fractionalized exciton Fermi surfaces and condensates in two-component quantized Hall states. Preprint at https://arxiv.org/abs/1611.01171 (2016)
Acknowledgements
We acknowledge experimental assistance of B. Odegard and J. Island, and discussions with M. Barkeshli, C. Dean, E.-A. Kim, R. Mong, C. Nayak, Z. Papic, S. Simon and A. Stern. Magnetocapacitance measurements were funded by the NSF under DMR-1636607. A portion of the nanofabrication and the transport measurements were funded by the ARO under proposal 69188PHH. A.F.Y. acknowledges the support of the David and Lucile Packard Foundation. Measurements above 14 T were performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation cooperative agreement number DMR-1157490 and the State of Florida. The numerical simulations were performed on computational resources supported by the Princeton Institute for Computational Science and Engineering (PICSciE). E.M.S. acknowledges the support of the Elings Fellowship. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and JSPS KAKENHI grant number JP15K21722.
Author information
Authors and Affiliations
Contributions
A.A.Z., E.M.S. and H.Z. fabricated devices A, B and C, respectively. T.T. and K.W. synthesized the hexagonal boron nitride crystals. A.F.Y. and C.K. built the measurement electronics. A.A.Z., H.Z., E.M.S. and A.F.Y. acquired and analysed the experimental data. M.P.Z. performed the DMRG calculations. A.A.Z., M.P.Z. and A.F.Y. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks D. Abanin, K. Park, K. Yang and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains methods, figures S1-S17 and tables S1-S3. (PDF 27030 kb)
Rights and permissions
About this article
Cite this article
Zibrov, A., Kometter, C., Zhou, H. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017). https://doi.org/10.1038/nature23893
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature23893
This article is cited by
-
Enhanced superconductivity in spin–orbit proximitized bilayer graphene
Nature (2023)
-
Nanoscale electrostatic control in ultraclean van der Waals heterostructures by local anodic oxidation of graphite gates
Nature Physics (2023)
-
Dirac revivals drive a resonance response in twisted bilayer graphene
Nature Physics (2023)
-
Superconductivity and strong interactions in a tunable moiré quasicrystal
Nature (2023)
-
Correlation-driven electron-hole asymmetry in graphene field effect devices
npj Quantum Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.