Abstract
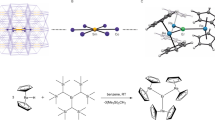
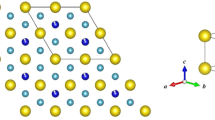
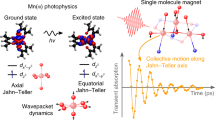
Lanthanides have been investigated extensively for potential applications in quantum information processing and high-density data storage at the molecular and atomic scale. Experimental achievements include reading and manipulating single nuclear spins1,2, exploiting atomic clock transitions for robust qubits3 and, most recently, magnetic data storage in single atoms4,5. Single-molecule magnets exhibit magnetic hysteresis of molecular origin6—a magnetic memory effect and a prerequisite of data storage—and so far lanthanide examples have exhibited this phenomenon at the highest temperatures. However, in the nearly 25 years since the discovery of single-molecule magnets7, hysteresis temperatures have increased from 4 kelvin to only about 14 kelvin8,9,10 using a consistent magnetic field sweep rate of about 20 oersted per second, although higher temperatures have been achieved by using very fast sweep rates11,12 (for example, 30 kelvin with 200 oersted per second)12. Here we report a hexa-tert-butyldysprosocenium complex—[Dy(Cpttt)2][B(C6F5)4], with Cpttt = {C5H2tBu3-1,2,4} and tBu = C(CH3)3—which exhibits magnetic hysteresis at temperatures of up to 60 kelvin at a sweep rate of 22 oersted per second. We observe a clear change in the relaxation dynamics at this temperature, which persists in magnetically diluted samples, suggesting that the origin of the hysteresis is the localized metal–ligand vibrational modes that are unique to dysprosocenium. Ab initio calculations of spin dynamics demonstrate that magnetic relaxation at high temperatures is due to local molecular vibrations. These results indicate that, with judicious molecular design, magnetic data storage in single molecules at temperatures above liquid nitrogen should be possible.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Vincent, R., Klyatskaya, S., Ruben, M., Wernsdorfer, W. & Balestro, F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature 488, 357–360 (2012)
Thiele, S. et al. Electrically driven nuclear spin resonance in single-molecule magnets. Science 344, 1135–1138 (2014)
Shiddiq, M. et al. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 531, 348–351 (2016)
Donati, F. et al. Magnetic remanence in single atoms. Science 352, 318–321 (2016)
Natterer, F. D. et al. Reading and writing single-atom magnets. Nature 543, 226–228 (2017)
Gatteschi, D ., Sessoli, R . & Villain, J. Molecular Nanomagnets (Oxford Univ. Press, 2006)
Sessoli, R., Gatteschi, D., Caneschi, A. & Novak, M. A. Magnetic bistability in a metal–ion cluster. Nature 365, 141–143 (1993)
Rinehart, J. D., Fang, M., Evans, W. J. & Long, J. R. A N23– radical-bridged terbium complex exhibiting magnetic hysteresis at 14 K. J. Am. Chem. Soc. 133, 14236–14239 (2011)
Liu, J. et al. A stable pentagonal bipyramidal Dy(III) single-ion magnet with a record magnetization reversal barrier over 1000 K. J. Am. Chem. Soc. 138, 5441–5450 (2016)
Ding, Y.-S., Chilton, N. F., Winpenny, R. E. P. & Zheng, Y.-Z. On approaching the limit of molecular magnetic anisotropy: a near-perfect pentagonal bipyramidal dysprosium(III) single-molecule magnet. Angew. Chem. Int. Ed. 55, 16071–16074 (2016)
Chen, Y.-C. et al. Symmetry-supported magnetic blocking at 20 K in pentagonal bipyramidal Dy(III) single-ion magnets. J. Am. Chem. Soc. 138, 2829–2837 (2016)
Gupta, S. K., Rajeshkumar, T., Rajaraman, G. & Murugavel, R. An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature. Chem. Sci. 7, 5181–5191 (2016)
Evans, W. J., Perotti, J. M., Brady, J. C. & Ziller, J. W. Tethered olefin studies of alkene versus tetraphenylborate coordination and lanthanide olefin interactions in metallocenes. J. Am. Chem. Soc. 125, 5204–5212 (2003)
Berkefeld, A. et al. Carbon monoxide activation via O-bound CO using decamethylscandocinium–hydridoborate ion pairs. J. Am. Chem. Soc. 134, 10843–10851 (2012)
Kaita, S. et al. Ultimately specific 1,4-cis polymerization of 1,3-butadiene with a novel gadolinium catalyst. Macromol. Rapid Commun. 24, 179–184 (2003)
Demir, S., Zadrozny, J. M., Nippe, M. & Long, J. R. Exchange coupling and magnetic blocking in bipyrimidyl radical-bridged dilanthanide complexes. J. Am. Chem. Soc. 134, 18546–18549 (2012)
Demir, S., Zadrozny, J. M. & Long, J. R. Large spin-relaxation barriers for the low-symmetry organolanthanide complexes [Cp*2Ln(BPh4)] (Cp*=pentamethylcyclopentadienyl; Ln = Tb, Dy). Chem. Eur. J. 20, 9524–9529 (2014)
Meng, Y.-S., Zhang, Y.-Q., Wang, Z.-M., Wang, B.-W. & Gao, S. Weak ligand-field effect from ancillary ligands on enhancing single-ion magnet performance. Chem. Eur. J. 22, 12724–12731 (2016)
Rinehart, J. D. & Long, J. R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2, 2078–2085 (2011)
Chilton, N. F., Collison, D., McInnes, E. J. L., Winpenny, R. E. P. & Soncini, A. An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes. Nat. Commun. 4, 2551 (2013)
Jiang, S.-D., Wang, B.-W., Sun, H.-L., Wang, Z.-M. & Gao, S. An organometallic single-ion magnet. J. Am. Chem. Soc. 133, 4730–4733 (2011)
Jiang, S.-D. et al. Series of lanthanide organometallic single-ion magnets. Inorg. Chem. 51, 3079–3087 (2012)
Jeletic, M. et al. An organometallic sandwich lanthanide single-ion magnet with an unusual multiple relaxation mechanism. J. Am. Chem. Soc. 133, 19286–19289 (2011)
Zhang, P. et al. Equatorially coordinated lanthanide single ion magnets. J. Am. Chem. Soc. 136, 4484–4487 (2014)
Stoyanov, E. S., Stoyanova, I. V. & Reed, C. A. The basicity of unsaturated hydrocarbons as probed by hydrogen-bond-acceptor ability: bifurcated N–H+···π hydrogen bonding. Chem. Eur. J. 14, 7880–7891 (2008)
Guo, F.-S. et al. A dysprosium metallocene single-molecule magnet functioning at the axial limit. Angew. Chem. Int. Ed. http://dx.doi.org/10.1002/anie.201705426 (2017)
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions Ch. 10 (Oxford Univ. Press, 1970)
Lunghi, A., Totti, F., Sessoli, R. & Sanvito, S. The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets. Nat. Commun. 8, 14620 (2017)
Escalera-Moreno, L., Suaud, N., Gaita-Ariño, A. & Coronado, E. Determining key local vibrations in the relaxation of molecular spin qubits and single-molecule magnets. J. Phys. Chem. Lett. 8, 1695–1700 (2017)
Shrivastava, K. N. Theory of spin–lattice relaxation. Phys. Status Solidi B 117, 437–458 (1983)
Gregson, M. et al. A monometallic lanthanide bis(methanediide) single molecule magnet with a large energy barrier and complex spin relaxation behaviour. Chem. Sci. 7, 155–165 (2016)
Acknowledgements
We acknowledge funding from the Engineering and Physical Sciences Research Council (studentship to C.A.P.G. and EP/P002560/1 for F.O. and D.R.), the Ramsay Memorial Fellowships Trust (fellowship to N.F.C.) and the University of Manchester. We thank the University of Manchester for access to the SQUID magnetometer and Computational Shared Facility and R. E. P. Winpenny, E. J. L. McInnes and D. Collison for comments.
Author information
Authors and Affiliations
Contributions
C.A.P.G. and D.P.M. provided the original concept. C.A.P.G. synthesized and characterized the compounds. F.O. carried out the single-crystal X-ray diffraction analysis and supporting synthetic/characterization work. N.F.C. collected and interpreted magnetic data. N.F.C. devised the relaxation dynamics model and wrote computer programs to perform these calculations. D.R. and N.F.C. performed the calculations. D.P.M. and N.F.C. wrote the manuscript with contributions from all authors. D.P.M. and N.F.C. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks R. Sessoli, P. Zhang and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Methods, Discussion, Data and Equations, Supplementary Tables 1-21, Supplementary Figures 1-64. It includes details of synthesis methods, crystallography, NMR, UV-Vis-NIR, vibrational spectra, magnetic data, theoretical analysis and additional references. This file was replaced on 4 September 2017 to correct a file corruption in the equations. (PDF 26419 kb)
Supplementary Data
Crystallographic Information File for 1 and 5-7. (CIF 4576 kb)
Rights and permissions
About this article
Cite this article
Goodwin, C., Ortu, F., Reta, D. et al. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 548, 439–442 (2017). https://doi.org/10.1038/nature23447
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature23447
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.