Abstract
The realization of long-range ferromagnetic order in two-dimensional van der Waals crystals, combined with their rich electronic and optical properties, could lead to new magnetic, magnetoelectric and magneto-optic applications1,2,3,4. In two-dimensional systems, the long-range magnetic order is strongly suppressed by thermal fluctuations, according to the Mermin–Wagner theorem5; however, these thermal fluctuations can be counteracted by magnetic anisotropy. Previous efforts, based on defect and composition engineering6,7,8,9,10, or the proximity effect, introduced magnetic responses only locally or extrinsically. Here we report intrinsic long-range ferromagnetic order in pristine Cr2Ge2Te6 atomic layers, as revealed by scanning magneto-optic Kerr microscopy. In this magnetically soft, two-dimensional van der Waals ferromagnet, we achieve unprecedented control of the transition temperature (between ferromagnetic and paramagnetic states) using very small fields (smaller than 0.3 tesla). This result is in contrast to the insensitivity of the transition temperature to magnetic fields in the three-dimensional regime. We found that the small applied field leads to an effective anisotropy that is much greater than the near-zero magnetocrystalline anisotropy, opening up a large spin-wave excitation gap. We explain the observed phenomenon using renormalized spin-wave theory and conclude that the unusual field dependence of the transition temperature is a hallmark of soft, two-dimensional ferromagnetic van der Waals crystals. Cr2Ge2Te6 is a nearly ideal two-dimensional Heisenberg ferromagnet and so will be useful for studying fundamental spin behaviours, opening the door to exploring new applications such as ultra-compact spintronics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Han, W., Kawakami, R. K., Gmitra, M. & Fabian, J. Graphene spintronics. Nat. Nanotechnol. 9, 794–807 (2014)
Ohno, H. et al. Electric-field control of ferromagnetism. Nature 408, 944–946 (2000)
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013)
Wang, Z., Tang, C., Sachs, R., Barlas, Y. & Shi, J. Proximity-induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys. Rev. Lett. 114, 016603 (2015)
Mermin, N. D . & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966)
Gonzalez-Herrero, H. et al. Atomic-scale control of graphene magnetism by using hydrogen atoms. Science 352, 437–441 (2016)
Nair, R. R. et al. Spin-half paramagnetism in graphene induced by point defects. Nat. Phys. 8, 199–202 (2012)
McCreary, K. M., Swartz, A. G., Han, W., Fabian, J. & Kawakami, R. K. Magnetic moment formation in graphene detected by scattering of pure spin currents. Phys. Rev. Lett. 109, 186604 (2012)
Červenka, J., Katsnelson, M. I. & Flipse, C. F. J. Room-temperature ferromagnetism in graphite driven by two-dimensional networks of point defects. Nat. Phys. 5, 840–844 (2009)
Uchoa, B., Kotov, V. N., Peres, N. M. R. & Neto, A. H. C. Localized magnetic states in graphene. Phys. Rev. Lett. 101, 026805 (2008)
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007)
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014)
Xia, F., Mueller, T., Lin, Y.-M., Valdes-Garcia, A. & Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 4, 839–843 (2009)
Kou, X. et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 137201 (2014)
Jung, J., Pereg-Barnea, T. & MacDonald, A. H. Theory of interedge superexchange in zigzag edge magnetism. Phys. Rev. Lett. 102, 227205 (2009)
Son, Y. W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006)
Dresselhaus, M. S. Intercalation in Layered Materials (Plenum Press, 1986)
Castro, E. V., Peres, N. M. R., Stauber, T. & Silva, N. A. P. Low-density ferromagnetism in biased bilayer graphene. Phys. Rev. Lett. 100, 186803 (2008)
Cao, T., Li, Z. & Louie, S. G. Tunable magnetism and half-metallicity in hole-doped monolayer GaSe. Phys. Rev. Lett. 114, 236602 (2015)
Carteaux, V., Brunet, D., Ouvrard, G. & Andre, G. Crystallographic, magnetic and electronic structures of a new layered ferromagnetic compound Cr2Ge2Te6 . J. Phys. Condens. Matter 7, 69–87 (1995)
Ji, H. et al. A ferromagnetic insulating substrate for the epitaxial growth of topological insulators. J. Appl. Phys. 114, 114907 (2013)
Xia, J., Beyersdorf, P. T., Fejer, M. M. & Kapitulnik, A. Modified Sagnac interferometer for high-sensitivity magneto-optic measurements at cryogenic temperatures. Appl. Phys. Lett. 89, 062508 (2006)
Li, Y. & Baberschke, K. Dimensional crossover in ultrathin Ni(111) films on W(110). Phys. Rev. Lett. 68, 1208–1211 (1992)
Zhang, R. & Willis, R. F. Thickness-dependent Curie temperatures of ultrathin magnetic films: effect of the range of spin-spin interactions. Phys. Rev. Lett. 86, 2665–2668 (2001)
Bloch, M. Magnon renormalization in ferromagnets near the Curie point. Phys. Rev. Lett. 9, 286–287 (1962)
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009)
Hirakawa, K. Kosterlitz-Thouless transition in two-dimensional planar ferromagnet K2CuF4 . J. Appl. Phys. 53, 1893–1898 (1982)
Weber, M. J. Handbook of Optical Materials section 1.6.3 (CRC Press, 2003)
Kaplan, B. & Gehring, G. A. The domain structure in ultrathin magnetic films. J. Magn. Magn. Mater. 128, 111–116 (1993)
Alegria, L. D. et al. Large anomalous Hall effect in ferromagnetic insulator-topological insulator heterostructures. Appl. Phys. Lett. 105, 053512 (2014)
Yu, Y. et al. Gate-tunable phase transitions in thin flakes of 1T-TaS2 . Nat. Nanotechnol. 10, 270–276 (2015)
Kuo, C.-T. et al. Exfoliation and Raman spectroscopic fingerprint of few-layer NiPS3 van der Waals crystals. Sci. Rep. 6, 20904 (2016)
Li, L. et al. Direct observation of the layer-dependent electronic structure in phosphorene. Nat. Nanotechnol. 12, 21–25 (2017)
Cococcioni, M. & de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 71, 035105 (2005)
Xiang, H., Lee, C., Kooc, H.-J., Gong, X. & Whangbo, M.-H. Magnetic properties and energy-mapping analysis. Dalton Trans. 42, 823–853 (2013)
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098–1113 (1940)
Corciovei, A. Spin-wave theory of ferromagnetic thin films. Phys. Rev. 130, 2223–2229 (1963)
Acknowledgements
We thank J.-G. Zheng for help with AFM measurement at UC Irvine, and R. Birgeneau for providing SQUID Magnetometry at UC Berkeley. This work was primarily supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231 (van der Waals heterostructures program, KCWF16). The computational resource was provided by the National Energy Research Scientific Computing Center, which is supported by the US DOE. The bulk crystal growth at Princeton University was supported by the NSF MRSEC programme, grant NSF DMR-1420541, and the measurements at UC Irvine were partially supported by NSF DMR-1350122.
Author information
Authors and Affiliations
Contributions
C.G. and X.Z. conceived and initiated the research and designed the experiments; C.G. performed the Sagnac MOKE measurements with assistance from L.L., A.S. and Y.X., under the guidance of J.X.; Z.L. and T.C. performed theoretical calculations under the guidance of S.G.L.; H.J. synthesized Cr2Ge2Te6 bulk crystals under the guidance of R.J.C.; C.G. prepared and characterized few-layer samples with assistance from Y.X., W.B. and C.W.; and C.G., Z.L., T.C., Y.W., Z.Q.Q., S.G.L., J.X. and X.Z. analysed the data and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 Magnetization characterizations of a bulk Cr2Ge2Te6 crystal.
a, Photo of bulk Cr2Ge2Te6 platelets. b, Magnetization characterization by SQUID at 4 K, showing that Cr2Ge2Te6 has an out-of-plane easy axis. c, Temperature-dependent magnetization characterization under a 0.075-T out-of-plane field, showing  by SQUID, consistent with our Kerr rotation result (
by SQUID, consistent with our Kerr rotation result ( ; in Fig. 2j).
; in Fig. 2j).
Extended Data Figure 2 Characterizations of monolayer and bilayer Cr2Ge2Te6 flakes.
a, A representative optical image of exfoliated bilayer flakes. White arrows point to bilayer flakes. b, An optical image of a specific bilayer flake. c, The environmental AFM image of the bilayer flake in b, showing that a large monolayer flake attaches to the bilayer flake (left). The corresponding AFM height profiles are also shown (right). d, e, Optical (d) and SEM (e) images of thin Cr2Ge2Te6 flakes. The SEM image reveals an additional flake (circled by a white dashed line in e, adjacent to the bilayer strip), which might be a degraded monolayer flake (degradation can be seen from the bubble-like features).
Extended Data Figure 3 Evolution of optical contrast and Raman spectra of bilayer Cr2Ge2Te6 flakes in air.
a, Evolution of optical contrast of a bilayer Cr2Ge2Te6 flake in air. After 90 min of exposure to air (highlighted by the yellow dashed arrow), the optical contrast of the bilayer flake begins to reduce slowly. Error bars are the standard deviation of the optical contrast of the flake of various regions. Insets show optical images of the flake as freshly exfoliated and after overnight exposure in air. b, The evolution of the Raman spectra of another bilayer Cr2Ge2Te6 flake. To avoid laser-triggered degradation, Raman spectra were acquired when the sample was pumped back to vacuum (10−5–10−6 torr). The peaks in the range 100–150 cm−1 are features of bilayer Cr2Ge2Te6 and the peak at 520 cm−1 is from Si.
Extended Data Figure 4 Optical and AFM images of few-layer samples.
a, b, Optical images of bilayer (2L) and three-layer (3L) flakes (a) and a four-layer (4L) flake (b). Numbers in a and b are the optical contrasts in the green channel of the flakes; errors are standard deviations. c, d, AFM images of five-layer (5L; c) and six-layer (6L; d) samples, with the corresponding height profiles.
Extended Data Figure 5 The sample-end experimental set-up of Sagnac MOKE.
a, For the temperature-dependent Kerr image study of 2–5-layer samples under a 0.075-T field, the specimen is loaded on a stage surrounded by a cylindrical permanent magnet and the effective magnetic field perpendicular to the specimen surface is approximately 0.075 T, measured by a Gauss meter. A quarter wave plate is placed on the quartz window. Therefore, the raw signal includes a sample Kerr rotation signal and a background signal, primarily from the Faraday effect of the quartz window. The background signal can readily be obtained by data acquisition on the bare SiO2 substrate. A description of the remaining part of the optical set-up connecting to the polarization maintaining fibre can be found in ref. 22. b, For the study of magnetic field control of transition temperatures, a slightly modified experimental set-up is used. The cylindrical magnet in a provides a magnetic field of only very limited strength. To compare the contrasting fields, we machined the heights of copper stages to accommodate the heights of different disk magnets with contrasting field strengths: 0.065 T and 0.3 T. c, For the hysteresis study, we made a superconducting coil to accommodate the chamber. Owing to the connection between the superconducting coil and the sample stage in our set-up, the superconducting coil cannot be used for temperature-dependent studies. WD, working distance.
Extended Data Figure 6 Temperature evolution of the remanent magnetization of a six-layer Cr2Ge2Te6 flake.
At 4.7 K, after ‘saturating’ the six-layer Cr2Ge2Te6 flake by a 0.6-T magnetic field, the remanent magnetization is obtained by removing the field. Subsequently, under zero-field, the temperature is increased, during which process the Kerr rotation angle is tracked. This measurement shows an intrinsic ferromagnetic phase transition temperature of a six-layer Cr2Ge2Te6 flake close to 10 K. Error bars, standard error of sample signals.
Extended Data Figure 7 Positioning a target flake.
a, The pre-defined patterns of metal pads. b, A scanned map of the reflectance of the specimen. The colour represents the reflected light intensity. The reflectance of metal pads can vary because some pads were peeled off during the exfoliation process. c, A smaller-size scanning. The units of the numbers on the axes in b and c are millimetres.
Extended Data Figure 8 Magnetic interlayer coupling and single-ion anisotropy as a function of on-site Hubbard U in bulk Cr2Ge2Te6.
Blue circles represent single-ion anisotropy, and the magnetic anisotropy is out-of-plane (negative single-ion anisotropy) for U > 0.2 eV. Red squares represent interlayer magnetic coupling, which is ferromagnetic (negative) for U < 1.7 eV. Bulk Cr2Ge2Te6 is a ferromagnet with an out-of-plane easy axis. Therefore, the range 0.2 eV < U < 1.7 eV (shaded area) could qualitatively reproduce the bulk magnetic property. We set U = 0.5 eV in the subsequent calculations, because the experimentally estimated single-ion anisotropy in the bulk is small.
Extended Data Figure 9 Crystal structure consisting of magnetic ion Cr only.
Illustration of in-plane (left) and out-of-plane (right) nearest-neighbour exchange interactions. The ABC-type stacked hexagonal lattice is a reduced illustration of atomic arrangement of Cr in bulk Cr2Ge2Te6 crystals. J1, J2 and J3 (Jz1, Jz2 and Jz3) represent the first, second and third in-plane (out-of-plane) nearest-neighbour spin–spin exchange interactions, respectively. Positive and negative J values represent antiferromagnetic and ferromagnetic exchange interactions. Each Cr site carries a spin S = 3/2 in theoretical simulations. Blue and orange circles represent the Cr ions on A and B sublattices, respectively.
Extended Data Figure 10 Magnetic-field-dependent 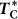 under different values of anisotropy in RSWT.
under different values of anisotropy in RSWT.
Calculated magnetic-field-dependent  of monolayer (1L), bilayer (2L), three-layer (3L) and six-layer (6L) samples using A = 0, A = −0.01 meV and A = −0.001 meV in RSWT, as well as that of the bulk, with A = −0.05 meV. The x axis (B field) is plotted on a logarithmic scale. The efficient field control of transition temperature is clearly seen for small anisotropies in 2D layers.
of monolayer (1L), bilayer (2L), three-layer (3L) and six-layer (6L) samples using A = 0, A = −0.01 meV and A = −0.001 meV in RSWT, as well as that of the bulk, with A = −0.05 meV. The x axis (B field) is plotted on a logarithmic scale. The efficient field control of transition temperature is clearly seen for small anisotropies in 2D layers.
Rights and permissions
About this article
Cite this article
Gong, C., Li, L., Li, Z. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017). https://doi.org/10.1038/nature22060
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature22060
This article is cited by
-
Ferromagnetism on an atom-thick & extended 2D metal-organic coordination network
Nature Communications (2024)
-
Visualizing thickness-dependent magnetic textures in few-layer Cr2Ge2Te6
Communications Materials (2024)
-
Electric control of optically-induced magnetization dynamics in a van der Waals ferromagnetic semiconductor
Nature Communications (2024)
-
Current-induced switching of a van der Waals ferromagnet at room temperature
Nature Communications (2024)
-
Topological Kerr effects in two-dimensional magnets with broken inversion symmetry
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 under different values of anisotropy in RSWT.
under different values of anisotropy in RSWT.