Abstract
The spectrum of the hydrogen atom has played a central part in fundamental physics over the past 200 years. Historical examples of its importance include the wavelength measurements of absorption lines in the solar spectrum by Fraunhofer, the identification of transition lines by Balmer, Lyman and others, the empirical description of allowed wavelengths by Rydberg, the quantum model of Bohr, the capability of quantum electrodynamics to precisely predict transition frequencies, and modern measurements of the 1S–2S transition by Hänsch1 to a precision of a few parts in 1015. Recent technological advances have allowed us to focus on antihydrogen—the antimatter equivalent of hydrogen2,3,4. The Standard Model predicts that there should have been equal amounts of matter and antimatter in the primordial Universe after the Big Bang, but today’s Universe is observed to consist almost entirely of ordinary matter. This motivates the study of antimatter, to see if there is a small asymmetry in the laws of physics that govern the two types of matter. In particular, the CPT (charge conjugation, parity reversal and time reversal) theorem, a cornerstone of the Standard Model, requires that hydrogen and antihydrogen have the same spectrum. Here we report the observation of the 1S–2S transition in magnetically trapped atoms of antihydrogen. We determine that the frequency of the transition, which is driven by two photons from a laser at 243 nanometres, is consistent with that expected for hydrogen in the same environment. This laser excitation of a quantum state of an atom of antimatter represents the most precise measurement performed on an anti-atom. Our result is consistent with CPT invariance at a relative precision of about 2 × 10−10.
Similar content being viewed by others
Main
Experimental comparison of the spectra of hydrogen and antihydrogen was one of the main scientific motivations for the construction of CERN’s Antiproton Decelerator5. Of utility is the 1S–2S transition, owing to the long lifetime (about 1/8 s) of the 2S state and the associated narrow frequency width of the transition (a few hertz at 2.5 × 1015 Hz). A comparison of the hydrogen and antihydrogen frequencies for this transition is therefore potentially an extremely sensitive test of CPT symmetry. However, the technological challenges related to addressing antihydrogen with laser light are extreme, because antihydrogen does not occur naturally and must be synthesized and judiciously protected from interaction with atoms of normal matter—with which it will annihilate. Working with only a few anti-atoms at a time represents a further challenge, when compared to spectroscopy on 1012 atoms of trapped hydrogen6.
Low-energy antihydrogen was first synthesized2 in 2002. This feat was later repeated7,8,9, and in 2010 antihydrogen was successfully trapped3 to facilitate its study. It was subsequently shown that anti-atoms could be held4 for up to 1,000 s, and various measurements have been performed on antihydrogen in the context of tests of CPT symmetry10,11,12 or gravitational studies13.
The central portion of ALPHA-2, our second-generation trapping device for antihydrogen, is shown schematically in Fig. 1. Antihydrogen is synthesized by mixing plasmas of antiprotons from the antiproton decelerator (about 90,000 particles) and positrons from a Surko-type accumulator14,15 (about 1.6 million particles). The techniques used in this experiment yield about 25,000 antihydrogen atoms per mixing attempt.
a, b, The various Penning traps (electrodes illustrated, external 1 T solenoid, not shown) confine and manipulate antiprotons  and positrons (e+) to produce antihydrogen. Cold (<0.5 K) anti-atoms are confined radially by the octupole field and axially by the magnetic well that is formed by the five mirror coils and is plotted in b. Earlier experiments in ALPHA used only the end mirror coils. The flattened profile (uniform to ±10−4 T on axis in the shaded region in b) extends the laser resonance volume and slightly improves the depth of the trap. Laser light enters from the antiproton side (left in a) and is aligned with the fixed cavity axis. The laser beam crosses the trap axis at an angle of 2.3°. The piezoelectric actuator on the output coupler is used to lock the cavity to the laser frequency. The axial scale in a and b is the same; the radial extent of the annihilation detector is larger than illustrated. The brown-shaded electrodes are used to apply blocking potentials during the experimental trials (see text). The two short solenoids are used in capture and preparation of the antiproton and positron plasmas.
and positrons (e+) to produce antihydrogen. Cold (<0.5 K) anti-atoms are confined radially by the octupole field and axially by the magnetic well that is formed by the five mirror coils and is plotted in b. Earlier experiments in ALPHA used only the end mirror coils. The flattened profile (uniform to ±10−4 T on axis in the shaded region in b) extends the laser resonance volume and slightly improves the depth of the trap. Laser light enters from the antiproton side (left in a) and is aligned with the fixed cavity axis. The laser beam crosses the trap axis at an angle of 2.3°. The piezoelectric actuator on the output coupler is used to lock the cavity to the laser frequency. The axial scale in a and b is the same; the radial extent of the annihilation detector is larger than illustrated. The brown-shaded electrodes are used to apply blocking potentials during the experimental trials (see text). The two short solenoids are used in capture and preparation of the antiproton and positron plasmas.
Antihydrogen atoms can be trapped in the multipolar, superconducting trap if they have a kinetic energy of less than about 0.5 K (in temperature units). The trap comprises a set of ‘mirror coils’—short solenoids that generate the axial confinement well—and an octupole for transverse confinement. Trapped antihydrogen is detected by ramping down the currents in the magnetic trap over 1.5 s and detecting the annihilation of the antiproton when the released atoms hit the wall of the trap. We use a three-layer silicon vertex detector16 to image the annihilation vertex position of each detected atom. Event topology is used to distinguish antiproton annihilations from cosmic rays, which continually trigger the detector at an average rate of 10.02 ± 0.04 s−1 (±1s.d.).
The particle manipulations that are necessary to produce trappable antihydrogen atoms have been described elsewhere3,4,17; we note only that recent innovations (Methods) in these techniques have provided a large improvement in the number of trapped anti-atoms available per trial compared to the best previous result12. The antihydrogen production method involves a new technique in which we ‘stack’ anti-atoms resulting from two successive mixing cycles, which originate from independent shots of antiprotons from the antiproton decelerator and accumulations of positrons. We trapped on average about 14 anti-atoms per trial, compared to 1.2 in previous work12.
The trapped anti-atoms are confined to a cylindrical volume of 44-mm diameter and 280-mm length. Windows in the vacuum chamber allow the introduction of 243-nm laser light into this cryogenic, ultrahigh-vacuum volume. Two counter-propagating photons can excite the 1S–2S transition at a frequency that is independent of the Doppler effect to first order. To have enough light intensity in each direction to excite the anti-atoms in a reasonable amount of time, ALPHA-2 includes a Fabry–Pérot power build-up cavity in the ultrahigh-vacuum system (Fig. 1).
The laser system (Fig. 2) features a Toptica TA-FHG pro laser that generates about 150 mW of 243-nm radiation, obtained by twice frequency doubling light from a tunable, 972-nm diode laser. The ultraviolet light is transported to the internal cavity, which is locked to the laser frequency using the Pound–Drever–Hall18 technique. A photodiode monitors the transmitted light to determine the cavity power.
a, Light from the 243-nm laser passes through an electro-optic modulator (EOM) for 6.25-MHz sideband creation, and through a Galilean telescope to mode-match the beam to the build-up cavity inside ALPHA-2. RF is the radio frequency; ‘position stabilization’ refers to the laser beam position. The 243-nm light is generated by frequency quadrupling the output of a 972-nm diode laser. The 972-nm light is shifted to resonance with an ultralow-expansion glass Fabry–Perot cavity (ULE) by an acousto-optic modulator (AOM), which also serves to stabilize the laser frequency. The ULE frequency is referenced to the SI second by an optical frequency comb, stabilized by a GPS-disciplined quartz oscillator. The ULE resonance together with the chosen frequency set point determines the modulation frequency of the AOM. b, The 243-nm laser beam is transported through air to the ALPHA-2 apparatus. Beam position and angle are stabilized through an active feedback system using position-sensitive detectors (PSDs) and piezo-actuated mirrors. The reflection from the input coupler of the build-up cavity is picked up with a photo diode (PD) and mixed with the sideband frequency to provide the Pound–Drever–Hall locking signal for the piezo-mounted output coupler (pzt). The transmitted light is continuously monitored both with a photo diode for power measurement and a charge-coupled device (CCD) camera for mode monitoring. The build-up cavity has a finesse of 230, providing a circulating power of greater than 1 W once losses are taken into account.
The laser is stabilized by locking to an ultra-low expansion (ULE) cavity (Menlo Systems). An acousto-optic modulator (AOM) is used to shift the laser frequency from the antihydrogen transitions to the nearest ULE cavity mode. A femtosecond frequency comb (Menlo Systems), referenced to a Global Positioning System (GPS)-disciplined quartz oscillator (K+K Messtechnik), monitors and corrects the drift of the ULE cavity and relates the laser frequency to atomic time.
The hypothesis to be investigated here is that the 1S–2S transition in antihydrogen is at the same frequency as that of hydrogen. Because our antihydrogen is confined in a magnetic field, we rely on the known physics of the hydrogen atom to calculate the expected frequency and excitation rates of the transition in trapped antihydrogen.
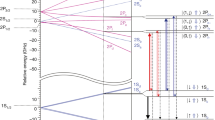
Figure 3 shows hyperfine energy levels of the 1S and 2S states in a magnetic field. The low-field-seeking ground-state sublevels, 1Sc and 1Sd, survive in the magnetic minimum trap and can be excited to the corresponding 2S hyperfine state. The transition frequencies fc–c and fd–d are different primarily because the hyperfine splitting of the 1S and 2S states are different.
Calculated energies (E; for hydrogen) of the hyperfine sublevels of the 1S (bottom) and 2S (top) states as functions of magnetic field strength. To show the structure of the sublevels, the centroid energy difference E1S–2S = 2.4661 × 1015 Hz has been suppressed on the vertical axis. Vertical black arrows indicate the two-photon transitions (which occur with frequency fc–c or fd–d) between the trappable 1S and 2S states.
To simulate the experiment, we propagate the trapped atoms in a model of the magnetic trap. Note that the longitudinal magnetic field profile (Fig. 1b) is ‘flattened’ using the central three mirror coils, to maximize the volume of resonance overlap with the laser. When the atom crosses the laser beam, we calculate the two-photon excitation probability, taking into account the transit time broadening, AC Stark shift and residual Zeeman effect. An atom in the 2S state can be ionized by a single additional photon from the 243-nm laser, or it can decay in one of two ways: (1) a two-photon decay, which returns the atom to the same hyperfine state in which it started; or (2) a one-photon decay via the 2P state, which can mix with the 2S state owing to the motional electric field that the atoms experience in the magnetic trap. The single-photon decays can result in trappable ground-state atoms, or they can induce a spin-flip of the positron, resulting in a non-trappable atom that escapes and annihilates.
In Fig. 4 we show the response of the simulated atoms to a 300-s exposure of both the c–c and d–d transitions, as a function of laser detuning, assuming 1 W of circulating laser power in the build-up cavity. The response is asymmetric, with a tail at higher frequencies due to the residual Zeeman effect. In the inset of Fig. 4, we show the population in the different end states after illuminating each of the transitions for a time t with zero laser detuning. The fraction of anti-atoms removed by the on-resonance laser, compared to off resonance, is estimated to be 0.47 at 300 s.
Results of simulating the illumination of both the c–c and d–d transitions for 300 s with 1 W of circulating laser power are shown. The survival (grey dotted line) or removal (by ionization, purple dashed line; or as a result of spin-flip, green solid line) fraction is plotted as a function of laser detuning, where zero detuning is resonant at the field minimum of the magnetic trap. The vertical red lines indicate the detuning for off-resonance and on-resonance illumination transitions in the experiment. Inset, time evolution of populations in the relevant end states in the case of zero detuning. The populations are normalized to the simulated null experiment, that is, the number of atoms after an equal hold time with no laser interaction.
The experimental protocol is straightforward and has been previously applied to a demonstration of microwave-induced transitions10 in trapped antihydrogen. A single experimental trial involves producing antihydrogen in the atom trap, pulsing axial electric fields to rid the trap of residual charged particles, holding the trapped anti-atoms for 600 s, and then ramping down the trapping fields to release and detect any anti-atoms in the trap.
Three types of trials were conducted. (1) ‘On resonance’: after the antihydrogen has been produced, trapped and allowed to decay to the ground state, the laser is tuned to an expected resonance frequency for one of the 1S–2S transitions, introduced into the trapping volume, and the internal cavity is locked. The d–d transition and then the c–c transition are driven for 300 s each. (2) ‘Off resonance’: same as above, but the laser is detuned 200 kHz (at 243 nm) below the relevant transition. (3) ‘No laser’: no laser radiation is present during the 600-s hold time. During the hold times, electrostatic blocking potentials are placed on electrodes on either side of the magnetic trap (Fig. 1) to ensure that antiprotons resulting from ionization can be lost only radially. Electric fields from these potentials are negligible in the anti-atom trapping volume.
In all aspects other than the laser configuration, the three trial sequences are identical. The on-resonance laser frequencies used correspond to transition frequencies (twice the laser frequency) of:

There is no measurable difference in laser power between these and their respective off-resonance counterparts.
We conducted 11 sets of the three types of trial, varying the order in each set to reduce the chance of systematic effects. Alternating the trials in this fashion ameliorates the effects of a slow decline in the trapping rate over the course of the experiment.
We use a multivariate analysis (MVA; Methods) algorithm10 to distinguish antiproton annihilations from cosmic rays. The MVA used for the 1.5-s shutdown window yields a cosmic ray background rate of 0.042 ± 0.001 s−1, or 0.062 events per trial. This is the only detector background of concern in the experiment. The event reconstruction efficiency (the ratio of the number of events identified as antiproton annihilations to the number of detector triggers) is 0.688 ± 0.002 (Methods).
The results of the experiment, summed over 11 trials, are shown in Table 1. They show a very significant difference between the on- and off-resonance trials (C-test19, one-sided P value of 4.2 × 10−10).
We use the ‘no laser’ trials to ensure that any fluctuation in the trapping rate is small compared to the difference between subsequent on-resonance and off-resonance trials. The comparison of off-resonance and no-laser rates confirms that there are no laser-related side effects (for example, vacuum degradation) that lead to antihydrogen loss from the trap.
The on- and off-resonance trials differ by 92 ± 15 counts. We conclude that the laser light has removed 58% ± 6% of the trapped antihydrogen atoms by resonant 1S–2S excitation followed by either a spin-flip or an ionization event. The removed fraction is in good agreement with the estimates of the hydrogenic rate in Fig. 4, for our build-up cavity power of 1 W.
Our sensitive vertex detector allows us to search for evidence of annihilations during the 2 × 300-s hold periods. Owing to the long exposure times, we use a different MVA protocol (Methods) to distinguish events from background. With this protocol, the cosmic background rate is reduced to 0.0043 ± 0.0003 s−1 at the expense of reducing the reconstruction efficiency to 0.376 ± 0.002. A summary of this analysis for the same 11 sets of trials is shown in Table 2.
Here, the summed off-resonance and no-laser trials are generally consistent with background only, and the difference between the on- and off-resonance totals of 52 ± 10 counts shows clear statistical significance (C-test19, one-sided P value of 2.2 × 10−7). If the relative efficiencies are taken into account, then the number of annihilations (52/0.376 ≈ 138) is in good agreement with the expected number of antihydrogen atoms lost (92/0.688 ≈ 134). These events may be due to either spin-flip of antihydrogen or radial loss of antiprotons resulting from ionization.
If we assume that there are no exotic asymmetries in the spectrum of antihydrogen (compared to that of hydrogen), then the 400-kHz resolution of the current observation, coupled with our model spectrum, can be interpreted as a test of CPT symmetry at a precision of 200 parts per trillion. A stronger statement of CPT invariance must await a detailed measurement of the transition line shape. For smaller detunings, the laser frequency determination, the laser linewidth and the uncertainty in determining the minimum magnetic field in the trap can become important. The long-term average laser frequency at 972 nm is determined to a relative accuracy of 8 × 10−13 using the frequency comb. The laser linewidth contributes at most 10 kHz to the uncertainty at the two-photon frequency, based on the measured excursions of the ULE cavity lock and worst-case fluctuations in the doubling stages. The uncertainty in the minimum magnetic field strength of the trap is determined from the measured electron cyclotron frequency20 of 28.46 ± 0.01 GHz. The field uncertainty leads to a frequency uncertainty of ±6,400 Hz and ±350 Hz for the c–c and d–d transitions, respectively (5.2 × 10−12 and 2.8 × 10−13 relative to the transition frequencies). Therefore, a straightforward extension of the current technique should provide a measurement of the line shape in the near future.
We have performed a laser-spectroscopic measurement on an atom of antimatter. This has been a long-sought achievement in low-energy antimatter physics. It marks a turning point from proof-of-principle experiments to serious metrology and precision CPT comparisons using the optical spectrum of an anti-atom. The greatly improved trapping rate demonstrated here bodes well for many other future antihydrogen experiments, including microwave hyperfine transitions, spectroscopy and laser cooling using Lyman-α light21, and gravitational studies with neutral antimatter. The current result, along with recently determined limits on the antiproton–electron mass ratio22 and antiproton charge-to-mass ratio23, demonstrate that tests of fundamental symmetries with antimatter are maturing rapidly.
We note that the sensitivity of this initial measurement, in terms of the absolute energy scale, is approximately 2 × 10−18 GeV, which is close to the absolute precision of the CPT test in the neutral kaon system of approximately 5 × 10−19 GeV (ref. 24). Our antihydrogen measurements are potentially very sensitive to the internal structure of the antiproton, at a level that is relevant to the current study of the proton charge radius25,26.
Methods
Time evolution of the dataset
The time evolution of the detected events in the three types of trials is depicted in Extended Data Fig. 1.
Sample size
No statistical methods were used to predetermine sample size.
Suppression of cosmic ray background
To determine the signal events in the 1.5-s and 2 × 300-s observation windows, we require two different suppression techniques. We tune the MVA for the two windows in a similar manner to that used in a recent study of the neutrality of antihydrogen12. Annihilation events are distinguished from background events (primarily cosmic rays) by their distinctive topologies. Nine selection variables sensitive to the difference between annihilation and background10 have been used as input to an MVA package27,28.
The signal data and background data used for MVA training, validation and testing is a set of 207,535 annihilation events and 1,596,579 background events. The signal events were produced during antiproton/positron mixing in the apparatus, and contain less than 1% background. Background events were collected during times when there was no antiproton beam.
The 1.5-s observation window. The analysis was tuned to give the same background rate (0.042 s−1) as our ‘online’ analysis. This gave an efficiency of 0.688 ± 0.002 (statistical error only) annihilations per detector trigger.
The 300-s observation windows. The experimental data were accumulated over an irradiation time of 600 s per trial, so a more severe suppression of the background was required. This MVA was optimized to give the best significance for the estimated number of annihilation events expected, suppressing the background rate to 0.0043 ± 0.0003 s−1, or an expected 2.57 ± 0.08 per 600-s trial. The corresponding efficiency is 0.376 ± 0.002 (statistical error only), or 54% of the value for the 1.5-s window.
Improved antihydrogen trapping rate
The improved trapping rate reported here is not the result of any single new technique or manipulation, but is due to very careful preparation and control of the charged species (electrons, antiprotons and positrons) used in the process of synthesizing antihydrogen. At every step in the process, the particle plasmas are optimized for temperature, density, number and radial extent. ALPHA-2 is equipped with extensive diagnostics for lepton and antiproton plasmas. Potential manipulations are carefully controlled to create and maintain temperatures as low as possible for the positrons and antiprotons during mixing. We use such techniques as strong drive rotating wall electric fields29 for controlling plasma sizes, and evaporative cooling30 for obtaining low temperatures. To maintain the lowest possible temperatures during mixing we synthesize antihydrogen by potential manipulation31 rather than the autoresonant drive technique32 used in more recent work. Our position-sensitive vertex detector is essential in analysing and optimizing the mixing process, giving rapid feedback on the antihydrogen production rate, the time evolution of the rate, and the spatial distribution of the produced anti-atoms31.
The stacking technique for accumulating two loads of antihydrogen in the atom trap relies on the same careful preparation techniques in order to load a second batch of charged particles (antiprotons and positrons) into the trapping volume after the trapping fields have been energized and antihydrogen produced. For all previous publications3,4,10,11,12, we prepared the plasmas before ramping up the trapping fields.
In a departure from previous work3, we do not use an extremely rapid (9-ms time constant) shutdown of the trapping fields to release trapped antihydrogen at the end of a trial. Instead, the fields are ramped down over 1.5 s. This leads to a higher overall duty cycle, because the rapid shutdown heats the Penning trap electrodes and quenches the superconducting magnets, which requires a wait of several minutes between trials to re-cool the apparatus to optimal cryogenic temperatures.
Data availability
The datasets generated during and/or analysed during this study are available from the corresponding author on reasonable request.
References
Parthey, C. G. et al. Improved measurement of the hydrogen 1S–2S transition frequency. Phys. Rev. Lett. 107, 203001 (2011)
Amoretti, M. et al. Production and detection of cold antihydrogen atoms. Nature 419, 456–459 (2002)
Andresen, G. B. et al. Trapped antihydrogen. Nature 468, 673–676 (2010)
Andresen, G. B. et al. Confinement of antihydrogen for 1,000 seconds. Nat. Phys. 7, 558–564 (2011)
Maury, S. The antiproton decelerator: AD. Hyperfine Interact. 109, 43–52 (1997)
Cesar, C. L. et al. Two-photon spectroscopy of trapped atomic hydrogen. Phys. Rev. Lett. 77, 255–258 (1996)
Gabrielse, G. et al. Background-free observation of cold antihydrogen with field-ionization analysis of its states. Phys. Rev. Lett. 89, 213401 (2002)
Andresen, G. B. et al. Production of antihydrogen at reduced magnetic field for anti-atom trapping. J. Phys. B 41, 011001 (2008)
Enomoto, Y. et al. Synthesis of cold antihydrogen in a cusp trap. Phys. Rev. Lett. 105, 243401 (2010)
Amole, C. et al. Resonant quantum transitions in trapped antihydrogen atoms. Nature 483, 439–443 (2012)
Amole, C. et al. An experimental limit on the charge of antihydrogen. Nat. Commun. 5, 3955 (2014)
Ahmadi, M. et al. An improved limit on the charge of antihydrogen from stochastic acceleration. Nature 529, 373–376 (2016)
Amole, C. et al. Description and first application of a new technique to measure the gravitational mass of antihydrogen. Nat. Commun. 4, 1785 (2013)
Murphy, T. J. & Surko, C. M. Positron trapping in an electrostatic well by inelastic collisions with nitrogen molecules. Phys. Rev. A 46, 5696–5705 (1992)
Surko, C. M., Greaves, R. G. & Charlton, M. Stored positrons for antihydrogen production. Hyperfine Interact. 109, 181–188 (1997)
Amole, C. et al. Silicon vertex detector upgrade in the ALPHA experiment. Nucl. Instrum. Methods A 732, 134–136 (2013)
Andresen, G. B. et al. Search for trapped antihydrogen. Phys. Lett. B 695, 95–104 (2011)
Drever, R. W. P. et al. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 31, 97–105 (1983)
Przyborowski, J. & Wilenski, H. Homogeneity of results in testing samples from Poisson series: with an application to testing clover seed for dodder. Biometrika 31, 313–323 (1940)
Amole, C. et al. In situ electromagnetic field diagnostics with an electron plasma in a Penning–Malmberg trap. New J. Phys. 16, 013037 (2014)
Donnan, P. H., Fujiwara, M. C. & Robicheaux, F. A proposal for laser cooling antihydrogen atoms. J. Phys. B 46, 025302 (2013)
Hori, M. et al. Buffer-gas cooling of antiprotonic helium to 1.5 to 1.7 K, and antiproton-to-electron mass ratio. Science 354, 610–614 (2016)
Ulmer, S. et al. High-precision comparison of the antiproton-to-proton charge-to-mass ratio. Nature 524, 196–199 (2015)
Beringer, J. et al. Review of particle physics. Phys. Rev. D 86, 010001 (2012)
Pohl, R. et al. The size of the proton. Nature 466, 213–216 (2010)
Pohl, R. et al. Laser spectroscopy of muonic deuterium. Science 353, 669–673 (2016)
Narsky, I. StatPatternRecognition: a C++ package for statistical analysis of high energy physics data. Preprint at http://arxiv.org/abs/physics/0507143 (2005)
Narsky, I. Optimization of signal significance by bagging decision trees. Preprint at http://arxiv.org/abs/physics/0507157 (2005)
Danielson, J. R. & Surko, C. M. Radial compression and torque-balanced steady states of single-component plasmas in Penning–Malmberg traps. Phys. Plasmas 13, 055706 (2006)
Andresen, G. B. et al. Evaporative cooling of antiprotons to cryogenic temperatures. Phys. Rev. Lett. 105, 013003 (2010)
Andresen, G. B. et al. Antihydrogen formation dynamics in a multipolar neutral anti-atom trap. Phys. Lett. B 685, 141–145 (2010)
Andresen, G. B. et al. Autoresonant excitation of antiproton plasmas. Phys. Rev. Lett. 106, 025002 (2011)
Acknowledgements
All authors are members of the ALPHA Collaboration. This work was supported by: the European Research Council through its Advanced Grant programme (J.S.H.); CNPq, FAPERJ, RENAFAE (Brazil); NSERC, NRC/TRIUMF, EHPDS/EHDRS, FQRNT (Canada); FNU (Nice Centre), Carlsberg Foundation (Denmark); JSPS Postdoctoral Fellowships for Research Abroad (Japan); ISF (Israel); STFC, EPSRC, the Royal Society and the Leverhulme Trust (UK); DOE, NSF (USA); and VR (Sweden). We are grateful for the efforts of the CERN Antiproton Decelerator team, without which these experiments could not have taken place. We thank J. Tonoli (CERN) and his staff for extensive, time-critical help with machining work. We thank the staff of the Superconducting Magnet Division at Brookhaven National Laboratory for collaboration and fabrication of the trapping magnets. We thank C. Marshall (TRIUMF) for his work on the ALPHA-2 cryostat. We acknowledge the influence of T. Hänsch on the methodology and the hardware used here. We thank F. Besenbacher (Aarhus) for timely support in procuring the ALPHA-2 external solenoid. We thank A. Charman (UC Berkeley) for discussions.
Author information
Authors and Affiliations
Contributions
This experiment was based on data collected using the ALPHA-2 antihydrogen trapping apparatus, designed and constructed by the ALPHA Collaboration using methods developed by the entire collaboration. The entire collaboration participated in the operation of the apparatus and the data taking activities. The laser and internal cavity system was conceived, implemented, commissioned and operated by W.B., N.M., J.S.H., S.E., C.Ø.R., S.A.J., C.L.C., B.X.R.A. and G.S. F.R., C.Ø.R., J.F. and N.M. developed the simulation program for laser interaction with magnetically trapped atoms. New techniques for obtaining a higher antihydrogen trapping rate and realising antihydrogen stacking were proposed and implemented by C.C., W.B., J.F., T.F., S.A.J., N.M., D.M., C.Ø.R., C.B. and M.S. Detailed analysis of the antiproton annihilation detector data was done by J.T.K.M. and A.O., using methods introduced to ALPHA by S.S. The positron accumulator is the responsibility of C.B., M.C., C.A.I. and D.P.W. The manuscript was written by J.S.H., S.E., S.A.J., N.M., C.Ø.R. and J.T.K.M., with extensive help from C.L.C., M.C.F., J.F., A.O. and M.E.H. The manuscript was then edited and improved by the entire collaboration. Much of the work in this article forms part of the PhD theses of C.Ø.R. and S.A.J.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Time evolution of the dataset.
The cumulative number of observed events for each type of trial (‘On res’, on resonance; ‘Off res’, off resonance) is plotted as a function of chronological trial number to illustrate the time history of the dataset. The errors are due to counting statistics  only.
only.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) licence. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons licence, users will need to obtain permission from the licence holder to reproduce the material. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ahmadi, M., Alves, B., Baker, C. et al. Observation of the 1S–2S transition in trapped antihydrogen. Nature 541, 506–510 (2017). https://doi.org/10.1038/nature21040
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature21040
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.