Abstract
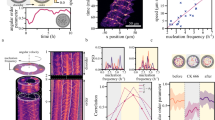
Collective oscillatory behaviour is ubiquitous in nature1, having a vital role in many biological processes from embryogenesis2 and organ development3 to pace-making in neuron networks4. Elucidating the mechanisms that give rise to synchronization is essential to the understanding of biological self-organization. Collective oscillations in biological multicellular systems often arise from long-range coupling mediated by diffusive chemicals2,5,6,7,8,9, by electrochemical mechanisms4,10, or by biomechanical interaction between cells and their physical environment11. In these examples, the phase of some oscillatory intracellular degree of freedom is synchronized. Here, in contrast, we report the discovery of a weak synchronization mechanism that does not require long-range coupling or inherent oscillation of individual cells. We find that millions of motile cells in dense bacterial suspensions can self-organize into highly robust collective oscillatory motion, while individual cells move in an erratic manner, without obvious periodic motion but with frequent, abrupt and random directional changes. So erratic are individual trajectories that uncovering the collective oscillations of our micrometre-sized cells requires individual velocities to be averaged over tens or hundreds of micrometres. On such large scales, the oscillations appear to be in phase and the mean position of cells typically describes a regular elliptic trajectory. We found that the phase of the oscillations is organized into a centimetre-scale travelling wave. We present a model of noisy self-propelled particles with strictly local interactions that accounts faithfully for our observations, suggesting that self-organized collective oscillatory motion results from spontaneous chiral and rotational symmetry breaking. These findings reveal a previously unseen type of long-range order in active matter systems (those in which energy is spent locally to produce non-random motion)12,13. This mechanism of collective oscillation may inspire new strategies to control the self-organization of active matter14,15,16,17,18 and swarming robots19.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Winfree, A. T. The Geometry of Biological Time (Springer, 1980)
Oates, A. C., Morelli, L. G. & Ares, S. Patterning embryos with oscillations: structure, function and dynamics of the vertebrate segmentation clock. Development 139, 625–639 (2012)
He, L., Wang, X., Tang, H. L. & Montell, D. J. Tissue elongation requires oscillating contractions of a basal actomyosin network. Nat. Cell Biol. 12, 1133–1142 (2010)
Herzog, E. D. Neurons and networks in daily rhythms. Nat. Rev. Neurosci. 8, 790–802 (2007)
Muller, P. et al. Differential diffusivity of Nodal and Lefty underlies a reaction-diffusion patterning system. Science 336, 721–724 (2012)
Gregor, T., Fujimoto, K., Masaki, N. & Sawai, S. The onset of collective behavior in social amoebae. Science 328, 1021–1025 (2010)
Danino, T., Mondragon-Palomino, O., Tsimring, L. & Hasty, J. A synchronized quorum of genetic clocks. Nature 463, 326–330 (2010)
Liu, J. et al. Metabolic co-dependence gives rise to collective oscillations within biofilms. Nature 523, 550–554 (2015)
De Monte, S. et al. Dynamical quorum sensing: population density encoded in cellular dynamics. Proc. Natl Acad. Sci. USA 104, 18377–18381 (2007)
Bennett, M. V. L. & Zukin, R. S. Electrical coupling and neuronal synchronization in the mammalian brain. Neuron 41, 495–511 (2004)
Koride, S. et al. Mechanochemical regulation of oscillatory follicle cell dynamics in the developing Drosophila egg chamber. Mol. Biol. Cell 25, 3709–3716 (2014)
Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1, 323–345 (2010)
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013)
Nédélec, F. J., Surrey, T., Maggs, A. C. & Leibler, S. Self-organization of microtubules and motors. Nature 389, 305–308 (1997)
Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A. R. Polar patterns of driven filaments. Nature 467, 73–77 (2010)
Sumino, Y. et al. Large-scale vortex lattice emerging from collectively moving microtubules. Nature 483, 448–452 (2012)
Sanchez, T., Chen, D. T. N., DeCamp, S. J., Heymann, M. & Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 491, 431–434 (2012)
Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95–98 (2013)
Rubenstein, M., Cornejo, A. & Nagpal, R. Programmable self-assembly in a thousand-robot swarm. Science 345, 795–799 (2014)
Kearns, D. B. A field guide to bacterial swarming motility. Nat. Rev. Microbiol. 8, 634–644 (2010)
Darnton, N. C., Turner, L., Rojevsky, S. & Berg, H. C. Dynamics of bacterial swarming. Biophys. J. 98, 2082–2090 (2010)
Wu, Y. & Berg, H. C. A water reservoir maintained by cell growth fuels the spreading of a bacterial swarm. Proc. Natl Acad. Sci. USA 109, 4128–4133 (2012)
Zhang, H. P., Be’er, A., Smith, R. S., Florin, E.-L. & Swinney, H. L. Swarming dynamics in bacterial colonies. Europhys. Lett. 87, 48011 (2009)
Sokolov, A. & Aranson, I. S. Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109, 248109 (2012)
Wensink, H. H. et al. Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. USA 109, 14308–14313 (2012)
López, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clément, E. Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115, 028301 (2015)
Lushi, E., Wioland, H. & Goldstein, R. E. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111, 9733–9738 (2014)
Pushkin, D. O., Shum, H. & Yeomans, J. M. Fluid transport by individual microswimmers. J. Fluid Mech. 726, 5–25 (2013)
Vicsek, T. et al. Novel type phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995)
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, 1984)
Turner, L., Zhang, R., Darnton, N. C. & Berg, H. C. Visualization of flagella during bacterial swarming. J. Bacteriol. 192, 3259–3267 (2010)
Hamhaber, U., Grieshaber, F. A., Nagel, J. H. & Klose, U. Comparison of quantitative shear wave MR-elastography with mechanical compression tests. Magn. Reson. Med. 49, 71–77 (2003)
Zhang, R., Turner, L. & Berg, H. C. The upper surface of an Escherichia coli swarm is stationary. Proc. Natl Acad. Sci. USA 107, 288–290 (2010)
Spikes, J. D. in The Science of Photobiology (ed. Smith, K. C. ) 79–110 (Springer, 1989)
Nagai, K. H., Sumino, Y., Montagne, R., Aranson, I. S. & Chaté, H. Collective motion of self-propelled particles with memory. Phys. Rev. Lett. 114, 168001 (2015)
Chaté, H., Grinstein, G. & Tang, L. H. Long-range correlations in systems with coherent (quasi)periodic oscillations. Phys. Rev. Lett. 74, 912 (1995)
Acknowledgements
We thank Y. Li and W. Zuo from our laboratory for building the microscope stage temperature control system, L. Xu (The Chinese University of Hong Kong) for providing silicone oil, H. C. Berg (Harvard University) for providing the bacterial strains, and J. Näsvall and J. Bergman (Uppsala University) for providing the mRFP plasmid. This work was supported by the Research Grants Council of Hong Kong SAR (RGC numbers 2191031 and 2130439 and CUHK Direct Grant numbers 3132738 and 3132739 to Y.W.), the National Natural Science Foundation of China (NSFC number 21473152, to Y.W.; NSFC number 11635002 to H.C. and X.S.; NSFC numbers 11474210, 11674236 and 91427302 to X.S.), and the Agence Nationale de la Recherche (project Bactterns, to H.C.).
Author information
Authors and Affiliations
Contributions
Y.W. discovered the phenomenon and designed the study. C.C. and S.L. performed experiments. C.C., S.L., Y.W. analysed and interpreted the data, with input from H.C. X.S. and H.C. developed the mathematical model. All authors wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks J. Hasty and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Figure 1 Illustration of a swarming colony.
a, Top view of the colony. E. coli cells were inoculated near the edge of the Petri dish (grey dot) to initiate swarming (Methods). The arrow indicates colony expansion direction before the colony covers the entire Petri dish (9 cm in diameter). At the time of observing collective oscillations in the colony, the colony has covered the entire available surface on the Petri dish and ceased expansion. Cells within 1–2 cm of the inoculum have already become sessile and turned into biofilm, while most cells in the area enclosed by the red line remain motile. Once emerged, collective oscillations span over the entire area enclosed by the red line. In the specified x–y coordinate system, the +x axis represents the colony expansion direction. b, Illustration of the average position of cells undergoing collective oscillation in the form of elliptical trajectories. The blue line indicates the long-axis orientation of the elliptical trajectory (that is, the orientation along which collective osillcations have the greatest amplitude), and θ denotes the angle between the long axis and the x axis in a. The distribution of θ across different colonies is given in Fig. 2a. It tends to be along the y-axis, that is, perpendicular to the colony-expanding direction. Colonies are typically more isotropic along the y-axis. So the result in Fig. 2a suggests that the development of collective oscillations is influenced by the large-scale anisotropy of the system. c, Side view of the colony. The swarming colony establishes a swarm-fluid film of thickness 5–10 μm in which a dense population of cells is dispersed. The top surface of the swarm-fluid film is in contact with air and covered by a monolayer of surfactant (see ref. 33), and the bottom surface is in contact with agar.
Extended Data Figure 2 Collective velocity of cells undergoes periodic oscillation.
a, Components of cells’ collective velocity obtained by PIV analysis (green, x-axis component; black, y-axis component; same data as in Fig. 1c) were fitted by the following sinusoidal functions: vx = 6.25 × sin(0.95t + 0.66) + 0.01 μm s−1, and vy = 11.9 × sin(0.95t − 1.49) μm s−1. b, Temporal correlation of collective velocity. The temporal correlation was first calculated for each grid of the velocity field obtained by PIV analysis and then averaged over the entire velocity field, using the following formula:  , where V(r, t) denotes the velocity vector in a grid located at position r and at time t, and the angular brackets denote averaging first over time t and then over all grids. The grey area represents standard error of the mean when averaging over all grids. c, Temporal evolution of collective velocity. This figure plots collective velocities average over an area of L × L and connects them in the order of time. Three window sizes (L) for averaging are chosen: 19.5 μm (black), 59.8 μm (red), and 100.1 μm (blue). Apparently collective velocity measured over larger areas tends to fluctuate less and better reveals the oscillatory nature of the collective velocity field. This is similar to what can be measured in ‘non-trivial collective behaviour’ in cellular automata and other dynamical systems; see ref. 36 and references therein. d, Speed fluctuation versus averaging window size. The normalized fluctuation (or fluctuation-speed ratio; denoted as F) at each window size L was calculated as
, where V(r, t) denotes the velocity vector in a grid located at position r and at time t, and the angular brackets denote averaging first over time t and then over all grids. The grey area represents standard error of the mean when averaging over all grids. c, Temporal evolution of collective velocity. This figure plots collective velocities average over an area of L × L and connects them in the order of time. Three window sizes (L) for averaging are chosen: 19.5 μm (black), 59.8 μm (red), and 100.1 μm (blue). Apparently collective velocity measured over larger areas tends to fluctuate less and better reveals the oscillatory nature of the collective velocity field. This is similar to what can be measured in ‘non-trivial collective behaviour’ in cellular automata and other dynamical systems; see ref. 36 and references therein. d, Speed fluctuation versus averaging window size. The normalized fluctuation (or fluctuation-speed ratio; denoted as F) at each window size L was calculated as  , where V(t) = (vx, vy) denotes the measured collective velocity vector averaged over an area of L × L at time t,
, where V(t) = (vx, vy) denotes the measured collective velocity vector averaged over an area of L × L at time t,  denotes the sinusoidal fit of collective velocity as shown in a, and the angle brackets denote averaging over time. The speed fluctuation drops down to about 20% of the fitted collective velocity beyond a window size of about 100 μm. Thus, averaging over an area greater than 100 μm × 100 μm is preferred for revealing collective oscillations.
denotes the sinusoidal fit of collective velocity as shown in a, and the angle brackets denote averaging over time. The speed fluctuation drops down to about 20% of the fitted collective velocity beyond a window size of about 100 μm. Thus, averaging over an area greater than 100 μm × 100 μm is preferred for revealing collective oscillations.
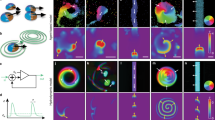
Extended Data Figure 3 Chirality distribution of collective oscillations.
a, The chirality of elliptical collective oscillations in a series of independent experiments shows no obvious bias towards clockwise (CW; 32 out of 71 cases) or counterclockwise (CCW; 36 out of 71). In some rare cases, the collective oscillation shows no apparent chirality (straight, 1 out of 71) or appears irregular (irregular, 2 out of 71). Straight collective oscillation is a special form of elliptical trajectory where the phase difference between the two orthogonal oscillation components is zero (or π). b, An example of irregular collective oscillation. The red line indicates the trajectory of a silicone oil tracer. Such trajectories resemble the one shown in Fig. 3a and may indicate that the collective oscillation had not stabilized yet.
Extended Data Figure 4 Chirality analysis of single-cell trajectories.
Representative single-cell trajectories near the bottom (in contact with agar; a) and near the top (in contact with air; b) of the swarm fluid film (Extended Data Fig. 1) in a colony undergoing counterclockwise collective oscillation are plotted in different colours. Each trajectory lasted 1–2 s before the cell moved out of focus. The coloured dot near a trajectory of the same colour indicates the ending point of the trajectory. e and f show the chirality distribution of single-cell trajectories in the colony (e, near the bottom of the colony; f, near the top of the colony), with ‘straight’ representing those trajectories with a fitted radius of curvature >1 mm. Single-cell trajectories and their chirality distribution are similarly plotted for a colony undergoing clockwise collective oscillation (c and g, near the bottom of the colony; d and h, near the top of the colony). Based on these results, the chirality of single-cell trajectories is conspicuously biased towards the chirality of collective oscillation of the colony, indicating that the chirality bias shares the same origin as the collective oscillation. One observation to note is that the chirality of single-cell trajectories near the top of colonies is less biased than that near the bottom of colonies (f and h).
Extended Data Figure 5 Statistics of abrupt turns made by cells undergoing collective oscillation.
An abrupt turn made by a cell is defined as the change of moving direction by 135° or more. During one period of collective oscillation (about 4–12 s), a cell may make several abrupt turns. a, The turning ratio, that is, the number of cells that made at least one abrupt turn during a 0.5-s interval divided by the total number of cells tracked during this 0.5-s interval, is plotted for 12 fluorescent cells undergoing collective oscillation that were tracked within a 20 s time-lapse video (see Methods for single-cell tracking). The result suggests that the abrupt turns occur at a constant rate over time. b, Distribution of the time interval between two consecutive abrupt turns made by the same cell. The distribution can be approximated as an exponential distribution in the following form: (59/T) × exp(−t/T), with the best fit of T (that is, the expected mean of time interval) being (2.3 ± 0.3) s, which agrees well with the average interval measured experimentally (2.1 ± 1.9 s, mean ± s.d., n = 118). This result suggests that cells do not engage in oscillatory motion at the single-cell level, that is, individual cells do not behave as oscillators.
Extended Data Figure 6 Temporal evolution of collective velocity during the emergence of collective oscillation and during chirality switching.
a and b plot the x- and y-axis components of the collective velocity associated with Fig. 3b obtained by PIV analysis, respectively. Prior to the onset of collective oscillation (before about 75 s in the plots), the velocity of single cells has already recovered to normal magnitude, although the collective velocity is small. c, Chirality switching from clockwise to counterclockwise during the competition of collective oscillations with opposite chirality. The average position of cells during the chirality switching process is plotted (colour scale shows time). The average position was reconstructed by integrating the collective velocity obtained by PIV analysis. d, Collective velocity in c fitted by smoothing spline method based on PIV data (red, x-axis component; black, y-axis component) (see Methods).
Extended Data Figure 7 Deactivation of cell motility during collective oscillation.
a, Response of single-cell motility to excitation of the photo-sensitizing dye FM4-64 in growth medium. Cell speed is plotted against time. Excitation light (560/40 nm) was turned on starting from the time indicated by the red line. Cell speed almost vanished within about 7 s upon illumination. Error bars represent standard deviation, n = 10. In this experiment, E. coli cells were collected from swarming colonies, transferred to a freshly poured swarm agar plate supplemented with FM4-64 (Methods), and covered by a coverslip. A thin layer of cell suspension formed in between the agar surface and the coverslip, in which cells remained motile. The motion of cells was imaged using a 100 × oil immersion objective (Nikon Plan Apochromat Lambda DM, numerical aperture 1.45, working distance 0.13 mm) and recorded by a sCMOS camera (Andor Neo 5.5) at 30 fps operating in global-shutter mode. b, Collective oscillation in response to deactivation of cell motility by exciting FM4-64 in growth medium (Methods). The collective velocity of cells obtained by PIV analysis (y-axis component, red line) and the velocity of a silicone-oil tracer (y-axis component, black line) in the light-illuminated area (about 160 μm in diameter) of a colony are plotted against time (the x–y coordinate system is the same as in Extended Data Fig. 1). Excitation light was turned on starting at time = 7.6 s (indicated by the red arrow). The time taken for the collective velocity to almost vanish in the light-illuminated area can be up to a few minutes, because cells frequently move in and out of the light-illuminated area. Nevertheless, oscillations do not vanish completely even in the centre of the illuminated area. In fact, silicone-oil droplets near the top surface still oscillate but with a very small amplitude. Both these droplets and the immotile cells are tracers of a residual oscillatory flow, strongly damped in the undriven illuminated area, reflecting the incompressibility of fluids (see Extended Data Fig. 8). c and d plot the period of collective oscillation and the amplitude of x-axis component of collective velocity against distance to the boundary of the light-illuminated area, with d = 0 representing the boundary position and the red lines being best fits of data. Collective oscillation of cells persisted within about 50 μm inside the boundary of light-illuminated area because some light-immobilized cells were mixed with motile cells near the boundary (Supplementary Video 4). Error bars represent standard deviation (n = 3).
Extended Data Figure 8 Deactivation of cell motility in mathematical model.
In the simulation, we created a deactivation zone in the centre of the simulation domain (as indicated by the region inside the black circle in a) by setting the self-propelled velocity v0 = 0 and the entraining force f = 0 inside a circular region of area 1,000 μm2. The angular and frequency couplings kθ and kω are also set to zero in the deactivation zone. All the parameters are the same as in Fig. 4c–e outside the deactivation zone. a, Snapshot of Supplementary Video 8 showing the deactivation zone. b, The time series of Vy components in the middle of the deactivation zone and in an active zone that is 750 μm away from the deactivation zone. The deactivation of cell activity is implemented at time = 0 s. The average of Vy is over an area of 300 μm2. c, The oscillation period as a function of distance from the centre of deactivation region. The period doesn’t change across the system. d, The amplitude of oscillation of Vy as a function of distance from the centre of deactivation region. It is clear that some residual oscillation in the deactivation zone persists in agreement with experiments (see Extended Data Fig. 7b).
Extended Data Figure 9 Clustering pattern during biofilm formation in swarming colonies.
a, Phase-contrast image. b, Fluorescent image. Scale bars, 100 μm. The images were taken at about 2 cm from the inoculum after 18 h growth (Methods). The clusters (dark spots in a, or bright spots in b) were sessile biofilms, while cells remained motile elsewhere. The colony consisted of mostly fluorescent cells. Fluorescence intensity at biofilm clusters appeared brighter than elsewhere because of the higher cell density in these clusters. The typical diameter of biofilm clusters was about 20 μm, and the typical distance between these clusters was about 50 μm (close to the typical length of long axis of elliptical collective trajectories during collective oscillations; see Fig. 1). This spatial patterning of biofilm clusters may be relevant to the transport of sessile cells via fluid flows associated with collective oscillations.
Extended Data Figure 10 Cell density dependence of collective oscillation.
We deposited drops of bacterial suspension on agar surface at controlled cell densities, and followed the emergence of collective oscillations after the liquid drop flattened to be a disk-shaped liquid film. a, Temporal correlation function of collective velocity at three different cell densities: 1.5 × 1010 cells ml−1 (magenta), 3.8 × 1010 cells ml−1 (green), and 6.0 × 1010 cells ml−1 (black). The temporal correlation function of collective velocity was calculated as  , where V(t) denotes the collective velocity at time t, and the angle brackets denote averaging over time. b, Power spectrum P(f) of the temporal correlation function of collective velocity at different cell densities. c, The maxima of the power spectrum curves in b plotted against cell density ρ. As shown in b and c, the power spectrum of the correlation function is featureless and there is no large-scale oscillation when the cell density is below about 2 × 1010 cells ml−1. A small but important peak arises near 0.2 Hz in the power spectrum when cell density is above 2 × 1010 cells ml−1, indicating the emergence of irregular and elusive collective oscillations. At cell densities higher than about 5 × 1010 ml−1 (approximately 20% volume fraction), regular periodic collective oscillation develops robustly, as manifested by the sharp peaks near 0.2 Hz in the power spectrum. These results demonstrate that cell density is the triggering factor of large-scale collective oscillation.
, where V(t) denotes the collective velocity at time t, and the angle brackets denote averaging over time. b, Power spectrum P(f) of the temporal correlation function of collective velocity at different cell densities. c, The maxima of the power spectrum curves in b plotted against cell density ρ. As shown in b and c, the power spectrum of the correlation function is featureless and there is no large-scale oscillation when the cell density is below about 2 × 1010 cells ml−1. A small but important peak arises near 0.2 Hz in the power spectrum when cell density is above 2 × 1010 cells ml−1, indicating the emergence of irregular and elusive collective oscillations. At cell densities higher than about 5 × 1010 ml−1 (approximately 20% volume fraction), regular periodic collective oscillation develops robustly, as manifested by the sharp peaks near 0.2 Hz in the power spectrum. These results demonstrate that cell density is the triggering factor of large-scale collective oscillation.
Supplementary information
Turbulent collective motion of E. coli cells in a colony prior to the onset of collection oscillation
This phase-contrast video is played in real time at 10 frames per second, with the real elapsed time indicated in the video control bar. Cells display a disordered state with collective motion at small spatial scales (~10 µm) taking the form of transient jets and vortices. (AVI 8768 kb)
Collective oscillation of E. coli cells in a colony
This phase-contrast video is played in real time at 15 frames per second, with the real elapsed time indicated in the video control bar. Two silicone oil tracers appeared as dark spots near the center of field of view, and they underwent synchronized oscillation in elliptical trajectories. This video is associated with Fig. 1 (panel a-c) and Extended Data Figure 2. The last frame of this video is associated with Fig. 1a. (AVI 8383 kb)
Single-cell trajectories during collective oscillation
This video (associated with Fig. 2e) is played in real time at 15 frames per second, with the real elapsed time indicated in the video control bar. The cells seen here were fluorescent (strain HCB1737 mRFP), and they were mixed with non-fluorescent cells at a ratio of 1:99. Individual cells moved in an erratic manner while the entire population was undergoing collective oscillation. Red trace indicates the trajectory of a cluster consisting of immotile cells that can serve as a flow tracer. The cluster is in fact larger than shown in the video because some cells in it are non-fluorescent. (AVI 6416 kb)
Collective oscillation near the boundary of an area of cells immobilized by the photosensitizing effect of FM4-64
This phase-contrast video (associated with Extended Data Figure 7c,d) is played in real time at 15 frames per second, with the real elapsed time indicated in the video control bar. The area of light illumination to excite FM 4-64 is of diameter ~160 μm, and the boundary of this area is near the bottom of the field of view. The collective oscillation of cells was almost unaffected by the light-immobilized area beyond a distance of ~50 μm away from the boundary. (AVI 7088 kb)
Simulations of dry model
Individual particles in the system show erratic trajectories (some particles are marked in different colors) while the whole system shows regular global oscillations of the mean velocity. The red trajectories are the time integration of average velocity of the system. This video is associated with Figure 4a. (MOV 4507 kb)
Travelling wave state of the ‘wet’ model
The system is of size 1536μm x 192μm. The particles are colored according to their moving directions relative to x-axis (see colormap). White particles are ten randomly chosen particles for easy visibility. Elliptic trajectories are generated by the integration of local average flow velocity in a domain of size 150 μm x 150 μm. This video is associated with Figure 4c. (MOV 948 kb)
Fluid flows in the travelling wave state
This video is associated with Figure 4d. Here the system has stronger flows perpendicular to the travelling wave direction. The colormap in the unit of μm/s represents the intensity of the speed of flows. (MOV 3026 kb)
Simulations with deactivation zone in the center of the simulation domain
The video is associated with Extended Data Figure 8. Particles are colored according to their moving direction relative to x-axis (see colormap). White particles are randomly chosen and marked for easy visibility. The system still maintains travelling wave state with the deactivation zone present. Particle motion inside the deactivation zone is driven by small residual oscillatory flows governed by the Stokes equation. (MOV 4535 kb)
Rights and permissions
About this article
Cite this article
Chen, C., Liu, S., Shi, Xq. et al. Weak synchronization and large-scale collective oscillation in dense bacterial suspensions. Nature 542, 210–214 (2017). https://doi.org/10.1038/nature20817
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature20817
This article is cited by
-
Self-enhanced mobility enables vortex pattern formation in living matter
Nature (2024)
-
Autonomous waves and global motion modes in living active solids
Nature Physics (2023)
-
Time irreversibility in active matter, from micro to macro
Nature Reviews Physics (2022)
-
Selective and collective actuation in active solids
Nature Physics (2022)
-
Heterogeneity-induced lane and band formation in self-driven particle systems
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.